Az előző részben kitöröltünk mindent a fejünkből, amit az általános iskolában a számokról tanultunk, és elkezdtük felépíteni a modern kriptográfiai eljárások alapját jelentő számelméletet a semmiből. Mindössze 4 egyszerű állításból indultunk ki, amelyeket Peano-axiómáknak nevezünk, és amelyek rögzítik a pozitív egész számok és a 0 alapvető tulajdonságait. Ezek halmazát természetes számoknak nevezzük és \N-nel jelöljük. Szigorúan az axiómákat használva bevezettünk az \N halmazon egy összeadásnak nevezett műveletet, amelyről megmutattuk, hogy – az axiómák logikai következményeként – valóban teljesíti az általános iskolában jól megszokott tulajdonságokat. De vajon mi minden következik még ebből a 4 axiómából? Milyen alaptulajdonságai vannak a szorzás műveletének és mi az oka, hogy ezek valóban teljesülnek? Mik azok a relációk és hogy jön ide a „kő-papír-olló” nevű játék? Mit nevezünk rendezett halmaznak és hogyan vezethetjük be a „kisebb-nagyobb” fogalmát a természetes számok között? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít az előző részben bevezetett alábbi definíciókra és tételekre, amelyekkel elkezdtük a számelmélet felépítését:
Legyen adott egy \N-nel jelölt halmaz, valamint egy s:\N \to \N függvény. Az \N halmaz elemeit természetes számoknak nevezzük, amennyiben teljesülnek a következő axiómák:
- Az s függvény az \N halmaz minden x eleméhez rendeljen hozzá valamilyen szintén \N-beli elemet, azaz létezzen az s(x) elem. Ezt az elemet az x rákövetkezőjének nevezzük.
- Ha x és y az \N halmaz két tetszőleges eleme, és s(x)=s(y), akkor x=y. Ilyenkor azt mondjuk, hogy a két elem egyenlő egymással.
- Az \N halmazban létezik pontosan egy olyan 0-val jelölt elem, amelyhez nem található olyan x elem, amelyre teljesül, hogy s(x)=0. Ezt az elemet nullának nevezzük.
- Tegyük fel, hogy a P halmaz az \N halmaznak egy valamilyen részhalmaza. Ha a 0 a P halmazban van, valamint ha abból, hogy egy tetszőleges x elem a P halmazban van következik, hogy s(x) is a P halmazban van, akkor \N összes eleme a P halmazban van – azaz P=\N.
Az \N halmazon értelmezett, +-szal jelölt kétváltozós műveletet összeadásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a+0=a.
- Amennyiben valamely a és b számokra az a+b eredménye már ismert, úgy teljesül, hogy a+s(b)=s(a+b).
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
Az \N tetszőleges a és b elemeire igaz az alábbi összefüggés:
a+b = b+aAz \N halmaz tetszőleges a, b és c elemeire igaz az alábbi összefüggés:
(a+b)+c = a+(b+c)E definíciók és tételek kontextusba helyezése miatt erőteljesen ajánlott tehát elolvasni az előző részt. A teljes cikksorozat elejét itt találod.
A matematika igazi természete kezdett el kibontakozni az előző részben. Nevezetesen: kiindulunk néhány egyszerű állításból, amelyeket igaznak fogadunk el – ez jelen példánkban a Peano-axiómarendszer 4 állítása. Nem azért fogadjuk el őket igaznak, mert valamiféle abszolút igazságokat állítanak – olyan talán nem is létezik, ha belegondolunk –, hanem azért, mert ezek rögzítik a felépítendő elmélet „játékszabályait”, akárcsak a sakkban. A fogalmainkat szigorúan az axiómákból építjük fel, és csak olyan további állításokat fogadunk el igaznak, amelyeket szigorú logikai érveléssel az axiómákra, az azok segítségével felépített fogalmakra, vagy korábban már bizonyított állításokra tudunk visszavezetni.
Ennek a tudománynak épp ez adja az erősségét is. Minden más természettudomány alapja ugyanis a kísérletezés. Akárhány kísérletet is végzünk, soha nem lehetünk teljesen biztosak egy tudományos elmélet igazságában, arra csupán megerősítést kapunk. Ha azonban akárcsak egyetlen kísérlet is megcáfolja az elméletünket, azt azonnal dobhatjuk ki a kukába. Ezzel szemben egy matematikai állítás igazsága örök érvényű. Egy bizonyított állítás igaz marad, ameddig világ a világ, arra nyugodtan lehet tovább építkezni, és nincs szükség arra, hogy azt kísérletekkel megerősítsük. Az előző részben például a Peano-axiómák segítségével bevezettük az összeadás fogalmát, és bizonyítottuk annak kommutativitását és asszociativitását. A továbbiakban tehát nyugodtan építkezhetünk ezekre a tulajdonságokra.
Építkezzünk hát tovább, és kényelmi okok miatt vezessünk be egy újabb műveletet az \N halmazon.
A természetes számok szorzása
Képzeljük el azt a szituációt, amikor egy számot önmagával sokszor kell összeadni. Jó volna valamilyen módon rövidíteni az olyan jellegű kifejezéseket, mint például ez: a+a+a+a+a. Itt az a számot 5-ször adtuk össze önmagával, ami – valljuk be – eléggé kényelmetlen. Ezt elkerülendő, most bevezetünk egy „szorzásnak” nevezett műveletet, amelyet \cdot-tal fogunk jelölni. A fenti kifejezést például így rövidíthetjük: a \cdot 5.
A szorzás műveletével kapcsolatban azonnal rögzíthetünk két megállapodást. Először is állapodjunk meg abban, hogy mi legyen az eredmény akkor, ha valamit 0-val szorzunk meg. Ezt ugye a fenti értelmezés alapján egy 0 tagú összegként foghatjuk fel. Természetes tehát, ha rögzítjük, hogy tetszőleges a esetén a \cdot 0 eredménye 0 legyen. A másik megállapodásunk pedig legyen az, hogy ha egy a számot egy b szám rákövetkezőjével szorozzuk meg, akkor az ennek megfelelő összegben éppen 1-gyel többször szerepeljen a, mintha csak b-vel szoroztunk volna.
Ennek megfelelően az alábbi definícióval vezetjük be a szorzás műveletét:
12.1. Definíció (Peano-szorzás):
Az \N halmazon értelmezett, \cdot-tal jelölt kétváltozós műveletet szorzásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a\cdot 0=0.
- Amennyiben valamely a és b számokra az a\cdot b eredménye már ismert, úgy teljesül, hogy a\cdot s(b)=(a\cdot b) + a.
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
♣Ez alapján kiszámítható bármely két természetes szám szorzata. Amennyiben például \N elemeit a szokásos módon, 10-es számrendszerben jelöljük, akkor a 2 \cdot 3 szorzat az alábbi lépésekben fejthető ki szigorúan a fenti definíció szerint:
\begin{aligned}2 \cdot 0&=0 \\ 2 \cdot 1&=2 \cdot s(0)=(2 \cdot 0) + 2 = 0 + 2 = 2 \\ 2 \cdot 2&=2 \cdot s(1) = (2 \cdot 1) + 2=2+2=4 \\ 2 \cdot 3&=2 \cdot s(2)=(2 \cdot 2) + 2=4 + 2=6 \end{aligned}Értelmeztünk tehát egy műveletet az \N halmazon, amelyet önkényesen „szorzásnak” neveztünk, és a \cdot műveleti jellel jelöltünk. Az összeadáshoz hasonlóan vizsgáljuk hát meg, hogy ez valóban teljesíti-e azokat a jól megszokott tulajdonságokat, amelyeket általános iskolai tanulmányaink alapján elvárnánk tőle.
A szorzás kommutativitása
Általános iskolában megtanultuk, hogy az összeadáshoz hasonlóan a szorzás esetén is felcserélhető a két tényező sorrendje. Első jogos kérdés tehát, hogy vajon a 12.1. Definícióban ismertetett „szorzásnak” nevezett művelet teljesíti-e ezt a kritériumot?
Ennek megmutatásához két segédtételre lesz szükségünk. Az első segédtétel azt mondja ki, hogy a definíció 1. pontjában szereplő esetben a tényezők felcserélhetők – azaz, hogy az a \cdot 0-hoz hasonlóan a 0 \cdot a eredménye is 0 lesz:
12.2. Lemma:
Az \N halmaz tetszőleges a elemére igaz az alábbi összefüggés:
0\cdot a=0 ♣Ez ugyan magától értetődőnek tűnik, de ismételten felhívjuk a figyelmet arra, hogy mindenben kételkednünk kell, amit nem vezettünk vissza az axiómákra, az azokból alkotott definíciókra vagy korábban már bizonyított állításokra. Márpedig a \cdot-tal jelölt Peano-szorzás jelenleg nem több pusztán egy általunk kreált definíciónál. A bizonyításhoz az előző részben már jól bejáratott teljes indukciót alkalmazzuk, amelynek használatát a 4. Peano-axióma teszi lehetővé:
Bizonyítás:
Az a-ra vonatkozó teljes indukciót alkalmazunk. Tegyük fel tehát, hogy valamilyen a=n természetes számra az állítás igaz. Az indukciós feltétel tehát 0\cdot n=0. Azt kell bizonyítanunk, hogy ekkor a=s(n)-re is igaz lesz, azaz:
0\cdot \underbrace{s(n)}_{=a}=0A Peano-szorzás 12.1. Definíciójának 2. pontja miatt:
0\cdot s(n)=(0\cdot n) + 0 = \ldotsA Peano-összeadás 11.4. Definíciójának 1. pontja miatt:
\ldots =0\cdot n = \ldotsVégül pedig az indukciós feltétel miatt:
\ldots =0Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Ezért most felborítjuk az első dominót, azaz igazoljuk, hogy az állítás igaz a=0-ra. Ez viszont nyilvánvalóan teljesül a Peano-szorzás 12.1. Definíciójának 1. pontja miatt:
0\cdot \underbrace{0}_{=a}=0Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a számra igaz, hogy 0\cdot a=0.
∎A kommutativitáshoz szükséges második segédtétel lényegében azt mondja ki, hogy mi történik a Peano-szorzás definíciójának (12.1. Definíció) 2. pontjában szereplő képlettel, ha felcseréljük a tényezőket:
12.3. Lemma:
Az \N halmaz tetszőleges a és b elemeire igaz az alábbi összefüggés:
s(b)\cdot a=(b\cdot a) + a ♣Bizonyítás:
Az a-ra vonatkozó teljes indukciót alkalmazunk, azaz feltesszük, hogy az állítás már igaz valamilyen a=n természetes számra. Indukciós feltevésünk szerint tehát s(b)\cdot n=(b\cdot n) + n. Azt kell bizonyítanunk, hogy ekkor az állítás a=s(n)-re is teljesül, azaz:
s(b)\cdot s(n) = (b\cdot s(n)) + s(n)A Peano-szorzás 12.1. Definíciójának 2. pontja miatt:
s(b)\cdot s(n) = (s(b)\cdot n) + s(b) = \ldotsAz indukciós feltétel miatt a zárójel átírható:
\ldots = (\underbrace{(b\cdot n) + n}_{=s(b)\cdot n}) + s(b) = \ldotsTekintve, hogy az összeadás asszociatív (lásd: 11.8. Tétel), ezért ezt a kifejezést átzárójelezhetjük:
\ldots = (b\cdot n) + (n + s(b)) = \ldotsA Peano-összeadás 11.4. Definíciójának 2. pontja miatt a zárójel átírható:
\ldots = (b\cdot n) + \underbrace{s(n+b)}_{=(n + s(b))} = \ldotsTekintve, hogy az összeadás kommutatív (lásd: 11.7. Tétel), ezért a jobboldali tagban szereplő s függvény paramétere átírható:
\ldots = (b\cdot n) + s(\underbrace{b+n}_{=n+b}) = \ldotsIsmételten a Peano-összeadás 11.4. Definíciójának 2. pontját alkalmazva:
\ldots = (b\cdot n) + \underbrace{(b+s(n))}_{=s(b+n)} = \ldotsAz összeadás asszociativitása miatt ez a kifejezés ismételten átzárójelezhető:
\ldots = ((b\cdot n) + b)+s(n) = \ldotsVégül a Peano-szorzás 12.1. Definíciójának 2. pontja miatt a zárójelben lévő kifejezés átírható:
\ldots = (\underbrace{b\cdot s(n)}_{=(b\cdot n)+b})+s(n)Vagyis azt kaptuk, hogy valóban s(b)\cdot \underbrace{s(n)}_{=a} = (b\cdot \underbrace{s(n)}_{=a}) + \underbrace{s(n)}_{=a}.
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Ezért most felborítjuk az első dominót, azaz igazoljuk, hogy az állítás igaz a=0-ra, azaz:
s(b)\cdot \underbrace{0}_{=a} = (b\cdot \underbrace{0}_{=a}) + \underbrace{0}_{=a}Ez viszont nyilvánvalóan teljesül, hiszen a Peano-szorzás 12.1. Definíciójának 1. pontja miatt:
s(b)\cdot 0 = 0 = \ldotsSzintén ugyanezen ok miatt:
\ldots = b\cdot 0 = \ldotsVégül a Peano-összeadás 11.4. Definíciójának 1. pontja miatt:
\ldots = (b\cdot 0) + 0Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden b és a számra igaz, hogy s(b)\cdot a = (b\cdot a) + a.
∎Ezután bizonyítjuk a szorzás kommutativitását:
12.4. Tétel (Peano-szorzás kommutativitása):
Az \N halmaz tetszőleges a és b elemeire igaz az alábbi összefüggés:
a\cdot b = b\cdot a ♣Bizonyítás:
Teljes indukciót alkalmazunk b-re vonatkozóan. Tegyük fel, hogy az állítás igaz valamilyen b=n természetes számra. Az tehát az indukciós feltétel, hogy a \cdot n=n \cdot a. Azt kell bizonyítanunk, hogy ebben az esetben b=s(n)-re is igaz lesz, azaz:
a \cdot \underbrace{s(n)}_{=b} = \underbrace{s(n)}_{=b} \cdot aA 12.1. Definíció 2. pontja miatt:
a\cdot s(n) = (a\cdot n) + a = \ldotsAz indukciós feltétel miatt:
\ldots =(n\cdot a) + a= \ldotsVégül az imént bizonyított 12.3. Lemma miatt:
\ldots = s(n) \cdot aVagyis azt kaptuk, hogy valóban a \cdot \underbrace{s(n)}_{=b} = \underbrace{s(n)}_{=b} \cdot a.
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Az első dominót pedig már fel is borítottuk, ugyanis a 12.2. Lemma alapján az állítás igaz b=0-ra.
Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a és b számra igaz, hogy a\cdot b=b\cdot a.
∎Látható tehát, hogy a 12.1. Definícióban értelmezett „szorzásnak” nevezett művelet valóban kommutatív, ahogy azt az általános iskolában már megszokhattuk tőle.
Most nézzünk meg egy rendkívül fontos kapcsolatot az előző részben definiált „összeadás” és a mostani részben definiált „szorzás” nevű műveletek között. Ez a tulajdonság szintén jól ismert az általános iskolából, most viszont vizsgáljuk meg, hogy tulajdonképpen miért is van ez így.
Az összeadás és a szorzás kapcsolata
Biztosan sokan emlékeznek még általános iskolából az úgynevezett „zárójelfelbontási szabályra”. Tegyük fel, hogy van két darab kétváltozós műveletünk egy valamilyen H halmazon. Jelöljük az egyik műveletet \circ-rel, a másikat pedig \bullet-tal. Szándékosan választottam két semleges szimbólumot annak érdekében, hogy nehogy véletlenül bárki bármilyen konkrét műveletre asszociáljon. Tegyük fel, hogy a következő kifejezést kell kiértékelnünk a H halmaz a, b és c elemeire:
a\bullet (b \circ c)Ennek a kifejezésnek a kiértékelését mutatja az alábbi ábra:
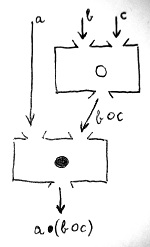
Elképzelhető, hogy a \circ és a \bullet művelet olyan, hogy a fenti kifejezés átalakítható erre:
(a\bullet b)\circ (a\bullet c)Ennek a kifejezésnek a kiértékelését mutatja az alábbi ábra:
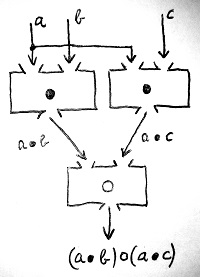
Látható, hogy a két fenti kifejezés kiértékelése teljesen máshogyan történik. Első esetben először a \circ műveletet kell elvégezni b-re és c-re, majd ennek az eredményét kell össze-\bullet-ozni a-val balról. Második esetben viszont először össze-\bullet-ozzuk b-t és c-t a-val balról, majd az így kapott két eredményt \circ-özzük össze.
Amennyiben a \circ és \bullet műveletek olyanok, hogy tetszőleges a-ra, b-re és c-re a két fenti kifejezés végeredménye mindig megegyezik egymással, azaz
a\bullet (b \circ c) = (a\bullet b) \circ (a\bullet c)teljesül, akkor azt mondjuk, hogy a \bullet művelet baldisztributív a \circ műveletre nézve. Amennyiben
(b \circ c)\bullet a = (b\bullet a) \circ (c\bullet a)teljesül, akkor azt mondjuk, hogy a \bullet művelet jobbdisztributív a \circ műveletre nézve. Amennyiben mindkét azonosság egyszerre teljesül, akkor egyszerűen azt mondjuk, hogy a \bullet művelet disztributív a \circ műveletre nézve.
Ha például a \bullet művelet kommutatív, akkor automatikusan mindkét oldali disztributivitás teljesül. Az állítás megfordítása azonban nem feltétlenül igaz, azaz a kétoldali disztributivitásból nem következik a \bullet művelet kommutativitása.
Ezen kívül a disztributivitási kapcsolat két művelet között általában nem szimmetrikus. Például ha a \bullet művelet disztributív a \circ műveletre nézve, abból még nem következik, hogy a \circ művelet is disztributív a \bullet műveletre nézve. Elképzelhetőek azonban olyan algebrai struktúrák, amelyekben még ez a szimmetria is teljesül. Például a halmazműveletek közül a metszetképzés (\cap) és az unió (\cup) műveletei kölcsönösen disztributívak egymásra nézve:
\begin{aligned}A\cap (B\cup C) &= (A\cap B)\cup (A\cap C) \\ A\cup (B\cap C) &= (A\cup B)\cap (A\cup C)\end{aligned}Most nézzük meg, hogy disztributivitási szempontból mit tudunk elmondani a 11.4. Definíció szerinti „összeadásnak” és a 12.1. Definíció szerinti „szorzásnak” nevezett műveletekről.
12.5. Tétel (Peano-szorzás disztributivitása):
Az \N halmaz tetszőleges a, b és c elemeire igazak az alábbi összefüggések:
a\cdot (b+c) = (a\cdot b) + (a\cdot c) (a+b)\cdot c = (a\cdot c) + (b\cdot c) ♣Bizonyítás:
Először is megjegyezzük, hogy elegendő csak a baloldali disztributivitást bizonyítani tekintve, hogy a Peano-szorzás kommutatív – ahogy azt a 12.4. Tételben már bizonyítottuk.
Teljes indukciót alkalmazunk c-re vonatkozóan. Tegyük fel, hogy az állítás igaz valamilyen c=n természetes számra. Az tehát az indukciós feltétel, hogy a \cdot (b+n)=(a \cdot b) + (a \cdot n). Azt kell bizonyítanunk, hogy ebben az esetben c=s(n)-re is igaz lesz, azaz:
a \cdot (b+ \underbrace{s(n)}_{=c})=(a \cdot b) + (a \cdot \underbrace{s(n)}_{=c})A 11.4. Definíció 2. pontja miatt:
a \cdot (b+ s(n))=a \cdot s(b+n) = \ldotsA 12.1. Definíció 2. pontja miatt:
\ldots =(a \cdot (b+n)) + a = \ldotsAz indukciós feltétel miatt:
\ldots =((a \cdot b)+(a \cdot n)) + a = \ldotsAz összeadás asszociativitása miatt (11.8. Tétel):
\ldots =(a \cdot b)+((a \cdot n) + a) = \ldotsVégül ismét a 12.1. Definíció 2. pontja miatt:
\ldots =(a \cdot b)+(a \cdot s(n))Vagyis azt kaptuk, hogy valóban a \cdot (b+ \underbrace{s(n)}_{=c})=(a \cdot b) + (a \cdot \underbrace{s(n)}_{=c}).
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Most felborítjuk az első dominót, tehát igazoljuk, hogy az állítás igaz c=0 esetén, azaz:
a \cdot (b+ \underbrace{0}_{=c})=(a \cdot b) + (a \cdot \underbrace{0}_{=c})A 11.4. Definíció 1. pontja miatt:
a \cdot (b+ 0)=a \cdot b = (a\cdot b) + 0 =\ldotsVégül a 12.1. Definíció 1. pontja miatt:
\ldots = (a\cdot b) + (a\cdot 0)Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a, b és c számra igaz, hogy a\cdot (b+c)=(a\cdot b) + (a\cdot c).
∎Mostantól tehát nyugodtan alkalmazhatjuk az általános iskolából már jól ismert zárójelfelbontási szabályt, mivel a Peano-axiómák segítségével értelmezett két műveletünk teljesíti ezt a követelményt is.
A Peano-szorzás asszociativitása
Most vizsgáljuk meg, hogy az összeadáshoz hasonlóan vajon a szorzás is asszociatív-e.
12.6. Tétel (Peano-szorzás asszociativitása):
Az \N halmaz tetszőleges a, b és c elemeire igaz az alábbi összefüggés:
(a\cdot b)\cdot c = a\cdot (b\cdot c) ♣Bizonyítás:
Ezúttal is c-re vonatkozó teljes indukcióval bizonyítunk. Indukciós feltételként feltételezzük, hogy valamilyen c=n-re a tétel már teljesül, azaz:
(a\cdot b)\cdot n = a\cdot (b\cdot n)Feladatunk megmutatni, hogy ekkor c=s(n)-re is teljesül, azaz:
(a\cdot b)\cdot s(n) = a\cdot (b\cdot s(n))A 12.1. Definíció 2. pontja miatt:
(a\cdot b)\cdot s(n) = ((a\cdot b) \cdot n) + (a\cdot b)=\ldotsAz indukciós feltétel miatt:
\ldots =(a\cdot (b \cdot n)) + (a\cdot b)=\ldotsA disztributivitási szabály miatt (12.5. Tétel):
\ldots =a\cdot ((b \cdot n) + b)=\ldotsVégül ismételten a 12.1. Definíció 2. pontja miatt:
\ldots =a\cdot (b \cdot s(n))A dominósor tehát felállítva, most elborítjuk az első dominót, azaz belátjuk, hogy c=0-ra a tétel igaz. Ez viszont nyilvánvalóan teljesül a 12.1. Definíció 1. pontjának háromszori alkalmazásával:
(a\cdot b) \cdot \underbrace{0}_{=c} = 0 = a\cdot 0 = a \cdot (b \cdot \underbrace{0}_{=c}) ∎Ezzel megmutattuk, hogy a Peano-axiómák segítségével bevezetett mindkét műveletünk az elvárt módon viselkedik. A fejezet további részében az \N halmazban fogunk egy kicsit rendetrakni. Ez szükséges lesz ugyanis ahhoz az absztrakcióhoz, amelyet a sorozat következő részében fogunk majd meglépni, és amelynek a segítségével nemcsak összeadni és szorozni, hanem kivonni is fogunk tudni.
Kő-papír-olló
A Peano-axiómákkal definiált \N halmaz jelenleg nem több csupán egy „zsáknál”, amelyben ott csücsül a végtelen sok természetes szám. E számkör kibővítéséhez azonban szükségünk lesz egy olyan fogalomra, amelynek a segítségével ezeket az objektumokat valamilyen módon sorba tudjuk állítani. Szeretnénk olyan kijelentéseket tenni, miszerint egy a szám „előrébb van” ebben a képzeletbeli sorban, mint egy b szám.
A kétváltozós műveletekhez (11.3. Definíció) hasonlóan szükségünk lesz tehát egy olyan képzeletbeli dobozra, amelybe ha felül bedobunk két tetszőleges számot az \N halmazból, akkor alul kipottyan egy igen vagy egy nem válasz egy adott eldöntendő kérdésre. Például arra a kérdésre, hogy a „előrébb van-e” a természetes számok halmazában, mint b? Ez nagyon hasonló azokhoz a Turing-gépekhez, amelyeket a 6. részben formális nyelvek felismeréséhez használtunk. Jelen esetben azonban a bemenet nem egy szimbólumsorozat, hanem két természetes szám, a kimenet pedig egy igen vagy egy nem válasz lesz. Ezt szemlélteti az alábbi ábra:
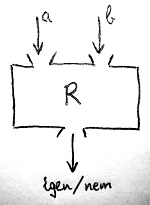
Az olyan kétbemenetű dobozokat, amelyek választ adnak valamilyen eldöntendő kérdésre a két felül bedobott szám közötti kapcsolatról, kétváltozós relációknak nevezzük. A fenti ábrán látható doboz például egy kétváltozós relációt reprezentál, amely relációt önkényesen R-rel jelöltünk, de választhattunk volna bármilyen más szimbólumot is. Most nézzük meg, hogyan tudjuk általánosságban megfogalmazni, hogy matematikailag tulajdonképpen mit is nevezünk relációnak.
Ennek megértéséhez fontos először tisztázni a „rendezett pár” fogalmát. Emlékezzünk vissza, hogy egy kétváltozós műveletet egy olyan függvényként definiáltuk (11.3. Definíció), amely az adott művelet alaphalmazából származó elemekből alkotott összes létező ún. rendezett párhoz hozzárendel egy-egy elemet szintén ebből az alaphalmazból. Vegyük például a már jól ismert \N halmazt, és válasszunk ki belőle két tetszőleges elemet, mondjuk 1-et és 2-t. Ebből a két elemből kétféleképpen tudunk egy rendezett párt alkotni, mivel nem mindegy, hogy melyik hol foglal helyet ebben a párban (ezért hívjuk rendezett párnak). Az egyik ilyen párt (1; 2)-vel, a másikat pedig (2; 1)-gyel jelöljük. Az (1; 2) és a (2; 1) rendezett párok tehát különbözőek, mivel nem azonos a bennük szereplő elemek sorrendje.
Egy tetszőleges H halmaz elemeiből alkotott összes létező rendezett pár szintén egy halmazt alkot. Ezt a halmazt H\times H-val jelöljük (kimondva: H „kereszt” H). Tegyük fel például, hogy a H halmaz a \text{kő}, a \text{papír} és az \text{olló} szavakat tartalmazza. Ekkor a H\times H halmaz az alábbi 9 rendezett párt fogja tartalmazni: (\text{kő}; \text{kő}), (\text{kő}; \text{papír}), (\text{kő}; \text{olló}), (\text{papír}; \text{kő}), (\text{papír}; \text{papír}), (\text{papír}; \text{olló}), (\text{olló}; \text{kő}), (\text{olló}; \text{papír}), és (\text{olló}; \text{olló}).
Ezek után a kétváltozós reláció fogalmát így definiáljuk:
12.7. Definíció (Kétváltozós reláció):
Ha H egy tetszőleges halmaz, akkor a H\times H halmaz egy valamilyen R részhalmazát kétváltozós relációnak nevezzük. Ha a és b a H halmaz két tetszőleges – nem feltétlenül különböző – eleme, és az (a; b) rendezett pár benne van az R halmazban, akkor azt mondjuk, hogy a és b között fennáll az R reláció. Ezt így jelöljük: aRb.
♣Az előző példánál maradva definiáljunk egy relációt a \text{kő}, a \text{papír} és az \text{olló} szavakat tartalmazó H halmazon. Jelöljük például a \succ szimbólummal a H\times H halmaznak azt a részhalmazát, amely csak a (\text{kő}; \text{olló}), (\text{olló}; \text{papír}) és (\text{papír}; \text{kő}) rendezett párokat tartalmazza. A definícióban szereplő jelöléssel például írhatjuk azt, hogy \text{kő} \succ \text{olló}. Ezt szavakkal így mondhatjuk: „\text{kő} üti \text{olló}-t”. Vegyük észre, hogy az imént épp a matematikai leírását adtuk meg a jól ismert kő-papír-olló játék ütési szabályainak.
Amikor egy végtelen halmazon értelmezünk valamilyen relációt, akkor természetesen nem tudjuk megtenni, hogy felsoroljuk az összes olyan párt, amelyek relációban állnak egymással. Ilyen esetekben valamilyen szabályt adunk meg arra vonatkozóan, hogy mikor tekintünk két elemet egymással relációban állónak, és mikor nem. Hamarosan bevezetünk majd egy relációt az \N halmazon, amelynek a segítségével sorba fogjuk tudni rendezni \N elemeit – azaz a természetes számokat. Előbb azonban vizsgáljuk meg, hogy pontosan mit értünk rendezési reláció alatt.
Rendezési relációk
A most következő néhány definíció egy-egy speciális tulajdonságot követel meg egy relációtól. Az első például azt, hogy bármely elem relációban álljon önmagával:
12.8. Definíció (Reflexív reláció):
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció. Ha H minden a elemére teljesül, hogy aRa, akkor azt mondjuk, hogy az R reláció reflexív.
♣A második definíció azt követeli meg egy relációtól, hogy két különböző elem esetén a közöttük lévő reláció – ha egyáltalán létezik – iránya egyértelmű legyen:
12.9. Definíció (Antiszimmetrikus reláció):
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a és b a H halmaz tetszőleges, de egymástól különböző elemei – azaz a\neq b. Ha minden ilyen esetben aRb és bRa közül legfeljebb az egyik teljesül, akkor azt mondjuk, hogy az R reláció antiszimmetrikus.
♣Másként megfogalmazva ha egy antiszimmetrikus reláció mindkét irányban fennáll két elem között, akkor a két elem azonos. Megjegyezzük azonban, hogy visszafelé nem feltétlenül teljesül, hogy a=b esetén bármelyik irányban is fennáll a reláció. Ezt a fentebb definiált reflexivitási tulajdonság hivatott biztosítani.
A harmadik definíció azt követeli meg, hogy az elempárok azon tulajdonsága, miszerint egymással relációban állnak, „láncszerűen” öröklődjön. Például: ha én „magasabb vagyok” az apámnál, apám pedig „magasabb” az anyámnál, akkor én „magasabb vagyok” az anyámnál. Ezt fejezi ki az alábbi definíció:
12.10. Definíció (Tranzitív reláció):
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a, b és c a H halmaz tetszőleges elemei. Ha minden ilyen esetben aRb és bRc együttes teljesülése esetén aRc is teljesül, akkor azt mondjuk, hogy az R reláció tranzitív.
♣Végül a negyedik definíció azt követeli meg, hogy két tetszőleges elemet kiválasztva azok mindenképpen legyenek egymással „összehasonlíthatók” az adott reláció segítségével.
12.11. Definíció (Trichotom reláció):
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a és b a H halmaz tetszőleges elemei. Ha minden ilyen esetben aRb és bRa közül legalább az egyik teljesül, akkor azt mondjuk, hogy az R reláció trichotóm.
♣Ezek a definíciók tehát mind egy-egy speciális követelményt fogalmaznak meg egy adott relációval kapcsolatban. Például az előző szakaszban a kő-papír-olló játékkal kapcsolatban definiált \succ reláció nyilvánvalóan nem reflexív, hiszen ha a két játékos ugyanazt mutatja – legyen az akár \text{kő}, akár \text{papír}, akár \text{olló} –, az eredmény döntetlen lesz. De nem is tranzitív, hiszen például \text{papír} \succ \text{kő} és \text{kő} \succ \text{olló}, de \text{papír} \nsucc \text{olló}. Végül a trichotómia sem teljesül ugyanazon okok miatt, mint a reflexivitás. Viszont antiszimmetrikus, hiszen ha a két játékos különbözőt mutat, akkor biztosan csak az egyikük fog nyerni.
Most bevezetjük a rendezett halmaz fogalmát, majd a definíció után megmutatjuk az elnevezés jogosságát:
12.12. Definíció (Rendezett halmaz):
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, antiszimmetrikus és tranzitív, úgy R-et H feletti részbenrendezésnek hívjuk, vagy pedig azt mondjuk, hogy a H egy részbenrendezett halmaz az R relációval.
Az R relációt teljes rendezésnek nevezzük H felett, ha a fentieken kívül a trichotómia is teljesül rá. Ilyenkor azt mondjuk, hogy a H egy rendezett halmaz az R relációval.
♣Minket jelenleg csak a teljes rendezések, és ennek megfelelően a rendezett halmazok érdekelnek, részbenrendezett halmazokkal egyelőre nem foglalkozunk. Vizsgáljuk meg tehát, hogy miért nevezhetünk jogosan „rendezésnek” egy olyan relációt, amely teljesíti a fenti definícióban szereplő mind a 4 kritériumot.
Tegyük fel, hogy van egy valamilyen H halmazon értelmezett rendezési reláció, amelyet a \leq szimbólummal jelölünk. Ne társítsunk most semmilyen számokkal kapcsolatos jelentést ehhez a szimbólumhoz, az a\leq b kifejezést egyszerűen csak olvassuk úgy, hogy „a legfeljebb annyiadik elem a sorban, mint b”. Ezek után a 12.12. Definícióban szereplő 4 kritériumot így is olvashatjuk:
- Reflexivitás: Tetszőleges elem „legfeljebb annyiadik a sorban”, mint önmaga.
- Antiszimmetria: Ha az a elem „legfeljebb annyiadik a sorban”, mint a b elem, és a b elem is „legfeljebb annyiadik a sorban”, mint az a elem, akkor a két elem megegyezik.
- Tranzitivitás: Ha az a elem „legfeljebb annyiadik a sorban”, mint a b elem, amely pedig „legfeljebb annyiadik a sorban”, mint a c elem, akkor az a elem „legfeljebb annyiadik a sorban”, mint a c elem.
- Trichotómia: Bármely két elemről el lehet dönteni, hogy melyikük van „legfeljebb annyiadik helyen a sorban”, mint a másik.
Ha végiggondoljuk, akkor pontosan ez az, amit elvárunk egy olyan relációtól, amelynek a segítségével egy egyértelmű sorrendet szeretnénk felállítani egy halmaz elemei között.
Most nézzük meg, hogyan tudunk egy ilyen tulajdonságokkal rendelkező relációt megadni a természetes számok \N halmazán.
A természetes számok rendezési relációja
A természetes számok \N-nel jelölt halmazán definiáljuk az alábbi relációt:
12.13. Definíció (Természetes számok rendezése):
Amennyiben az \N halmaz tetszőleges a és b elemeihez létezik olyan k szintén \N-beli elem, amelyre teljesül, hogy a+k=b, akkor azt mondjuk, hogy a\leq b. Kiolvasva: „a legfeljebb b” vagy „b legalább a”.
Ha ezen kívül a\neq b is teljesül – azaz a nem azonos b-vel –, akkor azt mondjuk, hogy a\lt b. Kiolvasva: „a kisebb, mint b” vagy „b nagyobb, mint a”. Egy ezzel azonos megfogalmazás így hangzik: ha tetszőleges a és b elemekhez létezik olyan k elem, amelyre teljesül, hogy a+k=b és k\neq 0, akkor a\lt b.
Fordított irányú reláció esetén értelemszerűen használhatjuk a \geq vagy a \gt szimbólumokat is.
♣Látható, hogy ennek az új fogalomnak a bevezetéséhez közvetett módon kizárólag az előző részben ismertetett Peano-axiómákat (11.1. Definíció), közvetlenül pedig az az alapján értelmezett összeadás nevű műveletet (11.4. Definíció) használtuk. Ezt szem előtt tartva tehát egyelőre semmit nem mondhatunk még erről a most bevezetett relációról, kiváltképpen azt nem, hogy ez valóban egy rendezési reláció lenne. Ezt ugyanis először bizonyítani kell.
Nézzük először a \leq reláció reflexivitását:
12.14. Tétel:
A 12.13. Definícióban bevezetett \leq reláció reflexív, azaz az \N halmaz tetszőleges a elemére teljesül, hogy a\leq a.
♣Bizonyítás:
Tekintve, hogy a Peano-összeadás 11.4. Definíciójának 1. pontja szerint tetszőleges a-ra teljesül, hogy a+0=a, ezért nyilvánvalóan létezik olyan természetes szám – nevezetesen a 0 –, amelyet hozzáadva bármihez azt a bármit kapjuk eredményül. Így tehát a\leq a tetszőleges a esetén teljesül.
∎A tranzitivitás hasonlóan egyszerűen adódik:
12.15. Tétel:
Az \N halmaz tetszőleges a, b és c elemére teljesül, hogy a\leq b és b\leq c együttes fennállása esetén a\leq c is fennáll – azaz a \leq reláció tranzitív.
♣Bizonyítás:
Ha a\leq b, akkor a 12.13. Definíció miatt létezik olyan természetes szám, amelyet a-hoz adva b-t kapunk. Jelöljük ezt a számot k_1-gyel, így tehát azt kapjuk, hogy a+k_1=b.
Hasonló okok miatt ha b\leq c, akkor létezik olyan természetes szám is, amelyet b-hez adva c-t kapunk. Jelöljük ezt a számot k_2-vel, így tehát azt kapjuk, hogy b+k_2=c.
Az első egyenlet baloldalát a második egyenletbe b helyére behelyettesítve azt kapjuk, hogy \underbrace{(a+k_1)}_{=b} + k_2=c. Tekintve, hogy az összeadás asszociatív (11.8. Tétel), ezért ez a kifejezés átzárójelezhető: a+(k_1+k_2)=c.
Létezik tehát olyan természetes szám is, amelyet a-hoz adva c-t kapunk – nevezetesen k_1+k_2. A \leq reláció definíciója miatt ez épp azt jelenti, hogy a\leq c.
∎Az antiszimmetria (12.9. Definíció) igazolásához először két segédtételre lesz szükségünk. Ezek közül az első egy olyan állítás, amely a későbbiekben is hasznos lesz:
12.16. Lemma:
Tetszőleges a, b és c természetes számok esetén ha a+c = b+c, akkor a=b.
♣Ne feledjük, hogy csak a már rendelkezésünkre álló fogalmakra és tételekre, valamint az axiómákra hivatkozhatunk. Tekintve, hogy „kivonás” egyelőre nem létezik, más úton kell bizonyítanunk a fenti állítást.
Bizonyítás:
A már jól ismert teljes indukciót alkalmazzuk. Először is megmutatjuk, hogy ha az állítás teljesül valamilyen c=n-re, akkor teljesülni fog c=s(n)-re is. Meg kell tehát mutatnunk, hogy ha a+n = b+n-ből a=b következik, akkor a+s(n) = b+s(n)-ből is a=b következik.
Az a+s(n)=b+s(n) egyenlet mindkét oldalát a Peano-összeadás definíciójának (11.4. Definíció) 2. pontja miatt átírhatjuk így: s(a+n)=s(b+n). Mármost a 2. Peano-axióma (11.1. Definíció) kimondja, hogy ha két természetes szám rákövetkezője megegyezik, akkor a két szám is megegyezik. Ebből tehát az következik, hogy a+n=b+n. Az indukciós feltétel szerint viszont az állítás teljesül n-re, ezért ebből a=b következik.
A dominósort felállítottuk, nincs más hátra, mint felborítani az első dominót, azaz megmutatni, hogy a+0=b+0-ból a=b következik. Ez viszont nyilvánvalóan teljesül, hiszen az egyenlet mindkét oldalát egyszerűsíthetjük 0-val a Peano-összeadás definíciójának (11.4. Definíció) 1. pontja miatt.
∎A második segédtétel – amelyre szükségünk lesz az antiszimmetria igazolásához – azt mondja ki, hogy mi az az egyetlen eset, amikor egy összeg eredménye 0 lehet.
12.17. Lemma:
A természetes számok körében ha a+b=0, akkor a=0 és b=0.
♣Ezt egy új bizonyítási módszerrel igazoljuk, amelyet indirekt bizonyításnak nevezünk. Ilyenkor nem magát az állítást igazoljuk, hanem megmutatjuk, hogy miért nem lehet hamis.
Bizonyítás:
Tegyük fel, hogy nem igaz az állítás, azaz a+b=0, de a és b közül legalább az egyik nem 0. Az összeadás kommutativitása (11.7. Tétel) miatt mindegy, hogy melyiket választjuk, a másikkal ugyanez a gondolatmenet végigjátszható. Legyen például most b\neq 0. Vizsgáljuk meg, hogy egy ilyen galád feltételezésnek milyen képtelen logikai következményei lennének.
Ha b\neq 0, akkor a Peano-axiómarendszer (11.1. Definíció) 3. pontja miatt létezik olyan természetes szám, amelynek épp b a rákövetkezője (hiszen egyedül a 0 nem rákövetkezője semminek). Jelöljük ezt a számot n-nel, amelyre tehát igaz, hogy s(n)=b.
Az a+b=0 kifejezést tehát így is írhatjuk: a+\underbrace{s(n)}_{=b}=0. Ez a Peano-összeadás (11.4. Definíció) 2. pontja miatt így írható fel: s(a+n)=0. Vagyis azt kaptuk, hogy az a+n rákövetkezője 0. Ez azonban lehetetlen, hiszen a Peano-axiómarendszer (11.1. Definíció) 3. pontja szerint a 0 nem rákövetkezője semminek.
Ha tehát a tételünk hamisságát továbbra is tartani szeretnénk, akkor hamisnak kellene tekintenünk a 3. axiómát is. Megfordítva: ha a 3. axiómát igaznak fogadjuk el – márpedig annak fogadjuk el –, akkor a tétel is szükségképpen igaz kell legyen.
∎A 12.16. Lemma és a 12.17. Lemma felhasználásával mostmár igazolhatjuk a \leq reláció antiszimmetriáját.
12.18. Tétel:
Az \N halmaz tetszőleges a és b elemére teljesül, hogy a\leq b és b\leq a együttes fennállása esetén szükségképpen a=b – azaz a \leq reláció antiszimmetrikus.
♣Bizonyítás:
Ha a\leq b, akkor a 12.13. Definíció miatt létezik olyan természetes szám, amelyet a-hoz adva b-t kapunk. Jelöljük ezt a számot k_1-gyel, így tehát azt kapjuk, hogy a+k_1=b.
Hasonló okok miatt ha b\leq a, akkor létezik olyan természetes szám is, amelyet b-hez adva a-t kapunk. Jelöljük ezt a számot k_2-vel, így tehát azt kapjuk, hogy b+k_2=a.
Az első egyenlet baloldalát a második egyenletbe b helyére behelyettesítve azt kapjuk, hogy \underbrace{(a+k_1)}_{=b} + k_2=a. Tekintve, hogy az összeadás asszociatív (11.8. Tétel), ezért ez a kifejezés átzárójelezhető: a+(k_1+k_2)=a.
A Peano-összeadás definíciójának (11.4. Definíció) 1. pontja miatt az egyenlet jobboldalához hozzáadhatunk 0-t: a+(k_1+k_2)=a+0. Az egyenlet mindkét oldala egyszerűsíthető a-val a 12.16. Lemma miatt, azaz k_1+k_2=0. Ebből viszont a 12.17. Lemma miatt az következik, hogy k_1=0 és k_2=0.
Helyettesítsük vissza mondjuk k_1-et az egyik kiindulási egyenletünkbe: a+\underbrace{0}_{=k_1}=b. Végül az egyenlet baloldala a Peano-összeadás definíciójának (11.4. Definíció) 1. pontja miatt 0-val egyszerűsíthető, azaz a=b.
∎Már csak a trichotómia igazolása van hátra. Ez az alábbi segédállításból fog következni:
12.19. Lemma:
Tetszőleges a és b természetes számok esetén az a\leq b reláció akkor és csak akkor teljesül, ha az s(a)\leq s(b) reláció is teljesül.
♣Bizonyítás:
Mivel ez egy „akkor és csak akkor” típusú állítás, ezért mindkét irányú következtetést igazolni kell.
Ha a\leq b, akkor ez azt jelenti a 12.13. Definíció definíció miatt, hogy létezik n, amelyre a+n=b. Ám ekkor nyilvánvalóan s(a+n)=s(b), és így s(a)+n=s(b) is igaz. Ez viszont szintén a definíció miatt épp azt jelenti, hogy s(a)\leq s(b).
Megfordítva: ha s(a)\leq s(b), akkor létezik n, amelyre s(a)+n=s(b). Ám ekkor nyilvánvalóan s(a+n)=s(b) is igaz, amiből a 2. Peano-axióma miatt (11.1. Definíció) a+n=b következik. Ez viszont épp azt jelenti, hogy a\leq b.
∎Ebből már következik a \leq reláció trichotómiája, ezért most ezt mondjuk ki:
12.20. Tétel:
Az \N halmaz tetszőleges a és b elemére teljesül, hogy az a\leq b és b\leq a relációk közül legalább az egyik fennáll – azaz a \leq reláció trichotóm.
♣Bizonyítás:
Indirekt bizonyítást fogunk alkalmazni, azaz nem közvetlenül a tételt bizonyítjuk, hanem megmutatjuk, miért lehetetlen, hogy nem igaz. Tegyük fel ezért, hogy az \N halmazban léteznek olyan galád a és b számok, amelyek között egyik irányban sem áll fenn a \leq reláció, azaz a\nleq b és b\nleq a.
Ebből az következik, hogy egyikük sem lehet 0, hiszen ha például a=0 lenne, akkor \underbrace{0}_{=a}\leq b teljesülne (ugyanis 0+b=b). Ha meg b=0 lenne, akkor pedig \underbrace{0}_{=b}\leq a teljesülne (ugyanis 0+a=a).
Mármost ha egyikük sem 0, akkor a 3. Peano-axióma (11.1. Definíció) miatt mindkettőhöz létezik egy-egy olyan szám, amelyeknek épp ők a rákövetkezői. Jelöljük ezt a két számot a_1-gyel és b_1-gyel, amelyekre tehát teljesül, hogy s(a_1)=a és s(b_1)=b.
Mármost ha a és b között nem teljesül a \leq reláció egyik irányban sem, akkor a 12.19. Lemma miatt utóbbiak között sem fog – azaz a_1\nleq b_1 és b_1\nleq a_1.
De ekkor ugyanezen gondolatmenet alapján léteznie kell egy a_2 és egy b_2 számnak is, amelyek rákövetkezői épp az a_1 és b_1 számok, és amelyek közül szintén egyik sem 0. És így tovább, ezt a gondolatmenetet a végtelenségig folytathatjuk, mindig találunk újabb és újabb nem 0 számokat, amelyek rákövetkezői épp az előző lépésben megtalált számok. Kapunk tehát két végtelen számsorozatot – amely sorozatokban nem szerepel a 0 –, az alábbi rákövetkezőségi viszonyokkal:
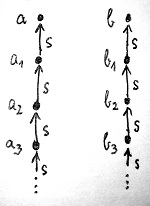
Ez viszont lehetetlen, hiszen a 4. Peano-axióma (11.1. Definíció) kimondja, hogy a 0-ból kiindulva a rákövetkezési függvény mentén az összes természetes számhoz el kell jutnunk előbb-utóbb. Márpedig egy ilyen gyűjtögetésben az ábrán lévő két sorozat tagjai biztosan nem lennének benne.
Ebből viszont az következik, hogy az a\leq b és a b\leq a relációk közül legalább az egyiknek teljesülnie kell tetszőleges a és b esetén, máskülönben ellentmondásba kerülnénk a 4. Peano-axiómával.
∎A \leq reláció tehát teljesíti mindazon követelményeket, amelyeket a 12.12. Definíció megkövetel tőle. Ezért mostmár nyugodtan kijelenthetjük, hogy a 12.13. Definícióban jogosan neveztük ezt a relációt rendezésnek, és jogosan nevezhetjük az \N halmazt rendezett halmaznak.
Hol tartunk most?
Ezen a ponton álljunk meg egy pillanatra, és szedjük össze, hogy jelenleg hol tartunk a számelmélet felépítésében, amit ugye a semmiből kezdtünk el az előző részben.
A Peano-axiómarendszer 4 állításával bevezettük a természetes számok halmazát:
Legyen adott egy \N-nel jelölt halmaz, valamint egy s:\N \to \N függvény. Az \N halmaz elemeit természetes számoknak nevezzük, amennyiben teljesülnek a következő axiómák:
- Az s függvény az \N halmaz minden x eleméhez rendeljen hozzá valamilyen szintén \N-beli elemet, azaz létezzen az s(x) elem. Ezt az elemet az x rákövetkezőjének nevezzük.
- Ha x és y az \N halmaz két tetszőleges eleme, és s(x)=s(y), akkor x=y. Ilyenkor azt mondjuk, hogy a két elem egyenlő egymással.
- Az \N halmazban létezik pontosan egy olyan 0-val jelölt elem, amelyhez nem található olyan x elem, amelyre teljesül, hogy s(x)=0. Ezt az elemet nullának nevezzük.
- Tegyük fel, hogy a P halmaz az \N halmaznak egy valamilyen részhalmaza. Ha a 0 a P halmazban van, valamint ha abból, hogy egy tetszőleges x elem a P halmazban van következik, hogy s(x) is a P halmazban van, akkor \N összes eleme a P halmazban van – azaz P=\N.
Ezen a halmazon bevezettünk két műveletet az alábbi definíciók szerint:
Az \N halmazon értelmezett, +-szal jelölt kétváltozós műveletet összeadásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a+0=a.
- Amennyiben valamely a és b számokra az a+b eredménye már ismert, úgy teljesül, hogy a+s(b)=s(a+b).
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
Az \N halmazon értelmezett, \cdot-tal jelölt kétváltozós műveletet szorzásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a\cdot 0=0.
- Amennyiben valamely a és b számokra az a\cdot b eredménye már ismert, úgy teljesül, hogy a\cdot s(b)=(a\cdot b) + a.
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
Bizonyítottuk, hogy e két művelet engedelmeskedik az általános iskolából már jól ismert számolási szabályoknak:
Az \N tetszőleges a és b elemeire igaz az alábbi összefüggés:
a+b = b+aAz \N halmaz tetszőleges a, b és c elemeire igaz az alábbi összefüggés:
(a+b)+c = a+(b+c)Az \N halmaz tetszőleges a és b elemeire igaz az alábbi összefüggés:
a\cdot b = b\cdot aAz \N halmaz tetszőleges a, b és c elemeire igaz az alábbi összefüggés:
(a\cdot b)\cdot c = a\cdot (b\cdot c)Az \N halmaz tetszőleges a, b és c elemeire igazak az alábbi összefüggések:
a\cdot (b+c) = (a\cdot b) + (a\cdot c) (a+b)\cdot c = (a\cdot c) + (b\cdot c)A 4 alapművelet közül tehát a két legfontosabb (az összeadás és a szorzás) már többé-kevésbé rendelkezésünkre áll. A kivonás azonban sajnos a természetes számok \N halmazán nem művelet (lásd a 11.3. Definíció), mivel bizonyos esetekben kivezet belőle. Például nincs olyan természetes szám, amely a 2-5 különbségképzés eredménye lenne (a -3 ugyanis nem természetes szám, holott a 2 és az 5 is az).
Kinőttük tehát az \N halmazt, ezért a következő részben át fogunk térni egy \N-nél bővebb számkörbe, amelyben már gond nélkül fogunk tudni kivonást is végezni. Sajnos azonban osztásról általánosságban még itt sem fogunk tudni beszélni – legalábbis nem a megszokott értelemben. Cserébe viszont elkezdhetünk majd végre ismerkedni azokkal a számokkal, amelyek alapvető szerepet játszanak a kriptográfiai eljárásokban, és úgy általában az egész számelméletben.
A számkör bővítésének előkészítése érdekében bevezettünk egy relációt az \N halmazon:
Amennyiben az \N halmaz tetszőleges a és b elemeihez létezik olyan k szintén \N-beli elem, amelyre teljesül, hogy a+k=b, akkor azt mondjuk, hogy a\leq b. Kiolvasva: „a legfeljebb b” vagy „b legalább a”.
Ha ezen kívül a\neq b is teljesül – azaz a nem azonos b-vel –, akkor azt mondjuk, hogy a\lt b. Kiolvasva: „a kisebb, mint b” vagy „b nagyobb, mint a”. Egy ezzel azonos megfogalmazás így hangzik: ha tetszőleges a és b elemekhez létezik olyan k elem, amelyre teljesül, hogy a+k=b és k\neq 0, akkor a\lt b.
Fordított irányú reláció esetén értelemszerűen használhatjuk a \geq vagy a \gt szimbólumokat is.
Végül – az indirekt bizonyítás módszerét bemutatva – megmutattuk, hogy ez a reláció egy teljes rendezést valósít meg a természetes számok között:
A 12.13. Definícióban bevezetett \leq reláció reflexív, azaz az \N halmaz tetszőleges a elemére teljesül, hogy a\leq a.
Az \N halmaz tetszőleges a, b és c elemére teljesül, hogy a\leq b és b\leq c együttes fennállása esetén a\leq c is fennáll – azaz a \leq reláció tranzitív.
Az \N halmaz tetszőleges a és b elemére teljesül, hogy a\leq b és b\leq a együttes fennállása esetén szükségképpen a=b – azaz a \leq reláció antiszimmetrikus.
Az \N halmaz tetszőleges a és b elemére teljesül, hogy az a\leq b és b\leq a relációk közül legalább az egyik fennáll – azaz a \leq reláció trichotóm.
A következő részben kilépünk a természetes számok köréből egy sokkal előnyösebb algebrai tulajdonságokkal bíró számkörbe. Ennek keretében bemutatjuk azt az absztrakciós utat, amelyet az emberiség hajnalán őseinknek is meg kellett tenniük, és ezzel párhuzamosan megismerkedünk néhány absztrakt algebrai fogalommal. Ezek segítségével általánosabb módon tudjuk majd tárgyalni azokat a számelméleti összefüggéseket, amelyek végül a prímszámok elméletén keresztül elvezetnek minket napjaink biztonságos kommunikációjának alapjaihoz.
A következő részt itt találod…



