Az előző részekben (a 11., 12., 13., 14. és 15. részekben) betekintést nyertünk abba a gondolkodásmódba, amelyet követve örök érvényű igazságokat tudunk kimondani és bizonyítani a matematikai logika rém egyszerű, ám annál szigorúbb szabályainak betartásával. Mindössze 4 állításból, az úgynevezett Peano-axiómákból (11.1. Definíció) indultunk ki, amelyek lényegében a természetes számokról alkotott intuitív elképzeléseinket fogalmazzák meg kellő precizitással. Ezekből kiindulva aztán definiáltuk az összeadás és a szorzás műveletét e számok között. Ezután e számkört kibővítettük a negatív számokkal, az így kapott halmazt pedig \Z-vel jelöltük és egész számoknak neveztük el őket. Itt már a kivonás is korlátlanul elvégezhető. Végül – elvonatkoztatva a „szám” fogalmától – általánosságban is megfogalmaztuk azokat a követelményeket, amelyeket egy tetszőleges halmaznak teljesítenie kell annak érdekében, hogy az elemeivel a „szokásos” módon „számolni” lehessen. Az ilyen konstrukciókat gyűrűknek neveztük el, amelyeknek számos hasznos tulajdonságát mutattuk meg az előző két részben.
De vajon mit kezdjünk azzal, hogy az „osztás” művelete általában nem végezhető el gyűrűkben? Mit jelent az „oszthatóság”? Mikor mondjuk egy gyűrű valamely elemére, hogy „felbonthatatlan” és mely elemeket nevezzük „prímeknek”? Miért van ezeknek kitüntetett szerepük bizonyos gyűrűkben? Mit állít a számelmélet alaptétele, és mitől függ, hogy egy gyűrűben teljesül-e vagy nem? Mi a helyzet az egész számok gyűrűjében? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 14. és 15. részben tárgyalt gyűrű fogalmára, valamint az ezekkel kapcsolatos alábbi definíciókra és tételekre:
Tegyük fel, hogy adva van egy valamilyen R halmaz, amelyen értelmezve van két darab kétváltozós művelet. Az egyiket nevezzük összeadásnak és jelöljük +-szal. A másikat nevezzük szorzásnak és jelöljük \cdot-tal. Az így kapott (R,+,\cdot ) algebrai struktúrát gyűrűnek nevezzük, amennyiben teljesülnek rá az alábbi tulajdonságok – az úgynevezett gyűrűaxiómák:
- A + művelet kommutatív és asszociatív.
- A + műveletre nézve létezik neutrális elem. Ezt a gyűrű nullelemének nevezzük és 0-val jelöljük.
- A + művelet invertálható. Egy tetszőleges a elem +-ra vonatkozó inverzét -a-val jelöljük és a additív inverzének vagy ellentettjének nevezzük.
- A \cdot művelet asszociatív.
- Tetszőleges R-beli a, b és c elemekre teljesülnek az alábbi disztributivitási szabályok:
Amennyiben a \cdot művelet is kommutatív, úgy (R,+,\cdot )-et kommutatív gyűrűnek nevezzük.
Amennyiben a \cdot műveletre nézve is létezik neutrális elem, úgy ezt az elemet a gyűrű egységelemének nevezzük és 1-gyel jelöljük, (R,+,\cdot )-et pedig egységelemes gyűrűnek nevezzük.
Azt a gyűrűt, amely kizárólag a 0 elemet (azaz a gyűrű nullelemét) tartalmazza, nullgyűrűnek nevezzük. Ezt definíció szerint nem tekintjük egységelemes gyűrűnek annak ellenére, hogy a 0 ebben az elfajult esetben nyilvánvalóan neutrális elem az összeadáson kívül a szorzásra nézve is.
Ferdetestnek nevezzük azokat az egységelemes gyűrűket, amelyekben a \cdot műveletre nézve a gyűrű nullelemén kívül minden elemnek létezik inverze. Ha emellett a \cdot művelet még kommutatív is, akkor (R,+,\cdot )-et kommutatív ferdetestnek vagy egyszerűen csak testnek nevezzük (a nullgyűrű tehát nem test, mivel nem is egységelemes a definíció szerint). Egy tetszőleges a elem \cdot-ra vonatkozó inverzét ebben az esetben \frac{1}{a}-val vagy a^{-1}-gyel jelöljük és a multiplikatív inverzének nevezzük.
Legyen (R,+,\cdot ) tetszőleges gyűrű a szokásos jelölésekkel, valamint legyen a és b a gyűrű két tetszőleges eleme. Ha a\cdot b=0, de sem a\neq 0, sem pedig b\neq 0, akkor azt mondjuk, hogy a baloldali nullosztó, b pedig jobboldali nullosztó.
Másként fogalmazva egy a elemet akkor nevezünk baloldali nullosztónak, ha a\neq 0, és létezik olyan b\neq 0 elem, amelyre a\cdot b=0 teljesül. Megint másként fogalmazva egy b elemet akkor nevezünk jobboldali nullosztónak, ha b\neq 0, és létezik olyan a\neq 0 elem, amelyre a\cdot b=0 teljesül.
Az (R,+,\cdot ) gyűrűt nullosztómentes gyűrűnek hívjuk, ha nincs benne sem jobb-, sem pedig baloldali nullosztó. Másként fogalmazva egy nullosztómentes gyűrűben a\cdot b=0-ból következik, hogy a=0 vagy b=0.
A szakirodalomban sok helyen találkozhatunk még a zérusosztó, illetve a zérusosztómentes gyűrű kifejezésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat, ettől függetlenül ezek mind ugyanazt jelentik.
A nullosztómentes és kommutatív gyűrűket integritástartományoknak nevezzük.
Megjegyezzük, hogy ez a definíció nem követeli meg egységelem – azaz a szorzásra nézve neutrális elem – létezését. Sajnos a magyar terminológiában sincs külön neve az egységelemmel is rendelkező integritástartományoknak, ezért a továbbiakban mi is kénytelenek leszünk körülírni az ilyen eseteket, amennyiben az szükséges.
Legyen (R, +, \cdot ) tetszőleges gyűrű a szokásos jelölésekkel. Ekkor tetszőleges a és b elemekre teljesülnek az alábbiak:
- 0a=a0=0
- -(-a)=a
- a(-b)=(-a)b=-(ab)
- (-a)(-b)=ab
- -(a+b)=(-a)+(-b)
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni az előző és az azelőtti részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Ebben a részben főként az oszthatóság fogalmával fogunk foglalkozni. Számunkra elsősorban az egész számok gyűrűje lesz az érdekes, azonban szeretnénk ezeket a fogalmakat minél általánosabb módon tárgyalni, lehetőleg a gyűrűk szintjén. A továbbiakban az egyszerűség kedvéért a kommutatív gyűrűkre szorítkozunk. Ezekben ugyanis az oszthatósággal kapcsolatos definíciók és tételek megfogalmazása jóval egyszerűbbé válik azáltal, hogy a szorzás esetén sem kell törődnünk a tényezők sorrendjével. Amennyiben ettől eltérünk, vagy egy tételhez illetve definícióhoz egyéb tulajdonságra is szükség van (például egységelem létezése vagy nullosztómentesség), úgy azt külön ki fogjuk hangsúlyozni.
Ezenkívül egy jelölésbeli egyszerűsítést is fogunk tenni a továbbiakban. Az előző részekben egy R alaphalmazú gyűrű jelölésekor mindig felsoroltuk a gyűrű két műveletének szimbólumát is. Például: (R,+,\cdot ). Mostantól – ha ez félreértést nem okoz – magát a gyűrűt fogjuk szimplán R-rel jelölni. A nullelem és az esetleges egységelem jelölésére rendre a 0 és az 1, az „összeadás” műveletre a +, a „szorzás” műveletre pedig a \cdot szimbólumot – vagy az egymás után írást – használjuk majd. Természetesen ha ettől esetleg eltérünk, azt minden ilyen esetben külön jelezni fogjuk.
Végül, ha egy a elemhez hozzáadjuk egy b elem ellentettjét, akkor az a+(-b) kifejezés helyett a rövidebb a-b írásmódot fogjuk használni, és kivonásról, illetve az a és b elem különbségéről fogunk beszélni.
Egy általános gyűrűben tehát korlátlanul elvégezhető a kivonás bármely két gyűrűelem között. Nézzük is meg, hogy pontosan mit értünk azalatt, hogy a kivonás lényegében az összeadás megfordítása. Legyen adva két gyűrűelem, jelöljük őket mondjuk a-val és b-vel. Annyit tudunk róluk, hogy ha az a elemet összeadjuk egy másik, ismeretlen gyűrűelemmel, akkor az eredmény b. Feladatunk megtalálni ezt az – alábbi ábrán k-val jelölt – ismeretlen gyűrűelemet:
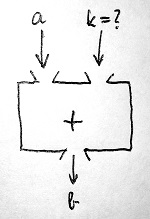
Ne feledjük, hogy „összeadás” alatt most a gyűrű + szimbólummal jelölt műveletét értjük, semmi egyebet. Erről mindössze annyit tudunk, hogy teljesíti a rá vonatkozó gyűrűaxiómákat (14.12. Definíció). A fenti ábrán látható szituációt az alábbi egyenlettel írhatjuk fel:
a+k=bFeladatunk megtalálni a keresett k gyűrűelemet. Szerencsére a 3. gyűrűaxióma hamar a segítségünkre siet, amely kimondja, hogy minden gyűrűelemnek létezik ellentettje (vagy más szóval additív inverze). Így például az a elemnek is létezik ilyen, -a-val jelölt „párja”. Az, hogy -a az a inverze a + műveletre nézve épp azt jelenti, hogy őket összeadva ugyanezen művelet neutrális elemét kapjuk (lásd a 14.9. Definíciót). A + művelet neutrális eleme viszont nem más, mint a gyűrű nulleleme. Ha tehát a fenti egyenlet mindkét oldalához a additív inverzét adjuk, akkor a következőt kapjuk:
\underbrace{(a+(-a))}_{=0}+k=b+(-a)A baloldalon tehát 0+k szerepel, ami a neutrális elem 14.7. Definíciója alaján k-val egyezik meg. A végeredmény tehát:
k=b-aAz összeadás megfordítása alatt tehát azt értjük, hogy az eredményhez hozzáadva az egyik bemenet additív inverzét, visszakapjuk a másik bemenetet. Vegyük észre, hogy ez épp az általános iskolából ismert kivonással analóg, amikoris a „van 3 forintunk, mennyi kell még ahhoz, hogy épp 5 legyen?” típusú kérdésekre kerestük a választ. A 3. gyűrűaxióma teszi lehetővé, hogy bármilyen számok is szerepeljenek a kérdésben, azt mindig meg tudjuk válaszolni. Nincs más dolgunk ugyanis, mint a második számhoz hozzáadni az első additív inverzét (vagy más szavakkal: a második számból kivonni az elsőt), pont úgy, ahogyan a fenti képlet is leírja. Természetesen ilyen módon adott esetben negatív számot is kaphatunk eredményül, amelyet a megfelelő módon kell értelmeznünk. Például a „van 5 forintunk, mennyi kell még ahhoz, hogy épp 3 legyen?” kérdésre a fenti képlet -2-t ad eredményül, amelyet úgy értelmezhetünk, hogy el kell költenünk 2 forintot ahhoz, hogy épp 3 legyen.
Oszthatóság
Most vizsgáljuk meg ugyanezt a kérdést a gyűrű másik műveletére vonatkozóan is. A bevezető szakaszt szóról szóra megismételve, ám a + műveletet a \cdot műveletre lecserélve ezúttal tehát a következő a feladat. Keressük azt az ismeretlen k gyűrűelemet, amellyel az a gyűrűelemet megszorozva a b gyűrűelemet kapjuk eredményül. Az alábbi ábra mutatja ezt a szituációt:
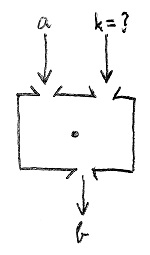
Az előző szakaszban ugyan nem hangsúlyoztuk ki, de nagyon fontos, hogy csak a gyűrű elemei között kutakodhatunk, amikor keressük az ismeretlen k elemet. Mondhatnánk, hogy egyszerű a feladatunk, hiszen ugyanazt kell csinálni, mint az összeadás megfordítása esetén, két apró különbségtől eltekintve. Egyrészt ezúttal összeadás helyett szorozni kell b-t, másrészt pedig ezt a szorzást a additív inverze helyett ezúttal a multiplikatív inverzével kell végrehajtani. A 14.12. Definíció multiplikatív inverzre vonatkozó jelölését használva ez így fejezhető ki képlettel:
k=b\cdot a^{-1}Sajnos azonban az összeadással ellentétben a szorzáshoz nincs olyan gyűrűaxiómánk, amely biztosítja tetszőleges elem multiplikatív inverzének létezését. Ez csak speciális gyűrűkben teljesül, amelyeket a 14.12. Definíció alapján testeknek neveztünk.
A számunkra fontos egész számok \Z gyűrűje azonban nem test, mivel kizárólag az egységelemnek és ellentettjének van multiplikatív inverze – mindkettőnek önmaga. Így ott ez a képlet egyetlen gyakorlatilag is hasznos esetben sem használható k „kiszámításához”. Ennek ellenére sok esetben adott a és b gyűrűelemekhez mégis létezik olyan k gyűrűelem, amelyre teljesül, hogy ak=b.
Ez elvezet minket a legfontosabb számelméleti fogalomhoz.
16.1. Definíció (Oszthatóság):
Tegyük fel, hogy R egy kommutatív gyűrű, valamint a és b a gyűrű két eleme. Amennyiben létezik olyan k gyűrűelem, hogy ak=b, akkor azt mondjuk, hogy a osztója b-nek az R gyűrűben. Ezzel egyenértékű megfogalmazások: b osztható a-val vagy b többszöröse a-nak.
Az oszthatóság tehát egy kétváltozós reláció az R gyűrűben. Azt a relációt, hogy „a osztója b-nek R-ben”, így jelöljük: a|_R b.
Amennyiben a és b között nem áll fenn az oszthatósági reláció – azaz a nem osztója b-nek az R gyűrűben –, azt így jelöljük: a{\nmid}_R b.
Ha a kontextusból egyértelmű, hogy melyik gyűrűben vizsgáljuk az oszthatóságot, akkor a relációt jelölő szimbólumból elhagyhatjuk a gyűrűre való hivatkozást. Ilyenkor például a|_R b helyett egyszerűen a|b-t írhatunk.
♣Megjegyzés:
Egy testben bármely a\neq 0 és b elem között fennáll az a|b oszthatóság. Itt ugyanis minden nemnulla elemnek van multiplikatív inverze. Így a k=b\cdot a^{-1} képlet minden esetben előállítja azt a k tényezőt, amellyel megszorozva az a elemet b-t kapunk eredményül, hiszen:
a\cdot \underbrace{(b\cdot a^{-1})}_{=k} = \underbrace{(a\cdot a^{-1})}_{=1}\cdot b = b ♣Most nézzünk néhány példát ennek a fogalomnak a megértéséhez. Az egész számok \Z gyűrűjében például 2|6, mivel létezik olyan egész szám, amellyel 2-t megszorozva 6-ot kapunk (nevezetesen a 3, hiszen 2\cdot 3=6). Ugyanakkor például 6\nmid2, mivel nem létezik olyan k egész szám, amelyre 6k=2 teljesülne.
Annak demonstrálására, hogy nagyon nem mindegy, melyik gyűrűben beszélünk oszthatóságról, nézzük például a páros (azaz 2-vel osztható) egész számok halmazát a szokásos összeadással és szorzással. Ezt a halmazt konvencionálisan 2\Z-vel szoktuk jelölni, és azonnal látszik, hogy ez egy kommutatív gyűrű, hiszen teljesíti a 14.12. Definíció szerinti gyűrűaxiómákat.
Az összeadásról és a szorzásról korábban már láttuk, hogy mindkettő kommutatív és asszociatív, valamint hogy a szorzás disztributív az összeadásra nézve. A nullelem (azaz a 0 egész szám) szintén páros, valamint egy páros szám ellentettje is páros, így teljesül a 2. és a 3. gyűrűaxióma is. Már csak annyit kell ellenőrizni, hogy az összeadás és a szorzás valóban művelet-e a 2\Z halmazon is, azaz nem vezet-e ki belőle. Ez viszont nyilván teljesül, hiszen két páros szám összege és szorzata is páros. Ez a gyűrű viszont nem egységelemes, hiszen a szorzás neutrális eleme az 1 egész szám, ami nem páros. Ugyanakkor nullosztómentes, hiszen ha semmilyen két nemnulla egész szám szorzata nem lehet 0, akkor ez speciálisan a páros számokra is nyilván igaz.
Most vizsgáljuk meg a 2|6 oszthatóságot a 2\Z gyűrűben is. A \Z gyűrűvel ellentétben itt már nem teljesül ez az oszthatóság, hiszen nem létezik olyan páros szám, amellyel a 2-t megszorozva 6-ot kapnánk. Azaz 2|_{\Z}6, ugyanakkor 2{\nmid}_{2\Z}6.
A 13. részben az úgynevezett ekvivalenciarelációk kapcsán ismertük meg a szimmetrikus relációk fogalmát (lásd a 13.3. Definíciót). Ezek olyan relációk, amelyek ha fennállnak az egyik irányban, akkor fennállnak a másik irányban is. Az oszthatósági reláció tehát a \Z gyűrűben NEM szimmetrikus, hiszen a fentebbi példa alapján 2|6, de 6\nmid 2.
A 12. részben az úgynevezett rendezési relációk kapcsán pedig az antiszimmetrikus relációk fogalmát (lásd a 12.9. Definíció) ismertük meg. Ezek olyan relációk, amelyek ha mindkét irányban fennállnak két elem között, akkor a két elem azonos. Korábban már említettük, hogy az antiszimmetria és a szimmetria egymással nem ellentétes fogalmak. A \Z gyűrűben értelmezett oszthatósági reláció például – amellett, hogy nem szimmetrikus – az antiszimmetria tulajdonságát SEM teljesíti.
Egyrészt ugyanis teljesül az 1|(-1) oszthatóság, hiszen létezik olyan egész szám, amellyel 1-et megszorozva -1-et kapunk (nevezetesen a -1). Másrészt teljesül a (-1)|1 oszthatóság is, hiszen létezik olyan egész szám is, amellyel -1-et megszorozva 1-et kapunk (nevezetesen ismét a -1). A reláció tehát fennáll mindkét irányban az 1 és a -1 között, ugyanakkor 1\neq -1. Ez a reláció tehát valóban nem antiszimmetrikus.
Most vizsgáljuk meg az oszthatósági reláció néhány tulajdonságát, amelyek egyszerűen adódnak a 16.1. Definícióból.
16.2. Tétel (Oszthatóság tulajdonságai):
Legyen R egy tetszőleges kommutatív gyűrű. Ekkor igazak az alábbiak:
- Ha a gyűrű egységelemes, akkor minden elem osztója önmagának.
- Ha a gyűrű nullosztómentes, és létezik olyan a\neq 0 elem, amely osztója önmagának, akkor a gyűrű egységelemes.
- Tetszőleges a-ra teljesül, hogy a|0. Azaz a nullelemnek minden elem osztója.
- A 0|a oszthatóság akkor és csak akkor teljesül, ha a=0. Azaz a nullelem csak önmagának osztója.
- Ha valamilyen a, b és c elemekre teljesülnek az a|b és a b|c oszthatóságok, akkor teljesül az a|c oszthatóság is. Azaz az oszthatósági reláció tranzitív (lásd a 12.10. Definíciót).
- Ha valamilyen a, b és c elemekre teljesülnek az a|b és az a|c oszthatóságok, akkor teljesülnek az a|b+c és az a|b-c oszthatóságok is. Azaz ha egy gyűrűelem osztója valamely két gyűrűelemnek, akkor osztója az összegüknek és a különbségüknek is.
- Ha valamilyen a és b elemekre teljesül az a|b oszthatóság, akkor tetszőleges c elemre teljesül az a|bc oszthatóság is. Azaz ha egy gyűrűelem osztója valamely gyűrűelemnek, akkor osztója a többszöröseinek is.
- Ha valamilyen a és b elemekre teljesül az a|b oszthatóság, akkor teljesülnek az a|(-b), a (-a)|b valamint a (-a)|(-b) oszthatóságok is. Azaz az ellentettképzés nem befolyásolja az oszthatósági relációt.
Bizonyítás:
Az 1. tulajdonság: Az egységelem a szorzás neutrális eleme. A 14.7. Definíció szerint ezzel tehát bármilyen a elemet megszorozva az eredmény marad a. Ez épp azt jelenti, hogy a|a.
A 2. tulajdonság: Az, hogy fennáll az a|a oszthatóság azt jelenti, hogy létezik olyan x gyűrűelem, amelyre teljesül az a\cdot x=a egyenlet. Ezt az egyenletet bármely r gyűrűelemmel megszorozva ezt kapjuk:
a\cdot x\cdot r=a\cdot rMivel azonban a gyűrű nullosztómentes, ezért a 15.4. Tétel miatt mindkét oldalt lehet egyszerűsíteni a-val. Így ezt kapjuk:
x\cdot r=rAz x elemre tehát igaz lesz, hogy őt bármilyen r gyűrűelemmel megszorozva r-et kapunk eredményül. Más szavakkal x a gyűrű egységeleme.
A 3. tulajdonság: A 15.1. Tétel 1. pontja alapján bármely a elemet a nullelemmel szorozva a nullelemet kapjuk eredményül. Ez épp azt jelenti, hogy a|0.
A 4. tulajdonság: Mivel az imént bizonyított 3. tulajdonság alapján minden gyűrűelem osztója a nullelemnek, így nyilván maga a nullelem is. Ha tehát a=0, akkor fennáll a 0|a oszthatóság. Visszafelé: ha fennáll a 0|a oszthatóság, akkor ez azt jelenti, hogy létezik olyan k gyűrűelem, amelyre 0\cdot k=a teljesül. Ebből viszont a 15.1. Tétel 1. pontja miatt a=0 következik.
Az 5. tulajdonság: Az, hogy fennállnak az a|b és a b|c oszthatóságok azt jelenti, hogy léteznek olyan k_1 és k_2 gyűrűelemek, amelyekre teljesülnek az alábbi egyenletek:
\begin{aligned}a\cdot k_1&=b\\b\cdot k_2&=c\end{aligned}A második egyenletbe b helyére behelyettesítve az első egyenlet baloldalát ezt kapjuk:
\underbrace{(a\cdot k_1)}_{=b}\cdot k_2=cMivel azonban a 14.12. Definícióban megfogalmazott 4. gyűrűaxióma alapján a szorzás asszociatív, ezért ennek az egyenletnek a baloldala átzárójelezhető:
a\cdot (k_1\cdot k_2)=cLétezik tehát olyan gyűrűelem, amellyel a-t megszorozva c-t kapunk (nevezetesen a k_1\cdot k_2). Ez viszont épp azt jelenti, hogy a|c.
A 6. tulajdonság: Az, hogy fennállnak az a|b és az a|c oszthatóságok azt jelenti, hogy léteznek olyan k_1 és k_2 gyűrűelemek, amelyekre teljesülnek az alábbi egyenletek:
\begin{aligned}a\cdot k_1&=b\\a\cdot k_2&=c\end{aligned}Ezt a két egyenletet egymással összeadva, illetve az elsőből a másodikat kivonva a következőket kapjuk:
\begin{aligned}ak_1+ak_2&=b+c \\ ak_1-ak_2&=b-c\end{aligned}Mivel azonban a 14.12. Definícióban megfogalmazott 5. gyűrűaxióma alapján teljesülnek a disztributivitási szabályok, ezért ennek a két egyenletnek a baloldalai átírhatók az alábbi módon:
\begin{aligned}a\cdot (k_1+k_2)&=b+c \\ a\cdot (k_1-k_2)&=b-c\end{aligned}Eszerint tehát léteznek olyan gyűrűelemek, amelyekkel a-t megszorozva b+c-t illetve b-c-t kapunk (nevezetesen a k_1+k_2 illetve a k_1-k_2). Ez viszont épp azt jelenti, hogy a|b+c illetve a|b-c.
A 7. tulajdonság: Az, hogy fennáll az a|b oszthatóság azt jelenti, hogy létezik olyan k gyűrűelem, amelyre teljesül az alábbi egyenlet:
a\cdot k = bAz egyenlet mindkét oldalát a c gyűrűelemmel megszorozva ezt kapjuk:
(a\cdot k)\cdot c = b\cdot cMivel azonban a 14.12. Definícióban megfogalmazott 4. gyűrűaxióma alapján a szorzás asszociatív, ezért ennek az egyenletnek a baloldala átzárójelezhető:
a\cdot (k\cdot c) = b\cdot cLétezik tehát olyan gyűrűelem, amellyel a-t megszorozva bc-t kapunk (nevezetesen a kc). Ez viszont épp azt jelenti, hogy a|bc.
Végül a 8. tulajdonság: Az, hogy fennáll az a|b oszthatóság azt jelenti, hogy létezik olyan k gyűrűelem, amelyre teljesül az alábbi egyenlet:
a\cdot k = bViszont a 15.1. Tétel 2., 3. és 4. pontjai miatt ekkor az alábbi egyenletek is teljesülnek:
\begin{aligned}a\cdot(-k)&=(-b) \\ (-a)\cdot k&=(-b)\\ (-a)\cdot (-k)&=-(-b)=b\end{aligned}Ez viszont épp azt jelenti, hogy fennállnak az a|(-b), (-a)|(-b) és (-a)|b oszthatóságok.
∎Most ismerkedjünk meg egy, a továbbiakban fontos fogalommal.
Egységek
Az oszthatóság tulajdonságairól szóló imént bizonyított 16.2. Tétel 4. pontja alapján egy gyűrű nulleleme egyfajta szélsőséget képvisel. Ő ugyanis kizárólag saját magának osztója. A másik szélsőséget azok a gyűrűelemek képviselik, amelyek viszont a gyűrű minden elemének osztói. Ezeknek külön nevük is van.
16.3. Definíció (Egység):
Legyen R egy tetszőleges kommutatív gyűrű. Ha egy adott e gyűrűelem esetén minden a gyűrűelemre teljesül az e|a oszthatósági reláció, akkor az e elemet egységnek nevezzük.
♣Megjegyzés:
Figyelem! Ez nem tévesztendő össze az egységelem fogalmával, amely a 14.12. Definíció alapján a gyűrű \cdot-tal jelölt műveletének neutrális eleme.
Igaz ugyanakkor, hogy egy gyűrű egységeleme – amennyiben létezik – mindig egység. Ugyanis bármely a gyűrűelem esetén 1\cdot a=a, amely viszont épp azt jelenti, hogy 1|a. Igaz továbbá, hogy az egységelem ellentettje is egység, hiszen a 16.2. Tétel 8. pontja alapján az 1|a oszthatóságból következik a (-1)|a oszthatóság.
Egyáltalán nem biztos azonban, hogy egy gyűrűben csak ez a két egység létezik. Egy testben például a nullelemen kívül minden elem egység, ugyanis az oszthatóság 16.1. Definíciója utáni megjegyzés alapján itt minden elem osztható bármilyen nemnulla elemmel.
Megjegyezzük ugyanakkor, hogy nem csak ez a két szélsőséges eset létezik. Vannak olyan gyűrűk is, amelyekben az egységelemen és ellentettjén kívül is létezik egység, ugyanakkor nem minden eleme az. Ilyen gyűrű például az egész számok egyfajta általánosításának tekinthető úgynevezett Gauss-egészek gyűrűje, amelyben összesen 4 egység van. Ennek részleteitől azonban – az úgynevezett komplex számok ismeretének hiányában – eltekintünk.
♣Az alábbi tétel arra ad választ, hogy mikor létezik egyáltalán egység egy gyűrűben.
16.4. Tétel:
Egy kommutatív és nullosztómentes gyűrűben akkor és csak akkor létezik egység, ha létezik egységelem.
Amennyiben a gyűrű csak kommutatív, de nem feltétlenül nullosztómentes, úgy csak annyit tudunk mondani, hogy ha létezik egységelem, akkor létezik egység is. Ebben az esetben egy egység létezéséből még nem következik az, hogy egységelem is létezik.
♣Bizonyítás:
Azt, hogy az esetleges egységelem egy gyűrűben mindig egység, már láttuk az egység 16.3. Definíciója utáni megjegyzésben. Így csak azt kell megmutatni, hogy ha létezik egység, akkor szükségképpen léteznie kell egységelemnek is nullosztómentes gyűrű esetén.
Tegyük fel tehát, hogy e egy egység. Az általánosság megsértése nélkül feltehetjük, hogy e\neq 0. Hiszen ha e=0 lenne, akkor a 16.2. Tétel 4. pontja miatt ő csak saját magának lenne osztója. Mivel azonban azt mondtuk róla, hogy osztója a gyűrű minden elemének (hiszen egység), ezért ebben az esetben a gyűrűnek szükségképpen ő lenne az egyetlen eleme. Azaz a 14.12. Definíció szerinti nullgyűrűről volna szó, amelyben a nullelem egyben egységelem is, így erre nyilván teljesülne az állítás.
Most nézzük az e\neq 0 esetet. Ő tehát osztója a gyűrű összes elemének, így saját magának is, azaz e|e. Ebből viszont a 16.2. Tétel 2. pontja miatt az következik, hogy a gyűrű egységelemes.
∎Azt tehát már tudjuk, hogy egy kommutatív, nullosztómentes gyűrűben pontosan akkor létezik egység, ha egységelem is létezik. Például az előző szakaszban vizsgált 2\Z gyűrűben emiatt nem létezik egység, hiszen egységelem sem létezik.
A most következő tétel ahhoz nyújt segítséget, hogy egy kommutatív, egységelemes gyűrűben megtaláljuk az összes egységet. Ehhez mindössze az egységelem ismerete szükséges, a nullosztómentesség nem.
16.5. Tétel:
Egy kommutatív, egységelemes gyűrűben egy elem akkor és csak akkor egység, ha osztója az egységelemnek.
♣Bizonyítás:
Mivel egy egység a definíció alapján minden gyűrűelemnek osztója, ezért nyilván az egységelemnek is.
Visszafelé: Tegyük fel, hogy egy e elem osztója az egységelemnek, azaz e|1. Az egység 16.3. Definíciója utáni megjegyzésben azonban már láttuk, hogy 1 szükségképpen egység, azaz minden a gyűrűelemre teljesül az 1|a oszthatóság. Fennállnak tehát az e|1 és 1|a oszthatóságok, így az oszthatósági reláció tranzitivitása miatt (lásd a 16.2. Tétel 5. pontját) fennáll az e|a oszthatóság is minden a gyűrűelemre. Ez viszont épp azt jelenti, hogy e egység.
∎Egy kommutatív, egységelemes gyűrűben tehát az egységek pontosan az egységelem osztói. Az egész számok \Z gyűrűjében ez alapján tehát az 1-en és a -1-en kívül nincs más egység, hiszen az 1 egész számnak nincs más osztója.
Megjegyezzük még, hogy az utóbbi két tétel semmit nem mond az egységekről abban az esetben, ha a gyűrű csak kommutatív, de nem egységelemes, és a nullosztómentesség sem teljesül. Az általunk vizsgált esetekben azonban ilyen nem fog előfordulni.
Asszociált elemek
Most az oszthatóság után egy másik relációval fogunk megismerkedni, amely az imént tárgyalt egységekhez kapcsolódik szorosan. Ez a fogalom a számelmélet alaptételének a pontos megfogalmazásában lesz segítségünkre. Azt fejezi ki, hogy két gyűrűelem az oszthatóság szempontjából ugyanúgy viselkedik, vagy más szavakkal megkülönböztethetetlen. Erről szól az alábbi definíció.
16.6. Definíció (Asszociált):
Egy kommutatív gyűrű valamely a és b elemeire akkor mondjuk, hogy egymás asszociáltjai, ha pontosan ugyanazok a többszöröseik és az osztóik is. Pontosabban fogalmazva, ha tetszőleges r gyűrűelem esetén a|r akkor és csak akkor teljesül, amikor b|r is teljesül, valamint r|a akkor és csak akkor teljesül, amikor r|b is teljesül.
Azt, hogy a és b egymás asszociáltjai így jelöljük: a\sim b.
♣Például a \Z gyűrűben az 5 és a (-5) egymás asszociáltjai.
Megjegyzés:
Egy testben bármely a\neq 0 és b\neq 0 elem között teljesül az a\sim b asszociáció. Itt ugyanis minden nemnulla elem osztója az összes elemnek (lásd a 16.1. Definíció utáni megjegyzést). Az a-nak és b-nek tehát minden elem többszöröse, és a nullelemen kívül minden elem osztója. Így az osztóik is megegyeznek és a többszöröseik is, ami épp azt jelenti, hogy egymás asszociáltjai.
♣Először is megmutatjuk, hogy ez a reláció egy ekvivalenciareláció (lásd a 13.4. Definíciót) a gyűrű alaphalmazán, és így a 13.5. Tétel alapján a gyűrű alaphalmazát úgynevezett ekvivalencia-osztályokra bontja. Erről a fogalomról bővebben a 13. részben írtunk, de dióhéjban arról van szó, hogy minden gyűrűelem pontosan egy ekvivalencia-osztályba fog bekerülni. Méghozzá abba, amely az ő asszociáltjait tartalmazza.
16.7. Tétel:
Legyen R egy tetszőleges kommutatív gyűrű. Ekkor a 16.6. Definíció szerinti asszociáltság egy ekvivalenciareláció a gyűrű R alaphalmazán. Más szavakkal tetszőleges a, b és c elemekre teljesülnek az alábbiak:
- a\sim a (reflexivitás).
- Ha a\sim b, akkor b\sim a (szimmetria).
- Ha a\sim b és b\sim c, akkor a\sim c (tranzitivitás).
Bizonyítás:
Teljesen nyilvánvalóan adódik az asszociáltság 16.6. Definíciójából. Ugyanis:
- Bármely elemnek nyilván pontosan ugyanazok az osztói és többszörösei is, mint önmagának.
- Ha egy a elemnek pontosan ugyanazok az osztói és többszörösei, mint egy b elemnek, akkor nyilván a b elemnek is pontosan ugyanazok az osztói és többszörösei, mint az a elemnek.
- Ha egy a elemnek pontosan ugyanazok az osztói és többszörösei, mint egy b elemnek, amelynek viszont pontosan ugyanazok az osztói és többszörösei, mint egy c elemnek, akkor nyilván az a elemnek is pontosan ugyanazok az osztói és többszörösei, mint a c elemnek.
Most vizsgáljuk meg, hogy mit tudunk mondani ezekről az ekvivalencia-osztályokról. Általános esetben – amikor a gyűrűről csak annyit tudunk, hogy kommutatív – az alábbiakat.
16.8. Tétel:
Tetszőleges kommutatív gyűrű esetén igazak az alábbiak:
- A gyűrű minden eleme és az ellentettje egymás asszociáltjai. Azaz minden a elemre fennáll az a\sim (-a) reláció.
- Ha fennáll az a\sim b asszociáció, akkor fennállnak az a\sim (-b), (-a)\sim b valamint (-a)\sim (-b) asszociációk is.
- A nullelemnek egyetlen asszociáltja van, méghozzá saját maga.
- Ha két elem egymásnak osztói, akkor asszociáltak. Azaz ha valamely a és b elemek között fennállnak az a|b és b|a oszthatóságok, akkor teljesül az a\sim b asszociáció.
- Bármely e egység akkor és csak akkor asszociáltja valamely f gyűrűelemnek, ha f is egység.
Bizonyítás:
A tétel 1. állításához két dolgot kell bizonyítani. Egyrészt azt, hogy bármely d gyűrűelem akkor és csak akkor osztója a-nak, ha (-a)-nak is. A 16.2. Tétel 8. pontja épp azt mondja ki, hogy ha teljesül d|a, akkor teljesül d|(-a) is. Ez azonban természetesen visszafelé is igaz a 15.1. Tétel 2. pontja miatt, miszerint minden elem ellentettjének az ellentettje önmaga. Azaz ha teljesül d|(-a) akkor teljesül d|\underbrace{(-(-a))}_{=a} is.
A másik dolog, ami bizonyítani kell, hogy bármely d gyűrűelem akkor és csak akkor többszöröse a-nak, ha (-a)-nak is. Azaz a|d akkor és csak akkor teljesül, ha (-a)|d is teljesül. A 16.2. Tétel 8. pontja azonban azt is kimondja, hogy ha teljesül a|d, akkor teljesül (-a)|d is, így az előző gondolatmenet szinte szó szerint érvényes itt is.
A 2. állítás az 1. állítás egyszerű következménye. Ugyanis például b-re a tétel alapján igaz, hogy b\sim (-b), így ha a\sim b teljesül, akkor a tranzitivitás miatt a\sim (-b) is. A másik két asszociáció ugyanezen okok miatt teljesül.
A 3. állítás: Mivel az asszociáció a 16.7. Tétel értelmében reflexív, ezért nyilván teljesül a 0\sim 0 asszociáció. Azt kell megmutatni, hogy a nullelemnek nincs más asszociáltja. Tegyük fel indirekt, hogy nem ez a helyzet, azaz létezik olyan a\neq 0 elem a gyűrűben, amelyre teljesül a 0\sim a asszociáció. Ez tehát azt jelenti, hogy a 0-nak és az a elemnek pontosan ugyanazok az osztóik. A 0-nak viszont a 16.2. Tétel 3. pontja alapján osztója minden gyűrűelem. Az asszociáltság miatt ekkor a-nak is osztója az összes gyűrűelem, tehát speciálisan a 0 is. A 16.2. Tétel 4. pontja alapján azonban a 0|a oszthatóságból következik, hogy a=0, ami ellentmond indirekt feltételezésünknek, miszerint a\neq 0.
A 4. állítás: Tegyük fel, hogy egyszerre teljesülnek az a|b és a b|a oszthatóságok. Ekkor ha bármely d_1 elemre fennáll a d_1|a oszthatóság (azaz d_1 osztója a-nak), akkor az oszthatóság tranzitivitása miatt – mivel ugye a|b teljesül – fennáll a d_1|b oszthatóság is (azaz d_1 osztója b-nek is). Ugyanezen okok miatt ha bármely d_2 elem osztója b-nek, akkor a-nak is. Az a elemnek tehát pontosan ugyanazok az osztói, mint a b elemnek.
Ugyanez a gondolatmenet a többszörösökre is végigjátszható. Ha bármely t_1 elemre fennáll az a|t_1 oszthatóság (azaz t_1 többszöröse a-nak), akkor az oszthatóság tranzitivitása miatt – mivel ugye b|a teljesül – fennáll a b|t_1 oszthatóság is (azaz t_1 többszöröse b-nek is). Ugyanezen okok miatt ha bármely t_2 elem többszöröse b-nek, akkor a-nak is. Az a elemnek tehát ponotosan ugyanazok a többszörösei is, mint a b elemnek.
Láttuk tehát, hogy a|b és b|a együttes fennállása esetén a és b osztói is és többszörösei is megegyeznek. Ez viszont épp azt jelenti, hogy a\sim b.
Végül az 5. állítás: Egyrészt mivel e egység, ezért ő minden elemnek osztója, vagy másként fogalmazva neki minden elem a többszöröse. Ha mármost e\sim f, akkor f-nek is minden elem a többszöröse, és így ő is egység. Visszafelé: Mivel e és f egység, ezért ők minden elemnek osztói. Speciálisan tehát egymásnak is, és így a tétel 4. állítása miatt valóban asszociáltak.
∎Megjegyzés:
A tétel alapján tehát biztos, hogy az összes egység egy ekvivalencia-osztályba kerül, amelyben az egységeken kívül nincs más elem. Ezenkívül minden elem azonos ekvivalencia-osztályba kerül az ellentettjével. Arról azonban a tétel semmit nem mond, hogy egy ilyen osztálynak kizárólag ők lennének-e az elemeik. Például az egység 16.3. Definíciója utáni megjegyzésben már említett úgynevezett Gauss-egészek körében minden nemnulla elemnek önmagán és az ellentettjén kívül van még 2 további asszociáltja. Ennek részleteitől azonban – az úgynevezett komplex számok ismeretének hiányában – eltekintünk.
Megjegyezzük ugyanakkor, hogy az asszociáció bármely testben mindössze két ekvivalencia-osztályt fog kijelölni. Az egyikben a tétel második állítása miatt egyetlen elem lesz, méghozzá a nullelem. A másik ekvivalencia-osztály pedig a 16.6. Definíció utáni megjegyzés alapján tartalmazni fogja az összes többi elemet – amelyek egyébként a 16.3. Definíció utáni megjegyzés alapján épp az egységek.
♣Most vizsgáljuk meg, hogy egységelemes gyűrűk esetén mennyivel tudunk többet mondani az asszociált elempárokról. Az alábbi tétel ahhoz nyújt segítséget, hogy két tetszőleges elemről könnyen el tudjuk dönteni, hogy egymás asszociáltjai-e vagy sem.
16.9. Tétel:
Egy kommutatív és egységelemes gyűrűben két elem akkor és csak akkor asszociáltjai egymásnak, ha egymás osztói. Azaz valamely a és b elemek között akkor és csak akkor teljesül az a\sim b asszociáció, ha fennállnak az a|b és b|a oszthatóságok.
Amennyiben a gyűrű csak kommutatív, de nem feltétlenül egységelemes, úgy csak annyit tudunk mondani, hogy az egymással való oszthatóságból következik az asszociáltság. Ebben az esetben az asszociáltságból még nem következik az egymással való oszthatóság.
♣Például az egész számok \Z gyűrűjében a 4 és a (-4) egymás asszociáltjai, és mivel egységelemes, ezért egymás osztói is. A páros egész számok 2\Z gyűrűjében azonban nem teljesül sem a 4|(-4), sem pedig a (-4)|4 oszthatóság, ennek ellenére ez a két szám ebben a gyűrűben is egymás asszociáltja.
Bizonyítás:
Az egyik irányt már bizonyítottuk a 16.8. Tétel 4. pontjában.
Most nézzük a másik irányt, azaz tegyük fel, hogy a gyűrű egységelemes, és a\sim b. A 16.2. Tétel 1. pontja alapján egységelemes gyűrűkben minden elem osztója önmagának, így tehát fennállnak az a|a valamint a b|b oszthatóságok. Mivel azonban a és b egymás asszociáltjai, ezért pontosan ugyanazok az osztóik. Ha tehát fennáll az a|a oszthatóság, akkor szükségképpen fennáll az a|b oszthatóság is. Ugyanilyen okból ha fennáll a b|b oszthatóság, akkor szükségképpen fennáll a b|a oszthatóság is.
∎Végül az alábbi tétel ahhoz nyújt segítséget, hogy egy adott elem összes asszociáltját meg tudjuk találni, amennyiben ismerjük az egységeket.
16.10. Tétel:
Egy kommutatív, egységelemes és nullosztómentes gyűrűben két elem akkor és csak akkor asszociáltjai egymásnak, ha az egyik a másiknak egységszerese.
Amennyiben a gyűrű csak kommutatív és egységelemes, de nem feltétlenül nullosztómentes, úgy csak annyit tudunk mondani, hogy ha két elem közül az egyik a másiknak egységszerese, akkor ők asszociáltak. Ebben az esetben az asszociáltságból még nem következik, hogy az egyik a másiknak egységszerese.
♣Például a \Z gyűrűben az egységek az 1 és a (-1), és rajtuk kívül nincs más egység. A tétel alapján tetszőleges egész számnak megkapjuk az összes asszociáltját, ha megszorozzuk ezzel a két egységgel. Ez alapján például az 5 asszociáltjai az 5\cdot 1=5 (azaz önmaga), valamint az 5\cdot (-1)=(-5) (azaz az ellentettje), és ezeken kívül nincs is más asszociáltja.
Bizonyítás:
Nézzük először a tétel második felét. Itt csak annyit kell feltételeznünk, hogy a gyűrű kommutatív és egységelemes. Tegyük most fel, hogy valamely a és b elemekhez létezik olyan e egység, hogy a\cdot e=b – azaz a b elem az a elem egységszerese. Feladatunk megmutatni, hogy ekkor a\sim b.
Az a\cdot e=b egyrészt a 16.1. Definíció alapján épp azt jelenti, hogy teljesül az a|b oszthatóság. Másrészt, mivel e egység, ezért a 16.5. Tétel alapján ő osztója az egységelemnek, azaz teljesül az e|1 oszthatóság is. Ez szintén a 16.1. Definíció miatt épp azt jelenti, hogy létezik olyan f gyűrűelem, amelyre teljesül az alábbi egyenlet:
e\cdot f=1Ha ezzel az f elemmel megszorozzuk a b gyűrűelemet, ezt kapjuk:
b\cdot f=\underbrace{a\cdot e}_{=b}\cdot fMivel azonban e és f szorzata épp az egységelemet adja, ezért végülis:
b\cdot f=a\cdot \underbrace{e\cdot f}_{=1}=aEz a 16.1. Definíció miatt épp azt jelenti, hogy teljesül a b|a oszthatóság is. Ebből viszont a 16.9. Tétel miatt következik, hogy a\sim b.
Most a tétel megfordítását bizonyítjuk. Ehhez már fel kell használnunk a nullosztómentességet is. Most azt tegyük fel, hogy valamely a és b elemek esetén teljesül az a\sim b asszociáció. Azt fogjuk megmutatni, hogy ekkor az a és b elemek egymás egységszeresei. Ha a=0, akkor a 16.8. Tétel 3. pontja miatt szükségképpen b=0, és ezek nyilván egymás egységszeresei. Így a továbbiakban feltesszük, hogy a\neq 0.
Mivel teljesül az a\sim b asszociáció, és a gyűrű egységelemes, ezért a 16.9. Tétel alapján teljesülnek az a|b és a b|a oszthatóságok. Ez épp azt jelenti, hogy léteznek olyan k_1 és k_2 gyűrűelemek, amelyekre teljesülnek az alábbi egyenletek:
\begin{aligned}a\cdot k_1&=b \\ b\cdot k_2&=a\end{aligned}A második egyenletbe b helyére az elsőt behelyettesítve, valamint a jobboldali a-t az egységelemmel megszorozva ezt kapjuk:
\underbrace{a\cdot k_1}_{=b}\cdot k_2=a\cdot 1Mivel a gyűrű nullosztómentes, ezért a 15.4. Tétel alapján mindkét oldalt egyszerűsíthetjük a-val (amiről ugye feltettük, hogy nem nulla):
k_1\cdot k_2=1A k_1 és a k_2 tehát mindketten osztói az egységelemnek, és így a 16.5. Tétel értelmében mindketten egységek. Vagyis az a és b elemek valóban egymás egységszeresei.
∎Felbonthatatlanok és prímek
Az oszthatóságról szóló szakasz elején az volt a feladatunk, hogy egy szorzás a bemenetét és b kimenetét ismerve keressünk egy gyűrűelemet a másik bemenetre. Akkor mondtuk, hogy teljesül az a|b oszthatóság, ha létezett ilyen elem a gyűrűben. Most ennél egy fokkal nehezebb a feladatunk. Képzeljük el azt a szituációt, hogy csak a szorzás kimenetét ismerjük, és mindkét bemenetre keresnünk kell egy-egy gyűrűelemet, amelyek szorzata épp a kimenet. Ezt mutatja az alábbi ábra:
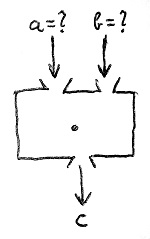
Ezt képlettel kifejezve: c=a\cdot b. Itt tehát az a feladat, hogy a c gyűrűelemnek megtaláljuk valamely osztóját. Algoritmikus szempontból ez egy roppant nehéz feladat, és – mint látni fogjuk a későbbiekben – épp ez biztosítja azt, hogy a modern kriptográfiai eljárások gyakorlatilag feltörhetetlenek. Most azonban tegyük félre az algoritmikus nehézséget, és vizsgáljuk meg ezt a feladatot elméleti szempontból. Egy gyűrűelemet adott esetben sokféleképpen felbonthatunk két másik gyűrűelem szorzatára. Az alábbi példában felsoroltuk az 50 egész szám összes lehetséges felbontását a \Z gyűrűben (a tényezők sorrendjétől eltekintve):
\begin{aligned}50&=1\cdot 50=\\&=2\cdot 25=\\&=5\cdot 10=\\&=(-1)\cdot (-50)=\\&=(-2)\cdot (-25)=\\&=(-5)\cdot (-10) \end{aligned}De vajon mi a helyzet akkor, ha például a 13 egész számot szeretnénk két másik egész szám szorzatára bontani? Érdekes módon ezt csak kétféleképpen tehetjük meg (a tényezők sorrendjétől eltekintve):
13=1\cdot 13=(-1)\cdot (-13)Látható, hogy mindkét felbontásban az egyik tényező egy egység volt, a másik tényező pedig az eredeti szám valamely asszociáltja (jelen esetben saját maga vagy az ellentettje). Amennyiben az a célunk, hogy oszthatósággal kapcsolatos újabb információt nyerjünk a felbontandó elemről, úgy az ilyen jellegű felbontásokkal nem sokra megyünk. Az egységtényezőből azért nem tudunk meg semmi újat, mert egy egységnek bármely osztója maga is egység (hiszen az oszthatóság tranzitivitásán keresztül örökli ezt a tulajdonságot). A másik tényezőből pedig azért nem derül ki semmi új, mert neki meg pontosan ugyanazok az osztói, mint a eredeti elemnek.
A \Z gyűrűben a 13 egész szám emiatt egyfajta „építőkockaként” funkcionál: résztvesz más számok felépítésében, ám ő maga már nem bontható tovább értelmes módon. Az általános iskolában „prímszámoknak” neveztük azokat a számokat, amelyeknek „olyan kevés osztójuk van, amilyen kevés csak lehet”. Elsőre talán zavart okozhat, hogy egyrészt a most következő definícióban teljesen más megnevezést használunk ezekre a kitüntetett gyűrűelemekre, másrészt pedig a „prím” kifejezést teljesen másra fogjuk használni. Ennek oka azonban hamarosan világossá válik.
16.11. Definíció (Felbonthatatlan elem):
Legyen R egy tetszőleges kommutatív gyűrű. Ha valamely a, b és c elemekre a=b\cdot c teljesül, akkor a b\cdot c szorzatot az a elem felbontásának nevezzük. Azokat a felbontásokat, amelyekben b és c közül az egyik egység, a másik pedig a asszociáltja, triviális felbontásoknak nevezzük. Ha egy gyűrűelem saját maga nem egység és nem létezik nemtriviális felbontása (azaz ha létezik is felbontása, az csak triviális lehet), akkor őt felbonthatatlannak vagy irreducibilisnek nevezzük. Ha egy elem nem felbonthatatlan és nem egység, akkor őt összetett elemnek nevezzük. Az egységeket nem tekintjük sem felbonthatatlannak, sem pedig összetettnek.
♣A páros számok 2\Z gyűrűjében például felbonthatatlanok a 2, 6, 10, …, 150, …, illetve ezek ellentettjei is. Ezeknek ugyanis egyáltalán nem létezik felbontása ebben a gyűrűben (azaz nem bonthatók fel páros számok szorzatára).
Az egész számok \Z gyűrűjében például felbonthatatlanok a 2, 3, 5, 7, 13, …, 919, …, 17180131327, …, illetve ezek ellentettjei is. Ezeknek léteznek ugyan felbontásaik, ám azok mind triviális felbontások a fenti értelemben.
Látható, hogy az oszthatósághoz hasonlóan nagyon nem mindegy, hogy melyik gyűrűben beszélünk felbonthatatlanságról. A 6 például felbonthatatlan a 2\Z gyűrűben – hiszen nincs két olyan páros szám, amelyeknek szorzata 6 lenne –, azonban nem felbonthatatlan a \Z gyűrűben – hiszen 6=2\cdot 3 egy nemtriviális felbontás.
Az 1 és a -1 egységek, így a definíció szerint ők nem számítanak felbonthatatlannak. Látszólag semmi nem indokolja, hogy az egységeket önkényesen kizárjuk a felbonthatatlanok közül. Ennek pusztán – mint azt látni fogjuk – praktikussági okai vannak a számelmélet alaptételének megfogalmazásakor. A nullelemet azért nem kellett külön kizárni a definícióban a felbonthatatlanok közül, mivel az amúgyis felbontható nemtriviálisan (például 0\cdot a tetszőleges a\neq 0 elem esetén egy nemtriviális felbontás).
A továbbiakban főként olyan gyűrűket fogunk vizsgálni, amelyekben a szorzás kommutativitásán kívül a nullosztómentesség is teljesül (azaz két nemnulla elem szorzata nem lehet nulla). Ezeket a gyűrűket integritástartományoknak neveztük (lásd a 15.5. Definíciót), és ezeket tekintettük „normálisan” viselkedő gyűrűknek sok szempontból. Az alábbi tétel alapján például integritástartományok esetén a „triviális felbontás” fogalma némiképp egyszerűbben fogalmazható meg a 16.11. Definícióhoz képest.
16.12. Tétel:
Legyenek a\neq 0, b és c egy integritástartomány valamely elemei, amelyekre teljesül az alábbi:
a=b\cdot cEkkor ha b és c közül valamelyik egység, akkor a másik a-nak asszociáltja.
Fordítva: ha b és c közül valamelyik a-nak asszociáltja, akkor a másik egység.
♣Ez alapján tehát integritástartományok esetén a 16.11. Definícióhoz képest a triviális felbontásokra elegendő annyit kikötni, hogy az egyik tényező egység, hiszen a fenti tétel alapján ekkor a másik tényező automatikusan a felbontandó elem asszociáltja lesz. A bizonyításhoz azonban erőteljesen kihasználjuk a nullosztómentességet.
Bizonyítás:
Tegyük fel, hogy a=b\cdot c, és b egység. A 16.4. Tétel értelmében a gyűrűben létezik egységelem, mivel egység is létezik (hiszen b az). Ekkor azonban alkalmazható a 16.10. Tétel, amely szerint ha két elem közül az egyik a másik egységszerese, akkor asszociáltak. Tekintve, hogy jelen esetben ugye a=b\cdot c, és b egység, ezért valóban a\sim c. Ugyanezen okok miatt ha b helyett c az egyég, akkor pedig az a\sim b asszociáció teljesül.
Visszafelé: tegyük fel, hogy a=b\cdot c, és teljesül az a\sim b asszociáció. Mivel a\neq 0, ezért b\neq 0 szintén igaz, hiszen a 16.8. Tétel 3. pontja alapján a nullelem csak önmaga asszociáltja. Mivel bc=a, ezért teljesül a b|a oszthatóság, azaz b osztója a-nak. De ekkor b önmagának is osztója kell legyen (azaz b|b-nek teljesülnie kell), hiszen a és b asszociáltak, tehát pontosan ugyanazok az osztóik. De ha teljesül a b|b oszthatóság, akkor a 16.2. Tétel 2. pontjának értelmében a gyűrű egységelemes.
Ekkor azonban alkalmazható a 16.10. Tétel, mely szerint a szükségképpen b egységszerese kell legyen, tekintve, hogy asszociáltak. Azaz léteznie kell olyan e egységnek a gyűrűben, hogy a=b\cdot e. Ezek szerint tehát teljesül az alábbi:
\underbrace{b\cdot c}_{=a}=b\cdot eMivel a gyűrű nullosztómentes, ezért ebből c=e következik, azaz c valóban egység. Ugyanezen okok miatt ha b helyett c asszociáltja a-nak, akkor pedig b lesz szükségképpen egység.
∎Azt tehát már tudjuk, hogy amiket általános iskolában „prímeknek” neveztünk, azok a gyűrűk absztrakciós szintjén a „felbonthatatlan elemeknek” felelnek meg. Jogos lehet a kérdés, hogy akkor ugyanezen az absztrakciós szinten mégis mire használjuk a „prím” kifejezést, ha nem erre. Az alábbi definíció ad erre választ.
16.13. Definíció (Prímtulajdonságú elem):
Egy R kommutatív gyűrű valamely p elemét prímtulajdonságú elemnek (vagy egyszerűen csak prímnek) nevezzük, ha nem a nullelem, nem egység, és csak úgy lehet osztója két gyűrűelem szorzatának, ha legalább az egyik tényezőnek osztója. Azaz ha valamely a és b gyűrűelemekre teljesül a p|ab oszthatóság, akkor a p|a vagy p|b oszthatóságok közül legalább az egyik ugyancsak teljesül.
♣Megjegyzés:
A definícióból és a szorzás asszociativitásából azonnal adódik, hogy ez a tulajdonság akárhánytényezős szorzatokra is ugyanúgy működik. Azaz ha p prím, és teljesül a p|a_1\cdot a_2\cdot \ldots \cdot a_n oszthatóság, akkor a p|a_1, p|a_2, ..., p|a_n oszthatóságok közül legalább az egyik ugyancsak teljesül. Ennek végiggondolását az Olvasóra bízzuk.
♣Ennek a fogalomnak látszólag semmi köze nincs ahhoz, ahogyan az általános iskolában a prímeket szokták meghatározni, ezért talán némi magyarázatra szorul.
Emlékeztetnénk az olvasót az oszthatóság tulajdonságairól szóló 16.2. Tétel 7. pontjára. Ez ugye azt mondja ki, hogyha egy elem osztója egy szorzat valamely tényezőjének, akkor osztója a szorzatnak is. Például az egész számok gyűrűjében 3|6, ezért nyilván 3|6\cdot 2 is teljesül.
Ennek megfordítása azonban általánosságban nem igaz. Azaz általánosságban nem igaz, hogyha egy elem osztója egy szorzatnak, akkor szükségképpen osztója valamelyik tényezőnek is. Például 8|2\cdot 12, ugyanakkor 8\nmid 2 és 8\nmid 12. A prímtulajdonságú elemek (vagy prímek) éppen azok az elemek egy gyűrűben, amelyeknél a megfordítás is érvényes minden esetben.
A nullelemet a felbonthatatlanság 16.11. Definíciójához hasonlóan a prímek közül is szeretnénk kizárni. Mivel azonban az általunk többnyire vizsgált integritástartományokban a nullelem egyébként teljesítené a definíció kritériumait, ezért külön ki kellett kötnünk, hogy őt mégsem tekintjük prímnek. Ha ugyanis valamely a és b elemekre teljesülne, hogy 0|ab, akkor az oszthatóság tulajdonságairól szóló 16.2. Tétel 4. pontja miatt ab=0 következne. Ez viszont az integritástartományok nullosztómentessége miatt csak úgy lehetne, ha a és b közül legalább az egyik 0 lenne. Ebből viszont következne, hogy a 0|a illetve 0|b oszthatóságok közül legalább az egyik teljesül. Azaz végsősoron a 0 prím lenne, ha nem kötnénk ki a definícióban külön, hogy mégsem az.
Jogosan merülhet fel a kérdés az Olvasóban, hogy vajon miért nevezik az általános iskolában „prímnek” azt, amit mi itt „felbonthatatlannak” neveztünk. És vajon miért definiáltuk teljesen másként a prímeket? Nem lehetséges-e, hogy valójában ugyanarról a fogalomról van szó? Általánosságban sajnos nem ennyire egyszerű a helyzet. Például a páros számok 2\Z gyűrűjében a 6 felbonthatatlan, hiszen nem bontható fel két páros szám szorzatára. Ugyanakkor nem prím, hiszen osztója a 2\cdot 18 szorzatnak, de nem osztója sem a 2-nek, sem pedig a 18-nak (hiszen nem léteznek olyan páros számok, amelyeket 6-tal szorozva 2-t vagy 18-at kapnánk eredményül).
Egy integritástartományban tehát ez a két fogalom általában nem ugyanazt jelenti. Az imént például láthattuk, hogy adott esetben létezhetnek olyan elemek, amelyek felbonthatatlanok, de nem prímek. De vajon létezhetnek-e olyan prímek, amik viszont nem felbonthatatlanok? Az alábbi tétel azokban az esetekben adja meg a választ erre a kérdésre, amikor az integritástartomány egységelemmel rendelkezik.
16.14. Tétel:
Legyen R egy integritástartomány, amelyben létezik egységelem is. Ekkor minden prímtulajdonságú elem felbonthatatlan R-ben.
♣Bizonyítás:
Tegyük fel, hogy p tetszőleges prím, és tekintsük ennek valamilyen felbontását:
p=a\cdot bAzt kell bizonyítani, hogy a és b közül az egyik szükségképpen egység kell legyen. A p=ab felbontásból egyrészt következik, hogy teljesülnek az a|p és b|p oszthatóságok.
Másrészt, mivel a gyűrű egységelemes, ezért a 16.2. Tétel 1. pontja miatt minden elem osztója önmagának. Így p=ab-ből következik, hogy teljesül a p|ab oszthatóság is. Ám p prímtulajdonsága miatt ekkor a p|a és p|b oszthatóságok közül legalább az egyik teljesül.
Tegyük fel, hogy p|a teljesül. A bizonyítás elején ugyanakkor megállapítottuk, hogy a|p is teljesül. A 16.9. Tétel miatt az egymással való oszthatóságból következik, hogy a és p egymás asszociáltjai, amiből a 16.12. Tétel alapján az következik, hogy b szükségképpen egység.
Ha p|a mégsem teljesül, akkor p prímtulajdonsága miatt p|b biztosan teljesül. Ebben az esetben az előbbi gondolatmenetet szinte szóról szóra megismételve azt fogjuk kapni, hogy a egység.
Igaz tehát, hogy bármely prímnek bármilyen felbontásában az egyik tényező mindenképpen egység. Azaz valóban minden prím felbonthatatlan.
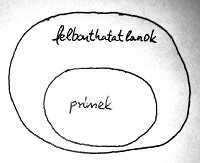
∎Az egységelemes integritástartományokban tehát biztos, hogy a következő a helyzet:
Érdekes kérdés, hogy mi a helyzet nem egységelemes integritástartományok esetén. Erre a kérdésre a következő szakaszban fogunk visszakanyarodni.
Számunkra az olyan integritástartományok lesznek érdekesek, amelyekben azon kívül, hogy minden prím felbonthatatlan még az is teljesül, hogy minden felbonthatatlan prím. Ezekben ugyanis teljesülni fog egy olyan tulajdonság, amely kriptográfiai szempontból alapvető fontosságú.
A számelmélet alaptétele
Az előző szakasz elején láttuk, hogy a \Z gyűrűben egy egész szám adott esetben többféleképpen bontható fel két egész szám szorzatára. Most képzeljük el, hogy az így kapott egész számokat további egész számokra bontjuk, és ezt a felbontást mindaddig folytatjuk minden ágon, ameddig felbonthatatlan számba nem ütközünk. Az előző szakasz alapján innen már nem érdemes tovább folytatni a felbontást (ha egyáltalán lehetséges), hiszen oszthatóságra vonatkozó újabb információt már nem fogunk kapni. Az alábbi ábrán a 100 egész szám néhány felbontását láthatjuk a \Z gyűrűben:
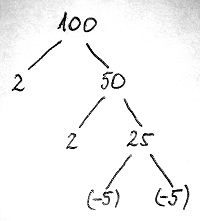
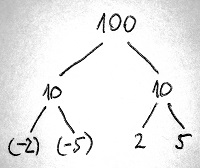
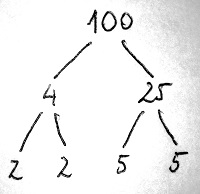
Nagyon úgy tűnik, hogy furcsamód minden így kapott felbontás – amennyiben a tényezők sorrendjétől és egymással való asszociáltságától eltekintünk – megegyezik. A következő részekben látni fogjuk, a \Z gyűrűben történetesen valóban teljesül, hogy minden 0-tól és egységtől különböző elem egyértelműen írható fel felbonthatatlanok szorzataként. Ez azonban egyáltalán nem magától értetődő tulajdonsága egy gyűrűnek. Például a páros számok 2\Z gyűrűjében a 100 egyrészt felírható 2\cdot 50-ként, másrészt pedig 10\cdot 10-ként, és ez a két felbontás „lényegesen” különbözik egymástól.
Az egyértelmű felbonthatóság – azaz a számelmélet alaptételének – teljesülése vagy nem teljesülése egy adott gyűrűben szoros összefüggésben van a prímek és a felbonthatatlanok közötti viszonnyal. Még mielőtt ezt részletesen megvizsgálnánk, először is fogalmazzuk meg mostmár precízen, hogy mikor mondjuk egy integritástartományra azt, hogy teljesül benne a számelmélet alaptétele.
16.15. Definíció (A számelmélet alaptétele):
Legyen R egy tetszőleges integritástartomány. Azt mondjuk, hogy R-ben érvényes a számelmélet alaptétele, ha R minden nemnulla és nem egység eleme egyértelműen felbontható R felbonthatatlan elemeinek szorzatára. Egy felbonthatatlan elem „felbontása” alatt önmagát, mint „egytényezős szorzatot” értjük.
A felbontás egyértelműsége a következőt jelenti. Tekintsük valamely r elem két tetszőleges felbontását:
\begin{aligned}r&=p_1\cdot p_2\cdot \ldots \cdot p_n = \\ &= q_1\cdot q_2\cdot \ldots \cdot q_k\end{aligned}Ekkor a tényezők száma ugyanannyi (azaz n=k), és a két felbontás tényezői egymással párba állíthatók úgy, hogy a párok tagjai egymásnak asszociáltjai legyenek.
♣A számelmélet alaptétele tehát tulajdonképpen két dolgot állít. Egyrészt azt állítja, hogy minden nemnulla és nem egység elemnek létezik felbontása. Másrészt pedig azt, hogy ez a felbontás „néhány apróságtól eltekintve” egyértelmű.
Most adunk egy szükséges feltételt ahhoz, hogy egy integritástartományban teljesüljön a számelmélet alaptétele. A szükségesség azt jelenti, hogy ha ez a feltétel nem teljesül, akkor az alaptétel sem. Azonban önmagában ebből a feltételből még nem következik, hogy a gyűrű „alaptételes”.
16.16. Tétel:
Legyen R egy integritástartomány, amelyben teljesül a számelmélet alaptétele. Ekkor minden felbonthatatlan elem prímtulajdonságú R-ben.
♣Bizonyítás:
Legyen p egy tetszőleges felbonthatatlan elem R-ben. Azt tudjuk, hogy p nem a nullelem (hiszen tetszőleges a esetén 0\cdot a egy nemtriviális felbontás), valamint a 16.11. Definíció miatt nem is egység. Azt kell megmutatni, hogy prímtulajdonságú, azaz hogy ha bármilyen r és s elemek esetén teljesül a p|rs oszthatóság, akkor a p|r vagy p|s oszthatóságok közül is legalább az egyik teljesül. A p|rs oszthatóság a 16.1. Definíció alapján azt jelenti, hogy létezik olyan t elem, amelyre teljesül az alábbi egyenlet:
pt=rsNézzük először, mi lehet a helyzet a jobboldalon. Ha r (vagy s) a nullelem, akkor nyilván fennáll a p|r (vagy p|s) oszthatóság, így ebben az esetben nyilván teljesül a prímtulajdonság.
Az általánosság megsértése nélkül tehát feltehetjük, hogy r\neq 0 és s\neq 0, azaz rs\neq 0 (a nullosztómentesség miatt). Ez viszont azt jelenti, hogy az egyenlet baloldalán álló pt sem lehet nulla, és így alkalmazható a 16.12. Tétel. Nevezetesen: ha r és s közül valamelyik egység, akkor a másik pt asszociáltja, azaz szintén osztható p-vel. Így ebben az esetben is teljesül a prímtulajdonság.
A speciális esetekből még azt kell megvizsgálni, amikor t egység (nullelem ugye nem lehet, hiszen azt mondtuk, hogy pt\neq 0). A 16.4. Tétel miatt ilyenkor a gyűrű egységelemes, alkalmazható tehát a 16.10. Tétel. Ez alapján a jobboldalon álló rs asszociáltja p-nek, hiszen egységszerese. De mivel p felbonthatatlan, ezért r és s közül az egyik p-nek asszociáltja, és így osztható vele (hiszen egységelemes gyűrűről van szó). A prímtulajdonság tehát ebben az esetben is teljesül.
A fennmaradó esetekben az r, s és t elemeket felírhatjuk felbonthatatlan elemek szorzataként, hiszen R-ben teljesül a számelmélet alaptétele. Így a fenti egyenletből ezt kapjuk:
p\cdot \underbrace{t_1\cdot t_2 \cdot \ldots \cdot t_k}_{=t} = \underbrace{r_1\cdot r_2 \cdot \ldots \cdot r_n}_{=r} \cdot \underbrace{s_1\cdot s_2 \cdot \ldots \cdot s_m}_{=s}A számelmélet alaptétele ugyanakkor azt is kimondja, hogy a felbontás asszociáltságtól és a tényezők sorrendjétől eltekintve egyértelmű. Ebből következik, hogy a baloldalon álló felbonthatatlan elemek mindegyikének kell legyen egy asszociált párja a jobboldalon, így p-nek is. Ha ez az r=r_1\cdot \ldots \cdot r_n szorzat valamelyik tényezője, akkor teljesül a p|r oszthatóság. Ha pedig az s=s_1\cdot \ldots \cdot s_m szorzat valamelyik tényezője, akkor pedig teljesül a p|s oszthatóság.
Minden esetben azt kapjuk, hogy p valóban prímtulajdonságú, ahogy a tétel állítja.
∎Megjegyezzük azonban, hogy habár a fenti feltétel csak szükséges, de nem elégséges feltétel az alaptételhez, azonban „nem hiányzik sok” hozzá, hogy elégséges legyen. Ugyanis a feltétel csak azt nem garantálja, hogy minden (nem nulla és nem egység) elemnek létezik-e felbontása. Az alábbi tétel szerint ha viszont létezik felbontás, akkor annak egyértelműségét már garantálja.
16.17. Tétel:
Legyen R egy integritástartomány, amelyben minden felbonthatatlan elem prímtulajdonságú. Ekkor R-ben teljesül a számelmélet alaptételének egyértelműségi állítása.
Azaz amennyiben egy nem nulla, nem egység elem felbontható R felbonthatatlan elemeinek szorzatára, úgy ez a felbontás asszociáltságtól és a tényezők sorrendjétől eltekintve egyértelmű.
♣Bizonyítás:
Tekintsük ugyanis egy felbontható x elem két tetszőleges felbontását:
x=p_1\cdot p_2\cdot \ldots \cdot p_n = q_1\cdot q_2\cdot \ldots \cdot q_kAzt kell bizonyítani, hogy a kétféle felbontásban ugyanannyi felbonthatatlan tényező van, és minden baloldali tényezőnek van egy asszociált párja a jobboldali felbontásban. Kezdjük p_1-gyel.
Mivel jelen esetben minden felbonthatatlan prímtulajdonságú, ezért p_1 is az, amely ugye a fenti egyenlet alapján osztója a jobboldali q_1\cdot \ldots \cdot q_k szorzatnak. A prímtulajdonság miatt ekkor osztója e szorzat legalább egy tényezőjének is. Az általánosság megsértése nélkül feltételezhetjük, hogy ez a tényező q_1. Ha mégsem ez lenne a helyzet, akkor a megfelelő módon átsorszámozzuk a jobboldali tényezőket.
Teljesül tehát a p_1|q_1 oszthatóság, de mivel q_1 felbonthatatlan, ezért ez a 16.11. Definíció alapján csak úgy teljesülhet, ha q_1=p_1\cdot e_1, ahol e_1 valamilyen egység. Az egység létezéséből a 16.4. Tétel miatt következik, hogy a gyűrű egységelemes. Ekkor azonban alkalmazható a 16.10. Tétel, amely szerint p_1 és q_1 egymás asszociáltjai – azaz megtaláltuk p_1 asszociált párját a jobboldalon. Az egyenletünk – amelyet a nullosztómentesség miatt egyszerűsíthetjük p_1-gyel – most így néz ki:
\cancel{p_1}\cdot p_2\cdot \ldots \cdot p_n = \underbrace{\cancel{p_1}\cdot e_1}_{=q_1}\cdot q_2\cdot \ldots \cdot q_kEzután p_2-vel folytatjuk ugyanezt az eljárást, majd p_3-mal, stb. Az előbb látott gondolatmenet alapján mindegyikhez megtaláljuk az asszociált párját a jobboldalon. Amikor az utolsó baloldali tényezővel is megtörtént az egyszerűsítés, akkor az egyenlet baloldalán az egységelem marad, a jobboldalon pedig az egyszerűsítések során előálló n darab egységtényező. Kérdés, hogy ezeken az egységeken kívül marad-e még további tényező a jobboldalon? Például:
1=e_1\cdot e_2\cdot \ldots \cdot e_n\cdot \underbrace{q_{n+1}\cdot q_{n+2} \cdot \ldots \cdot q_k}_{?}Ha ez így lenne, akkor az azt jelentené, hogy a q_{n+1}, q_{n+2}, ..., q_k tényezők mindegyike osztója lenne az egységelemnek, tehát végsősoron ők mind egységek lennének (a 16.5. Tétel értelmében). Ez viszont lehetetlen, hiszen ezek a tényezők felbonthatatlanok, és így a 16.11. Definíció szerint nem lehetnek egységek.
Ezért az egyszerűsítési eljárás során a baloldali és a jobboldali tényezők egyszerre fogynak el, és eközben mindegyik baloldali tényezőhöz megtaláljuk az ő asszociált párját a jobboldalon. Az x elem két felbontása tehát sorrendtől és asszociáltságtól eltekintve valóban megegyezik.
∎Az előző szakaszban a prímek és a felbonthatatlan elemek viszonyát vizsgáltuk, és megállapítottuk, hogy egységelemes integritástartományokban minden prím felbonthatatlan. Akkor feltettük a kérdést, hogy vajon mi a helyzet az olyan integritástartományokkal, amelyekben nem létezik egységelem?
Tekintve, hogy ez a kérdés a számelmélet alaptételének teljesülése szempontjából fontos, ezért inkább azt érdemes megvizsgálni, hogy teljesülhet-e egyáltalán az alaptétel ilyen integritástartományokban? Erre ad választ a következő tétel.
16.18. Tétel:
Legyen R egy integritástartomány, amelyben nem létezik egységelem. Ekkor R-ben nem teljesül a számelmélet alaptétele. Másként fogalmazva az alaptétel csak egységelemes integritástartományokban teljesülhet.
♣Bizonyítás:
Mivel nem létezik egységelem, így a 16.4. Tétel értelmében egység sem létezik. Azaz ha van felbonthatatlan elem, akkor neki még – a 16.11. Definíció szerinti értelemben vett – triviális felbontása sem létezik. Azzal az esettel nem kell foglalkoznunk, hogy mi van akkor, ha egyáltalán nem létezik felbonthatatlan elem. Ebben az esetben ugyanis nem teljesülne a számelmélet alaptételének felbonthatóságról szóló része, hiszen ha nincs felbonthatatlan elem, akkor semmilyen elemet sem lehet felbontani ilyen nem létező elemek szorzatára.
Az általánosság megsértése nélkül feltételezhetjük tehát, hogy létezik felbonthatatlan elem. A következő kérdés, hogy vajon prímtulajdonságú elem létezik-e? Tegyük fel, hogy létezik, és nézzük meg, hogy ennek mik lennének a következményei. Legyen például p egy prímtulajdonságú elem. Ő nyilván osztója bármelyik többszörösének, azaz tetszőleges a\neq 0 gyűrűelemre fennáll a p|pa oszthatóság (meg nyilván a=0-ra is, ám ez az eset számunkra most nem annyira érdekes).
Ebből viszont p prímtulajdonsága miatt következik, hogy a p|p és p|a oszthatóságok közül legalább az egyik teljesül. Mivel nem létezik egységelem, ezért a 16.2. Tétel 2. pontja miatt a p|p oszthatóság lehetetlen, így szükségképpen teljesül p|a. Azaz létezik olyan a_1 elem, amelyre p\cdot a_1 = a. Tekintve, hogy nem létezik egység, így a_1 sem lehet az, vagyis az a elem biztosan nem felbonthatatlan.
De ha fennáll a p|\underbrace{p\cdot a_1}_{=a} oszthatóság, akkor a prímtulajdonságot kihasználva és az előző gondolatmenetet megismételve adódik, hogy fennáll a p|a_1 oszthatóság is. Azaz létezik olyan a_2 elem, amelyre teljesül, hogy p\cdot a_2=a_1, és mivel a_2 szintén nem egység, ezért a_1 sem felbonthatatlan.
Ezt az eljárást a végtelenségig folytathatjuk anélkül, hogy felbonthatatlan elembe ütköznénk. Az így kialakuló végtelen oszthatósági láncot mutatja az alábbi ábra:
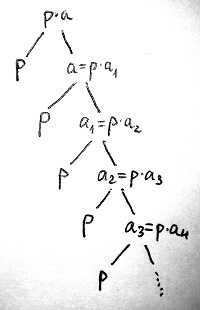
Ha tehát feltételezzük, hogy létezik prímtulajdonságú elem, akkor ennek többszörösei biztosan nem bonthatók fel felbonthatatlanok szorzatára, azaz nem teljesül a számelmélet alaptételének felbonthatóságról szóló része.
Ha viszont azt feltételezzük, hogy nem létezik prím, akkor pedig a 16.16. Tételben megfogalmazott szükséges feltétel nem teljesül, hiszen egyetlen felbonthatatlan sem lehet prím, ha prímek nem is léteznek. Azaz ilyenkor a számelmélet alaptételének egyértelműségről szóló része nem fog teljesülni.
∎A fentiek alapján nem egységelemes integritástartományokban teljesen mindegy, hogy mi a prímek és a felbonthatatlan elemek viszonya, hiszen ezekben amúgysem teljesülhet az alaptétel.
Így már nagyjából teljes a kép azzal kapcsolatban, hogy mikor teljesülhet a számelmélet alaptétele egy integritástartományban. Erre adtunk ebben a szakaszban egy szükséges feltételt. Ez a feltétel a teljes alaptételhez ugyan nem volt elégséges, azonban az egyértelműségi részhez már igen. Létezik olyan feltétel is az alaptétel teljesüléséhez, amely szükséges és egyben elégséges is. Ez azonban túlmutat ennek a résznek a keretein, és az úgynevezett ideálok elméletéhez vezet, így azt egy későbbi részben fogjuk bemutatni.
Ebben a részben tehát megismerkedtünk a legfontosabb számelméleti fogalommal, azaz az „oszthatósággal”, illetve annak alapvető tulajdonságaival. Ezután bevezettük az „egység”, „asszociált”, „felbonthatatlan” és „prím” fogalmát, amelyek segítségével a számelmélet alaptételét precízen meg tudtuk fogalmazni. Végül szükséges (de nem elégséges) feltételt mutattunk ahhoz, hogy egy integritástartományban teljesülhessen az alaptétel.
A következő részben ugyanerre egy elégséges (de nem szükséges) feltételt is mutatunk. Ennek keretében gyűrűk egy speciális osztályával fogunk megismerkedni, amelyeket euklidészi gyűrűknek nevezünk, és amelyekbe – nagy szerencsénkre – az egész számok \Z gyűrűje is beletartozik. Itt fogjuk óriási hasznát venni az előző részben erre a gyűrűre kiterjesztett \leq szimbólummal jelölt rendezési relációnak.
A következő részt itt találod…



