Az előző részben a legnagyobb közös osztó fogalmát általánosítva megismerkedtünk a kitüntetett közös osztó fogalmával. Megmutattuk, hogy amennyiben bármely két elemnek létezik a kitüntetett közös osztója egy integritástartományban, úgy az elemek prímtényezős felbontásai – ha egyáltalán léteznek – egyértelműek lesznek. A kitüntetett közös osztó kiszámításához ismertettük az euklidészi algoritmus alapgondolatát a pozitív egész számokon. Ezt az euklidészi norma fogalmának bevezetésével sikerült működésre bírni egyéb integritástartományokon is. Ezeket euklidészi gyűrűknek neveztük. Igazoltuk azt is, hogy a prímtényezős felbontás egyértelműségén túl annak létezése is biztosított ezekben a speciális gyűrűkben. Végül igazoltuk, hogy az egész számok \Z gyűrűje szintén euklidészi gyűrű, és így valóban teljesül benne a számelmélet alaptétele.
De vajon hogyan lehet „felcsavarni” a számegyenest úgy, hogy az alkalmas legyen kriptográfiai kódoló és dekódoló függvények képzéséhez? Mit jelent a „kongruencia” fogalma, és hogyan lehet ezt általánosítani az úgynevezett „ideálok” és „gyűrűhomomorfizmusok” segítségével? Mik azok a „maradékosztálygyűrűk” és hogyan kell bennük számolni? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 13. és 14. részben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, szimmetrikus és tranzitív, úgy R-et a H halmaz feletti ekvivalenciarelációnak hívjuk.
Tegyük fel, hogy A és B két valamilyen – műveletekkel és/vagy relációkkal ellátott – algebrai struktúra alaphalmaza. Egy közöttük lévő f:A\to B struktúratartó leképezést (függvényt) homomorfizmusnak nevezünk.
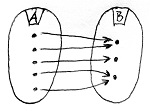
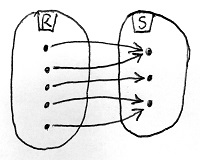
Amennyiben B minden eleme legalább egy A-beli elemhez hozzá van rendelve, akkor f-et szürjektív homomorfizmusnak vagy ráképzésnek nevezzük.
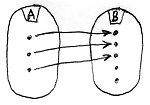
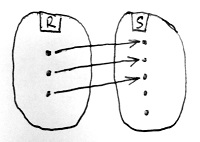
Amennyiben B minden eleme legfeljebb egy A-beli elemhez van hozzárendelve, akkor f-et injektív homomorfizmusnak vagy beágyazásnak nevezzük.
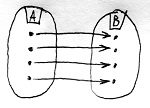
Amennyiben B minden eleme pontosan egy A-beli elemhez van hozzárendelve, akkor f-et bijektív homomorfizmusnak vagy izomorfizmusnak nevezzük.
Tegyük fel, hogy adva van egy valamilyen R halmaz, amelyen értelmezve van két darab kétváltozós művelet. Az egyiket nevezzük összeadásnak és jelöljük +-szal. A másikat nevezzük szorzásnak és jelöljük \cdot-tal. Az így kapott (R,+,\cdot ) algebrai struktúrát gyűrűnek nevezzük, amennyiben teljesülnek rá az alábbi tulajdonságok – az úgynevezett gyűrűaxiómák:
- A + művelet kommutatív és asszociatív.
- A + műveletre nézve létezik neutrális elem. Ezt a gyűrű nullelemének nevezzük és 0-val jelöljük.
- A + művelet invertálható. Egy tetszőleges a elem +-ra vonatkozó inverzét -a-val jelöljük és a additív inverzének vagy ellentettjének nevezzük.
- A \cdot művelet asszociatív.
- Tetszőleges R-beli a, b és c elemekre teljesülnek az alábbi disztributivitási szabályok:
Amennyiben a \cdot művelet is kommutatív, úgy (R,+,\cdot )-et kommutatív gyűrűnek nevezzük.
Amennyiben a \cdot műveletre nézve is létezik neutrális elem, úgy ezt az elemet a gyűrű egységelemének nevezzük és 1-gyel jelöljük, (R,+,\cdot )-et pedig egységelemes gyűrűnek nevezzük.
Azt a gyűrűt, amely kizárólag a 0 elemet (azaz a gyűrű nullelemét) tartalmazza, nullgyűrűnek nevezzük. Ezt definíció szerint nem tekintjük egységelemes gyűrűnek annak ellenére, hogy a 0 ebben az elfajult esetben nyilvánvalóan neutrális elem az összeadáson kívül a szorzásra nézve is.
Ferdetestnek nevezzük azokat az egységelemes gyűrűket, amelyekben a \cdot műveletre nézve a gyűrű nullelemén kívül minden elemnek létezik inverze. Ha emellett a \cdot művelet még kommutatív is, akkor (R,+,\cdot )-et kommutatív ferdetestnek vagy egyszerűen csak testnek nevezzük (a nullgyűrű tehát nem test, mivel nem is egységelemes a definíció szerint). Egy tetszőleges a elem \cdot-ra vonatkozó inverzét ebben az esetben \frac{1}{a}-val vagy a^{-1}-gyel jelöljük és a multiplikatív inverzének nevezzük.
Legyen adott egy R halmaz és egy ezen értelmezett *-gal jelölt kétváltozós művelet, valamint legyen n az R halmaz egy eleme.
Az n elemet jobboldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
a*n=aAz n elemet baloldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
n*a=aHa egy n elem egyszerre jobb- és baloldali neutrális elem, akkor őt kétoldali neutrális elemnek, vagy egyszerűen csak neutrális elemnek nevezzük.
A szakirodalomban sok helyen találkozhatunk még a semleges elem, a nullelem, a zéruselem vagy az egységelem kifejezésekkel, valamint a 0 illetve az 1 jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
Legyen adott egy R halmaz egy rajta értelmezett * művelettel. Létezzen továbbá neutrális elem erre a műveletre nézve, amelyet jelöljünk n-nel.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b*b^{-1}=n, akkor b^{-1}-et a b elem jobboldali inverzének nevezzük a * műveletre nézve.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b^{-1}*b=n, akkor b^{-1}-et a b elem baloldali inverzének nevezzük a * műveletre nézve.
Ha b^{-1} egyszerre jobb- és baloldali inverz, akkor őt a b elem kétoldali inverzének, vagy egyszerűen csak inverzének nevezzük a * műveletre nézve. Azt mondjuk, hogy a b elem invertálható, amennyiben létezik hozzá inverz elem a * műveletre nézve. Azt mondjuk, hogy a * művelet invertálható, ha minden R-beli elemhez létezik inverz erre a műveletre nézve.
A szakirodalomban sok helyen találkozhatunk még az ellentett elem vagy a reciprok kifejezésekkel, valamint a -b illetve az \frac{1}{b} jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 13. és 14. részt, mivel gyakran hivatkozni fogunk rájuk. Ezenkívül érdemes átismételni a Diffie-Hellman kulcscsere protokollról szóló 9. részt is, ugyanis az ott felületesen már érintett moduláris aritmetika matematikai hátterét fogjuk ebben a részben tárgyalni. A teljes cikksorozat elejét itt találod.
A Diffie-Hellman kulcscsere protokoll kapcsán a 9. részben már szóba kerültek az úgynevezett egyirányú függvények. Ezek olyan függvények, amelyek esetén a bemenetből algoritmikusan könnyű kiszámítani a kimenetet. Ezzel szemben ha csak a kimenet ismert, abból borzasztóan nehéz kitalálni, hogy mi lehetett a bemenet. Kriptográfiai szempontból az ilyen tulajdonságú függvények azért hasznosak Alice és Bob számára, mert ezek segítségével könnyen közölhetnek egymással olyan információt a nembiztonságos csatornán keresztül, ami a gonosz Eve számára rejtve marad. Eve csak valamilyen egyéb titkos információ birtokában tudná ezeket a függvényeket hatékonyan megfordítani. A számelméleti összefüggések azonban lehetővé teszik, hogy Alice-nak és Bob-nak ezt a – támadó számára létfontosságú – titkot egyáltalán ne kelljen közölniük.
A Diffie-Hellman kulcscsere protokoll során például Alice és Bob egy közös titkos kulcsban való megegyezéshez használt ilyen függvényeket. Ezenkívül az úgynevezett RSA-eljárás is hasonló függvényeket használ. Ez utóbbiról egy későbbi cikkben lesz szó részletesen, miután az ehhez szükséges számelméleti fogalmakkal megismerkedtünk. Mindkét eljárás az úgynevezett moduláris hatványozáson alapul. A hagyományos hatványozás a már jól ismert szorzásra vezethető vissza. Így például az a^n kifejezést egy olyan szorzatként kell értelmezni, amelynek n darab tényezője van, és minden tényezője a. Azaz:
a^n=\underbrace{a\cdot a\cdot a\cdot \ldots \cdot a}_{\text{n darab}}A moduláris hatványozást ugyanígy egy n tényezős szorzatként értelmezzük. A különbség pusztán annyi, hogy a szorzást ilyenkor nem a hagyományos módon, a mindkét irányban végtelen számegyenesen kell elvégezni, hanem egy véges sok számot tartalmazó „óralapon”. A 9. részben erről részletesen szó volt, ám az ott szereplő példát vizsgáljuk meg mégegyszer, de mostmár az előző részben az euklidészi algoritmus kapcsán tanult maradékos osztás ismeretében.
Az említett példában a 4\cdot 5 szorzatot kellett kiszámítani a 11 elemet tartalmazó óralapon számolva. Ezt a szorzást akkor úgy végeztük el, hogy először végrehajtottuk a hagyományos szorzást, amiből megkaptuk, hogy összesen 4\cdot 5=20 lépést kell megtenni az óralapon. Ezután a 0-ból kiindulva az óramutató járásával megegyező irányban megtettük a 20 lépést. A végeredmény az a szám lett, ahová megérkeztük, azaz 9. Ez látható az alábbi ábrán:
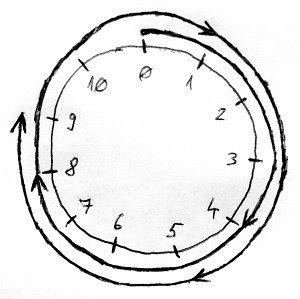
Vegyük észre, hogy itt tulajdonképpen egy maradékos osztásról van szó. Ha ugyanis a 11 elemű óralapon lépkedünk, akkor a lépegetés során a 11 egész számú többszöröseinél újra és újra visszajutunk a kiindulópontra. Így azt kell csak meghatározni, hogy az összlépésszám (jelen esetben 20) mennyi maradékot ad 11-gyel osztva. A végeredmény a keresett maradék lesz. Jelen esetben a 20 és a 11 közötti maradékos osztást elvégezve ez adódik:
20=\underbrace{1}_{\text{hányados}}\cdot 11 + \underbrace{9}_{\text{maradék}}A kapott hányados azt adja meg, hogy a lépegetés során összesen hányszor fogunk visszajutni a kezdőpontba. A maradékból pedig megkapjuk, hogy ezen felül még hány lépést kell pluszban megtennünk. A végeredmény szempontjából az óraaritmetikában csak a maradék fontos, a kapott hányadost elfelejtjük.
Számolás maradékokkal
A moduláris hatványozás alapja tehát az iménti példában látott moduláris szorzás. Problémát jelenthet azonban, ha a kitevő túl nagy. Például a 2^{328} hatvány óraaritmetikában való kiszámításához nem lenne szerencsés, ha előbb ki kellene számítanunk a 2\cdot 2\cdot 2\cdot \ldots \cdot 2 szorzatot, amelynek 328 tényezője van. Ilyenkor ugyanis még a maradékképzés előtt egy olyan nagy számot kapnánk részeredményként, amelynek hatására a számítógépünk tárolóregisztereiben úgynevezett „túlcsordulás” következne be.
A 2. részben a digitális áramkörökben történő számábrázolás kapcsán már volt szó arról, hogy a számítógépek általában maximum 64 bináris számjegyen tárolják a számokat. Mármost a 2^{328} részeredmény egészen pontosan 329 bináris számjegyen férne el. A számítógép ezt a problémát úgy „oldja meg”, hogy jobb esetben elszáll programhibával. Rosszabb esetben pedig az első 265 darab bináris számjegyet levágja a részeredmény elejéről, és az így kapott hibás részeredménnyel számol tovább. El lehet képzelni, hogy ennek milyen beláthatatlan következményei lennének.
Ahhoz, hogy ezt a problémát megoldjuk, előszöris igazolni fogjuk az egész számok közötti maradékos osztás egy fontos tulajdonságát. Az euklidészi norma 17.16. Definíciójában a maradékos osztás során képződő maradékokra csak annyit kötöttünk ki, hogy a normájuk legyen kisebb, mint az osztó normája. Ez általában nem vonja maga után azt, hogy a maradék egyértelmű lesz. Például az 5 és 3 egész számok között kétféleképpen is elvégezhetjük a maradékos osztást:
\begin{aligned}5&=1\cdot 3 + 2 \\ 5&=2\cdot 3 -1\end{aligned}Első esetben 2-t, második esetben pedig -1-et kaptunk maradékul. Mindkettő helyes, hiszen a \Z gyűrűben az abszolútérték-függvény az euklidészi norma. Márpedig mindkét maradéknak kisebb az abszolútértéke, mint az osztónak, ami ugye jelen esetben 3. Azt fogjuk megmutatni, hogy amennyiben a maradékra még azt is kikötjük, hogy nemnegatív, úgy a maradékos osztás továbbra is elvégezhető. Ebben az esetben azonban már csak egyféleképpen.
Ehhez először szükségünk lesz egy egyszerű segédtételre, amely a továbbiakban is hasznunkra lesz.
18.1. Lemma:
Tegyük fel, hogy a, b és c\neq 0 tetszőleges egész számok, melyekre teljesülnek az alábbi egyenlőtlenségek:
\begin{aligned}0&\leq a\lt |c| \\ 0&\leq b\lt |c|\end{aligned}Tegyük fel továbbá, hogy teljesül a c|a-b oszthatóság is. Ekkor a és b megegyezik.
♣Bizonyítás:
Mivel a-b és b-a egymás ellentettjei, ezért a c|a-b oszthatóság miatt a 16.2. Tétel 8. pontja alapján az alábbi oszthatóságok mind teljesülnek:
\begin{aligned}c&|a-b \\ c&|b-a \\ (-c)&|a-b \\ (-c)&|b-a\end{aligned}A fenti négy oszthatóság között biztosan van olyan, amelynek mindkét oldalán nemnegatív számok szerepelnek. Ezért az általánosság megsértése nélkül feltehetjük, hogy a c|a-b oszthatóság ilyen. Ha mégsem ez lenne a helyzet, akkor választunk egy olyat, amire ez teljesül, és az alábbi gondolatmenetet arra alkalmazzuk.
Tehát feltehetjük, hogy 0\leq a-b. Itt két eset lehetséges: vagy 0=a-b, vagy pedig a 0\lt a-b szigorú egyenlőtlenség teljesül. Ha az utóbbi, akkor a c|a-b oszthatóságra alkalmazható a 17.2. Lemma, miszerint bármely pozitív egész szám legalább akkora, mint az osztói. Azaz c\leq a-b. De ez ellentmondás, hiszen a és b szigorúan kisebbek c abszolútértékénél. De mivel c-ről feltettük, hogy nemnegatív, ezért az abszolútérték-függvény 17.18. Definíciója miatt a és b szigorúan kisebbek magánál c-nél is. Így – lévén hogy mindketten nemnegatívak – a különbségük méginkább szigorúan kisebb c-nél.
A fentiekből az következik, hogy a c|a-b oszthatóság csak a 0=a-b esetben teljesülhet. Ebből viszont a=b következik, ahogyan a tétel állítja.
∎Mostmár igazolhatjuk, hogy az egész számok közötti nemnegatív maradékos osztás egyértelmű.
18.2. Tétel:
Tetszőleges a és b\neq 0 egész számhoz pontosan egy olyan k hányados és r maradék létezik, melyekre teljesülnek az alábbiak:
\begin{aligned}a&=k\cdot b + r\\0&\leq r\lt |b|\end{aligned} ♣Bizonyítás:
Előszöris azt igazoljuk, hogy a maradékos osztás ezekkel a szigorúbb feltételekkel is elvégezhető, azaz mindenképpen létezik nemnegatív maradék is. Ezután fogjuk igazolni ennek egyértelműségét.
A 17.19. Tételből tudjuk, hogy az abszolútérték függvény egy euklidészi norma a \Z gyűrűn. Ez a 17.16. Definíció alapján azt jelenti, hogy tetszőleges a és b\neq 0 egész számhoz létezik olyan k_0 hányados és r_0 maradék, amelyekre teljesülnek az alábbiak:
\begin{aligned}a&=k_0\cdot b + r_0 \\ |r_0|&\lt |b|\end{aligned}Feladatunk megmutatni, hogy ezekből előállítható olyan k hányados és r maradék is, amelyek a tételben szereplő szigorúbb feltételeknek is eleget tesznek.
Amennyiben r_0\geq 0, akkor az abszolútérték-függvény 17.18. Definíciója miatt |r_0|=r_0. Ekkor az r=r_0 és a k=k_0 választás épp megfelel a feltételeknek.
Így elegendő csak azzal az esettel foglalkozni, amikor r_0\lt 0. Ekkor az abszolútérték-függvény definíciója miatt |r_0|=-r_0. Mivel r_0\lt 0, ezért a 15.9. Lemma 1. pontja miatt -r_0\gt 0. Ekkor az euklidészi normára vonatkozó |r_0|\lt|b| feltétel az alábbi két eset valamelyikével ekvivalens attól függően, hogy b pozitív vagy negatív:
- Ha b pozitív, akkor 0\lt \overbrace{-r_0}^{=|r_0|}\lt \overbrace{b}^{=|b|}.
- Ha b negatív, akkor 0\lt \underbrace{-r_0}_{=|r_0|}\lt \underbrace{-b}_{=|b|}.
A jobboldali egyenlőtlenségekhez r_0-t, a baloldali egyenlőtlenségekhez pedig az 1. esetben (r_0+b)-t, a 2. esetben pedig (r_0-b)-t adva az alábbiakat kapjuk:
- Ha b pozitív, akkor 0\lt r_0+b\lt \overbrace{b}^{=|b|}.
- Ha b negatív, akkor 0\lt r_0-b\lt \underbrace{-b}_{=|b|}.
Azaz ha meg tudnánk oldani, hogy az eredeti a=k_0b+r_0 egyenletből kiindulva olyan maradékos osztást végezzünk, amelynek eredményeképp az 1. esetben (r_0+b), a 2. esetben pedig (r_0-b) legyen a maradék, akkor ezek eleget tennének a tételben szereplő feltételeknek. Ezt viszont a 14.12. Definícióban szereplő 5. gyűrűaxióma szerinti disztributivitási szabályok kihasználásával és egy piszkos kis trükkel minden gond nélkül meg tudjuk tenni:
\begin{aligned}a&=k_0b+r_0=k_0b+r_0+b-b=(\overbrace{k_0-1}^{k})b + \overbrace{r_0+b}^{r}\\a&=k_0b+r_0=k_0b+r_0+b-b=(\underbrace{k_0+1}_{k})b + \underbrace{r_0-b}_{r}\end{aligned}Így tehát pozitív b esetén a k=k_0-1 és r=r_0+b választással, míg negatív b esetén a k=k_0+1 és r=r_0-b választással az r maradék garantáltan pozitív lesz. Ezzel minden esetet lefedtünk, az egész számok körében tehát valóban mindig elvégezhető a maradékos osztás úgy, hogy a kapott maradék nemnegatív.
Azt kell még megmutatni, hogy ilyen feltételekkel viszont már csak egyféleképpen végezhető el. Tegyük fel, hogy kétféleképpen is elvégezhető a nemnegatív maradékos osztás. Ez azt jelenti, hogy léteznek olyan k_1 és k_2 hányadosok, valamint nemnegatív r_1 és r_2 maradékok, amelyekre teljesülnek az alábbiak:
\begin{aligned}&a=k_1\cdot b + r_1 \\ &a=k_2\cdot b + r_2\\ &0\leq r_1 \lt |b| \\ &0\leq r_2\lt |b|\end{aligned}A két fenti egyenletet egymásból kivonva a következőt kapjuk:
0=(k_1-k_2)\cdot b + r_1 - r_2Mindkét oldalból (k_1-k_2)\cdot b-t kivonva az alábbi lesz a szituáció:
r_1-r_2=(k_2-k_1)\cdot bEz viszont az oszthatóság 16.1. Definíciója alapján épp azt jelenti, hogy teljesül a b|r_1-r_2 oszthatóság. Mivel r_1 és r_2 is a b-vel való maradékos osztás során kapott nemnegatív maradékok, így ők biztosan szigorúan kisebbek b abszolútértékénél. Ebből viszont a 18.1. Lemma alapján r_1=r_2 következik, azaz a maradékok valóban megegyeznek.
Ekkor azonban a korábban kapott r_1-r_2=(k_2-k_1)\cdot b egyenlet az alábbi alakra egyszerűsödik:
\underbrace{0}_{=r_1-r_2}=(k_2-k_1)\cdot bMivel a tétel szövegében kikötöttük, hogy b\neq 0, ezért a nullosztómentesség miatt ez csak akkor teljesülhet, ha k_2-k_1=0, amiből k_1=k_2 következik. Így tehát a hányadosok is megegyeznek.
Azaz valóban: tetszőleges a és b\neq 0 egész számok között pontosan egyféleképpen lehet elvégezni a maradékos osztást úgy, hogy a kapott maradék nemnegatív.
∎Ez azért jó hír a számunkra, mivel így minden a egész számhoz hozzá tudunk rendelni egy nemnegatív maradékot, amelyet a-nak egy valamilyen m\neq 0 egész számmal képzett maradékos osztása eredményezne. Ez a hozzárendelés ugye az iménti tétel értelmében egyértelmű lesz, azaz minden egész számhoz pontosan egy maradékot rendel. Így tulajdonképpen egy függvényt kapunk. Ennek a függvénynek az értékkészlete ráadásul véges lesz, hiszen pontosan m darab olyan nemnegatív egész létezik, amely maradékként szóba jöhet, azaz értéke kisebb, mint m abszolútértéke. Például m=3 vagy m=-3 esetén ezek a 0, az 1 és a 2 nemnegatív egész számok.
Ezek az osztási maradékok tehát egy véges halmazt alkotnak. Ennek elemei között két műveletet is tudunk értelmezni az imént említett függvény segítségével. Erről szól az alábbi definíció, valamint az alatta szereplő megjegyzések és példák.
18.3. Definíció (Moduláris összeadás és szorzás):
Legyen m\neq 0 tetszőleges nemnulla egész szám. Jelölje \Z_m azt a halmazt, amelynek elemei az m abszolútértékénél kisebb, nemnegatív (azaz a 0, 1, 2, ..., |m|-1) egész számok. E halmaz elemeit modulo m maradékoknak nevezzük.
Azt a \bmod_m:\Z \to \Z_m függvényt, amely minden egész számhoz az m-mel képzett nemnegatív osztási maradékát rendeli, modulo m maradékképző függvénynek nevezzük.
A \bmod_m függvény, valamint a szokásos összeadás és szorzás segítségével értelmezzünk két darab kétváltozós műveletet a \Z_m halmaz elemei között az alábbiak szerint:
\begin{aligned}a\oplus b &= \bmod_m(a+b) \\ a\odot b &= \bmod_m(a\cdot b)\end{aligned}A \oplus szimbólummal jelölt műveletet modulo m összeadásnak, a \odot szimbólummal jelölt műveletet modulo m szorzásnak, az m egész számot pedig modulusnak nevezzük. Amennyiben az adott kontextusban nem fontos a modulus, úgy a fenti műveleteket egyszerűen csak moduláris összeadásnak és moduláris szorzásnak hívjuk.
♣Megjegyzés:
A definícióból azonnal adódnak az alábbi észrevételek:
- A \bmod_m maradékképzés valóban egy függvény, mivel a hozzárendelés a 18.2. Tétel alapján egyértelmű. Ez alatt azt értjük, hogy minden egész számhoz pontosan egy modulo m maradék rendelhető, se több, se kevesebb. Megjegyezzük ugyanakkor, hogy a hozzárendelés nyilván nem kölcsönösen egyértelmű, hiszen egy adott \Z_m-beli elem végtelen sok egész szám modulo m maradéka lehet. Például végtelen sok olyan egész szám van, ami 2-vel osztva 1 maradékot ad: nevezetesen minden páratlan szám.
- Ennek következménye, hogy a definícióban szereplő \oplus és \odot szimbólummal jelölt műveletek valóban műveletek a szó algebrai értelmében is (lásd az erről szóló 11.3. Definíciót). Ugyanis a definíció szerint a hagyományos összeadás/szorzás elvégzése után alkalmazni kell a \bmod_m maradékképző függvény, amely a \Z_m halmazba képez. A két művelet tehát \Z_m-beli elemekből alkotott párokhoz valóban \Z_m-beli elemeket rendel hozzá, azaz nem vezet ki a \Z_m halmazból.
- Bármilyen a egész szám modulo m maradéka megegyezik a modulo -m maradékával. Azaz a \bmod_m és a \bmod_{-m} függvények minden m\neq 0 esetén ugyanazt a hozzárendelést valósítják meg. Ugyanis a 15.1. Tétel 4. pontja alapján a=km+r=(-k)(-m)+r, és ha 0\leq r\lt |m| teljesül, akkor az abszolútérték-függvény 17.18. Definíciója értelmében 0\leq r\lt |-m| is nyilván teljesül.
- A \bmod_m függvény az |m|=1 szélsőséges esetben is értelmes, csak épp nem túl változatos. Ilyenkor ugyanis a \Z_m halmaz a nullgyűrű (14.12. Definíció) lesz, azaz mindössze egyetlen elemet fog tartalmazni, méghozzá a 0 egész számot. A \bmod_m maradékképző függvény pedig minden egész számhoz a 0-t fogja hozzárendelni. Nyilván, hiszen az m=1 vagy m=-1 modulusok minden számnak osztói – mivel egységek –, és így a maradék minden esetben 0.
- A \bmod_m(a)=a egyenlőség akkor és csak akkor teljesül, ha az a egész szám maga is modulo m maradék, azaz teljesül a 0\leq a\lt |m| egyenlőtlenség. Nyilván, hiszen ebben az esetben a maradékos osztás az a=0\cdot m+a alakra egyszerűsödik, így a nemnegatív maradéka m-mel osztva önmaga. Megfordítva: ha a maradéka önmaga – azaz \bmod_m(a)=a –, akkor nyilván teljesül a 0\leq a\lt |m| egyenlőtlenség, hiszen ez a modulo m maradékok definíciója.
- Végül megjegyezzük, hogy a \Z_m-en értelmezett két moduláris műveletre nincs standard jelölés, a definícióban önkényesen használtuk a \oplus és \odot szimbólumokat. Ettől kontextustól függően eltérhetünk, ám ezt minden esetben jelezni fogjuk.
Nézzünk is egy egyszerű példát a fenti definícióban foglaltakra. Legyen például m=3. Ekkor ugye a \Z_3 halmazról van szó, amelynek mindössze a 0, az 1 és a 2 lesznek az elemei. Az alábbiakban a \bmod_3 függvény néhány hozzárendelését tüntettük fel:
\begin{aligned}\bmod_3(0)&=0\\\bmod_3(1)&=1\\\bmod_3(2)&=2\\\bmod_3(3)&=0\\\bmod_3(4)&=1\\\bmod_3(5)&=2\\&\vdots\end{aligned}Az alábbi két táblázatban pedig a \Z_3 halmazon értelmezett \oplus és \odot műveletek úgynevezett műveleti táblái láthatók:
\begin{array}{cc}\begin{array}{c|ccc}\oplus &0&1&2\\ \hline 0&0&1&2 \\1&1&2&0\\2&2&0&1\end{array} & \begin{array}{c|ccc}\odot &0&1&2\\ \hline 0&0&0&0 \\1&0&1&2\\2&0&2&1\end{array}\end{array}Például a 2\oplus 1 művelet eredményét a 2-es sor 1-es oszlopából tudjuk kiolvasni a baloldali táblázatból, ami ugye 0. A műveletet a fenti definíció szerint elvégezve valóban 0-t kapunk, hiszen \bmod_3(2+1)=\bmod_3(3)=0. Az 1\oplus 2 eredménye ehhez hasonlóan az 1-es sor 2-es oszlopában szerepel, ami – hatalmas meglepetésre – szintén 0. A moduláris szorzás táblázata ugyanígy értelmezendő. Például 2\odot 2=1. Nyilván, hiszen ha 2\cdot 2-t elosztjuk 3-mal, akkor épp 1 lesz a maradék.
Hamarosan visszatérhetünk a szakasz elején felvetett moduláris hatványozással kapcsolatos problémára. Előbb azonban megmutatjuk, hogy a moduláris összeadás és szorzás pontosan ugyanazokkal a „jól megszokott” tulajdonságokkal rendelkezik, mint a szokásos összeadás és szorzás.
18.4. Tétel:
Tetszőleges m\neq 0 egész szám esetén legyen \Z_m a 18.3. Definíció szerinti modulo m maradékok halmaza, és jelölje \oplus és \odot az ezen a halmazon definiált moduláris összeadás és szorzás műveletét. Ekkor \Z_m egy kommutatív gyűrűt alkot ezzel a két művelettel, amely |m|\neq 1 esetén egységelemes.
♣Bizonyítás:
A 14.12. Definícióban szereplő gyűrűaxiómák teljesülését kell igazolnunk. Nézzük őket sorban:
A műveletek kommutativitása: Ez egyszerűen adódik a 18.3. Definícióból, valamint a hagyományos összeadás és szorzás kommutativitásából:
\begin{aligned}a\oplus b&=\bmod_m(a+b)=\bmod_m(b+a)=b\oplus a \\ a\odot b&=\bmod_m(a\cdot b)=\bmod_m(b\cdot a)=b\odot a\end{aligned}Neutrális elem létezése: Az |m|=1 esetben a 18.3. Definíció utáni megjegyzés 4. pontja alapján \Z_m épp a nullgyűrű. Ebben az egyetlen elem a 0, amely nyilván mindkét műveletre nézve neutrális. Feltehetjük tehát, hogy |m|\neq 1. Mivel \Z_m elemei épp a modulo m maradékok, ezért rájuk alkalmazható a 18.3. Definíció utáni megjegyzés 5. pontja. Ez alapján könnyen adódik, hogy mindkét művelethez létezik neutrális elem, méghozzá a 0 és az 1:
\begin{aligned}a\oplus 0&=\bmod_m(a+0)=\bmod_m(a)=a \\ a\odot 1&=\bmod_m(a\cdot 1)=\bmod_m(a)=a\end{aligned}Ellentett elem létezése: Ehhez azt kell megmutatni, hogy tetszőleges a maradékhoz létezik olyan b maradék, amelyre a\oplus b=0 teljesül. Ha a=0, akkor a b=0 választás nyilván megfelelő, hiszen az előző pont alapján 0\oplus 0=0. Az a\neq 0 esetekben a b=|m|-a választás lesz a megfelelő, hiszen ekkor egyrészt nyilván teljesül a 0\leq b\lt |m| egyenlőtlenség (azaz b is egy modulo m maradék), másrészt pedig az a\oplus b moduláris összeadást kifejtve az alábbit kapjuk:
a\oplus b=\bmod_m(a+b)=\bmod_m(a+\underbrace{|m|-a}_{=b})=\bmod_m(|m|)Ha m pozitív, akkor \bmod_m(|m|)=\bmod_m(m), ha pedig negatív, akkor \bmod_m(|m|)=\bmod_m(-m). A 16.2. Tétel 8. pontja alapján viszont az ellentettképzés nem befolyásolja az oszthatóságot, így mindkét esetben 0 lesz a maradék, azaz b valóban a ellentettje.
A moduláris összeadás asszociativitása: Azt kell megmutatni, hogy (a\oplus b)\oplus c=a\oplus (b\oplus c). Fejtsük ki mindkét oldalt a 18.3. Definíció alapján. A végrehajtás során képződő részeredményeket jelöljük r_1-gyel és q_1-gyel, a végeredményeket pedig r_2-vel és q_2-vel:
\begin{aligned}(a\oplus b)\oplus c&=\overbrace{\bmod_m(a+b)}^{=r_1}\oplus c=\bmod_m(r_1+c)=r_2 \\ a\oplus (b\oplus c)&=a\oplus \underbrace{\bmod_m(b+c)}_{=q_1}=\bmod_m(a+q_1)=q_2\end{aligned}Azt kell megmutatnunk, hogy r_2=q_2, azaz mindegy, hogy milyen sorrendben végezzük el a két moduláris összeadást, a végeredmény ugyanaz lesz. A \bmod_m függvény szerinti maradékos osztásokat elvégezve négy egyenletet írhatunk fel az r_1 és q_1 valamint az r_2 és q_2 maradékokra valamilyen k_1 és n_1 valamint k_2 és n_2 hányadosokkal:
\begin{aligned}a+b&=k_1m+r_1 \\ b+c&=n_1m+q_1 \\ r_1+c&=k_2m+r_2 \\ a+q_1&=n_2m+q_2\end{aligned}Az első két egyenletet átrendezve megkapjuk r_1-et és q_1-et:
\begin{aligned}r_1&=a+b-k_1m \\ q_1&=b+c-n_1m\end{aligned}Ezeket behelyettesítve a másik két egyenletbe az alábbiakat kapjuk:
\begin{aligned}\overbrace{a+b-k_1m}^{=r_1}+c&=k_2m+r_2 \\ a+\underbrace{b+c-n_1m}_{=q_1}&=n_2m+q_2\end{aligned}Ezeket megint átrendezve kifejezhetjük az r_2 és a q_2 maradékokat:
\begin{aligned}r_2&=a+b-k_1m+c-k_2m \\ q_2&=a+b+c-n_1m-n_2m\end{aligned}Azt kell megmutatnunk, hogy ezek valójában megegyeznek. Írjuk hát fel a kettejük különbségét:
\begin{aligned}r_2-q_2&=\overbrace{\bcancel{a}+\bcancel{b}-k_1m+\bcancel{c}-k_2m}^{r_2}\overbrace{-\bcancel{a}-\bcancel{b}-\bcancel{c}+n_1m+n_2m}^{-q_2}=\\&=(n_1+n_2-k_1-k_2)\cdot m\end{aligned}Azt kaptuk tehát, hogy teljesül az m|r_2-q_2 oszthatóság. Mivel r_2 és q_2 nemnegatív maradékok, így alkalmazható rájuk a 18.1. Lemma, amiből r_2=q_2 következik. Az \oplus művelet tehát valóban asszociatív.
A moduláris szorzás asszociativitása: Azt kell megmutatni, hogy (a\odot b)\odot c=a\odot (b\odot c). Ismét fejtsük ki mindkét oldalt a részeredményeket r_1-gyel és q_1-gyel, a végeredményeket pedig r_2-vel és q_2-vel jelölve:
\begin{aligned}(a\odot b)\odot c&=\overbrace{\bmod_m(ab)}^{=r_1}\odot c=\bmod_m(r_1c)=r_2 \\ a\odot (b\odot c)&=a\odot \underbrace{\bmod_m(bc)}_{=q_1}=\bmod_m(aq_1)=q_2\end{aligned}A \bmod_m függvény szerinti maradékos osztásokat elvégezve négy egyenletet írhatunk fel az r_1 és q_1 valamint az r_2 és q_2 maradékokra valamilyen k_1 és n_1 valamint k_2 és n_2 hányadosokkal:
\begin{aligned}ab&=k_1m+r_1 \\ bc&=n_1m+q_1 \\ r_1c&=k_2m+r_2 \\ aq_1&=n_2m+q_2\end{aligned}A \oplus művelet asszociativitásánál látott módon ismét kifejezhetjük az r_2-q_2 különbséget – a részleteket az Olvasóra bízzuk –, amelyből megint azt fogjuk kapni, hogy teljesül az m|r_2-q_2 oszthatóság. Ebből viszont ugyancsak a 18.1. Lemma miatt r_2=q_2 következik, azaz a \odot művelet is asszociatív.
A disztributivitási szabályok teljesülése: Mivel a \odot művelet kommutativitását már igazoltuk, ezért elegendő az egyik oldali disztributivitást megmutatni, azaz hogy a\odot (b\oplus c)=(a\odot b)\oplus (a\odot c) teljesül. A recept a megszokott: ismét a definíció szerint kifejtjük mindkét oldalt, majd megmutatjuk, hogy a különbségük osztható az m modulussal, azaz végsősoron megegyeznek. A két oldal definíció szerinti kifejtése:
\begin{aligned}a\odot (b\oplus c)&=a\odot \overbrace{\bmod_m(b+c)}^{=r_1}=\bmod_m(ar_1)=r_2 \\ (a\odot b)\oplus (a\odot c)&=\underbrace{\bmod_m(ab)}_{=q_1} \oplus \underbrace{\bmod_m(ac)}_{=q_2}=\bmod_m(q_1+q_2)=q_3\end{aligned}Ez tehát az alábbi 5 maradékos osztást jelenti:
\begin{aligned}b+c&=k_1m+r_1 \\ ar_1&=k_2m+r_2 \\ ab&=n_1m+q_1 \\ ac&=n_2m+q_2 \\ q_1+q_2&=n_3m+q_3\end{aligned}Ebből az r_2-q_3 különbséget kell kifejezni – amelyet ugyancsak az Olvasóra bízunk –, amelyből az előzőekhez hasonlóan megkapjuk, hogy teljesül az m|r_2-q_3 oszthatóság. Ebből megint a 18.1. Lemma alkalmazásával r_2=q_3 adódik, azaz a \odot művelet disztributív a \oplus műveletre nézve.
Minthogy minden gyűrűaxióma teljesül, továbbá a moduláris szorzás is kommutatív, ezért \Z_m valóban egy kommutatív gyűrű. Láttuk továbbá, hogy a szorzásra nézve is létezik neutrális elem. Ezért \Z_m egységelemes, hacsak nem a nullgyűrűről – az |m|=1 esetről – van szó, amit a 14.12. Definíció szerint nem tekintünk annak.
∎Egyenletek megoldása a \Z_m gyűrűben
Eszerint tehát amikor osztási maradékokkal számolunk, akkor nyugodtan hagyatkozhatunk minden olyan eddigi tételre, amelyeket eddig kommutatív, egységelemes gyűrűkre bizonyítottunk az előző részekben. Nagyjából minden ugyanúgy fog működni, ahogyan azt az egész számok körében már megszoktuk.
De csak nagyjából! Az egyenletek megoldásánál a \Z_m gyűrűben körültekintően kell eljárnunk. A természetes számok körében a 14. részben felhoztunk egy egyszerű példát. Akkor a 2x+3=7 egyenletet kellett megoldanunk a természetes számok halmazán. A problémát az okozta, hogy „kivonás” és „osztás” ebben a számkörben – mint algebrai értelemben vett „művelet” – nem állt rendelkezésünkre. Ezért az alábbi két segédtételt voltunk kénytelenek felhasználni „kivonás” és „osztás” helyett:
Első lépésként az egyenlet jobboldalát 7 helyett egy kéttagú összegként írtuk fel:
2x+3=4+3Ebből a 12.16. Lemma alapján 2x=4 következett. Ezután második lépésként ennek jobboldalát 4 helyett egy kéttényezős szorzatként írtuk fel:
2x=2\cdot 2Ebből viszont a 14.2. Lemma alapján az x=2 megoldás következett. Azaz a természetes számok körében egy egyenlet megoldásakor mindkét oldalból büntetlenül szabad volt „kivonni” ugyanazt a tetszőleges számot, valamint mindkét oldalt szabad volt „elosztani” ugyanazzal a tetszőleges nemnulla számmal. Méghozzá annak ellenére, hogy ez a két „művelet” ezen a számhalmazon nem állt rendelkezésünkre. Megemlítettük ugyanakkor, hogy más algebrai struktúrákban nagyon könnyen kaphatunk hibás eredményt, ha az ehhez hasonló lépéseket nem kellő körültekintéssel végezzük el.
A fenti két segédtételt azután a 15. rész elején általánosítottuk tetszőleges gyűrűkre is. Itt a kivonással már nincs gond, hiszen az tetszőleges gyűrűben korlátlanul elvégezhető. Osztani azonban általában továbbra sem tudunk, mivel multiplikatív inverz létezése csak testekben garantált. Az alábbi tétel azonban mégis a segítségünkre siet:
Eszerint nullosztómentes gyűrűkben, és – ami talán még fontosabb – csak azokban továbbra is lehet tetszőleges nemnulla gyűrűelemmel „elosztani” egy egyenlet mindkét oldalát. Kérdés, hogy vajon a \Z_m gyűrű minden m\neq 0 esetén nullosztómentes-e?
Térjünk most vissza a fenti egyenletünkhöz, és ismét próbáljuk meg megoldani azt, ám ezúttal a \Z_8 gyűrűben keressük a megoldást. Az itt érvényes műveleti jelekkel ez az egyenlet az alábbi formát ölti – a könnyebb áttekinthetőség kedvéért a műveleti sorrendet zárójelekkel is kihangsúlyoztuk:
(2\odot x) \oplus 3=7A „kivonás” – mint említettük – gond nélkül elvégezhető. Emlékeztetjük az Olvasót, hogy egy gyűrűben „kivonás” alatt az ellentettel (additív inverzzel) való összeadást értjük. Így tehát most adjuk hozzá az egyenlet mindkét oldalához a 3 gyűrűelem additív inverzét. A \Z_8 gyűrűben ez az 5 egész szám lesz, hiszen a moduláris összeadás 18.3. Definíciója alapján 3\oplus 5=\bmod_8(3+5)=\bmod_8(8)=0. A baloldalon tehát 2\odot x marad, míg a jobboldalon 7\oplus 5=\bmod_8(7+5)=\bmod_8(12)=4-et kapunk. Azaz:
2\odot x=4Gondolhatnánk, hogy innen már egyszerű a dolgunk, hiszen – hasonlóan a természetes számok körében alkalmazott megoldáshoz – felírhatjuk a jobboldalon szereplő 4-et egy kéttényezős szorzatként 2\odot 2 alakban:
2\odot x=2\odot 2Ha azonban most meggondolatlanul alkalmazzuk szépen a 15.4. Tételt, és erre hivatkozva mindkét oldalt „egyszerűsítjük” 2-vel, akkor könnyen azt a következtetést vonhatjuk le, hogy a fenti egyenletből x=2 következik. EZ AZONBAN HIBÁS!
Az x=2 valóban megoldása a (2\odot x)\oplus 3=7 egyenletnek, azonban van még egy további megoldás is. Nevezetesen az x=6, amely fölött ezzel a lépéssel szépen átsiklunk. Ellenőrizzük csak le, hogy a \Z_8 gyűrűben a (2\odot 6)\oplus 3 valóban 7-tel egyezik meg.
Mi okozhatja hát a problémát? Ha tüzetesen megvizsgáljuk az egyenletek egyszerűsíthetőségéről szóló 15.4. Tételt, akkor feltűnhet, hogy az kizárólag nullosztómentes gyűrűkre érvényes. Márpedig ha \Z_8-ban ez a lépés nem működik, az csak úgy lehetséges, hogy ez a gyűrű bizony nem nullosztómentes. Ez azonnal látható is, ha megvizsgáljuk a \Z_8 gyűrű „szórzótábláját”:
\begin{array}{c|cccccccc}\odot &0&1&2&3&4&5&6&7 \\ \hline 0&0&0&0&0&0&0&0&0 \\ 1&0&1&2&3&4&5&6&7 \\ 2&0&2&4&6&0&2&4&6 \\ 3&0&3&6&1&4&7&2&5 \\ 4&0&4&0&4&0&4&0&4 \\ 5&0&5&2&7&4&1&6&3 \\ 6&0&6&4&2&0&6&4&2 \\ 7&0&7&6&5&4&3&2&1 \end{array}Ha megfigyeljük, ebben a táblázatban az első soron és oszlopon kívül is bőven szerepel a nullelem. Ez azt jelenti, hogy egy szorzat olyan esetekben is lehet 0, amikor történetesen egyik tényezője sem az. Ilyen például a 2\odot 4 szorzat, hogy csak egyet említsünk.
Jó lenne tehát valami általános szabály arra vonatkozóan, hogy mely esetekben nullosztómentes a \Z_m gyűrű, és mely esetekben nem. Erről szól az alábbi tétel.
18.5. Tétel:
Tetszőleges m\neq 0 egész szám esetén legyen \Z_m a modulo m maradékok gyűrűje a moduláris összeadás és szorzás műveletével. A \Z_m gyűrű akkor és csak akkor nullosztómentes, ha m prímszám.
♣Bizonyítás:
Tegyük fel, hogy m prímszám, és a \Z_m gyűrű valamely a és b elemeinek moduláris szorzata 0, azaz a\odot b=0. Azt kell megmutatni, hogy ekkor a és b közül legalább az egyik szükségképpen 0. Az a\odot b=0 a 18.3. Definíció alapján azt jelenti, hogy \bmod_m(ab)=0, vagyis az ab szorzat m-mel osztva 0 maradékot ad. Teljesül tehát az m|ab oszthatóság. De mivel m prím, ezért a 16.13. Definíció alapján ekkor az m|a vagy m|b oszthatóságok közül legalább az egyik szintén teljesül. Első esetben \bmod_m(a)=0, második esetben pedig \bmod_m(b)=0. Azonban a és b is modulo m maradékok, ezért a 18.3. Definíció utáni megjegyés 5. pontja alapján az első esetben a, a második esetben pedig b szintén 0. Ha tehát m prímszám, akkor \Z_m valóban nullosztómentes.
Azt kell még belátni, hogy minden más esetben viszont találhatunk nullosztót. Tegyük ezért most fel, hogy m nem prímszám és egyelőre tegyük fel azt is, hogy pozitív. Mivel az egész számok gyűrűjében teljesül a számelmélet alaptétele (lásd a 17.22. Tételt), ezért a 16.16. Tétel alapján minden felbonthatatlan szám egyben prímszám is. Mivel m nem prímszám, így felbonthatatlan sem lehet (lásd a 16.11. Definíciót). Léteznek tehát olyan a és b pozitív egész számok, amelyekre teljesülnek az alábbiak:
\begin{aligned}&m=ab\\&0\lt a\lt m\\&0\lt b\lt m\end{aligned}A két egyenlőtlenség alapján tehát a és b a \Z_m gyűrű olyan nemnulla elemei, amelyek hagyományos szorzata m-mel osztva 0 maradékot ad, azaz a\odot b=0. Így tehát ők nullosztók a \Z_m gyűrűben. A 18.3. Definíció utáni megjegyzés 3. pontja alapján azonban az ellentettképzés nem befolyásolja a \bmod_m maradékképző függvényt, és így a \Z_m gyűrű műveletei ugyanúgy fognak viselkedni, mint a \Z_{-m} gyűrű műveletei. Ezért ha a és b nullosztók voltak a \Z_m gyűrűben, akkor nullosztók lesznek a \Z_{-m} gyűrűben is. Így tehát a nullosztómentesség valóban csak akkor teljesül, ha a modulus prímszám (függetlenül attól, hogy pozitív vagy negatív).
∎A moduláris hatványozás tulajdonságai
Mostmár visszatérhetünk az eredeti problémánkhoz, és általánosan is megfogalmazhatjuk azt a fentiek alapján. Eszerint tehát a feladat az, hogy adott a és n\gt 0 egész számok esetén számítsuk ki azt a maradékot, amelyet az a^n hatvány ad valamilyen m\neq 0 egész számmal osztva. A konkrét feladatban a 2^{328} hatvány 11-gyel való osztási maradékát kellett kiszámítani. A probléma ugye az, hogy ezt az a^n hatvány tényleges kiszámítása nélkül kellene megtennünk, máskülönben a modulo m maradékképzés előtt kapott részeredmény kezelhetetlenül nagy lenne.
Azt viszont láttuk a előző szakaszban, hogy a \Z_m gyűrűben ilyen szempontból sokkal könnyebb számolni, hiszen itt minden részeredmény egy véges számhalmazból kerül ki. Érdemes volna tehát már az elején „áttérni” a \Z_m gyűrűre, és a hatványozást már az itteni moduláris szorzással végezni. Ehhez azonban az kell, hogy ez az „áttérés” ne befolyásolja a kapott végeredményt. Azaz ha előbb „áttérünk” a \Z_m gyűrűbe és ott végezzük el a moduláris szorzásokat, akkor ugyanazt kell kapnunk, mintha előbb a \Z gyűrűben végeznénk el a hagyományos szorzásokat, majd vennénk az így kapott eredmény \Z_m-beli megfelelőjét.
A 13. részben a természetes számok \Z-be való beágyazásánál már volt szó az úgynevezett struktúratartó leképezésekről, amelyeket homomorfizmusoknak neveztünk (lásd a 13.8. Definíciót). Nekünk most a fentiek alapján épp egy ilyen leképezésre lenne szükségünk a \Z és \Z_m gyűrűk között. Erről szól az alábbi definíció, amely tehát a 13.8. Definícióban definiált homomorfizmusfogalom speciális esete gyűrűkre, mint algebrai struktúrákra. Kivételesen feltüntettük a gyűrűk műveleti szimbólumait is annak érdekében, hogy világos legyen, mikor melyik gyűrűben kell az adott műveletet elvégezni.
18.6. Definíció (Gyűrűhomomorfizmus):
Tegyük fel, hogy adva van egy (R,+,\cdot) és egy (S,\oplus,\odot) gyűrű. Ekkor egy f:R\to S függvényt gyűrűhomomorfizmusnak nevezünk, amennyiben tetszőleges R-beli a és b elemekre teljesülnek az alábbi követelmények:
\begin{aligned}f(a+b)&=f(a)\oplus f(b)\\f(a\cdot b)&=f(a)\odot f(b)\end{aligned}Amennyiben S minden eleme legalább egy R-beli elemhez hozzá van rendelve, akkor f-et szürjektív gyűrűhomomorfizmusnak vagy gyűrűráképzésnek nevezzük.
Amennyiben S minden eleme legfeljebb egy R-beli elemhez van hozzárendelve, akkor f-et injektív gyűrűhomomorfizmusnak vagy gyűrűbeágyazásnak nevezzük.
Amennyiben S minden eleme pontosan egy R-beli elemhez van hozzárendelve, akkor f-et bijektív gyűrűhomomorfizmusnak vagy gyűrűizomorfizmusnak nevezzük.
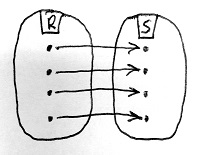
Ilyenkor azt mondjuk, hogy az R és az S gyűrű izomorf egymással. Ezt így jelöljük: R\simeq S.
♣Megjegyzés:
A gyűrűizomorfizmus szimmetrikus: Azaz ha R\simeq S teljesül, akkor S\simeq R is teljesül. Nyilván, hiszen ha az ábrán a nyilak irányát megfordítjuk, akkor az így kapott g megfeleltetés is kölcsönösen egyértelmű. Ez azt jelenti, hogy ha a_S és b_S az S gyűrű két tetszőleges eleme, akkor léteznek olyan a_R és b_R elemek az R-gyűrűben, amelyekre teljesülnek az alábbiak:
\begin{aligned}f(a_R)&=a_S \\ f(b_R)&=b_S \\ g(a_S)&=a_R \\ g(b_S)&=b_R\end{aligned}Ekkor azonban f művelettartó tulajdonságai, valamint a fentiek miatt teljesülnek az alábbi egyenletek:
\begin{aligned}g(a_S\oplus b_S)&=g(f(a_R)\oplus f(b_R))=g(f(a_R+b_R))=a_R+b_R=\\&=g(a_S)+g(b_S) \\ g(a_S\odot b_S)&=g(f(a_R)\odot f(b_R))=g(f(a_R\cdot b_R))=a_R\cdot b_R=\\&=g(a_S)\cdot g(b_S)\end{aligned}A g leképezés tehát szintén gyűrűizomomorfizmus, csak épp S-ből mutat R-be.
A gyűrűizomorfizmus tranzitív: Azaz tetszőleges R, S és T gyűrűk esetén ha R\simeq S és S\simeq T, akkor R\simeq T. Jelöljük ugyanis f_{RS}-sel az R-ből S-be mutató, f_{ST}-vel pedig az S-ből T-be mutató gyűrűizomorfizmust. Ezek után definiáljuk az R-ből közvetlenül T-be mutató g leképezést f_{RS} és f_{ST} egymás után alkalmazásaként. Azaz tetszőleges R-beli r elemre legyen g(r)=f_{ST}(f_{RS}(r)). Az alábbi ábráról azonnal látszik, hogy az R-ből T-be mutató g leképezés is kölcsönösen egyértelmű:
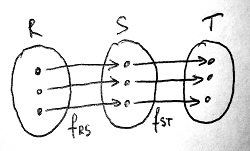
A művelettartó tulajdonságok könnyen adódnak az f_{RS} és f_{ST} gyűrűizomorfizmusok hasonló tulajdonságaiból. A három gyűrű műveleti jeleit az alábbi levezetésben nem különböztettük meg, ám javasoljuk az Olvasónak, hogy gondolja végig, melyik műveletet melyik gyűrűben kell elvégezni:
\begin{aligned}g(a+b)&=f_{ST}(f_{RS}(a+b))=f_{ST}(f_{RS}(a)+f_{RS}(b))=\\&=f_{ST}(f_{RS}(a))+f_{ST}(f_{RS}(b))=\\&=g(a)+g(b) \\ g(a\cdot b)&=f_{ST}(f_{RS}(a\cdot b))=f_{ST}(f_{RS}(a)\cdot f_{RS}(b))=\\&=f_{ST}(f_{RS}(a))\cdot f_{ST}(f_{RS}(b))=\\&=g(a)\cdot g(b)\end{aligned}Végül a gyűrűizomorfizmus reflexív: Azaz tetszőleges R gyűrű izomorf önmagával (R\simeq R), ugyanis az f(a)=a leképezés nyilvánvalóan gyűrűizomorfizmus R-ből önmagába.
♣Az alábbi tételben meg is adunk egy gyűrűhomomorfizmust az egész számok \Z gyűrűjéből a véges sok elemet tartalmazó \Z_m gyűrűbe. Nem lesz túl meglepő a dolog, hiszen ez a leképezés mindvégig itt volt az orrunk előtt.
18.7. Tétel:
Tegyük fel, hogy m\neq 0 egy tetszőleges nemnulla egész szám. Ekkor a 18.3. Definícióban szereplő \bmod_m:\Z \to \Z_m maradékképző függvény egy szürjektív gyűrűhomomorfizmus \Z és \Z_m között.
♣Bizonyítás:
Azt kell megmutatni, hogy a \bmod_m függvény tartja az eredeti \Z gyűrű mindkét műveletét. Nézzük először az összeadást. Itt az alábbi összefüggést kell igazolni:
\bmod_m(a+b)=\bmod_m(a)\oplus \bmod_m(b)Fejtsük ki mindkét oldalt a 18.3. Definíció alapján. A bal- és jobboldalon képződő maradékokat jelöljük r-rel, q_1-gyel, q_2-vel és q_3-mal:
\begin{aligned}&\bmod_m(a+b)=r \\ &\underbrace{\bmod_m(a)}_{=q_1}\oplus \underbrace{\bmod_m(b)}_{=q_2}=\bmod_m(q_1+q_2)=q_3\end{aligned}Azt kell megmutatnunk, hogy r=q_3, azaz mindegy, hogy melyik gyűrűben végezzük el az összeadást, a végeredmény ugyanaz lesz. A \bmod_m függvény szerinti maradékos osztásokat elvégezve négy egyenletet írhatunk fel az r, q_1, q_2 és q_3 maradékokra valamilyen k, n_1, n_2 és n_3 hányadosokkal:
\begin{aligned}a+b&=km+r \\ a&=n_1m+q_1 \\ b&=n_2m+q_2 \\ q_1+q_2&=n_3m+q_3\end{aligned}Az első egyenletből kifejezhetjük r-et, amely a \bmod_m(a+b) maradékképzés eredménye:
r=a+b-kmA második és harmadik egyenletből kifejezhetjük q_1-et és q_2-t, amely a \bmod_m(a)\oplus \bmod_m(b) moduláris összeg két tagját fogja adni:
\begin{aligned}q_1&=a-n_1m \\ q_2&=b-n_2m\end{aligned}A kapott q_1 és q_2 maradékokat a harmadik egyenletbe behelyettesítve ezt kapjuk:
\underbrace{a-n_1m}_{=q_1}+\underbrace{b-n_2m}_{=q_2}=n_3m+q_3Ezt átrendezve megkapjuk q_3-at:
q_3=\underbrace{a-n_1m}_{=q_1}+\underbrace{b-n_2m}_{=q_2}-n_3mAzt kell tehát igazolnunk, hogy r és q_3 valójában megegyeznek. Ehhez írjuk fel kettejük különbségét:
\begin{aligned}r-q_3&=\overbrace{\bcancel{a}+\bcancel{b}-km}^{r}\overbrace{-\bcancel{a}+n_1m-\bcancel{b}+n_2m+n_3m}^{-q_3}=\\&=(n_1+n_2+n_3-k)\cdot m\end{aligned}Azt kaptuk tehát, hogy teljesül az m|r-q_3 oszthatóság. Mivel r és q_3 nemnegatív maradékok, így alkalmazható rájuk a 18.1. Lemma, amiből r=q_3 következik. A \bmod_m függvény tehát valóban tartja az összeadást.
Most a szorzás tartását ellenőrizzük nagyjából ugyanezzel a módszerrel. Azt kell megmutatni, hogy \bmod_m(a\cdot b)=\bmod_m(a)\odot \bmod_m(b). Ismét fejtsük ki mindkét oldalt a kapott maradékokat r-rel, q_1-gyel, q_2-vel és q_3-mal jelölve:
\begin{aligned}&\bmod_m(a\cdot b)=r \\ &\underbrace{\bmod_m(a)}_{=q_1}\odot \underbrace{\bmod_m(b)}_{=q_2}=\bmod_m(q_1\cdot q_2)=q_3\end{aligned}A \bmod_m függvény szerinti maradékos osztásokat elvégezve ismét négy egyenletet írhatunk fel az r, q_1, q_2 és q_3 maradékokra valamilyen k, n_1, n_2 és n_3 hányadosokkal:
\begin{aligned}a\cdot b&=km+r \\ a&=n_1m+q_1 \\ b&=n_2m+q_2 \\ q_1\cdot q_2&=n_3m+q_3\end{aligned}Az összeadás tartásánál látott módon ismét kifejezhetjük az r-q_3 különbséget – a részleteket az Olvasóra bízzuk –, amelyből megint azt fogjuk kapni, hogy teljesül az m|r-q_3 oszthatóság. Ebből viszont ugyancsak a 18.1. Lemma miatt r=q_3 következik, azaz a \bmod_m függvény a szorzást is tartja, és így valóban egy gyűrűhomomorfizmus \Z és \Z_m között.
Azt kell még igazolni, hogy szürjektív, ami itt azt jelenti, hogy minden \Z_m-beli elemhez létezik legalább egy olyan egész szám, amelynek épp ő a modulo m maradéka. Ez viszont nyilvánvalóan következik a 18.3. Definíció utáni megjegyzés 5. pontjából. Eszerint ugyanis a 0, 1, 2, ..., |m|-1 egész számokat a \bmod_m függvény önmagukra képezi le, amelyek viszont pontosan a \Z_m elemei.
∎A szakasz elején közölt példára alkalmazva az iménti tételt mostmár könnyedén kiszámíthatjuk, hogy a 2^{328} hatvány mennyi maradékot ad 11-gyel osztva. Ehhez annyit kell tennünk, hogy a 328 darab tényezőre alkalmazzuk a \bmod_{11} maradékképző függvényt, és vesszük az így kapott maradékok moduláris szorzatát a \Z_{11} gyűrűben:
\bmod_{11}(\underbrace{2\cdot 2\cdot \ldots \cdot 2}_{\text{328 darab}})=\underbrace{\bmod_{11}(2)\odot \bmod_{11}(2)\odot \ldots \odot \bmod_{11}(2)}_{\text{328 darab}}Az a probléma tehát megoldódott, hogy a számolgatás közben nem fogunk olyan óriási részeredményeket kapni, amelyek túllépik a számítógép számábrázolási határait. Megjegyezzük ugyanakkor, hogy a gyakorlatban a kitevő nagyságrendje a többszázjegyű számok körében mozog. Ez a módszer tehát ebben a formában továbbra sem alkalmazható, mivel beláthatatlanul sok moduláris szorzást igényel. Egy későbbi részben azonban mutatni fogunk egy olyan módszert, amelynek a segítségével még ezek az óriási kitevős moduláris hatványok is pillanatok alatt kiszámíthatók.
Ez az ismételt négyzetre emelések módszere néven lesz ismeretes, és – anélkül, hogy most belemennénk a részletekbe – a moduláris hatványozás azonosságait fogja igen trükkös módon kihasználni. Ezek az azonosságok azonban tetszőleges kommutatív gyűrűben érvényesek, így az alábbi tételben ezt az általános esetet fogjuk igazolni.
18.8. Tétel (A hatványozás azonosságai):
Legyen R egy tetszőleges kommutatív gyűrű, amelynek „szorzás” műveletét jelöljük a szokásos \cdot szimbólummal vagy egymás után írással. Tegyük fel továbbá, hogy ha x a gyűrű valamely eleme, n pedig tetszőleges pozitív egész, akkor az x^n hatványon az alábbi n tényezős „szorzatot” értjük:
x^n=\underbrace{x\cdot x\cdot x\cdot \ldots \cdot x}_{\text{n darab}}Ekkor tetszőleges a és b gyűrűelemek, valamint tetszőleges n és k pozitív egész számok esetén teljesülnek az alábbi tulajdonságok:
- (a\cdot b)^n=a^n\cdot b^n
- (a^n)^k=a^{n\cdot k}
- a^n\cdot a^k=a^{n+k}
Bizonyítás:
A bizonyításban a 14.12. Definíció szerinti gyűrűaxiómákra fogunk hivatkozni.
Az 1. tulajdonság: Az (a\cdot b)^n hatvány egy olyan n tényezős szorzat, amelynek minden tényezője (a\cdot b). A 4. gyűrűaxióma alapján a szorzás asszociatív, valamint – mivel kommutatív gyűrűről van szó – kommutatív is, ezért ezt a szorzatot tetszőlegesen átrendezhetjük és átzárójelezhetjük. Így az a és b tényezőket csoportosítva két n tényezős szorzathoz jutunk. Az elsőnek minden tényezője a, a másodiknak pedig b:
\begin{aligned}(a\cdot b)^n&=\overbrace{(ab)\cdot (ab)\cdot \ldots \cdot (ab)}^{\text{n darab}}=\\&=(\underbrace{a\cdot a\cdot \ldots \cdot a}_{\text{n darab}})\cdot(\underbrace{b\cdot b\cdot \ldots \cdot b}_{\text{n darab}})=a^n\cdot b^n\end{aligned}A 2. tulajdonság: Az (a^n)^k egy olyan k tényezős szorzat, amelynek minden tényezője a^n. Ezen tényezők mindegyike viszont egy-egy olyan n tényezős szorzat, amelynek minden tényezője a. A 4. gyűrűaxióma alapján a szorzás asszociatív, ezért ez tulajdonképpen egy olyan n\cdot k tényezős szorzatként is felfogható, amelynek minden tényezője a.
A 3. tulajdonság: Az a^n és a^k szorzatoknak rendre n és k darab tényezője van. A 4. gyűrűaxióma alapján a szorzás asszociatív, ezért az ő szorzatuk tulajdonképpen felfogható egy olyan nagy szorzatként, amelyben ezen tényezők száma összeadódik. Azaz az a^n\cdot a^k szorzatnak n+k darab tényezője lesz.
∎A Diffie-Hellman kulcscsere protokoll helyessége
Mivel az iménti tétel tetszőleges kommutatív gyűrűre érvényes, így érvényes a \Z_m gyűrűre is. Ez szoros összefüggésben van a 9. részben már részletesen ismertetett Diffie-Hellman kulcscsere protokollal. Ennek helyességét akkor nem igazoltuk, így ezt most fogjuk megtenni. Ott ugye gyakorlatilag a \Z_m gyűrűben kell moduláris hatványozást végezni. Ha Alice és Bob titkos kulcsot akarnak megbeszélni, akkor először a nembiztonságos csatornán keresztül megállapodnak egy x egész számban és egy m\neq 0 modulusban, amelyet mindketten majd a moduláris hatványozáshoz fognak használni. Ezután mindketten kitalálnak maguknak egy-egy titkos kitevőt. Tegyük fel, hogy Alice titkos kitevője a, Bob-é pedig b. Ezeket a kitevőket egymásnak sem árulják el.
Ezután Alice a \Z_m gyűrűben kiszámítja az x^a moduláris hatványt, és az eredményt átküldi Bobnak. Bob ugyanígy kiszámítja az x^b moduláris hatványt, és az eredményt átküldi Alice-nak. Ezután a kapott számokat mindketten ismét modulárisan hatványozzák a saját titkos kitevőjükkel. Alice a Bob-tól kapott x^b számból kiszámítja az (x^b)^a, Bob pedig az Alice-tól kapott x^a számból kiszámítja az (x^a)^b moduláris hatványt. A fenti 18.8. Tétel tétel 2. pontja alapján azonban mindketten ugyanazt a számot fogják kapni:
\underbrace{(x^b)^a}_{\text{Alice eredménye}}=x^{b\cdot a}=x^{a\cdot b}=\underbrace{(x^a)^b}_{\text{Bob eredménye}}A Diffie-Hellman kulcscsere protokoll tehát valóban helyesen működik, mivel a moduláris hatványozás ugyanazokkal a tulajdonságokkal rendelkezik, mint a hagyományos hatványozás. Már csak azt a problémát kell megoldanunk, hogy ezeket a moduláris hatványokat óriási kitevők esetén is nagyon hatékonyan ki tudjuk számolni. Erre – mint már említettük – egy későbbi részben fogunk kitérni az ismételt négyzetre emelések módszere kapcsán, amely szintén a 18.8. Tételben felsorolt tulajdonságokat használja ki.
Kongruenciák
Most azonban ismerkedjünk meg további fontos fogalmakkal a 18.6. Definícióban ismertetett gyűrűhomomorfizmusok kapcsán. Tegyük fel, hogy adva van egy R és egy S gyűrű, valamint egy közöttük lévő f:R\to S művelettartó leképezés, azaz gyűrűhomomorfizmus. Ez tehát R minden eleméhez hozzárendel valamilyen S-beli elemet.
Elképzelhető azonban, hogy egy adott S-beli elem több R-beli elemhez is hozzá van rendelve. Így tehát R elemei között definiálhatunk egy relációt, amely azt fejezi ki két R-beli elem között, hogy nekik ugyanaz az f gyűrűhomomorfizmus szerinti képük az S gyűrűben. Erről szól az alábbi definíció.
18.9. Definíció (Gyűrűhomomorfizmus szerinti kongruencia):
Tegyük fel, hogy R és S tetszőleges gyűrűk, valamint adva van közöttük egy f:R\to S gyűrűhomomorfizmus. Amennyiben az R gyűrű valamilyen a és b elemeire teljesül, hogy f(a)=f(b), akkor azt mondjuk, hogy a és b kongruensek az f gyűrűhomomorfizmus szerint. Ezt a relációt így jelöljük:
a\equiv b\pod fAmennyiben a és b között nem áll fenn az imént definiált f szerinti kongruencia, akkor őket inkongruensnek nevezzük az f gyűrűhomomorfizmus szerint. Ezt így jelöljük:
a\ \cancel{\equiv}\ b\pod f ♣A 13. részben már megismerkedtünk az úgynevezett ekvivalenciarelációkkal. Ezek olyan relációk voltak, amelyek egy halmaz elemeit osztályokba sorolják, méghozzá olymódon, hogy minden elem pontosan egy osztályba kerül bele. Vagyis az egyes osztályok között nincs átfedés, és minden elem bekerül valamelyik osztályba. A kongruencia fenti definíciójából azonnak adódik, hogy ez a reláció szintén egy ekvivalenciareláció.
18.10. Tétel:
Tegyük fel, hogy adva van egy f:R\to S gyűrűhomomorfizmus valamilyen R és S gyűrűk között. Ekkor a 18.9. Definícióban bevezetett f szerinti kongruencia egy ekvivalenciareláció az R gyűrű elemei között. Az ehhez tartozó ekvivalencia-osztályokat f szerinti kongruenciaosztályoknak vagy f szerinti maradékosztályoknak nevezzük.
♣Bizonyítás:
A 13.4. Definíció alapján azt kell tehát bizonyítani, hogy az f szerinti kongruenciareláció reflexív (12.8. Definíció), tranzitív (12.10. Definíció) és szimmetrikus (13.3. Definíció). Az alábbiakban legyenek a, b és c az R gyűrű tetszőleges elemei.
Mivel nyilván f(a)=f(a) teljesül, ezért fennáll az a\equiv a\pod f reláció, így az reflexív. Az is nyilván igaz, hogy ha f(a)=f(b) és f(b)=f(c) teljesül, akkor f(a)=f(c) is teljesül. Így tehát az a\equiv b\pod f és b\equiv c\pod f relációkból következik az a\equiv c\pod f reláció, azaz teljesül a tranzitivitás is. Végül ha f(a)=f(b) igaz, akkor nyilván f(b)=f(a) is igaz, vagyis a\equiv b\pod f-ből következik b\equiv a\pod f, ami épp a szimmetriát jelenti.
∎Ez alapján tehát az f gyűrűhomomorfizmus az R gyűrűt maradékosztályokra bontja, és egy adott maradékosztályban minden elemnek ugyanaz lesz az f szerinti képe az S gyűrűben. Az alábbi ábrán például a \Z és \Z_3 gyűrűk között lévő, fentebb már ismertetett \bmod_3 maradékképző függvény – mint gyűrűhomomorfizmus – szerinti maradékosztályokat szemléltetjük:
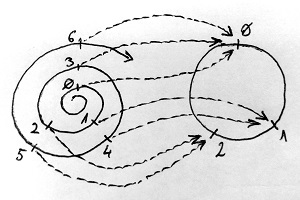
Az ábra baloldalán az egész számok \Z gyűrűjét reprezentáló, mindkét irányban végtelen számegyenes „felcsavarva” látható. Méghozzá olymódon, hogy az azonos maradékosztályba kerülő egész számok egy vonalba essenek. Ezek épp azok a számok lesznek, amelyek 3-mal osztva azonos maradékot adnak. Az ábra jobboldalán a \bmod_3 gyűrűhomomorfizmus képhalmaza, tehát jelen esetben a \Z_3 halmaz látható. Ennek elemeit egy óralapon helyeztük el ahhoz hasonlóan, ahogyan a 9. részben szemléltettük az óraaritmetikát a Diffie-Hellman kulcscsere protokoll kapcsán. A két halmaz közötti \bmod_3 leképezést nyilakkal szemléltettük, amely tehát minden egész számhoz az ő modulo 3 maradékát rendeli hozzá.
Felmerülhet az Olvasóban a kérdés, hogy a fenti 18.9. Definícióban, valamint a 18.10. Tételben miért kötöttük ki a két gyűrű közötti f függvényről, hogy az gyűrűhomomorfizmus legyen. Hiszen a kongruenciát, mint relációt az eddigiek alapján definiálhattuk volna tetszőleges függvény szerint is. Az ugyanúgy egy ekvivalenciareláció lenne, ugyanis a 18.10. Tétel bizonyításában egyáltalán nem használtuk ki az f leképezés művelettartó tulajdonságait. Rövidesen világos lesz, hogy miért olyan fontos ez a tulajdonság.
Gyűrűhomomorfizmus magja és képe
Képzeljük el azt a szituációt, hogy adva van egy valamilyen R gyűrű, valamint egy ezen értelmezett f gyűrűhomomorfizmus, de nem ismerjük azt az S gyűrűt, amelybe f képez. Szeretnénk azonban feltárni S szerkezetét. Hamarosan látni fogjuk, hogy ehhez előszöris az f szerinti kongruenciareláció által meghatározott R-beli maradékosztályokat kell meghatároznunk.
Első körben azt gondolnánk, hogy erre nincs más mód, mint R összes elemére alkalmazni az f függvényt, és a kapott függvényértékek alapján meghatározni ezeket a maradékosztályokat. Szerencsére van egy ennél sokkal egyszerűbb módszer, ám ehhez már szükségünk lesz f összegtartó tulajdonságára. Először ismertetünk egy hasznos segédtételt, amely ezt a tulajdonságot használja ki.
18.11. Lemma:
Legyen adva egy (R,+,\cdot) és egy (S,\oplus,\odot) gyűrű, valamint egy közöttük lévő f:R\to S összegtartó leképezés. Ekkor igazak az alábbiak:
- Ha rendre 0_R és 0_S jelöli az R és S gyűrűk nullelemét, akkor f(0_R)=0_S.
- Ha rendre a - és a \ominus szimbólumok jelölik az R-beli és S-beli ellentettképzést, akkor tetszőleges R-beli a elem esetén f(-a)=\ominus f(a).
Szavakkal: egy összegtartó leképezés az ellentettképzést és a nullelemet is tartja. Azaz egyrészt az R gyűrű nullelemének képe az S gyűrű nulleleme, másrészt bármely R-beli elem R-beli ellentettjének képe az elem képének S-beli ellentettje.
♣Bizonyítás:
Jelöljük az R gyűrű összeadását a +, míg az S gyűrű összeadását a \oplus szimbólummal.
Az 1. állítás: Mivel egyrészt 0_R az R gyűrű nulleleme, valamint f tartja az összeadást, ezért az R gyűrű tetszőleges a elemére felírható az alábbi:
f(a)=f(a+0_R)=f(a)\oplus f(0_R)Másrészt, mivel 0_S az S gyűrű nulleleme, ezért f(a)=f(a)\oplus 0_S is igaz. Ezt az előző egyenlettel összevetve az alábbit kapjuk:
\underbrace{f(a)\oplus f(0_R)}_{=f(a)}=f(a)\oplus 0_SHa mindkét oldalhoz hozzáadjuk az f(a) elem S-beli ellentettjét, akkor megkapjuk a tétel 1. állítását:
f(0_R)=0_SA 2. állítás: Legyen a az R gyűrű valamely tetszőleges eleme, amelynek R-beli ellentettjét jelöljük -a-val. Ekkor az 1. állítás miatt:
f(a+(-a))=f(0_R)=0_SMásrészt viszont f tartja az összeadást, így igaz az alábbi is:
f(a+(-a))=f(a)\oplus f(-a)A két egyenletet egymással összevetve ezt kapjuk:
f(a)\oplus f(-a)=0_SMivel f(a) és f(-a) összege épp az S gyűrű nulleleme, valamint az ellentettképzés a 14.10. Tétel alapján egyértelmű, ezért f(-a) valóban az f(a) elem S-beli ellentettjével egyezik meg. Azaz f(-a)=\ominus f(a), ahogyan a tétel állítja.
∎Térjünk most vissza az eredeti problémánkhoz, amikoris egy R gyűrűből kiinduló, S gyűrűbe mutató valamilyen f gyűrűhomomorfizmus szerinti kongruenciareláció maradékosztályait szeretnénk meghatározni. Az előző segédtétel következményeként most meg fogjuk mutatni, hogy ezek között van egy kitüntetett maradékosztály, amely már egyértelműen meghatározza az összes többit. Ez a kitüntetett maradékosztály épp azokból az R-beli elemekből áll, amelyekhez az f leképezés az S gyűrű nullelemét rendeli hozzá. Ennek a kitüntetett maradékosztálynak, valamint az f értékkészletének külön nevet is ad az alábbi definíció.
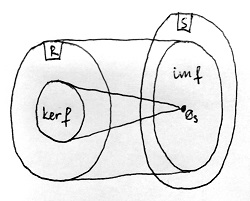
18.12. Definíció (Gyűrűhomomorfizmus magja és képe):
Legyenek R és S tetszőleges gyűrűk, valamint legyen adva közöttük egy f:R\to S gyűrűhomomorfizmus. Ekkor az f gyűrűhomomorfizmus magjának nevezzük azon R-beli elemek halmazát, melyeknek f szerinti képe az S gyűrű nulleleme. Az f magját – az angol „kernel” szóból eredeztetve – így jelöljük: \ker f.
Az f gyűrűhomomorfizmus képének nevezzük azoknak az S-beli elemeknek a halmazát, amelyek képei legalább egy R-beli elemnek. Az f képét – az angol „image” szóból eredeztetve – így jelöljük: \text{im} f.
Az alábbi ábra szemlélteti a fenti fogalmakat:
Megjegyzés:
A 18.9. Definícióban szereplő kongruenciára a most definiált fogalom segítségével egy alternatív definíciót is adhatunk. Nevezetesen: az R gyűrű valamely a és b elemei között akkor és csak akkor teljesül az f gyűrűhomomorfizmus szerinti kongruencia (azaz akkor és csak akkor teljesül az a\equiv b\pod f reláció), ha az a-b különbség benne van f magjában. Ugyanis a\equiv b\pod f pontosan azt jelenti, hogy f(a)=f(b). Mindkét oldalhoz f(b) ellentettjét adva, valamint kihasználva f összegtartó (lásd a 18.6. Definíciót) és ellentettképzéstartó (lásd a 18.11. Lemma 2. pontját) tulajdonságát, ezt kapjuk:
f(a)\oplus(\ominus f(b))=f(a-b)=0_S ♣Például az előző szakaszban felhozott \Z és \Z_3 közötti \bmod_3 maradékképző függvény – mint gyűrűhomomorfizmus – magja épp a 3-mal osztható egész számokból áll. A \bmod_3 maradékképző függvény ugyanis pontosan ezekhez rendeli hozzá a \Z_3 gyűrű nullelemét, azaz a 0 maradékot. A \bmod_3 függvény képe pedig a 18.3. Definíció utáni megjegyzés 5. pontja miatt maga a \Z_3 halmaz.
Megjegyezzük, hogy egy f:R\to S gyűrűhomomorfizmus magja soha nem lehet üres. A 18.11. Lemma 1. pontja alapján ugyanis szükségképpen tartalmazza legalább az R gyűrű nullelemét, hiszen ennek képe biztosan az S gyűrű nulleleme lesz.
Most azt mutatjuk meg, hogy egy gyűrűhomomorfizmus magja már egyértelműen meghatározza az általa indukált kongruenciarelációt.
18.13. Tétel:
Legyenek R, S és T valamilyen tetszőleges gyűrűk, és tegyük fel, hogy adva van egy f:R\to S, valamint egy g:R\to T gyűrűhomomorfizmus. Legyen továbbá a és b az R gyűrű két tetszőleges eleme.
Amennyiben \ker f=\ker g, úgy az a\equiv b\pod f kongruencia pontosan akkor teljesül, amikor az a\equiv b\pod g kongruencia is.
Visszafelé: Amennyiben az a\equiv b\pod f kongruencia pontosan akkor teljesül, amikor az a\equiv b\pod g kongruencia is, úgy \ker f=\ker g.
♣Bizonyítás:
Az áttekinthetőség kedvéért most az összeadást a +, az ellentettképzést és a kivonást pedig a - szimbólummal fogjuk jelölni mindhárom gyűrű esetén. Mindig gondoljuk azonban végig, hogy az adott kifejezésben szereplő műveleti jelek éppen melyik gyűrűre vonatkoznak. Ezzel szemben a nullelemek között továbbra is jelölésbeli különbségeket fogunk tenni. Ez alapján az R gyűrű nullelemét 0_R, az S gyűrű nullelemét 0_S, a T gyűrű nullelemét pedig 0_T fogja jelölni.
Először is tegyük fel, hogy \ker f=\ker g, azaz a két gyűrűhomomorfizmus magja megegyezik. Az a\equiv b\pod f reláció a 18.12. Definíció utánis megjegyzés alapján pontosan azt jelenti, hogy az a-b különbség benne van az f gyűrűhomomorfizmus magjában.
Mivel azonban azt mondtuk, hogy \ker f=\ker g – azaz f és g magjának ugyanazok az elemei –, így az a-b különbség benne van a g gyűrűhomomorfizmus magjában is. Ez viszont ismét a 18.12. Definíció utánis megjegyzés alapján pontosan azt jelenti, hogy teljesül az a\equiv b\pod g kongruencia.
Amennyiben tehát \ker f=\ker g, akkor a két gyűrűhomomorfizmus szerinti kongruencia egyszerre teljesül vagy nem teljesül, azaz teljesen ekvivalens egymással.
Visszafelé: Tegyük most fel, hogy a két kongruencia egymással ekvivalens. A fentiekhez hasonló lépéseket alkalmazva egyrészt azt fogjuk kapni, hogy az a\equiv b\pod f kongruencia pontosan akkor teljesül, ha az a-b különbség benne van az f magjában. Ehhez hasonlóan az a\equiv b\pod g kongruencia pontosan akkor teljesül, ha az a-b benne van a g magjában. Ha tehát a két kongruencia ekvivalens egymással, akkor az a-b különbség pontosan akkor van benne f magjában, amikor benne van g magjában is. Ez ugye tetszőleges a és b elempárra teljesül, így speciálisan azokban az esetekben is, amikor b=0_R. Ez viszont azt jelenti, hogy tetszőleges a=a-0_R pontosan akkor van benne f magjában, amikor g magjában is benne van. A \ker f és \ker g halmazoknak tehát pontosan ugyanazok az elemei, azaz a két halmaz valóban megegyezik.
∎Ez alapján tehát egy f gyűrűhomomorfizmus szerinti kongruenciarelációt kizárólag annak magja, nem pedig maga az f határozza meg. Még csak az sem érdekes, hogy f milyen gyűrűbe képez. Nézzünk is erre egy egyszerű példát.
Legyen most a kiindulási gyűrűnk az egész számok \Z gyűrűje, és legyen az egyik célgyűrű a \Z_2 gyűrű. A másik célgyűrű elsőre szokatlan lesz, mivel ennek alaphalmaza nem számokból, hanem az e és az o betűkből áll. Ezt a halmazt P-vel fogjuk jelölni a példában. Vezessünk be ezen a halmazon is két műveletet, és jelöljük őket a \boxplus és a \boxdot szimbólumokkal. Ezt a két műveletet önkényesen az alábbi műveleti táblákkal definiáljuk:
\begin{array}{cc}\begin{array}{c|cc}\boxplus &e&o\\ \hline e&e&o \\o&o&e \end{array} & \begin{array}{c|cc}\boxdot &e&o\\ \hline e&e&e \\o&e&o\\ \end{array}\end{array}Könnyű leellenőrizni, hogy a P halmaz ezzel a két művelettel szintén gyűrűt alkot, melynek nulleleme az e betű, egységeleme pedig az o betű. Ennek legegyszerűbb módja, ha meggondoljuk, hogy ez a gyűrű \Z_2-től pusztán abban különbözik, hogy máshogy jelöltük az elemeit és a két műveletét. Valóban, az Olvasó is könnyedén leellenőrizheti, hogy az alábbi h leképezés tulajdonképpen egy 18.6. Definíció szerinti izomorfizmus a \Z_2 és a P gyűrűk között, azaz \Z_2\simeq P:
\begin{aligned}h(0)&=e\\h(1)&=o\end{aligned}Hamarosan meg fogjuk mutatni, hogy ez az izomorfizmus nem véletlenül teljesül e két gyűrű között. Ám egyelőre tegyük félre ezt a dolgot. Van tehát egy kiindulási gyűrűnk, amely az egész számok \Z gyűrűje, valamint van két célgyűrűnk: a \Z_2 és az imént definiált, meglehetősen szokatlan P. Nincs más hátra, mint találni két \Z-ből kiinduló gyűrűhomomorfizmust, amelyeknek ugyanaz a magja \Z-ben, azonban az egyiknek a célgyűrűje \Z_2, a másiknak pedig P.
Az első viszonylag egyszerű, hiszen a 18.3. Definíció szerinti \bmod_2 maradékképző függvény a 18.7. Tétel alapján egy gyűrűhomomorfizmus \Z és \Z_2 között. Ennek magja a 2-vel osztható (tehát páros) számokból áll, hiszen pontosan ezek fognak 0 maradékot adni 2-vel osztva. A másik gyűrűhomomorfizmust az alábbi f függvénnyel adjuk meg:
f(x)=\begin{cases} e &\text{ha}\ x\ \text{páros} \\ o &\text{ha}\ x\ \text{páratlan}\end{cases}Az Olvasóra bízzuk annak átgondolását, hogy f valóban egy gyűrűhomomorfizmus \Z és P között. Mivel az e betű a P gyűrű nulleleme, ezért az f gyűrűhomomorfizmus magja szintén a páros számokból áll.
A három gyűrűt és a közöttük lévő \bmod_2:\Z\to \Z_2 és f:\Z\to P gyűrűhomomorfizmusokat, illetve ezek közös magját mutatja az alábbi ábra:
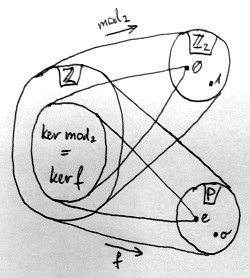
Erre a szituációra már alkalmazhatjuk a kongruenciák ekvivalenciájáról szóló 18.13. Tételt. Eszerint tehát a két gyűrűhomomorfizmus – habár azok teljesen más gyűrűkre képeznek – szerinti kongruenciarelációk teljesen azonosak lesznek. Ez azt jelenti, hogy az alábbi két reláció tetszőleges a és b egész számok között vagy egyszerre teljesül, vagy egyszerre nem teljesül:
\begin{aligned}a&\equiv b\pod {\bmod_2}\\a&\equiv b\pod f\end{aligned}Ezt a két kongruenciarelációt tehát teljesen felesleges megkülönböztetni egymástól. Sőt, általában is hasznos lenne bevezetni egy olyan kongruencia-fogalmat, amely nem támaszkodik közvetlenül egy adott konkrét gyűrűhomomorfizmusra, hanem annak csak a magjára. Erről szól a következő szakasz.
Részgyűrűk és ideálok
Tegyük fel, hogy van egy R gyűrű, amelyen egy kongruenciarelációt szeretnénk megadni. Nem szeretnénk ugyanakkor foglalkozni semmiféle más gyűrűvel, abba mutató gyűrűhomomorfizmusokkal meg aztán pláne nem. Szerencsére az előző szakaszban bizonyított 18.13. Tétel alapján nekünk elegendő R-ben egy olyan részhalmazt keresni, amely alkalmas arra, hogy valamilyen gyűrűhomomorfizmus magja legyen. Ezt azonban ennek a hipotetikus gyűrűhomomorfizmusnak a konkrét ismerete nélkül szeretnénk megtenni. Ehhez először is definiálunk egy, a továbbiakban is hasznos fogalmat.
18.14. Definíció (Részgyűrű):
Ha egy R gyűrű valamely S részhalmaza maga is gyűrű az R műveleteire nézve, akkor azt mondjuk, hogy S részgyűrű R-ben. Ezt így jelöljük: S\leq R.
A nullgyűrű és maga a teljes R nyilvánvalóan részgyűrűk R-ben. Ezeket triviális részgyűrűknek nevezzük. Azt, hogy S részgyűrű R-ben, de S\neq R így jelöljük: S\lt R. Ilyenkor azt mondjuk, hogy S valódi részgyűrű R-ben.
♣A 16. részben az oszthatóság kapcsán már láttuk, hogy például a páros számok 2\Z-vel jelölt halmaza maga is gyűrű a \Z-n értelmezett összeadásra és szorzásra nézve, így 2\Z részgyűrű \Z-ben. Mivel nem minden egész szám páros, ezért 2\Z\lt \Z, azaz 2\Z valódi részgyűrű \Z-ben. A páratlan számok szintén részhalmazt alkotnak \Z-n belül, ez a részhalmaz azonban nem részgyűrű, hiszen már a műveleti zártság sem teljesül az összeadásra. Például 3+5=8, ami nem páratlan szám.
Az alábbi tétel abban nyújt segítséget, hogy ne kelljen minden gyűrűaxiómát ellenőriznünk ahhoz, hogy egy részhalmazról eldöntsük, vajon részgyűrű-e vagy sem.
18.15. Tétel:
Egy tetszőleges R gyűrű valamely S részhalmaza akkor és csak akkor részgyűrű, ha teljesülnek az alábbi tulajdonságok:
- S zárt az R gyűrű összeadására.
- S zárt az R gyűrű szorzására.
- S tartalmazza az R gyűrű nullelemét.
- S zárt az R-beli ellentettképzésre.
Bizonyítás:
Tegyük fel, hogy S részgyűrű R-ben. Ekkor a műveleti zártság – azaz az 1. és 2. tulajdonság – nyilvánvalóan teljesül, máskülönben S nem lenne gyűrű az R-beli műveletekre nézve, és így részgyűrű sem lehetne R-ben.
Mivel S-nek létezik nulleleme – hiszen maga is gyűrű –, ezért a 3. tulajdonsághoz azt kell megmutatni, hogy ez a nullelem megegyezik R nullelemével. Jelöljük S nullelemét 0_S-sel, R nullelemét pedig 0_R-rel, és tegyük fel indirekt, hogy ez a kettő nem ugyanaz. Ha a kettő nem ugyanaz, akkor az sem mindegy, hogy melyik gyűrűben beszélünk ellentettképzésről. Jelölje most (-0_S) a 0_S elem R-beli ellentettjét. Őket összeadva tehát az R gyűrű nullelemét kell kapjuk, azaz:
0_S+(-0_S)=0_RMivel 0_S az S gyűrű nulleleme, ezért nyilvánvalóan igaz az alábbi:
0_S+0_S=0_SVégül, mivel 0_R az R gyűrű nulleleme, ezért az alábbi is teljesül:
0_S+0_R=0_SMivel S gyűrű, így az összeadás asszociativitása miatt:
(0_S+0_S)+(-0_S)=0_S+(0_S+(-0_S))A baloldalt kifejtve ezt kapjuk:
\underbrace{(0_S+0_S)}_{=0_S}+(-0_S)=0_S+(-0_S)=0_RA jobboldalt kifejtve pedig ezt:
0_S+\underbrace{(0_S+(-0_S))}_{=0_R}=0_S+0_R=0_SEz a kettő eredmény viszont a fentebb már említett asszociativitás miatt indirekt feltételezésünkkel ellentétben mégis meg kell egyezzen, így valóban 0_R=0_S.
Végül az ellentettképzésre való zártság – azaz a 4. tulajdonság – igazolásához képezzük az S gyűrű valamely a elemének ellentettjét mindkét gyűrűben, és megmutatjuk, hogy ezek valójában megegyeznek. Az S-beli ellentettet jelöljük x_S-sel, míg az R-beli ellentettet x_R-rel. Az a elemet az R-beli ellentettjével összeadva az R gyűrű nullelemét kell kapnunk, azaz:
a+x_R=0_RUgyanakkor az a elemet az S-beli ellentettjével összeadva az S gyűrű nullelemét kell kapnunk, amiről azonban már láttuk, hogy megegyezik az R gyűrű nullelemével. Azaz:
a+x_S=0_S=0_RMinthogy az R-beli ellentettképzés a 14.10. Tétel alapján egyértelmű, ezért szükségképpen x_S=x_R. Azaz az S gyűrű valóban zárt az R-beli ellentettképzésre.
Visszafelé: Most azt kell megmutatnunk, hogy amennyiben teljesül mind a 4 tulajdonság, úgy S részgyűrű R-ben. Az R gyűrű műveletei az 1. és 2. tulajdonságok alapján nem vezetnek ki S-ből, így azok algebrai értelemben műveletek ezen a szűkebb halmazon is (lásd a 11.3. Definíciót). Továbbá a 3. és 4. tulajdonság miatt létezik nullelem, és minden elemnek létezik ellentettje is S-ben. Így a 14.12. Definíció szerinti gyűrűaxiómákból már csak a két művelet asszociativitását, valamint a disztributivitási szabályokat kell igazolnunk. Ezeket azonban S megörökli az R-től a műveletekkel együtt. Így tehát S valóban részgyűrű R-ben.
∎Még mielőtt visszatérnénk egy R gyűrűből kiinduló gyűrűhomomorfizmusok magjainak azonosítására, vizsgáljuk meg azt a kérdést, hogy hogyan azonosíthatjuk egy S gyűrűbe mutató gyűrűhomomorfizmusok képeit. Az alábbi tétel alapján ezekről sajnos nem tudunk túl sokat mondani.
18.16. Tétel:
Legyen adva egy S gyűrű, és annak egy T részhalmaza. A T részhalmaz akkor és csak akkor képe egy S-be mutató gyűrűhomomorfizmusnak, ha részgyűrű S-ben.
♣Bizonyítás:
Tekintsük azt az f gyűrűhomomorfizmust, amelynek képe T. Ez egy valamilyen, számunkra ismeretlen X gyűrű elemein van értelmezve, amelynek nullelemét jelöljük most 0_X-szel, míg az S gyűrű nullelemét jelöljük 0_S-sel. Azt kell megmutatnunk, hogy T-re teljesülnek a 18.15. Tételben felsorolt feltételek.
A 18.11. Lemma 1. pontja alapján f(0_X)=0_S, így tehát az S gyűrű nulleleme valóban benne van T-ben.
Ha valamilyen a és b elemek benne vannak T-ben, akkor léteznek olyan x_a és x_b elemek X-ben, amelyeknek épp ő a képük, azaz f(x_a)=a és f(x_b)=b. A két egyenletet összeadva és összeszorozva, valamint kihasználva f művelettartó tulajdonságait az alábbiakat kapjuk:
\begin{aligned}f(x_a)+f(x_b)&=f(x_a+x_b)=a+b \\ f(x_a)\cdot f(x_b)&=f(x_a\cdot x_b)=a\cdot b\end{aligned}Léteznek tehát olyan elemek X-ben, amelyeknek a+b és a\cdot b a képei (nevezetesen x_a+x_b és x_a\cdot x_b), emiatt az a+b összeg és az a\cdot b szorzat is benne van T-ben, ami így valóban zárt az összeadásra és szorzásra nézve.
Végül ha valamilyen a elem benne van T-ben, akkor létezik olyan x_a elem X-ben, amelynek épp a a képe, azaz f(x_a)=a. A 18.11. Lemma 2. pontja alapján azonban f tartja az ellentettképzést is, így teljesül az alábbi:
f(-x_a)=-f(x_a)=-aLétezik tehát olyan elem X-ben, amelynek -a a képe (nevezetesen -x_a), emiatt -a is benne van T-ben, ami így zárt az ellentettképzésre nézve is. Minthogy a 18.15. Tételben felsorolt minden feltétel teljesül, ezért T valóban részgyűrű S-ben.
Visszafelé: Tegyük most fel, hogy T részgyűrű S-ben. Azt kell megmutatnunk, hogy van olyan S-be mutató gyűrűhomomorfizmus, amelynek képe T. Tekintsük például azt az f:T\to S függvényt, amely T minden eleméhez önmagát rendeli hozzá. Ez kétségkívül nem egy izgalmas függvény, viszont nyilvánvalóan gyűrűhomomorfizmus, aminek a képe ráadásul épp a T halmaz.
∎Egy S gyűrűben tehát az odamutató gyűrűhomomorfizmusok képeiről mindössze annyit tudunk mondani, hogy azok pontosan S részgyűrűi lesznek. Ezzel szemben egy R gyűrű azon részhalmazairól, amelyek valamilyen R-ből kiinduló gyűrűhomomorfizmusok magjai lehetnek, ennél többet is fogunk tudni mondani. Most erre mutatunk egy szükséges feltételt, majd a következő szakaszban igazoljuk azt az egyáltalán nem nyilvánvaló tényt, hogy ez a feltétel egyben elégséges is.
18.17. Tétel:
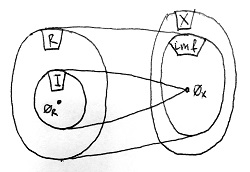
Tegyük fel, hogy egy R gyűrű valamely I részhalmaza egy R-ből kiinduló gyűrűhomomorfizmus magja. Tegyük fel továbbá, hogy a egy tetszőleges elem I-ben, és r egy tetszőleges elem R-ben. Ekkor teljesülnek az alábbiak:
- I részgyűrű R-ben.
- Az a\cdot r és az r\cdot a szorzatok benne vannak I-ben.
A 2. feltételben azért kellett mindkét irányú szorzást megemlíteni, mert ez a tétel tetszőleges – azaz nem feltétlenül csak kommutatív – gyűrűre érvényes. Vegyük észre, hogy ez a szorzásra szigorúbb feltételt ír elő annál, mintha I-ről egyszerűen csak annyit kötnénk ki, hogy részgyűrű legyen (azaz, hogy az I-beli elemek között végzett szorzás ne vezessen ki az I halmazból). A 2. feltétel ezen felül megköveteli még azt is, hogy bármely R-beli elemmel szorzunk is egy I-beli elemet – akár jobbról, akár balról –, az így kapott eredménynek is a szűkebb I halmazban kell maradnia.
Bizonyítás:
Tekintsük azt az f gyűrűhomomorfizmust, amelynek I a magja. Ez egy valamilyen, számunkra ismeretlen X gyűrűbe képez, amelynek nullelemét jelöljük most 0_X-szel, míg az R gyűrű nullelemét jelöljük 0_R-rel. Az f függvény tehát I minden eleméhez 0_X-et rendeli hozzá, hiszen \ker f=I. Ezt a szituációt mutatja az alábbi ábra.
Az 1. állítás igazolásához azt kell megmutatni, hogy I részgyűrű R-ben. Ez a 18.15. Tétel alapján pontosan akkor teljesül, ha I tartalmazza 0_R-t, valamint zárt az R gyűrű mindkét műveletére és az R-beli ellentettképzésre.
Mivel f gyűrűhomomorfizmus, ezért nyilván összegtartó is, így a 18.11. Lemma értelmében tartja a nullelemet és az ellentettképzést. Azaz egyrészt f(0_R)=0_X, és így 0_R valóban benne van f magjában, azaz I-ben. Másrészt ha valamilyen a benne van I-ben, akkor f(a)=0_X, és így az ellentettképzés tartása miatt f(-a)=-f(a)=-0_X=0_X. Azaz a ellentettjének is 0_X a képe, következésképp ő is benne van I-ben.
Az összeadásra való zártság szintén f összegtartó tulajdonságából ered. Ha ugyanis a és b az I két tetszőleges eleme, akkor egyrészt f(a)=0_X és f(b)=0_X. Másrészt viszont az összegtartás miatt az ő összegükre teljesül az alábbi:
f(a+b)=f(a)+f(b)=\underbrace{0_X}_{=f(a)}+\underbrace{0_X}_{=f(b)}=0_XTehát az a+b összeg is az X gyűrű nullelemére képeződik, következésképp ő is benne van I-ben. A szorzásra való zártság teljesen hasonló módon következik f szorzástartó tulajdonságából. Mivel teljesül a 18.15. Tétel minden feltétele, ezért I valóban részgyűrű R-ben.
A 2. állítás igazolásához tegyük fel, hogy r az R gyűrű tetszőleges – tehát nem feltétlenül I-beli – eleme. Azt kell megmutatni, hogyha ezzel akár balról, akár jobbról megszorzunk egy I-beli a elemet, akkor az eredmény is I-beli lesz. Mivel a benne van I-ben, ezért f(a)=0_X. Következésképp f szorzástartó tulajdonsága miatt az r\cdot a és a\cdot r szorzatok képére igazak lesznek az alábbiak:
\begin{aligned}f(r\cdot a)&=f(r)\cdot \overbrace{f(a)}^{=0_X}=0_X \\ f(a\cdot r)&=\underbrace{f(a)}_{=0_X}\cdot f(r)=0_X\end{aligned}Elképzelhető tehát, hogy a két szorzatnak nem ugyanaz lesz az eredménye az R gyűrűben (kivéve persze ha kommutatív gyűrűről van szó), de az biztos, hogy mindkét szorzat f szerinti képe az X gyűrű nulleleme lesz. Következésképp valóban benne vannak I-ben.
∎Az iménti tételben felsorolt két feltételt tehát egy gyűrű minden olyan részhalmaza teljesíti, amely egy valamilyen gyűrűhomomorfizmus magja lehet. Ezeknek a részhalmazoknak külön nevet is ad az alábbi definíció.
18.18. Definíció (Ideál):
Legyen adva egy R gyűrű, valamint annak egy I részhalmaza, amely részgyűrű R-ben. Tegyük fel továbbá, hogy r az R gyűrű egy tetszőleges – tehát nem feltétlenül I-beli – eleme.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az r\cdot a szorzat is I-ben van, akkor azt mondjuk, hogy I balideál R-ben.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az a\cdot r szorzat is I-ben van, akkor azt mondjuk, hogy I jobbideál R-ben.
Amennyiben egy I részgyűrű egyszerre bal- és jobbideál, akkor azt mondjuk, hogy I kétoldali ideál, vagy egyszerűen csak ideál R-ben. Ezt így jelöljük: I\triangleleft R.
A nullgyűrű és maga a teljes R nyilvánvalóan ideálok R-ben. Ezeket triviális ideáloknak nevezzük.
♣Természetesen kommutatív gyűrűk esetén nincs értelme külön jobb- vagy balideálokról beszélni, hiszen ott minden jobbideál egyben balideál is, és fordítva. Például az egész számok \Z gyűrűjében ideált alkot a páros számok 2\Z-vel jelölt halmaza, hiszen ha egy páros számot bármilyen tetszőleges egész számmal megszorzunk, az eredmény ugyancsak páros.
Ezzel a szóhasználattal élve a 18.17. Tétel úgy is megfogalmazható, hogy amennyiben egy R gyűrű valamely I részhalmaza magja valamilyen gyűrűhomomorfizmusnak, akkor I ideál R-ben. A következő szakaszban azt fogjuk megmutatni, hogy más részhalmaz nem is lehet gyűrűhomomorfizmus magja.
Maradékosztálygyűrűk
Előszöris bevezetünk egy új jelölésmódot, amelynek a segítségével tömören le tudunk írni bizonyos részhalmazokat egy gyűrűben. Az alábbi definíció azonban nem csak gyűrűk, hanem tetszőleges algebrai struktúrák esetén alkalmazható.
18.19. Definíció (Komplexusműveletek):
Tegyük fel, hogy H egy tetszőleges részhalmaza egy valamilyen G halmaznak, valamint legyen g egy tetszőleges G-beli elem.
Amennyiben a G halmazon értelmezve van egy \cdot-tal vagy egymás után írással jelölt, szorzásnak nevezett művelet, akkor g\cdot H-val vagy gH-val jelöljük azt a halmazt, amelynek elemei úgy képződnek, hogy H minden elemével balról összeszorozzuk a g elemet. Ehhez hasonlóan H\cdot g-vel vagy Hg-vel jelöljük azt a halmazt, amelynek elemei úgy képződnek, hogy H minden elemével jobbról összeszorozzuk a g elemet. Az így képzett gH és Hg halmazokat a H halmaz g elemmel vett komplexusszorzatának nevezzük.
Ehhez hasonlóan amennyiben a műveletet \cdot helyett + jelöli, akkor a g+H és H+g halmazokat a H halmaz g elemmel vett komplexusösszegének nevezzük.
♣Megjegyzés:
- Tegyük fel, hogy m egy nemnulla egész szám. Ekkor az m-mel osztható egész számok halmazát (vagy más szavakkal m többszöröseit) a fenti komplexusszorzást alkalmazva m\Z-vel jelölhetjük. Például a páros számok halmazát ezért jelöljük 2\Z-vel.
- A komplexusösszeadást is alkalmazva ennek megfelelően a páratlan számok halmazát 2\Z+1-gyel jelölhetjük.
- Egy gyűrű valamilyen S részhalmaza és r eleme esetén az r+S halmaz mindig megegyezik az S+r halmazzal, hiszen a 14.12. Definíció szerinti 1. gyűrűaxióma alapján az összeadás kommutatív, így mindegy, hogy melyik oldalról adjuk hozzá az r elemet az S elemeihez.
- Ezzel szemben az rS halmaz általában különbözik az Sr halmaztól, mivel a szorzás általában nem kommutatív (kivéve persze kommutatív gyűrűk esetén).
Most térjünk vissza az előző szakasz végén felvetett problémához. Azt már tudjuk, hogy ha egy R gyűrű valamely I részhalmaza magja valamilyen gyűrűhomomorfizmusnak, akkor I ideál R-ben. Most szeretnénk megmutatni, hogy ez visszafelé is igaz, azaz bármely I ideál magja valamilyen gyűrűhomomorfizmusnak.
Ehhez szükségünk van egy konstrukcióra, amelynek a segítségével egy tetszőleges I ideálhoz tudunk konstruálni egy olyan f gyűrűhomomorfizmust, amelynek épp I lesz a magja. Ehhez azonban kell egy célgyűrű is, ahová f mutatni fog. Ezt a gyűrűt és az f gyűrűhomomorfizmust is az R gyűrűből fogjuk képezni az I ideál segítségével.
Az ötletet a kongruenciákról szóló szakaszban már bemutatott \bmod_3 gyűrűhomomorfizmus szerinti maradékosztályokat szemléltető ábráról kölcsönözzük. Ezen az ábrán ugye felcsavartuk a számegyenest olymódon, hogy az azonos maradékosztályba eső elemek egyvonalba essenek:
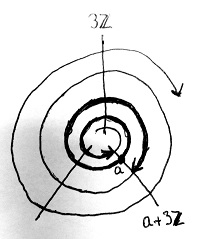
Ugyan jelen esetben egy általános gyűrűről beszélünk, ahol nem sok értelme van számegyenesről beszélni, ám az analógia meglehetősen hasznos a megértéshez. Az ábrán a függőleges irányban álló maradékosztály az, amelyik a \bmod_3 gyűrűhomomorfizmus magja. Ez ugye épp a 3-mal osztható egész számok halmaza lesz, amelyet a fentebbi komplexusszorzást alkalmazva 3\Z-vel jelölünk. Kérdés, hogy a többi maradékosztályt, mint halmazt hogyan tudjuk kifejezni 3\Z segítségével.
Tegyük fel, hogy a egy valamilyen előre rögzített egész szám, és jelöljük [a]_3-mal azt a maradékosztályt, amelynek ő eleme. A továbbiakban tehát ennek a maradékosztálynak a lesz a képviselője. A fenti ábrán látható, hogy a-ból kiindulva az [a]_3 maradékosztály tetszőleges eleméhez – és csak ezekhez – eljuthatunk, ha 3-nak valamilyen többszöröse számú lépést teszünk meg valamilyen irányban a felcsavart számegyenesen. Komplexusműveletekkel kifejezve ez azt jelenti, hogy teljesül az alábbi halmazegyenlőség:
[a]_3=a+3\ZEzek szerint tehát a \bmod_3 szerinti kongruencia minden maradékosztályát elő tudjuk állítani annak valamely önkényesen kiválasztott eleméből és a \bmod_3 magjából – azaz 3\Z-ből –, ami ugye a 18.17. Tétel alapján ideál \Z-ben.
Most térjünk vissza az eredeti R gyűrűnkhöz és annak valamely I ideáljához. Az előző példával analóg módon szeretnénk valamiféle „maradékosztályokat” előállítani r+I alakban, ahol r az adott „maradékosztály” egy eleme. Az idézőjeles megfogalmazást az indokolja, hogy a 18.10. Tétel gyűrűhomomorfizmus szerinti, nem pedig ideál szerinti maradékosztályokról beszél. Márpedig I-ről egyelőre nem tudjuk, hogy vajon magja-e bármiféle gyűrűhomomorfizmusnak, hiszen épp ezt szeretnénk bizonyítani.
A gyűrűhomomorfizmus szerinti maradékosztályok tulajdonképpen a 18.9. Definícióban bevezetett gyűrűhomomorfizmus szerinti kongruencia ekvivalencia-osztályai. A 18.12. Definíció utáni megjegyzés alapján két elem pontosan akkor volt kongruens egy f gyűrűhomomorfizmus szerint, ha a különbségük benne volt f magjában. Ezzel analóg módon talán praktikus lenne bevezetni az ideál szerinti kongruencia fogalmát.
18.20. Definíció (Ideál szerinti kongruencia):
Legyen R tetszőleges gyűrű és legyen I valamilyen ideál R-ben. Amennyiben az R gyűrű valamilyen a és b elemeire teljesül, hogy az a-b különbség az I ideálnak eleme, akkor azt mondjuk, hogy a és b kongruensek az I ideál szerint (vagy kongruensek modulo I). Ezt a relációt így jelöljük:
a\equiv b\pod IAmennyiben a és b között nem áll fenn az imént definiált modulo I kongruencia, akkor őket inkongruensnek nevezzük modulo I. Ezt így jelöljük:
a\ \cancel{\equiv}\ b\pod I ♣Nem lesz túl meglepő, hogy a gyűrűhomomorfizmus szerinti kongruenciához hasonlóan az ideál szerinti kongruencia is egy ekvivalenciareláció. Ennek ekvivalencia-osztályai ráadásul épp a kívánt alakban írhatók fel a komplexusműveletek segítségével.
18.21. Tétel:
Legyen R tetszőleges gyűrű, valamint I valamilyen ideál R-ben. Ekkor a 18.20. Definícióban bevezetett I szerinti kongruencia egy ekvivalenciareláció az R gyűrű elemei között. Az ehhez tartozó ekvivalencia-osztályokat I szerinti (modulo I) kongruenciaosztályoknak vagy I szerinti (modulo I) maradékosztályoknak nevezzük.
Ha r egy tetszőleges elem az R gyűrűben, akkor az r elemet tartalmazó modulo I maradékosztály épp az r+I halmaz lesz. Ilyenkor azt mondjuk, hogy az r elem reprezentálja az r+I maradékosztályt.
♣Bizonyítás:
A 13.4. Definíció alapján azt kell tehát bizonyítani, hogy az I ideál szerinti kongruenciareláció reflexív (12.8. Definíció), tranzitív (12.10. Definíció) és szimmetrikus (13.3. Definíció). Az alábbiakban legyenek a, b és c az R gyűrű tetszőleges elemei. A bizonyítás során végig arra fogunk támaszkodni, hogy I ideál, tehát egyben részgyűrű is.
Mivel nyilván a-a=0 teljesül, és az R nulleleme a 18.15. Tétel 3. pontja alapján benne van I-ben, ezért fennáll az a\equiv a\pod I reláció, így az reflexív.
Ha a-b és b-c benne vannak I-ben, akkor a 18.15. Tétel 1. pontja alapján az ő összegük, azaz a-b+b-c=a-c is benne van I-ben. Így tehát az a\equiv b\pod I és b\equiv c\pod I relációkból következik az a\equiv c\pod I reláció, azaz teljesül a tranzitivitás is.
Végül ha a-b benne van I-ben, akkor a 18.15. Tétel 4. pontja alapján az ő ellentettje, azaz b-a is benne van I-ben, vagyis a\equiv b\pod I-ből következik b\equiv a\pod I, ami épp a szimmetriát jelenti.
Az I szerinti kongruencia tehát valóban egy ekvivalenciareláció, amely az R gyűrű alaphalmazát ekvivalencia-osztályokra bontja. Ezek lesznek a modulo I maradékosztályok. Az r elemet tartalmazó maradékosztály pontosan azokból az x elemekből fog állni, amelyekre teljesül az x\equiv r\pod I kongruencia. A 18.20. Definíció alapján ez pontosan azt jelenti, hogy az x-r különbség benne van I-ben. Ez viszont a 18.19. Definícióban bevezetett komplexusműveletek nyelvén pontosan azt jelenti, hogy x benne van az r+I halmazban.
∎Megjegyzés:
Ez alapján tehát ha r és s az R gyűrű két tetszőleges eleme, akkor az r+I és s+I maradékosztályok viszonyaira vonatkozóan két eset lehetséges. Vagy teljesen megegyeznek egymással, azaz pontosan ugyanazok az elemeik, vagy pedig egyáltalán nincs közös elemük. Ha ugyanis teljesül az r\equiv s\pod I kongruencia, akkor az azt jelenti, hogy r és s ugyanabban a maradékosztályban van, következésképp r+I=s+I. Ha viszont a kongruencia nem teljesül, akkor ők külön maradékosztályba kerültek, amelyeknek a tétel alapján nem lehet közös elemük, hiszen ekvivalencia-osztályok (bővebben lásd a 13.5. Tételt).
♣Az ideálok szerinti kongruenciák tehát eddig láthatóan ugyanúgy „működnek”, mint a gyűrűhomomorfizmusok szerinti kongruenciák. Mindkettő maradékosztályokba sorolja a gyűrű elemeit, méghozzá minden elemet pontosan egybe. Eddig azonban az ideálok tulajdonságaiból csak azt használtuk ki, hogy részgyűrűk, a szorzásra vonatkozó tulajdonságot nem.
Mi azonban egy adott I ideálhoz keresünk egy olyan gyűrűhomomorfizmust, amelynek épp I a magja. Ehhez viszont szükségünk lesz egy célgyűrűre is. Ennek a célgyűrűnek – habár első hallásra furcsának tűnik – az I ideál szerinti maradékosztályok lesznek az elemei, így ezek között be szeretnénk vezetni két műveletet. Az ideálok szorzással kapcsolatos tulajdonságának most lesz jelentősége.
Hogy miért hangzik furcsának bevezetni két műveletet maradékosztályok között? Hát azért, mert a maradékosztályok halmazok, márpedig műveletet általában valamilyen halmaz elemei között szokás bevezetni. A matematikában azonban semmi nem tiltja, hogy bizonyos halmazok elemei maguk is halmazok legyenek. Emlékezzünk vissza, hogy a 13. részben magukat az egész számokat is hasonlóképpen építettük fel. Akkor egy-egy természetes számpárral írtunk le egy készpénz-adósság párost, amely számpárok között definiáltunk egy „azonos vagyoni helyzetet jelöl”-relációt, amelyről megmutattuk, hogy egy ekvivalenciareláció. Az egész számok tulajdonképpen ennek a relációnak az ekvivalencia-osztályai, amelyek között vígan értelmezni tudtuk az összeadást és a szorzást, mint műveletet.
A trükk az volt, hogy két ekvivalencia-osztály összegének vagy szorzatának képzéséhez először kiválasztottunk egy-egy tetszőleges elemet a két osztályból. Ezután ezeken elvégeztük az eredeti halmazon értelmezett megfelelő műveletet, és az eredményül kapott elem ekvivalencia-osztálya lett az ekvivalencia-osztályok közötti összegzés illetve szorzás eredménye.
Most ugyanezt a trükköt fogjuk alkalmazni, amikoris bevezetjük az összeadást és szorzást egy R gyűrű I ideáljának maradékosztályai között. Két maradékosztályt úgy fogunk összeadni, illetve összeszorozni, hogy kiválasztunk belőlük egy-egy tetszőleges elemet, amelyeket összeadunk, illetve összeszorzunk az eredeti R gyűrű műveleteivel, majd azt a maradékosztályt választjuk végeredménynek, amelybe az így kapott elem esik. Egy ilyen maradékosztályok közötti műveletnek nyilvánvalóan akkor van csak értelme, ha az eredményül kapott maradékosztály nem függ attól, hogy a két bemeneti maradékosztályból mely elemeket választottuk ki a művelet elvégzéséhez. Ilyenkor mondjuk azt, hogy a művelet jóldefiniált.
Az alábbi ábrán például az M és N maradékosztályok összeadása látható, amit két különböző elempár segítségével elvégezve ugyanaz az eredmény adódik:
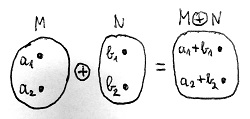
Megköveteljük tehát, hogy függetlenül attól, hogy az a_1+b_1 vagy az a_2+b_2 összeget számítjuk-e ki, az eredménynek mindkét esetben ugyanabba a maradékosztályba kell esnie. Természetesen ugyanezt megköveteljük a szorzásra is.
Egy R gyűrűben egy f gyűrűhomomorfizmus szerinti maradékosztályok közötti összeadás és szorzás jóldefiniáltságát f művelettartó tulajdonságai biztosítják. Ugyanis az a_1\equiv a_2\pod f, és a b_1\equiv b_2\pod f kongruenciák épp azt jelentik, hogy teljesülnek az f(a_1)=f(a_2) és f(b_1)=f(b_2) egyenletek. Ez viszont f összegtartó tulajdonságából következően a 18.12. Definíció utáni megjegyzés alapján épp azt jelenti, hogy az a_1-a_2 és b_1-b_2 különbségek benne vannak f magjában, azaz \ker f-ben. Ám \ker f a 18.17. Tétel miatt részgyűrű R-ben, és így zárt az összeadásra. Ez alapján e két különbség összege, azaz (a_1+b_1)-(a_2+b_2) szintén benne van \ker f-ben, azaz teljesül az a_1+b_1\equiv a_2+b_2\pod f kongruencia. Az összeadás tehát valóban jóldefiniált, hiszen ugyanabba a maradékosztályba eső eredményt kapunk, függetlenül attól, hogy mely elemeket választjuk ki a műveletvégzéshez a két bemeneti maradékosztályból.
A szorzás jóldefiniáltsága f szorzattartó tulajdonságából következik. Ha ugyanis a fenti két egyenletet összeszorozzuk, akkor f(a_1)\cdot f(b_1)=f(a_2)\cdot f(b_2) következik. A szorzattartó tulajdonság miatt ez viszont azt jelenti, hogy f(a_1\cdot b_1)=f(a_2\cdot b_2), azaz teljesül az a_1\cdot b_1\equiv a_2\cdot b_2\pod f kongruencia.
Kérdés, hogy ez a jóldefiniáltság vajon az ideál szerinti maradékosztályokra is teljesül-e. Ezt biztosítja az alábbi tétel.
18.22. Tétel:
Legyen R tetszőleges gyűrű, I pedig valamilyen ideál R-ben. Tegyük fel továbbá, hogy az R gyűrű valamilyen a_1 és a_2 valamint b_1 és b_2 elemeire teljesülnek az alábbi kongruenciák:
\begin{aligned}a_1&\equiv a_2\pod I \\ b_1&\equiv b_2\pod I\end{aligned}Ekkor teljesülnek az alábbi kongruenciák is:
\begin{aligned}a_1+b_1&\equiv a_2+b_2\pod I \\ a_1\cdot b_1&\equiv a_2\cdot b_2\pod I\end{aligned} ♣Bizonyítás:
Az első két kongruencia a 18.20. Definíció alapján épp azt jelenti, hogy az a_1-a_2 és a b_1-b_2 különbségek benne vannak I-ben. Minthogy I részgyűrű R-ben (hiszen ideál), ezért e két különbség összege, azaz (a_1+b_1)-(a_2+b_2) szintén I-ben van, és így valóban teljesül az a_1+b_1\equiv a_2+b_2\pod I kongruencia.
A szorzatra vonatkozó a_1b_1\equiv a_2b_2\pod I kongruencia viszont akkor teljesülne, ha a_1b_1-a_2b_2 is benne lenne I-ben, így most ezt fogjuk ellenőrizni. E kifejezés értéke nem változik, ha kivonunk belőle a_1b_2-t, majd hozzá is adjuk. Ezt felírva, és a_1-et, valamint b_2-t kiemelve ezt kapjuk:
a_1b_1-a_2b_2+a_1b_2-a_1b_2=a_1\cdot (b_1-b_2)+(a_1-a_2)\cdot b_2Nézzük meg a jobboldali kifejezés két tagját. Az első tag ugye az a_1\cdot (b_1-b_2) szorzat. A b_1-b_2 tényezőről tudjuk, hogy benne van I-ben. De mivel I ideál, így egyben balideál is, ezért az ő elemeit balról megszorozva bármilyen R-beli elemmel (például a_1-gyel) az eredmény szintén I-beli lesz (lásd a 18.18. Definíciót). Ugyanezen okok miatt – mivel I jobbideál is – a fenti összeg másik tagja, azaz az (a_1-a_2)\cdot b_2 szorzat is benne van I-ben. Így e két tag összege, azaz lényegében a_1b_1-a_2b_2 szintén benne van I-ben – hiszen I részgyűrű, azaz zárt az összeadásra –, tehát valóban teljesül az a_1b_1\equiv a_2b_2\pod I kongruencia is.
∎Ez tehát azt jelenti, hogy az ideál szerinti maradékosztályok közötti összeadás és szorzás valóban jóldefiniáltak, azaz műveletek a szó algebrai értelmében (lásd a 11.3. Definíciót).
Egyre több jel mutat tehát arra, hogy a gyűrűhomomorfizmusok szerinti kongruencia és az ideálok szerinti kongruencia fogalma tulajdonképpen egy és ugyanaz. Szedjük is össze az eddig megtalált párhuzamokat:
- Két elem között mindkettő pontosan akkor teljesül, ha a különbségük benne van egy bizonyos halmazban. Egyik esetben ez annak a gyűrűhomomorfizmusnak a magja, másik esetben pedig az az ideál, amely szerint képeztük az adott kongruenciát.
- Mindkettő ekvivalenciareláció.
- Mindkettőnek a maradékosztályai teljesen ugyanúgy fejezhetők ki a komplexusműveletek segítségével.
- E maradékosztályok között mindkettő esetben ugyanúgy értelmezhetünk jóldefiniált műveleteket.
Ha ez a két fogalom valóban ugyanaz, akkor az egyben azt is jelenti, hogy egy gyűrűből kiinduló gyűrűhomomorfizmusok magjai és az adott gyűrű ideáljai pontosan ugyanazok a halmazok lesznek. Visszautalnánk a 18.17. Tétel tételre, amelyben már láttuk, hogy a gyűrűhomomorfizmusok magjai mind ideálok. Most azt fogjuk megmutatni, hogy ez visszafelé is igaz.
Ez az alábbi tétel közvetlen következménye lesz, amely az ideál szerinti maradékosztályok halmazán imént bevezetett műveletek tulajdonságairól szól.
18.23. Tétel (Maradékosztálygyűrűk):
Legyen R egy tetszőleges gyűrű, és tegyük fel, hogy I ideál R-ben. Jelöljük R/I-vel azt a halmazt, amelynek elemei a 18.21. Tételben definiált I ideál szerinti maradékosztályok. Vezessünk be ezek között két műveletet az alábbiak szerint:
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek összege legyen az A\oplus B=(a+b)+I maradékosztály.
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek szorzata legyen az A\odot B=(a\cdot b)+I maradékosztály.
Ekkor az R/I halmaz ezzel a két művelettel gyűrűt alkot, amelyet az R gyűrű I ideál szerinti maradékosztálygyűrűjének vagy faktorgyűrűjének nevezünk.
Ha 0_R jelöli az R gyűrű nullelemét, akkor az R/I gyűrű nulleleme a 0_R+I maradékosztály.
Ha -a jelöli az R gyűrű egy a elemének ellentettjét, akkor az R/I gyűrű a+I elemének ellentettje a (-a)+I maradékosztály.
Ha R egységelemes, és 1_R jelöli az egységelemét, akkor R/I is egységelemes, az egységelem pedig az 1_R+I maradékosztály.
Ha R kommutatív, akkor R/I is az.
Tekintsük továbbá azt az f:R\to R/I függvényt, amely minden R-beli r elemhez az r+I maradékosztályt rendeli hozzá az R/I gyűrűből. Ekkor f egy gyűrűhomomorfizmus R és R/I között, melynek magja I. Ennek a neve természetes gyűrűhomomorfizmus.
♣Bizonyítás:
A 18.22. Tétel alapján a maradékosztályok közötti \oplus és \odot műveletek jóldefiniáltak, azaz az eredményként kapott maradékosztály nem függ az a és b reprezentánselemek megválasztásától. Így R/I-re elegendő a 14.12. Definíció szerinti gyűrűaxiómákat ellenőrizni.
Az asszociativitási és disztributivitási tulajdonságok, valamint a \oplus művelet kommutativitása: Azt kell megmutatni, hogy tetszőleges A=a+I, B=b+I és C=c+I maradékosztályok esetén teljesülnek az alábbiak:
\begin{aligned}A\oplus B&=B\oplus A \\ (A\oplus B)\oplus C&=A\oplus (B\oplus C) \\ (A\odot B)\odot C&=A\odot (B\odot C)\\A\odot (B\oplus C)&=(A\odot B)\oplus (A\odot C) \\ (A\oplus B)\odot C &= (A\odot C)\oplus (B\odot C)\end{aligned}A műveletek tételben szereplő definíciói alapján ezek így írhatók fel az a, b és c reprezentánselemek segítségével:
\begin{aligned}(a+b)+I &= (b+a)+I \\ ((a+b)+c)+I&=(a+(b+c))+I \\ ((a\cdot b)\cdot c)+I&=(a\cdot (b\cdot c))+I \\ (a\cdot (b+c))+I&=(ab+ac)+I \\ ((a+b)\cdot c)+I &= (ac+bc)+I\end{aligned}A reprezentánselemek között viszont teljesülnek ezek a tulajdonságok, hiszen ők az R gyűrű elemei.
Nullelem létezése: Az R/I gyűrűben kell egy olyan N maradékosztályt mutatni, amelyre tetszőleges A=a+I maradékosztály esetén teljesül az alábbi:
A\oplus N=N\oplus A=AMivel az \oplus műveletről már láttuk, hogy kommutatív, így elegendő csak az egyik irányú összeadást figyelembe venni. Ha az R gyűrű nulleleme 0_R, akkor az N=0_R+I maradékosztály épp megfelelő lesz nullelemnek az R/I gyűrűben, hiszen:
(\underbrace{a+I}_{=A})\oplus (\underbrace{0_R+I}_{=N})=(a+0_R)+I=a+I=AEllentett elem létezése: Itt azt kell megmutatni, hogy amennyiben N az R/I faktorgyűrű nulleleme, úgy tetszőleges A=a+I elemhez létezik olyan \ominus A-val jelölt elem, amelyre teljesül az alábbi:
A\oplus (\ominus A)=(\ominus A)\oplus A=NMivel az \oplus műveletről már láttuk, hogy kommutatív, így elegendő csak az egyik irányú összeadást figyelembe venni. A \ominus A=(-a)+I maradékosztály épp megfelelő lesz ellentett elemnek az R/I gyűrűben, hiszen:
(\underbrace{a+I}_{=A})\oplus (\underbrace{(-a)+I}_{=\ominus A})=(a-a)+I=0_R+I=NAz R/I halmaz tehát valóban gyűrűt alkot a tételben szereplő műveletekkel. Tegyük most fel, hogy R egységelemes, és jelöljük 1_R-rel az egységelemet. Feladatunk mutatni az R/I gyűrűben egy olyan E maradékosztályt, amelyre tetszőleges A=a+I maradékosztály esetén teljesül az alábbi:
A\odot E=E\odot A=AHa az R gyűrű egységeleme 1_R, akkor az 1_R+I maradékosztály épp megfelelő lesz egységelemnek az R/I gyűrűben, hiszen:
\begin{aligned}(\underbrace{a+I}_{=A})\odot (\underbrace{1_R+I}_{=E})&=(a\cdot 1_R)+I=a+I=A \\(\underbrace{1_R+I}_{=E})\odot (\underbrace{a+I}_{=A})&=(1_R\cdot a)+I=a+I=A\end{aligned}Most tegyük fel, hogy R kommutatív, és legyen az A=a+I valamint a B=b+I két tetszőleges maradékosztály az R/I gyűrűben. Ekkor R kommutativitása miatt teljesül az alábbi, azaz R/I is valóban kommutatív:
\begin{aligned}A\odot B&=(a+I)\odot (b+I)=(a\cdot b)+I=\\&=(b\cdot a)+I=(b+I)\odot (a+I)=B\odot A\end{aligned}Végezetül meg kell mutatni, hogy a tételben szereplő f:R\to R/I függvény egy gyűrűhomomorfizmus az eredeti és az R/I faktorgyűrű között. Az f függvény tehát minden R-beli r elemhez az r+I maradékosztályt rendeli hozzá. Tegyük fel, hogy r és s az R gyűrű tetszőleges elemei. Ekkor a művelettartó tulajdonságok az alábbiak alapján valóban teljesülnek:
\begin{aligned}f(r)\oplus f(s)&=(r+I)\oplus (s+I)=(r+s)+I=f(r+s) \\ f(r)\odot f(s)&=(r+I)\odot (s+I)=(r\cdot s)+I=f(r\cdot s) \end{aligned}Végül azt kell megmutatni, hogy f magja épp az I ideál. Egy tetszőleges R-beli s elemhez az f gyűrűhomomorfizmus pontosan akkor rendeli hozzá az R/I gyűrű nullelemét, azaz a 0_R+I maradékosztályt, ha f(s)=s+I=0_R+I. Minthogy I egy részgyűrű R-ben (hiszen ideál), ezért a 18.15. Tétel 3. pontja alapján ő az, aki tartalmazza 0_R-t, azaz 0_R+I=I. Az f(s)=0_R+I tehát akkor és csak akkor teljesül, ha s benne van I-ben. Az I ideál tehát valóban magja az f gyűrűhomomorfizmusnak.
∎Az imént bizonyított és a 18.17. Tétel következményeként mostmár egyértelműen azonosítani tudjuk egy gyűrű azon részhalmazait, amelyek valamilyen gyűrűhomomorfizmusok magjai lehetnek. Erről szól az alábbi következmény.
18.24. Következmény:
Legyen adva egy R gyűrű és annak egy I részhalmaza. Az I részhalmaz akkor és csak akkor magja egy valamilyen R-ből kiinduló gyűrűhomomorfizmusnak, ha ideál R-ben.
♣Bizonyítás:
Ha I magja egy gyűrűhomomorfizmusnak, akkor a 18.17. Tétel alapján ideál R-ben, azaz I\triangleleft R. Megfordítva: Ha I ideál R-ben, akkor a 18.23. Tétel alapján az R-ből kiinduló és az R/I faktorgyűrűbe mutató természetes gyűrűhomomorfizmusnak éppen I a magja.
∎Ez tehát azt jelenti, hogy a 18.9. Definícióban bevezetett gyűrűhomomorfizmus szerinti kongruencia fogalma helyett nyugodtan használhatjuk a továbbiakban a 18.20. Definícióban bevezetett ideál szerinti kongruencia fogalmát. A 18.13. Tétel alapján ugyanis egy kongruenciareláció nem függ konkrét gyűrűhomomorfizmusoktól, hanem azoknak csakis a magjától. Most viszont épp azt bizonyítottuk, hogy bármely R gyűrűben a belőle kiinduló gyűrűhomomorfizmusok magjai épp egybeesnek R ideáljaival. Így tehát egy gyűrű ideáljai alapján az összes létező kongruenciarelációt megkaphatjuk, ami csak értelmezhető az adott gyűrűn.
Gyűrűk homomorfizmustétele
A fenti meglehetősen absztrakt fogalmakra most egy kézenfekvő példát mutatunk. Fentebb már előkerült a 3\Z halmaz, amely a 3-mal osztható egész számokat tartalmazza. Erről már megállapítottuk, hogy ő egy ideál \Z-ben. Mi történik, ha \Z-t ezzel az ideállal faktorizáljuk, azaz képezzük a \Z/3\Z maradékosztálygyűrűt? Ennek 3 eleme lesz, méghozzá a 3\Z ideál szerinti maradékosztályok.
A komplexusműveletekkel jelölve a 3 maradékosztály a következő: a 0+3\Z, az 1+3\Z valamint a 2+3\Z. Ezek azokból az egész számokból fognak állni, amelyek 3-mal osztva rendre 0, 1 illetve 2 maradékot adnak. Az ezek közötti műveleteket a 18.23. Tétel alapján könnyen elvégezhetjük. Például az 1+3\Z és a 2+3\Z maradékosztályok összege a 0+3\Z, szorzata pedig a 2+3\Z maradékosztály lesz. Vezessük be a 3 maradékosztályra az alábbi jelöléseket:
\begin{aligned}[0]_3&=0+3\Z \\ [1]_3&=1+3\Z \\ [2]_3&=2+3\Z\end{aligned}Ekkor a \Z/3\Z faktorgyűrű műveleti táblái így néznek ki:
\begin{array}{cc} \begin{array}{c|ccc} \oplus & [0]_3 & [1]_3 & [2]_3 \\ \hline [0]_3 & [0]_3 & [1]_3 & [2]_3 \\ [1]_3 & [1]_3 & [2]_3 & [0]_3 \\ [2]_3 & [2]_3 & [0]_3 & [1]_3 \end{array} & \begin{array}{c|ccc} \odot & [0]_3 & [1]_3 & [2]_3 \\ \hline [0]_3 & [0]_3 & [0]_3 & [0]_3 \\ [1]_3 & [0]_3 & [1]_3 & [2]_3 \\ [2]_3 & [0]_3 & [2]_3 & [1]_3 \end{array} \end{array}Ha összehasonlítjuk ezeket a műveleti táblákat a fejezet elején bemutatott \Z_3 gyűrű műveleti tábláival, akkor azt tapasztaljuk, hogy szinte megegyeznek egymással. Algebrai szóhasználattal élve úgy tűnik, mintha a \Z_3 és \Z/3\Z gyűrűk izomorfak lennének. Íme a \Z_3 gyűrű műveleti táblái:
\begin{array}{cc}\begin{array}{c|ccc}\oplus &0&1&2\\ \hline 0&0&1&2 \\1&1&2&0\\2&2&0&1\end{array} & \begin{array}{c|ccc}\odot &0&1&2\\ \hline 0&0&0&0 \\1&0&1&2\\2&0&2&1\end{array}\end{array}Ez nem véletlenül van így! Emlékezzünk csak vissza, hogy a \Z_3 gyűrű tulajdonképpen nem más, mint egy \Z-ből kiinduló gyűrűhomomorfizmus, nevezetesen a \bmod_3 maradékképző függvény képe. Ráadásul ennek a gyűrűhomomorfizmusnak a magja épp a 3-mal osztható egész számok halmaza, azaz 3\Z. Ez éppenséggel az az ideál, amelynek a segítségével a \Z/3\Z faktorgyűrűt képeztük.
Az alábbi tétel szerint általánosságban is igaz, hogyha egy R gyűrűt egy belőle kiinduló f gyűrűhomomorfizmus magjával faktorizálunk, akkor az így kapott faktorgyűrű izomorf lesz f képével.
18.25. Tétel (Gyűrűk homomorfizmustétele):
Legyenek R és S tetszőleges gyűrűk, valamint tegyük fel, hogy adva van egy f:R\to S gyűrűhomomorfizmus. Ekkor R/\ker f \simeq \text{im} f, azaz az R-ből képzett f magja szerinti faktorgyűrű izomorf f képével.
♣Bizonyítás:
Előszöris megjegyezzük, hogy a 18.17. Tétel alapján \ker f ideál R-ben, így a baloldalon álló R/\ker f faktorgyűrű valóban értelmes. Igaz továbbá, hogy a 18.16. Tétel alapján \text{im} f részgyűrű abban a gyűrűben, ahová f mutat, így a tételben szereplő gyűrűizomorfia jobboldala is értelmes. Most megmutatjuk, hogy az izomorfia valóban teljesül.
Az R/\ker f faktorgyűrű elemei a \ker f, mint ideál szerinti maradékosztályok. Ezek a 18.12. Definíció utáni megjegyzés alapján pontosan ugyanazok a maradékosztályok lesznek, mint a 18.9. Definíció által definiált f gyűrűhomomorfizmus szerinti maradékosztályok.
Most definiálunk egy g:R/\ker f\to \text{im} f leképezést e faktorgyűrű és az f gyűrűhomomorfizmus képe között. Ennek a leképezésnek a képletét az R gyűrű elemeinek és az f gyűrűhomomomorfizmusnak a segítségével adjuk meg. Az alábbi képlet azt fejezi ki, hogy minden r elem esetén a g leképezés az r-et tartalmazó MARADÉKOSZTÁLYhoz épp azt az elemet rendeli hozzá a célgyűrűből, amelyet az f gyűrűhomomorfizmus is hozzárendel magához az r ELEMhez:
g(r+\ker f)=f(r)Az alábbi ábra mutatja a g leképezés iménti konstrukcióját.

Ez egy értelmes leképezés, ha ugyanis valamely r_1 és r_2 elemek ugyanabban a maradékosztályban vannak, akkor az ő különbségük benne van f magjában, ami épp azt jelenti, hogy az f szerinti képük megegyezik. Így tehát a g leképezés eredménye nem függ attól, hogy a bemeneti maradékosztály mely reprezentánselemének segítségével számítottuk azt ki a fenti képlettel.
Most igazoljuk, hogy a g leképezés kölcsönösen egyértelmű. Előszöris azt mutatjuk meg, hogy két különböző maradékosztály g szerinti képe is különbözik. Tegyük fel ezért indirekt, hogy az R gyűrű r és s elemei két különböző maradékosztályban vannak, ám e két maradékosztálynak ennek ellenére ugyanaz a g szerinti képe, azaz g(r+\ker f)=g(s+\ker f). Ez a g leképezés definíciója alapján azt jelentené, hogy f(r)=f(s). De ez ellentmondás, hiszen ez azt jelentené, hogy r és s mégis ugyanabban a maradékosztályban van. Azt tehát már tudjuk, hogy az \text{im} f célgyűrű minden eleme legfeljebb egy maradékosztálynak lehet a g szerinti képe, azaz g injektív.
A kölcsönös egyértelműséghez azt kell még igazolni, hogy a célgyűrűben nincs olyan elem, amely ne lenne képe valamely maradékosztálynak a g függvény szerint (azaz, hogy g szürjektív). Ez viszont természetesen teljesül, hiszen a célgyűrű nem más, mint \text{im} f, azaz az f gyűrűhomomorfizmus képe. Következésképp minden itt lévő s elemhez létezik olyan x elem az R gyűrűben, amelynek épp s a képe az f függvény szerint (azaz f(x)=s). Ez az x elem viszont benne van az x+\ker f maradékosztályban, amelyhez viszont a g függvény rendeli hozzá az s elemet a célgyűrűben. A g függvény tehát valóban kölcsönösen egyértelmű.
A g művelettartási tulajdonságai a fenti képletből már könnyen adódnak:
\begin{aligned}g((r+\ker f)\oplus (s+\ker f))&=g((r+s)+\ker f)=\\&=f(r+s)=f(r)+f(s)=\\&=g(r+\ker f)+g(s+\ker f) \\ g((r+\ker f)\odot (s+\ker f))&=g((r\cdot s)+\ker f)=\\&=f(r\cdot s)=f(r)\cdot f(s)=\\&=g(r+\ker f)\cdot g(s+\ker f)\end{aligned}Így tehát g valóban gyűrűizomorfizmus az R/\ker f faktorgyűrű és f képe között.
∎Ennek alkalmazásához most visszautalnánk a 18.13. Tétel kapcsán felvetett példára. Ez a tétel szólt arról, hogy egy f gyűrűhomomorfizmus szerinti kongruenciát kizárólag f magja, nem pedig maga f határoz meg. Ennek demonstrálásához képeztünk két különböző, de azonos magú gyűrűhomomorfizmust az egész számok \Z gyűrűjéből két másik gyűrűre. Ezek közül az egyik a már jól ismert kételemű \Z_2 gyűrű volt. A másik gyűrűt akkor P-vel jelöltük, és alaphalmaza az e és o betűket tartalmazta. Ennek a meglehetősen mesterkélt gyűrűnek a műveleteit a műveleti tábláival adtuk meg. Azt tapasztaltuk, hogy a két gyűrű csak az elemek elnevezésében és a használt műveleti jelekben tért el egymástól, de ezeken kívül teljesen ugyanaz volt a szerkezetük. Azaz izomorfak voltak egymással.
Nos, ez az imént bizonyított homomorfizmustétel következménye. A \Z_2 és P gyűrűkbe mutató két gyűrűhomomorfizmusnak ugyanis megegyezett a magja, amely ugye – mint ahogy azt a 18.24. Következmény alapján már tudjuk – egy ideál a \Z gyűrűben. Következésképp a homomorfizmustétel miatt mindkét gyűrű izomorf a \Z gyűrű ezen ideál szerinti faktorgyűrűjével, és így a 18.6. Definíció utáni megjegyzés alapján egymással is.
Ebben a részben tehát megismerkedtünk a Diffie-Hellman kulcscsere protokollban és az RSA-eljárásban használt moduláris aritmetika matematikai alapjaival. Ennek kapcsán megismerkedtünk olyan gyűrűkkel, amelyeknek csak véges sok elemük van, és meg is tanultunk számolni ezekben a gyűrűkben. Ehhez kulcsfontosságú volt a gyűrűhomomorfizmus fogalmának megismerése, amelynek a segítségével mellesleg igazoltuk a Diffie-Hellman kulcscsere protokoll helyességét. Ezután tetszőleges gyűrűkben azonosítottuk azokat a részhalmazokat, amelyek valamilyen gyűrűhomomorfizmusok magjai lehetnek. Mindeközben megismerkedtünk a kongruenciák, az ideálok és a maradékosztálygyűrűk fogalmával.
A következő részekben az ideálok segítségével végleg lezárjuk a számelmélet alaptételének kérdését. Ennek során megismerkedünk az úgynevezett főideálgyűrűkkel, majd az egész számokon értelmezett kongruenciákat fogjuk tanulmányozni.
A következő részt itt találod…




Kedves Dávid!
Köszönöm ezt a nagyszerű cikksorozatot!
A Facebookon láttam egy hozzászólást, hogy jó lenne, ha lehetne változatlan minőségben nyomtatni a részeket. Még a LaTeX formátum is szóba került ott.
Engem is foglalkoztatott ez a dolog már hetek óta, ezért hozzá is fogtam a megoldás kereséséhez. 3-féle megoldást találtam:
1) a html/css tartalom módosítása, ha van van jogosultsága a változtatáshoz;
2) az tartalom beillesztése a KaTeX scriptek után. Ekkor is megmarad az eredeti külalak;
3) készítettem egy Python programot, amellyel a htmlből LaTeX kódot kaphatok.
Én a 18. részt használtam a kísérletezéshez. Ha érdekli részletesebben, akkor keressen meg emailben.
Címem: nadsanyi@gmail.com
Üdvözlettel,
Nagy Sándor
Kedves Sándor!
Köszönöm a javaslatokat.
Az 1) pontnál gondolom arra gondol, hogy legyen külön media query a CSS-ben nyomtatás esetére. Ez járható út lenne rövidtávon, mivel teljesen az én kezemben van a tárhely.
A 2) pontot nem teljesen értem.
A 3) pontban említett program kimenete érdekelne, mivel én is valami hasonlót tervezek azzal a különbséggel, hogy az közvetlenül az adatbázisból dolgozna, és így képes volna kezelni a kereszthivatkozásokat is a teljes cikksorozat szintjén. Ezáltal egy komplett nyomdakész könyvkiadványt lehetne létrehozni akár egyetlen kattintással.
El tudná küldeni a 18. részről készült kimenetet az admin@youproof.hu címre?
Üdvözlettel,
Moldvai Dávid
Esetleg meg lehetne még próbálni WordPress-ből Markdown-ba. Nem próbáltam, de ha igaz akkor az összes posztot lehetne egyszerre (persze tudom, hogy M.D. alaposan belenyúlt a WordPress motorjába, tehát lehet még se olyan egyszerű):
https://kevq.uk/how-to-convert-wordpress-to-markdown/
Ez valószínűleg nem lenne teljesen magától értetődő, mivel – ahogy említetted – a tételek, definíciók, bizonyítások és magyarázatok külön entitásként (WordPress terminológiával élve post-ként) vannak kezelve adatbázis szinten. A cikkekbe ezek shortcode-okkal vannak beágyazva, a közöttük lévő asszociációk (például hogy egy bizonyítás melyik tételnek a bizonyítása, illetve hogy egy definíció melyik cikkhez tartozik) pedig eléggé trükkös módon taxonomy realtionship-ekkel vannak reprezentálva.