A 18. részben bevezettük a „gyűrűhomomorfizmus” és az ehhez szorosan kapcsolódó „gyűrűhomomorfizmus szerinti kongruencia” fogalmát. Megmutattuk ugyanakkor, hogy egy ilyen reláció nem függ egy konkrét gyűrűhomomorfizmustól, hanem annak csak a „magjától”. Ezeket a részhalmazokat „ideáloknak” neveztük el, definiáltuk az „ideál szerinti kongruenciát”, és igazoltuk, hogy ez a kétféle kongruencia-fogalom valójában egy és ugyanaz. Ennek során ismerkedtünk meg az úgynevezett „maradékosztálygyűrű” vagy „faktorgyűrű” fogalmával, amely ebben a részben kap fontos szerepet. Végül az előző részben az ideálok segítségével megadtunk egy szükséges és elégséges feltételt a számelmélet alaptételének teljesülésére, valamint megismerkedtünk a „főideálgyűrűk” fogalmával.
De vajon mit jelent a kongruencia és a maradékosztálygyűrű fogalma az egész számok esetén? Mik azok a teljes és redukált maradékrendszerek, és milyen tulajdonságaik vannak? Mit mér az Euler-féle \varphi-függvény? Mit nevezünk lineáris kongruenciának és mikor létezik megoldása? Mit állít az Euler-Fermat tétel és miért olyan fontos? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 17., 18. és 19. részekben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy a és b egy valamilyen R integritástartomány tetszőleges elemei. Az a és b elemek kitüntetett közös osztója a d elem, ha teljesül az alábbi két tulajdonság:
- Fennállnak a d|a és d|b oszthatóságok.
- Tetszőleges c elem esetén ha fennállnak a c|a és c|b oszthatóságok, akkor fennáll a c|d oszthatóság is.
Azaz a kitüntetett közös osztó minden közös osztónak többszöröse. Az a és b elemek kitüntetett közös osztójának jelölése: (a,b).
Legyen m\neq 0 tetszőleges nemnulla egész szám. Jelölje \Z_m azt a halmazt, amelynek elemei az m abszolútértékénél kisebb, nemnegatív (azaz a 0, 1, 2, ..., |m|-1) egész számok. E halmaz elemeit modulo m maradékoknak nevezzük.
Azt a \bmod_m:\Z \to \Z_m függvényt, amely minden egész számhoz az m-mel képzett nemnegatív osztási maradékát rendeli, modulo m maradékképző függvénynek nevezzük.
A \bmod_m függvény, valamint a szokásos összeadás és szorzás segítségével értelmezzünk két darab kétváltozós műveletet a \Z_m halmaz elemei között az alábbiak szerint:
\begin{aligned}a\oplus b &= \bmod_m(a+b) \\ a\odot b &= \bmod_m(a\cdot b)\end{aligned}A \oplus szimbólummal jelölt műveletet modulo m összeadásnak, a \odot szimbólummal jelölt műveletet modulo m szorzásnak, az m egész számot pedig modulusnak nevezzük. Amennyiben az adott kontextusban nem fontos a modulus, úgy a fenti műveleteket egyszerűen csak moduláris összeadásnak és moduláris szorzásnak hívjuk.
Tegyük fel, hogy R és S tetszőleges gyűrűk, valamint adva van közöttük egy f:R\to S gyűrűhomomorfizmus. Amennyiben az R gyűrű valamilyen a és b elemeire teljesül, hogy f(a)=f(b), akkor azt mondjuk, hogy a és b kongruensek az f gyűrűhomomorfizmus szerint. Ezt a relációt így jelöljük:
a\equiv b\pod fAmennyiben a és b között nem áll fenn az imént definiált f szerinti kongruencia, akkor őket inkongruensnek nevezzük az f gyűrűhomomorfizmus szerint. Ezt így jelöljük:
a\ \cancel{\equiv}\ b\pod fLegyen adva egy R gyűrű, valamint annak egy I részhalmaza, amely részgyűrű R-ben. Tegyük fel továbbá, hogy r az R gyűrű egy tetszőleges – tehát nem feltétlenül I-beli – eleme.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az r\cdot a szorzat is I-ben van, akkor azt mondjuk, hogy I balideál R-ben.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az a\cdot r szorzat is I-ben van, akkor azt mondjuk, hogy I jobbideál R-ben.
Amennyiben egy I részgyűrű egyszerre bal- és jobbideál, akkor azt mondjuk, hogy I kétoldali ideál, vagy egyszerűen csak ideál R-ben. Ezt így jelöljük: I\triangleleft R.
A nullgyűrű és maga a teljes R nyilvánvalóan ideálok R-ben. Ezeket triviális ideáloknak nevezzük.
Legyen R tetszőleges gyűrű és legyen I valamilyen ideál R-ben. Amennyiben az R gyűrű valamilyen a és b elemeire teljesül, hogy az a-b különbség az I ideálnak eleme, akkor azt mondjuk, hogy a és b kongruensek az I ideál szerint (vagy kongruensek modulo I). Ezt a relációt így jelöljük:
a\equiv b\pod IAmennyiben a és b között nem áll fenn az imént definiált modulo I kongruencia, akkor őket inkongruensnek nevezzük modulo I. Ezt így jelöljük:
a\ \cancel{\equiv}\ b\pod ILegyen R egy tetszőleges gyűrű, és tegyük fel, hogy I ideál R-ben. Jelöljük R/I-vel azt a halmazt, amelynek elemei a 18.21. Tételben definiált I ideál szerinti maradékosztályok. Vezessünk be ezek között két műveletet az alábbiak szerint:
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek összege legyen az A\oplus B=(a+b)+I maradékosztály.
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek szorzata legyen az A\odot B=(a\cdot b)+I maradékosztály.
Ekkor az R/I halmaz ezzel a két művelettel gyűrűt alkot, amelyet az R gyűrű I ideál szerinti maradékosztálygyűrűjének vagy faktorgyűrűjének nevezünk.
Ha 0_R jelöli az R gyűrű nullelemét, akkor az R/I gyűrű nulleleme a 0_R+I maradékosztály.
Ha -a jelöli az R gyűrű egy a elemének ellentettjét, akkor az R/I gyűrű a+I elemének ellentettje a (-a)+I maradékosztály.
Ha R egységelemes, és 1_R jelöli az egységelemét, akkor R/I is egységelemes, az egységelem pedig az 1_R+I maradékosztály.
Ha R kommutatív, akkor R/I is az.
Tekintsük továbbá azt az f:R\to R/I függvényt, amely minden R-beli r elemhez az r+I maradékosztályt rendeli hozzá az R/I gyűrűből. Ekkor f egy gyűrűhomomorfizmus R és R/I között, melynek magja I. Ennek a neve természetes gyűrűhomomorfizmus.
Legyen R tetszőleges gyűrű, I pedig valamilyen ideál R-ben. Amennyiben R-nek létezik olyan véges számú elemet tartalmazó X=\{a_1;a_2;\ldots;a_n\} részhalmaza, amely esetén \lang X\rang =I, akkor azt mondjuk, hogy az I ideál végesen generált. Ezt így jelöljük: I=(a_1,a_2,\ldots,a_n).
Speciálisan ha I generálható az R gyűrű egyetlen eleméből álló részhalmazával, akkor I-t főidálnak nevezzük. Az a\in R által generált I főideált így jelöljük: I=(a).
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Amennyiben R minden ideálja főideál (azaz generálható egyetlen elemmel), akkor R-t főideálgyűrűnek nevezzük.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 17., 18. és 19. részeket, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Első körben azt fogjuk megvizsgálni, hogy az egész számok \Z gyűrűjén pontosan mit jelent a 18.20. Definícióban bevezetett, meglehetősen absztrakt ideál szerinti kongruencia. Ehhez előszöris meg kell találnunk e gyűrű ideáljait. A 19.16. Tétel alapján minden euklidészi gyűrű – és így speciálisan maga \Z is – főideálgyűrű.
Ez a 19.15. Definíció szerint azt jelenti, hogy \Z összes ideálja egy-egy elemmel generálható. Ha tehát kiválasztunk egy tetszőleges m egész számot, akkor az m-et tartalmazó legszűkebb \Z-beli ideált úgy kapjuk meg, hogy képezzük m összes többszörösét. Ezt a halmazt a 19.11. Definíció alapján az m egész szám által generált főideálnak nevezzük, és (m)-mel jelöljük. Ha például m=3, akkor az ehhez tartozó főideál – az előző részben tanult halmazjelölésekkel – az alábbi halmaz lesz:
(3)=\{\ldots;-9;-6;-3;0;3;6;9;\ldots\}Ezután a 18.20. Definíciót szó szerint követve már könnyedén megmondhatjuk bármely a és b egész számokról, hogy vajon kongruensek-e a (3) főideál szerint vagy nem. Az említett definíció szerint ez a kongruencia pontosan akkor teljesül, ha az a-b különbség eleme ennek az ideálnak, azaz – szintén az előző részben tanult halmazjelölésekkel – (a-b)\in (3). Például a 13 és a 7 között fennál a (3) főideál szerinti kongruencia, mivel 13-7=6\in (3). Ezzel szemben a 18 és a 13 egész számok inkongruensek a (3) főideál szerint, hiszen 18-13=5\notin (3).
Ez persze nem túl intuitív, és nem is ez volt a kongruencia fogalmának eredeti jelentése. Ezt a relációt Carl Friedrich Gauss német matematikus vezette be a Disquisitiones Arithmeticae című művében, és kizárólag az egész számok között volt értelmezve. Ehhez képest az ideál fogalmának alapjait Ernst Kummer, szintén német matematikus fektette le jó 50 évvel később, amikor a mintegy 350 évig megoldatlan Nagy Fermat-sejtést akarta bizonyítani. Ez ugyan végül nem sikerült neki, de jelentős előrehaladást sikerült elérnie, és felfedezései a 20. században kifejlesztett számelméleti eszközöket is megalapozták.
Először tehát azt fogjuk megvizsgálni, hogy mi volt a kongruencia fogalmának eredeti jelentése, és hogyan kapcsolódik ez a 18.20. Definícióban bevezetett ideál szerinti kongruenciákhoz.
Kongruencia az egész számok között
Gauss eredetileg az osztási maradékokkal kapcsolatban használta a kongruencia fogalmát. Tegyük fel, hogy adva van egy m\neq 0 nemnulla egész szám, amelyet modulusnak fogunk nevezni. A gauss-féle értelmezésben két tetszőleges a és b egész számot akkor nevezünk kongruensnek az m modulus szerint, ha ugyanazt a nemnegatív maradékot adják m-mel osztva. Ezt – némiképp eltérve a 18.20. Definícióben szereplő általános jelöléstől – így jelöljük:
a\equiv b\pmod mA fentebbi példák ugyanúgy igazak maradnak ebben az értelmezésben is. Például a 13 és a 7 között fennál a kongruencia a 3 modulus szerint (vagy „modulo 3”), mivel mindkettőnek 1 lesz a nemnegatív maradéka 3-mal osztva. Ezzel szemben a 18 és a 13 egész számok inkongruensek modulo 3, hiszen a 18-nak 0, míg a 13-nak 1 lesz a nemnegatív maradéka 3-mal osztva.
Megjegyezzük, hogy a maradék nemnegativitását azért fontos megkövetelni, mivel a 18.2. Tétel ebben az esetben garantálja a maradék egyértelműségét. Ha ezt nem követelnénk meg, akkor például a 13 kétféle maradékot is adhatna 3-mal osztva:
\begin{aligned}13&=4\cdot 3+1 \\ 13&=5\cdot 3-2\end{aligned}Látható, hogy mindkét maradék teljesíti a 17.16. Definícióban szereplő euklidészi osztásra vonatkozó kritériumokat, hiszen mind az 1, mind pedig a -2 maradékok abszolútértéke kisebb 3-nál. Ha viszont a negatív maradékokat kizárjuk, akkor a 18.2. Tétel szerint az euklidészi osztás már csak egyféleképpen végezhető el.
Visszatérve tehát a kongruencia fogalmának gauss-féle értelmezésére, az látszólag megegyezik a 18.20. Definícióban szereplő ideál szerinti kongruencia-fogalommal. Legalábbis bármely két egész szám vagy mindkét értelmezés szerint kongruens lesz egymással, vagy egyik szerint sem. Az alábbi tételben ezt általánosságban is igazoljuk.
20.1. Tétel (Egész számok közötti kongruencia):
Legyenek a, b két tetszőleges, valamint m\geq 0 nemnegatív egész szám, és legyen I az m által generált főideál, azaz I=(m). Ekkor teljesülnek az alábbiak:
- Amennyiben m\gt 0, úgy a 18.20. Definíció szerinti a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha a és b ugyanazt a nemnegatív maradékot adja m-mel osztva.
- Amennyiben m=0, úgy az a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha a=b.
- Általánosságban az a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha fennáll az m|a-b oszthatóság.
- Speciálisan amennyiben m=1, úgy az a\equiv b\pod I kongruencia mindig teljesül.
Az a és b egész számok közötti, I=(m) főideál szerinti kongruenciát illetve inkongruenciát speciálisan így is jelölhetjük:
\begin{aligned}&a\equiv b\pmod m \\ &a\ \cancel{\equiv}\ b\pmod m \end{aligned}Ilyenkor azt mondjuk, hogy az a egész szám kongruens a b egész számmal az m modulus szerint, vagy modulo m.
♣Bizonyítás:
Az 1. állítás: Minthogy I egy ideál az egész számok \Z gyűrűjében, ezért a 18.24. Következmény miatt ő biztosan magja egy valamilyen \Z-ből kiinduló f gyűrűhomomorfizmusnak. Ugyanezen tétel, valamint a 18.12. Definíció utáni megjegyzés miatt azonban a 18.20. Definícióban definiált I ideál szerinti kongruencia és a 18.9. Definícióban definiált f gyűrűhomorfizmus szerinti kongruencia két egymással teljesen ekvivalens reláció. Ez azt jelenti, hogy az alábbi két kongruencia egyszerre teljesül, vagy nem teljesül:
\begin{aligned}a&\equiv b\pod I\\a&\equiv b\pod f\end{aligned}Azaz nincs más dolgunk, mint találni egy olyan f gyűrűhomomorfizmust, amelynek a magja éppen az I ideál. Vegyük észre, hogy mivel most m\neq 0, ezért a 18.3. Definícióban definiált \bmod_m-mel jelölt modulo m maradékképző függvény értelmezhető, és épp megfelel erre a célra. Ez a függvény ugyanis a 18.7. Tétel szerint egy szürjektív gyűrűhomomorfizmus az egész számok \Z és a modulo m maradékok \Z_m gyűrűje között. Ennek magja ráadásul épp az I=(m) főideál, hiszen ez pontosan az m egész szám többszöröseit tartalmazza, márpedig ezekhez – és csak ezekhez – a \bmod_m maradékképző függvény a 0 maradékot rendeli hozzá.
Eszerint tehát az a\equiv b\pod I ideál szerinti kongruencia pontosan akkor teljesül, amikor teljesül az a\equiv b\pod{\bmod_m} gyűrűhomomorfizmus szerinti kongruencia. Ez utóbbi viszont pontosan akkor teljesül, ha a \bmod_m maradékképző függvény a-hoz és b-hez ugyanazt a maradékot rendeli hozzá.
A 2. állítás: Amennyiben m=0, akkor nem értelmezett a \bmod_m maradékképző függvény, így ebben az esetben az ideál szerinti kongruencia 18.20. Definíciójából kell kiindulnunk. Eszerint az a\equiv b\pod I kongruencia pontosan akkor teljesül, ha az a-b különbség benne van az I ideálban. Ez az ideál azonban nem más, mint az m=0 által generált főideál. Minthogy a 16.2. Tétel 4. pontja alapján a 0-nak önmagán kívül nincs más többszöröse, ezért a (0) főideál mindössze a 0 egész számból fog állni. Eszerint tehát az a\equiv b\pod I pontosan akkor teljesül, ha a-b=0, vagy másként fogalmazva a=b.
A 3. állítás az 1. és a 2. állítások általánosítása. Az I=(m) főideál pontosan az m egész szám többszöröseit tartalmazza. Emiatt az a-b különbség pontosan akkor van benne ebben az ideálban – azaz teljesül az a\equiv b\pod I kongruencia –, ha fennáll az m|a-b oszthatóság.
Végül a 4. állítás a 3. állítás speciális esete. Ebben az esetben I=(1), de mivel az 1 egész szám a \Z gyűrű egységeleme, ezért a 16.3. Definíció utáni megjegyzés miatt egyúttal egység is. Minthogy egy egységnek minden gyűrűelem többszöröse, ezért az I=(1) főideál valójában a teljes \Z gyűrű lesz. Azaz ebben az esetben valóban mindig teljesül az a\equiv b\pod I kongruencia.
∎Megjegyzés:
Az a\equiv b\pmod m jelölés némiképp eltér az ideál szerinti kongruencia 18.20. Definíciójában szereplő jelöléstől. Történelmileg az előbbi volt hamarabb, és ekkor még kizárólag az osztási maradékokkal kapcsolatos jelentést értették alatta, amelyet épp a tétel 1. állítása fogalmaz meg. Ennek bizonyításában a \bmod_m gyűrűhomomorfizmus szerinti kongruenciához jutottunk, amelynek a\equiv b\pod{\bmod_m} jelölése nagyban hasonlít a gauss-féle a\equiv b\pmod m jelölésre.
Megjegyezzük még, hogy a modulusról látszólag feleslegesen kötöttük ki, hogy nemnegatív, hiszen a fenti bizonyítás ezt egyáltalán nem használja ki. A 18.3. Definíció utáni megjegyzés 3. pontja alapján azonban bármilyen egész szám modulo m maradéka megegyezik a modulo -m maradékával, így tehát a modulo m kongruencia pontosan ugyanaz a reláció lenne, mint a modulo -m kongruencia. Ez az oka annak, hogy negatív modulusokat nem használunk, hiszen azok helyettesíthetők a pozitív párjukkal.
♣Kongruenciák alapvető tulajdonságai
Az egész számok közötti kongruencia-fogalom tehát az ideál szerinti kongruencia-fogalom egy speciális esete, amelynek az előző szakaszban egy intuitív, osztási maradékokkal kapcsolatos értelmezését kaptuk. Az alábbi tételben összegyűjtöttük ennek a relációnak az alapvető tulajdonságait. Ezek mindegyikét valamilyen általános formában már igazoltuk a 18. részben.
20.2. Tétel:
Legyenek a, b, c, d tetszőleges, valamint m\geq 0 nemnegatív egész szám. Ekkor teljesülnek az alábbiak:
- Teljesül az a\equiv a\pmod m kongruencia, azaz minden egész szám kongruens önmagával modulo m.
- Ha a\equiv b\pmod m, akkor b\equiv a\pmod m.
- Ha a\equiv b\pmod m és b\equiv c\pmod m, akkor a\equiv c\pmod m.
- Ha a\equiv b\pmod m és c\equiv d\pmod m, akkor a+c\equiv b+d\pmod m és a-c\equiv b-d\pmod m.
- Ha a\equiv b\pmod m és c\equiv d\pmod m, akkor a\cdot c\equiv b\cdot d\pmod m.
- Ha a\equiv b\pmod m, akkor a+c\equiv b+c\pmod m és a-c\equiv b-c\pmod m.
- Ha a\equiv b\pmod m, akkor a\cdot c\equiv b\cdot c\pmod m.
- Ha a\equiv b\pmod m, akkor bármilyen pozitív egész n kitevő esetén a^n\equiv b^n\pmod m.
- Ha a\equiv b\pmod m, akkor m bármilyen nemnegatív k osztója esetén a\equiv b\pmod k.
Bizonyítás:
A 20.1. Tétel alapján az egész számok közötti modulo m kongruencia teljesen ekvivalens az (m) főideál szerinti kongruenciával, ezért minden olyan tétel vonatkozik rá, amelyet az ideálok szerinti kongruenciákkal kapcsolatban már bizonyítottunk.
Így például az 1., 2. és 3. állítás arról szól, hogy az egész számok közötti kongruencia egy reflexív, szimmetrikus és tranzitív reláció, azaz ekvivalenciareláció. Ezt az ideál szerinti kongruenciákra a 18.21. Tételben már igazoltuk.
A 4. és 5. állítás a 18.22. Tételből következik, aminek a segítségével az ideál szerinti maradékosztályok közötti műveletek jóldefiniáltságát igazoltuk (e műveletek definícióját lásd a maradékosztálygyűrűkről szóló 18.23. Tételben). Minthogy a különbségképzés tulajdonképpen ellentettel való összeadás, ezért a kivonásra vonatkozó állítás is teljesül.
A 6. és 7. állítások szintén teljesülnek, hiszen ezek a 4. és 5. állítások azon speciális esetei, amikoris c=d. A 8. állítás az 5. állítás azon speciális esetének n-szeri alkalmazásából adódik, amikoris a=c és b=d.
Végül a 9. állítás: Az I=(m) főideál szerinti kongruencia a 18.20. Definíció alapján azt jelenti, hogy az a-b különbség eleme az I=(m) főideálnak. Mármost ha k osztója m-nek – azaz teljesül a k|m oszthatóság –, akkor a 19.12. Tétel 1. pontja alapján teljesül az (m)\sube (k) tartalmazási reláció, és így az a-b különbség a (k) főideálnak is eleme. Ez ismételten a 18.20. Definíció alapján azt jelenti, hogy a és b a (k) főideál szerint is kongruens egymással. Mivel k-ról azt mondtuk, hogy nemnegatív, ezért a 20.1. Tételben szereplő jelölést alkalmazva a\equiv b\pmod k.
∎Megjegyzés:
Vegyük észre, hogy a tétel bizonyításához kizárólag néhány, ideál szerinti kongruenciákra vonatkozó korábbi állítást, valamint – a 9. állítás esetében – egy ideálok közötti tartalmazási relációt használtunk fel. Emiatt az összes most bizonyított azonosság automatikusan teljesül erre az általánosabb kongruencia-fogalomra is. Így tehát legyenek a, b, c és d egy tetszőleges R gyűrű elemei, valamint I és J tetszőleges ideálok R-ben. Ekkor teljesülnek az alábbiak:
- Teljesül az a\equiv a\pod I kongruencia, azaz minden gyűrűelem kongruens önmagával az I ideál szerint.
- Ha a\equiv b\pod I, akkor b\equiv a\pod I.
- Ha a\equiv b\pod I és b\equiv c\pod I, akkor a\equiv c\pod I.
- Ha a\equiv b\pod I és c\equiv d\pod I, akkor a+c\equiv b+d\pod I és a-c\equiv b-d\pod I.
- Ha a\equiv b\pod I és c\equiv d\pod I, akkor a\cdot c\equiv b\cdot d\pod I.
- Ha a\equiv b\pod I, akkor a+c\equiv b+c\pod I és a-c\equiv b-c\pod I.
- Ha a\equiv b\pod I, akkor a\cdot c\equiv b\cdot c\pod I.
- Ha a\equiv b\pod I akkor bármilyen pozitív egész n kitevő esetén a^n\equiv b^n\pod I.
- Ha a\equiv b\pod I és I\sube J, akkor a\equiv b\pod J.
A 8. állításban szereplő n-edik hatvány alatt ugyanazt értjük, mint a hatványozás azonosságairól szóló 18.8. Tétel esetén. Azaz ha x az R gyűrű valamely eleme, n pedig tetszőleges pozitív egész, akkor az x^n hatványon az alábbi n tényezős szorzatot értjük:
x^n=\underbrace{x\cdot x\cdot x\cdot \ldots \cdot x}_{\text{n darab}} ♣Eszerint tehát az összeadás, kivonás és szorzás műveletére vonatkozóan a kongruenciák ugyanúgy viselkednek, mint az egyenlőségek. Ha például adva van egy szorzásokból, összeadásokból és kivonásokból felépített kifejezés, és ennek bármilyen összetevőjét lecseréljük egy m modulus szerint vele kongruens kifejezéssel, akkor az így kapott kifejezés kongruens lesz az eredetivel szintén az m modulus szerint. Vegyünk egy egyszerű példát. Tekintsük például az alábbi kifejezést:
3^{3n+1}\cdot 5^{2n+1}+2^{5n+1}\cdot 11^nTegyük fel, hogy valamilyen okból kifolyólag azt kell bizonyítanunk, hogy ez a kifejezés n tetszőleges pozitív egész értéke esetén osztható 17-tel – legyen bármi is az az ok. Ez kongruenciával kifejezve az alábbit jelenti:
3^{3n+1}\cdot 5^{2n+1}+2^{5n+1}\cdot 11^n \equiv 0 \pmod{17}A hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontjai alapján a baloldali kifejezést átalakítva az alábbit kapjuk:
27^n\cdot 25^n\cdot 15 + 32^n\cdot 11^n\cdot 2 \equiv 0 \pmod{17}Nézzük először a baloldal első tagját, azaz a 27^n\cdot 25^n\cdot 15 kifejezést. A 15\equiv 15\pmod{17} kongruencia nyilván teljesül a 20.2. Tétel 1. pontja miatt. Továbbá, mivel teljesülnek a 27\equiv -7\pmod{17} és a 25\equiv 8\pmod{17} kongruenciák, ezért ugyanezen tétel 8. pontja miatt teljesülnek a 27^n\equiv (-7)^n\pmod{17} és a 25^n\equiv 8^n\pmod{17} kongruenciák is. De ekkor az így kapott 3 kongruenciát az 5. pont miatt összeszorozhatjuk, azaz teljesül az alábbi kongruencia is:
27^n\cdot 25^n\cdot 15 \equiv (-7)^n\cdot 8^n\cdot 15 \pmod{17}Ugyanígy az eredeti kongruencia baloldalának második tagját is lecserélhetjük egy vele kongruens kifejezéssel:
32^n\cdot 11^n\cdot 2 \equiv (-2)^n\cdot (-6)^n\cdot 2 \pmod{17}Az így kapott két kongruenciát a 20.2. Tétel 4. pontja miatt összeadhatjuk, így az alábbi kongruenciát kapjuk:
\begin{aligned}&27^n\cdot 25^n\cdot 15 + 32^n\cdot 11^n\cdot 2 \equiv \\ \equiv \ &(-7)^n\cdot 8^n\cdot 15 + (-2)^n\cdot (-6)^n\cdot 2 \pmod{17}\end{aligned}E konguencia jobboldala ismét a hatványozás azonosságairól szóló 18.8. Tétel 1. pontja miatt így írható fel:
\begin{aligned}&(-7)^n\cdot 8^n\cdot 15 + (-2)^n\cdot (-6)^n\cdot 2 \equiv \\ \equiv \ &(-56)^n\cdot 15 + 12^n\cdot 2 \pmod{17}\end{aligned}Mivel (-56)\equiv (-5)\pmod{17}, valamint 12\equiv (-5)\pmod{17}, ezért ismételten alkalmazva a 20.2. Tétel 4., 5. és 8. pontjait, ezt kapjuk:
\begin{aligned}&(-56)^n\cdot 15 + 12^n\cdot 2 \equiv \\ \equiv \ &(-5)^n\cdot 15 + (-5)^n\cdot 2 \pmod{17}\end{aligned}Erre már alkalmazhatjuk a gyűrűkre érvényes disztributivitási axiómát (14.12. Definíció 5. pont):
(-5)^n\cdot 15 + (-5)^n\cdot 2 \equiv (-5)^n\cdot 17 \pmod{17}Végül, mivel 17\equiv 0\pmod{17}, ezért teljesül az alábbi kongruencia is:
(-5)^n\cdot 17\equiv 0\pmod{17}Végeredményben tehát a sorozatos átalakításokat elvégezve, és az így kapott kifejezések részeit velük kongruens részkifejezésekkel helyettesítve az alábbi kifejezés valóban tetszőleges n pozitív egész szám esetén osztható 17-tel:
3^{3n+1}\cdot 5^{2n+1}+2^{5n+1}\cdot 11^nValljuk be, hogy kongruenciák nélkül ennek és az ehhez hasonló kérdéseknek a megválaszolása sokkal nehezebb lenne. Kénytelenek lennénk n-re vonatkozó teljes indukciót alkalmazni, amiből persze az oszthatóságról szóló 16.2. Tétel állításait használva ugyanezt az eredményt kapnánk, csak épp egy sokkal kényelmetlenebb úton. Ehelyett azonos átalakításokat és a kongruenciák tulajdonságait használva egy ilyen kérdés megválaszolása pár sorban megoldható. Most gyakorlásképpen vegyük át mégegyszer a fenti levezetést egyben:
\begin{aligned}3^{3n+1}\cdot 5^{2n+1}+2^{5n+1}\cdot 11^n &= \\ = 27^n\cdot 25^n\cdot 15 + 32^n\cdot 11^n\cdot 2 &\equiv \\ \equiv \ (-7)^n\cdot 8^n\cdot 15 + (-2)^n\cdot (-6)^n\cdot 2 &= \\ = (-56)^n\cdot 15 + 12^n\cdot 2 &\equiv \\ \equiv (-5)^n\cdot 15 + (-5)^n\cdot 2 &= \\ = (-5)^n\cdot 17 &\equiv 0\pmod{17}\end{aligned}Kongruenciák osztása
Ahogyan a fenti példa is mutatja, kongruenciákkal számolni hasonlóan egyszerű, mintha egyenletekkel volna dolgunk. Nagyjából minden ugyanúgy működik. A 18. részben azonban már láttuk, hogy az ilyen „nagyjából”-jellegű helyzetekben érhetik az embert kellemetlen meglepetések, ha nem kellő odafigyeléssel jár el. Ez a kongruenciák esetén sincs másként. Az összeadás, kivonás és szorzás esetén – mint láttuk – nincs gond. Az „osztással” azonban vigyázni kell!
Az „osztás” szót azért tettük idézőjelbe, mivel osztani általánosságban amúgy sem lehet egy gyűrűben, kivéve persze ha az adott gyűrű egyben test is (lásd a 14.12. Definíció ide vonatkozó részét). Amikor egy általános gyűrűben beszélünk osztásról, akkor ezalatt mindig az alábbi tétel szerinti egyszerűsítést értjük:
Ez alapján tehát nullosztómentes gyűrűkben – és csak ezekben – bármilyen egyenlet mindkét oldalát lehet tetszőleges nemnulla c gyűrűelemmel „elosztani”. Feltéve persze, hogy a megfelelő oszthatóságok fennállnak a c gyűrűelem és az egyenlet két oldalán lévő kifejezések között. Semmi gond – mondhatnánk –, egyszer már a 18. részben beleszaladtunk ebbe a hibába, így most majd nagyon oda fogunk figyelni. Le is ellenőrizzük, hogy az egész számok \Z gyűrűje a 15.6. Tétel alapján egy integritástartomány, tehát nullosztómentes, így könnyelműen azt gondoljuk, hogy semmi gond nem lehet a kongruenciákkal.
Jól vigyázzunk azonban! Az egyszerűsíthetőségről szóló 15.4. Tétel ugyanis EGYENLETEKRŐL, nem pedig kongruenciákról szól. A 20.2. Tétel 7. pontja ugyan kimondja, hogy ha teljesül az a\equiv b\pmod m kongruencia, akkor mindkét oldalt megszorozhatjuk valamilyen c egész számmal, azaz teljesül az ac\equiv bc\pmod m kongruencia is. Ez tehát ugyanúgy működik, mint az egyenlőségeknél. A kongruenciák esetén azonban ennek megfordítása nem feltétlenül igaz még nullosztómentes gyűrűk esetén sem. Tehát abból, hogy teljesül az ac\equiv bc\pmod m kongruencia, még nem következik, hogy az a\equiv b\pmod m kongruencia is teljesül. Tekintsük az alábbi egyszerű példát:
28\equiv 46\pmod 6Ez a kongruencia teljesül, hiszen mindkét oldal 4-et ad maradékul 6-tal osztva. Ráadásul ennek a kongruenciának mindkét oldala osztható 2-vel, azaz felírható az alábbi alakban:
14\cdot 2\equiv 23\cdot 2\pmod 6Ha most könnyelműen azt gondoljuk, hogy ezt a kongruenciát 2-vel egyszerűsíthetjük – ahogy mondjuk egy egyenlet esetén minden további nélkül megtehetnénk, hiszen \Z nullosztómentes –, akkor egy végzetes logikai hibát ejtenénk. Az alábbi kongruencia ugyanis NEM teljesül:
14\equiv 23\pmod 6Nyilván, hiszen a 14 és a 23 nem ugyanazt a maradékot adja 6-tal osztva.
De mi is volt itt a gond?! Vizsgáljuk meg általánosságban ezt a kérdést. Tegyük fel, hogy teljesül az alábbi, egész számok közötti kongruencia valamilyen m\gt 0 modulusra nézve:
ac\equiv bc\pmod mEz ugye a 20.1. Tétel 1. pontja alapján pontosan azt jelenti, hogy teljesül a 18.3. Definíció szerinti \bmod_m maradékképző függvény, mint gyűrűhomomorfizmus szerinti alábbi kongruencia:
ac\equiv bc\pod{\bmod_m}A \bmod_m az egész számok \Z gyűrűjéből a 18.3. Definíció szerinti \Z_m gyűrűbe képez. A fenti kongruencia tehát azt jelenti, hogy teljesül az alábbi egyenlet a \Z_m gyűrűben:
\bmod_m(ac)=\bmod_m(bc)Ha a \Z_m gyűrű szorzását az \odot szimbólummal jelöljük, akkor \bmod_m művelettartó tulajdonsága miatt ez az egyenlet így írható fel:
\bmod_m(a)\odot \bmod_m(c)=\bmod_m(b)\odot \bmod_m(c)Ha itt most lehetne az egyenlet mindkét oldalát \bmod_m(c)-vel egyszerűsíteni, akkor azt kapnánk, hogy teljesül a \bmod_m(a)=\bmod_m(b) egyenlőség. Ez más szavakkal valóban az a\equiv b\pmod m egész számok közötti kongruencia teljesülését jelentené. De sajnos általában nem ez a helyzet, hiszen ezt az egyszerűsítést a 15.4. Tétel alapján csak nullosztómentes gyűrűkben lehet elvégezni büntetlenül, márpedig ez a \Z_m gyűrű esetén nem garantált.
Összefoglalva tehát a gondot itt az okozza, hogy ugyan maga a 14\cdot 2\equiv 23\cdot 2\pmod 6 kongruencia az egész számok \Z gyűrűjének elemein van értelmezve, azonban ez tulajdonképpen az alábbi \Z_6 gyűrűben felírt egyenletnek felel meg:
\bmod_6(14)\odot \bmod_6(2)=\bmod_6(23)\odot \bmod_6(2)Elvégezve a 18.3. Definíció szerinti maradékos osztásokat ezt kapjuk:
2\odot 2=5\odot 2Ez az egyenlet valóban teljesül, hiszen a \Z_6 gyűrűben mindkét oldal 4. Ebben a gyűrűben azonban általánosságban nem szabad egyszerűsíteni egy egyenlet mindkét oldalát ugyanazzal a nemnulla elemmel – jelen esetben 2-vel –, hiszen a 6 nem prímszám, és így a \Z_6 gyűrű a 18.5. Tétel alapján nem nullosztómentes.
Ebből ugyanakkor az is következik, hogyha viszont a modulus prímszám lett volna, akkor egy hasonló szituációban minden további nélkül lehetne egyszerűsíteni a kongruenciákat is. Az alábbi tétel általánosan is megfogalmazza, hogy pontosan mikor és milyen körülmények szerint lehet egyszerűsíteni egy egész számokon értelmezett kongruenciát.
20.3. Tétel:
Legyen a, b, és c tetszőleges, m\gt 0 pozitív egész szám, d pedig a c és m egész számok kitüntetett közös osztója, azaz d=(c,m).
Ebben az esetben az ac\equiv bc\pmod m kongruencia akkor és csak akkor teljesül, amikor teljesül az alábbi kongruencia is:
a\equiv b\pmod{\frac{m}{d}}Itt \frac{m}{d} alatt azt az egész számot értjük, amelyet a d=(c,m) kitüntetett közös osztóval megszorozva az m modulust kapjuk eredményül.
♣Az előző példára vonatkoztatva ez azt jelenti, hogy a 28\equiv 46\pmod 6 kongruenciát lehet egyszerűsíteni 2-vel, ám ekkor a 6 modulust is egyszerűsíteni kell a (2,6)=2 kitüntetett közös osztóval. Valóban, a 14\equiv 23\pmod 3 kongruencia már tényleg teljesül, hiszen mindkét oldal 2-t ad maradékul 3-mal osztva.
Bizonyítás:
Az ac\equiv bc\pmod m kongruencia a 20.1. Tétel 3. pontja alapján akkor és csak akkor teljesül, ha fennáll az m|ac-bc, azaz a disztributivitási szabály miatt az alábbi oszthatóság:
m|(a-b)cUgye \frac{m}{d}-vel jelöltük azt az egész számot, amelyet a d kitüntetett közös osztóval megszorozva az m modulust kapjuk. Ehhez hasonlóan jelöljük \frac{c}{d}-vel azt az egész számot, amelyet ugyancsak d-vel megszorozva a c egész számot kapjuk. Azaz:
\begin{aligned}m&=\frac{m}{d}\cdot d \\ c&=\frac{c}{d}\cdot d\end{aligned}Nyilván az \frac{m}{d} és a \frac{c}{d} egész számok léteznek, hiszen d osztója m-nek is és c-nek is, mivel ő épp kettejük kitüntetett közös osztója. Ezek után a fenti oszthatóság így néz ki:
\underbrace{\frac{m}{d}\cdot d}_{=m}|(a-b)\underbrace{\frac{c}{d}\cdot d}_{=c}A 17.8. Tétel alapján egy integritástartományban – mint amilyen a 15.6. Tétel alapján az egész számok \Z gyűrűje is – egy oszthatóság mindkét oldalát szabad egyszerűsíteni bármilyen nemnulla elemmel. A d\neq 0 feltétel teljesül, hiszen ő nem más, mint c és m kitüntetett közös osztója, amely az m\neq 0 feltétel és a 16.2. Tétel 4. pontja miatt biztosan nem lehet 0. A fenti oszthatóság tehát az egyszerűsítési szabály miatt pontosan akkor teljesül, amikor teljesül az alábbi oszthatóság:
\frac{m}{d}|(a-b)\frac{c}{d}Nézzük most meg, hogy mit tudunk elmondani a (\frac{c}{d},\frac{m}{d}) kitüntetett közös osztóról. Azt ugye tudjuk, hogy (c,m)=d, így tehát igaz az alábbi:
(\underbrace{\frac{c}{d}\cdot d}_{=c},\underbrace{\frac{m}{d}\cdot d}_{=m})=dA kitüntetett közös osztó kiemelési tulajdonsága miatt (lásd a 17.9. Tételt) teljesül az alábbi asszociáció:
\underbrace{(\frac{c}{d}\cdot d,\frac{m}{d}\cdot d)}_{=d}\sim d\cdot (\frac{c}{d},\frac{m}{d})Minthogy a 16.10. Tétel alapján egy egységelemes integritástartományban valamely elem asszociáltjai pontosan az egységszeresei, emiatt a (\frac{c}{d},\frac{m}{d}) kitüntetett közös osztó szükségképpen egység kell legyen. Ez a 17.10. Definíció utáni megjegyzés alapján pontosan azt jelenti, hogy a \frac{c}{d} és az \frac{m}{d} egész számok egymáshoz relatív prímek. Mindeközben azonban – ahogyan fentebb már láttuk – teljesül az alábbi oszthatóság:
\frac{m}{d}|(a-b)\frac{c}{d}Mármost ez az oszthatóság egyrészt a 16.2. Tétel 7. pontja miatt akkor, másrészt pedig – mivel \frac{m}{d} relatív prím \frac{c}{d}-hez – az euklidészi lemma miatt (17.11. Tétel) csak akkor teljesül, amikor teljesül az alábbi oszthatóság is:
\frac{m}{d}|(a-b)Ez viszont a 20.1. Tétel 3. pontja alapján pontosan azt jelenti, hogy – a tétel állításának megfelelően – teljesül az alábbi kongruencia:
a\equiv b\pmod{\frac{m}{d}} ∎Megjegyzés:
E tétel egy egyszerű következménye, hogy ha a c szorzó tényező relatív prím az m modulushoz, akkor a c-vel való egyszerűsítés után a kongruencia változatlan modulus mellett érvényben marad. Azaz ebben az esetben az ac\equiv bc\pmod m kongruenciából következik az a\equiv b\pmod m kongruencia. Ekkor ugyanis a 17.10. Definíció utáni megjegyzés miatt d=(c,m)=1, és így az egyszerűsített \frac{m}{d} modulus meg fog egyezni az eredeti m modulussal.
♣Egész számok maradékosztályai és maradékosztálygyűrűi
Ebben a szakaszban az egész számok \Z gyűrűjének maradékosztályait vizsgáljuk meg. Általánosságban egy R gyűrűben a 18.20. Definíció szerinti értelemben vezettük be az ideál szerinti kongruencia fogalmát.
E definíció szerint amennyiben adva van egy I ideál R-ben, úgy az I ideál szerinti a\equiv b\pod I kongruencia pontosan akkor teljesül, ha az a-b különbség benne van az I ideálban. A 18.21. Tétel alapján ez egy ekvivalenciareláció R elemei között, amely tehát az R gyűrűt páronként diszjunkt halmazok uniójára (19.3. Definíció) bontja. Ezeket a halmazokat neveztük modulo I maradékosztályoknak. Az R gyűrű minden eleme tehát pontosan egy modulo I maradékosztályba kerül bele.
Most vizsgáljuk meg ezt a fogalmat az egész számok \Z gyűrűjére vonatkoztatva. Mivel a 19.16. Tétel alapján \Z egy főideálgyűrű (19.15. Definíció), ezért annak minden I ideáljához található olyan m egész szám, amely egymaga generálja I-t, azaz I=(m). A 20.1. Tételben épp az ilyen I=(m) főideál szerinti kongruenciákra használtuk az a\equiv b\pmod m jelölést. Kérdés tehát, hogy vajon mik lesznek egy ilyen kongruencia által meghatározott maradékosztályok? Erre ad választ az alábbi tétel.
20.4. Tétel (Egész számok maradékosztályai):
Legyen adva egy tetszőleges m\geq 0 nemnegatív egész szám. A 20.1. Tételben bevezetett modulo m kongruencia egy ekvivalenciareláció az egész számok \Z gyűrűjén. Az ehhez tartozó ekvivalencia-osztályokat modulo m kongruenciaosztályoknak vagy modulo m maradékosztályoknak nevezzük.
Ha m\gt 0, akkor pontosan m darab modulo m maradékosztály létezik. Legyen a egy tetszőleges egész szám. Ekkor az a-t tartalmazó modulo m maradékosztály bármely eleme felírható km + a alakban valamilyen alkalmas k egész számmal. Visszafelé: Minden k egész szám esetén a km + a egész szám benne van az a-t tartalmazó modulo m maradékosztályban.
Ha m=0, akkor végtelen sok modulo m maradékosztály létezik, és minden ilyen maradékosztályban pontosan egy egész szám van.
♣Bizonyítás:
A 20.1. Tételben bevezetett modulo m kongruencia ekvivalens az I=(m) főideál szerinti kongruenciával. Ez utóbbi a 18.21. Tétel alapján valóban egy ekvivalenciareláció, így tehát a modulo m kongruencia is az. Mivel e két kongruencia ekvivalens, ezért pontosan ugyanazok lesznek a maradékosztályaik.
Ha a egy tetszőleges egész szám, akkor az a-t tartalmazó modulo I maradékosztály épp az a+I halmaz lesz (lásd a 18.19. Definícióban bevezetett komplexusösszeadást). Ez tehát meg fog egyezni az a-t tartalmazó modulo m maradékosztállyal, ezért elég meghatároznunk az a+I halmazt. Minthogy az I=(m) főideál épp m többszöröseit tartalmazza, ezért az a+I halmaz valóban éppen a km + a alakban felírható egész számokból áll. Speciálisan ha m=0, akkor ilymódon minden egész szám külön maradékosztályba kerül, így ezek száma valóban végtelen.
Ha m\gt 0, akkor az I=(m) szerinti kongruencia ekvivalens a 18.3. Definícióban bevezetett \bmod_m maradékképző függvény, mint gyűrűhomomorfizmus szerinti kongruenciával, hiszen az I=(m) főideál épp ennek a gyűrűhomomorfizmusnak a magja. Mármost ennek a kongruenciának a maradékosztályai – amelyek tehát megegyeznek az I=(m) főideál szerinti és így a modulo m kongruencia maradékosztályaival – a 18.9. Definíció alapján épp azok a halmazok lesznek \Z-ben, amelyeknek az elemeihez a \bmod_m függvény azonos elemet rendel hozzá a 18.3. Definíció szerinti \Z_m képhalmazból. Ez látható az alábbi ábrán:
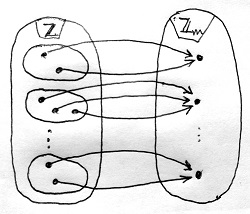
Következésképp m\gt 0 esetben a modulo m maradékosztályok száma épp meg fog egyezni a \Z_m gyűrű elemszámával, amely valóban m.
∎Megjegyzés:
A 20.1. Tétel utáni megjegyzésben szereplő okok miatt negatív modulus szerinti maradékosztályokról sem szoktunk beszélni. Ugyanis a modulo m kongruencia pontosan ugyanaz a reláció, mint a modulo -m kongruencia, és így az általuk meghatározott maradékosztályok is megegyeznek.
♣Például modulo 8 maradékosztályból pontosan 8 darab van. Ezeket, illetve ezek néhány elemét mutatja az alábbi ábra:

Nézzük meg például a 13-at tartalmazó maradékosztályt (ezt az ábrán nyíllal jelöltük). A tétel szerint ennek elemei pontosan a 8k+13 alakban felírható egész számok. Valóban, az ábrán megjelenített elemek például így írhatók fel ebben az alakban:
\begin{aligned}-19&=8\cdot (-4)+13 \\ -11&=8\cdot (-3)+13 \\ -3&=8\cdot (-2)+13 \\ 5&=8\cdot (-1)+13 \\ 13&=8\cdot 0+13 \\ 21&=8\cdot 1+13 \\ 29&=8\cdot 2+13\end{aligned}A 18.23. Tételben vezettük be a maradékosztálygyűrű (vagy faktorgyűrű) fogalmát. Ezek olyan gyűrűk, amelyeknek a fenti maradékosztályok voltak az elemei, és ezek között értelmeztünk két műveletet. Eszerint egy A és egy B maradékosztály A\oplus B összege szintén egy maradékosztály lesz. Ezt úgy kapjuk meg, hogy veszünk egy-egy tetszőleges a\in A és b\in B elemet az eredeti gyűrűből, képezzük ezek a+b összegét szintén az eredeti gyűrűben, és azt a maradékosztályt választjuk végeredményként, amelybe ez az a+b összeg esik. Az A\odot B szorzatot ehhez hasonlóan értelmeztük az eredeti gyűrű szorzásának segítségével.
Az egész számokon imént bevezetett modulo m maradékosztályokból ugyanígy a 18.23. Tételben leírt módon alkothatunk egy gyűrűt.
20.5. Tétel (Egész számok maradékosztálygyűrűi):
Legyen m\geq 0 egy tetszőleges nemnegatív egész szám, és jelöljük \Z/m\Z-vel azt a halmazt, amelynek elemei a 20.4. Tételben definiált modulo m maradékosztályok. Ha a valamilyen egész szám, akkor jelöljük [a]_m-mel az a-t tartalmazó modulo m maradékosztályt. Ilyenkor azt mondjuk, hogy az a egész szám reprezentálja az [a]_m maradékosztályt. Vezessünk be e maradékosztályok között két műveletet az alábbiak szerint:
- Ha [a]_m és [b]_m két maradékosztály, akkor ezek összege legyen az [a]_m\oplus [b]_m=[a+b]_m maradékosztály.
- Ha [a]_m és [b]_m két maradékosztály, akkor ezek szorzata legyen az [a]_m\odot [b]_m=[a\cdot b]_m maradékosztály.
Ekkor a \Z/m\Z halmaz ezzel a két művelettel egy kommutatív és egységelemes gyűrűt alkot, amelyet modulo m maradékosztálygyűrűnek nevezünk. E gyűrű nulleleme a [0]_m, egységeleme pedig az [1]_m maradékosztály.
Tekintsük továbbá azt az f:\Z\to \Z/m\Z függvényt, amely minden a egész számhoz az [a]_m maradékosztályt rendeli hozzá. Ekkor f egy gyűrűhomomorfizmus \Z és \Z/m\Z között, melynek magja az m egész szám többszöröseinek halmaza. Ennek a neve természetes gyűrűhomomorfizmus.
♣Bizonyítás:
A modulo m maradékosztályok pontosan az (m) főideál szerinti maradékosztályokkal egyeznek meg. Emiatt a \Z/m\Z halmaz a tételben bevezetett \oplus és \odot műveletekkel nem más, mint a \Z gyűrűnek az (m) főideál szerinti faktorgyűrűje, azaz a 18.23. Tételben bevezetett jelölésekkel \Z/(m). Innentől kezdve a bizonyítás teljesen megegyezik a 18.23. Tétel bizonyításával.
Mivel \Z kommutatív és egységelemes, ezért a 18.23. Tétel alapján a \Z/(m)=\Z/m\Z faktorgyűrű is az. A nullelem az említett tételnek megfelelően a 0+(m) maradékosztály, ami a [0]_m modulo m maradékosztálynak felel meg. Ehhez hasonlóan az egységelem az 1+(m) maradékosztály, ami pedig az [1]_m modulo m maradékosztálynak felel meg.
Végül a természetes gyűrűhomomorfizmus magja az (m) főideál lesz, amely valóban az m egész szám többszöröseit tartalmazza.
∎Eszerint tehát ha két maradékosztályt szeretnénk összeadni vagy összeszorozni egymással a fenti értelemben, akkor teljesen mindegy, hogy a művelet elvégzéséhez mely reprezentánselemeket használjuk. Tekintsük ismét a modulo 8 maradékosztályokat:
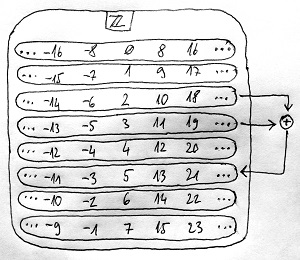
Az ábrán megjelöltünk két maradékosztályt, illetve ezek összegét is, amely egy harmadik maradékosztály. Látható, hogy bármely elemekkel is reprezentáljuk a két bemeneti maradékosztályt, e reprezentánselemek összege mindenképp a kimeneti maradékosztályt fogja reprezentálni. Például a -14+19=5 és a 10+11=21 összegek ugyanazt a maradékosztályt reprezentálják a fenti tétel miatt.
Tegyük fel most, hogy adva van egy m\gt 0 egész szám, és tekintsük a 20.5. Tétel szerinti modulo m maradékosztálygyűrűt. Ebben a gyűrűben ugyanúgy kell számolni, mint a 18.3. Definícióban bevezetett \Z_m gyűrűben. Ez a gyűrűk homomorfizmustételének következménye, amelyről a 18. részben volt szó bővebben.
A fentebbi példában szereplő modulo 8 maradékosztálygyűrű műveleti táblái emiatt megegyeznek a \Z_8 gyűrű műveleti tábláival. A \Z_8 gyűrű szorzótáblája például így néz ki:
\begin{array}{c|cccccccc}\odot &0&1&2&3&4&5&6&7 \\ \hline 0&0&0&0&0&0&0&0&0 \\ 1&0&1&2&3&4&5&6&7 \\ 2&0&2&4&6&0&2&4&6 \\ 3&0&3&6&1&4&7&2&5 \\ 4&0&4&0&4&0&4&0&4 \\ 5&0&5&2&7&4&1&6&3 \\ 6&0&6&4&2&0&6&4&2 \\ 7&0&7&6&5&4&3&2&1 \end{array}Az ezzel a homomorfizmustétel miatt (18.25. Tétel) izomorf modulo 8 maradékosztálygyűrű szorzótáblája ezzel gyakorlatilag megegyezik, az egyetlen különbség az elemek jelölésében van:
\begin{array}{c|cccccccc}\odot & [0]_8 & [1]_8 & [2]_8 & [3]_8 & [4]_8 & [5]_8 & [6]_8 & [7]_8 \\ \hline [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 \\ [1]_8 & [0]_8 & [1]_8 & [2]_8 & [3]_8 & [4]_8 & [5]_8 & [6]_8 & [7]_8 \\ [2]_8 & [0]_8 & [2]_8 & [4]_8 & [6]_8 & [0]_8 & [2]_8 & [4]_8 & [6]_8 \\ [3]_8 & [0]_8 & [3]_8 & [6]_8 & [1]_8 & [4]_8 & [7]_8 & [2]_8 & [5]_8 \\ [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 \\ [5]_8 & [0]_8 & [5]_8 & [2]_8 & [7]_8 & [4]_8 & [1]_8 & [6]_8 & [3]_8 \\ [6]_8 & [0]_8 & [6]_8 & [4]_8 & [2]_8 & [0]_8 & [6]_8 & [4]_8 & [2]_8 \\ [7]_8 & [0]_8 & [7]_8 & [6]_8 & [5]_8 & [4]_8 & [3]_8 & [2]_8 & [1]_8 \end{array}A 14.12. Definíció alapján egy gyűrűben a szorzás általában nem invertálható művelet (lásd a 14.9. Definíciót). Ez azonban nem jelenti azt, hogy egyáltalán ne létezhetne olyan nemnulla elem a gyűrűben, amely a szorzásra nézve invertálható – csupán azt, hogy nem mindegyik elem ilyen. Például az egész számok \Z gyűrűjében mindössze az 1-hez és a -1-hez létezik inverz elem. Mindkettő inverze önmaga, hiszen 1\cdot 1=1 és (-1)\cdot (-1)=1.
Ezzel szemben a modulo 8 maradékosztálygyűrűben több invertálható elem is van. A fenti szorzótábla alapján ezek a következő maradékosztályok: [1]_8, [3]_8, [5]_8 és [7]_8. Például a [3]_8 inverze szintén önmaga, mivel [3]_8\odot [3]_8 = [1]_8.
Ezzel ellentétben a [0]_8, a [2]_8, a [4]_8 és a [6]_8 maradékosztályok nem ivertálhatók, mivel a szorzótáblában a nekik megfelelő sorokban sehol nem szerepel az [1]_8 maradékosztály. Azaz nincs olyan maradékosztály, amellyel őket megszorozva [1]_8-et kapnánk.
A fenti példákban csupa olyan invertálható elem szerepelt, amelyek mindegyikének az inverze önmaga volt. Ez nem feltétlenül van mindig így. Ha például a modulo 10 maradékosztálygyűrűt vizsgáljuk, ebben a gyűrűben olyan invertálható elem is van, amelynek inverze nem önmaga. Például a [3]_{10} maradékosztály inverze a [7]_{10} maradékosztály, hiszen őket összeszorozva a 21 egész szám által reprezentált maradékosztályt kapjuk, ami megegyezik az [1]_{10} maradékosztállyal.
Az invertálható maradékosztályoknak – fontosságuk miatt – külön nevük is van.
20.6. Definíció (Redukált maradékosztály):
Legyen m\gt 0 egy tetszőleges pozitív egész szám. Ekkor a \Z/m\Z-vel jelölt modulo m maradékosztálygyűrű (lásd a 20.5. Tételt) invertálható elemeit modulo m redukált maradékosztályoknak nevezzük.
♣A 20.5. Tételben már láttuk, hogy amennyiben a modulus egy m\gt 0 pozitív egész szám, akkor a modulo m maradékosztálygyűrű elemszáma pontosan m, vagy más szavakkal pontosan m darab modulo m maradékosztály létezik. Felmerül a kérdés, hogy vajon mi lesz az ugyanezen modulus szerinti redukált maradékosztályok száma? Pontosan ezt méri a számelmélet egyik legfontosabb függvénye, amelyet az alábbi definícióban vezetünk be, és amely Leonhard Euler svájci matematikusról kapta a nevét.
20.7. Definíció (Az Euler-függvény):
Legyen m\gt 0 tetszőleges pozitív egész szám. Ekkor a modulo m redukált maradékosztályok számát a \varphi(m)-mel jelölt függvény értéke adja meg. Ezt a függvényt Euler-féle \varphi-függvénynek (ejtsd: „fi”) nevezzük.
♣Az alábbiakban megadjuk a \varphi-függvény értékét az első néhány pozitív egész számra:
\begin{aligned}\varphi(1)&=1 \\ \varphi(2)&=1 \\ \varphi(3)&=2 \\ \varphi(4)&=2 \\ \varphi(5)&=4 \\ \varphi(6)&=2 \\ \varphi(7)&=6 \\ \varphi(8)&=4 \\ \varphi(9)&=6 \\ \varphi(10)&=4 \\ &\vdots\end{aligned}Az alábbi ábrán a \varphi-függvény grafikonja látható az első 1000 pozitív egész számig bezárólag.
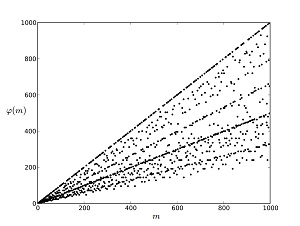
Látható, hogy a függvény bizonyos szempontból meglehetősen hektikusan viselkedik. Felmerül a kérdés, hogy vajon hogyan számítható ki az értéke tetszőleges m\gt 0 pozitív egész számra? Ehhez ugye a modulo m redukált maradékosztályokat kéne tudnunk megszámolni. Ennek viszont előfeltétele, hogy egy adott maradékosztályról egyáltalán el tudjuk dönteni, hogy redukált-e vagy nem, azaz létezik-e inverze a modulo m maradékosztálygyűrű szorzására nézve vagy nem.
Vizsgáljuk ezért meg, hogy ennek mi a feltétele. Tegyük fel, hogy elénk kerül egy valamilyen a egész számmal reprezentált [a]_m maradékosztály, és azt kell eldöntenünk, hogy létezik-e olyan X maradékosztály, amelyre teljesül az alábbi egyenlet a maradékosztálygyűrűben:
[a]_m\odot X=[1]_mItt [1]_m jelöli a maradékosztálygyűrű egységelemét, azaz azt a maradékosztályt, amelyben benne van az 1 egész szám. Ekkor a keresett X maradékosztály lesz az [a]_m maradékosztály inverze – amennyiben létezik. A 20.4. Tétel alapján elegendő X egyetlen elemét megtalálni, hiszen ebből könnyedén megkapható az összes többi. Jelöljük ezt a keresett elemet x-szel, azaz X=[x]_m. Ekkor a fenti egyenlet – követve a \odot művelet 20.5. Tételbeli definícióját – így módosul:
[a]_m\odot [x]_m=[a\cdot x]_m=[1]_mSzavakkal megfogalmazva tehát kell keresnünk egy olyan x egész számot, amely esetén az a\cdot x szorzat ugyanabban a maradékosztályban van, mint az 1 egész szám. A kongruenciák nyelvén ez épp az alábbit jelenti:
ax\equiv 1\pmod mAz [a]_m maradékosztály inverzének létezése tehát azon áll vagy bukik, hogy létezik-e olyan x egész szám, amely kielégíti a fenti kongruenciát – azaz a fenti úgynevezett kongruenciaegyenlet megoldható-e. A következő szakaszban ennek feltételeit tekintjük át.
Lineáris kongruenciák
A kongruenciaegyenletek legegyszerűbb képviselői az úgynevezett lineáris kongruenciák, mint amilyen a fenti kongruenciaegyenlet is. Ezeknek kulcsszerepe van a kriptográfiai eljárásokban, ezért ebben a szakaszban fontos tételeket mondunk ki velük kapcsolatban. Előszöris definiáljuk pontosan, hogy mit is értünk lineáris kongruencia, illetve annak megoldásai és megoldásszáma alatt.
20.8. Definíció (Lineáris kongruenciák):
Legyen a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám. Ekkor az alábbi kongruenciaegyenletet lineáris kongruenciának nevezzük:
a\cdot x\equiv b\pmod mEgy lineáris kongruencia egy megoldásán egy olyan modulo m maradékosztályt értünk, amelynek tetszőleges elemét x helyére behelyettesítve a kongruencia teljesül.
Egy lineáris kongurencia megoldásszáma alatt azon modulo m maradékosztályok számát értjük, amelyek megoldásai az adott lineáris kongruenciának.
♣Megjegyzés:
Nyilvánvaló, hogyha egy s egész számot x helyére behelyettesítve a kongruencia teljesül – azaz a\cdot s\equiv b\pmod m –, akkor ez igaz lesz az s által reprezentált [s]_m maradékosztály összes többi elemére is. Ha ugyanis egy t egész szám benne van ebben a maradékosztályban, az pontosan azt jelenti, hogy teljesül az alábbi kongruencia:
s\equiv t\pmod mEkkor azonban a 20.2. Tétel 7. pontja miatt teljesül az alábbi kongruencia is:
a\cdot s\equiv a\cdot t\pmod mHa tehát a\cdot s\equiv b\pmod m fennáll, akkor ugyanezen tétel 2. és 3. pontjai miatt a\cdot t\equiv b\pmod m is fennáll. Ez az oka annak, hogy egy lineáris kongruencia megoldása alatt nem egy-egy egész számot, hanem teljes maradékosztályokat értünk.
♣Egy lineáris kongruencia esetén – hasonlóan egy hagyományos egyenlethez – az alábbi kérdésekre keressük a választ:
- Mi a megoldhatóság szükséges és elégséges feltétele?
- Hány megoldás létezik (a fenti definíció szerinti értelemben)?
- Hogyan kaphatjuk meg ezeket a megoldásokat?
Ahhoz, hogy ezeket a kérdéseket megválaszoljuk, először is szükségünk van egy fontos állításra az előző részben tárgyalt, végesen generált ideálok elemeivel kapcsolatban. Az alábbi tétel az egységelemes gyűrűk esetére szorítkozik, és arról szól, hogy hogyan tudjuk megkapni egy ideál összes elemét a generátorelemek segítségével. Általános esetben a helyzet némiképp bonyolultabb, és jelenleg nincs is rá szükségünk, így ennek részleteit most mellőzzük.
20.9. Tétel:
Legyen R egy tetszőleges egységelemes gyűrű, továbbá legyenek a_1, a_2, ..., a_n az R gyűrű tetszőleges elemei.
Ekkor az ezen elemek által generált balideál minden eleme felírható r_1a_1+r_2a_2+\ldots +r_na_n alakban az R gyűrű alkalmasan választott r_1, r_2, ..., r_n elemeinek segítségével. Visszafelé: Ha egy r\in R gyűrűelem felírható r=r_1a_1+r_2a_2+\ldots +r_na_n alakban az R gyűrű alkalmasan választott r_1, r_2, ..., r_n elemeinek segítségével, akkor r benne van az a_1, a_2, ..., a_n elemek által generált balideálban.
Ehhez hasonlóan az a_1, a_2, ..., a_n elemek által generált jobbideál minden eleme felírható a_1s_1+a_2s_2+\ldots +a_ns_n alakban az R gyűrű alkalmasan választott s_1, s_2, ..., s_n elemeinek segítségével. Visszafelé: Ha egy s\in R gyűrűelem felírható s=a_1s_1+a_2s_2+\ldots +a_ns_n alakban az R gyűrű alkalmasan választott s_1, s_2, ..., s_n elemeinek segítségével, akkor s benne van az a_1, a_2, ..., a_n elemek által generált jobbideálban.
Végül az (a_1,a_2,\ldots,a_n) (kétoldali) ideál minden eleme felírható r_1a_1+r_2a_2+\ldots +r_na_n és a_1s_1+a_2s_2+\ldots +a_ns_n alakban az R gyűrű alkalmasan választott r_1, r_2, ..., r_n és s_1, s_2, ..., s_n elemeinek segítségével. Visszafelé: Ha egy r\in R gyűrűelem felírható r=r_1a_1+r_2a_2+\ldots +r_na_n=a_1s_1+a_2s_2+\ldots +a_ns_n alakban az R gyűrű alkalmasan választott r_1, r_2, ..., r_n és s_1, s_2, ..., s_n elemeinek segítségével, akkor r benne van az (a_1, a_2, ..., a_n) ideálban.
♣Bizonyítás:
Először is a balideálok elemeire vonatkozó állítást igazoljuk. Jelöljük I-vel azt a halmazt, amely pontosan az r_1a_1+r_2a_2+\ldots +r_na_n alakban felírható elemeket tartalmazza. Azt kell bizonyítani, hogy I a legszűkebb olyan balideál, amely tartalmazza az a_1, a_2, ..., a_n elemeket.
Kezdjük annak igazolásával, hogy I balideál. Ehhez a 18.18. Definíció alapján azt kell megmutatni, hogy I részgyűrű – amihez a 18.15. Tétel feltételeit fogjuk felhasználni –, valamint, hogy tetszőleges elemét balról megszorozva bármelyik R-beli elemmel az eredmény benne van I-ben.
Összeadásra való zártság: Legyen r és s az I halmaz két tetszőleges eleme. Mivel ők I elemei, ezért felírhatók a tételben szereplő alakban:
\begin{aligned}r &= r_1a_1+r_2a_2+\ldots +r_na_n \\ s &= s_1a_1+s_2a_2+\ldots +s_na_n\end{aligned}Ekkor ezek összege szintén a tételben szereplő alakban írható fel:
r+s = (r_1+s_1)a_1+(r_2+s_2)a_2+\ldots +(r_n+s_n)a_nEmiatt az r+s összeg szintén benne van I-ben, amely tehát valóban zárt az összeadásra nézve.
Szorzásra való zártság: Legyen s az I halmaz tetszőleges eleme. Mivel s\in I, ezért ő felírható a tételben szereplő alakban:
s=s_1a_1+s_2a_2+\ldots +s_na_nEzt balról megszorozva tetszőleges r\in R elemmel az így kapott szorzat szintén a tételben szereplő alakban írható fel:
r\cdot s=r\cdot (s_1a_1+s_2a_2+\ldots +s_na_n)=(rs_1)a_1+(rs_2)a_2+\ldots +(rs_n)a_nEmiatt az rs szorzat szintén benne van I-ben. Mivel r tetszőleges R-beli elem lehet – beleértve persze az I-beli elemeket is –, ezért I nemcsak az önmagán belüli szorzásra nézve zárt, hanem a tetszőleges R-beli elemekkel való baloldali szorzásokra nézve is.
Tartalmazza a nullelemet: Ez nyilvánvaló, hiszen a nullelem felírható a tételben szereplő alakban:
0=0\cdot a_1+0\cdot a_2+\ldots +0\cdot a_nEllentettképzésre való zártság: Legyen r az I halmaz tetszőleges eleme. Mivel r\in I, ezért ő felírható a tételben szereplő alakban:
r=r_1a_1+r_2a_2+\ldots +r_na_nDe ekkor ennek ellentettje szintén felírható ilyen alakban:
-r=(-r_1)a_1+(-r_2)a_2+\ldots +(-r_n)a_nEmiatt (-r) szintén benne van I-ben, amely tehát zárt az ellentettképzésre is.
Az I halmaz tehát teljesíti a balideálokra vonatkozó 18.18. Definíció szerinti követelményeket, így valóban balideál.
Most azt kell megmutatni, hogy I tartalmazza az a_1, a_2, ..., a_n generátorelemeket. Ez nyilvánvaló, hiszen mindegyikük felírható a tételben szereplő alakban:
\begin{aligned}a_1&=1\cdot a_1 + 0\cdot a_2 + 0\cdot a_3 +\ldots +0\cdot a_n \\ a_2&=0\cdot a_1 + 1\cdot a_2 + 0\cdot a_3 +\ldots +0\cdot a_n \\ a_3&=0\cdot a_1 + 0\cdot a_2 + 1\cdot a_3 +\ldots +0\cdot a_n \\ &\vdots \\ a_n&=0\cdot a_1 + 0\cdot a_2 + 0\cdot a_3 +\ldots +1\cdot a_n \end{aligned}Azt tehát már tudjuk, hogy I egy olyan balideál, amely tartalmazza az a_1, a_2, ..., a_n generátorelemeket. Annyit kell még igazolni, hogy ő a legszűkebb ilyen balideál.
A 19.7. Definíció értelmében ez azt jelenti, hogy ha J egy tetszőleges balideál, amely szintén tartalmazza a generátorelemeket, akkor I\sube J. Meg kell tehát mutatni, hogy tetszőleges t\in I esetén t\in J is teljesül.
Mivel t\in I, ezért ő felírható a tételben szereplő alakban:
t=t_1a_1+t_2a_2+\ldots +t_na_nAzt ugye tudjuk, hogy J tartalmazza az a_1, a_2, ..., a_n generátorelemeket. Tekintve, hogy J balideál, ezért tartalmazza a t_1a_1, t_2a_2, ..., t_na_n szorzatokat is, valamint ezek összegét is, azaz valóban teljesül t\in J.
Az I halmaz tehát valóban a legszűkebb olyan balideál, amely tartalmazza az a_1, a_2, ..., a_n generátorelemeket – épp ahogyan a tétel állítja.
A jobbideálok elemeire vonatkozó állítás a fentiekhez nagyon hasonlóan igazolható, csak épp jobboldali szorzásokat kell alkalmazni. Végül a (kétoldali) ideálok elemeire vonatkozó állítás automatikusan adódik, hiszen egy (kétoldali) ideál egyszerre jobb- és balideál.
∎Például tekintsük a (8,6) ideált az egész számok gyűrűjében. A tétel alapján ennek összes elemét megkapjuk, ha a 8x+6y kifejezésbe az x és y helyére behelyettesítjük az összes lehetséges egész számpárt. Az alábbi táblázatban néhány nemnegatív számpárra számítottuk ki az eredményt, de a táblázat természetesen folytatható lenne a negatív számtartományokban is:
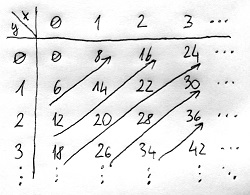
A kapott számok az ábrán feltüntetett vonalak mentén kettesével követik egymást. Úgy tűnik tehát, hogy a (8,6) ideál épp a páros számokat tartalmazza, azaz megegyezik a (2) főideállal. A 2 ráadásul épp a 8 és a 6 kitüntetett közös osztója. Az előző részben mutattunk már egy fontos összefüggést egy integritástartomány ideáljai és a kitüntetett közös osztók között:
Eszerint tehát az (a,b) és (d) ideálok közötti egyenlőségből következik, hogy d kitüntetett közös osztója a-nak és b-nek. Vigyázzunk azonban! Visszafelé ugyanis általánosságban nem igaz az összefüggés. Vagyis abból, hogy d kitüntetett közös osztója a-nak és b-nek még nem következik, hogy az (a,b) és a (d) ideálok megegyeznek. Ennek a megfordításnak a pontos feltételeit az alábbi tétel fogalmazza meg.
20.10. Tétel:
Legyen R tetszőleges integritástartomány, amelyben létezik egységelem. Legyenek továbbá a, b és d az R tetszőleges elemei. Ekkor teljesülnek az alábbiak:
- Ha d kitüntetett közös osztója a-nak és b-nek, akkor (a,b)\sube (d).
- Az (a,b)=(d) halmazegyenlőség akkor és csak akkor teljesül, ha d kitüntetett közös osztója a-nak és b-nek ÉS felírható u\cdot a+v\cdot b alakban az R gyűrű alkalmasan választott u és v elemeinek segítségével.
Bizonyítás:
Az 1. állítás: Legyen tehát d kitüntetett közös osztója a-nak és b-nek. Azt kell bizonyítani, hogy ekkor fennáll az (a,b)\sube (d) tartalmazási reláció, azaz az (a,b) ideál bármely eleme egyúttal a (d) főideálnak is eleme.
Legyen tehát x az (a,b) ideál egy tetszőleges eleme. Mivel az R integritástartomány egységelemes, ezért a 20.9. Tétel értelmében x kifejezhető az a és b generátorelemek segítségével az alábbi alakban:
x=u\cdot a + v\cdot bMármost, mivel fennállnak a d|a és d|b oszthatóságok – hiszen d közös osztója a-nak és b-nek –, ezért a 16.2. Tétel 7. pontja miatt fennállnak a d|ua és d|vb oszthatóságok is. Ám ekkor ugyanezen tétel 6. pontja miatt fennáll az alábbi oszthatóság is:
d|\underbrace{u\cdot a +v\cdot b}_{=x}Azaz x többszöröse d-nek, ami azt jelenti, hogy benne van a (d) főideálban, tehát valóban teljesül az (a,b)\sube (d) tartalmazási reláció.
A 2. állítás: Azt már a 19.19. Tételben igazoltuk, hogy az (a,b)=(d) halmazegyenlőség esetén d kitüntetett közös osztója a-nak és b-nek. Így most csak annyit kell megmutatni, hogy felírható d=u\cdot a+v\cdot b alakban. Mivel nyilván d\in (d), ezért az (a,b)=(d) halmazegyenlőség miatt d\in (a,b). Ám ekkor d a 20.9. Tétel alapján valóban felírható a kívánt alakban.
Visszafelé: Legyen most d kitüntetett közös osztója a-nak és b-nek, és tegyük fel, hogy d felírható d=u\cdot a+v\cdot b alakban. Azt kell megmutatni, hogy ebben az esetben teljesül az (a,b)=(d) halmazegyenlőség. Mivel d kitüntetett közös osztó, ezért az 1. állítás miatt fennáll az (a,b)\sube (d) tartalmazási reláció, így már csak a másik irányú tartalmazás – azaz (d)\sube (a,b) – fennállását kell bizonyítani.
Legyen x a (d) főideál tetszőleges eleme. Ez azt jelenti, hogy teljesül a d|x oszthatóság, azaz létezik olyan k gyűrűelem, hogy x=k\cdot d. De mivel d-ről tudjuk, hogy felírható d=ua+vb alakban, ezért ugyanez igaz lesz x-re:
x=k\cdot (\underbrace{ua+vb}_{=d})=(ku)\cdot a+(kv)\cdot bÍgy x a 20.9. Tétel alapján benne van az (a,b) ideálban, tehát valóban teljesül a (d)\sube (a,b) tartalmazási reláció is. Minthogy (d) és (a,b) között mindkét irányban fennáll a tartalmazási reláció, ezért a 19.2. Definíció utáni megjegyzés 5. pontja miatt a két halmaz megegyezik.
∎Most alkalmazzuk a fenti példára a tételt. Mivel a 2 a 8 és 6 kitüntetett közös osztója, továbbá 2=1\cdot 8 + (-1)\cdot 6, ezért a (8,6) ideál nem csak látszólag, hanem valóban megegyezik a (2) főideállal.
Az előző tételnek van egy egyszerű következménye az előző részben tárgyalt főideálgyűrűkre nézve, amely Bézout-lemma néven ismeretes. Ez Étienne Bézout 18. századi francia matematikusról kapta a nevét, és eredetileg az egész számok körében volt ismeretes, ám az ennél általánosabb főideálgyűrűkre is érvényes.
20.11. Tétel (Bézout-lemma):
Legyen R főideálgyűrű, továbbá legyenek a és b az R tetszőleges elemei. Ekkor az a és b elemek kitüntetett közös osztója kifejezhető u\cdot a+v\cdot b alakban az R gyűrű alkalmasan választott u és v elemeinek segítségével. Ezt az összeget az a és b elemek u és v elemekkel vett lineáris kombinációjának nevezzük.
♣Bizonyítás:
Jelöljük d-vel az a és b elemek kitüntetett közös osztóját. Mivel R főideálgyűrű, ezért az (a,b) ideál is szükségképpen főideál, azaz generálható egyetlen elemmel is. Létezik tehát olyan e gyűrűelem, hogy (a,b)=(e). Ekkor azonban a 20.10. Tétel 2. pontja alapján e is kitüntetett közös osztója a-nak és b-nek.
Mármost a kitüntetett közös osztó a 17.6. Tétel szerint asszociáltság erejéig egyértelmű, azaz teljesül az e\sim d asszociáció. Ez viszont az asszociáltság 16.6. Definíciója alapján azt jelenti, hogy e-nek és d-nek pontosan ugyanazok a többszöröseik, vagyis az általuk generált főideálok megegyeznek, azaz (e)=(d). Teljesül tehát az alábbi halmazegyenlőség:
(d)=\underbrace{(a,b)}_{=(e)}Ebből viszont a 20.10. Tétel 2. pontja miatt következik, hogy d valóban kifejezhető u\cdot a+v\cdot b alakban az R integritástartomány alkalmas u és v elemeinek segítségével.
∎Most térjünk vissza az ax\equiv b\pmod m lineáris kongruencia megoldhatóságának kérdésére. Az alábbi tételben megmutatjuk, hogy ez szoros összefüggésben van egy egész számokon értelmezett egyenlet – úgynevezett lineáris diofantoszi egyenlet – megoldhatóságával.
20.12. Tétel:
Legyen a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám. Ekkor az a\cdot x\equiv b\pmod m lineáris kongruencia akkor és csak akkor oldható meg, ha megoldható az alábbi úgynevezett lineáris diofantoszi egyenlet:
a\cdot x+m\cdot y=bItt megoldáson egy olyan egész számpárt értünk, amelyeket a fenti lineáris diofantoszi egyenletbe x és y helyére behelyettesítve teljesül az egyenlőség. Egy tetszőleges s egész szám által reprezentált [s]_m maradékosztály akkor és csak akkor megoldása az ax\equiv b\pmod m lineáris kongruenciának, ha létezik olyan t egész szám, hogy az (s;t) számpár megoldása az ax+my=b lineáris diofantoszi egyenletnek – azaz fennáll az as+mt=b egyenlőség.
Jelöljük (a,m)-mel az a és m egész számok kitüntetett közös osztóját. A fenti lineáris diofantoszi egyenletnek – és így a neki megfelelő ax\equiv b\pmod m lineáris kongruenciának – akkor és csak akkor létezik megoldása, ha teljesül az (a,m)|b oszthatóság.
♣Bizonyítás:
Elsőként megmutatjuk, hogy az ax\equiv b\pmod m lineáris kongruencia pontosan akkor oldható meg, amikor megoldható az ax+my=b lineáris diofantoszi egyenlet.
Az ax\equiv b\pmod m megoldhatósága azt jelenti, hogy létezik olyan [s]_m maradékosztály, amely megoldása ennek a kongruenciának. Az [s]_m maradékosztályt tehát az s egész számmal reprezentáltuk, azaz teljesül az as\equiv b\pmod m kongruencia. Ez viszont a 20.1. Tétel 3. pontja alapján pontosan akkor teljesül, ha fennáll az m|b-as oszthatóság. Az oszthatóság 16.1. Definíció definíciója miatt ez pontosan azt jelenti, hogy létezik olyan t egész szám, amelyre teljesül az mt=b-as egyenlet. Mindkét oldalhoz as-t hozzáadva azt kapjuk tehát, hogy az ax\equiv b\pmod m kongruencia megoldhatósága pontosan azt jelenti, hogy léteznek olyan s és t egész számok, amelyek kielégítik az alábbi lineáris diofantoszi egyenletet:
ax+my=bAz utóbbi megoldhatóságának szükséges és elégséges feltétele ezért egyúttal az előbbi megoldhatóságának is szükséges és elégséges feltétele lesz – épp ahogyan a tétel állítja. A fentiekből továbbá kiderült, hogy egy s egész szám által reprezentált [s]_m maradékosztály valóban akkor és csak akkor megoldása az ax\equiv b\pmod m lineáris kongruenciának, ha létezik olyan t egész szám, amelyre fennáll az as+mt=b egyenlőség.
Most azt igazoljuk, hogy az ax+my=b egyenlet megoldhatóságának szükséges és elégséges feltétele az (a,m)|b oszthatóság. Tegyük ezért fel, hogy az x_0, y_0 egész számpár egy megoldása ennek az egyenletnek, azaz:
ax_0+my_0=bMivel az (a,m) az a és m egész számok közös osztója, ezért nyilván fennállnak az (a,m)|a és (a,m)|m oszthatóságok. Emiatt a 16.2. Tétel 7. pontja alapján fennállnak az (a,m)|ax_0 valamint az (a,m)|my_0 oszthatóságok is. Ám ekkor ugyanezen tétel 6. pontja miatt fennáll az alábbi oszthatóság is:
(a,m)|\underbrace{ax_0 +my_0}_{=b}Visszafelé: Ha fennáll az (a,m)|b oszthatóság, az azt jelenti, hogy létezik olyan t egész szám, amelyre teljesül az alábbi egyenlet:
(a,m)\cdot t=bMivel az egész számok \Z gyűrűje főideálgyűrű (19.16. Tétel), ezért alkalmazható a Bézout-lemma (20.11. Tétel). Ez alapján az (a,m) kitüntetett közös osztóhoz léteznek olyan u és v egész számok, hogy teljesül az alábbi:
(a,m)=au+mvEzt behelyettesíthetjük az előző egyenletbe:
(\underbrace{au+mv}_{(a,m)})\cdot t=bA zárójelet felbontva végül ezt kapjuk:
a\cdot (ut) + m\cdot (vt)=bAzaz lényegében megkaptuk az ax+my=b lineáris diofantoszi egyenlet egy megoldását, nevezetesen az x=ut, y=vt egész számpárt.
∎Ez tehát azt jelenti, hogy az ax\equiv b\pmod m lineáris kongruencia és az ax+my=b lineáris diofantoszti egyenlet kölcsönösen visszavezethetők egymásra. Ennek alapján bármely, a lineáris kongruenciákkal kapcsolatos eredmény felhasználható a lineáris diofantoszi egyenletek vizsgálatánál és viszont.
Felhívjuk azonban a figyelmet, hogy jelentős eltérés van a kettő között! Egy lineáris kongruencia megoldásai modulo m maradékosztályok, és így a megoldások száma véges. Ezzel szemben egy lineáris diofantoszi egyenlet megoldásai egész számpárok, és ezekből végtelen sok lehet.
Amikor egy lineáris kongruenciát kell megoldanunk, akkor általában az iménti tétel alapján visszavezetjük azt egy lineáris diofantoszi egyenletre. Egy ilyen egyenlet megoldására a következő részben fogunk mutatni egy roppant hatékony módszert, amely tulajdonképpen a 17. részben bemutatott euklidészi algoritmusnak egy kibővített változata. Ennek az eljárásnak a segítségével kiszámítjuk a diofantoszi egyenlet egy x, y megoldását. Ekkor a 20.12. Tétel alapján az x által reprezentált [x]_m maradékosztály épp az eredeti lineáris kongruencia egyik megoldása lesz.
Jogosan merül fel a kérdés, hogy mi van akkor, ha egy lineáris kongruenciának több megoldása is létezik? Vajon összesen hány megoldás van? Hogyan kapható meg egy megoldásból az összes többi? Ezt az alábbi tételben válaszoljuk meg, majd a bizonyítás után egy egyszerű példán demonstráljuk ennek alkalmazását.
20.13. Tétel:
Legyen a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám. Jelöljük továbbá az a és m egész számok pozitív kitüntetett közös osztóját d-vel, azaz d=(a,m). Ekkor igazak az alábbi állítások:
- Ha az ax\equiv b\pmod m kongruencia megoldható, akkor a 20.8. Definíció szerinti értelemben vett megoldásszáma d.
- Ha egy valamilyen s egész szám által reprezentált [s]_m maradékosztály megoldása az ax\equiv b\pmod m kongruenciának, akkor pontosan az alábbi – egymástól páronként különböző – maradékosztályok lesznek a kongruencia megoldásai:
Itt \frac{m}{d} alatt azt az egész számot értjük, amelyet a d=(a,m) kitüntetett közös osztóval megszorozva az m modulust kapjuk eredményül.
♣Bizonyítás:
Elegendő a 2. állítást igazolni, abból ugyanis automatikusan következik a megoldásszámra vonatkozó 1. állítás. Azt mondtuk, hogy az s egész szám által reprezentált [s]_m maradékosztály megoldása a kongruenciának, azaz:
as\equiv b\pmod mVálasszunk most egy tetszőleges t egész számot. Az általa reprezentált [t]_m maradékosztály akkor és csak akkor lesz megoldása a kongruenciának, ha teljesül at\equiv b\pmod m. Mivel a kongruencia szimmetrikus és tranzitív (20.2. Tétel 2. és 3. pont), ezért ez pontosan az alábbit jelenti:
as\equiv at\pmod mA kongruenciák egyszerűsítéséről szóló 20.3. Tétel alapján mindkét oldalt egyszerűsíthetjük a-val, ám eközben a modulust is „el kell osztanunk” az (a,m) kitüntetett közös osztóval, azaz jelen esetben d-vel. A fenti kongruencia tehát pontosan az alábbi esetben teljesül:
s\equiv t\pmod{\frac{m}{d}}Vagyis a t által reprezentált [t]_m maradékosztály pontosan akkor lesz megoldás, ha t ugyanabba a modulo \frac{m}{d} maradékosztályba esik, mint s, azaz:
[s]_{\frac{m}{d}}=[t]_{\frac{m}{d}}Ez a 20.4. Tétel alapján épp azt jelenti, hogy t felírható az alábbi alakban valamilyen alkalmasan választott k egész számmal:
t=s+k\cdot \frac{m}{d}Azt kaptuk tehát, hogy amennyiben ismerünk egy [s]_m megoldást, akkor az összes többi megoldást előállíthatjuk [s+k\cdot \frac{m}{d}]_m alakban. Így már csak azt kell igazolni, hogy k-val végigfutva az összes egész számon épp a tétel 2. állításában szereplő d darab modulo m maradékosztályt kapjuk.
Nézzük meg ezért, hogy két különböző k_1 és k_2 esetén az s+k_1\frac{m}{d} és s+k_2\frac{m}{d} kifejezések mikor fogják ugyanazt a maradékosztályt reprezentálni, azaz mikor fog teljesülni az alábbi:
[s+k_1\frac{m}{d}]_m=[s+k_2\frac{m}{d}]_mEz ugye pontosan akkor teljesül, ha fennáll az alábbi kongruencia:
s+k_1\frac{m}{d}\equiv s+k_2\frac{m}{d} \pmod mA 20.2. Tétel 6. pontja miatt mindkét oldalból kivonhatunk s-t:
k_1\frac{m}{d}\equiv k_2\frac{m}{d} \pmod mA 20.3. Tétel alapján mindkét oldalt egyszerűsíthetjük \frac{m}{d}-vel. Vigyáznunk kell azonban, mivel ilyenkor ugye a modulust is egyszerűsíteni kell \frac{m}{d} és m kitüntetett közös osztójával! Azaz a fenti kongruencia pontosan akkor teljesül, amikor az alábbi kongruencia is:
k_1\equiv k_2 \pmod{\frac{m}{(\frac{m}{d}, m)}}Most vizsgáljuk meg, hogy tulajdonképpen mivel egyezik meg az itt szereplő modulus. Ne feledjük, hogy itt nem törtekről van szó, hiszen az egész számok \Z gyűrűjében vagyunk, ahol nem értelmezhető az osztás művelete. Ehelyett például az \frac{m}{d} csak egy jelölés, amely azt az egész számot jelöli, amellyel a d egész számot megszorozva az m egész számot kapjuk eredményül. Azaz:
\frac{m}{d} \cdot d = mFeltéve persze, ha ilyen létezik, aminek ugye a feltétele az d|m oszthatóság. Ez jelen esetben nyilván fennáll, mivel azt mondtuk, hogy d az a és m kitüntetett közös osztója. Ám ekkor teljesül az \frac{m}{d}|m oszthatóság is, így az (\frac{m}{d},m) kitüntetett közös osztó a 17.5. Tétel 4. pontja miatt \frac{m}{d}-vel egyezik meg. A fenti kongruenciában tehát a modulus így hozható egyszerűbb formára:
\frac{m}{(\frac{m}{d}, m)}=\frac{m}{(\frac{m}{d})}Ez tehát azt az egész számot jelöli, amellyel az \frac{m}{d} egész számot megszorozva az m egész számot kapjuk eredményül. A fentebbi \frac{m}{d} \cdot d = m összefüggés alapján ez épp d-vel egyezik meg. A fenti kongruencia tehát tulajdonképpen így néz ki:
k_1\equiv k_2\pmod dAzt kaptuk tehát, hogy az [s+k_1\frac{m}{d}]_m és [s+k_2\frac{m}{d}]_m modulo m maradékosztályok akkor és csak akkor egyeznek meg, amikor a [k_1]_d és [k_2]_d modulo d maradékosztályok megegyeznek.
Ez viszont pontosan azt jelenti, hogy épp annyi megoldása van az ax\equiv b\pmod m lineáris kongurenciának, ahány modulo d maradékosztály létezik, ezek száma viszont a 20.4. Tétel alapján d. Így tehát ha k végigfut a 0, 1, 2, ..., d-1 egész számokon, akkor épp a 2. állításban szereplő [s]_m, [s+\frac{m}{d}]_m, [s+2\frac{m}{d}]_m, ..., [s+(d-1)\frac{m}{d}]_m maradékosztályokat kapjuk megoldásként.
∎Most nézzünk meg egy egyszerű példát az iménti tétel alkalmazására. A 18. részben szó volt arról, hogy nagyon óvatosan kell eljárnunk, amikor a 18.3. Definíció szerinti \Z_m gyűrűben akarunk egyenleteket megoldani. Példaként a \Z_8 gyűrűben írtuk fel az alábbi egyenletet:
(2\odot x)\oplus 3=7Az említett példában megmutattuk, hogyha a „szokásos” módon próbáljuk megoldani ezt az egyenletet, akkor elveszhetnek bizonyos megoldások. Ha például mindkét oldalból kivonunk 3-at, majd mindkét oldalt „elosztjuk” 2-vel, akkor megkapjuk ugyan az x=2 megoldást, ám elveszítjük az x=6 megoldás. Ennek az oka az volt, hogy a \Z_8 gyűrű nem nullosztómentes – hiszen például 2\odot 4=0, holott egyik tényező sem 0. Az imént bizonyított, lináris kongruenciákkal kapcsolatos tétel segítségével azonban már könnyen kezelhetjük az ilyen egyenleteket. Nézzük is meg, hogyan.
Mint már említettük, a homomorfizmustétel miatt (18.25. Tétel) a \Z_8 gyűrű izomorf a \Z/8\Z gyűrűvel – azaz a modulo 8 maradékosztálygyűrűvel –, tehát pontosan ugyanúgy kell benne számolni. Emiatt a \Z_8 gyűrűben felírt (2\odot x)\oplus 3=7 egyenletet áttranszformálhatjuk a \Z/8\Z maradékosztálygyűrűbe:
([2]_8\odot X)\oplus [3]_8=[7]_8A [3]_8 maradékosztály ellentettje az [5]_8 maradékosztály, mivel ezek összege épp a [0]_8 maradékosztály. Így mindkét oldalhoz [5]_8-öt hozzáadva ezt kapjuk:
[2]_8\odot X=[4]_8Keressük tehát azt az X maradékosztályt, amelyet a [2]_8 maradékosztállyal megszorozva a [4]_8 maradékosztályt kapjuk eredményül. Ha megnézzük a \Z/8\Z maradékosztálygyűrű alábbi szorzótábláját, akkor látszik, hogy két megoldás van. Nevezetesen az X=[2]_8 és az X=[6]_8 maradékosztályok:
\begin{array}{c|cccccccc}\odot & [0]_8 & [1]_8 & [2]_8 & [3]_8 & [4]_8 & [5]_8 & [6]_8 & [7]_8 \\ \hline [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 & [0]_8 \\ [1]_8 & [0]_8 & [1]_8 & [2]_8 & [3]_8 & [4]_8 & [5]_8 & [6]_8 & [7]_8 \\ [2]_8 & [0]_8 & [2]_8 & [4]_8 & [6]_8 & [0]_8 & [2]_8 & [4]_8 & [6]_8 \\ [3]_8 & [0]_8 & [3]_8 & [6]_8 & [1]_8 & [4]_8 & [7]_8 & [2]_8 & [5]_8 \\ [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 & [0]_8 & [4]_8 \\ [5]_8 & [0]_8 & [5]_8 & [2]_8 & [7]_8 & [4]_8 & [1]_8 & [6]_8 & [3]_8 \\ [6]_8 & [0]_8 & [6]_8 & [4]_8 & [2]_8 & [0]_8 & [6]_8 & [4]_8 & [2]_8 \\ [7]_8 & [0]_8 & [7]_8 & [6]_8 & [5]_8 & [4]_8 & [3]_8 & [2]_8 & [1]_8 \end{array}Igenám, csakhogy egy sokkal nagyobb – például a kriptográfiai gyakorlatban előforduló többszázjegyű – modulus esetén nem írhatjuk fel a szorzótáblát, mivel az ehhez használt papírlap sokszorosan beborítaná az egész bolygót. Ehelyett a megoldáshoz a fenti tételt fogjuk alkalmazni.
A 20.4. Tétel alapján elegendő a keresett X maradékosztály(ok) egyetlen elemét megtalálni, hiszen ebből könnyedén megkapható az összes többi. Jelöljük ezt a keresett elemet x-szel, azaz X=[x]_m. Ekkor a fenti egyenlet – követve a \odot művelet 20.5. Tételbeli definícióját – így módosul:
[2]_8\odot [x]_8=[2\cdot x]_8=[4]_8Szavakkal megfogalmazva tehát kell keresnünk egy olyan x egész számot, amely esetén a 2\cdot x szorzat ugyanabban a maradékosztályban van, mint a 4 egész szám. Ez épp az alábbi lineáris kongruencia megoldásainak megkeresését jelenti:
2\cdot x\equiv 4\pmod 8A 20.12. Tétel alapján ez a kongruencia megoldható, mivel a (2,8)=2 kitüntetett közös osztónak többszöröse a kongruencia jobboldalán szereplő 4 egész szám. A 20.13. Tétel alapján ekkor a megoldásszám valóban 2.
Tegyük fel, hogy valahogyan megtaláltuk a [2]_8 megoldást. Ezt például az úgynevezett kibővített euklidészi algoritmus segítségével tudjuk majd kiszámítani, amelyet a következő részben fogunk bemutatni. Ekkor a 20.13. Tétel alapján valóban pontosan az alábbi maradékosztályok lesznek a megoldások:
\begin{aligned}[2+0\cdot \frac{8}{(2,8)}]_8&=[2]_8 \\ [2+1\cdot \frac{8}{(2,8)}]_8&=[2+4]_8=[6]_8\end{aligned}Így tehát a \Z_8 gyűrű és a \Z/8\Z maradékosztálygyűrű izomorfiája miatt az eredeti (2\odot x)\oplus 3=7 egyenlet megoldásai az x=2 és x=6 elemek lesznek a \Z_8 gyűrűben.
Teljes és redukált maradékrendszerek
Most tehát egy lépéssel közelebb kerültünk az Euler-féle \varphi-függvény kiszámításához, ami ugye a 20.7. Definíció alapján épp a modulo m redukált maradékosztályok számát adja meg. Az előző szakaszban tanultak felhasználásával ugyanis egy adott maradékosztályról könnyedén el tudjuk dönteni, hogy redukált-e vagy nem, azaz létezik-e inverze a \Z/m\Z maradékosztálygyűrű szorzására nézve vagy nem. Ennek pontos feltételét az alábbi tételben adjuk meg.
20.14. Tétel:
Legyen m\gt 0 tetszőleges pozitív egész szám. Egy a egész szám által reprezentált [a]_m maradékosztály akkor és csak akkor redukált – azaz invertálható –, ha a relatív prím m-hez.
Ha [a]_m=[b]_m, akkor az (a,m) és (b,m) kitüntetett közös osztók asszociáltak, azaz (a,m)\sim (b,m). Emiatt teljesen mindegy, hogy a vizsgált maradékosztályt melyik elemével reprezentáljuk, ugyanis vagy mindegyik eleme relatív prím lesz a modulushoz, vagy egyik sem.
♣Bizonyítás:
Az [a]_m maradékosztály a 20.6. Definíció alapján pontosan akkor redukált, ha invertálható, azaz egyértelműen létezik olyan X=[x]_m maradékosztály, amelyre teljesül az alábbi:
[a]_m\odot X=[a]_m\odot [x]_m=[a\cdot x]_m=[1]_mEz pontosan az alábbi lineáris kongruencia egyértelmű megoldhatóságát jelenti:
ax\equiv 1\pmod mEz viszont a 20.12. Tétel szerint pontosan akkor oldható meg, ha teljesül az (a,m)|1 oszthatóság. Ez a 16.5. Tétel alapján azt jelenti, hogy az (a,m) kitüntetett közös osztó egység, vagy más szavakkal a relatív prím az m modulushoz (lásd a 17.10. Definíció utáni megjegyzést).
Válasszuk a pozitív egységet kitüntetett közös osztónak, azaz legyen (a,m)=1. Ebben az esetben a megoldások száma a 20.13. Tétel értelmében (a,m)=1. Vagyis a megoldás valóban egyértelmű.
Most igazoljuk a tétel másik állítását, miszerint egy maradékosztály minden elemének asszociáltság erejéig ugyanaz az m modulussal vett kitüntetett közös osztója. Az [a]_m=[b]_m egyenlőség azt jelenti, hogy a ugyanabban a maradékosztályban van, mint b. Így tehát a 20.4. Tétel alapján a b egész szám felírható az alábbi alakban valamilyen alkalmas k_1 egész szám segítségével:
b=k_1m+aMivel az (a,m) kitüntetett közös osztó osztója a-nak és m-nek, ezért a 16.2. Tétel 7. és 6. pontjai miatt osztója k_1m+a=b-nek is. Így tehát (a,m) közös osztója b-nek és m-nek, vagyis a 17.4. Definíció alapján osztója ezek kitüntetett közös osztójának, azaz teljesül az (a,m)|(b,m) oszthatóság.
Ugyanígy a 20.4. Tétel alapján az a egész szám is felírható az alábbi alakban valamilyen alkalmas k_2 egész szám segítségével:
a=k_2m+bEbből az előző gondolatmenetet megismételve azt fogjuk kapni, hogy teljesül a (b,m)|(a,m) oszthatóság. Minthogy mindkét irányban fennáll az oszthatóság, ezért a 16.9. Tétel miatt (a,m) és (b,m) valóban asszociáltak.
Speciálisan ha a relatív prím m-hez, akkor (a,m) egység, és így az asszociáltság miatt (b,m) is egység, azaz b is relatív prím m-hez.
∎Az Euler-féle \varphi-függvény tehát az imént bizonyított feltételnek eleget tevő maradékosztályok számát adja meg. Mi azonban szeretnénk egy olyan alternatív definíciót adni ennek a függvénynek, amely könnyebben kiszámítható. Ehhez szükségünk van néhány további fogalomra és összefüggésre.
20.15. Definíció (Teljes és redukált maradékrendszer):
Legyen m\gt 0 egy pozitív egész szám. Ha minden modulo m maradékosztályból pontosan egy elemet kiveszünk, akkor az így kapott számhalmazt modulo m teljes maradékrendszernek nevezzük. Ehhez hasonlóan ha minden modulo m redukált maradékosztályból pontosan egy elemet kiveszünk, akkor az így kapott számhalmazt modulo m redukált maradékrendszernek nevezzük.
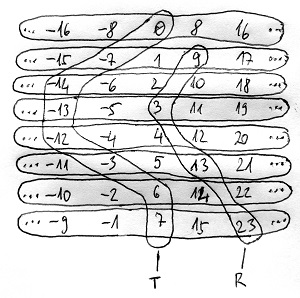
♣Az alábbi ábrán a \Z/8\Z-vel jelölt modulo 8 maradékosztályok, illetve egy-egy belőlük képzett teljes és redukált maradékrendszer látható. Előbbit T-vel, utóbbit pedig R-rel jelöltük. Látható, hogy a T halmaz minden maradékosztályból pontosan egy elemet tartalmaz. Ehhez hasonlóan az R halmaz minden redukált maradékosztályból tartalmaz pontosan egy elemet:
Az alábbi tétel abban nyújt segítséget, hogy egy tetszőleges egész számokból álló halmazról könnyen el tudjuk dönteni, hogy az egy teljes illetve redukált maradékrendszer-e vagy sem.
20.16. Tétel:
Legyen m\gt 0 tetszőleges pozitív egész szám. Egy egész számokból álló H halmaz akkor és csak akkor alkot modulo m teljes maradékrendszert, ha teljesülnek az alábbi feltételek:
- A H halmaz elemeinek száma m.
- A H halmaz tetszőleges a és b elemeire a\neq b esetén a\ \cancel{\equiv}\ b\pmod m.
A H halmaz akkor és csak akkor alkot modulo m redukált maradékrendszert, ha teljesülnek az alábbi feltételek:
- A H halmaz elemeinek száma \varphi(m).
- A H halmaz tetszőleges a és b elemeire a\neq b esetén a\ \cancel{\equiv}\ b\pmod m.
- A H halmaz minden eleme relatív prím m-hez.
Bizonyítás:
Nézzük először a teljes maradékrendszerekre vonatkozó állítást! Tegyük fel, hogy H teljes maradékrendszer modulo m. Mivel a modulo m maradékosztályok száma a 20.4. Tétel alapján m, és H minden maradékosztályból pontosan egy elemet tartalmaz, ezért elemszáma szükségképpen m. Továbbá H elemei páronként inkongruensek modulo m, hiszen mindegyik különböző maradékosztályból származik.
Visszafelé: Tegyük fel, hogy a H halmaz m darab páronként inkongruens számot tartalmaz. Ekkor a páronkénti inkongruencia miatt ezek mindegyike különböző maradékosztályokba tartozik. Továbbá mivel a számuk m, ezért m darab maradékosztályt reprezentálnak, azaz a 20.4. Tétel alapján az összeset. A H halmaz tehát valóban egy modulo m teljes maradékrendszer.
Most nézzük a redukált maradékrendszerekre vonatkozó állítást! Tegyük fel, hogy H redukált maradékrendszer modulo m. Mivel a modulo m redukált maradékosztályok száma a 20.7. Definíció alapján \varphi(m), és H minden redukált maradékosztályból pontosan egy elemet tartalmaz, ezért elemszáma szükségképpen \varphi(m). Továbbá H elemei páronként inkongruensek modulo m, hiszen mindegyik különböző redukált maradékosztályból származik. Végül H minden eleme relatív prím m-hez, hiszen ezeket redukált maradékosztályokból választottuk ki, márpedig a 20.14. Tétel alapján egy redukált maradékosztálynak minden eleme relatív prím m-hez.
Visszafelé: Tegyük fel, hogy a H halmaz \varphi(m) darab páronként inkongruens számot tartalmaz, amelyek mindegyike relatív prím m-hez. Ekkor a páronkénti inkongruencia miatt ezek mindegyike különböző maradékosztályokba tartozik, amelyek mindegyike az m-hez relatív prímség miatt redukált maradékosztály. Továbbá mivel a számuk \varphi(m), ezért \varphi(m) darab redukált maradékosztályt reprezentálnak, azaz a 20.7. Definíció alapján az összeset. A H halmaz tehát valóban egy modulo m redukált maradékrendszer.
∎E tétel egyik alkalmazásaként most egy alternatív definíciót is adunk az Euler-féle \varphi-függvényre.
20.17. Következmény:
Legyen m\gt 0 tetszőleges pozitív egész szám. Ekkor az Euler-féle \varphi-függvény a 0, 1, 2, ..., m-1 egész számok közül az m-hez relatív prímek számát adja meg.
♣Bizonyítás:
A 18.3. Definíció utáni megjegyzés 5. pontja alapján a \bmod_m maradékképző függvény a 0, 1, 2, ..., m-1 egész számokhoz mind különböző modulo m maradékot rendel. Így a 20.1. Tétel 1. pontja alapján ezek a számok páronként inkongruensek. Továbbá, mivel a számuk épp m, ezért a 20.16. Tétel alapján egy teljes maradékrendszert alkotnak modulo m.
Mivel ez egy teljes maradékrendszer, ezért tartalmazza egy-egy reprezentánsát minden modulo m maradékosztálynak, így a redukált maradékosztályoknak is. Ez utóbbiak viszont biztosan mind relatív prímek m-hez, hiszen az általuk reprezentált redukált maradékosztályok a 20.14. Tétel alapján csupa m-hez relatív prím elemekből állnak.
A 20.7. Definíció szerint az Euler-féle \varphi-függvény a modulo m redukált maradékosztályok számát adja meg. A fentiek alapján ez a szám valóban meg fog egyezni azon egészek számával, amelyek 0, 1, 2, ..., m-1 teljes maradékrendszer elemei közül relatív prímek m-hez.
∎Egy másik alkalmazásként megmutatjuk, hogy egy teljes (illetve redukált) maradékrendszerből hogyan kaphatunk egy újabb teljes (illetve redukált) maradékrendszert. Ennek rettentő fontos következménye lesz számunkra az úgynevezett Euler-Fermat tétel, amelyet a következő szakaszban mutatunk be.
20.18. Tétel:
Legyen b tetszőleges, m\gt 0 valamilyen pozitív, a pedig egy m-hez relatív prím egész szám.
Amennyiben az r_1, r_2, ..., r_{m} egész számok egy modulo m teljes maradékrendszert alkotnak, akkor az alábbi számok is: ar_1+b, ar_2+b, ..., ar_{m}+b.
Amennyiben az s_1, s_2, ..., s_{\varphi(m)} egész számok egy modulo m redukált maradékrendszert alkotnak, akkor az alábbi számok is: as_1, as_2, ..., as_{\varphi(m)}.
♣Bizonyítás:
Nézzük először a teljes maradékrendszerre vonatkozó állítást! Mivel az új maradékrendszer elemszáma is m, ezért a 20.16. Tétel alapján elegendő a páronkénti inkongruenciát ellenőrizni. Legyen tehát ar_i+b és ar_j+b az új maradékrendszer két tetszőleges eleme, és tegyük fel, hogy ezek között fennáll a kongruencia, azaz:
ar_i+b\equiv ar_j+b\pmod mA 20.2. Tétel 6. pontja alapján mindkét oldalból kivonhatunk b-t. Így az alábbit kapjuk:
ar_i\equiv ar_j\pmod mMivel a-ról azt mondtuk, hogy relatív prím m-hez, így a 20.3. Tétel utáni megjegyzés alapján a-val egyszerűsíthetjük mindkét oldalt:
r_i\equiv r_j\pmod mEz viszont csak akkor lehetséges, ha r_i=r_j, hiszen az eredeti teljes maradékrendszer elemei páronként inkongruensek modulo m. Így tehát az ar_i+b=ar_j+b egyenlőség is szükségképpen fennáll. Megfordítva a gondolatmenetet: ha az új maradékrendszernek vesszük két egymástól különböző tetszőleges elemét, akkor ők szükségképpen inkongruensek modulo m.
Most nézzük a redukált maradékrendszerre vonatkozó állítást! Mivel az új maradékrendszer elemszáma is \varphi(m), ezért a 20.16. Tétel alapján elegendő a páronkénti inkongruenciát, valamint az m-hez relatív prímséget ellenőrizni. Legyen tehát as_i és as_j az új maradékrendszer két tetszőleges eleme, és tegyük fel, hogy ezek között fennáll a kongruencia, azaz:
as_i\equiv as_j\pmod mInnentől a gondolatmenet teljesen megegyezik az előzővel.
Azt kell még megmutatni, hogy az új maradékrendszer minden eleme relatív prím m-hez. Legyen tehát as_i az új maradékrendszer tetszőleges eleme. Azt ugye a tétel szövegéből tudjuk, hogy a relatív prím m-hez. Továbbá s_i is relatív prím m-hez, mivel ő az eredeti redukált maradékrendszer egyik eleme.
Ez azt jelenti, hogy sem a-nak, sem pedig s_i-nek nincs m-mel közös osztója az egységeken kívül. Mivel a 17.22. Tétel szerint az egész számok \Z gyűrűjében teljesül a számelmélet alaptétele, ezért ez azt is jelenti, hogy a és s_i prímtényezői mind különböznek m prímtényezőitől, és így a szorzatuknak sincs m-mel közös prímtényezője, tehát osztója sem az egységeken kívül. Azaz as_i valóban relatív prím m-hez.
∎Az Euler-Fermat tétel
Végül ebben a szakaszban megismerjük az RSA kriptográfiai eljárás alapját képező Euler-Fermat tételt. Ezt a tételt 1736-ban publikálta Leonhard Euler egy másik hasonlóan fontos tétel, a kis Fermat-tétel általánosításaként. Ez utóbbi Pierre de Fermat francia műkedvelő matematikustól származik 100 évvel korábbról, 1636-ból, és majd a prímtesztelő eljárások kapcsán lesz róla szó bővebben egy későbbi részben.
20.19. Tétel (Euler-Fermat tétel):
Legyen m\gt 0 tetszőleges pozitív, a pedig egy m-hez relatív prím egész szám. Ekkor teljesül az alábbi kongruencia:
a^{\varphi(m)} \equiv 1\pmod mItt az a^{\varphi(m)} kifejezés alatt egy olyan \varphi(m) tényezős szorzatot értünk, amelynek minden tényezője a.
♣Bizonyítás:
Tekintsünk egy tetszőleges R=\{r_1; r_2; \ldots; r_{\varphi(m)}\} modulo m redukált maradékrendszert. Mivel a relatív prím m-hez, ezért a 20.18. Tétel alapján az S=\{ar_1; ar_2; \ldots; ar_{\varphi(m)}\} számhalmaz is egy modulo m redukált maradékrendszert alkotnak.
Ez azt jelenti, hogy mindkét számhalmaz tartalmaz egy-egy reprezentánselemet az összes létező redukált maradékosztályból. Tehát az S halmazban minden ar_i elemnek van egy r_j párja az R halmazban, amely ugyanannak a redukált maradékosztálynak a reprezentánseleme, vagyis vele kongruens modulo m. Most átmenetileg nevezzük át az R elemeit úgy, hogy az ar_i ilyen értelemben vett párját jelöljük s_i-vel. Ebből tehát \varphi(m) darab kongruenciát lehet felírni, ahol a baloldalon az S, míg a jobboldalon – a most bevezetett jelölésekkel – az R halmaz elemei szerepelnek:
\begin{aligned}ar_1&\equiv s_1\pmod m \\ ar_2&\equiv s_2\pmod m \\ ar_3&\equiv s_3\pmod m \\ &\vdots \\ ar_{\varphi(m)}&\equiv s_{\varphi(m)}\pmod m\end{aligned}A 20.2. Tétel 5. pontja alapján ez a \varphi(m) darab kongruencia összeszorozható:
\underbrace{aa \ldots a}_{\varphi(m)\ \text{darab}} \cdot r_1r_2\ldots r_{\varphi(m)} \equiv s_1s_2\ldots s_{\varphi(m)} \pmod mA jobboldalon tehát az R halmaz elemei szerepelnek, csak épp átmenetileg az s_1, s_2, ..., s_{\varphi(m)} nevekkel láttuk el őket. Az eredeti neveikkel szerepeltetve és az eszerinti indexelés alapján sorbarendezve őket a fenti kongruencia tulajdonképpen így néz ki:
a^{\varphi(m)} \cdot r_1r_2\ldots r_{\varphi(m)} \equiv r_1r_2\ldots r_{\varphi(m)} \pmod mMivel az R=\{r_1; r_2; \ldots; r_{\varphi(m)}\} számhalmaz egy modulo m redukált maradékrendszer, ezért minden eleme relatív prím m-hez. Emiatt a fenti kongruenciát a 20.3. Tétel utánis megjegyzés alapján ezekkel az elemekkel mind egyszerűsíthetjük, megkapva így a tétel állítását:
a^{\varphi(m)} \equiv 1\pmod m ∎Alkalmazzuk például az m=8 modulusra és hozzá relatív prím a=5-re a tételt. Ekkor a kongruencia baloldala így néz ki:
a^{\varphi(m)}=5^{\varphi(8)}=5^4=625Ez 8-cal osztva valóban 1-et ad maradékul.
Az, hogy a tételben szereplő a relatív prím a modulushoz más szavakkal azt jelenti, hogy ő egy redukált maradékosztály reprezentánseleme. A tétel tehát tulajdonképpen azt mondja, hogy a \Z/m\Z maradékosztálygyűrűben a redukált maradékosztályok bármelyikét a \varphi(m)-edik hatványra emelve mindig az [1]_m maradékosztályt, vagyis a \Z/m\Z gyűrű egységelemét kapjuk eredményül. Ez a tény alapvető fontosságú az RSA kriptográfiai eljárás szempontjából, mint ahogyan azt látni fogjuk.
Végül megjegyezzük, hogy az Euler-Fermat tétel megfordítása is igaz. Vagyis az imént említett feltétel – miszerint a relatív prím a modulushoz – az Euler-Fermat tételben szereplő kongruencia teljesülésének nemcsak elégséges, hanem szükséges feltétele is. Sőt, az alábbi tételben egy ennél erősebb állítást is igazolunk.
20.20. Tétel:
Legyen m\gt 0 tetszőleges pozitív, a pedig egy tetszőleges egész szám. Tegyük fel, hogy létezik olyan k\gt 0 pozitív kitevő, amelyre teljesül az alábbi kongruencia:
a^k\equiv 1\pmod mEkkor a relatív prím m-hez.
♣Bizonyítás:
Tekintsük az alábbi lineáris kongruenciát:
ax\equiv 1\pmod mEnnek a lineáris kongruenciának a 20.12. Tétel értelmében akkor és csak akkor létezik megoldása, ha teljesül az (a,m)|1 oszthatóság. Minthogy az 1 egész szám a \Z gyűrű egységeleme, így ez az oszthatóság akkor és csak akkor teljesülhet, ha (a,m) egység, azaz a relatív prím m-hez.
Márpedig k\gt 1 kitevő esetén az a^k\equiv 1\pmod m kongruencia így írható fel:
a\cdot \overbrace{a^{k-1}}^{=x}\pmod mHa pedig a k kitevő 1, akkor pedig így:
a\cdot \overbrace{1}^{=x}\pmod mElső esetben a fenti lineáris kongruenciát az x=a^{k-1}, második esetben pedig az x=1 egész szám kielégíti, azaz van megoldása, és így a 20.12. Tétel értelmében a valóban relatív prím m-hez.
∎Ebben a részben tehát megvizsgáltuk, hogy a 18. részben bevezetett kongruencia fogalma mit jelent az egész számok \Z gyűrűjére vonatkoztatva. Megmutattuk, hogy a kongruenciákkal nagyjából ugyanúgy kell számolni, mint a hagyományos egyenletekkel, de azért bizonyos esetekben vigyázni kell. Ezután megvizsgáltuk, hogy hogyan néznek ki az egész számok maradékosztályai és maradékosztálygyűrűi, és megismerkedtünk az Euler-féle \varphi-függvénnyel, amely a modulo m redukált maradékosztályok számát adja meg. A lineáris kongruenciák megoldhatóságának feltételei kapcsán erre a függvényre adtunk egy alternatív definíciót is. Végül megismerkedtünk az RSA-eljárás alapját képező Euler-Fermat tétellel.
A következő részekben kibővítjük a 17. részben megismert euklidészi algoritmust, amely így már alkalmas lesz a most tanult lineáris kongruenciák megoldására is. Megvizsgáljuk továbbá, hogy hogyan lehet kiszámítani az Euler-féle \varphi-függvény értékét egy adott számra annak prímtényezőinek ismeretében. Így már minden számelméleti ismeret rendelkezésre áll az RSA-eljárás részleteinek bemutatásához. Végül rátérünk arra a kérdésre, hogy hogyan lehet az RSA biztonságához szükséges óriási – a gyakorlatban többszázjegyű – prímszámokat találni.
A következő részt itt találod…



