Tegyük fel, hogy adva van egy (R,+,\cdot) és egy (S,\oplus,\odot) gyűrű. Ekkor egy f:R\to S függvényt gyűrűhomomorfizmusnak nevezünk, amennyiben tetszőleges R-beli a és b elemekre teljesülnek az alábbi követelmények:
\begin{aligned}f(a+b)&=f(a)\oplus f(b)\\f(a\cdot b)&=f(a)\odot f(b)\end{aligned}Amennyiben S minden eleme legalább egy R-beli elemhez hozzá van rendelve, akkor f-et szürjektív gyűrűhomomorfizmusnak vagy gyűrűráképzésnek nevezzük.
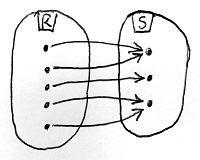
Amennyiben S minden eleme legfeljebb egy R-beli elemhez van hozzárendelve, akkor f-et injektív gyűrűhomomorfizmusnak vagy gyűrűbeágyazásnak nevezzük.
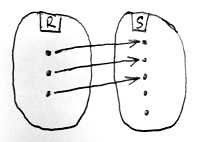
Amennyiben S minden eleme pontosan egy R-beli elemhez van hozzárendelve, akkor f-et bijektív gyűrűhomomorfizmusnak vagy gyűrűizomorfizmusnak nevezzük.
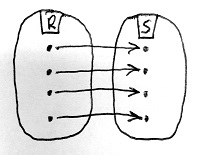
Ilyenkor azt mondjuk, hogy az R és az S gyűrű izomorf egymással. Ezt így jelöljük: R\simeq S.


