Induljunk ki a tétel első felében szereplő R ekvivalenciarelációból. Olyan nyilván nem fordulhat elő, hogy egy a elem nincs benne egyik osztályban sem. A reflexivitás miatt ugyanis a legalább önmagával relációban áll, így ő legrosszabb esetben is benne van egy egyelemű (csak a-t tartalmazó) osztályban. Tegyük most fel, hogy a két olyan osztályban is benne van, amelyek tartalmaznak további elemeket és különböznek egymástól. Legyen például a következő a szituáció:
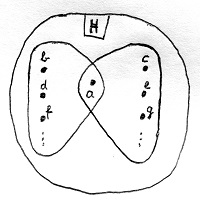
Mivel a és b egy osztályba kerültek, ezért aRb teljesül. Hasonló okok miatt teljesül aRc is. De ha aRc teljesül, akkor a szimmetria miatt cRa is teljesül. De mivel cRa és aRb egyszerre teljesül, ezért a tranzitivitás miatt cRb is teljesül. Ez viszont azt jelenti, hogy c-nek és b-nek mégiscsak ugyanabba az osztályba kellett volna kerülnie, ami ellentmond annak a feltételezésünknek, hogy kialakulhat a fenti ábrán lévő szituáció. Az R ekvivalenciareláció által a tételben szereplő módon meghatározott osztályozás tehát valóban egy partíció a H halmazon.
Megfordítva: Tekintsük most H egy tetszőleges partícióját, amelyben tehát minden elem pontosan egy osztályban van. Képezzük ebből az S relációt a tétel szerint. Az S reláció reflexív, mivel tetszőleges a elem nyilvánvalóan ugyanabban az osztályban van, mint önmaga, legyen szó bármilyen partícióról. Hasonlóan az S reláció szimmetrikus, mivel ha egy tetszőleges a elem ugyanabban az osztályban van, mint egy tetszőleges b elem, akkor nyilván b elem is ugyanabban az osztályban van, mint a elem, legyen szó bármilyen partícióról.
Végezetül tegyük fel, hogy S nem tranzitív, azaz léteznek olyan galád a, b és c elemek, amelyekre aSb és bSc teljesül, ugyanakkor a\cancel{S} c. Ez csak akkor fordulhat elő, ha a és c két különböző osztályban van, b viszont mindkét osztálynak eleme:
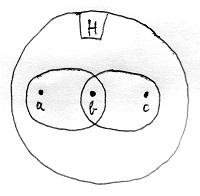
Ez viszont ellentmond annak, hogy az osztályozás, amiből a tétel szerinti S relációt képeztük egy partíció volt. Az S reláció tehát mégiscsak tranzitív. Mivel beláttuk, hogy teljesül mindhárom követelmény, ezért S valóban egy ekvivalenciareláció.


