Vigyázat! Az f(C) kifejezés ebben az esetben nem valamiféle matematikai objektumot jelöl, amelyet az f függvény a C halmazhoz hozzárendel. Ehelyett azt a halmazt jelöli, amely pontosan a C-beli elemek f szerinti képeit tartalmazza. Ehhez hasonlóan az f^{-1}(D) nem egy olyan matematikai objektumot jelöl, amelyhez az f függvény épp a D halmazt rendeli hozzá. Ehelyett azt a halmazt jelöli, amely pontosan azokat az A-beli elemeket tartalmazza, amelyeknek f szerinti képe D-ben van.

A definícióból következik, hogy ha f^{-1}(D)=C teljesül, akkor f(C)=D is teljesül. Nyilván, hiszen a definíció szerint C is egy olyan részhalmaz A-ban, amelynek f szerinti képe D – történetesen a legbővebb.

Vigyázzunk azonban, ugyanis ez utóbbi állítás megfordítása nem igaz! Azaz f(C)=D-ből a C=f^{-1}(D) állítás még nem, csupán az ennél gyengébb C\sube f^{-1}(D) állítás következik. Elképzelhető ugyanis, hogy létezik egy C-nél bővebb E\sube A halmaz is, amelynek szintén D a képe. Ezt a szitációt mutatja az alábbi ábra:

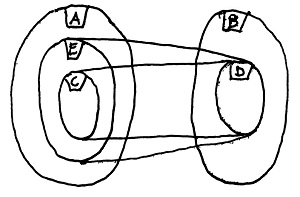
Végül megjegyezzük, hogy az f(C) halmaz tetszőleges C esetén létezik, mivel az f egy függvény, amely A minden eleméhez, és így speciálisan az összes C-beli elemhez is szükségképpen hozzárendel valamit a B halmazból. Így f(C) legrosszabb esetben legalább egy elemet mindenképpen tartalmaz – kivéve persze ha C az üreshalmaz, amikoris f(C) is az üreshalmaz.

Ezzel szemben az f^{-1}(D) teljes inverz kép adott D esetén nem biztos, hogy létezik. Sőt, még csak az sem biztos, hogy létezik egyáltalán olyan részhalmaz A-ban, amelynek D az f szerinti képe. Elképzelhető ugyanis, hogy D-ben van olyan elem, amely egyetlen A-beli elemhez sincs hozzárendelve. Természetesen most is igaz, hogy ha D az üreshalmaz, akkor f^{-1}(D) létezik, és szintén az üreshalmaz.