Az előző részben láttuk, hogy a számítógépek megjelenésével az Alice és Bob közötti titkos kommunikáció igénye a továbbiakban nem pusztán emberi nyelven írt bizalmas szövegek küldözgetésére korlátozódik. Ezért elkezdtük felépíteni az információátviteli rendszerek absztrakt modelljét annak érdekében, hogy megfelelően általánosan tudjuk tárgyalni ezt a kérdést a továbbiak során. Ennek első állomásaként eddig két összetevővel ismerkedtünk meg: az egyik volt az információforrás, a másik pedig a forráskódoló.

De vajon hogyan történik a digitális információ reprezentációja az informatikai rendszerekben? Mik azok a számrendszerek? Hogyan kell elképzelni a számítógépek memóriáját és mi van benne? Hogyan épül fel egy képet tartalmazó file és mit tartalmaz? Ebben a részben erről lesz szó…

Az előző részben megismert digitális információforrás felfogható egy olyan absztrakt objektumnak, amely egy véges (például N elemű) halmazból vett elemek sorozatát produkálja. Mivel az N elemű halmaz véges, ezért ennek elemeihez egyértelműen hozzárendelhetjük a 0, 1, …, N-1 egész számokat. Egy szöveges információforrás esetén ezek lehetnek a különböző karakterekhez rendelt egész számok például az ASCII kódtábla alapján, egy hangforrás vagy bármilyen más fizikai folyamat esetén pedig az őt leíró analóg jel digitalizált változatát alkotó számok (lásd az előző rész végét). Látható, hogy matematikai szempontból a közölt információ konkrét tartalmának nincs jelentősége. Ezért azt csupán egy egész számokból álló sorozatnak fogjuk tekinteni. Ráadásul másnak tekinteni nem is lenne értelme, mivel egy informatikai rendszer a vizsgálatunk tárgya, amely számokon kívül semmi mást nem tud értelmezni és feldolgozni.

Ez a számsorozat azután a forráskódoló bemenetére kerül. Ennek feladata ebből egy olyan bitsorozat (az adat) előállítása, amely már átküldhető a kommunikációs csatornán. A forráskódolás témakörének vizsgálata messzire vezetne, ezért itt ezt nem fogjuk részletezni. Azt azonban fontos tudnunk, hogy a számokat hogyan lehet leírni bitsorozatokkal, ezért először a különböző számrendszerekről ejtünk néhány szót.

Számrendszerek

A mindenkinek ismerős tízes (vagy más néven decimális) számrendszer kialakulásához mindenképpen szükség volt az úgynevezett helyiértékes írásmódra, amelyet először az ókori Mezopotámiában vezettek be. A történelmi áttekintés mellőzésével egy példán keresztül mutatjuk be ennek lényegét. Tegyük fel, hogy meg kell számlálnunk bizonyos dolgokat, és kavicsokkal szeretnénk jelölni a számlálás eredményét. Az egyik megoldás, hogy a számlálás során dobáljuk le a kavicsokat a homokba, így a végeredmény a homokban lévő kavicsok száma lesz. Ennek hátránya, hogy egyrészt sok tárgy megszámlálásához rengeteg kavicsra van szükségünk, másrészt pedig a végeredmény egy rakás kavics lesz, amivel nem vagyunk sokkal előrébb. Nem könnyű például megmondani két közel azonos méretű kavicshalomról, hogy melyik a több.

Egy ennél jóval hatékonyabb eljárás a következő. Rajzoljunk egymás mellé köröket a homokba, és határozzuk meg, hogy maximum hány kavicsot engedünk meg egy körön belül. Legyen ez például most 2. Ezután kezdjük el a jobb szélső körbe dobálni a kavicsokat. Ezt mindaddig folytathatjuk, amíg el nem értük a maximális 2 kavicsot a jobb szélső körben. Ekkor a következő kavicsot már az eggyel balra lévő körbe dobjuk, az első kört pedig kiürítjük.

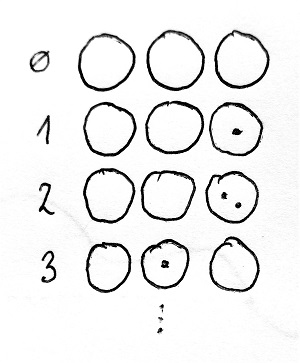
Ezután ismét dobálhatunk az első körbe. Amikor az újra megtelt, a következő kavicsot megint a második körbe dobjuk és ismét kiürítjük az első kört.

Ezt folytatva egy idő után elérkezünk egy olyan pontra, amikor megtelik az első és a második kör is. Ekkor a következő kavicsot már a harmadik körbe dobjuk, és kiürítjük mind az első, mind pedig a második kört.

És így tovább, ezt az eljárást a végtelenségig folytathatjuk. Vegyük észre, hogy így nagy számok esetén lényegesen kevesebb kavicsra van szükségünk ahhoz képest, mint amekkora mennyiséget jelölünk velük. A módszer hatékonysága abban rejlik, hogy a kavicsoknak különböző értékei vannak attól függően, hogy melyik körben helyezkednek el. Az első körben lévő kavicsoknak 1 az értéke, és minden további körben az értékük megháromszorozódik. A második körben egy kavics értéke már 3, a harmadik körben már 3²=9, a negyedik körben 3³=27 és így tovább, a k-adik körben 3^k-1 egy-egy kavics értéke. Az alábbi ábrán például a 2019 kavicsokkal történő reprezentációját láthatjuk, és ehhez mindössze 9 kavicsra van szükségünk. Az egyes körök alatt láthatjuk, hogy mekkora az értéke egy-egy kavicsnak az adott körben:

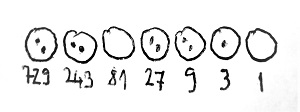
Gratulálhatunk magunknak, ugyanis lényegében feltaláltuk a helyiértékes számábrázolást. Konkrétan a fenti példában a 3-as számrendszert. A dolgot továbbfejleszthetjük azzal, ha különböző szimbólumokat találunk ki egy-egy kör lehetséges tartalmainak leírására. Jelen esetben 3 féle szimbólumra van szükségünk, mivel egy kör tartalma 3 féle lehet: üres, egy kavics, két kavics. Legyen ez a 3 féle szimbólum például rendre a 0, az 1 és a 2. Ekkor kavicsok helyett a 2019-es szám leírására használhatjuk például a 2202210 szimbólumsorozatot.

Ehhez hasonlóan leírhatjuk a számokat tetszőleges n-alapú számrendszerben, ha n>1. Egy n-alapú számrendszer semmiben sem különbözik a fenti kavicsos példától. Ekkor az egyes körökben elhelyezhető kavicsok maximális száma n-1 lesz, egy adott körben lévő kavicsok értéke pedig n megfelelő hatványa lesz a kör pozíciójának (amit helyiértéknek nevezünk) függvényében. A jobb szélső kör helyiértéke n⁰=1, míg a további körök helyiértékei rendre n¹, n², n³, és így tovább. Egy adott kör helyiértéke mindig a tőle jobbra lévő kör helyiértékének n-szerese.

A megszokott 10-es számrendszerben ezek a helyiértékek például: 10⁰ (azaz 1), 10¹ (azaz 10), 10² (azaz 100), stb. A maja, valamint a pre-kolumbiai és közép-amerikai civilizációk 20-as alapú számrendszereket használtak. Ennek eredete feltehetőleg összefügg az emberek kéz- és lábujjainak számával. A 60-as alapú rendszert a sumér és az azt követő mezopotámiai kultúrák használták. Ez a ma használt időmérő rendszerben is visszaköszön: egy órát 60 percre osztunk, illetve 1 percet 60 másodpercre. A 12-es számrendszer maradványai is fellelhetők például abban, hogy az év 12 hónapra oszlik. Csaknem minden nyelvben külön szó van a 12 dologból álló csoportra, például a magyar „tucat”, az angol „dozen”, a német „das Dutzend”, az olasz „dozzina”, az orosz „djuzsina” stb.

A 2-es (bináris) számrendszer

Most nézzük meg, hogy n=2 esetén (azaz 2-es számrendszerben) hogyan tudjuk leírni az előző példában szereplő 2019-es számot. A 2-es számrendszer helyiértékei rendre 2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=16, és így tovább. A helyiértékeket reprezentáló körök tartalma ebben az esetben 2 féle lehet: vagy nincs kavics az adott körben, vagy pedig van. Ezt a két esetet rendre a 0 és az 1 szimbólumokkal fogjuk jelölni a számábrázolásban. Ezután megkeressük azt a legnagyobb helyiértéket, amely még éppen nem nagyobb az ábrázolni kívánt számunknál, azaz 2019-nél. Ez a 2¹⁰=1024 lesz, így az ennek megfelelő körbe annyi kavicsot helyezünk, amennyinek az összértéke még éppen nem haladja meg a 2019-et. Ez jelen esetben a maximális 1 darab kavics lesz, így leírjuk az ennek megfelelő 1 szimbólumot, és az elhelyezett kavics értékét (1024) levonjuk a 2019-ből, eredményül 995-öt kaptunk. Ezután ezzel az 995-tel megyünk tovább az eggyel alacsonyabb helyiértékre, ez a 2⁹=512 lesz. Ebbe a körbe megint annyi kavicsot helyezünk, hogy ezek összértéke ne legyen nagyobb 995-nél. Ez megint a maximális 1 darab kavics lesz, tehát leírjuk az ennek megfelelő 1 szimbólumot is, és az elhelyezett kavics értékét (512) levonjuk az 995-ből. Így a számunk ábrázolása eddig az 11 szimbólumsorozat, a maradék pedig 483. Ezt az eljárást folytatjuk egészen a legalacsonyabb helyiértékig. Végeredményül az 11111100011 szimbólumsorozatot kapjuk, amely tehát a 2019-es szám 2-es számrendszerbeli ábrázolása:

A most bemutatott 2-es (vagy más néven bináris) számrendszer rendkívül fontos az informatikai rendszerek szempontjából. A 0 és 1 szimbólumokat ugyanis könnyű elektronikus eszközökkel kezelni. Például folyik-e áram egy vezetékben vagy nem? Van-e töltés egy kondenzátorban vagy nincs? Van-e lyuk égetve egy DVD lemezre vagy nincs? Egy bináris szám számjegyeit bit-eknek nevezzük, amely kifejezés az angol „binary digit” (azaz bináris számjegy) rövidített változata. Megfelelő áramkörökkel bináris számokon műveleteket tudunk végezni az őket reprezentáló fizikai jelek manipulálása által, méghozzá veszettül gyorsan. Például 64-bites egész számok szorzásának időtartama egy mai átlagos processzor esetén a néhány nanoszekundumos nagyságrendbe esik. Ez egyetlen másodperc alatt nagyságrendileg 1 milliárd szorzás elvégzését jelenti. A bináris számok szorzása, összeadása, és egyéb műveletek végzése helyiértékenként történik nagyon hasonlóan ahhoz, mint ahogyan az írásban számolást tanultuk általános iskolában, 10-es számrendszerben. Az alábbi ábrán például ugyanazon két szám írásbeli összeadásának folyamata látható bináris és 10-es számrendszerben:

\begin{array}{rr}{\begin{array}{rr} & \ 11010 \\ + & \ 10011 \\ \hline \ & 101101 \end{array}} & {\begin{array}{rr} & \ 26 \\ + & \ 19 \\ \hline \ & 45 \end{array}}\end{array}

A 16-os (hexadecimális) számrendszer

Annak érdekében, hogy ne kelljen állandóan olyan sok bináris számjegyet leírnunk, bevezethetünk egy praktikus rövidítést. Ha a biteket képzeletben 4-esével csoportosítjuk, és ezeket a csoportokat egy-egy szimbólummal helyettesítjük, akkor egy sokkal rövidebb írásmódot kapunk. Ez az ábrázolás épp a 16-os (vagy más néven hexadecimális) számrendszernek felel meg, mivel 4 bináris helyiértéken épp 16 féle bitsorozat írható le. Méghozzá pontosan azok, amelyek megfelelnének a 0, 1, 2, …, 15 darab kavics elhelyezésének az adott csoportnak megfelelő 16-os számrendszerbeli helyiértéken.

A hexadecimális számjegyek jelöléséhez 16 különböző szimbólumra van szükségünk. Ezért a szokásos 0, 1, 2, …, 9 szimbólumok mellé be kell vezetnünk 6 darab további szimbólumot is: A, B, C, D, E és F (vagy ezek kisbetűs változatai), amelyek rendre a 10, 11, 12, 13, 14 és 15 kavics elhelyezését jelentik. Amikor egy hexadecimális számot leírunk, akkor általában a számjegyek felsorolása elé a „0x” prefixumot szoktuk írni a 16-os számrendszer jelölésére. Az alábbi ábrán a 2019-es szám bináris leírásának hexadecimális rövidítése látható:

\underbrace{0111}_{\text{7}}\underbrace{1110}_{\text{E}}\underbrace{0011}_{\text{3}}=\text{0x7E3}

Ehhez hasonlóan az előző részben ismertetett ASCII kódtábla szerint kódolt Bob üzenet 24 bites kódját a 0x42, 0x6F, 0x62 hexadecimális számsorozattal is leírhatjuk. Ne feledjük azonban, hogy ez csupán a bitsorozatok leírásának egy rövidítése. A digitális áramkörök ettől függetlenül természetesen továbbra is 2-es számrendszerben számolnak. Most vizsgáljuk meg, hogyan mi van egy informatikai eszköz memóriájában vagy például egy bináris adatokat tartalmazó file-ban.

A memória felépítése

Egy informatikai rendszerben futó folyamat bemenő adatai, valamint a folyamat által végrehajtandó program utasításai a futás megkezdése előtt egy memóriának nevezett tárolóba kerülnek. Erre azért van szükség, mert a memóriát sokkal gyorsabban lehet írni és olvasni, mint a hosszútávú tárolásra szolgáló úgynevezett háttértárat (ami a legtöbbször a merevlemez). A folyamat a memóriát használja munkaterületként. Innen olvassa a végrehajtandó utasításokat és a bemenetet, itt tárolja a részeredményeket, valamint a kimenet is itt fog megjelenni, amelyet aztán vissza lehet írni a háttértárra, ha a hosszabb távú tárolás szükséges.

A tárolás/adattovábbítás szempontjából a byte (azaz bitek 8-as csoportja) tekinthető atomi egységnek vagy legalsóbb szintnek. A memória ennek megfelelően kis rekeszekből áll, amelyek mindegyike egy-egy byte-ot tárol. A rekeszek 0-tól kezdődően sorszámozva vannak, egy ilyen sorszámot az adott rekesz memóriacímének nevezünk. A folyamat ezekkel a címekkel hivatkozik a memóriában lévő rekeszekre, amikor írni vagy olvasni akarja őket. Ez a memóriamodell látható az alábbi ábrán:

\begin{array}{c}{\begin{array}{cc}\text{c\'\i m} & \text{adat}\end{array}}\\{\begin{array}{|c|c|} \hline 0. & \text{0x13} \\ \hline 1. & \text{0xF1} \\ \hline 2. & \text{0x2A} \\ \hline 3. & \text{0x58} \\ \hline \end{array}}\\\vdots\end{array}

Egy informatikai rendszerben azonban egynél több folyamat is futhat párhuzamosan. Ezek mindegyike ugyanazt a fizikai memóriát használja munkaterületként, ezért biztosítani kell, hogy mindegyik folyamat csak a saját adataihoz férjen hozzá. Nem lenne jó például, ha az egyik folyamat valamely részeredményét egy párhuzamosan futó másik folyamat véletlenül felülírhatná. Ennek biztosítása az operációs rendszer feladata, amely úgy mutatja a memóriát az egyes folyamatok számára, mintha mindegyik kizárólagosan rendelkezne a teljes címtartománnyal. Ezt a mechanizmust virtuális memóriakezelésnek nevezzük. A folyamatok tehát virtuális címeket használnak az adataik eléréséhez, és az operációs rendszer képezi le ezeket a valódi, fizikai címekre. Erről bővebben itt lehet olvasni. Számunkra azonban most csak annyi a fontos, hogy egy adott folyamat szempontjából a memória a fenti képen látható módon néz ki.

Hasonló mondható el a háttértáron lévő file-ok tartalmáról is, valamint a hálózati kommunikáció során továbbított adatok is lényegében tekinthetők byte-ok sorozatának. A továbbiakban tehát általánosságban byte-sorozatokról lesz szó, függetlenül attól, hogy ezek a memóriában vagy egy file-ban lévő, netán valamilyen kommunikációs csatornán továbbított adatokból származnak.

Előjel nélküli egészek

Az, hogy egy byte-sorozatban az egyes byte-ok mit jelentenek, az adott alkalmazástól függ, vagy valamilyen szabványban van leírva. Ennek a résznek a végén mutatunk erre egy példát, amikoris megvizsgáljuk egy képet leíró file szerkezetét. Az azonban általánosságban elmondható, hogy van néhány alap adattípus, ami a legtöbb alkalmazásban előfordul.

A legegyszerűbb példa az úgynevezett előjel nélküli egész számok (unsigned integer) ábrázolása. Ez tipikusan 1, 2, 4 vagy 8 byte-on (azaz rendre 8, 16, 32 vagy 64 biten) szokott történni attól függően, hogy milyen értéktartományra van szükségünk, és mennyi memóriát szánunk egy-egy érték tárolására. Ezek azonban csak a „beépített” típusok. Ha ennél nagyobb számokkal akarunk dolgozni, annak természetesen nincs elvi akadálya. Viszont ekkor ezek aritmetikáját (az egyes műveletek végrehajtásának módját) magunknak kell leprogramozni. A legtöbb alkalmazáshoz azonban a 64 bit (azaz 8 byte) bőven elegendő, hiszen ennyi helyiértékkel 2⁶⁴=18446744073709551616 különböző egész számot tudunk leírni. Az előjel nélküli egész számokat leíró byte-ok sorrendje általában kétféle szokott lenni. Little endiannak nevezzük azt a sorrendet, amikor a kisebb helyiértékű byte-ok vannak elöl, és ezt követik az egyre nagyobb helyiértékűek. Az ezzel ellentétes sorrendet big endiannak nevezzük.

Tekintsük például a 18365-ös számot, és nézzük meg, hogy ez 32-bites little endian byte-sorrendű előjel nélküli egészként ábrázolva hogyan nézne ki egy byte-sorozatban. A 18365-ös szám bináris alakja 32 biten 00000000000000000100011110111101. Ezt byte-okra osztjuk és felsoroljuk ezeket a byte-okat a legkisebb helyiértéktől kezdve. Ekkor a következő byte-sorozatot kapjuk: 0xBD, 0x47, 0x00, 0x00. Ugyanezt a számot 64 biten ábrázolva további 4 darab 0x00 byte is szerepelne a fenti 4 byte után. Az alábbi ábrán a 18365-ös számot leíró byte-ok láthatók 32-bites little endian ábrázolásban az n-edik memóriacímtől kezdve:

\begin{array}{c}\vdots\\{\begin{array}{|c|c|} \hline (n+0). & \text{0xBD} \\ \hline (n+1). & \text{0x47} \\ \hline (n+2). & \text{0x00} \\ \hline (n+3). & \text{0x00} \\ \hline \end{array}}\\\vdots\end{array}

Ugyanez a szám 32-bites big endian ábrázolásban:

\begin{array}{c}\vdots\\{\begin{array}{|c|c|} \hline (n+0). & \text{0x00} \\ \hline (n+1). & \text{0x00} \\ \hline (n+2). & \text{0x47} \\ \hline (n+3). & \text{0xBD} \\ \hline \end{array}}\\\vdots\end{array}

Úgy tűnik, nincs jelentős előnye egyik ábrázolási módnak sem a másikkal szemben, és használatuk az adott számítógép-architektúrától függ. A legtöbb szabvány mindenesetre a little endian módot írja elő. Ennek oka talán abban keresendő, hogy az ezt használó Intel x86/x64 processzor-architektúra a legelterjedtebb.

Előjeles egészek

Természetesen előjeles egész számokat (signed integer) is tárolhatunk. Itt is választhatunk a 8, 16, 32 vagy 64 bites ábrázolásmódok közül. Az ilyen számok ábrázolása a következőképpen történik: amennyiben az ábrázolni kívánt szám pozitív, azt ugyanúgy ábrázoljuk, mint az előjel nélküli esetben. Ha viszont a szám negatív, akkor leírjuk őt binárisan úgy, mintha pozitív lenne, majd minden így kapott bitet az ellentettjére cserélünk (ahol 0 volt, oda 1 kerül, és viszont, ezt invertálásnak nevezzük), végül az eredményhez hozzáadunk 1-et. Az így kapott bitsorozatot tároljuk le ugyanúgy byte-onként, mint az előjel nélküli esetben.

Tekintsük például a -18365-ös számot, vagyis az előző példa negatív változatát. Ennek pozitív változata 32 biten ábrázolva a 00000000000000000100011110111101 bitsorozat. Ezt a bitsorozatot invertáljuk, és adjunk az eredményhez 1-et. A kapott bitsorozat: 11111111111111111011100001000011. Ezt little endian sorrendben letárolva a kapott byte-ok: 0x43, 0xB8, 0xFF, 0xFF. Ugyanezt a számot 64 biten ábrázolva további 4 darab 0xFF byte is szerepelne a fenti 4 byte után. Az alábbi ábrán a -18365-ös számot leíró byte-ok láthatók 32-bites little endian ábrázolásban az n-edik memóriacímtől kezdve:

\begin{array}{c}\vdots\\{\begin{array}{|c|c|} \hline (n+0). & \text{0x43} \\ \hline (n+1). & \text{0xB8} \\ \hline (n+2). & \text{0xFF} \\ \hline (n+3). & \text{0xFF} \\ \hline \end{array}}\\\vdots\end{array}

Ugyanez a szám 32-bites big endian ábrázolásban:

\begin{array}{c}\vdots\\{\begin{array}{|c|c|} \hline (n+0). & \text{0xFF} \\ \hline (n+1). & \text{0xFF} \\ \hline (n+2). & \text{0xB8} \\ \hline (n+3). & \text{0x43} \\ \hline \end{array}}\\\vdots\end{array}

Ezt kettes komplemens számábrázolásnak nevezzük. Ilyenkor tehát a legnagyobb helyiértékű bitet előjelként használjuk: ha ez a bit 0, akkor az ábrázolt számot pozitívnak, ha pedig 1, akkor negatívnak értelmezzük. Az invertálásnak és az eredmény 1-gyel való megnövelésének praktikussági okai vannak. Egyrészt, ha egy számnak képezzük a kettes komplemensét, majd az eredménynek ismét képezzük a kettes komplemensét, akkor az eredeti számot kapjuk vissza (épp úgy, mintha kétszer vennénk egy szám ellentettjét). Ezen kívül a digitális összeadó áramköröket kivonásra is használhatjuk változtatás nélkül. Ha ugyanis egy bináris számhoz hozzáadjuk egy másik szám kettes komplemensét, akkor épp olyan eredményt kapunk, mintha kivonást végeztünk volna. Ráadásul, ha egy kisebb számból vonunk ki egy nagyobbat ilyen módon, akkor épp az így keletkező negatív eredményt kapjuk szintén kettes komplemens ábrázolásban. Ezek általános bizonyításától most eltekintünk, de érdemes kipróbálni papíron, hogy tényleg működik.

Itt csak megemlítjük, hogy természetesen nem csak egész, hanem tört számokat is tudunk ábrázolni (és rajtuk műveleteket végezni) a számot leíró bitek megfelelő értelmezésével. Ennek leggyakoribb formája az úgynevezett lebegőpontos számábrázolás. Ennek nagyjából az a lényege, hogy a számot leíró bitek egyik csoportja a „hasznos” számjegyeket írja le, a bitek egy másik csoportja pedig azt, hogy ebben a számjegysorozatban hol helyezkedik el a tizedesvessző. Ennek részleteire azonban itt nem térünk ki.

Egy kép bináris leírása

Most egy példán keresztül bemutatjuk, hogyan kell a fentieket elképzelni a gyakorlatban. Az előző részben megpróbáltunk megnyitni egy MP3 file-t a jól ismert Notepad alkalmazással, és azt tapasztaltuk, hogy egy látszólag értelmetlen adathalmaz van benne. Most egy hasonló példát fogunk megnézni, azonban vizsgálatunk tárgya az egyszerűség kedvéért MP3 helyett egy BMP típusú kép lesz.

Ehhez elkészítettem egy tesztképet. Ez mindössze 2×2 képpontból áll, és innen lehet letölteni (jobb klikk, mentés másként). Ha a letöltött képet megnyitjuk a Paint nevű egyszerű képszerkesztőben, és kellőképpen ránagyítunk a képre, akkor láthatjuk, hogy a bal-felső és a jobb-alsó képpont fekete, míg a bal-alsó és a jobb-felső képpont fehér színű. Az alábbi ábrán ez látható kinagyítva:

Most a fehér képpontokat szürkékre fogjuk cserélni, ám ezt nem a képszerkesztővel, hanem a file-ban szereplő megfelelő byte-ok átírásával fogjuk megtenni. A képszerkesztőt tehát egy időre bezárhatjuk. Ha megnyitnánk a képfile-t Notepad-ban, az MP3-hoz hasonlóan megint egy látszólag értelmetlen ASCII karaktersorozatot látnánk. Ehelyett nyissuk meg a file-t egy olyan programmal, amely a file-ban lévő byte-okat jeleníti meg hexadecimális alakban. Sokféle ilyen szerkesztőt találhatunk a neten, ilyen például a HxD – Hexeditor nevű program. Ezzel láthatóvá válik az a file-ban lévő 70 darab byte, amely ezt az egyszerű 2×2 pixeles képet leírja. A byte-ok az alábbi ábrán látható sorrendben sorfolytonosan követik egymást (balról jobbra olvasva):

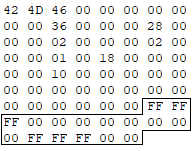
Azt, hogy ebből a 70 byte-ból melyik mit jelent, a BMP szabvány írja le. A részletekbe most nem megyünk bele, a számunkra ebből most annyi fontos, hogy a file alapvetően 2 részből áll. Az első rész az úgynevezett fejléc, amely információkat tartalmaz a képpel kapcsolatban, míg a második rész tartalmazza a konkrét képpont adatokat. Ez utóbbi a fenti ábrán a feketével bekeretezett rész.

Egy BMP file fejléce minden esetben a B és M karakterek ASCII-kódjával, azaz a 0x42 és 0x4D értékű byte-okkal kezdődik (ez az ábrán is látszik). Ez egy előzetes ellenőrzést tesz lehetővé az alkalmazás számára, hogy valóban egy BMP formátumú képpel van-e dolga. A fejléc továbbá – többek között – tartalmazza, hogy hány képpont a kép szélessége és magassága, hogy milyen módon van leírva egy-egy képpont színe a képpont adatoknál, illetve hogy hanyadik byte-tól kezdődnek konkrétan ezek a képpont adatok. Ez utóbbi információt a fejlécben a 10. sorszámú pozíciótól (a számozás 0-tól indul) kezdődő 4 byte tartalmazza (0x36, 0x00, 0x00, 0x00). Ezeket a szabvány szerint 32-bites little endian byte-sorrendű előjel nélküli egészként kell értelmezni. Ennek értéke tehát 54. Valóban, a feketével bekeretezett pixel adatok kezdete épp az 54. sorszámú byte. A fejléc tartalmát a továbbiakban nem részletezzük, ehelyett ugorjunk a bekeretezett részhez, azaz a képpont adatokhoz.

Az egyes képpontok ebben a BMP file-ban 3-3 byte-tal vannak leírva, amelyek rendre az adott képpont színének kék, zöld és vörös színösszetevőit adják meg. A színösszetevők intenzitását a megfelelő byte értéke határozza meg: a 0x00 érték az adott színösszetevő teljes hiányát, míg a 0xFF érték a maximális intenzitását jelenti. Ezeket RGB-színkódoknak nevezik, utalva a „red”, „green” és „blue” szavak kezdőbetűire.

A kép soronként lentről felfelé tárolódik, vagyis a képpont adatok a legalsó sorral kezdődnek. Az első 3 byte (0xFF, 0xFF, 0xFF) tárolja tehát a bal alsó pixel RGB-színkódját, amely a fehér színnek felel meg. Ha megnézzük a képet, a bal alsó pixel valóban fehér. A következő 3 byte (0x00, 0x00, 0x00) a következő, azaz a jobb alsó pixel színét tárolja, amely valóban a fekete. Ezzel vége az alsó sornak, azonban van itt még 2 darab 0x00 értékű byte, a szabvány szerint ugyanis minden sort szükség szerint 0 bitekkel kell feltölteni oly módon, hogy az egyes sorokhoz 4-gyel osztható számú byte tartozzék. Ez programozástechnikailag megkönnyíti az ilyen file-ok kezelését, ennek részleteire most nem térünk ki.

A következő 3 byte (0x00, 0x00, 0x00) már a következő sor első pixelét, azaz a bal felső fekete pixelt tárolja. Ezután pedig az utolsó, jobb felső fehér pixel RGB-kódja következik (0xFF, 0xFF, 0xFF). Végül ismét 2 darab 0x00 értékű kitöltő byte következik az előző sorhoz hasonlóan. Ezzel vége a pixel adatoknak, és egyben a BMP file-nak is.

Most módosítani fogjuk a bal alsó és a jobb felső pixel színét leíró byte-okat. Azt szeretnénk, hogy ezek szürkék legyenek. A szürke színben a fehérhez hasonlóan mindhárom színösszetevő szerepel, csak éppen nem a maximális (0xFF) intenzitással. Egy közepes intenzitású szürke színt kapunk, ha például mindhárom összetevőt 0x80-ra állítjuk. Az alábbi ábra mutatja a módosított byte-okat feketével bekeretezve:

Miután elmentettük a file-t, bezárhatjuk a Hexeditor-t. Ha ezek után Paint-ben megnyitjuk a módosított file-unkat és kellőképpen ránagyítunk a képre, akkor láthatjuk, hogy a bal-alsó és a jobb-felső képpont színe a várakozásoknak megfelelően fehérről szürkére módosult. Az alábbi ábrán ez látható kinagyítva:

Láthatjuk tehát, hogy egy kép egy informatikai eszköz memóriájában vagy egy file-ban semmi más, mint egy bináris számsorozat. A képszerkesztő szoftverek abban segítenek nekünk, hogy értelmezik ezt a számsorozatot, vizuálisan megjelenítik a számunkra az általuk kódolt képet, és lehetővé teszik, hogy szintén vizuális eszközökkel ezen a képen módosítsunk. Egy Adobe Photoshop persze nagyon bonyolult képfeldolgozó algoritmusokat is megvalósít, de valójában a legalacsonyabb szinten nem történik más, mint bináris adatok manipulálása. Pontosan úgy, ahogy mi most azt manuálisan megtettük, képszerkesztő program nélkül.

Ebben a fejezetben tehát megismerkedtünk a számrendszerek fogalmával, és képet kaptunk arról, hogy az informatikai eszközök milyen módokon tárolják a különböző számokat. Ennek gyakorlati bemutatására megnéztük, hogy egy egyszerű BMP formátumú képet leíró file milyen byte-okat tartalmaz, illetve, hogy melyik byte-nak mi a jelentése a BMP szabvány szerint. Meg is változtattuk néhány képpont színét pusztán néhány byte átírásával. E rövid kitérő után a következő részben az információátviteli rendszerek absztrakt modelljét építjük tovább, és ennek keretében megismerkedünk magával az átviteli csatornával, továbbá a vele kapcsolatban felmerülő problémákkal.

A következő részt itt találod…