Az előző részben Alice és Bob történetén keresztül bemutattuk, hogy milyen problémákkal kell szembesülnie azoknak, akik bizalmas információkat szeretnének közölni egymással egy nembiztonságos csatornán keresztül. Egy rövid áttekintés keretében bemutattunk néhány történelmi példát rejtjelezési eljárásokra és megismerkedtünk a kriptográfia alapfogalmaival.

A rejtjelezés a 20. század második felére egy modern informatikai tudományággá nőtte ki magát. Ez biztosítja az Internet és a számítógéphálózatok biztonságos működését. Mivel az Alice és Bob közötti kommunikáció napjainkban nem pusztán írott szövegekre korlátozódik, ezért most egy kis kitérő keretében megismerkedünk az információelmélet néhány alapfogalmával. Mi a különbség az információ és az adat között? Mit jelent az információs entrópia és a forráskódolás? Mi határozza meg, hogy egy adat milyen mértékben tömöríthető? Mit nevezünk analóg és digitális információnak? Ebben a részben erről lesz szó…

A kriptográfia tudományának elsődleges célja tehát az információ elrejtése a kíváncsiskodó szemek elől. Ami az ellenoldalt illeti (például Eve), az ő céljuk az elrejtett titkok felfedése. Ehhez természetesen ők is tudományos módszereket használnak. Ezt a tudományágat – amely tehát a titkok felfedésével foglalkozik – kriptoanalízisnek nevezzük. A kriptográfia és a kriptoanalízis örökös háborút vív egymással. Ám ezt nem két szembenálló fél háborújaként kell elképzelni, hiszen aki az egyikkel foglalkozik, nyilván foglalkoznia kell a másikkal is. Ismernie kell ugyanis az ellenfél eszköztárát a hatékony védelem (vagy épp támadás) kidolgozásához. Ahogy az ebből a cikksorozatból ki fog derülni, ebben a háborúban jelenleg a kriptográfia áll nyerésre. Ám ez nem jelenti azt, hogy mindig ez lesz a helyzet.

Információ és adat

A 20. század második felére a számítógépek megjelenésével az információ fogalmának jelentése már nem csak az emberi nyelven íródott szövegekre korlátozódott, hanem egy ennél absztraktabb jelentést kapott. Az információ latin eredetű szó, amely értesülést, hírt, tájékoztatást jelent. Különböző tudományágak különböző módon definiálják, ám általánosságban elmondható, hogy információnak olyan valamit tekintünk, amely számunkra ismerethiányt, bizonytalanságot csökkent. Az informatikai definíció alapján az információmennyiség mértékegysége a bit: ha egy eldöntendő kérdésre egyforma valószínűséggel várható „igen” vagy „nem” válasz, akkor egy ilyen kérdésre adott konkrét válasz pontosan 1 bit információt hordoz.

Gondoljunk például a jól ismert barkochba nevű játékra. A játékosoknak eldöntendő kérdésekre adott válaszok alapján kell rájönniük a gondolt szóra. Tegyük fel, hogy az összes lehetséges szavak száma véges, és valaki egy olyan eldöntendő kérdést tesz fel, amelyre adott „igen” vagy „nem” válasz a lehetőségek felét kizárja. Ekkor egy ilyen válasz 1 bit információt hordoz a játékosok számára.

Ha például 65536 féle lehetséges szó közül gondolt valaki egyre, akkor ezt mindössze 16 jól megfogalmazott eldöntendő kérdésből ki lehet találni. Itt a „jól megfogalmazás” azt jelenti, hogy minden kérdés épp a felére csökkenti a szóba jöhető megfejtések számát. Vagyis 16 bit az az információmennyiség, amelynek megismerése szükséges ahhoz, hogy megtudjuk, mire gondolt valaki egy 65536 elemű halmazból, hiszen 2¹⁶=65536. Amennyiben a játékosok nem elég ügyesen kérdeznek, akkor ennél több kérdésre is szükség lehet. Ilyenkor ugyanis egy-egy válasz 1 bitnél kevesebb információt hordoz. Tegyük fel például, hogy egy korábbi kérdésre adott válaszból már tudjuk, hogy a gondolt dolog élőlény. Ebben az esetben nem érdemes megkérdezni, hogy műanyagból van-e, mivel az erre adott „nem” válasz nem hordoz semmilyen új információt, ugyanis a lehetséges megfejtések közül nem zár ki további elemeket.

Sokan összekeverik az információ és az adat fogalmát. Ennek fő oka talán az, hogy e két fogalom szorosan összefügg egymással, ráadásul mindkettő mértékegysége a bit. Az adatoknak önmagukban nincs jelentésük. Például az az adat, hogy 30, önmagában nem jelent semmit. Az adatok azáltal nyernek értelmet, és válnak információvá, hogy valamilyen értelmezést társítunk hozzájuk. Egy adathalmaz értelmezése mindig valamilyen közös egyezmény alapján történik, ezeket az informatikában például különböző szabványok írják le. Egy-egy ilyen egyezmény lényegében azt definiálja, hogy egy véges szimbólumkészlet segítségével hogyan tudjuk leírni az információt oly módon, hogy az kinyerhető legyen ebből a leírásból bárki számára, aki szintén ismeri az adott egyezményt.

Erre a legősibb példa az írott nyelv. Itt az információ az a gondolat, tudás vagy ismeretanyag, amelyet a küldő fél a fogadó féllel (vagy felekkel) közölni szeretne. Tegyük fel, hogy ennek leírására a küldő az ábécé betűit, a számokat és a szokásos írásjeleket szeretné használni, mint véges szimbólumkészletet. A közös egyezmény ebben a példában a nyelvtani szabályoknak az összessége. Ezek definiálják, hogy a szimbólumokat hogyan kell egymás után papírra vetni ahhoz, hogy a fogadó fél fejében ugyanaz a gondolat, tudás vagy ismeretanyag legyen, miután elolvasta és ugyanazon nyelvtani szabályok szerint értelmezte a papíron lévő szimbólumsorozatot. Ha belegondolunk, ez az egyik legfontosabb fejlődési lépcsőfok az emberi faj történetében. Ez tette lehetővé az információ áramlását téren és időn át.

Bináris kódolás

Az informatikai eszközök az információ leírására technikai okok miatt egy, a fentinél sokkal szerényebb szimbólumkészletet kénytelenek használni. Ez a szimbólumkészlet mindössze 2 elemű. E szimbólumok fizikai megjelenési formái a legkülönfélébbek lehetnek a használt médiumtól függően: alacsony vagy magas feszültségérték egy vezetéken, lyuk vagy lyuk hiánya egy DVD-n vagy lyukkártyán, egy rádióhullám vagy fénysugár valamilyen fizikai jellemzőjének alacsony vagy magas értéke, stb. Ezeket összefoglaló néven bináris jeleknek vagy bináris szimbólumoknak nevezzük, utalva arra, hogy mindössze 2 féle van belőlük. A bináris szimbólumok konkrét fizikai megjelenési formáival főként a híradástechnika tudománya foglalkozik. Ebben a cikksorozatban ettől elvonatkoztatunk, és egyszerűen a 0 vagy 1, illetve az igaz vagy hamis szimbólumokkal fogunk rájuk hivatkozni.

Az informatikában az információ leírása (tehát az adat) nem más, mint bináris szimbólumok egymás után írt sorozata. Hasonlóan az írott nyelvhez, ahol viszont betűket használunk szimbólumként. Egy ilyen sorozat által reprezentált adat mennyiségén a sorozat hosszát értjük, melynek mértékegysége – az információ mértékegységéhez hasonlóan – szintén a bit. Például a 010000100110111101100010 sorozat egy 24 bites adatot reprezentál. Látható, hogy az adatmennyiség mérése egy viszonylag egyszerű dolog. De vajon mi az az információ, amit ez a 24 bites adat leír, és ennek az információnak mi a mennyisége?

Az első kérdésre a válasz attól függ, hogy mi az a közös egyezmény (szabvány) amely alapján a küldő fél a „fejében” lévő információt épp ezzel a 24 bittel írta le. A fogadó félnek ez alapján kell értelmeznie ezt a sorozatot annak érdekében, hogy ő is ugyanazon információ birtokába kerüljön. Ez jelen példában egy, az Egyesült Államokban az 1960-as években kidolgozott és szabványosított kódrendszer alapján történt. Ennek a szabványnak a neve American Standard Code for Information Interchange (ASCII).

Az ASCII kódrendszer alkalmazásának célja eredetileg a távgépírókon és távnyomtatókon való felhasználás volt. A szöveget egy villamos írógéphez hasonló eszközbe gépelték, amely az ASCII kódtábla alapján bináris szimbólumsorozattá alakította az üzenetet. Ezt elektromos jelek formájában továbbította a telefonvonalon keresztül a fogadó állomásnak, amely általában egy nyomtató volt. A fogadó állomás szintén az ASCII kódtábla alapján a papírra nyomtatta a bináris szimbólumsorozat által leírt betűket és egyéb karaktereket.

Lényeges, hogy a karakterek bináris sorozatokká való leképezése egységesen történjen. Ha például a 65-ös ASCII kódot elküldik, akkor a fogadó eszköznek ezt minden esetben A karakternek kell értelmeznie. Máskülönben lehetetlenné válna szövegek tárolása, kinyomtatása vagy átvitele egy másik gépre. Az ASCII kódtábla 128 különböző karaktert a 0-127 közötti előjel nélküli egész számokra képezi le. Ezek közül a 32-127 közötti rész tartalmazza a látható karaktereket, tehát a kis- és nagybetűket valamint különböző írásjeleket és a számokat. A 0-31 közötti rész különböző nem látható vezérlőkaraktert tartalmaz (pl. soremelés, törlés, adatátvitel végének jelzése, stb.) Az alábbi ábrán az ASCII kódtábla látható karaktereket tartalmazó része látható:

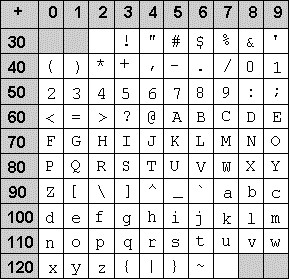
Az A karakter ASCII-kódja például a 65. Ez kettes számrendszerben felírva épp a 01000001 bináris sorozatnak felel meg (a számrendszerekről bővebben a következő részben lesz szó). Az ASCII kódtábla alapján az eredeti 010000100110111101100010 sorozat tehát úgy értelmezendő, hogy azt 8 bites csoportokra osztjuk (ezeket byte-oknak nevezik), és mindegyik ilyen csoportra megkeressük a neki megfelelő karaktert a kódtáblában. Ezek alapján a kódolt szöveg a Bob volt, mivel a 01000010 byte a 66-os, a 01101111 byte a 111-es, végül a 01100010 byte a 98-as ASCII kódnak felel meg.

Az eredeti ASCII kódtábla nem használta ki mind a 8 bitet, így ezzel mindössze 128 féle karaktert lehet kódolni. Később a 8. bit kihasználásával ezt kibővítették újabb 128 karakterrel, amelybe bekerültek a leggyakoribb nyugat-európai nyelvek ékezetes betűi és további speciális karakterek. Ennek neve ISO 8859-1, vagy más néven Latin-1 kódolás. Ám ez még mindig nem tartalmazza például a magyar ő és ű karaktereket. Napjainkban a még újabb Unicode szabvány használata a legelterjedtebb, amely 8 helyett 16 bitet használ a karakterek kódolására. Ez 65536 különböző szimbólum kódolását teszi lehetővé, és ezáltal egy egységes kódtáblába foglalja a világ különböző nyelveinek legtöbb szimbólumát.

De mi történik akkor, ha a fogadó fél nem ugyanolyan szabvány alapján értelmez egy bináris adatot, mint ami alapján azt a küldő kódolta? Próbáljunk megnyitni egy MP3 file-t egy egyszerű szövegszerkesztővel, például Notepad-dal. Az MP3 file-ban lévő bináris adatot a Notepad egyszerű ASCII kódolású szövegként próbálja meg értelmezni és megjeleníteni. Ez a következő ábrán látható „szöveget” eredményezi:

Ez nyilvánvalóan egy értelmetlen zagyvaság. Azonban ez nem jelenti azt, hogy az MP3 file-ban lévő binárisan kódolt adatnak ne lenne információtartalma. Mindössze arról van szó, hogy az információ itt nem egy szöveg, hanem egy, az MP3 szabvány alapján tömörített hang. Következésképp az értelmezéséhez nem az ASCII, hanem az MP3 szabványt kell követni. Amennyiben a Notepad helyett egy olyan szoftvert – például egy médialejátszót – használunk, amely ismeri az MP3 szabványt, akkor ugyanennek a bitsorozatnak az „információtartalma” egy, a számítógéphez kötött megfelelő hangrendszeren felcsendülő techno zene formájában fog materializálódni.

Az információ mennyiségének mérése

Azt a kérdést tehát megválaszoltuk, hogy milyen információt kódol a példaként felhozott 24 bites 010000100110111101100010 adat. Az ASCII kódtábla értelmezése szerint a Bob szöveget. A második kérdésünk viszont az volt, hogy mennyi ennek az információnak a mennyisége (amelynek a mértékegysége ugye szintén bit)? Ez már egy sokkal nehezebben megfogható dolog, ugyanis az információ mennyisége nem feltétlenül azonos az őt leíró adat mennyiségével. Például ha ugyanezt a szöveget a 16 bites karaktereket használó Unicode szabvány szerint kódoltuk volna, akkor 24 helyett 48 bitre lett volna szükségünk, mégis ugyanazt az információt tartalmazná ez a hosszabb bitsorozat. Következésképp a mennyiségének is ugyanannyinak kéne lennie.

Az információmennyiség méréséhez – fura módon – el kell vonatkoztatnunk a konkrét szimbólumsorozat által reprezentált tartalomtól. Ehelyett egy, az adott információforrásra jellemző mennyiséget kell meghatároznunk. Az információforrás absztrakt modellje egy olyan objektum, amely egy véges szimbólumkészlet – a forrásábécé – elemeit bocsájtja ki magából szép sorban. Az információforrás jellege meghatározza, hogy a forrásábécé egy-egy eleme milyen kontextusokban milyen valószínűségekkel fordul elő a forrásból érkező sorozatokban. Minél egyenletesebb az egyes szimbólumok eloszlása, annál bizonytalanabb, hogy milyen konkrét sorozat fog érkezni a forrásból.

Az előző részben már említett Claude Shannon amerikai matematikus és híradástechnikai szakember ennek a bizonytalanságnak a mérésére vezette be az 1940-es évek végén az információs entrópia fogalmát. Ennek tanulmányozása az információelmélet egyik alapja, és ennek a segítségével válik mérhetővé a forrásból érkező információ mennyisége. Az entrópia érdekessége abban áll, hogy független a konkrét tartalomtól. Ehelyett az egy, az adott információforrásra jellemző statisztikai mennyiség. Minél nagyobb a forrás entrópiája, annál kevésbé megjósolható, hogy mi lesz a forrásból érkező következő szimbólum. Következésképp egy-egy szimbólumnak annál nagyobb lesz a hírértéke.

A fenti, 010000100110111101100010 bináris sorozatra vonatkozó kérdés helyett tehát azt a kérdést kell feltennünk, hogy átlagosan mennyi információt tartalmaz egy-egy forrásszimbólum egy olyan információforrás esetén, amely magyar nyelven íródott szövegek betűit bocsájtja ki magából. Az információforrás entrópiája pontosan ez a mennyiség lesz, amely statisztikai módszerekkel mérhető. Minél több korábbi szimbólumsorozat áll rendelkezésünkre, annál pontosabban. A természetes nyelveken íródott szövegek implicit módon rengeteg szabályosságot tartalmaznak. Figyeljük meg például, hogy a magyar nyelvben nem túl gyakori, hogy egymás után két magánhangzó áll. Előfordul persze, de alapvetően nem jellemző.

Az ehhez hasonló nyelvi jellemzők által okozott statisztikai összefüggések miatt az ilyen jellegű információforrások viselkedése „kiszámíthatóbb”, mint mondjuk egy olyan információforrás, amely teljesen véletlenszerűen bocsájtja ki magából a szimbólumokat. Ha megmérnénk e két információforrás entrópiáját, akkor azt tapasztalnánk, hogy a magyar nyelvű szövegek entrópiája lényegesen alacsonyabb, mint a teljesen véletlenszerű betűsorozatoké. Mivel ennek a cikksorozatnak nem ez a fő témája, ezért ennek matematikai részleteibe nem megyünk bele. Azonban egy egyszerű kísérlettel megpróbáljuk érzékeltetni, hogy mi a gyakorlati jelentősége az információs entrópiának.

Az adatok tömöríthetőségének elvi korlátai

Az információelmélet egyik fontos területe az úgynevezett forráskódolással foglalkozik. Ennek fő kérdése az, hogy egy információforrásból érkező szimbólumsorozatot milyen módszerrel célszerű bitsorozattá alakítani oly módon, hogy annak hossza lehetőleg minél kisebb legyen. Ennek gyakorlati alkalmazását mindenki ismeri, aki használt már valamilyen adattömörítési eljárást. Ezeknek egyik fajtája a veszteségmentes tömörítés, amely azt garantálja, hogy a tömörítés során nem veszik el információ. Ez a gyakorlatban azt jelenti, hogy az eredeti bitsorozat teljes egészében visszaállítható a tömörített bitsorozatból. Érezhetően kell lennie egy alsó korlátnak arra vonatkozóan, hogy egy bitsorozatot milyen mértékben lehet veszteségmentesen tömöríteni.

Ezt az alsó korlátot határozza meg az információs entrópia. Minél nagyobb egy adott bitsorozat entrópiája, az annál kevésbé lesz tömöríthető. Ennek érzékeltetésére elvégeztem egy viszonylag egyszerű kísérletet. Az Internetről kimásoltam Madách Imre – Az ember tragédiája című művét és az egészet elhelyeztem egy szöveges file-ba. Ennek a file-nak a mérete 199612 byte lett. Ezek után létrehoztam két másik ugyanilyen méretű file-t. Az egyik teljesen véletlenszerű byte-okat tartalmazott, a másik pedig periodikusan ugyanazt az 5 byte-ot ismételgette teljes hosszában. Mindhárom file-ra lefuttattam a mindenki által jól ismert ZIP nevű tömörítő eljárást, és megvizsgáltam, hogy melyiket milyen mértékben sikerült tömöríteni. Az alábbi eredmények születtek:

• Az ember tragédiája: 81884 byte (az eredeti méret 41 %-a)
• Véletlenszerű: 199835 byte (az eredeti méret 100,1 %-a)
• Periodikus: 480 byte (az eredeti méret 0,2 %-a)

Az eredményekből egyértelműen látható az összefüggés a három különböző forrás entrópiája és tömöríthetősége között. Madách műve a hossza miatt viszonylag reprezentatív statisztikai mintát ad a magyar nyelvről. Látható, hogy kevesebb, mint a felére össze lehetett nyomni még egy olyan általános tömörítővel is, mint a ZIP. Ez arról árulkodik, hogy az emberi nyelven íródott szövegek entrópiája nem túl magas a sok redundancia és szabályosság miatt.

Ezzel szemben az ugyanolyan hosszú, de teljesen véletlenszerű byte-okkal megtöltött inputot egyáltalán nem sikerült tömöríteni. Sőt, a tömörített file még hosszabb is lett, mint az eredeti. Ezt a kis növekedést az okozza, hogy a ZIP eljárás egyfajta szótárat próbál építeni a bemenetből annak érdekében, hogy a gyakran előforduló byte sorozatokat rövidebbekkel helyettesítse. Ezt a szótárat viszont tárolni kell a tömörített file-ban, és ennek van bizonyos adminisztrációs költsége. Mivel azonban ennek a véletlenszerű forrásnak az entrópiája nagyon magas, ezért a tömörítés hatásfoka itt gyakorlatilag 0 volt, az eljárás során felépített szótár pedig csak a helyet foglalta.

Végül a harmadik forrásból jövő információt az 500-ad részére tudta tömöríteni a ZIP. Ez nem is meglepő, hiszen ez a file 5 darab byte periodikus ismétléséből állt, vagyis nem sok információ volt benne. Az entrópia – azaz a byte-onkénti átlagos információtartalom – tehát ebben az esetben majdnem 0 volt.

A fenti kísérlet tehát rávilágít arra, hogy az információs entrópia egyértelműen meghatároz egyfajta elvi alsó korlátot, aminél tömörebben nem lehet leírni az adott információt.

Amennyiben ezt a korlátot mégis át szeretnénk lépni, akkor kompromisszumot vagyunk kénytelenek kötni. Ennek ugyanis az az ára, hogy az eredeti adat nem állítható vissza teljes egészében a tömörített adatból. Az úgynevezett veszteséges tömörítések esetén tehát információ veszik el a tömörítés során. Cserébe viszont a tömörítés hatásfoka lényegesen nagyobb lehet attól függően, hogy mekkora és milyen jellegű veszteséget engedünk meg. Erre a legkézenfekvőbb példák a hang-, kép- és videótömörítési eljárások. Egy JPEG-be mentett kép esetén például a dekódolás után nem kapjuk vissza pixelről pixelre az eredeti képet, csak egy ahhoz olyannyira hasonlót, hogy az apró különbségeket nem veszi észre a szemünk. Egy MP3 tömörítő a fülünk fogyatékosságait használja ki hasonló módon hangok tömörítéséhez.

Analóg és digitális információforrások

A fizikai világban az „információt” valamilyen vizsgált objektumok bizonyos fizikai jellemzői hordozzák, amelyeket általában az idő függvényében változó számértékekkel írhatunk le. Egy-egy ilyen fizikai jellemző időbeli változását jelnek nevezzük, és egy grafikonon ábrázolhatjuk. A vízszintes tengely az időt jelenti, a függőleges tengely pedig a jel lehetséges értékeit tartalmazza. A jelet reprezentáló görbe egy adott pontját leolvasva láthatjuk, hogy az adott jel az adott időpillanatban milyen értéket vesz fel. Analóg (folytonos) jelről beszélünk abban az esetben, ha a jel bármely tetszőleges időpontban bármilyen tetszőleges értéket felvehet egy adott intervallumon belül. Az alábbi ábrán egy analóg jel látható, amely a 4,3 helyen a 2,85 értéket veszi fel (bármit is jelentsen ez a jel által reprezentált fizikai jellemző szempontjából):

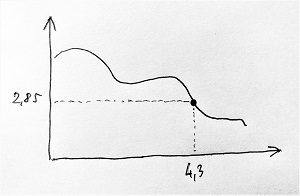
Ezzel szemben digitális (diszkrét) jelről beszélünk akkor, ha a jel csak bizonyos időpillanatokban van értelmezve, és csak véges sok különböző értéket vehet fel. A továbbiakban jel alatt mindig digitális jelet fogunk érteni, ugyanis bármely analóg jel átalakítható digitális jellé tetszőleges pontossággal. Az ilyen átalakításokat digitalizálásnak nevezzük, amely két részből áll. Egyrészt adott időközönként mintát veszünk a folytonos idejű analóg jelből. Ezt mintavételezésnek nevezzük. Másrészt pedig a vett minták folytonos értéktartományát adott számú részre osztjuk, és minden mintáról azt írjuk le, hogy melyik részbe esett az értéke. Ezt kvantálásnak nevezzük, amely tehát azt biztosítja, hogy egy-egy minta véges sok tizedesjeggyel leírható legyen.

Azt, hogy az eredeti analóg jelet mennyire pontosan tükrözi a digitalizált változata, egyrészt a mintavételezés gyakorisága, azaz a mintavételi frekvencia, másrészt pedig az értéktartomány felosztásának finomsága, azaz a kvantálási mélység határozza meg. Az alábbi ábrán egy 1 másodperces analóg jel digitalizálásának folyamatát láthatjuk. Itt 16 Hz-es mintavételezési frekvenciát és 2 bites kvantálási mélységet alkalmaztunk. Ez azt jelenti, hogy az 1 másodperces jelből 16 mintát vettünk, és 2²=4 részre osztottuk az értéktartományt a kvantáláskor. Eredményül egy számsorozatot kaptunk, amely leírja minden mintáról, hogy az adott minta melyik résztartományba esett. Az egyes résztartományokat a 0, 1, 2 és 3 számokkal azonosítottuk ebben az esetben:

A kapott digitalizált jel az 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 2, 1 számsorozat lesz. Ez nem egy túl pontos digitalizálás, de nyilván minden esetben megadható egy olyan ésszerű mintavételezési frekvencia és kvantálási mélység, amely elegendően nagy pontosságot eredményez az adott alkalmazás szempontjából. Vegyünk például egy analóg hangjelet, amely egy mikrofon vezetékén keresztül valamilyen elektromos jel formájában érkezik a digitalizáló egységhez. Ekkor egy 44100 Hz-es mintavételezési frekvencia (azaz másodpercenként 44100 mintavétel) és egy 16-bites kvantálási mélység (azaz az értéktartomány 2¹⁶=65536 részre osztása) bőven elegendő ahhoz, hogy az emberi fül által hallható hangokat leírjuk. Ez azt jelenti, hogy ebben az esetben az eredeti analóg jel és a digitalizált jel közötti különbség (vagyis a digitalizálás során fellépő hiba) olyan csekély mértékű, amelyet az emberi fül nem tud érzékelni. Egy audió CD gyakorlatilag ezeket a mintákat tartalmazza bináris adatként.

Összefoglalás

Ebben a részben tehát az információátviteli rendszerek absztrakt modelljének egy részével ismerkedtünk meg. Egy ilyen rendszer bemenetét ebben a modellben valamilyen információforrás adja. Például egy emberi nyelven íródott szöveg, egy digitalizált hanghullám vagy akár egy kép. Ebből az információból azután egy adott szabvány szerinti forráskódolásnak köszönhetően bináris adat lesz. Ezt láthatjuk az alábbi ábrán vázlatosan:

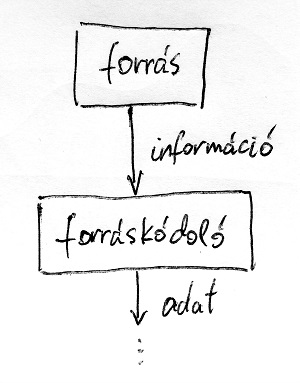
Sejthető, hogy innentől kezdve az Alice és Bob (illetve az általuk használt számítógépek) közötti kommunikáció gyakorlatilag számok küldözgetéséből fog állni. Ez az a pont, amikortól kezdve a kriptográfiára már nem nyelvészeti, hanem egyértelműen informatikai/matematikai tudományként kell tekintenünk. A következő részben a számrendszerekre fogunk kitérni és megvizsgáljuk, hogy az informatikai eszközök milyen formában tárolják az adatokat.

A következő részt itt találod…