Ez a cikksorozat a titkok elrejtésének tudományába kalauzolja el az Olvasót. E tudomány neve kriptográfia, amely az ógörög „kryptós” (rejtett) és „gráphein” (írni) szavakból ered, és amely szó szerint titkosírást, rejtjelezést jelent. A sorozat bevezető részében a kriptográfia tudományának történetén keresztül megismerkedünk az alapfogalmakkal és azokkal a problémákkal, amelyek megoldása nélkül ma nem létezne mobiltelefon, bankkártyás fizetés és Internet. De kezdjük a legelején, és ismerkedjünk meg főhőseinkkel…
A mindenki által jól ismert bibliai teremtéstörténetben leírtakkal ellentétben a legújabb kutatások szerint az első két ember neve nem Ádám és Éva, hanem Alice és Bob volt. Ez a történet főként róluk szól, amibe időnként más (olykor gonosz) mellékszereplők is be fognak kapcsolódni. A történet számunkra érdekes része akkor kezdődik, amikor a Paradicsomból való kiűzésük és a Föld benépesítésének fáradalmai után Alice és Bob ismeretlen okokból nagyon távol kerültek egymástól.
Szerencsére ekkorra már az emberek postaszolgálatokat hoztak létre, így a nagy távolság ellenére Alice és Bob képesek voltak üzeneteket küldeni egymásnak. Mivel korábban rendkívül közeli (amit nevezhetünk akár intimnek is) viszony alakult ki közöttük, ezért nyilván bizalmas üzeneteket is váltottak egymással, amelyekben a titkaikat beszélték meg. Sajnos azonban volt egy nagyon gonosz nőszemély, aki szerette mások titkait kifürkészni, és adott esetben akár még anyagi hasznot is húzni ezekből a bizalmas információkból. Őt Eve-nek hívták, aki a postán dolgozott, és így mindig látta, amikor Alice és Bob éppen üzenetet küldött egymásnak. Eve nagyon körültekintő volt ilyenkor: óvatosan felbontotta a borítékokat és elolvasta a bizalmas üzeneteket, azután visszazárta és visszatette a többi közé. Mindig nagyon figyelt arra, hogy senki se vegye őt észre, így Alice és Bob mit sem sejtett arról, hogy a bizalmas üzenetváltásaikat a gonosz Eve pofátlanul elolvassa.
Történt egyszer, hogy Alice sok pénzt szeretett volna küldeni Bob-nak, ezért elment a közeli bankfiókba. Nyitott egy bankszámlát, és befizette a pénzt erre a számlára. Ezután kitalált egy jelszót, és meghagyta a banknak, hogy csak annak adhatják oda ezt a pénzt, aki a jelszót meg tudja mondani. Alice arra gondolt, hogy nem túl biztonságos ilyen sok pénzt postán küldeni, hiszen akkoriban sajnos már elszaporodtak a postarablások. Ehelyett Alice-nak csupán értesítenie kell Bob-ot, hogy pénzösszeget helyezett el számára a bankban, valamint meg kell adnia neki a pénzfelvételhez szükséges jelszót.
Írt is gyorsan erről egy üzenetet Bob számára, és pénz helyett ezt az üzenetet küldte el postán. Természetesen a szemtelen Eve ezt az üzenetet is elolvasta titokban, és egyből kikerekedett a szeme annak láttán, hogy milyen értékes információhoz jutott. Nem is vesztegette az idejét, gyorsan elutazott egy közeli bankfiókba, és a titkos jelszó ismeretében Bob-ot megelőzve fel is vette a pénzt a számláról. Mire szerencsétlen Bob megkapta a bizalmas levelet, és elment a bankba felvenni a pénzt, a bankszámla már üres volt. Eve tehát közvetlen anyagi hasznot húzott az Alice és Bob közötti bizalmas üzenet megismeréséből.
A kriptográfia megjelenése
Minden rosszban van valami jó, hiszen ezáltal Alice és Bob rájöttek, hogy a posta nem megbízható, ha bizalmas üzenetváltásokról van szó. Megbeszéltek hát egy személyes találkozót, hogy együtt kitalálják, mihez kezdjenek ezzel a problémával. Azt tudták, hogy a továbbiakban is kénytelenek lesznek a nem megbízható postát használni a közöttük lévő nagy távolság miatt. Ugyanakkor nem szerették volna, ha az üzenetekben lévő bizalmas információk illetéktelen kezekbe kerülnének.
Ezért azt találták ki, hogy a küldő fél minden üzenet elküldése előtt lecseréli az üzenet betűit más betűkre egy adott szisztéma szerint. Ezt a szisztémát titokban tartják, a fogadó fél pedig a cserélgetést ugyanazon szisztéma szerint visszafelé elvégzi, miután megkapta az üzenetet. Így biztonságosan használhatják a postát az üzenetküldésre, hiszen a postán garázdálkodó Eve (vagy bárki más) hiába bontja fel a borítékot, abban csak egy számára értelmetlen betűhalmazt fog találni. Eve ugyanis nem ismeri Alice és Bob közös titkát, így nem tudja visszacserélgetni a betűket és megismerni a bizalmas üzenetek tartalmát.
Alice és Bob tehát megegyeztek abban, hogy rejtjelezni fogják az üzeneteiket.
A Caesar-kód
Vegyünk egy egyszerű példát erre. Tegyük fel, hogy Alice és Bob abban egyeztek meg, hogy az üzeneteikben kizárólag az angol ábécé 26 betűjét használják. Az egyszerűség kedvéért nem használnak szóközöket, írásjeleket és ékezetes betűket. A megegyezés szerint küldés előtt mindegyik betűt lecserélik az ábécében valamennyivel utána lévő betűre. Amennyiben ilyen módon elérnék az ábécé végét, akkor az elejétől folytatódik a számolás. A rejtjelezési eljárás ebben az esetben a betűk ábécé szerinti „eltolása”. Az pedig, hogy konkrétan Alice és Bob mekkora eltolásban egyeznek meg, ennek az eljárásnak egy paramétere, amelyet kulcsnak (key) nevezünk.
Tegyük fel, hogy Alice és Bob kulcsként a 15-ös számban egyeznek meg, vagyis hogy a rejtjelezéskor a betűket 15-tel fogják eltolni. Alice ezután a sziabobmiahelyzet üzenetet szeretné elküldeni Bob-nak. Ezt nyílt szövegnek (plain text) nevezzük, mivel ez az, amit el szeretnének rejteni Eve elől arra az időszakra, amíg a nem biztonságos kommunikációs csatornán (channel) keresztülhalad. Ez jelen példánkban a posta. Alice-nak ezt a nyílt szöveget küldés előtt át kell alakítania a Bob-bal kötött megegyezés szerint. A rejtjelezési eljárás és a megbeszélt kulcs alapján ez jelen esetben a nyílt szöveg minden betűjének lecserélését jelenti az ábécében 15-tel utána következő betűre. Ezt kódolásnak (encoding) nevezzük. Így Alice előállítja a hoxpqdqbxpwtanoti szimbólumsorozatot, amelyet kódszövegnek (cypher text) nevezünk, és ezt adja fel postán Bob-nak címezve.
Bob, miután megkapta a postán keresztül a kódszöveget, nincs más dolga, mint visszafelé alkalmazni a rejtjelezési eljárást az Alice-szal megbeszélt kulcsot használva. Azaz a kódszöveg minden betűjét le kell cserélnie az ábécében 15-tel megelőző betűre. Ezt dekódolásnak (decoding) nevezzük. Így Bob visszakapja a sziabobmiahelyzet nyílt szöveget, amelyre hasonló módon válaszolhat Alice-nak. Ekkor ő lesz a küldő, Alice pedig a fogadó fél, azaz a szerepük felcserélődik.
A történet kényes pontja az, amikor a borítékot Alice már feladta a postán, de az még nem érkezett meg Bob-hoz. A gonosz Eve-nek ugyanis újabb anyagi haszon reményében nyilván érdekében áll megismerni a nem neki címzett titkos üzenetek tartalmát. Ezzel meg is fog próbálkozni, így őt ebben a történetben támadónak (attacker) nevezzük. Amikor azonban Eve titokban felbontja az Alice által küldött borítékot, bajba kerül, mivel csak a hoxpqdqbxpwtanoti kódszöveget fogja látni. Eve még abban az esetben is bajban van, ha ismeri a használt rejtjelezési eljárást. Ez könnyen lehet, például azért mert az részletesen le van írva egy bárki számára elérhető szabványban. Azt viszont nem ismeri, hogy mi volt az a kulcs, amiben Alice és Bob előzetesen megegyeztek. Ez jelen esetben a 15.
Eve-nek tehát az a célja, hogy a kódszövegből a kulcs ismerete nélkül, de az eljárás ismeretében előállítsa a nyílt szöveget. Azt nyilván meg tudja tenni, hogy kipróbálja az 1-es kulcsot. Ekkor a gnwopcpawovszmnsh betűsorozatot fogja kapni. Ennek nyilván nincs értelme, így Eve azt már tudja, hogy az Alice és Bob által megbeszélt kulcs nem az 1-es volt. Ezután megpróbálkozhat a 2-es kulccsal, ám ekkor is értelmetlen szöveget fog kapni. Eve így kénytelen kipróbálni újabb és újabb kulcsokat is. Egy idő után végül sikerrel jár ugyan, viszont ez 15-ször annyi erőfeszítésébe került, mintha eleve ismerte volna a kulcsot.
A fent ismertetett kriptográfiai eljárást Caesar-kódnak nevezzük, amely az úgynevezett monoalfabetikus behelyettesítő kódolásoknak egy egyszerű fajtája. A monoalfabetikus kódolások nem számítanak túl erős rejtjelnek, mivel a kódszöveg előállításakor a nyílt szöveg betűit mindig ugyanolyan betűkkel helyettesítjük. Például a bob szövegrész megfelelője qdq lesz a kódszövegben. Ha Eve elegendően sok azonos kulccsal rejtjelezett kódszöveget tud elfogni Alice és Bob kommunikációjából, akkor könnyedén készíthet statisztikát a kódszövegekben előforduló betűk gyakoriságáról, amelyből értékes információkat nyerhet a kulcs ismerete nélkül is.
Ha például azt tapasztalja, hogy a kódszövegekben a t betűnek a leggyakoribb az előfordulása, akkor könnyen megsejtheti, hogy a t rejtjelezett betűk a nyílt szöveg e betűinek felelhetnek meg, hiszen a magyar nyelvben – amelyen Eve szerint vélhetően Alice és Bob kommunikál – az e betűnek a leggyakoribb az előfordulása. Ha Eve még azt is tudja, hogy Caesar-kóddal áll szemben, akkor gyorsan kipróbálhat néhány kódszöveget visszafejteni a 15-ös kulccsal, mivel a t betű az e betű után 15-tel van az ábécében. Amennyiben azt tapasztalja, hogy értelmes szövegeket kapott, akkor már meg is találta a kulcsot. Ráadásul sokkal könnyebben, mintha ész nélkül végigpróbálta volna az 1, 2, …, 15 kulcsokat egyenként. A kulcs ismeretében pedig Eve könnyedén dekódolhat minden további üzenetet. Ekkor azt mondjuk, hogy Eve feltörte (crack) az Alice és Bob által használt rejtjelezési eljárást.
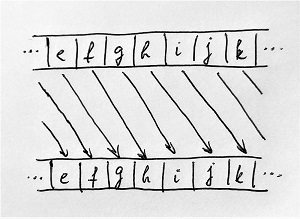
Egy fokkal bonyolultabb Eve helyzete, ha nem Caesar-kódról van szó, hanem valamilyen általánosabb monoalfabetikus kódolásról, amely jobban összekeveri az ábécé betűit. Azonban gyakoriságelemzéssel az ilyen kódszövegek megfejtése sem jelent túl nagy problémát.
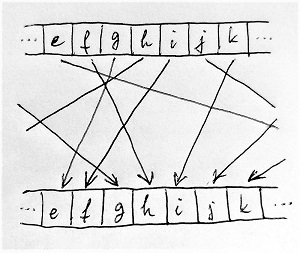
A Vigenére-kód
Alice és Bob tehát továbbra sincs biztonságban, ezért egy újabb személyes találkozót kénytelenek megbeszélni egymással annak érdekében, hogy még jobban megnehezítsék Eve dolgát. Megállapodnak abban, hogy az üzenetek kódolásakor betűnként fogják váltogatni az adott betűre alkalmazott eltolás értékét. Így a kulcs mostantól nem egy darab szám lesz, hanem egy valahány számból álló sorozat. A módosított kriptográfiai eljárás a következő: a nyílt szöveg betűi alá kezdjük el felírni a kulcsot alkotó számokat egyenként. Ismételgessük a kulcs számait mindaddig, amíg a nyílt szöveg összes betűje alá nem kerül valamilyen szám. Ezután minden betűre akkora eltolást alkalmazzunk, amilyen szám szerepel alatta.
Az előző példánál maradva tegyük fel, hogy Alice és Bob a (3, 5, 2) kulcsban állapodtak meg, és Alice ismét a sziabobmiahelyzet nyílt szöveget szeretné rejtjelezve elküldeni Bob-nak. Az alábbiakban látható az Alice által alkalmazott kódolás:
sziabobmiahelyzet
35235235235235235
vekdgqerkdmgodbhy
A kódolás eredményeképpen előálló kódszöveg tehát vekdgqerkdmgodbhy lesz. Látható, hogy Eve-nek ebben az esetben sokkal nehezebb dolga van, ugyanis például a bob szövegrészből gqe lesz a kódszövegben, vagyis az első b betűre más eltolás lett alkalmazva, mint a második b betűre. Hiába készít tehát statisztikát Eve a kódszöveg betűinek gyakoriságára, az sokkal kevésbé fogja tükrözni a magyar nyelv sajátosságait. Persze elkezdhet különböző kulcsokkal próbálkozni, azonban most nem 26 féle kulcsot kell kipróbálnia, hanem sokkal többet. A kulcs ugyanis most egy számsorozat, amelynek minden tagja 26 féle lehet, ráadásul Eve még azt sem tudja, hogy milyen hosszú a kulcs. Reménytelennek tűnik tehát Eve helyzete.
Ezt az eljárást Vigenére-kódnak nevezzük, amely egy egyszerű fajtája az ún. polialfabetikus behelyettesítő kódolásoknak. Ezeknél tehát változó, hogy a nyílt szöveg betűit milyen más betűkkel helyettesítjük. A Vigenére-kódot sokáig használták a középkorban, mivel a számtalan variációs lehetőség miatt sokáig feltörhetetlennek hitték. Azonban Leonhard Euler (18. századi matematikus, a matematikatörténet egyik legjelentősebb alakja) felfedezte, hogy a kulcsnál lényegesen hosszabb szöveg esetén periodikus ismétlődések lesznek a kódszövegben. A részletektől itt most eltekintünk, de ezeknek a periódusoknak a hosszából a kulcs hosszára lehet következtetni, amely által a feltörés lényegesen egyszerűbbé válik. A törési eljárás akkor igazán hatékony, ha hosszú a szöveg, és rövid a kulcs. Ezért célszerű olyan kulcsot választani, ami összemérhető a nyílt szöveg hosszával. Egy gyakorlott rejtjelfejtőnek különböző gyakoriságtáblázatok birtokában egy nem túl hosszú kulcs esetén mindössze 6-9 órába telt megfejteni a kódolt szöveget. Alice és Bob tehát még mindig nem érezhette magát eléggé biztonságban.
A kriptográfia alapelve
Általánosságban elmondható, hogy a rejtjelezési rendszerek tervezésekor két okból is célszerű különválasztani magát az eljárást, illetve az eljáráshoz használt kulcsot. Egyrész praktikussági okokból, hiszen ekkor minden olyan esetben, amikor Alice Bob helyett valaki mással szeretne kommunikálni, újabb és újabb eljárások kitalálása helyett elég csak egy másik kulcsban megegyezniük.
Másrészt biztonsági okokból, ugyanis érdemes mindig fejben tartani azt a Claude Shannon által megfogalmazott alapelvet, miszerint:
„Az ellenség ismeri a használt rendszert.”
Átfogalmazva: egy rejtjelezési rendszer biztonságának sosem szabad az eljárás titokban tartásától függenie. Ehelyett a biztonságnak egyedül a kulcs titokban tartásán kell múlnia. Egy kriptográfiai rendszert ezek szerint akkor mondunk biztonságosnak, ha a kódszövegből a kulcs ismerete nélkül akkora erőfeszítésbe kerül a nyíltszöveget előállítani, hogy nem éri meg megkísérelni még abban az esetben sem, ha maga az eljárás ismert a támadó számára.
Az Enigma
Ezt az alapelvet hagyták részben figyelmen kívül a híres német rejtjelező rendszer, az Enigma tervezői. Az Enigma első változatát Arthur Scherbius német mérnök fejlesztette ki az első világháború végén, és az 1920-as években kereskedelmi céllal kezdték el alkalmazni. Annyira sikeresnek bizonyult, hogy a második világháborúban a teljes német hadsereg kommunikációjának titkosítását is az Enigma későbbi katonai változataival végezték. Az Enigma előtt még „kézzel” történt a kódolás és a dekódolás, ezért a gép bevezetése erre a célra innovatív kezdeményezés volt. Az Enigmát használói abszolút biztonságosnak tartották, mivel az ezzel kódolt szövegek hagyományos – kézi – módszerekkel megfejthetetlenek voltak.
Tervezői azonban nem számoltak azzal, hogy a gép által generált titkos szöveget egy másik géppel – és persze a különböző tervezési hiányosságokat kihasználva – meg lehet fejteni. Az Enigmát először a lengyel Marian Rejewski vezette matematikusokból álló csoport törte fel 1932-ben. Azonban a németek a háború kitörése előtt lényegesen megbonyolították a szerkezetet. A lengyel kódtörők – a fenyegető veszélyt látva – összes tudásukat átadták a szövetségeseknek még hazájuk lerohanása előtt. Ez aztán nagyban hozzájárult az Egyesült Királyság kódfejtőinek későbbi sikereihez, akik Alan Turing vezetésével 1940-től a háború végéig a legtöbb elfogott német katonai üzenetet meg tudták fejteni.
Ezeket a hírszerzési információkat szigorú titoktartás övezte. Külön csapat gondoskodott „legendák” gyártásáról és álhírek kiszivárogtatásáról, nehogy az ellenség túl korán gyanút fogjon. Többek között ennek köszönhető, hogy a normandiai partraszállás abszolút váratlanul érte a németeket, akik az álhíreknek köszönhetően teljesen máshol várták a nyugati front megnyitását, és ez vezetett el végül a szövetségesek győzelméhez 1945 tavaszán.

Az Enigma működése
Az Enigma egy elektromechanikus rejtjelező gép, amely egy alfanumerikus billentyűzetből, egy kijelzőből, néhány közös tengelyen forgó tárcsából, valamint egy, a billentyűk leütésével működtetett tárcsaléptető mechanizmusból állt. Az egyik tárcsa minden egyes leütés után egyet lépett, míg a többi tárcsa csak adott leütésenként lépett egyet-egyet. Ezek a tárcsaléptetések állandóan változó áramkört hoztak létre, amely a kódolandó betű leütésekor zárult, kivillantva a kódszöveg aktuális betűjének megfelelő lámpát a kijelzőn. Az alábbi ábra egy 3 tárcsás Enigma működési alapelvét mutatja:
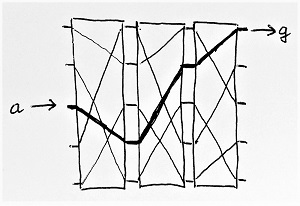
Amikor a kezelő leüti a billentyűzeten a nyílt szöveg soron következő betűjét (legyen ez például a), az aktuális tárcsaállásoknak megfelelően a tárcsák belső huzalozásán keresztül záródik az áramkör. Ekkor felvillan a kódszöveg következő betűje (a fenti példában g), majd a tárcsaléptető mechanizmus megforgat bizonyos tárcsákat. Így a nyílt szöveg következő betűje már egy teljesen más huzalozáson keresztül fogja zárni az áramkört.
Látható, hogy önmagában egy tárcsa csupán egy egyszerű monoalfabetikus helyettesítő kódolást állítana elő. Egy betűt kicserél egy másikra a belső huzalozásától függően. Az Enigma bonyolultságát a több tárcsa egyidejű használata, valamint az egyes tárcsák egymáshoz képest eltérő elforgatása adta, így egy polialfabetikus helyettesítő kódolást hozva létre. Az üzenetek megfelelő kódolásához és dekódolásához mindkét kommunikáló félnek azonos módon kellett az Enigmát beállítania. Egyforma tárcsákat kellett ugyanabban a sorrendben és megegyező kezdeti helyzetben használniuk. A németek ezen kívül később újabb és újabb bonyolításokat vezettek be. Például 3 helyett több tárcsa használata, egy kézzel megváltoztatható extra huzalozás, amellyel a tárcsák elé egy fix keverést be lehetett iktatni, stb. E beállítások összessége alkotja a kulcsot az Enigma esetén.
A kódfejtés további nehezítése érdekében a németek 1936-tól kezdődően áttértek a napi kulcsok használatára, azaz naponta változtatták az Enigma beállításait. Ezen kívül tilos volt 250 betűnél hosszabb üzeneteket küldeni. Az ennél hosszabb üzeneteket több részre bontották, és minden részt különböző véletlenszerűen választott egyszer használatos kulcsokkal kódoltak. Az első részüzenet kulcsát az Enigma aznapi beállítása alapján kódolták, majd a további részüzenetek kulcsait a megelőző részüzenet végén közölték. A fogadó fél a napi beállításból kiindulva szépen vissza tudta fejteni az üzenet részeit. Ezzel a protokollal a gyakoriságelemzésen alapuló törési kísérletek kudarcra voltak ítélve.
Az Enigma feltörése
Az Enigma elméleti kulcstere (a lehetséges beállítások száma) óriási, nagyságrendileg 1023 lehetőség. Ez már összevethető a modern rejtjelezők kulcsterének nagyságával. Egy ekkora kulcstér és a bevezetett óvintézkedések mellett érthetetlennek tűnik, hogy a szövetségeseknek hogyan sikerült mégis feltörniük az Enigmát. Ez több okra vezethető vissza, melynek egyik tényezője, hogy az Enigma biztonsága nagymértékben függött a tárcsák belső huzalozásának titokban tartásától. Mivel ezt a felhasználó nem tudta megváltoztatni, így ez nem a kulcs, hanem az eljárás részének tekinthető. Ez ellentmond a fentebb már említett kriptográfiai alapelvnek, miszerint feltételezni kell, hogy az ellenség részletesen ismeri a rejtjelező eljárást. Ez valóban így is volt, köszönhetően a szövetséges hírszerzés által zsákmányolt Enigma készülékek tüzetes vizsgálatának.
Ezeknek a vizsgálatoknak az eredményeképp a kódfejtők rájöttek egy sor tervezési hiányosságra. Ezeket kihasználva az átvizsgálandó kulcstér mérete lényegesen csökkenthető volt. Hogy csak a legfontosabbakat említsük: kényelmi szempontból az Enigma úgy volt kialakítva, hogy az eljárást kétszer alkalmazva az eredeti szöveget kapjuk vissza. Például ha egy u betű egy adott helyen x-be menne át, akkor, ha ugyanazon a helyen x lenne, az u-ba menne át. Ezen kívül további fontos tulajdonság volt, hogy egy betű soha nem kódolódott önmagába. Ez látszólag biztonságnövelő hatású, ám valójában további fontos támpontokat adott a kódfejtőknek rengeteg kulcs kizárására. Olyannyira, hogy az átvizsgálandó kulcstér mérete így alig 1 millióra csökkent.
Ezt kézzel átvizsgálni még mindig reménytelen lett volna. Azonban a kódfejtők Alan Turing vezetésével egy elektromechanikus gépet építettek erre a célra. Ennek továbbfejlesztett változata – a Colossus – 1943-ra mindössze pár perc alatt képes volt megtalálni az aznapi kulcsot a „nyers erő” módszerével, azaz a kulcsok végigpróbálgatásával. A Colossus-ból összesen 10 darab készült. A gépeket és leírásaikat megsemmisítették a háború után, egyetlen leírás kivételével. Ennek titkosságát csak 2000 szeptemberében oldotta fel a brit kormány.
Végül további logisztikai problémát okozott annak megoldása, hogy a hadsereg minden egysége naponta biztonságosan megkapja az aznapra érvényes kulcsot. A kommunikációs eszközökön keresztül nem küldhették, hiszen akkor ugyanabba a hibába estek volna, mint Alice, amikor Eve sikeresen ellopta a Bob-nak szánt pénzt. Ezért maradt a hagyományos módszer: a futárok alkalmazása. Ennek érthető limitációi miatt kénytelenek voltak egy nagyobb időszak (például egy hét vagy hónap) napi kulcsait egyszerre kiküldeni az egységeknek. Ezek a futárok kiváló célpontjai voltak a szövetséges hírszerzésnek, amely több alkalommal sikeresen lopott el adott időszakra érvényes komplett kódkönyveket. Az ilyen küldetések esetén persze fontos volt, hogy a lopás tényéről a németek ne szerezzenek tudomást. Ekkor ugyanis azonnal lecserélték volna az adott időszakra szánt kulcsokat, és így az ellopott kódkönyvek már semmit sem értek volna.
A kulcsmegosztás problémája
Figyeljük meg, hogy az összes eddig bemutatott esetben volt valami közös. Nevezetesen: ahhoz, hogy kettő vagy több résztvevő titkosított kommunikációt folytathasson egymással egy nembiztonságos csatornán, meg kell egyezniük egy közös kulcsban. Ezzel el is érkeztünk a kriptográfia tudományának egyik fő kérdéséhez, az úgynevezett kulcsmegosztás problémájához. A kulcsmegosztás problémája arról szól, hogy ezt hogyan tudják megtenni biztonságosan. A 20. század második feléig alapvetésnek tartották, hogy a kulcsmegosztáshoz mindenképpen szükség van egy biztonságos csatornára (például személyes találkozó). A szakma őrültségnek nevezte az ezzel ellentétes felvetéseket.
Nagy szerencsénkre az 1970-es években akadt néhány őrült, akik megmutatták a világnak, hogy a kulcsmegosztás problémája megoldható nembiztonságos csatornán is. Ezzel pedig megteremtették az alapját mindannak, amit napjainkban információs társadalomnak nevezünk. Nélkülük ma nem létezne mobiltelefon, bankkártyás fizetés és Internet. Ez a cikksorozat előttük próbál meg tisztelegni azáltal, hogy részletesen bemutatja és közérthetővé teszi eredményeiket, melyek alapjaiban változtatták meg világunkat.
A sorozat következő részeiben érdekes gyakorlati példákon keresztül vázlatosan áttekintjük az információátviteli rendszerek absztrakt modelljét. Ebből világos lesz, hogy a kriptográfia tudománya hol kapcsolódik be ebbe a játszmába. Ezután pedig részletesen rátérünk a kulcsmegosztás problémájának megoldására, és sok egyéb, a modern kriptográfiai eljárások kapcsán felmerülő kérdés megválaszolására.
A következő részt itt találod…




Nélkülük ma nem létezne mobiltelefon, bankkártyás fizetés és Internet. – Ez a mondat azért kicsit túlzás.
A bankkártyás fizetést el tudom fogadni, de Internet és (analóg) mobiltelefon is létezett a kulcsmegosztás elterjedése előtt.
Hát nem tudom. Lehet, hogy létezne Internet valamilyen formában, de hogy egy szimpla jelszavas bejelentkezést nem tudnál megcsinálni biztonságosan, az tuti.