A bizonyításban a 24.7. Tételben definiált baloldali mellékosztályokat fogjuk használni, de értelemszerűen ugyanígy használhatnánk a jobboldali mellékosztályokat is.

Az említett tételben definiált \sim reláció egy ekvivalenciareláció, melynek ekvivalencia-osztályai a H szerinti baloldali mellékosztályok. Ezek az ekvivalenciarelációkról szóló 13.5. Tétel alapján G egy partícióját alkotják. Azaz semelyik két baloldali mellékosztálynak nincs közös eleme, és uniójuk a teljes G. Ez az elrendezés látható az alábbi ábrán:

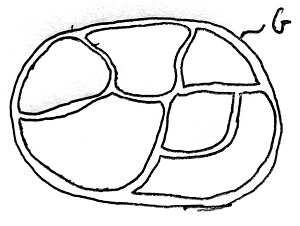
Tekintsük most a G csoportnak egy tetszőleges H szerinti baloldali mellékosztályát, és válasszunk ki belőle egy tetszőleges g elemet, amelyet reprezentánselemként fogunk használni a továbbiakban. A kérdéses mellékosztály tehát a gH halmaz lesz. Most egy kölcsönösen egyértelmű megfeleltetést fogunk létesíteni a gH mellékosztály és a H részcsoport elemei között.

A 24.7. Tétel illetve a hozzá tartozó megjegyzés alapján a gH mellékosztály tetszőleges x eleme esetén a g^{-1}x szorzat a H részcsoportnak egy eleme. Definiáljunk tehát egy f:gH\to H függvényt a következőképpen:

f(x)=g^{-1}x

Azt kell megmutatni, hogy f kölcsönösen egyértelmű megfeleltetés gH és H között. Ez az alábbi két dolgot jelenti:

1. Tetszőleges x\in gH és y\in gH esetén f(x)=f(y) akkor és csak akkor, ha x=y. Azaz az f függvény H minden elemét legfeljebb egy gH-beli elemhez rendeli hozzá.
2. Tetszőleges h\in H-hoz létezik olyan x\in gH, amelyre f(x)=h teljesül. Azaz az f függvény H minden elemét legalább egy gH-beli elemhez rendeli hozzá.

Nézzük az 1. állítást! Ha x=y, akkor nyilván teljesül az f(x)=f(y) egyenlőség, hiszen:

f(x)=g^{-1}x=g^{-1}y=f(y)

Visszafelé: ha f(x)=f(y), akkor az azt jelenti, hogy teljesül az alábbi egyenlőség:

g^{-1}x=g^{-1}y

Szorozzuk meg mindkét oldalt balról g-vel (itt e-vel jelöltük a G csoport egységelemét):

\underbrace{gg^{-1}}_{=e}\cdot x=\underbrace{gg^{-1}}_{=e}\cdot y

Ez viszont épp a kívánt x=y egyenlőség.

Most nézzük a 2. állítást! Keresnünk kell tehát egy olyan x elemet a gH mellékosztályban, amelyhez az f függvény épp a H részcsoport h elemét rendeli hozzá. Keressük tehát az alábbi egyenlet megoldását:

\underbrace{g^{-1}x}_{=f(x)}=h

Szorozzuk meg mindkét oldalt balról g-vel (itt e-vel jelöltük a G csoport egységelemét):

\underbrace{gg^{-1}}_{=e}\cdot x=gh

A baloldalról az egységelem elhagyható, így végülis a keresett x előállításának képletét kapjuk: x=gh.

Összefoglalva tehát a fenti f függvény mintájára kölcsönösen egyértelmű megfeleltetés létesíthető a H részcsoport, és bármely H szerinti baloldali mellékosztály között. Néhány mellékosztály esetére ez látható az alábbi ábrán:

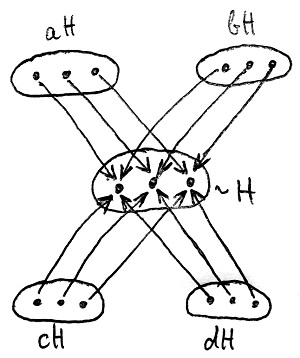
Ez azt jelenti, hogy bármely H szerinti baloldali mellékosztálynak pontosan ugyanannyi eleme van, mint magának H-nak. Ha tehát H rendjét megszorozzuk a baloldali mellékosztályok számával, akkor épp G rendjét kapjuk eredményül, hiszen a baloldali mellékosztályok G egy partícióját alkotják. Más szavakkal találtunk egy olyan egész számot – a H szerinti baloldali mellékosztályok számát –, amellyel megszorozva H rendjét épp G rendjét kapjuk. Az oszthatóság 16.1. Definíciója alapján ez épp azt jelenti, hogy |H| osztója |G|-nek.