24.1. Definíció (Félcsoport, csoport):

Tegyük fel, hogy adva van egy valamilyen G halmaz, amelyen értelmezve van egy kétváltozós művelet. Nevezzük ezt a műveletet szorzásnak és jelöljük \cdot-tal, vagy egymás után írással. Például egy a és egy b elem szorzatát jelöljük a\cdot b-vel vagy ab-vel.

Az így kapott (G,\cdot ) algebrai struktúrát félcsoportnak nevezzük, amennyiben az említett művelet asszociatív. Azaz tetszőleges a, b és c elemek esetén teljesül az alábbi:

Csoportnak nevezzük az olyan félcsoportokat, amelyek esetén az asszociativitáson kívül a műveletre nézve létezik neutrális elem is (14.7. Definíció), továbbá a művelet invertálható (14.9. Definíció). Egy csoport esetén a neutrális elemet általában e-vel vagy 1-gyel szoktuk jelölni, és ilyenkor egységelemről beszélünk. Egy a elem inverzét a^{-1}-gyel szoktuk jelölni. Tetszőleges a elem esetén teljesülnek tehát az alábbiak:

Amennyiben a művelet a fentieken felül még kommutatív is, úgy Abel-csoportról vagy kommutatív csoportról beszélünk. Abel-csoportok esetén a csoportműveletet tipikusan a + szimbólummal, a neutrális elemet 0-val, egy a elem inverzét pedig -a-val szoktuk jelölni. Ilyenkor a neutrális elemet nullelemnek, az a elem inverzét pedig a ellentettjének nevezzük.

24.2. Tétel (Szorzat inverze):

Legyen H egy tetszőleges halmaz, amelyen értelmezve van egy *-gal jelölt asszociatív művelet, és tegyük fel, hogy létezik H-ban neutrális elem (14.7. Definíció) erre a műveletre nézve. Legyenek továbbá x és y a H halmaz két olyan eleme, amelyek invertálhatók (14.9. Definíció) a * műveletre nézve. Jelöljük ezek inverzeit rendre x^{-1}-gyel és y^{-1}-gyel. Ekkor teljesül az alábbi azonosság:

Ha x és y felcserélhetők, azaz x*y=y*x, akkor teljesül az alábbi azonosság is:

Bizonyítás:

Ha e-vel jelöljük a * művelet neutrális elemét, akkor egyrészt:

Másrészt:

Azaz a 14.9. Definíció alapján (x*y) és y^{-1}*x^{-1} valóban egymás inverzei. Ha x és y felcserélhetők, akkor pedig nyilván (x*y)^{-1}=(y*x)^{-1}=x^{-1}*y^{-1} is igaz.

24.3. Definíció (Gyűrű additív és multiplikatív csoportja):

A 14.12. Definíció-ban szereplő gyűrűaxiómák a 24.1. Definícióban ismertetett félcsoport és csoport fogalmának segítségével átfogalmazhatók. Eszerint tegyük fel, hogy adva van egy R halmaz, amelyen értelmezve van egy +-szal és egy \cdot-tal jelölt kétváltozós művelet. Az (R,+,\cdot) algebrai struktúrát gyűrűnek nevezzük, ha teljesülnek az alábbiak:

1. Az R halmaz a + művelettel Abel-csoportot alkot.
2. Az R halmaz a \cdot művelettel félcsoportot alkot.

Az 1. pontban szereplő (R,+) Abel-csoportot az R gyűrű additív csoportjának nevezzük és R^+-szal jelöljük. Amennyiben az R gyűrű egységelemes, akkor vannak olyan elemei, amelyeknek a \cdot műveletre nézve is létezik inverze – az egységelem és ellentettje például mindenképpen ilyen. Ezeknek az invertálható elemeknek a halmaza – amely tehát R-nek egy nemüres részhalmaza – a \cdot művelettel szintén csoportot alkot, amelyet az R gyűrű multiplikatív csoportjának nevezzük és R^{\times}-tel jelöljük.

Megjegyzés:

A 24.1. Definíció alapján könnyen leellenőrizhető, hogy az R^{\times} halmaz valóban csoportot alkot az R gyűrű \cdot műveletével.

Előszöris R^{\times} zárt a \cdot műveletre nézve. Legyen ugyanis a és b az R gyűrű két invertálható eleme – azaz a\in R^{\times} és b\in R^{\times}. Ekkor az ab szorzat is invertálható – azaz ab\in R^{\times} –, méghozzá a 24.2. Tétel alapján:

Más szavakkal tehát az R halmazon értelmezett \cdot művelet algebrai értelemben művelet az R-nél szűkebb R^{\times} halmazon is (lásd a 11.3. Definíciót). Így ha a \cdot művelet R-en asszociatív volt, akkor nyilván R^{\times}-en is az.

Másodszor R^{\times}-ben létezik neutrális elem, méghozzá az R gyűrű egységeleme. Neki ugyanis nyilván létezik R-beli inverze a \cdot műveletre nézve: önmaga.

Harmadszor minden R^{\times}-beli elemnek az inverze szintén R^{\times}-ben van – azaz R^{\times} zárt az R-beli inverzképzésre is. Tegyük fel ugyanis, hogy egy a\in R^{\times} elem R-beli inverze a^{-1}, azaz aa^{-1}=1 és a^{-1}a=1. Mivel 1 benne van R^{\times}-ben, ezért a-nak az R^{\times}-beli inverze szintén csak a^{-1} lehet, hiszen a 14.10. Tétel alapján az inverzképzés egyértelmű.

Az R^{\times} halmaz tehát valóban csoportot alkot az R gyűrű \cdot műveletével.

Végül felhívjuk a figyelmet, hogy amennyiben R kommutatív és egységelemes, akkor érvényes a 16.5. Tétel. Ez alapján R valamely eleme akkor és csak akkor invertálható, ha egység. Az egységek ugyanis ilyenkor épp az egységelem osztói, ami ugye a 16.1. Definíció alapján azt jelenti, hogy létezik hozzájuk olyan elem, amellyel őket összeszorozva az egységelemet kapjuk eredényül. Egy kommutatív, egységelemes R gyűrű multiplikatív csoportja tehát R egységeiből áll. Speciálisan ha R test, akkor a 16.3. Definíció utáni megjegyzés alapján R^{\times} a nullelemen kívül minden R-beli elemet tartalmaz.

24.4. Definíció (Részcsoport):

Ha egy G csoport valamely H részhalmaza maga is csoport a G műveletére nézve, akkor azt mondjuk, hogy H részcsoport G-ben. Ezt így jelöljük: H\leq G.

Ha H részcsoport G-ben, de H\neq G, akkor azt mondjuk, hogy H valódi részcsoport G-ben. Ezt így jelöljük: H\lt G.

Megjegyzés:

A 19.6. Tételben igazoltuk, hogy a \sube szimbólummal jelölt tartalmazási reláció egy részbenrendezés bármilyen halmazrendszer elemei között, azaz reflexív, antiszimmetrikus és tranzitív. Továbbá azt is igazoltuk, hogy a \sub szigorú tartalmazási reláció ezek közül csak a tranzitivitást teljesíti.

Minthogy egy G csoport bármely H részcsoportja tulajdonképpen G-nek részhalmaza, továbbá örökli a G műveletét, ezért ezek a tulajdonságok természetesen a \leq szimbólummal jelölt „részcsoportjának lenni”-relációra is érvényesek.

24.5. Tétel:

Egy tetszőleges G csoport valamely H részhalmaza akkor és csak akkor részcsoport G-ben, ha teljesülnek az alábbi feltételek:

1. H zárt a G csoport műveletére.
2. H tartalmazza a G csoport egységelemét.
3. H zárt a G-beli inverzképzésre.

Bizonyítás:

Tegyük fel, hogy H részcsoport G-ben. Ekkor a műveleti zártság – azaz az 1. tulajdonság – nyilvánvalóan teljesül, máskülönben H nem lenne csoport a G műveletére nézve, és így részcsoport sem lehetne G-ben.

Mivel H-nak létezik egységeleme – hiszen maga is csoport –, ezért a 2. tulajdonsághoz azt kell megmutatni, hogy ez az egységelem megegyezik G egységelemével. Jelöljük H egységelemét e_H-val, G egységelemét pedig e_G-vel, és tegyük fel indirekt, hogy ez a kettő nem ugyanaz. Ha a kettő nem ugyanaz, akkor az sem mindegy, hogy melyik csoportban beszélünk inverzképzésről. Jelölje most {e_H}^{-1} az e_H elem G-beli inverzét. Őket összeszorozva tehát a G csoport egységelemét kell kapjuk, azaz:

Mivel e_H a H csoport egységeleme, ezért nyilvánvalóan igaz az alábbi:

Végül, mivel e_G a G csoport egységeleme, ezért az alábbi is teljesül:

Mivel H csoport, így a csoportművelet asszociativitása miatt:

A baloldalt kifejtve ezt kapjuk:

A jobboldalt kifejtve pedig ezt:

Ez a kettő eredmény viszont a fentebb már említett asszociativitás miatt indirekt feltételezésünkkel ellentétben mégis meg kell egyezzen, így valóban e_G=e_H.

Végül az inverzképzésre való zártság – azaz a 3. tulajdonság – igazolásához képezzük a H csoport valamely a elemének inverzét mindkét csoportban, és megmutatjuk, hogy ezek valójában megegyeznek. A H-beli inverzet jelöljük x_H-val, míg a G-beli inverzet x_G-vel. Az a elemet a G-beli inverzével összeszorozva a G csoport egységelemét kell kapnunk, azaz:

Ugyanakkor az a elemet a H-beli inverzével összeszorozva a H csoport egységelemét kell kapnunk, amiről azonban már láttuk, hogy megegyezik a G csoport egységelemével. Azaz:

Minthogy a G-beli inverzképzés a 14.10. Tétel alapján egyértelmű, ezért szükségképpen x_H=x_G. Azaz a H csoport valóban zárt a G-beli inverzképzésre.

Visszafelé: Most azt kell megmutatnunk, hogy amennyiben teljesül mind a 3 tulajdonság, úgy H részcsoport G-ben. A G csoport művelete az 1. tulajdonság alapján nem vezet ki H-ból, így az algebrai értelemben művelet ezen a szűkebb halmazon is (lásd a 11.3. Definíciót). Továbbá a 2. és 3. tulajdonság miatt létezik egységelem, és minden elemnek létezik inverze is H-ban. Így a 24.1. Definíció szerinti csoportaxiómákból már csak a művelet asszociativitását kell igazolnunk. Ezeket azonban H megörökli a G-től a művelettel együtt. Így tehát H valóban részcsoport G-ben.

24.6. Definíció (Csoport rendje):

Egy G csoport rendje alatt a benne lévő elemek számát értjük. Pontosabban fogalmazva ha G csak véges sok elemet tartalmaz, és elemeinek száma n, akkor azt mondjuk, hogy G véges, és rendje n. Ezt így jelöljük: |G|=n. Ezzel szemben ha G végtelen sok elemet tartalmaz, akkor végtelen rendű csoportról beszélünk. Ezt így jelöljük: |G|=\infty.

Mivel egy csoport részcsoportjai a 24.4. Definíció értelmében maguk is csoportok, ezért egy részcsoport rendje alatt szintén a fenti értelemben vett rendet értjük.

24.7. Tétel (Mellékosztályok):

Legyen G tetszőleges csoport, H pedig valamilyen részcsoport G-ben. Definiáljunk egy \sim szimbólummal jelölt relációt a G csoport elemei között a következőképpen: a\sim b akkor és csak akkor, ha a^{-1}b\in H.

Ekkor a \sim reláció egy ekvivalenciareláció a G csoport elemei között. Az ehhez tartozó ekvivalencia-osztályokat a G csoport H részcsoportja szerinti baloldali mellékosztályoknak nevezzük. Ha g egy tetszőleges elem a G csoportban, akkor a g elemet tartalmazó H szerinti baloldali mellékosztály épp a 18.19. Definícióban bevezetett komplexusszorzással képzett gH halmaz lesz.

Ehhez hasonlóan, ha az a\sim b relációt úgy definiáljuk, hogy akkor és csak akkor teljesüljön, ha ba^{-1}\in H, akkor ugyanígy egy ekvivalenciarelációt kapunk. Ebben az esetben az ekvivalencia-osztályokat a H részcsoport szerinti jobboldali mellékosztályoknak nevezzük, a g elemet tartalmazó jobboldali mellékosztály pedig a Hg halmaz lesz.

Bizonyítás:

A 13.4. Definíció alapján azt kell tehát bizonyítani, hogy a \sim szimbólummal jelölt reláció reflexív (12.8. Definíció), tranzitív (12.10. Definíció) és szimmetrikus (13.3. Definíció). Az alábbiakban legyenek a, b és c a G csoport tetszőleges elemei, az egységelemet pedig jelöljük e-vel. A bizonyítás során végig arra fogunk támaszkodni, hogy H részcsoport G-ben.

Mivel nyilván a^{-1}a=e teljesül, és a G csoport egységeleme a 24.5. Tétel 2. pontja alapján benne van a H részcsoportban, ezért fennáll az a\sim a reláció, így az reflexív.

Ha a^{-1}b és b^{-1}c benne vannak H-ban, akkor a 24.5. Tétel 1. pontja alapján az ő szorzatuk is benne van H-ban. Az ő szorzatuk viszont épp az a^{-1}c elem, hiszen:

Így tehát az a\sim b és b\sim c relációkból következik az a\sim c reláció, azaz teljesül a tranzitivitás is.

Végül ha a^{-1}b benne van H-ban, akkor a 24.5. Tétel 3. pontja alapján az ő inverze, is benne van H-ban. Az ő inverze viszont a 24.2. Tétel szerint épp b^{-1}a, hiszen:

Vagyis a\sim b-ből következik b\sim a, ami épp a szimmetriát jelenti.

A \sim reláció tehát valóban egy ekvivalenciareláció, amely a G csoport alaphalmazát ekvivalencia-osztályokra bontja. Ezek lesznek a H szerinti baloldali mellékosztályok. A g elemet tartalmazó mellékosztály pontosan azokból az x elemekből fog állni, amelyekre teljesül a g\sim x reláció. A tétel szövege alapján ez pontosan azt jelenti, hogy a g^{-1}x szorzat benne van H-ban. Ez viszont a 18.19. Definícióban bevezetett komplexusműveletek nyelvén pontosan azt jelenti, hogy x benne van a gH halmazban.

A tétel jobboldali mellékosztályokra vonatkozó állítása pontosan ugyanezzel a gondolatmenettel igazolható, csak ott a szorzásokat fordított sorrendben kell felírni.

Megjegyzés:

A figyelmes Olvasó észreveheti, hogy ez a bizonyítás szinte szó szerint megegyezik a 18.21. Tétel bizonyításával. A különbség pusztán annyi, hogy abban a tételben a G csoport szerepét az ott szereplő R gyűrű additív csoportja, míg a H részcsoport szerepét az ott szereplő I ideál, mint részgyűrű, végül a \sim relációt az I ideál szerinti kongruenciareláció tölti be. Az I szerinti maradékosztályok tehát tulajdonképpen az R gyűrű additív csoportjának I szerinti mellékosztályai.

Ebben az esetben azonban nincs értelme külön bal- illetve jobboldali mellékosztályokról beszélnünk, hiszen az R gyűrűn értelmezett + művelet kommutativitása miatt ezek nyilván megegyeznek. Egy általános csoport esetén azonban nem követeljük meg a csoportművelet kommutativitását, ezért ilyenkor a jobb- és baloldali mellékosztályok is általában különböző halmazok lesznek, azaz általában gH\neq Hg.

A 18.21. Tételben definiált maradékosztályokhoz – vagy speciálisan az egész számok maradékosztályaihoz – hasonlóan a mellékosztályok esetén is beszélhetünk reprezentánselemekről. Tegyük fel például, hogy egy H szerinti baloldali (vagy jobboldali) mellékosztályból a g elemet választottuk reprezentánselemnek. Ekkor egyrészt az iménti tétel alapján az adott mellékosztályt, mint halmazt gH (vagy jobboldali mellékosztály esetén Hg) alakban tudjuk leírni. Másrészt pedig tetszőleges a csoportelemről könnyen eldönthető, hogy g-vel azonos mellékosztályban van-e, azaz teljesül-e a tételben szereplő g\sim a reláció. Ehhez csak azt kell megvizsgálni, hogy a g^{-1}a (vagy jobboldali mellékosztály esetén az ag^{-1}) szorzat benne van-e a H részcsoportban.

24.8. Tétel (Lagrange tétele):

Legyen G tetszőleges véges csoport, H pedig tetszőleges részcsoport G-ben. Ekkor a H részcsoport rendje osztója G rendjének, azaz teljesül az alábbi oszthatóság:

Azaz létezik olyan egész szám, amellyel H rendjét megszorozva épp G rendjét kapjuk. Ez az egész szám a H részcsoport szerint bal- illetve jobboldali mellékosztályok számával egyezik meg, amelyet a H részcsoport G-beli indexének nevezzük, és |G:H|-val jelöljük. Azaz teljesül az alábbi összefüggés:

Bizonyítás:

A bizonyításban a 24.7. Tételben definiált baloldali mellékosztályokat fogjuk használni, de értelemszerűen ugyanígy használhatnánk a jobboldali mellékosztályokat is.

Az említett tételben definiált \sim reláció egy ekvivalenciareláció, melynek ekvivalencia-osztályai a H szerinti baloldali mellékosztályok. Ezek az ekvivalenciarelációkról szóló 13.5. Tétel alapján G egy partícióját alkotják. Azaz semelyik két baloldali mellékosztálynak nincs közös eleme, és uniójuk a teljes G. Ez az elrendezés látható az alábbi ábrán:

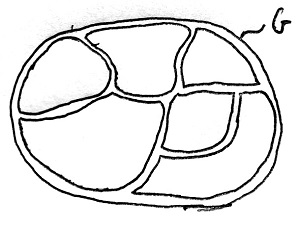
Tekintsük most a G csoportnak egy tetszőleges H szerinti baloldali mellékosztályát, és válasszunk ki belőle egy tetszőleges g elemet, amelyet reprezentánselemként fogunk használni a továbbiakban. A kérdéses mellékosztály tehát a gH halmaz lesz. Most egy kölcsönösen egyértelmű megfeleltetést fogunk létesíteni a gH mellékosztály és a H részcsoport elemei között.

A 24.7. Tétel illetve a hozzá tartozó megjegyzés alapján a gH mellékosztály tetszőleges x eleme esetén a g^{-1}x szorzat a H részcsoportnak egy eleme. Definiáljunk tehát egy f:gH\to H függvényt a következőképpen:

Azt kell megmutatni, hogy f kölcsönösen egyértelmű megfeleltetés gH és H között. Ez az alábbi két dolgot jelenti:

1. Tetszőleges x\in gH és y\in gH esetén f(x)=f(y) akkor és csak akkor, ha x=y. Azaz az f függvény H minden elemét legfeljebb egy gH-beli elemhez rendeli hozzá.
2. Tetszőleges h\in H-hoz létezik olyan x\in gH, amelyre f(x)=h teljesül. Azaz az f függvény H minden elemét legalább egy gH-beli elemhez rendeli hozzá.

Nézzük az 1. állítást! Ha x=y, akkor nyilván teljesül az f(x)=f(y) egyenlőség, hiszen:

Visszafelé: ha f(x)=f(y), akkor az azt jelenti, hogy teljesül az alábbi egyenlőség:

Szorozzuk meg mindkét oldalt balról g-vel (itt e-vel jelöltük a G csoport egységelemét):

Ez viszont épp a kívánt x=y egyenlőség.

Most nézzük a 2. állítást! Keresnünk kell tehát egy olyan x elemet a gH mellékosztályban, amelyhez az f függvény épp a H részcsoport h elemét rendeli hozzá. Keressük tehát az alábbi egyenlet megoldását:

Szorozzuk meg mindkét oldalt balról g-vel (itt e-vel jelöltük a G csoport egységelemét):

A baloldalról az egységelem elhagyható, így végülis a keresett x előállításának képletét kapjuk: x=gh.

Összefoglalva tehát a fenti f függvény mintájára kölcsönösen egyértelmű megfeleltetés létesíthető a H részcsoport, és bármely H szerinti baloldali mellékosztály között. Néhány mellékosztály esetére ez látható az alábbi ábrán:

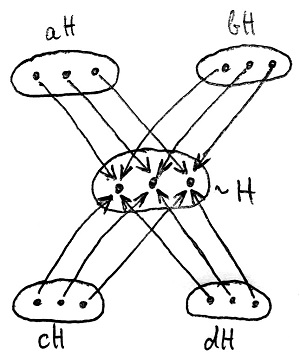
Ez azt jelenti, hogy bármely H szerinti baloldali mellékosztálynak pontosan ugyanannyi eleme van, mint magának H-nak. Ha tehát H rendjét megszorozzuk a baloldali mellékosztályok számával, akkor épp G rendjét kapjuk eredményül, hiszen a baloldali mellékosztályok G egy partícióját alkotják. Más szavakkal találtunk egy olyan egész számot – a H szerinti baloldali mellékosztályok számát –, amellyel megszorozva H rendjét épp G rendjét kapjuk. Az oszthatóság 16.1. Definíciója alapján ez épp azt jelenti, hogy |H| osztója |G|-nek.

Megjegyzés:

A 24.7. Tétel utáni megjegyzésben megemlítettük, hogy egy G csoportnak egy H részcsoportja szerinti bal- illetve jobboldali mellékosztályai általában nem azonos halmazok. Azaz ha g a G csoport egy eleme, akkor általában gH\neq Hg. Azonban a Lagrange-tételből azonnal következik, hogy véges G csoport esetén a számuk viszont megegyezik és ez a szám épp |G:H|-val egyezik meg.

Ennél azonban több is igaz. Viszonylag könnyen belátható, hogy a bal- és jobboldali mellékosztályok száma akkor is megegyezik, ha G rendje esetleg végtelen. Sőt, a bal- és jobboldali mellékosztályok között kölcsönösen egyértelmű megfeleltetés létesíthető akkor is, ha történetesen ezek száma is végtelen – és így ebben a végtelen számosságú esetben is „ugyanannyi van belőlük”. Ezek igazolását – illetve az index fogalmának ilyen jellegű általánosítását – azonban most mellőzzük.

24.9. Definíció (Egész kitevős hatvány):

Legyen H tetszőleges halmaz, amelyen értelmezve van egy *-gal jelölt asszociatív művelet. Ha x a H halmaz valamely eleme, n pedig tetszőleges pozitív egész, akkor az x^n hatványon az alábbi kifejezést értjük:

Tegyük fel, hogy a * műveletre nézve létezik neutrális elem (14.7. Definíció), amelyet jelöljünk e-vel. Ekkor az x^0 hatványon az alábbit értjük:

Végül tegyük fel, hogy az x elem invertálható (14.9. Definíció), és jelöljük az ő (kétoldali) inverzét x^{-1}-gyel. Ekkor az x^{-n} hatványon az alábbit értjük:

Azaz x-nek a -n-edik hatványa alatt x inverzének az n-edik hatványát értjük.

Megjegyzés:

E definíció tehát kiterjeszti a 18.8. Tételben bevezetett jelölésmódot a csak pozitív kitevőkről tetszőleges egész kitevőre, beleértve a 0 és a negatív kitevőket is. Egy x elem 0 kitevős hatványának természetesen csak abban az esetben van értelme, ha a műveletre nézve létezik neutrális elem. Ehhez hasonlóan a negatív kitevős hatványoknak pedig csak akkor van értelme, ha x-nek a műveletre nézve létezik inverze. Ezen túlmenően a definíció a 18.8. Tételben szereplő értelmezéssel ellentétben tetszőleges algebrai struktúra tetszőleges asszociatív műveletére – tehát nem kizárólag egy gyűrű „szorzás” műveletére – vonatkoztatható.

A hatványkifejezések segítségével tehát tömören tudjuk kifejezni azt, hogy egy műveletet sokszor kell elvégezni. Gyakori a szakirodalomban, hogy amennyiben a műveletet a + szimbólum jelöli – ez tipikusan kommutatív műveletek esetén szokott így lenni –, akkor x^n helyett az nx írásmódot alkalmazzuk, és hatvány helyett többszörösről beszélünk. Ez azonban nem tévesztendő össze az oszthatóság kapcsán a 16.1. Definíció megismert „többszörös” fogalmával. Ott ugyanis egy R gyűrű esetén az ak kifejezés alatt az a gyűrűelem k gyűrűelemmel vett többszörösét értettük, ami tehát egy darab „szorzás” az R gyűrűben. Ezzel szemben a most megismert na jelölés azt jelenti, hogy az a elemet n-szer kell „összeadni” saját magával az R gyűrűben. Azaz:

24.10. Tétel (Egész kitevős hatványozás azonosságai):

Legyen H tetszőleges halmaz, amelyen értelmezve van egy \cdot szimbólummal vagy egymás után írással jelölt asszociatív művelet. Tegyük fel továbbá, hogy e műveletre nézve létezik neutrális elem, és legyenek a és b a H két invertálható eleme. Ekkor tetszőleges – tehát nem feltétlenül csak pozitív – n és k egész számok esetén teljesülnek az alábbi tulajdonságok:

1. Ha a és b felcserélhetők, azaz ab=ba, akkor (a\cdot b)^n=a^n\cdot b^n
2. (a^n)^k = a^{n\cdot k}
3. a^n\cdot a^k=a^{n+k}
4. a^{-n}=(a^n)^{-1}, azaz az a^{-n} hatvány az a^n hatvány inverze.

Bizonyítás:

Tegyük fel először, hogy n és k mindketten pozitívak.

Ekkor az 1., 2., és 3. tulajdonságok igazolása szinte szóról szóra megegyezik a 18.8. Tétel bizonyításának gondolatmenetével. Mindössze két különbség van. Egyrészt most a tétel szövegéből tudjuk, hogy a \cdot művelet asszociatív, emiatt nem kell hivatkoznunk a 14.12. Definíció szerinti 4. gyűrűaxiómára – amit amúgy nem is tudnánk megtenni, hiszen most nem gyűrűről van szó. Másrészt pedig az 1. tulajdonság esetén ugyancsak a tétel szövegéből tudjuk, hogy ab=ba, így nem kell hivatkoznunk a művelet kommutativitására sem.

A 4. tulajdonsághoz az inverz elem 14.9. Definíciója alapján az alábbi két dolgot kell igazolni (itt e-vel jelöltük a \cdot művelet neutrális elemét):

Egyrészt a 24.9. Definíció alapján a^{-n}=(a^{-1})^n, továbbá a és a^{-1} felcserélhetők, hiszen a 14.9. Definíció szerint a\cdot a^{-1}=a^{-1}\cdot a=e. Másrészt, mivel az 1. tulajdonságot már bizonyítottuk pozitív n esetén, ezért ezt most felhasználhatjuk. Ez alapján egyrészt:

Másrészt:

Így tehát pozitív n esetén a^n és a^{-n} valóban egymás inverzei.

Most tegyük fel, hogy a két kitevő közül legalább az egyik 0. Ekkor a 24.9. Definícióból azonnal adódik mind a 4 tulajdonság. Ha például n=0:

1. (a\cdot b)^0=e^0=e=e\cdot e=a^0\cdot b^0, méghozzá függetlenül attól, hogy a és b felcserélhető-e vagy nem.
2. (a^0)^k=e^k=e=a^0=a^{0\cdot k}. Itt az e^k=e lépésnél kihasználtuk, hogy a neutrális elem önmaga inverze, így ez valóban teljesül függetlenül attól, hogy k pozitív, negatív vagy esetleg 0.
3. a^0\cdot a^k=e\cdot a^k=a^k=a^{0+k}
4. Egyrészt mivel a 0 ellentettje önmaga, azaz 0=-0, ezért a^{-0}=a^0=e. Másrészt mivel a neutrális elem önmaga inverze, ezért (a^0)^{-1}=e^{-1}=e. Vagyis valóban a^{-0}=(a^0)^{-1}.

Ha pedig k=0, akkor a 2. és 3. tulajdonságok nyilván teljesülnek, hiszen egyrészt (a^n)^0=e=a^0=a^{n\cdot 0}, másrészt a^n\cdot a^0=a^n\cdot e=a^n=a^{n+0}. Az 1. és 4. tulajdonságokkal ebben az esetben nem kell foglalkoznunk, mivel azokban nem szerepel a k kitevő.

Már csak azok az esetek maradtak, amikor a két kitevő közül legalább az egyik negatív. Legyen például n negatív. Az átláthatóság érdekében vezessük be az m=-n jelölést. Ekkor m pozitív, és ezt a továbbiakban kihasználjuk.

Most igazoljuk az 1. tulajdonságot negatív n-re. A bevezetett jelölésünket alkalmazhatjuk: (ab)^n=(ab)^{-m}. Mivel ugye m pozitív, ezért felhasználhatjuk a 4. tulajdonságot, hiszen azt pozitív kitevőkre már igazoltuk. Ez alapján tehát:

A külső zárójelen belüli kifejezésre ugyancsak m pozitivitása miatt alkalmazható az 1. tulajdonság, hiszen azt szintén igazoltuk pozitív kitevőkre:

Mivel a tétel szövege alapján most azt feltételezzük, hogy a és b felcserélhetők, ezért ebből következik, hogy a zárójelen belüli a^m és b^m szintén felcserélhetők. Ezek szorzata ugyanis az alábbi 2m tényezős szorzat:

Itt egymás mellett álló a és b tényezők cserélgetésével nyilván elérhető, hogy minden b tényező a baloldalra kerüljön. Mivel tehát a^m és b^m felcserélhetők, ezért a 24.2. Tétel alapján az (a^mb^m)^{-1} kifejezés tovább alakítható:

Most viszont ismét lehet alkalmazni a 4. tulajdonságot, hiszen m pozitív:

Összefoglalva azt kaptuk tehát, hogy (ab)^{-m}=a^{-m}b^{-m}. Visszafelé alkalmazva az m=-n jelölést, ez végülis az 1. tulajdonságnak felel meg.

Most a 4. tulajdonságot igazoljuk negatív n esetén. Maradjunk továbbra is az m=-n jelölésnél. Mivel m pozitív, és a 4. tulajdonságot pozitív kitevőkre már igazoltuk, ezért igaz az alábbi:

Visszafelé alkalmazva az m=-n jelölést ez tehát azt jelenti, hogy, hogy a^n és a^{-n} negatív n esetén is egymás inverzei. Tehát a 4. tulajdonság szerinti a^{-n}=(a^n)^{-1} összefüggés valóban teljesül negatív n esetén is.

Most igazoljuk a 2. tulajdonságot negatív n-re és pozitív k-ra. Maradjunk továbbra is az m=-n jelölésnél, azaz (a^n)^k=(a^{-m})^k. Ekkor mivel m pozitív, ezért a 24.9. Definíció alapján:

Ha most k pozitív, akkor alkalmazhatjuk a pozitív kitevőkre már bizonyított 2. tulajdonságot. Eszerint tehát:

Mivel pedig m is és k is pozitív, ezért mk is az, vagyis ismét a 24.9. Definíció alapján:

Visszafelé alkalmazva az m=-n jelölést, ez végülis a 2. tulajdonságnak felel meg.

Most igazoljuk a 2. tulajdonságot negatív n-re és szintén negatív k-ra. Maradjunk továbbra is az m=-n jelölésnél, de emellé vezessük be az l=-k jelölést is, azaz (a^n)^k=(a^{-m})^{-l}. Ekkor mivel m pozitív, ezért a 24.9. Definíció alapján:

Alkalmazhatjuk a már igazolt 4. tulajdonságot:

Mivel m is és l is pozitív, ezért alkalmazhatjuk a pozitív kitevőkre már igazolt 2. tulajdonságot:

Itt ugye ml pozitív, ezért ismét a 24.9. Definíció alapján:

Végül ismét a már igazolt 4. tulajdonság miatt:

Visszafelé alkalmazva az m=-n és az l=-k jelöléseket, ez végülis a 2. tulajdonságnak felel meg.

Végül igazolni kell a 2. tulajdonságot pozitív n-re és negatív k-ra. Ismét vezessük be az l=-k jelölést, azaz (a^n)^k=(a^n)^{-l}. Ekkor a már igazolt 4. tulajdonság miatt:

Mivel n és l pozitívak, és a 2. tulajdonságot már igazoltuk pozitív kitevőkre, ezért az ebben az esetben alkalmazható:

Ez viszont újból a 4. tulajdonság miatt az alábbival egyezik meg:

Visszafelé alkalmazva az l=-k jelölést, ez végülis a 2. tulajdonságnak felel meg.

Már csak a 3. tulajdonságot kell bizonyítani azokban az esetekben, amikor n és k közül legalább az egyik negatív. Mivel itt n és k szerepe teljesen szimmetrikus, ezért csak azt az esetet fogjuk igazolni, amikor n negatív, k pedig bármi más. Fordított esetben – tehát amikor k negatív, n pedig bármi más – ugyanezt a gondolatmenetet kellene végigjátszani k és n szerepének felcserélésével. A k=0 esettől most nyugodtan eltekinthetünk, hiszen azt már igazoltuk.

Vezessük be a jól megszokott m=-n jelölést, azaz a^na^k=a^{-m}a^k. Ekkor ugye m pozitív lesz, tehát a 24.9. Definíció szerint az alábbi szorzatot kaptuk:

Ha k negatív, akkor vezessük be ismét az l=-k jelölést is. Ekkor a fenti szorzatban további l darab, tehát összesen m+l darab a^{-1} tényező fog szerepelni. Mivel m+l pozitív, ezért:

Visszafelé alkalmazva az m=-n és az l=-k jelöléseket, a kitevőben végülis valóban n+k szerepel, ahogyan a 3. tulajdonság állítja.

Ha k pozitív, akkor a fenti szorzatban m darab a^{-1} tényező és k darab a tényező szerepel, azaz:

Az egymás mellett álló a és a^{-1} tényezők ugye szép sorban kiütik egymást, mivel egymás inverzei. Kérdés tehát, hogy melyikből van több. Ha m\leq k, akkor legalább annyi a tényező van, mint a^{-1} tényező, így ebben az esetben az a tényezőkből fog megmaradni k-m darab. Azaz ebben az esetben:

Visszafelé alkalmazva az m=-n jelölést, a kitevőben végülis valóban n+k szerepel, ahogyan a 3. tulajdonság állítja.

Ha viszont m\gt k, akkor több a^{-1} tényező van, mint a, ezért ebben az esetben az a^{-1} tényezőkből fog megmaradni m-k darab. Azaz:

Az m-k kitevő m\gt k miatt biztosan pozitív, ezért a 24.9. Definíció alapján ezt kapjuk:

Visszafelé alkalmazva az m=-n jelölést, a kitevőben ebben az esetben is n+k szerepel, ahogyan a 3. tulajdonság állítja.

24.11. Definíció (Csoportelem rendje):

Legyen G tetszőleges csoport, g pedig ennek valamely eleme. Ekkor g egymástól különböző hatványainak a számát g rendjének nevezzük, és az angol „order” kifejezésre utalva o(g)-vel jelöljük. Ha g-nek végtelen sok különböző hatványa létezik a G csoportban, akkor azt mondjuk, hogy g rendje végtelen. Jelekkel: o(g)=\infty.

24.12. Tétel:

Legyen G tetszőleges csoport, g ennek valamely eleme, e pedig az egységelem. Ha g rendje véges, akkor tetszőleges n és k egész számok esetén igazak az alábbiak:

1. g^k=g^n akkor és csak akkor teljesül, ha fennáll az o(g)|k-n oszthatóság, ami a 20.1. Tétel 3. pontja alapján a k\equiv n\pmod{o(g)} kongruenciát jelenti.
2. g^k=e akkor és csak akkor teljesül, ha fennáll az o(g)|k oszthatóság, ami a 20.1. Tétel 3. pontja alapján a k\equiv 0\pmod{o(g)} kongruenciát jelenti.
3. A g elem hatványai o(g) szerint periodikusan ismétlődnek.
4. A g elem o(g) rendje a legkisebb pozitív kitevő, amelyre g-t emelve az egységelemet kapjuk.
5. o(g)=1 akkor és csak akkor, ha g=e.

Ha g rendje végtelen, akkor g bármely két hatványa különbözik.

Bizonyítás:

Jelöljük I-vel azt a halmazt, amely olyan i egész számokból áll, amelyekre teljesül az alábbi:

Azaz I azon kitevők halmaza, amelyekre a g elemet emelve a G csoport egységelemét kapjuk.

Az I halmaz zárt az egész számok összeadására nézve, hiszen ha i\in I és j\in I, akkor I definíciója miatt ugye g^i=e és g^j=e. Ám ekkor a 24.10. Tétel 3. pontja alapján g^{i+j}=g^i\cdot g^j=e\cdot e=e, és így szintén I definíciója miatt i+j\in I.

Továbbá az I halmaz zárt tetszőleges egész számmal való szorzásra is, hiszen ha i\in I és s tetszőleges – tehát nem feltétlenül I-beli egész szám –, akkor egyrészt I definíciója miatt g^i=e. Másrészt viszont a 24.10. Tétel 2. pontja alapján g^{i\cdot s}=(g^i)^s=e^s=e, és így szintén I definíciója miatt i\cdot s\in I.

Végül egyrészt I tartalmazza a 0 egész számot, hiszen a 24.9. Definíció szerint g^0=e. Másrészt az I halmaz zárt az egész számok ellentettképzésére is, hiszen ha i\in I, akkor I definíciója miatt g^i=e, ám ekkor a 24.10. Tétel 4. pontja miatt g^{-i}=(g^i)^{-1}=e^{-1}=e, és így szintén I definíciója miatt -i\in I.

Az I halmaz tehát a 18.15. Tétel és a 18.18. Definíció alapján egy ideál az egész számok \Z gyűrűjében.

Ezek után tegyük fel, hogy g^k=g^n. Szorozzuk meg az egyenlet mindkét oldalát g^n inverzével, azaz a 24.10. Tétel 4. pontja alapján g^{-n}-nel. Ekkor az alábbit kapjuk:

Ez viszont a 24.10. Tétel 3. pontja miatt az alábbival ekvivalens:

Vagyis g^k=g^n pontosan akkor teljesül, ha k-n\in I. Ez viszont a 18.20. Definíció értelmében épp azt jelenti, hogy teljesül az alábbi, I ideál szerinti kongruencia:

Mivel a 17.19. Tétel alapján \Z euklidészi gyűrű, ezért a 19.16. Tétel miatt I szükségképpen csak főideál lehet, azaz egyetlen elemmel generálható. Jelöljük ezt a generátorelemet d-vel. Az I ideál tehát a 20.9. Tétel értelmében d többszöröseiből áll, amelyről az általánosság megsértése nélkül feltehető, hogy nemnegatív. Ha ugyanis d negatív lenne, akkor az ő ellentettje lenne pozitív, és így a 16.8. Tétel 1. pontja értelmében d-nek asszociáltja lenne. Azaz pontosan ugyanazok lennének a többszörösei, mint d-nek, és így őt választhatnánk I generátorelemének.

Feltételezve tehát, hogy d nemnegatív, a fenti ideál szerinti kongruencia a 20.1. Tétel alapján az alábbi kongruenciával ekvivalens:

A g csoportelem bármely két hatványa tehát pontosan akkor egyezik meg, ha a két hatványkitevő ugyanabba a modulo d maradékosztályba esik. Másként fogalmazva g rendje épp a modulo d maradékosztályok száma lesz. Két eset lehetséges: d=0 vagy d\gt 0.

Első esetben a 20.4. Tétel alapján bármely két kitevő különböző maradékosztályba tartozik, tehát g bármely két különböző kitevős hatványa különböző lesz, és így g rendje valóban végtelen.

Második esetben szintén a 20.4. Tétel miatt a modulo d maradékosztályok száma, és így g rendje d, azaz:

Ezt behelyettesítve a fenti kongruenciába tehát megkaptuk a tétel 1. állítását. A 2. állítás ennek speciális esete, amikoris n=0. A 3. állítás könnyen adódik a 20.4. Tételből. Ez alapján ugyanis ha rögzítünk egy tetszőleges a kitevőt, akkor pontosan az i\cdot o(g) + a alakban felírható kitevők lesznek a-val azonos maradékosztályban – ahol i tetszőleges egész szám –, azaz g hatványai valóban o(g) periódussal ismétlődnek.

A 4. állítás a 17.2. Lemma következménye. Az egységelemet adó kitevők ugyanis épp az I ideál elemei, amelyek – mint láttuk – mindannyian o(g) többszörösei, és így biztosan nem kisebbek o(g)-nél.

Végül az 5. állítás: Ha o(g)=1, akkor a 20.1. Tétel 4. pontja alapján a k\equiv n\pmod{o(g)} kongruencia mindig teljesül, és így bármely kitevő esetén az egységelemet kapjuk – beleértve természetesen az 1-es kitevőt is. Visszafelé: Ha g=e, akkor g-nek már az első hatványa is az egységelem. Mivel az 1 kitevőnél nincs kisebb pozitív egész kitevő, ezért a már bizonyított 4. állítás alapján o(g)=1.

24.13. Következmény:

Legyen G tetszőleges véges csoport, H pedig ennek egy tetszőleges nemüres részhalmaza. A H halmaz akkor és csak akkor részcsoport G-ben, ha zárt a G csoport műveletére nézve.

Bizonyítás:

Ha H részcsoport, akkor teljesíti a 24.5. Tétel feltételeit, így a műveleti zártságot is.

Visszafelé: Tegyük fel, hogy H olyan részhalmaz, amely zárt a csoportműveletre nézve, legyen g tetszőleges H-beli elem, továbbá jelöljük G egységelemét e-vel. Mivel G véges, ezért g-nek nem lehet végtelen sok különböző hatványa, és így az o(g) rend is véges. Azt tudjuk, hogy H zárt a csoportműveletre nézve, azaz tartalmazza g minden hatványát, így a g^{o(g)} hatványt is. A 24.12. Tétel 4. pontja alapján azonban g^{o(g)}=e, így tehát H valóban tartalmazza az egységelemet.

Végül szintén a műveleti zártság miatt H tartalmazza a g^{o(g)-1} hatványt is. Ez viszont épp g inverze, hiszen a 24.10. Tétel 3. pontja alapján őket összeszorozva épp az egységelemet kapjuk:

A H halmaz tehát zárt az inverzképzésre is. Teljesülnek tehát a 24.5. Tétel feltételei, következésképp H valóban részcsoport.

Megjegyzés:

A tétel bizonyításában G végességére pusztán azért volt szükség, mert ebből következett, hogy minden elem rendje szintén véges – ami ugye a bizonyítás kulcsa volt. Azonban visszafelé ez nem feltétlenül van így. Azaz abból, hogy minden elem rendje véges még nem következik, hogy maga a csoport is véges. Torziócsoportoknak nevezzük az olyan csoportokat, amelyeknél csak az elemrendek végességét követeljük meg, de magának a csoport rendjének a végességét nem feltétlenül. Nyilván minden véges csoport torziócsoport, ám léteznek végtelen torziócsoportok is. Ilyenre azonban az eddig definiált fogalmak alapján sajnos nem tudunk példát mutatni. Mindenesetre a tétel szövegében elegendő lett volna annyit kikötni, hogy G legyen torziócsoport.

24.14. Következmény:

Ha G véges csoport, akkor G bármely elemének rendje osztója G rendjének.

Bizonyítás:

Legyen g a G csoport tetszőleges eleme, és jelöljük H-val azt a halmazt, amely pontosan g hatványaiból áll. Ekkor H nyilván nemüres, hiszen tartalmazza legalább g-t. Továbbá zárt a G csoport műveletére nézve, ugyanis g bármely két hatványát összeszorozva ugyancsak g-nek egy hatványát kapjuk, hiszen a 24.10. Tétel 3. pontja miatt:

Mivel G véges, ezért a 24.13. Következmény értelmében H részcsoport G-ben. A Lagrange-tétel (24.8. Tétel) miatt tehát teljesül az alábbi oszthatóság:

Mivel azonban H a g elem összes létező hatványaiból áll, ezért |H|=o(g). Ezt behelyettesítve a fenti oszthatóságba megkapjuk a tétel állítását.

24.15. Definíció (Egész szám p-adikus rendje):

Legyen a\neq 0 egy tetszőleges nemnulla egész szám, p\gt 0 pedig valamilyen pozitív prímszám. Azt mondjuk, hogy az a egész szám p-adikus rendje k (ennek jele: v_p(a)=k), amennyiben igazak az alábbiak:

A 0 egész szám p-adikus rendjét végtelennek definiáljuk, azaz v_p(0)=\infty.

24.16. Lemma:

Legyenek adottak x és y tetszőleges egész számok, valamint egy p pozitív prímszám, amelyekre teljesülnek az alábbiak:

Ekkor érvényes az alábbi összefüggés:

Bizonyítás:

Mivel x\neq y, ezért x-y\neq 0, és így v_p(x-y) a 24.15. Definíció alapján egy véges nemnegatív szám, amiről a tétel szövege alapján tudjuk, hogy nemnulla, tehát v_p(x-y)\geq 1. Jelöljük ezt a számot k-val, azaz vezessük be az alábbi jelölést:

Ez a p-adikus rend 24.15. Definíciója szerint azt jelenti, hogy az x-y különbség prímtényezős felbontásában a p prímtényező a k-adik hatványon szerepel. Létezik tehát olyan m egész szám, amely tovább már nem osztható p-vel, és teljesül rá az alábbi:

Az x tehát kifejezhető a következőképpen:

Most vizsgáljuk meg, hogyan néz ki x=p^km+y-nak a p-edik hatványa:

Ez ugye egy p darab tényezőből álló kifejezés, amelyben minden tényező egy-egy kéttagú összeg, nevezetesen ez: (p^km+y). Az áttekinthetőség kedvéért a zárójelekben szereplő első tagra átmenetileg vezessük be a z=p^km jelölést. Ekkor tulajdonképpen az alábbi szorzást kéne tehát elvégezni:

Vizsgáljuk meg, hogy milyen alakot ölt az eredmény, ha felbontjuk ezt a p darab zárójelet. A 14.12. Definícióban szereplő disztributivitási szabályok alapján ezt úgy kell elvégezni, hogy minden zárójelből az összes lehetséges kombinációban kiválasztunk pontosan egy tagot, ezeket összeszorozzuk egymással, és az így kapott szorzatokat összeadjuk.

Megtehetjük például, hogy mind a p darab zárójelből a z tagot választjuk, és 0 darab zárójelből választjuk az y tagot. Ez a választás a z^py^0=z^p szorzatot fogja eredményezni, és nyilván csak egyféleképpen tudjuk megtenni. A végeredmény tehát így fog kezdődni:

Egy másik választás lehet, amikor 1 darab zárójelből választjuk ki az y tagot, és a maradék p-1 darab zárójelből továbbra is a z tagot választjuk. Ezek a választások mind a z^{p-1}y^1 szorzatot fogják eredményezni. Ilyen szorzatból viszont már p darab van, hiszen azt az egyetlen y tagot választhatjuk az 1., a 2., a 3., ..., és végül a p-edik zárójelből. A végeredmény tehát így folytatódik:

A következő kombinációk azok lesznek, amelyek esetén 2 darab zárójel esetén választjuk ki az y tagot. Ekkor a fennmaradó p-2 zárójelből a z tagot kell választanunk, tehát ezek a kombinációk mind a z^{p-2}y^2 szorzatot fogják eredményezni. Ezért a z^{p-2}y^2 szorzatból épp annyi fog szerepelni a végeredményben, ahányféleképpen p darab zárójelből ki tudjuk választani azt a 2 darabot, amelyek az y tényezőt adják az adott szorzathoz. Anélkül, hogy bonyolultabb kombinatorikai fejtegetésbe bonyolódnánk, jelöljük ezt a számot A_2-vel. A végeredmény tehát így folytatódik:

Általánosságban ha 0-tól kezdve sorszámozzuk a végeredmény tagjait, akkor az i-edik tag azokat a kombinációkat fogja tartalmazni, amelyek esetén i darab zárójel esetén választjuk ki az y tagot. Ekkor a fennmaradó p-i zárójelből kell a z tagot választanunk, tehát ezek a kombinációk mind a z^{p-i}y^i szorzatot fogják eredményezni. Ilyenből épp annyi fog szerepelni a végeredményben, ahányféleképpen p darab zárójelből ki tudjuk választani azt az i darabot, amelyek az y tényezőt adják az adott szorzathoz. Mivel ismét nem szeretnénk kombinatorikával szórakozni, ezért jelöljük ezt a számot nagyvonalúan A_i-vel. Ezért a végeredmény i-edik tagja így néz ki:

Mindent összevetve tehát (z+y)^p teljes kifejtése így néz ki:

Ahogyan megállapítottuk már, itt A_0=1 és A_1=p. Továbbá, mivel egyrészt p-féleképp lehet p darab zárójelből kiválasztani azt az egyet, amelyből NEM az y, hanem a z tagot választottuk ki, ezért természetesen A_{p-1}=p. Másrészt pedig egyféleképpen lehet az összes zárójelből az y tagot választani, ezért A_p=1. A többi A_i együttható pontos értékét az úgynevezett binomiális tétel alapján lehet kiszámítani, ám a bizonyítás szempontjából ez most nem érdekes számunkra.

Ha most visszafelé alkalmazzuk a z=p^km jelölést, akkor az x^p=(\underbrace{p^km}_{=z}+y)^p hatványra lényegében ezt a kifejezést kaptuk:

Alkalmazva a hatványozás azonosságairól szóló 18.8. Tétel mindhárom pontját:

Minket ugye az x_p-y_p különbség p-adikus rendje érdekel. Ezt a különbséget megkapjuk, ha a fenti összegzésből elhagyjuk az utolsó, y^p tagot:

Azt kell meghatározni tehát, hogy a fenti kifejezés p-nek legfeljebb hányadik hatványával osztható. Mivel a bizonyítás elején megállapítottuk, hogy k\geq 1, ezért p^{k+1}-gyel minden fenti tag osztható, teljesül tehát az alábbi oszthatóság:

Most nézzünk ennél 1-gyel magasabb hatványt, azaz p^{k+2}-t. Az utolsó előtti tagig bezárólag szintén minden fenti tag osztható p^{k+2}-vel. Kérdés, hogy mi a helyzet az utolsó, p^{k+1}my^{p-1} taggal.

Az m egész szám biztosan nem tartalmazza a p prímtényezőt, hiszen a bizonyítás elején őt épp így állítottuk elő. Továbbá a tétel szövege szerint v_p(xy)=0, ami a 24.15. Definíció alapján épp azt jelenti, hogy az xy szorzat sem tartalmazza a p prímtényezőt, így tehát maga y sem. A p^{k+1}my^{p-1} szorzat prímtényezős felbontásában p így csak a k+1-edik hatványon szerepel, azaz nem osztható p^{k+2}-vel. Így viszont a teljes összeg sem osztható p^{k+2}-vel, azaz:

Ezt összevetve a fentebb megállapított p^{k+1}|x^p-y^p oszthatósággal, a 24.15. Definíció szerint lényegében megkaptuk a tétel állítását:

24.17. Következmény:

Legyen p egy pozitív prímszám, a pedig egy tetszőleges egész szám, amely p-vel osztva 1-et ad maradékul, azaz amelyre teljesül az alábbi kongruencia:

Ekkor tetszőleges c\geq 1 egész kitevő esetén teljesül az alábbi kongruencia is:

Bizonyítás:

Egyrészt az általánosság megsértése nélkül feltehetjük, hogy a\neq 1, ebben az esetben ugyanis a tétel nyilvánvalóan igaz. Továbbá azt is feltehetjük, hogy a\neq -1, mivel ebben az esetben a -1\equiv 1\pmod p feltétel alapján p csak 2 lehet, és ekkor a tétel ismét nyilvánvalóan igaz.

Másrészt az a egész szám biztosan nem osztható p-vel, hiszen a tétel szövegében szereplő a\equiv 1\pmod p kongruencia alapján 1-et ad maradékul p-vel osztva. Az 1 szintén nem osztható p-vel. Emiatt a 24.15. Definíció szerint a szorzatuk p-adikus rendje biztosan 0.

Harmadrészt az a\equiv 1\pmod p a 20.1. Tétel 3. pontja alapján azt is jelenti, hogy teljesül az alábbi oszthatóság:

Így ismételten a 24.15. Definíció szerint az a-1 különbség p-adikus rendje biztosan nem 0.

Összefoglalva tehát az a és az 1 egész számokra teljesül a 24.16. Lemma mindhárom feltétele, azaz:

Ekkor viszont ugye teljesül az alábbi összefüggés:

Ez tehát azt jelenti, hogy az a^p-1 különbség prímtényezős felbontásában 1-gyel többször szerepel p, mint az a-1 felbontásában. Következésképp, mivel ugye teljesül a p|a-1 oszthatóság, ezért szükségképpen teljesülnie kell a p^2|a^p-1 oszthatóságnak is, ami a 20.1. Tétel 3. pontja alapján az alábbi kongruenciát jelenti:

Most ugyanezt a gondolatmenetet eljátszhatjuk az a^p és az 1 egész számokra is. Egyrészt mivel a\neq 1 és a\neq -1, ezért nyilván a^p\neq 1 is teljesül. Másrészt mivel a-ról tudjuk, hogy nem osztható p-vel, ezért nyilván a^p sem osztható p-vel, azaz v_p(a^p\cdot 1)=0. Harmadrészt mivel teljesül a p^2|a^p-1 oszthatóság, ezért nyilván v_p(a^p-1)\neq 0. Ám ekkor ismét a 24.16. Lemma alapján:

Vagyis az (a^p)^p-1=a^{p^2}-1 különbség prímtényezős felbontásában 1-gyel többször szerepel p, mint az a^p-1 felbontásában. Következésképp, mivel ugye teljesül a p^2|a^p-1 oszthatóság, ezért szükségképpen teljesülnie kell a p^3|a^{p^2}-1 oszthatóságnak is, ami a 20.1. Tétel 3. pontja alapján az alábbi kongruenciát jelenti:

A fenti gondolatmenetet akárhányszor megismételhetjük, melynek során a c-1-edik lépésben épp a tétel állítását kapjuk:

24.18. Tétel:

Legyen n egy tetszőleges, 1-nél nagyobb páratlan szám, amely valamilyen prímhatvány. Azaz n=p^c, ahol p valamilyen pozitív, páratlan prímszám, c pedig tetszőleges pozitív kitevő. Jelöljük G_n-nel azon modulo n maradékosztályok halmazát, amelyek NEM Miller-Rabin-tanúi n-nek. Ekkor igazak az alábbiak:

1. Egy valamilyen a egész szám által reprezentált [a]_n maradékosztály esetén [a]_n\in G_n akkor és csak akkor teljesül, ha fennáll az a^{p-1}\equiv 1\pmod n kongruencia.
2. A G_n halmaz a \Z/n\Z maradékosztálygyűrű multiplikatív csoportjának egy részcsoportja, azaz G_n\leq (\Z/n\Z)^{\times}.
3. A G_n halmaz akkor és csak akkor valódi részcsoport – azaz G_n\lt(\Z/n\Z)^{\times} –, ha c\gt 1. Egyébként c=1 esetben G_n=(\Z/n\Z)^{\times}.

Bizonyítás:

Mivel a tételben szereplő G_n halmaz elemei a NEM Miller-Rabin-tanúk, ezért a 23.9. Definíció utáni megjegyzés alapján az biztos, hogy itt csak redukált maradékosztályok lehetnek, azaz G_n\sube (\Z/n\Z)^{\times}.

Ha c=1, akkor n=p^c=p egy prímszám, amelynek a 23.10. Tétel értelmében egyáltalán nincsenek Miller-Rabin-tanúi, azaz ebben az esetben G_n=(\Z/n\Z)^{\times}. Ezzel c=1-re igazoltuk a 2. és 3. állításokat. Mivel n=p most egy prímszám, ezért az 1. állítás a kis Fermat-tételből (22.1. Tétel) azonnal következik, mely szerint bármilyen n=p-hez relatív prím a egész számra teljesül az a^{p-1}\equiv 1\pmod p kongruencia. A 20.14. Tétel alapján az n=p-hez relatív prím egész számok pontosan a redukált maradékosztályokat, azaz a (\Z/n\Z)^{\times} multiplikatív csoport elemeit reprezentálják, ami ugye – mint láttuk – megegyezik a NEM Miller-Rabin-tanúk G_n halmazával.

Az általánosság megsértése nélkül feltehetjük tehát, hogy c\geq 2.

Nézzük az 1. állítást ebben az esetben! Azt kell tehát bizonyítani, hogy az n=p^c egész szám NEM Miller-Rabin-tanúinak a reprezentánselemei, és csak azok elégítik ki az alábbi kongruenciát:

Ha az [a]_n maradékosztály nem Miller-Rabin-tanú, akkor egyrészt a 23.9. Definíció utáni megjegyzés alapján csak redukált maradékosztály lehet, és így a 20.14. Tétel szerint a és n=p^c relatív prímek. Ekkor viszont érvényes az Euler-Fermat tétel (20.19. Tétel), miszerint:

Másrészt viszont ha [a]_n nem Miller-Rabin-tanú, akkor szintén a 23.9. Definíció utáni megjegyzés szerint nem lehet Fermat-tanú sem. Ez a 23.3. Definíció alapján azt jelenti, hogy fennáll az alábbi kongruencia is:

A 24.12. Tétel 2. pontja alapján tehát a (\Z/n\Z)^{\times} csoportban az [a]_n elem rendje közös osztója \varphi(n)-nek és n-1-nek. Ez viszont a 17.4. Definíció miatt azt jelenti, hogy osztója a (\varphi(n), n-1) kitüntetett közös osztónak is, azaz teljesül az alábbi oszthatóság:

Alkalmazva az n=p^c helyettesítést a jobboldalon szereplő kitüntetett közös osztóra a 21.5. Tétel alapján, továbbá a 14.12. Definícióban szereplő 5. gyűrűaxióma szerint a következőt kapjuk:

Szintén a gyűrűaxiómák következménye, hogy a jobboldalon szereplő p^c-1 kifejezésből is kiemelhető a p-1 tényező, méghozzá az alábbi összefüggés miatt, amelyet az Olvasó maga is leellenőrizhet a zárójelek felbontásával:

Alkalmazhatjuk tehát a kitüntetett közös osztó kiemelési tulajdonságát (17.9. Tétel), azaz a fenti kitüntetett közös osztóból kiemelhetjük p-1-et:

Vegyük észre, hogy az itt szereplő jobboldali p^{c-1}+p^{c-2}+\ldots+p+1 összeg minden tagja osztható p-vel, kivéve az utolsó. Ez az összeg tehát p-vel osztva 1 maradékot ad, azaz a prímtényezői biztosan mind különböznek p-től. Ezzel szemben a baloldali p^{c-1} prímtényezői között csak p szerepel. A két mennyiség emiatt egymáshoz relatív prím, azaz:

Azt kaptuk tehát, hogy ha az [a]_n maradékosztály nem Miller-Rabin-tanú, akkor az ő rendje a (\Z/n\Z)^{\times} csoportban osztója lesz a (\varphi(n),n-1)=p-1 kitüntetett közös osztónak. Ez viszont a 24.12. Tétel 2. pontja alapján épp azt jelenti, hogy valóban teljesül az alábbi kongruencia, ahogyan a tétel állítja:

Most nézzük visszafelé! Tegyük fel, hogy teljesül az iménti kongruencia egy a egész számra. Most azt kell bizonyítani, hogy ekkor az [a]_n maradékosztály nem Miller-Rabin-tanú. Mivel n=p^c páratlan, ezért n-1=p^c-1 páros, és így valahányszor osztható 2-vel. Azaz létezik olyan e\geq 1 kitevő és k\geq 1 páratlan egész, hogy:

Ehhez hasonlóan p-1-hez is létezik olyan f\geq 1 kitevő és l\geq 1 páratlan egész, hogy:

A korábban már említett p^c-1=(p-1)(p^{c-1}+p^{c-2}+\ldots+p+1) azonosság alapján tudjuk, hogy teljesül az alábbi oszthatóság:

Mivel l és k páratlan, így ezek prímtényezői között biztosan nem szerepel a 2-es. Ezért a fenti oszthatóság csak úgy teljesülhet, ha fennáll az alábbi két feltétel:

Ugye abból indultunk ki, hogy teljesül az a^{p-1}\equiv 1\pmod n kongruencia. Ez az imént bevezetett p-1=2^fl jelölést alkalmazva így írható:

Ez a hatványozás azonosságairól szóló 18.8. Tétel 2. pontja miatt így is írható:

A 24.12. Tétel 2. pontja alapján tehát az [a^l]_n maradékosztály rendje osztója 2^f-nek. Ez csak úgy lehet, ha ez a rend is valamilyen 2-hatvány egy f-nél nemnagyobb, nemnegatív j kitevővel, azaz o([a^l]_n)=2^j.

Ha j=0, akkor ugye (a^l)^{2^0}=a^l és így teljesül az alábbi kongruencia:

De mivel tudjuk, hogy l|k – azaz k az l-nek többszöröse –, ezért ekkor teljesül az a^k\equiv 1\pmod n kongruencia is. Ez épp a 23.9. Definícióban szereplő első kongruencia, amely szerint tehát [a]_n valóban nem lehet Miller-Rabin-tanú.

Ha j\geq 1, akkor ez az elemrend 24.11. Definíciója miatt azt jelenti, hogy 2^j a legkisebb olyan kitevő, amely esetén az alábbi kongruencia teljesül:

Az ennél kisebb kitevőkre ez már nem teljesül, tehát például:

A felső kongruencia baloldala épp az alsó kongruencia baloldalának négyzete, hiszen:

Ha most az áttekinthetőség kedvéért bevezetjük az x=(a^l)^{2^{j-1}} jelölést, akkor fenti két kongruencia tulajdonképpen az alábbi két állításnak felel meg:

Az alsó kongruencia a 20.1. Tétel 3. pontja alapján az alábbi oszthatóságot jelenti:

Ennek az oszthatóságnak a jobboldala a 14.12. Definícióban ismertetett gyűrűaxiómák miatt szorzatba fejthető:

Ez az oszthatóság tehát biztosan teljesül. Ugyanakkor az is bizonyos, hogy x+1 és x-1 közül legfeljebb az egyikük prímtényezői között szerepelhet p, hiszen közöttük mindössze 2 a különbség. Más szavakkal az egyikük biztosan relatív prím lesz n=p^c-hez, és így az euklidészi lemma (17.11. Tétel) alapján a másik viszont biztosan osztható lesz n-nel. Azaz az alábbi oszthatóságok közül pontosan az egyik teljesül:

Azonban a második oszthatóság lehetetlen, hiszen az a 20.1. Tétel 3. pontja szerint azt jelentené, hogy mégiscsak teljesülne az x\equiv 1\pmod n kongruencia, amiről már láttuk, hogy nem teljesülhet. Következésképp csak az első oszthatóság teljesülhet. Ez viszont ismét a 20.1. Tétel 3. pontja miatt épp az alábbi kongruenciát jelenti:

Azonban emlékezzünk rá, hogy x-szel tulajdonképpen az (a^l)^{2^{j-1}}=a^{2^{j-1}l} kifejezést jelöltük, ezért ez a kongruencia ennek felel meg:

Mivel korábban már láttuk, hogy k többszöröse l-nek, azaz létezik olyan t egész szám, amely esetén lt=k. Ráadásul mivel a k és l számokról tudjuk, hogy páratlan számok, ezért a t is szükségképpen páratlan. Ha tehát a fenti kongruencia mindkét oldalát t-edik hatványra emeljük (amelyet ugye a 20.2. Tétel 8. pontja alapján tehetünk meg), akkor ezt kapjuk:

Itt a jobboldal valóban -1 marad, hiszen negatív szám páratlanadik hatványa ugyancsak negatív. Végeredményben tehát ezt kaptuk:

Tekintve, hogy j-1 biztosan kisebb a bevezetett e kitevőnél, ezért az alábbi kongruenciák közül biztosan teljesül az egyik:

Ez viszont a 23.9. Definíció alapján azt jelenti, hogy az [a]_n maradékosztály ebben az esetben sem lehet Miller-Rabin-tanú. Ezzel a tétel 1. állítását igazoltuk, miszerint valóban pontosan azok a maradékosztályok nem Miller-Rabin-tanúk – azaz tartoznak bele a tétel szövegében szereplő G_n halmazba –, amelyekre teljesül az alábbi kongruencia:

Most igazoljuk a 2. állítást, amely azt állítja, hogy G_n részcsoportja a (\Z/n\Z)^{\times} multiplikatív csoportnak. Mivel (\Z/n\Z)^{\times} rendje véges, ezért a 24.13. Következmény szerint elegendő azt ellenőrizni, hogy G_n nemüres és zárt a maradékosztályok közötti szorzásra, mint műveletre. Az első feltétel nyilván teljesül, hiszen 1^{p-1}\equiv 1\pmod n, és így az 1. állítás értelmében az [1]_n maradékosztály benne van G_n-ben.

Legyen most [a]_n és [b]_n két tetszőleges maradékosztály, amelyek a G_n halmaz elemei. Ez az imént bizonyított 1. állítás alapján azt jelenti, hogy teljesülnek az alábbi kongruenciák:

A két kongruenciát a 20.2. Tétel 5. pontja alapján összeszorozhatjuk egymással, így ezt kapjuk:

A baloldalt a hatványozás azonosságairól szóló 18.8. Tétel 1. pontját felhasználva átírhatjuk:

Ez viszont ismét az imént bizonyított 1. állítás miatt azt jelenti, hogy az [ab]_n maradékosztály is a G_n halmaz eleme. Az [ab]_n maradékosztály azonban a 20.5. Tételben szereplő definíciónak megfelelően épp az [a]_n és [b]_n maradékosztályok szorzata. A G_n halmaz tehát valóban részcsoport (\Z/n\Z)^{\times}-ban.

Végül a 3. állítást igazoljuk. Azt már láttuk, hogy c=1 esetben G_n=(\Z/n\Z)^{\times}, így elegendő azt igazolni, hogy c\geq 2 esetén viszont valódi részcsoportról van szó. Azaz kell találni egy olyan redukált maradékosztályt, amely nincs benne a G_n halmazban. Más szavakkal kell találnunk egy olyan a egész számot, amely relatív prím n=p^c-hez, de amelyre a^{p-1}\ \cancel{\equiv}\ 1\pmod{p^c}. Hiszen ekkor egyrészt a 20.14. Tétel alapján [a]_n egy redukált maradékosztály, másrészt pedig a már bizonyított 1. állítás alapján [a]_n\notin G_n.

Nézzük meg először, hogy mi következik abból, ha egy a szám teljesíti a fenti kongruenciát. Ekkor ugye a (\Z/n\Z)^{\times} csoportban a 24.12. Tétel 2. pontja alapján az [a]_n maradékosztály rendje osztója p-1-nek, azaz teljesül az alábbi oszthatóság:

Ám p-1 prímtényezős felbontásában biztosan nem szerepel p, így nem szerepelhet p-1 egyetlen osztójának prímtényezős felbontásában sem, emiatt o([a]_n) felbontásában sem, azaz:

Megfordítva a gondolatmenetet, ha tehát találunk egy olyan [a]_n redukált maradékosztályt, amelynek rendje osztható p-vel, akkor az kizárja azt, hogy teljesüljön az a^{p-1}\equiv 1\pmod{p^c} kongruencia, ami a már bizonyított 1. állítás alapján azt jelentené, hogy [a]_n\notin G_n.

Vegyük észre, hogy a [p+1]_n maradékosztály teljesíti ezt a feltételt. Egyrészt ugyanis p+1 nyilván relatív prím p-hez – azaz [p+1]_n egy redukált maradékosztály –, másrészt pedig teljesül az alábbi kongruencia:

Ekkor azonban alkalmazható a 24.17. Következmény, amely szerint teljesül az alábbi kongruencia is:

Ez viszont a 24.12. Tétel 2. pontja alapján azt jelenti, hogy a [p+1]_n maradékosztály rendje osztója p^{c-1}-nek. Továbbá ugyanezen tétel 5. pontja miatt ez a rend biztosan nem 1, hiszen [p+1]_n\neq [1]_n. Minthogy p^{c-1} prímtényezős felbontásában csak p szerepel, ezért ennek bármilyen 1-től különböző osztója szükségképpen osztható p-vel.

A [p+1]_n redukált maradékosztály tehát valóban nincs benne G_n-ben, és így G_n tényleg valódi részcsoportja (\Z/n\Z)^{\times}-nek, ahogyan a tétel állítja.

24.19. Tétel:

Legyen n egy tetszőleges 1-nél nagyobb páratlan szám, amelynek legalább két egymástól különböző prímtényezője is van, azaz nem prímhatvány. Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyekre teljesül az alábbi:

Ekkor létezik legalább egy olyan j kitevő a \{0; 1;2; \ldots ; e-1\} számok között, amelyekhez külön-külön találhatók olyan x egész számok, hogy teljesül az alábbi kongruencia:

Jelöljük az ilyen kitevők közül a legnagyobbat j_{\text{max}}-szal, és legyen H_n azon [a]_n maradékosztályok halmaza, amelyek esetén az a^{2^{j_{\text{max}}}k} hatvány 1-gyel vagy -1-gyel kongruens modulo n, azaz:

Ekkor H_n-re igazak az alábbiak:

1. A H_n halmaz minden eleme redukált maradékosztály. Másként fogalmazva H_n részhalmaza a (\Z/n\Z)^{\times} multiplikatív csoportnak, azaz H_n\sube (\Z/n\Z)^{\times}.
2. A H_n halmaz ezen felül a (\Z/n\Z)^{\times} multiplikatív csoport egy részcsoportja, azaz H_n\leq (\Z/n\Z)^{\times}.
3. A H_n részcsoport tartalmazza az összes NEM Miller-Rabin-tanút.
4. A H_n egy valódi részcsoport, azaz létezik olyan modulo n redukált maradékosztály, amely nincs benne H_n-ben.

Bizonyítás:

Előszöris nyilván létezik legalább egy a tételben említett feltételnek megfelelő j kitevő, hiszen például j=0 és x=-1 választással teljesül az alábbi kongruencia:

Tehát az ilyen kitevők között létezik legnagyobb is, amelyet ugye j_{\text{max}}-szal jelöltünk.

Nézzük először az 1. állítást, és mutassuk meg, hogy a H_n-ben lévő összes [a]_n maradékosztály redukált. A H_n halmaz definíciója miatt:

Akár 1, akár -1 szerepel a jobboldalon, a kongruenciát négyzetre emelve a következőt kapjuk:

Találtunk tehát egy olyan pozitív kitevőt – nevezetesen 2^{j_{\text{max}}+1}k-t – amelyre emelve a-t az eredmény kongruens lesz 1-gyel modulo n. Ebből viszont a 20.20. Tétel alapján következik, hogy a relatív prím n-hez, azaz a 20.14. Tétel értelmében [a]_n redukált maradékosztály. Ezzel igazoltuk a tétel 1. állítását.

A 2. állítás igazolásához a 24.13. Következmény értelmében azt kell megmutatni, hogy H_n nemüres és zárt a maradékosztályok közötti szorzásra, azaz a (\Z/n\Z)^{\times} csoport műveletére nézve. Mivel 1^{2^{j_{\text{max}}}k}\equiv 1\pmod n, ezért a tétel szövege alapján H_n nemüres, hiszen tartalmazza legalább az [1]_n maradékosztályt. Legyen most [a]_n és [b]_n a H_n halmaz két tetszőleges eleme. A H_n halmaz definíciója miatt ekkor teljesülnek az alábbi kongruenciák:

A 20.2. Tétel 5. pontja szerint ez a két kongruencia összeszorozható. Ekkor a 18.8. Tétel 1. pontjának alkalmazása után ezt kapjuk:

Azt kaptuk tehát, hogy az [ab]_n maradékosztály is a H_n halmaz eleme. Minthogy az [ab]_n maradékosztály a 20.5. Tételben bevezetett műveletek definíciója alapján épp az [a]_n és [b]_n maradékosztályok szorzata, ezért H_n zárt a (\Z/n\Z)^{\times} multiplikatív csoport műveletére nézve, azaz a 24.13. Következmény értelmében annak valóban részcsoportja. Ezzel igazoltuk a tétel 2. állítását.

A 3. állítás igazolásához tekintsünk egy tetszőleges [a]_n maradékosztályt, amely nem Miller-Rabin-tanú. Ekkor a Miller-Rabin-tanúk 23.9. Definíciója alapján vagy teljesül az a^k\equiv 1\pmod n kongruencia, vagy pedig létezik olyan j kitevő a \{0; 1;2; \ldots ; e-1\} számok között, amelyre teljesül az alábbi kongruencia:

Amennyiben az a^k\equiv 1\pmod n kongruencia teljesül, akkor mindkét oldalt j_{\text{max}}-szor négyzetre emelve, továbbá alkalmazva a 18.8. Tétel 2. pontját, az alábbit kapjuk:

Következésképp az [a]_n maradékosztály benne van a H_n halmazban.

Most nézzük meg, mi a helyzet akkor, ha nem teljesül az a^k\equiv 1\pmod n kongruencia. Ekkor ugye – mint már említettük – létezik olyan j kitevő a \{0; 1;2; \ldots ; e-1\} számok között, amelyre teljesül az alábbi kongruencia:

Alkalmazva a hatványozás azonosságairól szóló 18.8. Tétel 2. pontját ez így írható fel:

Az a^k tehát egy olyan egész szám, amelyet a 2-nek a j-edik hatványára, mint kitevőre emelve egy olyan egész számot kapunk, amely -1-gyel kongruens modulo n. A tétel szövegében bevezetett j_{\text{max}} definíciója alapján ekkor j\leq j_{\text{max}}.

Amennyiben egyenlőség áll fenn, azaz j=j_{\text{max}}, akkor teljesül az alábbi kongruencia:

Ez a H_n halmaz definíciója alapján azt jelenti, hogy [a]_n\in H_n.

Amennyiben nem áll fenn egyenlőség, akkor j\lt j_{\text{max}}. Az alábbi kongruenciáról ugye már tudjuk, hogy teljesül:

Mindkét oldalt sorozatosan négyzetre emelve az alábbi kongruenciákat kapjuk:

Mivel j\lt j_{\text{max}}, ezért a sorozatos négyzetre emelések hatására előbb-utóbb a alábbi kongruenciát fogjuk kapni:

Alkalmazva a hatványozás azonosságairól szóló 18.8. Tétel 2. pontját ez így írható fel:

Ez a H_n halmaz definíciója alapján ugyancsak azt jelenti, hogy [a]_n\in H_n. Igazoltuk tehát a tétel 3. állítását, miszerint minden nem Miller-Rabin-tanú a H_n részcsoportban van.

Végül a 4. állításhoz azt kell igazolni, hogy H_n valódi részcsoport (\Z/n\Z)^{\times}-ben, azaz találni kell egy olyan redukált maradékosztályt, amely nincs benne H_n-ben. Az n-ről a tétel szövegében kikötöttük, hogy ő egy olyan 1-nél nagyobb páratlan összetett szám, amelynek legalább két egymástól különböző prímtényezője van. Legyen n egyik prímtényezője p. Ekkor létezik olyan c\geq 1 kitevő és m\gt 1 páratlan egész szám, hogy egyrészt m tovább már nem osztható p-vel, másrészt pedig n felírható az alábbi alakban:

A 24.15. Definíció alapján úgy is mondhatjuk, hogy az n egész szám p-adikus rendje c\geq 1.

Ekkor p^c-nek és m-nek nincs közös prímtényezője, mert ha lenne, akkor az csak p valamilyen nulladiknál nagyobb hatványa lehetne, és így az n egész szám p-adikus rendje biztosan nagyobb lenne c-nél. Így tehát p^c és m relatív prímek. Ebben az esetben érvényes a kínai maradéktétel (22.2. Tétel), amelynek következményeként a 22.8. Tétel alapján fennáll az alábbi gyűrűizomorfizmus:

A tétel szövegéből tudjuk, hogy a j_{\text{max}} kitevőhöz létezik olyan egész szám, amelyet x helyére behelyettesítve teljesül az alábbi kongruencia:

Jelöljük az egyik ilyen egész számot s-sel, és tekintsük az [s]_n maradékosztályt a \Z/n\Z gyűrűben. Neki a 22.8. Tételben szereplő g gyűrűizomorfizmus az alábbi maradékosztálypárt felelteti meg a \Z/p^c\Z \times \Z/m\Z gyűrűben:

Ha a baloldali [s]_n maradékosztályt a 2^{j_{\text{max}}}k-adik hatványra emeljük a \Z/n\Z gyűrűben, akkor a g gyűrűizomorfizmus a művelettartó tulajdonság miatt ehhez épp a jobboldali maradékosztálypárnak a \Z/p^c\Z \times \Z/m\Z gyűrűben vett 2^{j_{\text{max}}}k-adik hatványát fogja hozzárendelni. Azaz:

A jobboldalon szereplő szorzatgyűrűbeli szorzást – és így a hatványozást – a 22.7. Tétel alapján komponensenként kell elvégezni, azaz:

A maradékosztályok közötti szorzást – és így a hatványozást – viszont a 20.5. Tétel szerint a reprezentánselemeken kell elvégezni, azaz:

A baloldalon szereplő modulo n maradékosztály reprezentánseleme tehát s^{2^{j_{\text{max}}}k}, amely a hatványozás azonosságairól szóló 18.8. Tétel 2. pontja alapján (s^{2^{j_{\text{max}}}})^k-val egyezik meg. Az s definíciójából tudjuk azonban, hogy:

Mindkét oldalt k-adik hatványra emelve a kongruencia jobboldalán továbbra is -1 marad, hiszen k a tétel szövege alapján páratlan:

Vagyis a fenti g szerinti hozzárendelés baloldalán tulajdonképpen a [-1]_n maradékosztály szerepel. Ám ekkor a g gyűrűizomorfizmus 22.8. Tételben szereplő definíciója alapján a jobboldalon pedig a ([-1]_{p^c};[-1]_m) maradékosztálypár kell szerepeljen:

Vagyis azt kaptuk, hogy az s^{2^{j_{\text{max}}}k} hatvány -1-gyel kongruens modulo p^c is, azaz:

Ezt a kongruenciát hamarosan felhasználjuk, amikoris a g gyűrűizomorfizmus segítségével megmutatjuk, hogy létezik olyan X\in \Z/n\Z redukált maradékosztály, amely nincs benne H_n-ben. A H_n definíciója alapján ez a keresett X maradékosztály pontosan akkor nincs benne H_n-ben, ha az ő \Z/n\Z gyűrűben vett 2^{j_{\text{max}}}k-adik hatványa különbözik mind az [1]_n, mind pedig a [-1]_n maradékosztálytól.

Legyen ez a keresett X az a maradékosztály, amely esetén a g gyűrűizomorfizmus épp az alábbi hozzárendelést valósítja meg:

Ilyen X ugye létezik, hiszen g kölcsönösen egyértelmű leképezés, azaz minden \Z/p^c\Z \times \Z/m\Z-beli maradékosztálypárt hozzárendeli valamelyik \Z/n\Z-beli maradékosztályhoz – jelen esetben az ([s]_{p^c};[1]_m) párt X-hez. A g művelettartó tulajdonsága alapján ekkor teljesül az alábbi hozzárendelés is:

A jobboldalon szereplő szorzatgyűrűbeli szorzást – és így a hatványozást – a 22.7. Tétel alapján komponensenként kell elvégezni, azaz:

A maradékosztályok közötti szorzást – és így a hatványozást – viszont a 20.5. Tétel szerint a reprezentánselemeken kell elvégezni, azaz:

Azt azonban már tudjuk, hogy teljesül az alábbi kongruencia:

Így tehát a fenti g szerinti hozzárendelés valójában az alábbi:

Így viszont a baloldalon szereplő X^{2^{j_{\text{max}}}k} hatvány biztosan nem lehet az [1]_n maradékosztály. Ebben az esetben ugyanis a g gyűrűizomorfizmus a 22.8. Tétel alapján az alábbi hozzárendelést valósítaná meg:

Ez csak akkor volna lehetséges, ha [1]_{p^c}=[-1]_{p^c} teljesülne, azaz fennállna az alábbi kongruencia:

Ez viszont azt jelentené, hogy teljesül az alábbi oszthatóság:

Ez viszont lehetetlen, hiszen p az n prímtényezője, amely páratlan, ezért p is, és így p^c is páratlan, azaz legalább 3. Márpedig a 17.2. Lemma alapján egy pozitív egész szám bármely osztója legfeljebb akkora lehet, mint maga a szám.

Hasonló gondolatmenet alapján az X^{2^{j_{\text{max}}}k} hatvány biztosan nem lehet a [-1]_n maradékosztály sem, hiszen ekkor a g gyűrűizomorfizmus a 22.8. Tétel alapján az alábbi hozzárendelést valósítaná meg:

Ez csak akkor volna lehetséges, ha [-1]_m=[1]_m teljesülne, azaz fennállna az alábbi kongruencia:

Ez viszont azt jelentené, hogy teljesül az alábbi oszthatóság:

Ez viszont ugyancsak lehetetlen, hiszen m-ről azt mondtuk, hogy 1-nél nagyobb páratlan egész, azaz legalább 3.

Azt kaptuk tehát, hogy az X maradékosztály 2^{j_{\text{max}}}k-adik hatványa különbözik az [1]_n és [-1]_n maradékosztályoktól, és így valóban nem lehet H_n-ben.

Annyit kell még igazolni, hogy X redukált maradékosztály, és ennek ellenére nincs H_n-ben – azt ugyanis már az 1. állításban igazoltuk, hogy nem redukált maradékosztályok amúgysem lehetnek benne H_n-ben. Az X konstrukciója alapján a g gyűrűizomorfizmus ugye az alábbi hozzárendelést valósítja meg:

Most tegyük fel, hogy az a egész szám az X maradékosztály egy reprezentánseleme, azaz legyen X=[a]_n. A 22.8. Tétel alapján azonban teljesül az alábbi hozzárendelés is:

Mivel a g által megvalósított hozzárendelés kölcsönösen egyértelmű, ezért a fenti két hozzárendelés egyszerre csak akkor teljesülhet, ha a jobboldalakon szereplő két maradékosztálypár egy és ugyanaz, azaz fennállnak a maradékosztályok közötti alábbi egyenlőségek:

A második egyenlőségből a 20.14. Tétel alapján következik, hogy a relatív prím m-hez. Az [a]_m=[1]_m maradékosztály ugyanis nyilván invertálható a \Z/m\Z gyűrűben, hiszen ő ennek a gyűrűnek az egységeleme, amelynek inverze önmaga.

Az első egyenlőségből szintén a 20.14. Tétel alapján következik, hogy a pontosan akkor relatív prím p^c-hez, ha s is az, hiszen ők ugyanannak a modulo p^c maradékosztálynak a reprezentánselemei. Az s-ről azonban korábban már megmutattuk, hogy teljesül rá az alábbi kongruencia:

A 20.2. Tétel 8. pontja alapján mindkét oldalt négyzetre emelhetjük:

Találtunk tehát egy olyan pozitív kitevőt – nevezetesen 2^{j_{\text{max}}+1}k-t – amelyre emelve s-t az eredmény kongruens lesz 1-gyel modulo p^c. Ebből viszont a 20.20. Tétel alapján következik, hogy s relatív prím p^c-hez, és így a is.

Egyrészt azt kaptuk tehát, hogy a relatív prím m-hez, vagyis nincs vele közös prímtényezője. Másrészt a relatív prím p^c-hez is, tehát vele sincs közös prímtényezője. Ekkor viszont a p^cm=n szorzattal sincs közös prímtényezője, tehát n-hez is relatív prím. Vagyis a 20.14. Tétel szerint az X=[a]_n valóban egy redukált maradékosztály a \Z/n\Z gyűrűben.

24.20. Következmény:

Legyen n\gt 1 egy tetszőleges páratlan egész szám. Ha n összetett, akkor a modulo n redukált maradékosztályoknak legalább a fele Miller-Rabin-tanú.

Bizonyítás:

1. eset: n valamilyen prímhatvány

Ekkor tehát n=p^c, ahol p valamilyen páratlan prímszám, továbbá c\geq 2, máskülönben n=p nem lenne összetett. A 24.18. Tétel 2. és 3. pontjai alapján a nem Miller-Rabin-tanúk G_n-nel jelölt halmaza egy valódi részcsoportot alkot a (\Z/n\Z)^{\times} multiplikatív csoportban. A Lagrange-tétel (24.8. Tétel) alapján a G_n részcsoport rendje osztója a (\Z/n\Z)^{\times} csoport rendjének. Minthogy G_n valódi részcsoport, ezért ez alapján az elemeinek a száma legfeljebb feleannyi, mint a (\Z/n\Z)^{\times} csoport elemeinek a száma. A redukált maradékosztályoknak tehát legfeljebb a fele lehet nem Miller-Rabin-tanú. Másként fogalmazva legalább a felük Miller-Rabin-tanú kell legyen.

2. eset: n nem prímhatvány, azaz legalább két prímtényezője van.

Ekkor a nem Miller-Rabin-tanúk ugyan nem alkotnak részcsoportot (\Z/n\Z)^{\times}-ben, azonban a 24.19. Tétel alapján létezik olyan H_n-nel jelölt valódi részcsoport, amely viszont minden nem Miller-Rabin-tanút tartalmaz. Azaz a következő a helyzet:

Ismét a Lagrange-tétel (24.8. Tétel) miatt a redukált maradékosztályoknak legfeljebb a fele – köztük az összes nem Miller-Rabin-tanú – tartozhat H_n-be. Következésképp ebben az esetben is legalább a felük Miller-Rabin-tanú.