Az előző részben megismerkedtünk a legfontosabb számelméleti fogalmakkal: oszthatóság, egység, asszociált, felbonthatatlan és prímtulajdonságú elemek. Ezután ismertettük a számelmélet alaptételét, amely azt biztosítja egy integritástartományban, hogy annak minden elemét egyértelműen elő lehessen állítani felbonthatatlan elemek szorzataként. Láttuk, hogy ez nem minden integritástartományban teljesül. Végül megmutattuk, hogy ha viszont teljesül, akkor a felbonthatatlanok és a prímek fogalma szükségképpen egybe kell essen. Azt is megemlítettük ugyanakkor, hogy ez csupán szükséges, de nem elégséges feltétel az alaptétel teljesüléséhez.
De vajon milyen elégséges feltételt tudunk mutatni erre vonatkozóan? Az egész számok gyűrűje teljesíti-e ezt a kritériumot? Mit jelent a „legnagyobb közös osztó” fogalma és hogyan lehet villámgyorsan kiszámolni az euklidészi algoritmus segítségével? Mit tudunk mondani erről általános integritástartományokra? Mik azok az euklidészi gyűrűk és mi közük a számelmélet alaptételéhez? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít az előző részben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy R egy kommutatív gyűrű, valamint a és b a gyűrű két eleme. Amennyiben létezik olyan k gyűrűelem, hogy ak=b, akkor azt mondjuk, hogy a osztója b-nek az R gyűrűben. Ezzel egyenértékű megfogalmazások: b osztható a-val vagy b többszöröse a-nak.
Az oszthatóság tehát egy kétváltozós reláció az R gyűrűben. Azt a relációt, hogy „a osztója b-nek R-ben”, így jelöljük: a|_R b.
Amennyiben a és b között nem áll fenn az oszthatósági reláció – azaz a nem osztója b-nek az R gyűrűben –, azt így jelöljük: a{\nmid}_R b.
Ha a kontextusból egyértelmű, hogy melyik gyűrűben vizsgáljuk az oszthatóságot, akkor a relációt jelölő szimbólumból elhagyhatjuk a gyűrűre való hivatkozást. Ilyenkor például a|_R b helyett egyszerűen a|b-t írhatunk.
Legyen R egy tetszőleges kommutatív gyűrű. Ha egy adott e gyűrűelem esetén minden a gyűrűelemre teljesül az e|a oszthatósági reláció, akkor az e elemet egységnek nevezzük.
Egy kommutatív gyűrű valamely a és b elemeire akkor mondjuk, hogy egymás asszociáltjai, ha pontosan ugyanazok a többszöröseik és az osztóik is. Pontosabban fogalmazva, ha tetszőleges r gyűrűelem esetén a|r akkor és csak akkor teljesül, amikor b|r is teljesül, valamint r|a akkor és csak akkor teljesül, amikor r|b is teljesül.
Azt, hogy a és b egymás asszociáltjai így jelöljük: a\sim b.
Legyen R egy tetszőleges kommutatív gyűrű. Ha valamely a, b és c elemekre a=b\cdot c teljesül, akkor a b\cdot c szorzatot az a elem felbontásának nevezzük. Azokat a felbontásokat, amelyekben b és c közül az egyik egység, a másik pedig a asszociáltja, triviális felbontásoknak nevezzük. Ha egy gyűrűelem saját maga nem egység és nem létezik nemtriviális felbontása (azaz ha létezik is felbontása, az csak triviális lehet), akkor őt felbonthatatlannak vagy irreducibilisnek nevezzük. Ha egy elem nem felbonthatatlan és nem egység, akkor őt összetett elemnek nevezzük. Az egységeket nem tekintjük sem felbonthatatlannak, sem pedig összetettnek.
Egy R kommutatív gyűrű valamely p elemét prímtulajdonságú elemnek (vagy egyszerűen csak prímnek) nevezzük, ha nem a nullelem, nem egység, és csak úgy lehet osztója két gyűrűelem szorzatának, ha legalább az egyik tényezőnek osztója. Azaz ha valamely a és b gyűrűelemekre teljesül a p|ab oszthatóság, akkor a p|a vagy p|b oszthatóságok közül legalább az egyik ugyancsak teljesül.
Legyen R egy tetszőleges integritástartomány. Azt mondjuk, hogy R-ben érvényes a számelmélet alaptétele, ha R minden nemnulla és nem egység eleme egyértelműen felbontható R felbonthatatlan elemeinek szorzatára. Egy felbonthatatlan elem „felbontása” alatt önmagát, mint „egytényezős szorzatot” értjük.
A felbontás egyértelműsége a következőt jelenti. Tekintsük valamely r elem két tetszőleges felbontását:
\begin{aligned}r&=p_1\cdot p_2\cdot \ldots \cdot p_n = \\ &= q_1\cdot q_2\cdot \ldots \cdot q_k\end{aligned}Ekkor a tényezők száma ugyanannyi (azaz n=k), és a két felbontás tényezői egymással párba állíthatók úgy, hogy a párok tagjai egymásnak asszociáltjai legyenek.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni az előző részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
A modern kriptográfiai eljárások szempontjából alapvető fontosságú, hogy az egész számok \Z gyűrűjében teljesüljön a számelmélet alaptétele. Egyrészt ez teszi lehetővé, hogy minden egész szám egyértelműen előáll prímszámok szorzataként, és így a számelméleti kapcsolatot biztosítja a publikus és a titkos kulcsok között ezekben az eljárásokban. Másrészt a prímfaktorizáció feladatának algoritmikus nehézsége biztosítja azt, hogy egy támadó számára beláthatatlanul sok ideig tartson kiszámítani a titkos kulcsot a hozzá tartozó publikus kulcsból. Ezért ebben a részben alapvető célunk annak igazolása, hogy az egész számok \Z gyűrűjében valóban teljesül a számelmélet alaptétele.
Ennek keretében meg fogunk ismerkedni az ókorból származó euklidészi algoritmussal. Ezzel két egész szám úgynevezett legnagyobb közös osztóját fogjuk tudni elképesztően hatékonyan kiszámítani. Ez az eljárás a továbbiakban is fontos lesz számunkra, mivel mind az RSA-ban, mind pedig a prímtesztelési eljárásokban alapvető szerepet játszik. Ezután ezt az eljárást fogjuk általánosítani oly módon, hogy ne csak az egész számok gyűrűjén, hanem minden olyan integritástartományon működjön, amely bizonyos kritériumoknak eleget tesz. Ezeket euklidészi gyűrűknek fogjuk nevezni. Végül megmutatjuk, hogy minden euklidészi gyűrűben – és így speciálisan az egész számok gyűrűjében is – teljesül a számelmélet alaptétele.
A legnagyobb közös osztó
Először is tisztázzuk, hogy mit értünk két egész szám legnagyobb közös osztóján. Tegyük fel, hogy a és b valamilyen egész számok. Azt mondjuk, hogy a c egész szám a és b közös osztója, ha egyidejűleg teljesülnek a c|a és c|b oszthatóságok. Például a 18 és 24 közös osztói az 1, 2, 3 és 6 egész számok, valamint ezek ellentettjei. A legnagyobb közös osztó alatt értelemszerűen ezek közül a legnagyobbat, azaz a 6 egész számot értjük. Általánosságban az a és b egész számok legnagyobb közös osztóját (a,b)-vel szoktuk jelölni. Az iménti példában tehát (18,24)=6.
A legnagyobb közös osztó definícióját a fentiek alapján tehát megadhatnánk a következőképpen.
17.1. Definíció (Legnagyobb közös osztó):
Tegyük fel, hogy a és b tetszőleges egész számok a \Z gyűrűben. Az a és b legnagyobb közös osztója a d egész szám, ha teljesül az alábbi két tulajdonság:
- Fennállnak a d|a és d|b oszthatóságok.
- Tetszőleges c egész szám esetén ha fennállnak a c|a és c|b oszthatóságok, akkor c\leq d.
Azaz a legnagyobb közös osztónál nincs nagyobb közös osztó. Az a és b egész számok legnagyobb közös osztójának jelölése: (a,b).
♣Megjegyzés:
A definícióból következik, hogy a=b=0 esetén nem létezik az (a,b) legnagyobb közös osztó, hiszen a 0-nak minden egész szám osztója (lásd a 16.2. Tétel 3. pontját), így közöttük nincs legnagyobb.
♣Kérdés, hogy az iménti megjegyzésben közölt eseten kívül vajon minden más esetben létezik-e a legnagyobb közös osztó. Ennek megmutatásához először ismertetünk egy segédtételt:
17.2. Lemma:
Ha a és b tetszőleges egész számok, és 0\lt b, akkor az a|b oszthatóságból következik, hogy a\leq b. Azaz tetszőleges pozitív egész szám legalább akkora, mint bármely osztója.
♣Bizonyítás:
Az biztos, hogy a\neq 0, hiszen máskülönben b=0 lenne a 16.2. Tétel 4. pontja miatt. A rendezési reláció trichotómiájából (lásd a 12.11. Definíciót), valamint a\neq 0-ból következően a\lt 0 vagy a\gt 0 közül pontosan az egyik teljesül.
Az a\lt 0 esettel nem kell különösebben foglalkoznunk, hiszen ekkor 0\lt b miatt nyilván következik a\leq b a rendezési reláció tranzitivitása miatt (lásd a 12.10. Definíciót).
Nézzük tehát a 0\lt a esetet. Az oszthatóság 16.1. Definíciója miatt a|b-ből következik, hogy létezik olyan k egész szám, amelyre teljesül az alábbi egyenlet:
a\cdot k = bA 13.10. Definíció szerinti pozitív és negatív egész számok, valamint a 0 a 13.9. Tétel értelmében lefedik a teljes \Z halmazt. Emiatt az egészek szorzásának 14.3. Definíciója alapján egy szorzat előjele az alábbiak szerint alakulhat a tényezők előjelének függvényében:
\begin{aligned}\text{pozitív}\cdot \text{pozitív} &= \text{pozitív} \\ \text{pozitív}\cdot \text{negatív} &= \text{negatív} \\ \text{negatív}\cdot \text{pozitív} &= \text{negatív} \\ \text{negatív}\cdot \text{negatív} &= \text{pozitív} \end{aligned}Mivel a fenti egyenletben a is és b is pozitív, ezért szükségképpen k is pozitív kell legyen, azaz 0\lt k. Továbbá az egyenlet a disztributivitási szabályok miatt átalakítható a következőképpen:
a\cdot k=a\cdot (1+k-1)=a+a\cdot (k-1)=bItt teljesül, hogy 0\leq a\cdot (k-1), hiszen a ugye pozitív, k-1 pedig pozitív vagy 0. Létezik tehát olyan természetes szám (vagy más szavakkal nemnegatív egész szám), amelyet a-hoz adva b-t kapunk, nevezetesen az a\cdot (k-1). Ez viszont a 15.18. Definíció miatt épp azt jelenti, hogy a\leq b.
∎Ennek a segédtételnek a felhasználásával mostmár könnyen meg tudjuk mutatni, hogy a \Z gyűrűben mindig létezik a és b legnagyobb közös osztója, amennyiben legalább az egyikük nem 0.
17.3. Tétel:
Ha a és b tetszőleges egész számok, és közülük legalább az egyik nem 0, akkor létezik az (a,b) legnagyobb közös osztó.
♣Bizonyítás:
Először azt mutatjuk meg, hogy egy tetszőleges n\neq 0 egész számnak mindig véges sok osztója van. Elegendő azt az esetet vizsgálni, amikor n pozitív. Ha ugyanis n negatív, akkor egyrészt a 15.9. Lemma 1. pontja miatt az ellentettje pozitív lenne, amelynek a 16.8. Tétel 1. pontjának értelmében pontosan ugyanazok lennének az osztói, mint n-nek.
Az általánosság megsértése nélkül feltehetjük tehát, hogy 0\lt n. A 17.2. Lemma miatt ekkor n egyetlen osztója sem lehet nagyobb n-nél. Ebből következik, hogy n-nek legfeljebb n darab pozitív osztója lehet. A 16.2. Tétel 8. pontja miatt ekkor azonban ezek ellentettjei is osztók, amelyek a 15.9. Lemma 1. pontja miatt mind negatívak lennének.
Tekintve, hogy a pozitív és negatív egész számok a 0-val együtt lefedik a teljes \Z halmazt, valamint a 16.2. Tétel 4. pontja miatt 0 \nmid n, ezért n-nek biztosan nincs ezeken kívül több osztója, így osztóinak száma biztosan nem több 2n-nél – azaz véges.
Ebből azonnal következik, hogy a tételben szereplő a és b egész számok közös osztóinak száma is véges. Igaz továbbá, hogy az 1 minden egész számnak osztója, hiszen ő a \Z gyűrű egységeleme, és így a 16.3. Definíció utáni megjegyzés alapján egyúttal egység is. A közös osztók halmaza tehát – azonkívül, hogy véges – nem üres, így biztosan van az elemei között legnagyobb. A legnagyobb közös osztó tehát valóban létezik.
∎A legnagyobb közös osztó definíciójával azonban van egy kis probléma. Nevezetesen: felhasználtuk hozzá az egész számok \Z gyűrűjének rendezési relációját. Mi azonban szeretnénk ezt a fogalmat tetszőleges integritástartományokra kiterjeszteni. Ugyanakkor nem szeretnénk csak a definíció kedvéért megkövetelni valamiféle rendezési reláció létezését. Ráadásul a 15. részben láthattuk, hogy bizonyos gyűrűk egyáltalán nem, vagy akár végtelen sokféleképpen rendezhetők. Ez utóbbi esetben például nem is lenne egyértelmű, hogy melyik rendezés szerinti legnagyobb közös osztóról beszélünk.
A kitüntetett közös osztó
Ebben a szakaszban tehát általánosítjuk a legnagyobb közös osztó fogalmát. Így már tetszőleges integritástartományra átvihető lesz ez a fogalom rendezési reláció nélkül is. Ezért bevezetjük a kitüntetett közös osztó fogalmát.
17.4. Definíció (Kitüntetett közös osztó):
Tegyük fel, hogy a és b egy valamilyen R integritástartomány tetszőleges elemei. Az a és b elemek kitüntetett közös osztója a d elem, ha teljesül az alábbi két tulajdonság:
- Fennállnak a d|a és d|b oszthatóságok.
- Tetszőleges c elem esetén ha fennállnak a c|a és c|b oszthatóságok, akkor fennáll a c|d oszthatóság is.
Azaz a kitüntetett közös osztó minden közös osztónak többszöröse. Az a és b elemek kitüntetett közös osztójának jelölése: (a,b).
♣A definícióból azonnal következnek az alábbi egyszerű állítások.
17.5. Tétel:
Tegyük fel, hogy a és b valamilyen R integritástartomány tetszőleges elemei. Ekkor igazak az alábbiak:
- A (0,0) kitüntetett közös osztó mindig létezik, és (0,0)=0.
- Ha létezik az (a,b) kitüntetett közös osztó, akkor a (b,a) kitüntetett közös osztó is létezik, és (a,b)=(b,a).
- Ha a és b közül legalább az egyik nem 0, és létezik az (a,b) kitüntetett közös osztó, akkor R egységelemes.
- Amennyiben a\neq 0 és teljesül az a|b oszthatóság, úgy (a,b) akkor és csak akkor létezik, ha R egységelemes. Ilyenkor (a,b)=a. Speciálisan b=0 esetén: (a,0)=a.
Bizonyítás:
Az 1. tulajdonság: A nullelem osztója önmagának, így közös osztó. Ugyanakkor neki minden elem osztója, így az összes többi potenciális közös osztó is, ezért ő kitüntetett is. Rajta kívül viszont más kitüntetett közös osztó nem létezhet, hiszen akkor annak a nullelem többszörösének kéne lennie, ami a 16.2. Tétel 4. pontja miatt lehetetlen. Tehát valóban (0,0)=0.
A 2. tulajdonság: Az a és b közös osztóinak halmaza nem változik, ha a pozíciójukat felcseréljük az (a,b) kifejezésben, így a kitüntetett közös osztó sem.
A 3. tulajdonság: A 17.4. Definíció 2. pontja alapján az (a,b) kitüntetett közös osztó önmagának is osztója, és ha a illetve b közül legalább az egyik nem 0, akkor a 16.2. Tétel 4. pontja miatt (a,b) sem lehet 0. Ám ekkor ugyanezen tétel 2. pontja alapján R egységelemes.
Végül a 4. tulajdonság: Ha (a,b) létezik, akkor az a\neq 0 feltétel miatt a 3. tulajdonság alapján R egységelemes. Megfordítva: Ha R egységelemes, akkor a 16.2. Tétel 1. pontja alapján teljesül az a|a oszthatóság. Az a|b feltétel miatt tehát a valóban közös osztó. Ezenkívül nyilván kitüntetett is, hiszen bármilyen elem csak akkor lehet közös osztó, ha osztója a-nak. Az (a,b) kitüntetett közös osztó tehát valóban létezik, és a-val egyezik meg.
∎A legnagyobb közös osztóval ellentétben kitüntetett közös osztóból létezhet több is. Például az előző szakasz elején közölt példában szereplő 24 és 18 egész számoknak a 6-on kívül a -6 is kitüntetett közös osztója. Szerencsére ez nem fog gondot okozni, mivel az alábbi tétel biztosít egyfajta egyértelműséget a kitüntetett közös osztóra.
17.6. Tétel:
Ha egy R integritástartományban valamely a és b elemeknek létezik kitüntetett közös osztója, akkor az asszociáltságtól eltekintve egyértelmű.
Ezalatt egyrészt azt értjük, hogy egy kitüntetett közös osztó bármely asszociáltja is kitüntetett közös osztó, másrészt pedig azt, hogy bármely két kitüntetett közös osztó szükségképpen egymás asszociáltja.
♣Bizonyítás:
Nézzük a tétel első állítását. Tegyük fel, hogy d_1 kitüntetett közös osztója a-nak és b-nek, valamint d_2-re teljesül, hogy d_1 \sim d_2 – azaz d_1 és d_2 asszociáltak. Azt kell megmutatni, hogy ekkor d_2 is kitüntetett közös osztó. Az asszociáltság 16.6. Definíciója alapján d_2-nek pontosan ugyanazok az osztói, mint d_1-nek. Emiatt, mivel d_1-nek osztója az összes közös osztó (hiszen kitüntetett), ezért d_2-nek is, így ő is kitüntetett.
Most nézzük a második állítást. Tegyük fel, hogy d_1 és d_2 is kitüntetett közös osztója a-nak és b-nek. Azt kell megmutatni, hogy ekkor d_1 \sim d_2 – azaz d_1 és d_2 asszociáltak. Mivel d_1 közös osztó, ezért osztója d_2-nek, hiszen d_2 ugye kitüntetett. Fordítva: mivel d_2 közös osztó, ezért osztója d_1-nek, hiszen d_1 is kitüntetett. A két kitüntetett közös osztó tehát kölcsönösen osztói egymásnak, és így a 16.9. Tétel értelmében egymás asszociáltjai.
∎Jogosan merülhet fel a kérdés az Olvasóban, hogy miért használtuk ugyanazt a jelölést a kitüntetett és a legnagyobb közös osztó esetén, amikor ezek látszólag teljesen különböző fogalmak. Ennek tisztázása érdekében most megmutatjuk, hogy HA két egész számnak egyáltalán létezik kitüntetett közös osztója, akkor az csak a legnagyobb közös osztó valamelyik asszociáltja lehet. Erről szól az alábbi tétel.
17.7. Tétel:
Tegyük fel, hogy a d egész szám valamely a és b egész számok legnagyobb közös osztója. Tegyük fel továbbá, hogy a-nak és b-nek létezik legalább 1 kitüntetett közös osztója, amelyet jelöljünk most e-vel. Ekkor d és e egymás asszociáltjai, és így a 17.6. Tétel értelmében d is kitüntetett közös osztó.
♣Bizonyítás:
Az a=b=0 esetet egyből ki is zárhatjuk, hiszen a 17.1. Definíció utáni megjegyzés miatt ekkor nem létezne legnagyobb közös osztó. Minthogy létezik (hiszen d az), ezért biztos, hogy a és b közül legalább az egyik nem 0. Ebből viszont következik, hogy a feltételezett e kitüntetett közös osztó biztosan nem 0 (hiszen a 16.2. Tétel 4. pontja miatt a 0 csak saját magának osztója). Így tehát e a rendezési reláció trichotómiája miatt vagy pozitív, vagy pedig negatív.
Legyen f=e, ha e pozitív, és f=-e ha e negatív. Ekkor egyrészt a 15.9. Lemma 1. pontja miatt f biztosan pozitív, másrészt pedig e-nek asszociáltja (vagy azért, mert megegyezik vele, vagy pedig a 16.8. Tétel 1. pontja miatt). Ebből viszont a 17.6. Tétel miatt következik, hogy f is kitüntetett közös osztó.
Mivel f közös osztó, és d a legnagyobb közös osztó, ezért egyrészt teljesül az f\leq d reláció. Másrészt mivel d szintén közös osztó, és f kitüntetett, ezért teljesül a d|f oszthatóság is. Ekkor azonban 0\lt f miatt alkalmazható a 17.2. Lemma, ami alapján teljesül a d\leq f reláció is.
Minthogy f\leq d és d\leq f egyszerre teljesül, ezért a \leq reláció antiszimmetriája (lásd a 12.9. Definíciót) miatt d=f. Azaz d valóban asszociáltja a tételben szereplő e kitüntetett közös osztónak, és így a 17.6. Tétel értelmében ő maga is kitüntetett közös osztó.
∎Ez mind szép és jó, azonban vigyázzunk! Ez a tétel csak annyit garantál, hogy HA valamely egész számpárnak létezik kitüntetett közös osztója, AKKOR e számok legnagyobb közös osztója is rendelkezni fog a 17.4. Definícióban szereplő kitüntetett tulajdonsággal (azaz, hogy ő többszöröse bármely közös osztónak). A legnagyobb közös osztó a 17.3. Tétel miatt egy esetet leszámítva mindig létezik, ám a kitüntetett közös osztó létezése egyáltalán nem magától értetődő.
Szerencsére a \Z gyűrűben valóban mindig létezik a kitüntetett közös osztó, amelyre hamarosan egy úgynevezett konstruktív bizonyítást adunk. Ez azt jelenti, hogy a bizonyítás egy meglehetősen hatékony eljárást is fog szolgáltatni a kitüntetett közös osztó kiszámításához. Ez az eljárás az ókorból ered, és euklidészi algoritmus néven ismeretes.
Mielőtt azonban erre rátérnénk, vizsgáljuk meg, hogy miért is olyan fontos nekünk a kitüntetett közös osztó létezése egy adott integritástartományban.
A kitüntetett közös osztó jelentősége
Ebben a szakaszban azt fogjuk megmutatni, hogy amennyiben egy R integritástartományban bármely két elemnek létezik kitüntetett közös osztója, akkor R minden felbonthatatlan eleme prímtulajdonságú, következésképp a 16.17. Tétel alapján teljesül a számelmélet alaptételének egyértelműségi része (lásd a 16.15. Definíciót).
Ehhez szükségünk lesz 3 segédtételre. Először az oszthatósági reláció egy újabb egyszerű tulajdonságát igazoljuk, amely nagyon hasonló a 16.2. Tétel 7. pontjában megfogalmazott állításhoz, ám annál egy kicsit többet mond. Ez hasznunkra lesz a továbbiakban.
17.8. Tétel:
Legyen R egy tetszőleges integritástartomány. Ekkor tetszőleges a, b és c\neq 0 elemekre az a|b oszthatóság akkor és csak akkor teljesül, amikor az ac|bc oszthatóság is. Egy integritástartományban tehát egy oszthatóság mindkét oldalát szabad egyrészt megszorozni bármilyen elemmel, másrészt egyszerűsíteni bármilyen nemnulla elemmel.
Ha a gyűrű csak kommutatív, de a nullosztómentesség nem teljesül, akkor csak annyi igaz, hogy az a|b oszthatóságból tetszőleges (tehát akár 0) c esetén következik az ac|bc oszthatóság.
♣Például az egész számok \Z gyűrűjében teljesül a 6|18 oszthatóság, és így a tétel alapján teljesül a 3|9 oszthatóság is.
Bizonyítás:
Az, hogy fennáll az a|b oszthatóság azt jelenti, hogy létezik olyan k gyűrűelem, amelyre teljesül az alábbi egyenlet:
a\cdot k = bAz egyenlet mindkét oldalát a c gyűrűelemmel megszorozva ezt kapjuk:
(a\cdot k)\cdot c = b\cdot cMivel azonban a 14.12. Definícióban megfogalmazott 4. gyűrűaxióma alapján a szorzás asszociatív, valamint – kommutatív gyűrűről lévén szó – kommutatív is, ezért ennek az egyenletnek a baloldala átzárójelezhető és átrendezhető:
(a\cdot c)\cdot k = b\cdot cLétezik tehát olyan gyűrűelem, amellyel ac-t megszorozva bc-t kapunk (nevezetesen a k). Ez viszont épp azt jelenti, hogy ac|bc. Vegyük észre, hogy ehhez nem használtuk fel a nullosztómentességet, valamint a c=0 esetre is működik. Így tehát bármely kommutatív gyűrűben tetszőleges a, b és c elemekre igaz, hogy az a|b oszthatóságból következik az ac|bc oszthatóság.
A visszafele irányhoz már fel kell használni a nullosztómentességet is. Ebben az esetben az ac|bc oszthatóságból az előző lépéseket visszafele eljátszva következik az alábbi egyenlet:
(a\cdot k)\cdot c = b\cdot cEzt a c\neq 0 feltétel, valamint a nullosztómentesség miatt a 15.4. Tétel alapján egyszerűsíteni lehet c-vel. Így:
a\cdot k = bEz viszont épp azt jelenti, hogy a|b.
∎Az oszthatóságnak ezt a tulajdonságát most fel fogjuk használni egy, a kitüntetett közös osztóval kapcsolatos fontos összefüggés igazolásához.
17.9. Tétel (A kitüntetett közös osztó kiemelési tulajdonsága):
Legyen R egy tetszőleges integritástartomány, amelyben bármely két elemnek létezik kitüntetett közös osztója. Ekkor tetszőleges a, b és c elemekre érvényes az alábbi összefüggés:
(ac,bc)\sim (a,b)\cdot cAzaz (ac,bc) és (a,b)c mindig egymás asszociáltjai.
♣Például a \Z gyűrűben (6,9)=3, és így (18,27)=(6\cdot 3, 9\cdot 3)=(6,9)\cdot 3=9.
Bizonyítás:
Ha c=0, akkor nyilván igaz az állítás, hiszen a 17.5. Tétel 1. pontja miatt egyrészt (a\cdot 0,b\cdot 0)=(0,0)=0, másrészt a 15.1. Tétel 1. pontja miatt (a,b)\cdot 0 = 0.
Ha a=b=0, akkor hasonló okok miatt szintén nyilvánvalóan teljesül a tétel, hiszen egyrészt (0\cdot c,0\cdot c)=(0,0)=0, másrészt (0,0)\cdot c=0\cdot c=0.
Az általánosság megsértése nélkül feltehetjük tehát, hogy c\neq 0, valamint a és b közül legalább az egyik nem 0, és így egyrészt a 16.2. Tétel 4. pontja miatt (a,b)\neq 0, másrészt a 17.5. Tétel 3. pontja miatt R-ben létezik egységelem.
Mivel (a,b) közös osztó, ezért teljesülnek az alábbi oszthatóságok:
\begin{aligned}(a,b)&|a \\ (a,b)&|b\end{aligned}Ekkor azonban a 17.8. Tétel miatt teljesülnek az alábbi oszthatóságok is:
\begin{aligned}(a,b)c&|ac \\ (a,b)c&|bc\end{aligned}Ez viszont azt jelenti, hogy (a,b)c közös osztója ac-nek és bc-nek. Mivel feltételeztük, hogy bármely két elemnek létezik kitüntetett közös osztója, ezért nyilván létezik az (ac,bc) kitüntetett közös osztó is. Ez viszont – kitüntetett lévén – többszöröse bármely más közös osztónak, így (a,b)c-nek is. Azt tehát már tudjuk a tételben szereplő két kifejezésről, hogy teljesül közöttük az alábbi oszthatóság:
(a,b)c|(ac,bc)Ez viszont az oszthatóság 16.1. Definíciója alapján épp azt jelenti, hogy létezik olyan k elem, amelyre teljesül az alábbi egyenlet:
(a,b)c \cdot k = (ac,bc)Azt fogjuk megmutatni, hogy k egység, mivel ebből a 16.10. Tétel miatt már következik az (a,b)c\sim (ac,bc) asszociáció. Vizsgáljuk hát meg a fenti egyenletet.
Ennek jobboldala ac és bc közös osztója, így az egyenlet baloldala is. Fennállnak tehát az alábbi oszthatóságok:
\begin{aligned}(a,b)c\cdot k &|ac \\ (a,b)c\cdot k &|bc\end{aligned}Mivel a bizonyítás elején az általánosság megsértése nélkül feltehettük, hogy c\neq 0, így mindkét oszthatóságot egyszerűsíteni lehet vele a 17.8. Tétel miatt. Ekkor ezt kapjuk:
\begin{aligned}(a,b)k &|a \\ (a,b)k &|b\end{aligned}Azt kaptuk tehát, hogy (a,b)k közös osztója a-nak és b-nek, és így osztója az ő kitüntetett közös osztójuknak. Azaz:
(a,b)k|(a,b)Mivel a bizonyítás elején láttuk, hogy létezik egységelem, valamint (a,b)\neq 0, így mindkét oszthatóságot egyszerűsíteni lehet (a,b)-vel a 17.8. Tétel miatt. Ekkor ezt kapjuk:
k|1A k elem tehát osztója az egységelemnek, emiatt a 16.5. Tétel értelmében valóban egység, és így (a,b)c\cdot k=(ac,bc)-ből következik az (a,b)c\sim (ac,bc) asszociáció, ahogyan a tétel állítja.
∎Végül igazoljuk az úgynevezett euklidészi lemmát. Ez arra ad feltételt, hogy egy elem mely esetekben osztója egy adott szorzat valamelyik tényezőjének, ha egyébként magának a szorzatnak osztója. Az előző részben már megemlítettük, hogy ez általánosságban nem igaz. Például 8|2\cdot 12, ugyanakkor sem a 8|2, sem pedig a 8|12 oszthatóság nem teljesül. A 16.13. Definícióban épp azokat az elemeket neveztük prímeknek, amelyek bármely olyan szorzatra teljesítik ezt a kritériumot, amelynek egyébként osztói.
Az euklidészi lemma a prímtulajdonságnál gyengébb feltételt határoz meg erre vonatkozóan. Ez alapján egy elemnek nem kell prímnek lennie ahhoz, hogy egy szorzat valamely tényezőjének osztója legyen. Viszont szükséges, hogy a másik tényezőjével a „lehető legkevesebb közös osztójuk legyen”. Először is tisztázzuk, hogy mikor mondjuk két elemről, hogy a „lehető legkevesebb közös osztójuk van”. Ennek az esetnek külön neve is van, amelyet a továbbiakban gyakran fogunk használni.
17.10. Definíció (Relatív prímek):
Legyen R tetszőleges integritástartomány. Amennyiben valamely a és b elemeknek minden közös osztója egység, akkor azt mondjuk, hogy a és b relatív prímek egymáshoz.
♣Megjegyzés:
Figyelem! Ez a fogalom nem azonos sem a felbonthatatlanok sem pedig a prímek fogalmával. Abból ugyanis, hogy két elem egymáshoz relatív prím, még nem következik, hogy közülük bármelyik is akár felbonthatatlan, akár prím lenne. Például a \Z gyűrűben a 8 és a 9 egész számoknak nincs a -1-en és az 1-en (tehát a gyűrű egységein) kívül más közös osztójuk, így relatív prímek. Ám egyikük sem felbonthatatlan (és így a 16.14. Tétel miatt nem is prím), hiszen a 8=2\cdot 4 és a 9=3\cdot 3 nemtriviális felbontások.
Megjegyezzük még, hogy egységelemes integritástartomány esetén az az állítás, miszerint a és b relatív prím ekvivalens azzal az állítással, hogy (a,b)\sim 1. Hiszen egyrészt ha létezik egységelem, akkor léteznek egységek is, amelyek minden elemnek osztói, így a-nak és b-nek közös osztói. Másrészt más közös osztójuk nem is lehet, mivel relatív prímek. Ebből következik, hogy pontosan az egységek a kitüntetett közös osztók, mivel ők egymásnak is osztói.
♣Ezek után az euklidészi lemma a következőképpen fogalmazható meg.
17.11. Tétel (Euklidészi lemma):
Legyen R egy tetszőleges integritástartomány, amelyben bármely két elemnek létezik kitüntetett közös osztója. Ekkor ha valamely a, b és c elemek esetén teljesül az a|bc oszthatóság és a relatív prím b-hez, akkor teljesül az a|c oszthatóság is.
♣Például a \Z gyűrűben 4|9\cdot 8, és mivel 4 és 9 relatív prímek, ezért 4|8.
Bizonyítás:
Az általánosság megsértése nélkül feltételezhetjük, hogy R nem a 14.12. Definíció szerinti nullgyűrű. Ha ugyanis az lenne, akkor az egyetlen elem a 0 lenne, így nyilván teljesülne a tétel állítása bármiféle feltétel nélkül is.
Ha R nem a nullgyűrű, akkor legalább két eleme van, amelyek közül az egyik nyilván nem a nullelem. Mivel azt mondtuk, hogy bármely két elemnek létezik kitüntetett közös osztója, így ennek a kettőnek is, emiatt a 17.5. Tétel 3. pontja alapján R egységelemes.
A tétel szövegének megfelelően tegyük fel, hogy teljesül az a|bc oszthatóság, valamint a és b relatív prímek, azaz a 17.10. Definíció utáni megjegyzés miatt (a,b)\sim 1.
Mivel R egységelemes, ezért a 16.2. Tétel 1. pontja miatt teljesül az a|a oszthatóság, és így ugyanezen tétel 7. pontja miatt az a|ac oszthatóság, továbbá a tétel szövegéből tudjuk, hogy teljesül a|bc is. Az a elem tehát közös osztója ac-nek és bc-nek, így osztója ezek kitüntetett közös osztójának. Azaz:
a|(ac,bc)A 17.9. Tétel miatt azonban teljesül az (ac,bc)\sim (a,b)c asszociáció, így:
a|(a,b)cVégül, mivel (a,b)\sim 1 – tehát (a,b) egység –, ezért teljesül az (a,b)c\sim c asszociáció is, azaz valóban a|c, ahogy a tétel állítja.
∎Az euklidészi lemma felhasználásával mostmár igazolhatjuk a kitüntetett közös osztó létezésének jelentőségét a számelmélet alaptétele kapcsán.
17.12. Tétel:
Legyen R egy tetszőleges integritástartomány. Ha bármely két elemnek létezik kitüntetett közös osztója, akkor R-ben minden felbonthatatlan elem prímtulajdonságú.
♣Bizonyítás:
Tegyük fel, hogy p felbonthatatlan elem R-ben. Azt kell megmutatni, hogy prímtulajdonságú, azaz hogy ha valamilyen a és b elemek esetén teljesül a p|ab oszthatóság, de p\nmid a, akkor szükségképpen teljesül a p|b oszthatóság.
Tegyük hát fel, hogy p\nmid a. Mivel azt mondtuk, hogy bármely két elemnek létezik kitüntetett közös osztója R-ben, ezért nyilván p-nek is és a-nak is létezik a (p,a) kitüntetett közös osztója.
Mivel (p,a) közös osztó, ezért nyilván teljesül a (p,a)|p oszthatóság. De mivel p felbonthatatlan, ezért a 16.11. Definíció miatt az alábbi két eset lehetséges:
\begin{aligned}(p,a)&\sim p \\ (p,a)&\sim 1\end{aligned}Azaz (p,a) vagy egység, vagy pedig p valamely asszociáltja. Ez utóbbi azonban lehetetlen, hiszen – lévén, hogy (p,a) közös osztó – teljesül a (p,a)|a oszthatóság, és így (p,a)\sim p miatt teljesülne a p|a oszthatóság is, ami ellentmond a feltételezésünknek, miszerint p\nmid a.
Azt kaptuk tehát, hogy (p,a) csak egység lehet, azaz p és a relatív prímek. Ebből viszont a p|ab oszthatóság és az euklidészi lemma (17.11. Tétel) miatt következik, hogy p|b. Azaz p valóban prímtulajdonságú, ahogy a tétel állítja.
∎Mostmár tehát tudjuk, hogy ha egy integritástartományban bármely két elemnek létezik a kitüntetett közös osztója, akkor minden felbonthatatlan elem prímtulajdonságú. Ebből viszont a 16.17. Tétel miatt következik, hogy teljesül a számelmélet alaptételének egyértelműségi állítása.
Az előző szakasz végén a 17.7. Tételben már láttuk, hogy a kriptográfiai szempontból számunkra fontos \Z gyűrűben HA egy elempárnak létezik kitüntetett közös osztója, AKKOR a legnagyobb közös osztójuk is kitüntetett. Megemlítettük ugyanakkor, hogy ez a tétel még nem garantálja azt, hogy bármely két egész számnak létezik a kitüntetett közös osztója. Ennek igazolására most megismerkedünk egy igen fontos számelméleti algoritmussal.
Az euklidészi algoritmus alapgondolata
Az euklidészi algoritmus az egyik legősibb, igen gyakran használt számelméleti algoritmus. Nevét az ókori görög matematikusról, Euklidészről kapta, aki Kr.e. 300 körül írta le az Elemek című művében. Ez egy rendkívül hatékony módszert határoz meg két egész szám kitüntetett közös osztójának előállítására.
Az általános iskolából nyilván mindenki emlékszik arra a módszerre, amely a két számnak a számelmélet alaptétele szerinti prímtényezős felbontásából indul ki. Mivel egy egész szám és az ellentettje ugyanúgy viselkedik oszthatóság szempontjából (lásd a 16.8. Tétel 1. pontját), ezért elegendő csak a pozitív egészekre és a pozitív prímtényezőkre szorítkozni. Ha tehát rendelkezésünkre áll a két szám prímtényezős felbontása, akkor a keresett kitüntetett közös osztó prímtényezős felbontása pontosan azokból a prímtényezőkből fog állni, amelyek mindkét szám felbontásában szerepelnek. Így például a 18 és a 45 kitüntetett közös osztója 9, mivel a két eredeti szám felbontása 18=2\cdot 3\cdot 3 és 45=3\cdot 3\cdot 5. A két felbontás közös prímtényezői adják a kitüntetett közös osztót, azaz 3\cdot 3=9.
Ezzel a módszerrel – bár helyes – két alapvető probléma van. Egyrészt azt még nem bizonyítottuk, hogy a \Z gyűrűben valóban teljesül a számelmélet alaptétele, így azt elméletben még nem használhatnánk. Másrészt viszont – és ez egy jóval nagyobb, gyakorlati probléma – ehhez a módszerhez szükségünk van a két szám prímtényezős felbontására. Ennek meghatározására jelenlegi tudásunk szerint azonban nem létezik hatékony eljárás, habár ez még bizonyításra vár. Hogy mit értünk „hatékony eljárás” alatt, arról a 6., 7. és 8. részekben volt szó részletesen, így azt nem ismételnénk meg. Azonban saját bőrünkön is érzékelhetjük a problémát, ha megpróbáljuk megtalálni például a 12\space 439\space 705\space 049 és a 15\space 828\space 713\space 003 kitüntetett közös osztóját ezzel a módszerrel.
Az említett „iskolás” módszert követve persze elkezdhetjük a prímtényezőkre bontást. Hamar beletörik azonban a bicskánk, mivel ezt a két számot szándékosan nagy prímtényezőkből állítottam össze. Nevezetesen:
\begin{aligned}12\space 439\space 705\space 049 &= 2797\cdot 2999\cdot 1483 \\ 15\space 828\space 713\space 003 &= 2999\cdot 1483\cdot 3559 \end{aligned}Innen persze a közös prímtényezők kiválogatása, és a kitüntetett közös osztó kiszámítása már egyszerű:
(12\space 439\space 705\space 049, 15\space 828\space 713\space 003)=2999\cdot 1483=4\space 447\space 517Mondhatnánk, hogy számítógéppel pillanatok alatt prímtényezőire bonthatjuk ezt a két számot. Ez minden bizonnyal így is van az ilyen nagyságrendű számok esetén. A problémát az okozza, hogy a bemeneti számjegyek számának növelésével a prímtényezők kiszámításához szükséges idő nagyon meredeken kezd emelkedni. Olyannyira, hogy például egy 500 számjegyből álló szám prímtényezőire bontása még a világ összes számítógépének is beláthatatlanul sok ideig tartana. A kriptográfiában használt RSA-eljárás algoritmikus biztonsága épp a prímtényezős felbontás feladatának e roppant nehézségén alapszik.
Az euklidészi algoritmus ezzel szemben egy olyan eljárást ad két egész szám kitüntetett közös osztójának kiszámítására, amelyhez nincs szükség a két szám prímtényezőire. Az algoritmus alapötlete az oszthatóság tulajdonságairól szóló 16.2. Tétel 6. és 7. pontjainak egy egyszerű következményén alapul. Nézzük is meg ezt az összefüggést.
17.13. Tétel:
Legyen R egy tetszőleges integritástartomány. Ekkor ha valamely a és b elemeknek létezik az (a,b) kitüntetett közös osztója, akkor tetszőleges k elem esetén érvényes az alábbi összefüggés:
(a,b)=(b, a-kb) ♣Bizonyítás:
Mivel (a,b) közös osztó, ezért teljesülnek az alábbi oszthatóságok:
\begin{aligned}(a,b)&|a \\ (a,b)&|b \end{aligned}A második oszthatóság jobboldala a 16.2. Tétel 7. pontja miatt tetszőleges k elemmel megszorozható:
(a,b)|kbAz (a,b) tehát osztója a-nak és kb-nek, így ugyanezen tétel 6. pontja miatt osztója a különbségüknek is:
(a,b)|a-kbAzt kaptuk, hogy az (a,b) elem a-n és b-n kívül közös osztója b-nek és a-kb-nek is. Már csak azt kell megmutatni, hogy ennek az elempárnak szintén kitüntetett közös osztója, azaz bármely más közös osztónak többszöröse. Tegyük fel például, hogy d egy ilyen közös osztó, azaz:
\begin{aligned}d&|b \\ d&|a-kb \end{aligned}Az első oszthatóság jobboldalát a 16.2. Tétel 7. pontja miatt k-val megszorozhatjuk:
d|kbA d elem tehát osztója a-kb-nek és kb-nek, így ugyanezen tétel 6. pontja miatt osztója az összegüknek is:
d|a-\cancel{kb}+\cancel{kb}Azt kaptuk tehát, hogy d közös osztója a-nak és b-nek, emiatt osztója az ő kitüntetett közös osztójuknak, azaz (a,b)-nek is. Igenám, de fentebb már láttuk, hogy (a,b) nem csak az a és b elemek közös osztója, hanem a b és a-kb elemeknek is. Így ő végülis ezeknek az elemeknek is kitüntetett közös osztója, azaz valóban:
(a,b)=(b,a-kb) ∎Nézzük is meg, hogy miképpen tudunk profitálni ebből az imént kapott (a,b)=(b, a-kb) összefüggésből. Egyelőre tegyük fel, hogy az egész számok \Z gyűrűjében vagyunk, mind a, mind pedig b pozitív egészek, valamint a\gt b. Később majd általánosítani fogjuk az algoritmust tetszőleges esetre, sőt tetszőleges integritástartományra, most azonban a működés alapelvének megértése a cél.
Rajzoljunk fel két „rudat”, amelyek méretarányosan tükrözik e két szám nagyságát. Kezdjünk el lenyesegetni b-nek megfelelő hosszúságú darabokat az a-t jelölő rúdból mindaddig, amíg a maradék kisebb nem lesz, mint b, vagy akár el nem tűnik teljesen. Ezt a folyamatot láthatjuk az alábbi ábrán, amelyen a maradék rudacska hosszának megfelelő számot r_1-gyel jelöltük:
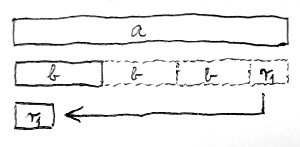
Ha belegondolunk, tulajdonképpen az történt, hogy az a pozitív egész számot sikerült kifejeznünk „valahányszor b, meg egy kis maradék” alakban:
a=k_1b+r_1Ráadásul – és ez kulcsfontosságú – az r_1 maradékra teljesül, hogy legalább 0, viszont szigorúan kisebb b-nél:
b\gt r_1\geq 0A fenti egyenletből az r_1 maradékot ki tudjuk fejezni r_1=a-k_1b alakban. Ez azért baromi jó, mivel az imént bizonyított tétel alapján az (a,b) kitüntetett közös osztó meg fog egyezni a (b,r_1) kitüntetett közös osztóval. Az eredeti számok közös osztójának kiszámítását tehát sikerült két kisebb szám közös osztójának kiszámítására visszavezetni. Most folytassuk ugyanezt a lenyesegetős eljárást a b és r_1 számokkal. Ez látható az alábbi ábrán kinagyítva:
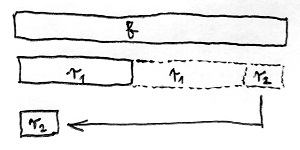
Ekkor tulajdonképpen a b egész számot sikerült kifejeznünk „valahányszor r_1, meg egy kis maradék” alakban. Ezt az eljárást folytatva a következő sorozathoz jutunk:
\begin{aligned}a&=k_1b+r_1 \\ b&=k_2r_1+r_2 \\ r_1&=k_3r_2+r_3 \\ r_2&=k_4r_3+r_4 \\ &\vdots \end{aligned}A kapott maradékok így alakulnak:
b\gt r_1\gt r_2\gt r_3\gt r_4\gt \ldots \geq 0Mindeközben pedig a keresett kitüntetett közös osztóra igaz lesz az alábbi egyenlőségsorozat:
(a,b)=(b,r_1)=(r_1,r_2)=(r_2,r_3)=\ldotsA maradékok tehát egyre kisebbek és kisebbek lesznek, miközben mindegyikről tudjuk, hogy 0-nál semmiképpen sem lehetnek kisebbek. Ezért érezhetően véges számú lépés után valamelyik maradék előbb-utóbb biztosan 0 lesz. A következő szakaszban megmutatjuk, hogy ez valóban a Peano-axiómarendszer egy következménye. Egyelőre tegyük fel, hogy ez tényleg így van, és az utolsó nemnulla maradék r_n. Ekkor befejezhetjük az eljárást, hiszen r_n\neq 0 és r_n|0 ugye teljesül, így alkalmazhatjuk a 17.5. Tétel 4. pontjában foglaltakat. Ez alapján megkaptuk a keresett kitüntetett közös osztót:
(a,b)=(r_n,0)=r_nMaradékos osztásnak nevezzük azt a műveletet, melynek során kiszámítjuk, hogy egy szám egy másikkal osztva mennyi maradékot ad. A maradékos osztás – itt nem részletezett digitális áramköri okok miatt – egy számítógép számára rendkívül hatékonyan elvégezhető. Ráadásul megmutatható – habár erre most nem térünk ki –, hogy az algoritmushoz szükséges maradékos osztások száma a kisebbik bemenet számjegyeinek a számával egyenesen arányos. Ez azt jelenti, hogy még az 500-jegyű számok tartományában is nagyságrendileg pár száz maradékos osztásból megkaphatjuk a kitüntetett közös osztót. Egy átlagos számítógép számára ez egy szemvillanás alatt elvégezhető. Ezzel szemben a prímtényezős módszer az idők végezetéig is eltartana ebben a számtartományban.
E gyorsaság demonstrálására nézzük is meg, hogy mennyire gyorsan kapjuk meg a fentebbi példában szereplő 12\space 439\space 705\space 049 és 15\space 828\space 713\space 003 számok kitüntetett közös osztóját. A maradékos osztás műveletét könnyedén el tudjuk végezni a legegyszerűbb kalkulátorral is. Ezt általában a mod (vagy hasonló) feliratú nyomógombbal érhetjük el. Ez egyetlen lépésben képezni fogja nekünk a képződő maradékot. Például a 8\space \text{mod}\space 3 műveletet elvégezve az eredmény 2, mivel a 8-at 3-mal osztva a maradék 2.
Az euklideszi algoritmust a két bemeneti számunkon lefuttatva az alábbi lépéseken keresztül jutunk el a keresett kitüntetett közös osztóig:
\begin{aligned}&(15828713003,12439705049) = \\ =&(12439705049,3389007954) = \\ =&(3389007954, 2272681187) = \\ =&(2272681187,1116326767) = \\ = &(1116326767, 40027653) = \\ =&(40027653, 35580136) =\\= &(35580136,4447517) =\\=&(4447517, 0)\end{aligned}A keresett kitüntetett közös osztó tehát 4\space 447\space 517. Valóban ugyanazt az eredményt kaptuk, mint a prímtényezős felbontást használó módszerrel, csak épp nem sok ezer (vagy épp millió) osztáspróbával, hanem mindössze 7 maradékos osztással. Úgy gondolom ez eléggé meggyőző, amikor hatékonyságról beszélünk.
A végtelen leszállás módszere
Hamarosan azt fogjuk megvizsgálni, hogy az imént tanult eljárást hogyan tudjuk olyan integritástartományokra is kiterjeszteni, amelyek nem feltétlenül számokat tartalmaznak. Ehhez először megismerkedünk a végtelen leszállás néven ismeretes indirekt bizonyítási módszerrel. Ezzel fogjuk tudni igazolni, hogy az euklidészi algoritmus véges számú lépés után valóban befejeződik.
A módszer a természetes számok \N halmazának most következő, fontos tulajdonságán alapszik.
17.14. Tétel (A természetes számok minimumtétele):
Ha P a természetes számok \N halmazának tetszőleges nemüres részhalmaza, akkor P-nek van minimuma a 12.13. Definíció szerinti \leq relációra nézve. Minimum alatt egy olyan p_0 elem létezését értjük, amelyre tetszőleges P-beli p elem esetén teljesül a p_0\leq p reláció.
♣Eszerint tehát sehogyan sem lehet kiválogatni véges vagy akár végtelen sok természetes számot úgy, hogy ezek között ne lenne legkisebb. Vegyük észre, hogy ez az egész számok \Z halmazára például nem érvényes, mivel bármilyen egész számnál létezik nála kisebb egész szám, hiszen itt a számegyenes mindkét irányban végtelen. De bizonyos számkörökben még csak erre sincs feltétlenül szükség. Habár a törtszámokat még nem építettük fel az axiómák segítségével, de intuitív módon belátható, hogy bármely két törtszám között végtelen sok további törtszám létezik. Következésképp a számegyenes semmilyen véges hosszú szakaszára nem igaz a fenti tétel. Az tehát, hogy a természetes számokra mégis igaz, egyáltalán nem magától értetődő, akármennyire is annak látszik. Nézzük is meg, hogy miért.
Bizonyítás:
Tegyük fel indirekt, hogy P egy olyan galád részhalmaza \N-nek, amelynek nincs minimuma. Jelöljük ezen kívül Q-val \N-nek azt a részhalmazát, amely minden olyan természetes számot tartalmaz, amely kisebb P bármely eleménél. Azaz egyrészt a Q halmaz minden q elemére teljesül, hogy bármely P-beli p elem esetén q\lt p, másrészt semmilyen Q halmazon kívüli elemre nem tejesül ez a tulajdonság. Egyelőre még nem tudjuk, hogy mely természetes számok tartoznak P-be, és melyek Q-ba. Az viszont bizonyos, hogy ha egy q természetes szám Q-ba tartozik, akkor nem tartozhat egyúttal P-be is, máskülönben teljesülne a q\lt q reláció, ami a 12.13. Definíció alapján lehetetlen. A következő tehát a szituáció:
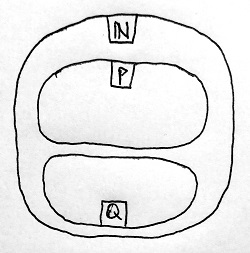
Azt kell megmutatnunk, hogy valójában minden természetes szám Q-ba tartozik, azaz Q=\N, hiszen ebből következne, hogy P csak az üres halmaz lehet. Ezt teljes indukcióval fogjuk bizonyítani, amelyre a Peano-axiómarendszer 11.1. Definíciójának 4. pontja ad lehetőséget.
Kezdjük a 0-val. Tegyük fel indirekt, hogy a 0 nincs benne Q-ban, azaz létezik olyan P-beli p elem, amelyre nem teljesül a 0\lt p reláció. Ekkor viszont a rendezési reláció trichotómiája miatt (lásd a 12.20. Tételt) szükségképpen teljesülne a p\leq 0 reláció. Ez a 12.13. Definíció miatt azt jelentené, hogy létezik olyan k természetes szám, amelyre p+k=0. A 12.17. Lemma alapján azonban a természetes számok körében egy összeg csak úgy lehet 0, ha mindkét tagja 0, és így p=0 lenne.
Azt kaptuk tehát, hogy ha a 0 nem lenne benne Q-ban, akkor szükségképpen benne kellene lennie P-ben. Ez viszont lehetetlen, hiszen bármely n természetes számra teljesül 0\leq n reláció, és így P-nek a 0 minimuma lenne. Tehát hibás volt az indirekt feltételezésünk, így a 0-nak szükségképpen Q-ban kell lennie.
Tegyük most fel, hogy egy valamilyen n természetes számról már tudjuk, hogy Q-ban van (az előbb láttuk, hogy a 0 például ilyen). Azt szeretnénk megmutatni, hogy ekkor s(n) (azaz n rákövetkezője) is benne van a Q-ban. Ezt ismét indirekt módon bizonyítjuk. Tegyük ezért fel az állítás ellenkezőjét, azaz hogy s(n) nincs benne a Q halmazban. Ez egyrészt azt jelentené, hogy létezne olyan p-vel jelölt elem a P halmazban, amelyre nem teljesül az s(n)\lt p reláció. Ismét a trichotómia miatt ekkor szükségképpen teljesülne a p\leq s(n) reláció. Másrészt, mivel ugye n az indukciós feltétel miatt benne van a Q halmazban, így teljesül az n\lt p reláció. Azaz összefoglalva:
n\lt p\leq s(n)Egyrészt a baloldali \lt reláció a 12.13. Definíció miatt azt jelenti, hogy n+k_1=p teljesül valamilyen k_1\neq 0 természetes számra. Másrészt a Peano-összeadás 11.4. Definíciója miatt a jobboldali kifejezés így írható át: s(n)=s(n+0)=n+s(0). Ezt kapjuk tehát:
\underbrace{n+k_1}_{=p} \leq n+s(0)Ez ismét a 12.13. Definíció miatt azt jelenti, hogy létezik olyan k_2 természetes szám, amelyre teljesül az alábbi egyenlet:
\underbrace{n+k_1}_{=p} + k_2 = n+s(0)A 12.16. Lemma alapján mindkét oldalt egyszerűsíthetjük n-nel, így ezt kapjuk:
k_1+k_2=s(0)Azonban tudjuk, hogy k_1\neq 0, így a Peano-axiómarendszer 11.1. Definíciójának 3. pontja alapján van olyan k_0 természetes szám, aminek k_1 a rákövetkezője, azaz s(k_0)=k_1. Így:
\underbrace{s(k_0)}_{=k_1} + k_2=s(k_0+k_2)=s(0)A Peano-axiómarendszer 11.1. Definíciójának 2. pontja miatt ekkor k_0+k_2=0 adódik, amelyből a 12.17. Lemma alapján k_0=0 és k_2=0 következik. Így tehát k_1=s(k_0)=s(0). Azaz:
\overbrace{n+\underbrace{s(0)}_{=k_1}}^{=p}+\underbrace{0}_{=k_2}=n+s(0)=s(n)És így:
p+0=p=s(n)Egyrészt tehát azt kaptuk, hogy ha s(n) nem lenne Q-ban, akkor szükségképpen P-ben kellene lennie. Másrészt viszont az iménti gondolatmenetet bármely P-beli x elemre megismételve azt kapnánk, hogy x\leq s(n) csak úgy teljesülhet, ha x=s(n). Így tehát a P halmaznak mégiscsak lenne minimuma, nevezetesen s(n). Tehát hibás volt az indirekt feltételezésünk, ezért ha n benne van Q-ban, akkor az ő rákövetkezője is szükségképpen Q-ban kell legyen.
Ezzel kész a teljes indukció, hiszen láttuk, hogy a 0 benne van Q-ban, így az iménti gondolatmenet alapján az ő rákövetkezője is, majd annak a rákövetkezője, és így tovább a végtelenségig. A Peano-axiómarendszer 11.1. Definíció 4. pontja alapján így minden természetes számot lefedünk, azaz Q=\N. A bizonyítás elején azonban láttuk, hogy ekkor P csak az üres halmaz lehet, azaz valóban nem létezik olyan nemüres részhalmaza \N-nek, amelynek nincs minimuma – épp ahogyan a tétel állítja.
∎A fenti tételen kívül szükségünk lesz még egy állításra, amely a \leq-nél szigorúbb \lt reláció tranzitivitását garantálja. Az előbbi tranzitivitását (tehát azt, hogy a\leq b és b\leq c esetén a\leq c) már megmutattuk a 12.15. Tételben. Nem meglepő módon ez a tulajdonság a szigorú rendezésre is teljesül, ráadásul nem csak a természetes számok között, hanem a teljes \Z halmazon is. Így most ezt mutatjuk meg.
17.15. Tétel:
Tetszőleges a, b és c egész számok esetén ha a\leq b és b\leq c teljesül, valamint az ennél szigorúbb a\lt b vagy b\lt c közül legalább az egyik teljesül, akkor a\lt c is teljesül.
♣Bizonyítás:
Az a\leq b és b\leq c relációk teljesülése, valamint az a\lt b vagy b\lt c relációk közül legalább az egyik teljesülése a 15.18. Definíció miatt azt jelenti, hogy léteznek n és k természetes számok, amelyek közül legalább az egyik nem 0, valamint a+n=b és b+k=c. A második egyenletbe b helyére az első egyenlet baloldalát behelyettesíthetjük: \underbrace{(a+n)}_{=b}+k=c. Ez a kifejezés az összeadás asszociativitása miatt átzárójelezhető: a+(n+k)=c. Az n+k összegről viszont tudjuk, hogy mindkét tagja természetes szám, melyek közül legalább az egyik nem 0. Márpedig a 12.17. Lemma kimondja, hogy ebben az esetben maga az összeg sem 0.
Összefoglalva: létezik olyan nem 0 természetes szám – nevezetesen az n+k –, amelyet a-hoz adva c-t kapunk. Ez a 15.18. Definíció miatt épp azt jelenti, hogy a\lt c.
∎Ezek után már alkalmazhatjuk majd a végtelen leszállás módszerét. Ezt Pierre de Fermat fejlesztette ki a 17. században, és számos fontos eredményhez jutott ennek segítségével. A végtelen leszállás módszere egy indirekt érvelés, melynek során megmutatjuk, hogy ha a szóban forgó állítás hamis, akkor elő lehet állítani egy olyan természetes számokból álló sorozatot, amelynek az imént bizonyított tranzitivitás miatt nincs minimuma. Ez ugye ellentmondana a fenti minimumtételnek, és így a Peano-axiómáknak. A bizonyítandó állítás tehát nem lehet hamis, következésképp igaznak kell lennie. A hátralévő részben ezt a módszert fogjuk felhasználni annak megmutatásához, hogy a számelmélet alaptétele teljesül gyűrűk egy speciális osztályában, az úgynevezett euklidészi gyűrűkben.
Euklidészi gyűrűk
Az euklidészi algoritmus alapgondolatának fentebbi ismertetésekor feltételeztük, hogy az a és b bemenet egy-egy pozitív egész szám, amelyeknek tehát a kitüntetett közös osztóját keressük. Az alapötletet a 17.13. Tétel tétel szolgáltatta, mely szerint ha a és b között el tudjuk végezni a maradékos osztást, akkor az (a,b) kitüntetett közös osztó – amennyiben egyáltalán létezik – meg fog egyezni a (b,r_1) kitüntetett közös osztóval, ahol r_1 a maradékos osztás során képződő maradék. Ezek után a b és r_1 között kell maradékos osztást végezni, így ha a képződő maradék r_2, akkor a (b,r_1) kitüntetett közös osztó – amennyiben létezik – meg fog egyezni az (r_1,r_2) kitüntetett közös osztóval.
Ezt az eljárást tovább folytatjuk mindaddig, míg valamelyik lépésben a képződő maradék 0 nem lesz. Ha az utolsó nemnulla maradék r_n, akkor végülis azt kaptuk, hogy az (a,b) kitüntetett közös osztó meg fog egyezni az (r_n,0) kitüntetett közös osztóval. Ez viszont a 17.5. Tétel 4. pontja alapján egységelemes gyűrűkben – és csak azokban – biztosan létezik, és r_n-nel egyezik meg.
Már csak azt kell belátni, hogy véges számú lépés után biztosan 0 lesz a képződő maradék. Ezt fentebb csak feltételeztük, most azonban a végtelen leszállás módszerével könnyedén adódik. Az a és b elemek maradékos osztásánál ugyanis fontos követelmény volt, hogy az a elemet úgy tudjuk kifejezni „valahányszor b, meg egy kis maradék” alakban, hogy a maradék mindig szigorúan kisebb legyen, mint b. Ha – feltételezve, hogy a maradékos osztást mindig el tudjuk végezni – az eljárás nem érne véget véges számú lépés után, akkor az r_1 \gt r_2 \gt r_3 \gt \ldots sorozat a \gt reláció 17.15. Tétel szerinti tranzitivitása miatt a természetes számoknak egy olyan részhalmaza lenne, amelynek nem lenne minimuma. Ez viszont, mint azt a 17.14. Tételben láttuk, lehetetlen.
Igenám, csakhogy mi tetszőleges integritástartományra szeretnénk kiterjeszteni ezt az algoritmust. Márpedig például az egész számok \Z gyűrűjére nem érvényes a minimumtétel, más integritástartományok pedig még csak nem is feltétlenül számokból, hanem egyéb objektumokból állhatnak. Vegyük azonban észre, hogy minket nem konkrétan a képződő maradékok érdekelnek, hanem azoknak a gyűrű nullelemétől való – bizonyos absztrakt értelemben vett – „távolsága”. Ha valahogy sikerülne az adott gyűrűben értelmezni egy olyan távolságfogalmat, amely biztosítja, hogy az euklidészi algoritmus során bármely lépésében a képződő maradék nullelemtől mért absztrakt „távolsága” szigorúan kisebb legyen, mint az előző lépésben képződő maradék ugyanilyen értelemben vett nullelemtől való „távolsága”, akkor nyert ügyünk lenne.
A most következő definíció külön nevet ad az olyan integritástartományoknak, amelyekben értelmezhető ilyen absztrakt távolságfogalom.
17.16. Definíció (Euklidészi gyűrű):
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Tegyük fel, hogy R elemein értelmezve van egy olyan f:R\to \N függvény, amely eleget tesz az alábbi követelményeknek:
- Tetszőleges a elem esetén f(a)=0 akkor és csak akkor teljesül, ha a=0_R, ahol 0_R az R gyűrű nullelemét, míg 0 a „nullának” nevezett természetes számot jelöli.
- Tetszőleges a és b\neq 0_R elemek esetén létezik olyan k hányados és r maradék az R gyűrűben, hogy a=k\cdot b + r és f(r)<f(b). Ezt a „műveletet” az a és b elemek közötti maradékos osztásnak vagy euklidészi osztásnak nevezzük.
Ekkor az f függvényt az R integritástartományon értelmezett euklidészi normának nevezzük. Amennyiben az R integritástartományon létezik (definiálható) euklidészi norma, úgy R-et euklidészi gyűrűnek nevezzük.
♣Megjegyzés:
Az euklidészi gyűrű fogalmának bevezetése mögött az a motiváció, hogy az euklidészi algoritmus ne csak a nemnegatív egész számok halmazán működhessen, hanem azt ki lehessen terjeszteni általános integritástartományok lehetőleg minél szélesebb körére is. A „működés” alatt egyrészt azt értjük, hogy az eljárás véges számú lépés után garantáltan befejeződjön. Ezt az euklidészi normának a definícióban szereplő 2. tulajdonsága fogja biztosítani a végtelen leszállás módszerén keresztül.
Másrészt viszont azt is szeretnénk, hogy a keresett kitüntetett közös osztó mindenképpen létezzen. Ehhez az kell, hogy az algoritmus leállása után az utolsó nemnulla r_n maradékból képzett (r_n,0) kitüntetett közös osztó is létezzen, máskülönben semmit nem érnénk azzal, hogy befejeződött az algoritmus. Ez viszont a 17.5. Tétel 4. pontja alapján csak egységelemes gyűrűkben létezik.
Ez az oka annak, hogy az euklidészi gyűrűk definíciójában megköveteljük, hogy létezzen egységelem.
♣Nem meglepő módon tehát a keresett távolságfogalom egy függvény lesz, amely az R integritástartomány elemeit a természetes számok \N halmazára képezi le. Egy elemhez hozzárendelt szám fogja „mérni” az adott elemnek a nullelemtől való absztrakt „távolságát”. A definícióban szereplő első követelmény logikus módon azt fogalmazza meg, hogy csak és kizárólag a nullelem távolsága legyen 0. A második követelmény pedig lényegében a pozitív egész számokon értelmezett maradékos osztás általánosításaként fogható fel.
Fontos megjegyezni még, hogy egy euklidészi gyűrűnek, mint algebrai struktúrának nem része a konkrét euklidészi norma. A fenti definíció szerint elegendő, ha létezik ilyen norma az adott gyűrűn. Sőt, ha egy integritástartomány euklidészi gyűrű, akkor általában több euklidészi norma is értelmezhető rajta. Általában azonban igen nehéz annak eldöntése, hogy egy R integritástartomány euklidészi gyűrű-e vagy sem. Természetesen ha találunk egy olyan függvényt, amely euklidészi norma, akkor R nyilván euklidészi gyűrű. Ha azonban nem találunk ilyen függvényt, akkor ez még önmagában nem elég a nemleges válaszhoz. Ehhez azt kéne igazolni, hogy ilyen függvény egyáltalán nem is létezik az adott R-hez. Ez számos nyitott kérdéshez és sejtéshez vezet, melyek a mai napig bizonyítatlanul várják az utókor ötleteit.
Meg fogjuk ugyanakkor mutatni, hogy az egész számok \Z gyűrűje euklidészi gyűrű. Ehhez a 15. részben bevezetett rendezési reláció felhasználásával mutatni fogunk egy olyan függvényt, amely \Z-ből \N-be képez, és amely eleget tesz az euklidészi normákra vonatkozó követelményeknek. Előbb azonban azt fogjuk megvizsgálni, hogy miért olyan fontosak az euklidészi gyűrűk a számelmélet alaptételének szempontjából. Például azért, mert ezekben bármely két elemnek létezik kitüntetett közös osztója, és így a 17.12. Tétel értelmében teljesül bennük a számelmélet alaptételének egyértelműségi állítása. Ezt az alábbi tétel mondja ki.
17.17. Tétel:
Ha egy R integritástartomány euklidészi gyűrű, akkor bármely két R-beli elemnek létezik kitüntetett közös osztója.
♣Bizonyítás:
A bizonyításhoz az euklidészi algoritmus általánosított változatát fogjuk felhasználni. Legyen a és b az R integritástartomány két tetszőleges eleme, és jelöljük 0_R-rel a nullelemet, 0-val pedig a „nulla” természetes számot. Ha a vagy b közül bármelyik 0_R, akkor létezik kitüntetett közös osztójuk. Ha mindkettő 0_R, akkor a 17.5. Tétel 1. pontja miatt. Ha pedig csak az egyikük, akkor viszont – mivel minden euklidészi gyűrű a 17.16. Definíció alapján egységelemes – ugyanezen tétel 4. pontja miatt.
Feltételezhetjük tehát, hogy a\neq 0_R és b\neq 0_R. Mivel R euklidészi gyűrű, ezért értelmezhető rajta valamilyen f euklidészi norma. Ekkor a és b között elvégezhető a maradékos osztás az f norma szerint. Azaz létezik k_1 hányados és r_1 maradék R-ben úgy, hogy egyrészt fennálljon az f(r_1)<f(b) szigorú egyenlőtlenség, másrészt teljesüljön az alábbi egyenlet:
a=k_1b+r_1Ha f(r_1)=0, akkor az euklidészi norma 17.16. Definíciója miatt r_1=0_R, és így a 17.13. Tétel, valamint a 17.5. Tétel 4. pontja alapján b lesz a kitüntetett közös osztó, hiszen (a,b)=(b,r_1)=(b,0_R)=b. Ha f(r_1)\neq 0, akkor r_1\neq 0_R, és így b és r_1 között ismét el tudjuk végezni az f norma szerinti maradékos osztást.
Ezt az eljárást mindaddig folytatjuk, amíg meg nem kapjuk a nullelemet maradékként valamelyik lépésben. Ekkor – szintén a 17.13. Tétel, valamint a 17.5. Tétel 4. pontja miatt – az utolsó olyan maradék lesz a kitüntetett közös osztó, amely nem a nullelem.
Az eljárás garantáltan véget fog érni véges számú lépés után, máskülönben a maradékos osztások során előállna az alábbi, természetes számokból álló végtelen sorozat:
f(b)\gt f(r_1)\gt f(r_2)\gt f(r_3)\gt \ldotsEz a 17.15. Tétel miatt \N-nek egy olyan részhalmaza lenne, amelynek nincs minimuma. Ez viszont a 17.14. Tétel miatt lehetetlen, így az euklidészi algoritmus garantáltan leáll véges számú lépés után, és előállítja az a és b kitüntetett közös osztóját, amely az utolsó nemnulla maradék lesz.
∎Hamarosan látni fogjuk, hogy ennél több is igaz. Nevezetesen: nemcsak a prímtényezős felbontás egyértelműsége, hanem a létezése is garantált euklidészi gyűrűkben.
Euklidészi norma a \Z gyűrűn
Előbb azonban megmutatjuk, hogy az egész számok \Z gyűrűje euklidészi gyűrű. Ehhez a 15. részben bevezetett rendezési reláció lesz a kulcs (lásd a 15.18. Definíciót). Ennek segítségével egy függvényt fogunk értelmezni a \Z halmazon, majd megmutatjuk, hogy az egy euklidészi norma. Nézzük először a kérdéses függvényt.
17.18. Definíció (Egész számok abszolútértéke):
Definiáljunk egy f:\Z \to \N függvényt a következőképpen:
f(a) = \begin{cases} a &\text{ha } a\geq 0 \\ -a &\text{ha } a\lt 0 \end{cases}Ekkor az f(a) természetes számot az a egész szám abszolútértékének nevezzük. Ennek jelölése: |a|.
♣Amennyiben az egész számokat a mindkét irányban végtelen számegyenesen ábrázoljuk, akkor ez a függvény intuitív módon valóban a 0 egész számtól való „távolságot” méri ezen az egyenesen. Ez alapján például az 5 és a -5 egész számok egyaránt 5 „távolságra” vannak a 0-tól. Azaz: |5|=|-5|=5. Ezt a „távolságmérést” szemlélteti az alábbi ábra:
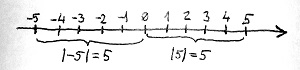
Az abszolútérték-függvénynek a következő tétel miatt van jelentősége számunkra.
17.19. Tétel:
A 17.18. Definíció szerinti f(a)=|a| abszolútérték-függvény egy euklidészi norma a \Z gyűrűn. Más szavakkal: \Z egy euklidészi gyűrű.
♣Bizonyítás:
Az abszolútérték-függvény képhalmaza a 17.18. Definíció alapján valóban a természetes számok \N halmaza, hiszen az abszolútérték biztosan nemnegatív. A \Z gyűrű nullelemének képe szintén a definíció alapján a 0 természetes szám. Visszafelé: ha |a|=0, akkor az alábbi két eset lehetséges:
\begin{aligned}a&=0\\-a&=0\end{aligned}Az \Z gyűrűben tehát pontosan a nullelemnek lesz 0 az abszolútértéke, azaz teljesül az euklidészi normákra vonatkozó 1. követelmény (lásd a 17.16. Definíciót). Így már csak azt kell megmutatni, hogy tetszőleges a és b\neq 0 egész számok között elvégezhető a maradékos osztás az abszolútérték-függvény, mint norma szerint. Azaz léteznek k és r egész számok úgy, hogy teljesülnek az alábbiak:
\begin{aligned}a=&kb+r \\ |r|&\lt |b|\end{aligned}Ehhez ki fogjuk használni, hogy a 15.18. Definíció szerinti \leq reláció teljesíti a 15.11. Definícióban megfogalmazott rendezési axiómákat. A bizonyítás konstruktív lesz, azaz k és r létezését azáltal igazoljuk, hogy egy eljárást mutatunk a kiszámításukra. Ez az eljárás a gyakorlatban nem lenne túl hatékony, ám nekünk a bizonyításhoz épp elegendő lesz.
Először szorítkozzunk arra az esetre, amikor egyik bemeneti számunk sem negatív, azaz a\geq 0 és b\gt 0. Tegyük fel továbbá, hogy k_1=0 és r_1=a. Ekkor nyilván teljesül az alábbi:
a=\underbrace{k_1}_{=0}b+\underbrace{r_1}_{=a}Ha r_1\lt b, akkor az eljárást befejezhetjük, és r_1 lesz a keresett maradék. Ha nem – azaz r_1\geq b –, akkor folytatnunk kell az eljárást. A jobboldalhoz hozzáadva és levonva b-t az eredmény nyilván nem változik. Így a fenti egyenlet a disztributivitási szabályokat kihasználva az alábbi alakba írható, megkapva ezáltal a k_2 és r_2 számokat:
a=k_1b+r_1-b+b=\underbrace{(k_1+1)}_{=k_2}b+\underbrace{r_1-b}_{=r_2}Mivel ugye r_1\geq b, és a 15.11. Definíció 1. pontja alapján a rendezési reláció kompatibilis az összeadással, ezért az egyenlőtlenség mindkét oldalához -b-t adva \underbrace{r_1-b}_{=r_2}\geq 0. Igaz továbbá, hogy r_2+b=r_1, és mivel b-ről kikötöttük, hogy nem 0, ezért ez azt jelenti, hogy r_2\lt r_1. Találtunk tehát egy r_1-nél kisebb nemnegatív jelöltet a keresett maradékra.
Ha r_2\lt b, akkor az eljárást befejezhetjük, és r_2 lesz a keresett maradék. Ha nem, akkor az előbbi gondolatmenetet megismételve tudunk találni újabb és újabb nemnegatív jelölteket, melyek mindegyike kisebb, mint az előző lépésben kapott jelölt. Az eljárásnak garantáltan véget kell érnie egyszer, máskülönben az alábbi végtelen hosszú nemnegatív egészekből álló sorozatot kapnánk:
r_1\gt r_2\gt r_3\gt \ldotsEz a természetes számoknak egy olyan részhalmaza lenne, amelynek nem létezne minimuma, ami a 17.14. Tétel alapján lehetetlen. Így megmutattuk, hogy a\geq 0 és b\gt 0 esetén az a elem felírható a=kb+r alakban úgy, hogy teljesüljön a 0\leq r\lt b egyenlőtlenség. Ez az egyenlőtlenség viszont ebben a speciális esetben épp azt jelenti, hogy |r|\lt |b|.
Most általánosítsuk ezt az eredményt először a b\lt 0 esetre. Ekkor a 15.9. Lemma 1. pontja miatt (-b)\gt 0. Így a fenti gondolatmenet alapján az a egész szám felírható a=k(-b)+r=(-k)b+r alakban úgy, hogy teljesüljön a 0\leq r\lt (-b) egyenlőtlenség. Minthogy 0\lt r és b\lt 0, ezért ez az egyenlőtlenség az abszolútértékekre vonatkozóan épp azt jelenti, hogy |r|\lt \underbrace{|b|}_{=|-b|}. Így lefedtük az összes olyan esetet, amikor a\geq 0 és b\neq 0.
Végül nézzük meg, mi van akkor, ha a\leq 0. Ekkor szintén a 15.9. Lemma miatt (-a)\geq 0, és így a fentiek alapján ő felírható (-a)=kb+r alakban úgy, hogy |r|\lt |b|. De ekkor mindkét oldal ellentettjét véve azt kapjuk, hogy a=(-k)b+(-r), miközben teljesül, hogy \underbrace{|-r|}_{=|r|}\lt |b|.
Ezzel már minden esetet lefedtünk, azaz tetszőleges a és b\neq 0 elemek között elvégezhető az abszolútérték-függvény szerinti maradékos osztás. Ez a függvény tehát valóban egy euklidészi norma a \Z gyűrűn.
∎Most tehát már tudjuk, hogy az egész számok \Z gyűrűje egy euklidészi gyűrű. A 17.17. Tétel miatt ez azt jelenti, hogy bármely két egész számnak létezik kitüntetett közös osztója. Ebből viszont a 17.12. Tétel alapján következik, hogy minden felbonthatatlan egész szám prímtulajdonságú, és így a 16.17. Tétel miatt teljesül a számelmélet alaptételének (16.15. Definíció) egyértelműségi állítása. Az utolsó szakaszban megmutatjuk, hogy ennél több is igaz.
A számelmélet alaptétele euklidészi gyűrűkben
A számelmélet alaptételének egyértelműségi állítása pusztán annyit állít, hogy HA egy elemnek egyáltalán létezik felbontása, AKKOR az a tényezők sorrendjétől és asszociáltságtól eltekintve egyértelmű. Most azt fogjuk igazolni, hogy euklidészi gyűrűkben ezen felül a felbontás LÉTEZÉSE is garantált. Ehhez a kulcsot a következő tétel fogja jelenteni.
17.20. Tétel:
Legyen R tetszőleges euklidészi gyűrű, azaz tegyük fel, hogy R-ben létezik valamilyen f:R \to \N euklidészi norma. Ekkor létezik olyan g:R \to \N euklidészi norma is, amely a 17.16. Definícióban megfogalmazott tulajdonságokon kívül tetszőleges a és b\neq 0_R elemekre teljesíti az alábbi egyenlőtlenségi tulajdonságot is:
g(a)\leq g(ab)A fentiekben 0_R-rel jelöltük az R gyűrű nullelemét.
♣Bizonyítás:
A bizonyítás konstruktív lesz, azaz az f euklidészi norma segítségével definiálni fogunk egy olyan g függvényt, amely maga is euklidészi norma, de ezen felül teljesíti a tételben szereplő egyenlőtlenségi tulajdonságot is.
Tegyük fel, hogy valamilyen tetszőleges k elemre szeretnénk kiszámítani a g(k) függvényértéket. Ehhez először képezzük a k elem összes nemnulla többszörösének az f norma szerinti értékét, azaz minden R-beli x\neq 0 elemre kiszámítjuk az f(kx) természetes számokat. Ezután válasszuk g(k) értékének ezek közül a legkisebbet, amely ugye a 17.14. Tétel miatt biztosan létezik. Más szavakkal a g(k) függvényérték legyen az eredeti f normának a k elem nemnulla többszörösein felvett minimuma.
A g függvény fenti definíciója alapján tehát a tételben szereplő a és b\neq 0_R elemek esetén létezik olyan c\neq 0_R elem, amelyre g(ab)=f(abc) teljesül (nevezetesen épp az a c elem, amelyre az f(abc) felveszi a minimumát). Mivel ugyanakkor az abc szorzat az ab elemen kívül az a elemnek is egy nemnulla többszöröse, ezért ismét a g függvény fenti definíciója miatt g(a)\leq f(abc), azaz valóban teljesül a tételben szereplő egyenlőtlenség:
g(a)\leq \underbrace{g(ab)}_{=f(abc)}Már csak annyit kell igazolni, hogy g is euklidészi norma R-ben. Legyen b\neq 0_R egy tetszőleges nemnulla R-beli elem, valamint válasszuk ki b-nek egy olyan nemnulla többszörösét, amelyre az eredeti f norma épp a minimumát veszi fel (ez ugye biztosan létezik, mint azt már láttuk fentebb). Azaz válasszunk ki egy olyan c\neq 0_R elemet, amelyre g(b)=f(bc) teljesül.
Minthogy b\neq 0_R és c\neq 0_R ezért a nullosztómentesség miatt bc\neq 0_R. Azaz tetszőleges a elem maradékosan elosztható a bc elemmel az eredeti f norma szerint. Ez azt jelenti, hogy létezik olyan k hányados és r maradék, amelyekre teljesülnek az alábbiak:
\begin{aligned}a&=k\cdot (bc) + r \\ f(r)&\lt f(bc)\end{aligned}Egyrészt a g függvény definíciója miatt g(r)\leq f(r\cdot 1) = f(r). Másrészt viszont a c elemet épp úgy választottuk ki, hogy f(bc)=g(b) teljesüljön. Létezik tehát olyan hányados (nevezetesen kc) és maradék (nevezetesen r), amelyre teljesülnek az alábbiak:
\begin{aligned}a&=(kc)\cdot b + r \\ \underbrace{g(r)}_{\leq f(r)}&\lt \underbrace{g(b)}_{=f(bc)}\end{aligned}Azaz tetszőleges a elem tetszőleges b\neq 0_R elemmel elosztható maradékosan a g függvény szerint is, így g valóban egy euklidészi norma.
∎Az iménti tételben szereplő egyenlőtlenségi tulajdonság tehát azt jelenti, hogy egy ilyen euklidészi norma tetszőleges elem bármely nemnulla többszörösére legalább akkora „távolságot” fog mérni, mint magára az elemre. A most következő tétel arra ad választ, hogy mely esetekben teljesül egyenlőség a két oldal között, és mely esetekben nem.
17.21. Tétel:
Legyen R tetszőleges euklidészi gyűrű, g:R\to \N pedig egy olyan euklidészi norma ezen a gyűrűn, amelyre teljesül a 17.20. Tételben szereplő egyenlőtlenségi tulajdonság.
Ekkor tetszőleges a\neq 0_R és b\neq 0_R elemek esetén g(a)=g(ab) akkor és csak akkor teljesül, ha b egység. Minden más esetben szigorú egyenlőtlenség áll fenn, azaz g(a)\lt g(ab).
A fentiekben 0_R-rel jelöltük az R gyűrű nullelemét.
♣Bizonyítás:
Előszöris, mivel R euklidészi gyűrű, így a 17.16. Definíció alapján létezik egységelem.
Ha b egység, akkor a 16.5. Tétel tétel értelmében osztója az egységelemnek. Létezik tehát olyan c elem, amelyre bc=1 teljesül. Mivel c\neq 0_R (máskülönben a bc szorzat a nullelem lenne), ezért a g norma egyenlőtlenségi tulajdonsága miatt g(ab)\leq g(a\underbrace{bc}_{=1})=g(a). Ugyanakkor szintén az egyenlőtlenségi tulajdonság miatt g(a)\leq g(ab). Mindkét irányban fennáll tehát a \leq reláció, így az antiszimmetria miatt szükségképpen g(a)=g(ab).
Azt tehát már tudjuk, hogy ha b egység, akkor valóban teljesül az egyenlőség. Azt kell még megmutatni, hogy más esetben viszont nem teljesül. Ezért most indirekt tegyük fel, hogy b nem egység, ám ennek ellenére teljesül g(a)=g(ab).
Mivel a-ról és b-ről tudjuk, hogy egyik sem a nullelem, ezért a nullosztómentesség miatt az ab szorzat sem lehet az. Emiatt az a elem elosztható maradékosan az ab elemmel a g norma szerint. Azaz létezik olyan k hányados és r maradék, hogy teljesülnek az alábbiak:
\begin{aligned}a&=kab + r \\ g(r)&\lt g(ab)\end{aligned}Az egyenlet mindkét oldalából kab-t levonva ezt kapjuk:
a-kab=rA baloldalt a disztributivitási szabályok miatt (14.12. Definíció 5. pont) így írhatjuk át:
a\cdot (1-kb)=rMivel b-ről indirekt azt mondtuk, hogy nem egység, ezért a 16.5. Tétel miatt nem lehet osztója az egységelemnek. Emiatt kb\neq 1, és így 1-kb biztosan nem a nullelem. A tétel szövegéből tudjuk ugyanakkor, hogy a sem a nullelem, azaz a nullosztómentesség miatt r az a-nak egy nemnulla többszöröse (egész konkrétan 1-kb-szerese), és így a g norma egyenlőtlenségi tulajdonsága miatt teljesül a következő egyenlőtlenség:
g(a)\leq g(\underbrace{a\cdot (1-kb)}_{=r})Azt kaptuk tehát, hogy g(a)\leq g(r). Ugyanakkor indirekt feltételeztük, hogy g(a)=g(ab), így a fentebbi maradékos osztásból kapott g(r)\lt g(ab) szigorú egyenlőtlenségből g(r)\lt g(a) következik.
Ez ellentmondás, hiszen g(r) nem lehet egyszerre legalább akkora, mint g(a), és határozottan kisebb is nála. Az indirekt feltételezésünk hibás volt, azaz a g(a)=g(ab) egyenlőség nem állhat fenn, amennyiben b nem egység.
∎Az utolsó két tételt felhasználva már könnyedén beláthatjuk ennek a résznek a főtételét, amely az euklidészi gyűrűk legfontosabb tulajdonságát mondja ki.
17.22. Tétel:
Minden euklidészi gyűrűben – és így a 17.19. Tétel miatt az egész számok \Z gyűrűjében is – teljesül a számelmélet alaptétele.
♣Bizonyítás:
A 17.17. Tétel alapján egy euklidészi gyűrűben bármely két elemnek létezik kitüntetett közös osztója. Így a 17.12. Tétel miatt minden felbonthatatlan elem prím. Ebből viszont a 16.17. Tétel szerint következik a számelémélet alaptételének egyértelműségi állítása. Ha tehát valamely elemnek egyáltalán létezik felbontása, akkor az – sorrendtől és asszociáltságtól eltekintve – egyértelmű.
Így már csak azt kell megmutatni, hogy bármely nemnulla és nem egység elemnek ténylegesen létezik felbontása. Tegyük fel, hogy g:R\to \N egy olyan euklidészi norma, amely eleget tesz a 17.20. Tételben szereplő egyenlőtlenségi tulajdonságnak is. Ilyen euklidészi norma ugyanezen tétel miatt garantáltan létezik. A bizonyításhoz a g norma értékkészletén, azaz a természetes számok \N halmazán fogunk teljes indukciót alkalmazni.
Ennek során minden n természetes számra megmutatjuk, hogy az összes olyan nemnulla és nem egység gyűrűelemnek létezik prímtényezős felbontása, amelynek a g norma szerinti „távolsága” a nullelemtől legfeljebb n. Az alábbi ábrán a gyűrű elemeinek azon A_0, A_1, A_2, ... részhalmazai láthatók, amelyek az első néhány természetes számhoz tartoznak ebben az értelemben. Az elemeket pontokkal jelöltük, valamint ábrázoltuk a g norma által hozzájuk rendelt értékeket is:
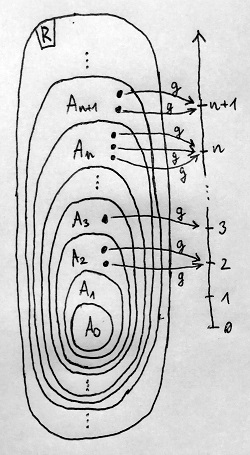
Először is indukciós feltételként feltesszük, hogy valamilyen n-re már igaz az állítás, azaz bármely n-nél nemnagyobb normájú nemnulla és nem egység gyűrűelemnek létezik prímtényezős felbontása. Ezt az elemhalmazt a fenti ábrán A_n-nel jelöltük. Azt kell megmutatnunk, hogy ekkor az A_{n+1} halmaz elemeire is teljesülni fog az állítás. Tegyük fel, hogy a egy tetszőleges A_{n+1}-beli elem. Feltételezhetjük, hogy nincs benne A_n-ben, hiszen máskülönben az indukciós feltétel miatt róla már amúgyis tudnánk, hogy létezik prímtényezős felbontása. Így tehát g(a)=n+1.
Ha a felbonthatatlan elem (16.11. Definíció), akkor az ő prímtényezős felbontása alatt a 16.15. Definíció alapján önmagát, mint „egytényezős szorzatot” értjük, így az nyilván létezik. Feltételezhetjük tehát, hogy a nem felbonthatatlan, azaz felírható a=bc alakban úgy, hogy b és c közül egyik sem egység. Ekkor azonban a g normára a 17.21. Tétel miatt fennállnak az alábbi szigorú egyenlőtlenségek, hiszen a nem egységszerese sem b-nek, sem pedig c-nek:
\begin{aligned}g(b)&\lt g(a) \\ g(c)&\lt g(a)\end{aligned}Ez viszont g(a)=n+1 miatt azt jelenti, hogy g(b)\leq n és g(c)\leq n. Az indukciós feltételünk alapján azonban emiatt b-nek és c-nek létezik prímtényezős felbontása, hiszen mindketten benne vannak az A_n halmazban. Így ha az a=bc szorzatba b és c helyére beírjuk e két felbontást, akkor épp a-nak a felbontását kapjuk.
Eddig tehát azt bizonyítottuk, hogy HA valamilyen n-re az A_n halmaz minden elemének létezik felbontása, AKKOR ez igaz lesz az őt tartalmazó A_{n+1} halmaz elemeire is. Már csak el kell indítani az indukciós „dominósor” ledöntését valahol, azaz kell találni valamilyen n-et, amelyre valóban teljesül a tétel állítása.
Ez ebben az esetben egyszerű lesz, hiszen az n=0 épp megfelelő erre a célra, habár az érvelés némileg szokatlan lesz. Az n=0 esethez az A_0 halmaz fog tartozni, amely tehát azokat a nemnulla és nem egység gyűrűelemeket tartalmazza, amelyeknek a g szerinti normája legfeljebb 0. Minthogy a norma értéke csak természetes (azaz nemnegatív) szám lehet, ezért ez azt jelenti, hogy az A_0 minden elemének pontosan 0 a normája. Igenám, de a norma a 17.16. Definíció miatt csak a nullelem esetében lehet 0, és mivel azt mondtuk, hogy A_0 nem tartalmazza a nullelemet, ezért ő csak az üres halmaz lehet (az a halmaz, amelynek nincs egyetlen eleme sem).
Viszont az üres halmaz elemeire tett bármilyen univerzális állítás igaz, így az is, hogy e nem létező elemek mindegyikének létezik prímtényezős felbontása. Ezt a furcsaságot a bizonyítás utáni megjegyzésben egy picit részletesebben is kifejtjük, most azonban térjünk vissza a befejezéshez.
Azt kaptuk tehát, hogy az A_0 halmazra – furcsamód ugyan, de – igaz lesz a tétel állítása. Ekkor azonban a fentebb bizonyított indukció miatt igaz lesz A_1-re is, majd emiatt A_2-re is, és így tovább, egészen a végtelenségig. Minthogy a g norma összes lehetséges értékét lefedtük, ezért biztosan nem hagytunk ki egyetlen nemnulla és nem egység gyűrűelemet sem a buliból. Mindegyikre igaz tehát a prímtényezős felbontás létezése, és így a számelmélet alaptétele.
∎Megjegyzés a bizonyításhoz:
A bizonyításban azt állítottuk, hogy az üres halmaz minden elemének létezik prímtényezős felbontása. Ez elsőre ellentmondásnak tűnik, azonban furcsamód nem az. Tegyük fel ugyanis indirekt, hogy az állítás nem igaz, azaz az üres halmazban nem minden elemnek létezik felbontása. Ez másként fogalmazva épp azt jelenti, hogy létezik olyan elem az üres halmazban, amelynek nem létezik felbontása. Ez viszont ellentmondás, ugyanis az üres halmaznak egyáltalán nincs eleme.
Az ilyen érvelés egy tipikus esete annak a furcsa jelenségnek, miszerint bármilyen, az üres halmaz elemeire tett univerzális állítás igaz. Például a „minden ismert egyszarvú fekete” és a „minden ismert egyszarvú fehér” mondatok egyaránt igaz állítások, tekintve, hogy mindkettő az üres halmaz elemeiről, nevezetesen az „ismert egyszarvúakról” tesz valamilyen univerzális kijelentést. A külföldi matematikai logikai szakirodalom „vacuous truth”-nak hívja az ilyesfajta kijelentéseket.
♣Ez a tétel tehát egy elégséges feltételt biztosít ahhoz, hogy egy integritástartományban teljesüljön a számelmélet alaptétele. Megjegyezzük azonban, hogy ez a feltétel nem szükséges az alaptételhez. Léteznek olyan integritástartományok is, amelyekben semmilyen értelemben nem végezhető el a maradékos osztás, és így nem euklidészi gyűrűk, ám mégis teljesül bennük a számelmélet alaptétele.
Ebben a részben megismerkedtünk a kitüntetett közös osztó fogalmával, és az euklidészi algoritmussal, amely azt képes hihetetlen sebességgel kiszámítani. A kitüntetett közös osztó létezése azért volt nagyon fontos számunkra, mivel annak fontos következményei vannak a számelmélet alaptételének egyértelműségi állítására nézve. Ezért általánosságban is megvizsgáltuk, mi kell ahhoz, hogy az euklidészi algoritmus valamilyen integritástartományon működhessen. Ezzel eljutottunk a maradékos osztás és az euklidészi gyűrűk fogalmához, és megmutattuk, hogy az ilyen gyűrűkben mindig teljesül a számelmélet alaptételének mindkét állítása. Végül igazoltuk, hogy az egész számok gyűrűje is euklidészi gyűrű – például az abszolútérték-függvényre, mint euklidészi normára nézve.
A 9. részben a Diffie-Hellman kulcscsere protokoll kapcsán már felületesen megismerkedtünk az úgynevezett óra-, vagy becsületesebb nevén moduláris aritmetikával. Ez szintén egy fontos összetevője az aszimmetrikus kulcsú titkosítási eljárásoknak, ezért a következő részben ezt a témakört újra elővesszük. Ám ezt ezúttal a gyűrűk absztrakciós szintjén fogjuk megtenni, melynek keretében megismerkedünk az úgynevezett maradékosztálygyűrűkkel. Ezenkívül minimálisan érinteni fogjuk az ideálok elméletét is.
A következő részt itt találod…



