Az előző részben tovább folytattuk a számelmélet felépítését a semmiből. A Peano-axiómarendszer és a 11. részből már ismert összeadás műveletének segítségével bevezettünk egy második műveletet is az \N halmazon. Ezt szorzásnak neveztük el, amelyről megmutattuk, hogy valóban teljesíti mindazon tulajdonságokat, amiket az általános iskolában megszokhattunk tőle. Ezután megismerkedtünk a reláció és a rendezett halmaz fogalmával, és definiáltunk egy olyan relációt az \N halmazon, amelynek a segítségével egy egyértelmű sorrendet tudtunk felállítani e halmaz elemei, azaz a természetes számok között. Megemlítettük ugyanakkor, hogy ez a számkör túl szűkös olyan kellőképpen általános számelméleti összefüggések feltárásához, amelyeket a matematika más területein is kamatoztatni tudnánk. De vajon mi volt az az absztrakciós folyamat, amelyet őseink is követtek, amikor elkezdtek a „semminél kevesebb” mennyiségekről elmélkedni? Mit lehet az ilyen mennyiségekkel modellezni? Tulajdonképpen mik azok a negatív számok? Hogyan köthető egy ilyen látszólag értelmetlen fogalom a valósághoz? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít az előző és az azelőtti részekben bevezetett alábbi definíciókra:
Legyen adott egy \N-nel jelölt halmaz, valamint egy s:\N \to \N függvény. Az \N halmaz elemeit természetes számoknak nevezzük, amennyiben teljesülnek a következő axiómák:
- Az s függvény az \N halmaz minden x eleméhez rendeljen hozzá valamilyen szintén \N-beli elemet, azaz létezzen az s(x) elem. Ezt az elemet az x rákövetkezőjének nevezzük.
- Ha x és y az \N halmaz két tetszőleges eleme, és s(x)=s(y), akkor x=y. Ilyenkor azt mondjuk, hogy a két elem egyenlő egymással.
- Az \N halmazban létezik pontosan egy olyan 0-val jelölt elem, amelyhez nem található olyan x elem, amelyre teljesül, hogy s(x)=0. Ezt az elemet nullának nevezzük.
- Tegyük fel, hogy a P halmaz az \N halmaznak egy valamilyen részhalmaza. Ha a 0 a P halmazban van, valamint ha abból, hogy egy tetszőleges x elem a P halmazban van következik, hogy s(x) is a P halmazban van, akkor \N összes eleme a P halmazban van – azaz P=\N.
Az \N halmazon értelmezett, +-szal jelölt kétváltozós műveletet összeadásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a+0=a.
- Amennyiben valamely a és b számokra az a+b eredménye már ismert, úgy teljesül, hogy a+s(b)=s(a+b).
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
Az \N halmazon értelmezett, \cdot-tal jelölt kétváltozós műveletet szorzásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a\cdot 0=0.
- Amennyiben valamely a és b számokra az a\cdot b eredménye már ismert, úgy teljesül, hogy a\cdot s(b)=(a\cdot b) + a.
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
Amennyiben az \N halmaz tetszőleges a és b elemeihez létezik olyan k szintén \N-beli elem, amelyre teljesül, hogy a+k=b, akkor azt mondjuk, hogy a\leq b. Kiolvasva: „a legfeljebb b” vagy „b legalább a”.
Ha ezen kívül a\neq b is teljesül – azaz a nem azonos b-vel –, akkor azt mondjuk, hogy a\lt b. Kiolvasva: „a kisebb, mint b” vagy „b nagyobb, mint a”. Egy ezzel azonos megfogalmazás így hangzik: ha tetszőleges a és b elemekhez létezik olyan k elem, amelyre teljesül, hogy a+k=b és k\neq 0, akkor a\lt b.
Fordított irányú reláció esetén értelemszerűen használhatjuk a \geq vagy a \gt szimbólumokat is.
E definíciók kontextusba helyezése, valamint a hozzájuk kapcsolódó tételek megismerése miatt erőteljesen ajánlott tehát elolvasni a 11. és a 12. részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Az általános iskolában vélhetően mindenki megtanulta a négy alapműveletet, illetve azok alapvető tulajdonságait. Mi ezek közül eddig mindössze az összeadással és a szorzással ismerkedtünk meg. Ezután azonban láthatóan falba ütköztünk, hiszen a természetes számok \N halmazán algebrai értelemben nem értelmezhető sem a kivonás, sem pedig az osztás. Ez alatt azt értjük, hogy ezek a „művelet-szerűségek” általánosságban kivezetnek a természetes számok köréből. Algebrai értelemben az olyan függvényeket neveztük műveleteknek, amelyek \N-beli elemekből alkotott párokhoz szintén \N-beli elemeket rendelnek hozzá. Például a + szimbólummal jelölt művelet egy olyan függvény, amely a (3;2) párhoz – és a kommutativitása miatt természetesen a (2;3) párhoz is – az 5 szimbólummal jelölt \N-beli elemet rendeli hozzá.
Ilyen értelemben sajnos a szokásos kivonást nem nevezhetjük műveletnek. Az még rendben is lenne, hogy a (3;2) párhoz hozzárendeli az 1 szimbólummal jelölt természetes számot – hiszen 3-2=1. De mit rendeljen hozzá mondjuk a (2;3) párhoz? Az \N halmazban nincs olyan elem, amely ehhez a párhoz rendelhető, mint egy kivonás eredménye. Márpedig a művelet fogalmának definíciója egyértelműen kimondja, hogy egy ilyen függvénynek minden elempárhoz hozzá kell rendelnie valamilyen elemet az alaphalmazból.
Megtehetjük persze – hiszen a matematikában mindent szabad mindaddig, míg a logika egyszerű de annál szigorúbb szabályait betartjuk –, hogy átírjuk a művelet definícióját, és nem kötjük ki, hogy minden elempárra értelmezve legyen. Ám ekkor roppant kényelmetlen dolgunk lenne, hiszen bármilyen olyan definíciót, tételt vagy bizonyítást, amely a művelet fogalmát használja szintén át kellene fogalmaznunk. Meg kellene ugyanis különböztetnünk azokat az eseteket, amelyekben egy művelet értelmezve van egy adott elempárra azoktól, amelyekben nincs. Nem állítom, hogy ez lehetetlen lenne, de semmiképpen sem kényelmes.
A matematikusok alapvetően lusták, ezért ilyen esetekben rendszeresen az általánosítás és az absztrakció eszközéhez nyúlnak. Ez azt jelenti, hogy olyan általánosabb fogalmakat és elméleteket dolgoznak ki, amelyekben az adott probléma sokkal kényelmesebben kezelhető. Mi is ezt az utat fogjuk követni. A problémánk tehát az, hogy a természetes számok között általánosságban nem végezhető el a kivonás. Az ezen a halmazon ugyanis nem művelet. Ezért ebben és a következő részben át fogunk térni egy másik számhalmazra, amelyben ez a probléma egy csapásra megszűnik. Ezt azonban nem a szokásos módon fogjuk megtenni, hanem továbbra is szigorúan az eddig felépített fogalmainkra, tételeinkre, valamint a Peano-axiómarendszerre támaszkodva. Így válik ugyanis világossá, hogy a korai gondolkodók számára mennyire nem volt magától értetődő absztrakció a számegyenes 0-tól balra lévő részének felfedezése (vagy megalkotása?).
Az eddigiekhez hasonlóan tehát töröljünk most ki mindent a fejünkből, amit a negatív számokról tudunk. Számunkra most kizárólag a természetes számok \N halmaza létezik a rajta értelmezett két művelettel és az előző részben megismert rendezési relációval.
Kompánia bankárai
A 7. részben már megismert Kompánia országában az állampolgárok már időtlen idők óta aranytallérokat használtak fizetőeszközként. Sajnos azonban – ahogy az lenni szokott – egyre jobban kezdett elterjedni a bűnözés. Ezért az emberek egy idő után már nem szívesen tárolták aranytallérjaikat otthon a párna alatt. Volt, aki elásta a kertben, mások elrejtették a padláson vagy egyéb helyeken. Azaz egyre nagyobb piaci igény kezdett el kialakulni egy olyan szolgáltatásra, amely biztosítani tudja az állampolgárok számára pénzük biztonságos tárolását.
Megjelentek tehát a bankok, akik vállalták, hogy megőrzik és nyilvántartják az emberek aranytallérjait némi jutalékért cserébe. Minden ügyfelük számára nyitottak tehát egy úgynevezett betéti számlát. Ez azt tartalmazta, hogy a banknál tárolt összes aranytallér közül hány darab tartozik az adott ügyfélhez. Ennek leírására logikus módon a természetes számok már jól ismert \N halmazának elemeit használták.
A kapzsi bankárok azonban hamar felismerték, hogy mivel kereshetnének jóval több pénzt annál, mint amit a betéti számlák után jutalékként kapnak az ügyfelektől. Elkezdtek hát további jutalékért cserébe kölcsönadni aranytallérokat az embereknek. Egyre többet és többet. Egy idő után már annál is többet, mint amennyi aranytallért összesen őriztek a páncéltermeikben. Ezt a látszólagos ellentmondást egy roppant egyszerű trükkel oldották fel. Minden ügyfél számára nyitottak egy úgynevezett hitelszámlát is a már meglévő betéti számla mellé. Ez azt tartalmazta, hogy az adott ügyfél a banknak mennyi aranytallérral tartozik. Logikus módon ennek leírására is a természetes számok \N halmazának elemeit használták.
Természetesen sok esetben nem történt valódi aranytallér kifizetés az ügyfél számára, hiszen nem is mindig volt rá szükség. Tegyük fel például, hogy Alice vásárol valamit Bobtól n aranytallérért, de nincs rá pénze. Megkéri ezért a bankot, hogy adjon hozzá a saját hitelszámlájához n aranytallérnyi összeget, Bob betéti számlájához pedig szintén adjon hozzá egy ugyanekkora összeget. Vegyük észre, hogy habár nem történt valódi aranytallér fizetés Alice és Bob között, a banknál nyilvántartott számláik alapján azonban mégis elmondhatjuk, hogy Bob „vagyona” n aranytallérral növekedett, miközben Alice „vagyona” ugyanekkora összeggel csökkent.
Ebből mindaddig nincs probléma, ameddig az ügyfelek nem kezdik el tömegesen kivenni az aranytallérjaikat a bankokból. Ha azonban ez mégis megtörténik valami miatt, akkor nagy meglepetésben lesz részük. A bank páncéltermében tárolt valódi aranytallérok száma ugyanis jóval kevesebb, mint amennyinek a betéti és hitelszámlák alapján ott kéne lennie. Nyilvánvaló tehát, hogy szabályozni kell, hogy a bankok mennyi aranytallérnyi összeget tarthatnak nyilván az ügyfelek számláin ahhoz képest, mint amennyit valóban tárolnak a páncéltermükben. Kompánia országában például 8:1 ez az arány. Ez azt jelenti, hogy ha egy bank páncéltermében 100 valódi aranytallér van, akkor az ügyfelek számláin összesen 800 virtuális aranytallér lehet nyilvántartva. De természetesen Kompánia csak egy képzeletbeli ország…
Számunkra most nem is a hitelkihelyezés állami szabályozásának módja az érdekes, ezért feltételezzük, hogy a bankok természetesen tisztességesen és a törvényeknek megfelelően működnek. Szándékosan az „és”, nem pedig az „azaz” szót használtam. Most inkább azt vizsgáljuk meg, hogy mi az, ami egy ügyfél vagyonát jellemzi a fenti felállásban.
A vagyon, mint mennyiség
Az előző szakaszban tehát egy mérhető mennyiség fogalma kezdett el körvonalazódni, amely – mint látni fogjuk – alapjában véve más, mint azok a mennyiségek, amelyeket eddig az \N halmaz elemeivel tudtunk mérni. A fenti bankos példában ezt a mennyiséget „vagyonnak” neveztük, amit a „betéti” és a „hitelszámla” egyenlegével, azaz lényegében egy természetes számokból álló párral jellemeztünk. A továbbiakban is használni fogjuk ezeket a bankokhoz köthető fogalmakat a könnyebb érthetőség kedvéért, azonban tartsuk szem előtt, hogy absztrakt szinten ezek lényegtelenek.
Egy vagyont, mint mennyiséget leíró matematikai objektum tehát a természetes számpárok halmazának egy eleme. Ezt a halmazt az előző rész fényében \N \times \N-nel jelöljük. Ennek a halmaznak egy eleme például a (3;2) számpár, egy másik eleme pedig mondjuk a (4;3) számpár. Általánosságban egy (a;b) számpár – ahol a is és b is természetes számok – egy olyan ügyfél vagyonát jelöli, akinek a betéti számláján a darab, míg a hitelszámláján b darab aranytallér van nyilvántartva.
Vegyük észre, hogy egy ügyfél vagyona nem változik, ha mind a hitel-, mind pedig a betéti számlájának egyenlegét ugyanazzal az összeggel növeljük. Előfordulhat tehát az, hogy egy (a;b) számpár ugyanazt a vagyont jelöli, mint egy (c;d) számpár, holott a\neq c és b\neq d. Az előző részben megismertük a kétváltozós reláció fogalmát (12.7. Definíció), amellyel egy halmaz elemei között valamilyen viszony meglétét, vagy meg nem létét fejezhetjük ki. Jelen esetben az \N\times \N halmazban lévő számpárok között szeretnénk azt a viszonyt kifejezni, hogy két ilyen számpár „ugyanazt a vagyont jelöli”-e vagy nem.
Most öntsük matematikai formába ezt az „ugyanazt a vagyont jelöli”-relációt az előző bekezdésben foglaltak alapján.
13.1. Definíció:
Az \N \times \N halmaz elemei között vezessünk be egy \sim szimbólummal jelölt relációt. Tetszőleges (a;b) és (c;d) számpárok esetén (a;b)\sim (c;d) akkor és csak akkor, ha az alábbi két feltétel közül legalább az egyik teljesül:
- Létezik olyan n természetes szám, hogy a+n=c és b+n=d.
- Létezik olyan k természetes szám, hogy c+k=a és d+k=b.
A definíció első pontja tehát azt fejezi ki, hogy ha a reláció baloldalán lévő számpár mindkét komponensét ugyanazzal az n értékkel növeljük meg, akkor az így kapott jobboldali számpár ugyanazt a vagyont jelölje. A második pont ugyanezt mondja ki, csak a másik irányban. Erre azért van szükség, mivel szeretnénk, ha az „ugyanazt a vagyont jelöli”-reláció szimmetrikus lenne. Ha tehát két számpár között fennáll az egyik irányban, akkor fennálljon a másik irányban is. Nyilvánvaló, hogy egy valamiféle egyenlőséget vagy azonosságot kifejező relációtól elvárjuk ezt a tulajdonságot. Ezt azonban rögzíteni kell a definícióban, ha a továbbiakban hivatkozni szeretnénk rá. Ez alapján például (3;2)\sim (4;3) a definíció 1. pontja miatt, míg (4;3)\sim (3;2) a definíció 2. pontja miatt teljesül.
A fenti definíció jól leírja azt az intuitív gondolatot, hogy mikor tekintünk két vagyont leíró számpárt azonosnak. Ez azonban a gyakorlatban nem túl praktikus. Ha például az a kérdés, hogy (2738;12993)\sim (3625; 13885) teljesül-e, akkor máris gondba kerülünk. Mondhatnánk azt, hogy mivel a 3625-2738 és a 13885-12993 különbségek nem egyeznek meg, ezért ez a reláció nem teljesül. De ne feledjük, hogy ez csalás lenne, mivel a kivonás fogalma még nem létezik számunkra. Ezért szükségünk van egy olyan kritériumra, amelyet a már létező fogalmainkkal könnyen tudunk ellenőrizni, és pontosan azokban az esetekben teljesül, amikor a definíció követelménye is. Egy ilyen kritériumot fogalmaz meg az alábbi tétel.
13.2. Tétel:
A 13.1. Definícióban szereplő \sim reláció két tetszőleges (a;b) és (c;d) számpárok között akkor és csak akkor teljesül, ha a+d=b+c.
♣Vegyük észre, hogy ez már egy olyan feltétel, amely kizárólag a 11.4. Definícióban bevezetett Peano-összeadást használja. Ha ez a tétel igaz, akkor az azt jelenti, hogy akár ezzel a kritériummal is definiálhattuk volna a \sim relációt. Ebből azonban nem látszódna egyértelműen a vagyoni helyzetek mérésére vonatkozó analógia. Most nézzük a tétel bizonyítását. Egy kicsit hosszadalmas lesz, de érdemes végigkövetni.
Bizonyítás:
Mivel ez egy „akkor és csak akkor” típusú állítás, ezért mindkét irányú implikációt bizonyítani kell. Nézzük először az egyik irányt. Ha (a;b)\sim (c;d), akkor e reláció 13.1. Definíciójának két követelménye közül legalább az egyik teljesül. Nézzük, hogy mi van akkor, ha az első követelmény teljesül. Ebben az esetben létezik olyan n természetes szám, amelyre teljesülnek az alábbiak:
\begin{aligned}a+n&=c\\b+n&=d\end{aligned}Ekkor megtehetjük, hogy a felső egyenlet mindkét oldalához b-t, az alsó egyenlet mindkét oldalához pedig a-t adunk hozzá. Így ezt kapjuk:
\begin{aligned}a+n+b&=c+b\\b+n+a&=d+a\end{aligned}Tekintve, hogy a két egyenlet baloldalain álló kifejezések a Peano-összeadás kommutativitása (11.7. Tétel) és asszociativitása (11.8. Tétel) miatt megegyeznek, ezért az egyenletek jobboldalain szereplő kifejezések is megegyeznek, azaz c+b=d+a. Ez viszont szintén az összeadás kommutativitása miatt épp a tételben szereplő kritérium teljesülésének bizonyítéka.
Ha a reláció 13.1. Definíciójának nem teljesül az első követelménye, akkor a második követelmény teljesül (hiszen legalább az egyiknek teljesülnie kell). Ezzel viszont ugyanez a gondolatmenet végigjátszható. Azt kaptuk tehát, hogy ha (a;b)\sim (c;d), akkor a+d=b+c szükségképpen teljesül.
Most nézzük meg, hogy vajon az állítás megfordítása is teljesül-e. Most azt tudjuk, hogy az (a;b) és (c;d) számpárokra teljesül, hogy a+d=b+c, és az a kérdés, hogy ekkor a 13.1. Definícióban teljesül-e legalább az egyik kritérium az (a;b) és (c;d) számpárokra.
Az előző részben bevezetett \leq reláció (12.13. Definíció) trichotómiája (12.20. Tétel) miatt tudjuk, hogy a\leq c és a \geq c közül legalább az egyik teljesül. Ugyanezen okok miatt b\leq d és b\geq d közül is teljesül legalább az egyik. Emiatt az alábbi 4 eset közül legalább az egyiknek teljesülnie kell a és c valamint b és d kisebb-nagyobb viszonyaival kapcsolatban:
- a\leq c és b\leq d
- a\leq c és b\geq d
- a\geq c és b\leq d
- a\geq c és b\geq d
Vizsgáljuk meg sorban mind a 4 esetet.
Első eset: a\leq c és b\leq d
Ez ugye a \leq reláció 12.13. Definíciója miatt azt jelenti, hogy léteznek n_1 és n_2 természetes számok, amelyekre teljesül, hogy
\begin{aligned}a+n_1&=c\\b+n_2&=d\end{aligned}Azt kell belátnunk, hogy valójában n_1=n_2, hiszen ekkor épp a \sim reláció 13.1. Definíciójának 1. pontját kapnánk. Azt ugye tudjuk, hogy az (a;b) és (c;d) számpárokra teljesül az a+d=b+c összefüggés, amelybe c és d helyére a fenti két egyenlet baloldalát behelyettesítve a következőt kapjuk:
a+\underbrace{b+n_2}_{=d}=b+\underbrace{a+n_1}_{=c}Ezt az egyenletet viszont a 12.16. Lemma miatt egyszerűsíthetjük (a+b)-vel, így valóban n_1=n_2.
Második eset: a\leq c és b\geq d
Ez ugye épp azt jelenti, hogy léteznek olyan n és k természetes számok, amelyekre teljesül, hogy
\begin{aligned}a+n&=c\\d+k&=b\end{aligned}Azt kell belátnunk, hogy ekkor valójában n=0 és k=0, hiszen ebből a=c és b=d következne, azaz az (a;b) és (c;d) számpárok valójában megegyeznének, így nyilván teljesülne közöttük a \sim reláció. Azt ugye tudjuk, hogy az (a;b) és (c;d) számpárokra teljesül az a+d=b+c összefüggés, amelybe c és b helyére a fenti két egyenlet baloldalát behelyettesítve a következőt kapjuk:
a+d=\underbrace{d+k}_{=b}+\underbrace{a+n}_{=c}Ezt az egyenletet most (a+d)-vel egyszerűsíthetjük ismételten a 12.16. Lemma miatt, azaz azt kapjuk, hogy 0=k+n. Ebből viszont a 12.17. Lemma miatt az következik, hogy valóban k=0 és n=0.
Harmadik eset: a\geq c és b\leq d
Ez ugye épp azt jelenti, hogy léteznek k és n természetes számok, amelyekre teljesül, hogy
\begin{aligned}c+k&=a\\b+n&=d\end{aligned}Hasonlóan az előző esethez, azt ugye tudjuk, hogy az (a;b) és (c;d) számpárokra teljesül az a+d=b+c összefüggés, amelybe a és d helyére a fenti két egyenlet baloldalát behelyettesítve a következőt kapjuk:
\underbrace{c+k}_{=a}+\underbrace{b+n}_{=d}=b+cEzt az egyenletet (b+c)-vel egyszerűsíthetjük, azaz k+n=0. Ebből viszont ismételten a 12.17. Lemma miatt az következik, hogy valóban k=0 és n=0.
Végül a negyedik eset: a\geq c és b\geq d
Ekkor az első esethez hasonlóan léteznek k_1 és k_2 természetes számok, amelyekre teljesül, hogy
\begin{aligned}c+k_1&=a\\d+k_2&=b\end{aligned}Azt kell belátnunk, hogy valójában k_1=k_2, hiszen ekkor épp a \sim reláció 13.1. Definíciójának 2. pontját kapnánk. Azt ugye tudjuk, hogy az (a;b) és (c;d) számpárokra teljesül az a+d=b+c összefüggés, amelybe a és b helyére a fenti két egyenlet baloldalát behelyettesítve a következőt kapjuk:
\underbrace{c+k_1}_{=a}+d=\underbrace{d+k_2}_{=b}+cEzt az egyenletet viszont egyszerűsíthetjük (c+d)-vel, így valóban k_1=k_2.
Mind a 4 esetben bizonyítottuk, hogy a 13.1. Definícióban szereplő követelmények közül legalább az egyik teljesül az (a;b) és a (c;d) számpárokra, amennyiben a+d=b+c.
∎Most tehát van egy olyan relációnk, amellyel a vagyoni helyzeteket mérő számpárok – tehát lényegében az \N \times \N halmaz elemei – között valamiféle egyenlőséget tudunk kifejezni. Azt fogjuk megvizsgálni, hogy milyen hatása van ennek a relációnak az \N \times \N halmazra. Ehhez egy újabb fontos fogalommal fogunk megismerkedni.
Ekvivalenciarelációk
Az előző részben megismerkedtünk az úgynevezett rendezési relációkkal. Ezek ugye arra szolgálnak, hogy egy halmaz elemei között valamilyen egyértelmű sorrendet tudjunk felállítani. A rendezési relációk semmiben nem különböznek bármilyen más relációtól azt leszámítva, hogy az alábbi 4 speciális tulajdonságot kell teljesíteniük:
- Reflexivitás (12.8. Definíció): Minden elem álljon relációban önmagával.
- Antiszimmetria (12.9. Definíció): Ha két elem nem azonos, akkor közöttük legfeljebb az egyik irányban teljesüljön a reláció (ahogyan azt egy „kisebb-nagyobb” jellegű fogalomtól elvárnánk).
- Tranzitivitás (12.10. Definíció): A reláció láncszerűen öröklődjön az elemek között (vagyis ha a és b, valamint b és c között is fennáll, akkor álljon fenn közvetlenül a és c között is).
- Trichotómia (12.11. Definíció): Két tetszőleges elem között legalább az egyik irányban teljesüljön (vagyis bármely két elem legyen „összehasonlítható” egymással).
Ebben a szakaszban relációk egy másik fajtájával fogunk megismerkedni, amelyeket ekvivalenciarelációknak nevezünk. Ezek nem arra szolgálnak, hogy sorrendet állítsunk fel egy halmaz elemei között, hanem arra, hogy azokat csoportosítani, osztályozni tudjuk. Méghozzá oly módon, hogy a halmaz minden eleme pontosan egy osztályba kerüljön. Ez azt jelenti, hogy minden elemről egyértelműen meg lehessen mondani, hogy ő melyik osztályba került. Ezenkívül ne legyen olyan elem, amely nem került bele egyik osztályba sem. Egy valamilyen H halmaz ilyen tulajdonságú osztályozását H partíciójának, magukat az osztályokat pedig ekvivalencia-osztályoknak nevezzük.
Az alábbi ábra egy 10 elemű H halmaz egy lehetséges partícióját mutatja:
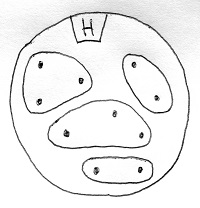
Ezzel szemben az alábbi ábrán lévő osztályozás nem partíció, mivel van olyan elem, amely nem került be egyetlen osztályba sem, valamint van olyan elem, amely egynél több osztályba is bele került:
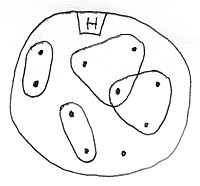
Egy ekvivalenciarelációnak tehát azt kell tudnia megmondani két tetszőleges elemről, hogy ők azonos osztályba kerültek-e, vagy sem. Most vizsgáljuk meg, hogy milyen speciális tulajdonságok szükségesek ahhoz, hogy ez az osztályozás valóban egy partíció legyen. Érezhető, hogy a reflexivitás és a tranzitivitás mindenképpen szükséges lesz. Nyilvánvaló ugyanis, hogy egy elem önmagával azonos osztályba kerül bármilyen partíció esetén (az „azonos osztályban van”-reláció tehát reflexív). Ezenkívül az is nyilvánvaló, hogy ha a és b azonos osztályba kerültek, valamint b és c is azonos osztályba kerültek, akkor a és c is azonos osztályba kerültek (a reláció tehát tranzitív).
E két speciális tulajdonságon kívül azonban szükség van még egy harmadikra is. Ezt a nem kevésbé nyilvánvaló tulajdonságot rögzíti az alábbi definíció:
13.3. Definíció:
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a és b a H halmaz tetszőleges elemei. Ha minden ilyen esetben aRb teljesülése esetén bRa is teljesül, akkor azt mondjuk, hogy az R reláció szimmetrikus.
♣Ez egész egyszerűen annyit fejez ki, hogyha két elem között fennáll a reláció valamelyik irányban, akkor fennáll a másik irányban is. Megjegyezzük még, hogy a nevével ellentétben ez a tulajdonság nem ellentéte a 12.9. Definícióban szereplő antiszimmetria tulajdonságának. Létezik ugyanis olyan reláció, amely egyszerre szimmetrikus és antiszimmetrikus. Triviális példa erre egy tetszőleges halmaz elemeinek egyenlősége, mint reláció. Létezik továbbá olyan reláció is, amely se nem szimmetrikus, se nem antiszimmetrikus. Erre egy későbbi részben fogunk példát mutatni, amikor bevezetjük az oszthatóság fogalmát, amely alapvető fontosságú lesz minden további vizsgálatunk szempontjából.
Ezek után a rendezési relációkhoz hasonlóan most az ekvivalenciareláció fogalmát rögzítjük:
13.4. Definíció (Ekvivalenciareláció):
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, szimmetrikus és tranzitív, úgy R-et a H halmaz feletti ekvivalenciarelációnak hívjuk.
♣Most vizsgáljuk meg, hogy egy ekvivalenciareláció valóban alkalmas-e egy halmaz elemeinek osztályozására oly módon, hogy ez az osztályozás egy partíció legyen. Az alábbi tétel azt mondja ki, hogy a reflexivitáson, tranzitivitáson és szimmetrián kívül nincs szükség egyéb tulajdonságra ehhez.
13.5. Tétel:
Tegyük fel, hogy H egy tetszőleges halmaz, valamint R egy tetszőleges ekvivalenciareláció ezen a halmazon. Képezzük a H halmaznak egy osztályozását a következőképpen: tetszőleges a és b elemek pontosan akkor kerüljenek egy osztályba, ha aRb teljesül. Ekkor ez az osztályozás egy partíció lesz.
Megfordítva: Tekintsük a H halmaznak egy tetszőleges partícióját. Képezzünk egy S relációt ezen a halmazon a következőképpen: tetszőleges a és b elemekre aSb pontosan akkor teljesüljön, ha a és b az adott partíció ugyanazon osztályában vannak. Ekkor S egy ekvivalenciareláció lesz.
♣Bizonyítás:
Induljunk ki a tétel első felében szereplő R ekvivalenciarelációból. Olyan nyilván nem fordulhat elő, hogy egy a elem nincs benne egyik osztályban sem. A reflexivitás miatt ugyanis a legalább önmagával relációban áll, így ő legrosszabb esetben is benne van egy egyelemű (csak a-t tartalmazó) osztályban. Tegyük most fel, hogy a két olyan osztályban is benne van, amelyek tartalmaznak további elemeket és különböznek egymástól. Legyen például a következő a szituáció:
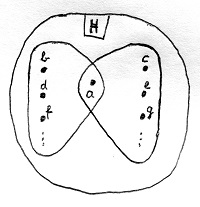
Mivel a és b egy osztályba kerültek, ezért aRb teljesül. Hasonló okok miatt teljesül aRc is. De ha aRc teljesül, akkor a szimmetria miatt cRa is teljesül. De mivel cRa és aRb egyszerre teljesül, ezért a tranzitivitás miatt cRb is teljesül. Ez viszont azt jelenti, hogy c-nek és b-nek mégiscsak ugyanabba az osztályba kellett volna kerülnie, ami ellentmond annak a feltételezésünknek, hogy kialakulhat a fenti ábrán lévő szituáció. Az R ekvivalenciareláció által a tételben szereplő módon meghatározott osztályozás tehát valóban egy partíció a H halmazon.
Megfordítva: Tekintsük most H egy tetszőleges partícióját, amelyben tehát minden elem pontosan egy osztályban van. Képezzük ebből az S relációt a tétel szerint. Az S reláció reflexív, mivel tetszőleges a elem nyilvánvalóan ugyanabban az osztályban van, mint önmaga, legyen szó bármilyen partícióról. Hasonlóan az S reláció szimmetrikus, mivel ha egy tetszőleges a elem ugyanabban az osztályban van, mint egy tetszőleges b elem, akkor nyilván b elem is ugyanabban az osztályban van, mint a elem, legyen szó bármilyen partícióról.
Végezetül tegyük fel, hogy S nem tranzitív, azaz léteznek olyan galád a, b és c elemek, amelyekre aSb és bSc teljesül, ugyanakkor a\cancel{S} c. Ez csak akkor fordulhat elő, ha a és c két különböző osztályban van, b viszont mindkét osztálynak eleme:
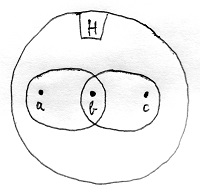
Ez viszont ellentmond annak, hogy az osztályozás, amiből a tétel szerinti S relációt képeztük egy partíció volt. Az S reláció tehát mégiscsak tranzitív. Mivel beláttuk, hogy teljesül mindhárom követelmény, ezért S valóban egy ekvivalenciareláció.
∎Az iménti tételből következik, hogy egy tetszőleges halmaz ekvivalenciarelációi és partíciói kölcsönösen egyértelmű megfeleltetésben állnak egymással. Ha ugyanis egy ekvivalencarelációból a tételben szereplő módon képezzük a hozzá tartozó partíciót, majd ebből a partícióhoz tartozó ekvivalenciarelációt, akkor e konstrukció „pontosan akkor”-jellege miatt az eredeti relációt kapjuk vissza. Ehhez hasonlóan ha egy partícióból képezzük a hozzá tartozó ekvivalenciarelációt, majd ebből a relációból a hozzá tartozó partíciót, akkor az eredeti partíciót kapjuk vissza.
Az egész számok, mint ekvivalencia-osztályok
A fentiek fényében térjünk most vissza az előző szakaszban definiált \sim relációnkhoz, amelyet az \N\times \N halmazon – azaz a természetes számpárokon – értelmeztünk a 13.1. Definíció alapján. Megjegyezzük, hogy a 13.2. Tétel miatt e reláció vonatkozásában mindegy, hogy a tételben vagy a reláció eredeti definíciójában szereplő feltételeket használjuk a továbbiakban, hiszen az említett tétel épp azt mondja ki, hogy vagy mindkét tulajdonság teljesül, vagy egyik sem. Az alábbi tétel igazolásához – amely a \sim reláció kulcsfontosságú tulajdonságát mondja ki – az utóbbi tulajdonságot fogjuk használni.
13.6. Tétel:
A 13.1. Definíció szerinti \sim reláció egy ekvivalenciareláció az \N \times \N halmazon.
♣Bizonyítás:
Az ekvivalenciareláció definíciója alapján azt kell igazolnunk, hogy a \sim reláció reflexív, szimmetrikus és tranzitív.
A reflexivitás nyilván teljesül, hiszen tetszőleges (a;b) számpár esetén (a;b)\sim (a;b). Ez ugyanis a 13.2. Tétel miatt épp azt jelenti, hogy a+b=b+a, amely a Peano-összeadás kommutativitása miatt természetesen igaz.
A szimmetria is nyilván teljesül. Tegyük fel ugyanis, hogy tetszőleges (a;b) és (c;d) számpárok esetén (a;b)\sim (c;d). Ez a 13.2. Tétel miatt azt jelenti, hogy a+d=b+c. A kommutativitás miatt természetesen ekkor c+b=d+a is igaz. Ez viszont ismét a tétel miatt épp azt jelenti, hogy (c;d)\sim (a;b).
Végül a tranzitivitás is könnyen adódik. Tegyük fel ugyanis, hogy valamely (a;b), (c;d) és (e;f) számpárokra (a;b)\sim (c;d) valamint (c;d)\sim (e;f) is teljesül. Ebből a 13.2. Tétel alapján az alábbi két egyenletet írhatjuk fel:
\begin{aligned}a+d&=b+c \\ c+f&=d+e \end{aligned}Adjuk össze a két egyenletet:
a+d+c+f=b+c+d+eÁm ekkor a 12.16. Lemma miatt az egyenlet mindkét oldalát (c+d)-vel egyszerűsíthetjük:
a+f=b+eEz viszont a 13.2. Tétel szerint épp azt jelenti, hogy (a;b)\sim (e;f). A \sim tehát valóban egy ekvivalenciareláció az \N\times \N halmazon.
∎Ha viszont \sim egy ekvivalenciareláció, akkor a 13.5. Tétel alapján ez a reláció ekvivalencia-osztályokra bontja az \N\times \N halmazt. Vizsgáljuk meg, hogyan néznek ki ezek az ekvivalencia-osztályok. Ábrázoljuk az \N\times \N halmaz elemeit egy kétdimenziós koordinátarendszer rácspontjaiként, és csoportosítsuk ezeket a pontokat az ekvivalencia-osztályok alapján. Az alábbi ábrán ezek az ekvivalencia-osztályok láthatók bekarikázva:
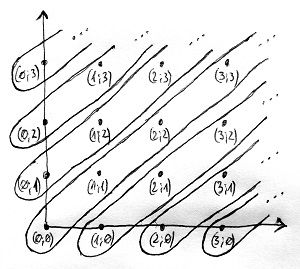
A vagyoni helyzetek analógiájával élve az azonos csoportba került számpárok mind ugyanazt a vagyoni helyzetet írják le. Ha például egy ügyfélnek 2 aranytallér van a betéti számláján és 3 aranytallér a hitelszámláján, akkor ugyanolyan a vagyoni helyzete, mintha 0 aranytallér lenne a betéti számláján és 1 a hitelszámláján. Az első esetet a (2;3), míg a második esetet a (0;1) számpár írja le. Mivel vagyoni helyzet szempontjából mindegy, hogy melyik leírást választjuk, ezért ennek megfelelően e két számpár ugyanabba az ekvivalencia-osztályba került. Ezt úgy is mondhatjuk, hogy a (2;3) és a (0;1) számpárok ugyanazt az ekvivalencia-osztályt reprezentálják.
Minket ezért a továbbiakban nem külön-külön az egyes számpárok, azaz az \N\times \N halmaz elemei érdekelnek, hanem azok az ekvivalencia-osztályok, amelyeket reprezentálják. A most következő, elsőre furcsának tűnő definíció bevezet egy olyan halmazt, amelynek az elemei ezek az ekvivalencia-osztályok lesznek. Ez a halmaz annyira fontos lesz a továbbiakban, hogy a definíció külön nevet is ad ezeknek az ekvivalencia-osztályoknak, mint e halmaz elemeinek.
13.7. Definíció (Az egész számok halmaza):
Az \N\times \N halmazon értelmezett 13.1. Definíció szerinti \sim reláció ekvivalencia-osztályainak halmazát az egész számok halmazának nevezzük, és \Z-vel jelöljük. Ha az (a;b) természetes számpár az \N\times \N egy tetszőleges eleme, akkor [(a;b)]-vel jelöljük az (a;b) természetes számpár által reprezentált egész számot.
♣Jól vigyázzunk a fenti jelölésekkel, az (a;b) ugyanis egy egyszerű természetes számpárt jelöl, amely az \N\times \N halmaz eleme. Ezzel szemben [(a;b)] egy ekvivalencia-osztályt, azaz – a fenti definíció szerinti elnevezés alapján – egy egész számot jelöl, amely viszont a \Z halmaz eleme. Igaz továbbá, hogy egy egész számot végtelen sok különböző számpárral reprezentálhatunk. Ha például (c;d) egy olyan számpár, hogy (a;b)\sim (c;d), akkor a [(c;d)] is ugyanazt az egész számot jelöli, mint [(a;b)]. Ez nagyon hasonló ahhoz, mint amikor törtszámokat írunk le többféleképpen. Például \frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\dots.
A fenti definíció azért tűnik elsőre furcsának, mert nem vagyunk hozzászokva, hogy egy egész számot [(a;b)] alakban jelöljünk. Ezért hamarosan be fogunk vezetni egy olyan jelölést, amelyet az általános iskolában már megszoktunk. Egyelőre azonban tekintsük ezeket az [(a;b)] alakú furcsaságokat az egész számoknak.
A természetes számok beágyazása \Z-be
Most tehát egyrészt van egy \N-nel jelölt halmazunk a rajta értelmezett két művelettel és a \leq relációval, amelyek definiálásához áttételesen vagy közvetlenül a Peano-axiómákat (11.1. Definíció) használtuk. Ennek elemeit természetes számoknak neveztük. Másrészt van egy \Z-vel jelölt halmazunk, amelynek elemei az \N\times \N halmazon értelmezett \sim-vel jelölt reláció ekvivalencia-osztályai. Ezeket az ekvivalencia-osztályokat – bármilyen furcsa egyelőre, de – egész számoknak neveztük.
Látható, hogy \N és \Z a mostani értelmezésünk szerint két, teljesen más jellegű objektumokat tartalmazó halmaz, így nyilván egyik sem lehet részhalmaza a másiknak. Mivel mi jelenleg az eddig megismert természetes számok általánosításán dolgozunk, ezért ez nem elfogadható számunkra. Egy általánosítás során ugyanis az a kívánatos, hogy a speciálisabb kiindulási objektumok halmaza az általánosabb objektumok halmazának részhalmaza legyen.
Az eddigi \N-nek nevezett halmazról tehát át szeretnénk térni a továbbiakban egy olyan halmazra, amely \Z-nek valamilyen részhalmaza, és „ugyanúgy viselkedik”, mint a „régi” \N halmaz. Az „ugyanúgy viselkedik” kifejezés jelentésére hamarosan rátérünk, de az már biztos, hogy szükségünk van egy függvényre, amely a „régi” és az „új” \N halmaz elemeit kölcsönösen egyértelműen megfelelteti egymással. Jelöljük most átmenetileg a „régi” halmazt \N_1-gyel, az „újat” \N_2-vel (amely ugye már része \Z-nek), a közöttük lévő kölcsösen egyértelmű függvényt pedig f-fel. Ez az elrendezés látható az alábbi ábrán:
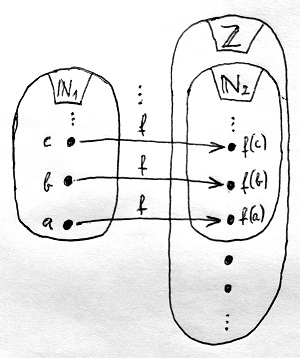
A kölcsönösen egyértelműség tehát azt jelenti, hogy minden \N_2-beli elem pontosan egy – azaz se nem több, se nem kevesebb – \N_1-beli elemhez legyen hozzárendelve az f függvény által, és fordítva, minden \N_1-beli elemhez legyen hozzárendelve pontosan egy \N_2-beli elem.
Most térjünk rá arra a kérdésre, hogy mit jelent az, hogy \N_2 „ugyanúgy viselkedik”, mint \N_1. Vegyük észre, hogy az \N_1 halmaz nem csupán egy halmaz, hanem definiálva van rajta egy +-szal és egy \cdot-tal jelölt művelet (11.4. Definíció és 12.1. Definíció), valamint egy \leq-val jelölt rendezési reláció (12.13. Definíció).
Annak érdekében, hogy az általánosítási projektünk teljes legyen, be szeretnénk vezetni a \Z halmazon is két műveletet, valamint egy teljes rendezést. De nem akárhogyan, hanem úgy, hogy amennyiben ezt a két új műveletet, valamint az új rendezési relációt csak az \N_2 halmazon vizsgáljuk – amely ugye \Z részhalmaza –, akkor azok „ugyanúgy viselkedjenek”, mint a régi \N_1 halmazon értelmezett műveleteink és rendezési relációnk. Az absztrakt algebrában ilyenkor azt mondjuk, hogy az \N_1 és az \N_2 halmazok közötti f leképezés egy művelet- és rendezéstartó leképezés – vagy összefoglaló néven struktúratartó leképezés – kell legyen.
Vezessünk be tehát a \Z halmazon is két műveletet, és egyelőre jelöljük az egyiket \oplus-szal, a másikat pedig \odot-tal, amelyek rendre a régi \N_1 halmazon értelmezett + és \cdot műveletek megfelelői lesznek. Az alábbi ábrán láthatjuk, mit jelent pontosan az, hogy az f leképezés „tartja” a + műveletet. A \cdot művelet „tartása” ugyanígy értelmezhető:
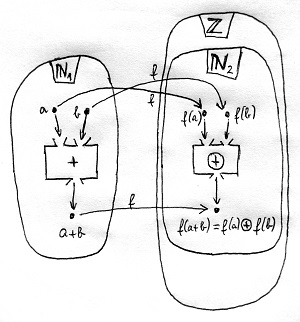
Ha tehát a régi \N_1 halmaz két tetszőleges a és b elemei esetén a + művelet eredménye a szintén \N_1-beli a+b elem, akkor elvárjuk az f leképzéstől, hogy az \N_2-beli f(a) és f(b) elemek esetén az f(a)\oplus f(b) művelet eredménye a szintén \N_2-beli f(a+b) elem legyen. Azaz tetszőleges \N_1-beli elemek közötti + művelet eredményének képe épp az eredeti elemek képei közötti \oplus művelet eredménye legyen. A \cdot és az újonnan bevezetett \odot műveletek tekintetében ugyanezt várjuk el az f leképezéstől.
A műveletekhez hasonlóan vezessünk be egy relációt is a \Z halmazon, amelyet egyelőre jelöljünk \lesssim-vel. Ez a régi \N_1 halmazon értelmezett \leq reláció megfelelője lesz a \Z halmazban. Az alábbi ábrán láthatjuk, mit jelent az, hogy az f leképezés „tartja” a \leq relációt:
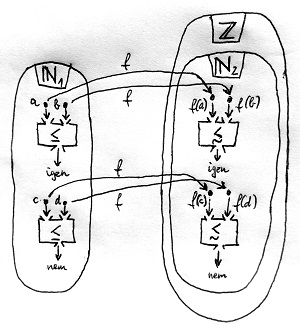
Azaz tetszőleges \N_1-beli elemek között pontosan akkor teljesüljön a \leq reláció, ha az \N_2-beli képeik között teljesül a \lesssim reláció.
Az absztrakt algebrában ezek a különleges, „tartási tulajdonságokkal” rendelkező függvények vagy leképezések központi jelentőségűek. Segítségükkel ugyanis a különböző úgynevezett algebrai struktúrák (azaz műveletekkel és/vagy relációkkal ellátott halmazok) mélyebb szerkezete vizsgálható anélkül, hogy elvesznénk az egyes konkrét reprezentációk részleteiben. Ezért fontos, hogy megismerkedjünk az alábbi fogalmakkal, amelyek tehát alapvetőek az algebrában:
13.8. Definíció (Homomorfizmus, izomorfizmus, beágyazás):
Tegyük fel, hogy A és B két valamilyen – műveletekkel és/vagy relációkkal ellátott – algebrai struktúra alaphalmaza. Egy közöttük lévő f:A\to B struktúratartó leképezést (függvényt) homomorfizmusnak nevezünk.
Amennyiben B minden eleme legalább egy A-beli elemhez hozzá van rendelve, akkor f-et szürjektív homomorfizmusnak vagy ráképzésnek nevezzük.
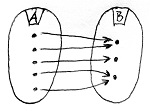
Amennyiben B minden eleme legfeljebb egy A-beli elemhez van hozzárendelve, akkor f-et injektív homomorfizmusnak vagy beágyazásnak nevezzük.
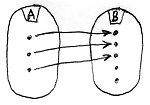
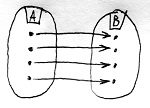
Amennyiben B minden eleme pontosan egy A-beli elemhez van hozzárendelve, akkor f-et bijektív homomorfizmusnak vagy izomorfizmusnak nevezzük.
Ezzel a szóhasználattal élve tehát szeretnénk egy injektív homomorfizmust – azaz egy beágyazást – létesíteni a régi \N_1 és az imént megkonstruált \Z halmaz között. Ekkor \Z-nek az \N_2 részhalmaza izomorf lenne a régi \N_1 halmazzal a + és a \cdot műveletek, valamint a \leq reláció tekintetében. Az izomorfia ebben az esetben azt jelentené, hogy az \N_1 és az \N_2 halmazok feletti algebrai struktúrák lényegében azonosak lennének – attól eltekintve, hogy másként jelöljük az elemeiket, a műveleteket és a rendezési relációkat.
A beágyazáshoz tehát két dolgot kell tennünk. Először is definiálnunk kell egy f:\N_1 \to \Z függvényt. Ezután pedig értelmeznünk kell a \Z halmazon az újdonsült \oplus és \odot műveleteket, valamint a \lesssim relációt úgy, hogy f az \N_1 halmaz \Z-be való beágyazását valósítsa meg, és \N_1 képe épp az \N_2 halmaz legyen \Z-n belül. Amint ez megvan, onnantól kezdve az eddigi \N_1 halmaz helyett nyugodtan tekinthetjük majd \N_2-t a természetes számok halmazának. Az izomorfia miatt ugyanis arra ugyanúgy érvényesek lesznek a Peano-axiómák és minden eddig bizonyított tételünk. Ezen kívül nyugodtan használhatjuk majd azokat a jelöléseket, amelyeket az általános iskolából már megszokhattunk.
Intuitív módon konstruáljuk most meg az f:\N_1 \to \Z függvényt, amely a beágyazást fogja megvalósítani. Ehhez megint a vagyoni helyzetekre vonatkozó analógiára gondoljunk. Legyen szó bármilyen vagyoni helyzetről, az alábbi 3 eset lehetséges:
- Az ügyfélnek több betétje van a banknál, mint hitele.
- Az ügyfélnek kevesebb betétje van a banknál, mint hitele.
- Az ügyfélnek ugyanannyi a betétje, mint a hitele.
A következő tétel arról szól, hogy bármely vagyoni helyzet mindhárom esetben biztosan reprezentálható egy olyan számpárral is, amelynek az egyik komponense 0.
13.9. Tétel:
Tegyük fel, hogy (a;b) az \N \times \N egy tetszőleges eleme. Ha a\geq b, akkor pontosan egy olyan n természetes szám létezik, amelyre teljesül, hogy (a;b)\sim (n;0). Ehhez hasonlóan, ha a\leq b akkor pontosan egy olyan m természetes szám létezik, amelyre teljesül, hogy (a;b)\sim (0;m). Végül (a;b)\sim (0;0) akkor és csak akkor teljesül, ha a=b.
A fentiekben \sim jelöli a 13.1. Definíció szerinti ekvivalenciarelációt, 0 pedig a Peano-axiómák szerinti „nulla” természetes számot.
♣Bizonyítás:
Az a\geq b feltétel a 12.13. Definíció alapján azt jelenti, hogy létezik olyan n természetes szám, amelyre teljesül, hogy a=b+n. A Peano-összeadás 11.4. Definíciójának 1. pontja miatt ez egyenértékű ezzel: a+0=b+n. Ez viszont a 13.2. Tétel miatt épp azt jelenti, hogy (a;b)\sim (n;0).
Ezzel bizonyítottuk a tételben szereplő n létezését. Tegyük most fel, hogy ez nem egyértelmű, azaz létezik egy másik n' természetes szám is, amelyre (a;b)\sim (n';0), de n\neq n'. A 13.2. Tétel miatt ez azt jelenti, hogy a+0=b+n'. Összevetve ezt az a=b+n egyenlettel azt kapnánk, hogy b+n=b+n'. Ezt az egyenletet viszont a 12.16. Lemma alapján b-vel egyszerűsíthetjük, így n=n' adódik, ami ellentmondás. A tételben szereplő n tehát mégis egyértelmű.
Az m-re vonatkozó állítás pontosan ugyanezen a módon igazolható, csak ekkor az a és b számok szerepét fel kell cserélni.
Végül ha a=b, akkor (a;\underbrace{a}_{=b})\sim (0;0) valóban teljesül, hiszen nyilván a+0=\underbrace{a}_{=b}+0. Másrészt, ha (a;b)\sim (0;0), akkor a 13.2. Tétel miatt a+0=b+0, azaz a Peano-összeadás 11.4. Definíciójának 1. pontja miatt a=b.
∎Ez tehát azt jelenti, hogy a \Z halmazban lévő összes [(a;b)]-vel jelölt ekvivalencia-osztály (azaz egész szám) leírható [(n;0)], [(0;n)] vagy [(0;0)] alakban is. Ezekre hamarosan az alábbi – az általános iskolában már megszokott – megnevezéseket és jelöléseket fogjuk használni:
13.10. Definíció (Pozitív és negatív egész számok):
Tegyük fel, hogy n egy természetes szám, és n\neq 0.
Ekkor a \Z halmaz [(n;0)] alakban felírható elemeit pozitív egész számoknak nevezzük, és így jelöljük: n vagy +n.
A \Z halmaz [(0;n)] alakban felírható elemeit negatív egész számoknak nevezzük és így jelöljük: -n.
A \Z halmaz [(0;0)] alakban felírható elemét nullának nevezzük, és így jelöljük: 0.
♣Egyelőre azonban maradjunk még az ekvivalencia-osztályokat használó jelölésnél. A fentebb már említett f:\N_1 \to \Z beágyazófüggvényt az alábbi módon fogjuk definiálni:
f(n)=[(n;0)]Ahogy az alábbi ábrán látható, a beágyazófüggvény az \N_1 elemeihez – amiket egészen idáig természetes számoknak neveztünk – a nulla és a pozitív egész számokat felelteti meg. Ezek alkotják az \N_2 részhalmazt a \Z halmazon belül:
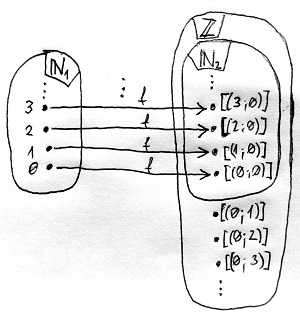
Az is látható, hogy a negatív egész számoknak nincs megfelelője a természetes számok között, ez tehát egy valódi beágyazás. Ez épp megfelel az elvárásainknak, tekintve, hogy most a számfogalom bővítését hajtjuk végre éppen. Most már csak azt kell biztosítani, hogy a \oplus és \odot műveleteket, valamint a \lesssim relációt úgy definiáljuk a \Z halmazon, hogy azok \N_2-re való megszorításai épp az \N_1 halmazon értelmezett + és \cdot műveletek, valamint a \leq reláció megfelelői legyenek. Azaz – algebrai szóhasználattal és jelölésmóddal élve – az (\N_1 ,+,\cdot , \leq) algebrai struktúra legyen izomorf az (\N_2 , \oplus , \odot , \lesssim ) algebrai struktúrával.
Összeadás a \Z halmazon
Értelmezzük hát az „összeadás” műveletét az egész számok \Z halmazán, amelyet ugye egyelőre a \oplus műveleti jellel jelölünk. Ezzel szeretnénk ugyanis hangsúlyozni, hogy ez látszólag teljesen független attól a + szimbólummal jelölt művelettől, amelyet a 11.4. Definícióban Peano-összeadásnak neveztünk. A Peano-összeadás ugyanis – a mostani jelölésekkel – az \N_1 halmazon volt értelmezve, amelynek az elemei ugye a természetes számok. Ezzel szemben a \oplus művelet az imént megkonstruált \Z halmazon van értelmezve, amelynek az elemei ugye a vagyoni helyzeteket jelölő természetes számpárok ekvivalencia-osztályai. Látni fogjuk azonban, hogy e két művelet között az előző szakaszban megadott f:\N_1 \to \Z beágyazófüggvény fog szoros kapcsolatot teremteni.
Na de mégis hogyan lehet ekvivalencia-osztályok közötti „műveletről” beszélni? Mi értelme van ennek? Ennek értelmezéséhez megint a vagyoni helyzetekről szóló analógiához nyúlunk. Tegyük fel, hogy Alice vagyonát egy (a;b) számpár reprezentálja. Ez ugye azt jelenti, hogy Alice betéti számláján a, hitelszámláján pedig b darab aranytallér van nyilvántartva. Hasonlóan tegyük fel, hogy Bob vagyonát egy (c;d) számpár reprezentálja ugyanilyen értelmezéssel. Teljesen értelmes feltenni egy olyan kérdést, hogy mennyi lesz az ő közös vagyonuk, ha összeházasodnak?
Kézenfekvő, ha azt mondjuk, hogy ebben az esetben ezt a közös vagyont – Alice és Bob vagyonának „összegét” – az (a+c;b+d) számpár reprezentálja. Ezzel tehát logikusan azt fejezzük ki, hogy a betéti számlák egyenlegén kívül a hitelszámlák egyenlegeit is össze kell adni. Vegyük észre, hogy ilyen módon a \oplus művelet definícióját visszavezethetjük egy már definiált fogalomra, nevezetesen a Peano-összeadásra (11.4. Definíció).
Fontos azonban megjegyezni, hogy nekünk valójában vagyoni helyzeteknek megfelelő ekvivalencia-osztályokat kellene tudni „összeadni”. Márpedig az imént csak egy-egy természetes számpárt adtunk össze. Azonban a 13.9. Tétel értelmében tetszőleges számpárról egyértelműen azonosítani lehet, hogy ő melyik ekvivalencia-osztályhoz tartozik. Ha tehát adva van két ekvivalencia-osztály, amelyeket szeretnénk „összeadni”, akkor az a kérdés, hogy vajon mindegy-e, hogy e két ekvivalencia-osztálynak mely elemein végezzük el a „számlánkénti” összeadást?
Nézzük például a [(3;0)] és a [(0;5)] ekvivalencia-osztályok „összegét”. Ennek a két osztálynak az alábbiakban felsoroltuk néhány elemét az egyenlőségjelek utáni kapcsoszárójelek között:
\begin{aligned} [(3;0)]&=\{ (3;0), (4;1), (5;2), (6;3), \dots \} \\ [(0;5)]&=\{ (0;5), (1;6), (2;7), (3;8), \dots \} \end{aligned}E két osztálynak egy-egy eleme a (3;0) és a (0;5) számpár. Ezeken elvégezve a „számlánkénti” összeadást a (3;5) számpárt kapjuk, amely a [(0;2)] ekvivalencia-osztályba tartozik. Ennek az „eredmény-osztálynak” az elemeit soroltuk fel alább:
[(0;2)]=\{ (0;2), (1;3), (2;4), (3;5), (4;6), (5;7), \dots \}Kérdés, hogy mondhatjuk-e nyugodt szívvel azt, hogy [(3;0)]\oplus [(0;5)]=[(0;2)]? Nem lehetséges-e, hogy ha a [(3;0)] és a [(0;5)] osztályok valamely más elemeit összegezzük, akkor eredményül egy olyan számpárt kapunk, amely nem a [(0;2)] osztályba tartozik? Elvégre minden osztályban végtelen sok számpár van, miért ne választhatnánk épp ilyen szerencsétlenül?
A most következő tétel azt állítja, hogy ilyen nem fordulhat elő.
13.11. Tétel:
Jelölje \sim a 13.1. Definíció szerinti relációt. Ebben az esetben ha (a_1;b_1)\sim (a_2;b_2) és (c_1;d_1)\sim (c_2;d_2), akkor (a_1+c_1;b_1+d_1)\sim (a_2+c_2;b_2+d_2).
♣Bizonyítás:
Az (a_1;b_1)\sim (a_2;b_2) valamint a (c_1;d_1)\sim (c_2;d_2) relációkból a 13.2. Tétel miatt az alábbi két egyenletet írhatjuk fel:
\begin{aligned}a_1+b_2 &= b_1+a_2 \\ c_1+d_2 &= d_1+c_2\end{aligned}A két egyenletet összeadva a következőt kapjuk:
(a_1+c_1)+(b_2+d_2) = (b_1+d_1)+(a_2+c_2)Ez viszont szintén a 13.2. Tétel miatt épp azt jelenti, hogy (a_1+c_1;b_1+d_1)\sim (a_2+c_2;b_2+d_2).
∎Eszerint tehát mindegy, hogy a két ekvivalencia-osztály mely elemein végezzük el a „számlánkénti” összegzést. Az eredmény minden esetben ugyanabból az ekvivalencia-osztályból fog kikerülni. Azt mondhatjuk tehát, hogy a \Z halmaz elemei között az alábbi definícióval értelmezett \oplus művelet jóldefiniált.
13.12. Definíció (Egész számok összeadása):
A \Z halmazon az alábbi képlet szerint értelmezett \oplus-szal jelölt kétváltozós műveletet összeadásnak nevezzük:
[(a;b)] \oplus [(c;d)] = [(a+c; b+d)]A fentiekben + a 11.4. Definíció szerinti Peano-összeadást, [(x;y)] pedig a \Z halmaznak azon elemét jelöli, amelynek – mint ekvivalencia-osztálynak – eleme az (x;y) természetes számpár.
♣Most vizsgáljuk meg, hogy az előző szakaszban definiált f beágyazófüggvény valóban tartja-e a + műveletet.
13.13. Tétel:
Tegyük fel, hogy \N_1 a Peano-axiómarendszer (11.1. Definíció) szerint definiált természetes számok halmaza, valamint adva van egy f:\N_1 \to \Z függvény az alábbiak szerint:
f(n)=[(n;0)]Ekkor tetszőleges a és b természetes számokra teljesül, hogy f(a+b)=f(a)\oplus f(b). Más szavakkal f egy injektív homomorfizmus az (\N_1, +) és a (\Z ,\oplus ) algebrai struktúrák között.
♣Bizonyítás:
Az f függvény definíciója alapján egyrészt f(a+b)=[(a+b;0)]. Másrészt az egész számok összedásának definíciója miatt (13.12. Definíció) igaz az alábbi:
f(a)\oplus f(b)=[(a;0)]\oplus [(b;0)] = [(a+b;0)]Az eredményül kapott két kifejezés megegyezik, tehát valóban f(a+b)=f(a)\oplus f(b).
∎Végezetül vizsgáljuk meg, hogy vajon az egész számok \Z halmazán értelmezett \oplus művelet is teljesíti-e az általános iskolában már megszokott tulajdonságokat a természetes számok között értelmezett Peano-összeadáshoz hasonlóan.
13.14. Tétel:
A \Z halmaz tetszőleges [(a;b)], [(c;d)] és [(e;f)] elemeire igazak az alábbi összefüggések:
[(a;b)] \oplus [(c;d)] = [(c;d)] \oplus [(a;b)] ([(a;b)] \oplus [(c;d)]) \oplus [(e;f)] = [(a;b)] \oplus ([(c;d)] \oplus [(e;f)])Más szavakkal a \oplus művelet kommutatív és asszociatív.
♣Bizonyítás:
Az első egyenlet baloldala az egész számok összeadásának 13.12. Definíciója miatt így írható:
[(a;b)] \oplus [(c;d)] = [(a+c;b+d)] = \dotsEbből a Peano-összeadás kommutativitása miatt (11.7. Tétel) következik, hogy az egész számok összeadása is kommutatív:
\dots = [(c+a;d+b)] = [(c;d)] \oplus [(a;b)]Ehhez hasonlóan a második egyenletben megfogalmazott asszociativitás pedig a Peano-összeadás asszociativitására vezethető vissza:
([(a;b)] \oplus [(c;d)]) \oplus [(e;f)] = [(a+c;b+d)] \oplus [(e;f)] = \dots \dots = [((a+c)+e;(b+d)+f)] = [(a+(c+e);b+(d+f))] = \dots \dots = [(a;b)] \oplus [(c+e;d+f)] = [(a;b)] \oplus ([(c;d)] \oplus [(e;f)]) ∎Hol tartunk most?
Ismételten álljunk meg, és szedjük össze, hol tartunk most a számelmélet felépítésében.
Megállapítottuk, hogy a természetes számok \N halmaza algebrai értelemben túlságosan szűkösnek bizonyul. Elkezdtük ezért végigkövetni azt a nem kis absztrakciós utat, amelynek eredményeként őseink felfedezték a számegyenes nullától balra lévő részét, azaz a negatív számokat.
Egy banki analógiával élve és a Peano-axiómáknál maradva ezeket az absztrakt objektumokat természetes számpárokkal próbáltuk leírni, amelyek első komponense banki betétet, második komponense pedig banki adósságot jelöl. Az alábbi definícióval bevezettünk e számpárok között egy relációt, amely az ugyanolyan vagyoni helyzeteket jelölő számpárokat azonosítja:
Az \N \times \N halmaz elemei között vezessünk be egy \sim szimbólummal jelölt relációt. Tetszőleges (a;b) és (c;d) számpárok esetén (a;b)\sim (c;d) akkor és csak akkor, ha az alábbi két feltétel közül legalább az egyik teljesül:
- Létezik olyan n természetes szám, hogy a+n=c és b+n=d.
- Létezik olyan k természetes szám, hogy c+k=a és d+k=b.
Megismerkedtünk az ekvivalenciareláció fogalmával:
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, szimmetrikus és tranzitív, úgy R-et a H halmaz feletti ekvivalenciarelációnak hívjuk.
Ezután megmutattuk, hogy a \sim reláció egy ekvivalenciareláció az \N \times \N halmazon, amely ezt a halmazt ekvivalencia-osztályokra bontja. Ezeket az osztályokat neveztük egész számoknak:
Az \N\times \N halmazon értelmezett 13.1. Definíció szerinti \sim reláció ekvivalencia-osztályainak halmazát az egész számok halmazának nevezzük, és \Z-vel jelöljük. Ha az (a;b) természetes számpár az \N\times \N egy tetszőleges eleme, akkor [(a;b)]-vel jelöljük az (a;b) természetes számpár által reprezentált egész számot.
Ezekre egy, az iskolai tanulmányainkból már jól ismert jelölést is bevezettünk:
Tegyük fel, hogy n egy természetes szám, és n\neq 0.
Ekkor a \Z halmaz [(n;0)] alakban felírható elemeit pozitív egész számoknak nevezzük, és így jelöljük: n vagy +n.
A \Z halmaz [(0;n)] alakban felírható elemeit negatív egész számoknak nevezzük és így jelöljük: -n.
A \Z halmaz [(0;0)] alakban felírható elemét nullának nevezzük, és így jelöljük: 0.
Ezután definiáltunk egy – egyelőre – \oplus-szal jelölt műveletet a \Z halmazon, amelyet az egész számok összeadásának neveztünk, és amelyről megmutattuk, hogy kommutatív és asszociatív:
A \Z halmazon az alábbi képlet szerint értelmezett \oplus-szal jelölt kétváltozós műveletet összeadásnak nevezzük:
[(a;b)] \oplus [(c;d)] = [(a+c; b+d)]A fentiekben + a 11.4. Definíció szerinti Peano-összeadást, [(x;y)] pedig a \Z halmaznak azon elemét jelöli, amelynek – mint ekvivalencia-osztálynak – eleme az (x;y) természetes számpár.
A \Z halmaz tetszőleges [(a;b)], [(c;d)] és [(e;f)] elemeire igazak az alábbi összefüggések:
[(a;b)] \oplus [(c;d)] = [(c;d)] \oplus [(a;b)] ([(a;b)] \oplus [(c;d)]) \oplus [(e;f)] = [(a;b)] \oplus ([(c;d)] \oplus [(e;f)])Más szavakkal a \oplus művelet kommutatív és asszociatív.
Végül megadtunk egy függvényt, amellyel elkezdtük algebrai értelemben beágyazni a természetes számokat az egész számok \Z halmazába. Egyelőre azt mutattuk meg, hogy ez a függvény valóban tartja a Peano-összeadás műveletét:
Tegyük fel, hogy \N_1 a Peano-axiómarendszer (11.1. Definíció) szerint definiált természetes számok halmaza, valamint adva van egy f:\N_1 \to \Z függvény az alábbiak szerint:
f(n)=[(n;0)]Ekkor tetszőleges a és b természetes számokra teljesül, hogy f(a+b)=f(a)\oplus f(b). Más szavakkal f egy injektív homomorfizmus az (\N_1, +) és a (\Z ,\oplus ) algebrai struktúrák között.
A következő részekben tovább folytatjuk az egész számok felépítését. Az összeadáshoz hasonlóan a Peano-szorzást, valamint a rendezési relációnkat is intuitív módon ki fogjuk terjeszteni erre a számkörre. Ezzel teljessé fog válni a természetes számok beágyazása a \Z halmazba. Végül általánosságban is megvizsgáljuk, hogy az így kapott új algebrai struktúrával milyen előnyökhöz jutottunk. Ennek keretében további absztrakt algebrai fogalmakkal fogunk megismerkedni, amelyeknek majd a prímszámok elméletének általánosabb tárgyalásakor vesszük hasznát.
A következő részt itt találod…



