Az előző részben kényelmi okok miatt elkezdtük kibővíteni a szám fogalmát. Azon a nem is olyan egyszerű absztrakciós úton kezdtünk el haladni, amelyen őseinknek is végig kellett menniük. Eddig a számokat bizonyos dolgok, sokaságok megszámlálására használtuk, így látszólag semmi értelme sincs a „semminél kevesebb” mennyiségekről beszélni. Ezt félretéve azonban láthattuk, hogy például adósság, vagy valamilyen hiány kifejezésére igen praktikus eszközt kaphatunk a kezünkbe. Ennek az absztrakciónak a keretében új algebrai fogalmakkal ismerkedtünk meg.
Az egész számokat természetes számpárok ún. ekvivalencia-osztályaiként határoztuk meg, amelyek között egy összeadásnak nevezett műveletet is definiáltunk. Ezután elkezdtük beágyazni ebbe az új számhalmazba a Peano-axiómarendszer szerinti \N halmazt egy úgynevezett injektív homomorfizmus – azaz struktúratartó leképezés – segítségével. De vajon hogyan tudjuk a szorzás műveletét is ésszerű módon kiterjeszteni a számegyenes 0-tól balra eső részére? Mit jelent az absztrakt algebrában a „neutrális elem”, az „inverz”, a „gyűrű” és a „test” fogalma? Hogyan definiálható a kivonás művelete az egész számok között? Mi a helyzet az osztással? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít az előző részben bevezetett alábbi definíciókra és a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, szimmetrikus és tranzitív, úgy R-et a H halmaz feletti ekvivalenciarelációnak hívjuk.
Az \N\times \N halmazon értelmezett 13.1. Definíció szerinti \sim reláció ekvivalencia-osztályainak halmazát az egész számok halmazának nevezzük, és \Z-vel jelöljük. Ha az (a;b) természetes számpár az \N\times \N egy tetszőleges eleme, akkor [(a;b)]-vel jelöljük az (a;b) természetes számpár által reprezentált egész számot.
Tegyük fel, hogy A és B két valamilyen – műveletekkel és/vagy relációkkal ellátott – algebrai struktúra alaphalmaza. Egy közöttük lévő f:A\to B struktúratartó leképezést (függvényt) homomorfizmusnak nevezünk.
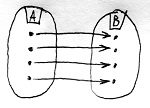
Amennyiben B minden eleme legalább egy A-beli elemhez hozzá van rendelve, akkor f-et szürjektív homomorfizmusnak vagy ráképzésnek nevezzük.
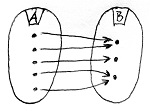
Amennyiben B minden eleme legfeljebb egy A-beli elemhez van hozzárendelve, akkor f-et injektív homomorfizmusnak vagy beágyazásnak nevezzük.
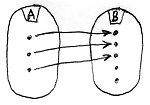
Amennyiben B minden eleme pontosan egy A-beli elemhez van hozzárendelve, akkor f-et bijektív homomorfizmusnak vagy izomorfizmusnak nevezzük.
Tegyük fel, hogy n egy természetes szám, és n\neq 0.
Ekkor a \Z halmaz [(n;0)] alakban felírható elemeit pozitív egész számoknak nevezzük, és így jelöljük: n vagy +n.
A \Z halmaz [(0;n)] alakban felírható elemeit negatív egész számoknak nevezzük és így jelöljük: -n.
A \Z halmaz [(0;0)] alakban felírható elemét nullának nevezzük, és így jelöljük: 0.
A \Z halmazon az alábbi képlet szerint értelmezett \oplus-szal jelölt kétváltozós műveletet összeadásnak nevezzük:
[(a;b)] \oplus [(c;d)] = [(a+c; b+d)]A fentiekben + a 11.4. Definíció szerinti Peano-összeadást, [(x;y)] pedig a \Z halmaznak azon elemét jelöli, amelynek – mint ekvivalencia-osztálynak – eleme az (x;y) természetes számpár.
E definíciók kontextusba helyezése, valamint a hozzájuk kapcsolódó tételek és egyéb fogalmak megismerése miatt erőteljesen ajánlott elolvasni a 11., a 12. és a 13. részt mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Ahhoz, hogy a szorzást is kiterjesszük az előző részben bevezetett új számkörre, ismét az intuíciónkra kell hagyatkoznunk. Kezdhetnénk persze azzal, hogy megadunk egy képletet, mint a \Z halmaz elemei közötti szorzás definícióját. Ezzel azonban elveszne az az információ, hogy miért éppen azt a képletet használjuk, nem pedig mást. Először is jelöljük ki a céljainkat.
Az előző részben ugye azt mondtuk, hogy a Peano-axiómarendszer (11.1. Definíció) által definiált \N halmazt szeretnénk beágyazni a \Z halmazba egy úgynevezett struktúratartó leképezéssel. Az eredeti \N halmazt átmenetileg \N_1-gyel, míg annak \Z-beli képét \N_2-vel jelöltük. A 13.12. Definíció szerinti \oplus műveletről megmutattuk (13.13. Tétel), hogy az az f(n)=[(n;0)] leképezés mellett valóban „ugyanúgy viselkedik” az \N_2 halmazon, mint a Peano-összeadás az \N_1 halmazon.
Hasonló a célunk a most bevezetendő \odot művelettel kapcsolatban ugyanezen leképezés mellett. Ezt a műveletet szorzásnak fogjuk nevezni, és ugyanúgy a teljes \Z halmazon szeretnénk értelmezni, mint az \oplus műveletet. Ennek a halmaznak az elemei ugye a természetes számpárok ekvivalencia-osztályai (13.7. Definíció). Mi lehet hát két ilyen ekvivalencia-osztály „szorzata”?
Szorzás a \Z halmazon
Az előző részben a 13.10. Definícióban bevezettük a pozitív és negatív egész számok általános iskolából már megszokott jelölését a meglehetősen szokatlan [(a;b)] jelölésmód helyett. Eszerint az [(n;0)] alakú egész számokat – amelyek ugye n aranytallérnyi betétet jelentenek – pozitív egész számoknak neveztük, és +n-nel jelöltük. Ezzel szemben a [(0;n)] alakú egész számokat – amelyek tehát n aranytallérnyi adósságot jelölnek – negatív egész számoknak neveztük, és -n-nel jelöltük. Végül a [(0;0)] alakban felírható egész számot „nullának” neveztük, és 0-val jelöltük. Ezt a 13.9. Tétel miatt tehettük meg, amely szerint minden egész szám felírható valamelyik alakban e három közül. Egyelőre azonban maradjunk a „szokatlan” jelölésmódnál mindaddig, amíg a megszokott számolási szabályok be nem bizonyosodnak.
Tegyük fel, hogy van egy [(a;b)]-vel és egy [(c;d)]-vel jelölt egész számunk. Kérdés, hogy mi legyen a [(a;b)] \odot [(c;d)] szorzás, mint művelet eredménye? Szabad kezet kaptunk a képlet megalkotásához, így azt úgy alakíthatjuk ki, ahogy nekünk tetszik. Az egyetlen megkötés, hogy kizárólag az eddig már megalkotott fogalmainkat használhatjuk, mint amilyen például a Peano-összeadás (11.4. Definíció) és a Peano-szorzás (12.1. Definíció). Nyilván azt szeretnénk elérni, hogy a megszokott számolási szabályok teljesüljenek a most bevezetendő \odot és az előző részben bevezetett \oplus műveletekre. Ennek szellemében kell tehát megalkotnunk a képletet.
Ehhez azonban egyenleteket kell tudnunk megoldani a Peano-axiómarendszer által meghatározott (\N ,+,\cdot ) algebrai struktúrában, azaz a természetes számok halmazán. Lévén hogy nem áll rendelkezésünkre mind a négy alapművelet, ezért ehhez szükségünk lesz némi segítségre.
Egyenletek megoldása az (\N , +, \cdot ) algebrai struktúrában
Most lépjünk vissza egy kicsit a korábbi részekben felépített \N halmazhoz és az azon értelmezett Peano-összeadáshoz (11.4. Definíció) és Peano-szorzáshoz (12.1. Definíció). Tegyük fel, hogy a 2\cdot x+3=7 egyenletet szeretnénk megoldani. Általános iskolában mindenki megtanulta, hogy ha egy érvényes egyenlet mindkét oldalából kivonunk egy tetszőleges számot, vagy mindkét oldalt elosztjuk egy tetszőleges NEM NULLA számmal, akkor az így kapott egyenletek továbbra is érvényben maradnak. Nincs más dolgunk hát, mint ilyen lépésekkel addig rendezgetni az egyenletet, míg az egyik oldalon kizárólag az ismeretlen marad. Ekkor a másik oldal épp a megoldás lesz.
Ezzel a gondolatmenettel tehát vonjunk ki mindkét oldalból 3-at, majd mindkét oldalt osszuk el kettővel, így megkapjuk a megoldást:
\begin{aligned}2\cdot x + 3 &= 7 \\ 2\cdot x &= 4 \\ x&=2 \end{aligned}Csakhogy van ezzel egy kis probléma: nem ismerünk olyan fogalmat, mint „kivonás” vagy „osztás”. Ne feledjük, hogy jelenleg a számelméletet az axiómákból szeretnénk felépíteni! Márpedig ebben az esetben nem hivatkozhatunk olyan fogalmakra, amiket nem definiáltunk pontosan.
Szerencsére azonban ez a probléma könnyen áthidalható két okos kis segédtétellel. Az egyiket ezek közül már megismertük egy korábbi részben:
A fenti példában szereplő 2\cdot x + 3 = 7 egyenlet megoldásának első lépésében tehát ahelyett, hogy „kivonnánk” mindkét oldalból 3-at – ezáltal nem definiált fogalmat használva –, az egyenlet jobboldalát cselesen felírjuk két természetes szám összegeként:
2\cdot x + 3 = 4 + 3Ebből már a 12.16. Lemma miatt következik, hogy 2\cdot x = 4. Mondhatnánk, hogy ez szőrszálhasogatás, azonban később látni fogjuk, mennyire könnyen tehetünk olyan logikailag helyesnek tűnő lépéseket, amelyek valójában hibásak. Például amikor majd az úgynevezett maradékosztályokkal kell számolnunk, amelyek a modern kriptográfiai eljárásokban – és úgy általában az egész számelméletben – alapvető fontosságúak.
Na de mi a helyzet a következő lépéssel, amikoris az egyenlet mindkét oldalát „elosztjuk” 2-vel? Az osztás fogalmát szintén nem ismerjük, ezért itt is megpróbáljuk megkerülni ezt a problémát, és az egyenlet jobboldalát felírjuk két természetes szám szorzataként:
2\cdot x = 2\cdot 2Kérdés, hogy vajon ebből következik-e, hogy x=2? És úgy általában abból, hogy a\cdot c = b \cdot c, vajon következik-e, hogy a = b? Az alábbiakban ezt fogjuk bizonyítani.
Előszöris emlékeztetnénk az Olvasót egy korábban már szintén bizonyított segédtételre:
Eszerint tehát a természetes számok körében egy összeg csak úgy lehet 0, ha mindkét tagja 0. Egy ehhez hasonló állításra van szükségünk a Peano-szorzásra vonatkozóan:
14.1. Lemma:
A természetes számok körében ha a\cdot b=0, akkor a=0 vagy b=0.
♣Eszerint tehát egy szorzat csak úgy lehet 0, ha legalább az egyik tényezője 0. Ez a tulajdonság persze nyilvánvalónak tűnik, ám hamarosan fogunk találkozni olyan algebrai struktúrákkal, amelyekben ez nem teljesül. Most nézzük ennek az állításnak a bizonyítását:
Bizonyítás:
A korábbi részekben már jól bejáratott indirekt bizonyítást fogjuk alkalmazni. Azaz megmutatjuk, hogy milyen képtelen következményekhez vezetne, ha az állítás nem lenne igaz.
Tegyük fel tehát, hogy léteznek olyan galád a és b természetes számok, amelyek esetén a\cdot b=0, ugyanakkor a\neq 0 és b\neq 0.
Mivel b\neq 0, ezért a Peano-axiómarendszer (11.1. Definíció) 3. pontja miatt létezik olyan természetes szám, amelynek épp b a rákövetkezője. Jelöljük ezt a számot c-vel, azaz s(c)=b.
Ekkor viszont b helyére behelyettesítve s(c)-t, a következőt kapjuk:
a\cdot \underbrace{s(c)}_{=b} = 0A Peano-szorzás definíciójának (12.1. Definíció) 2. pontja miatt ez a kifejezés így is írható:
a\cdot c + a = 0Viszont a 12.17. Lemma miatt a természetes számok körében egy összeg csak akkor lehet 0, ha mindkét tagja 0. Azaz jelen esetben a\cdot c=0 és a=0. Ezek közül a második viszont ellentmond annak az indirekt feltételezésünknek, miszerint a\neq 0.
∎Ennek segítségével mostmár megfogalmazhatjuk azt a segédtételt, amely általánosságban is lehetővé teszi, hogy egy egyenlet mindkét oldalát ugyanazzal a tényezővel egyszerűsíthessük:
14.2. Lemma:
Tetszőleges a, b és c természetes számok esetén ha c\neq 0 és a\cdot c = b\cdot c, akkor a=b.
♣Bizonyítás:
Tegyük fel, hogy nem igaz az állítás, azaz valamilyen c\neq 0 mellett léteznek olyan galád a és b természetes számok, amelyekre a\cdot c=b\cdot c teljesül, ugyanakkor a\neq b.
Ekkor a és b kisebb-nagyobb viszonyaira vonatkozóan a \leq reláció (12.13. Definíció) trichotómiája (12.20. Tétel) miatt két eset lehetséges: a\lt b vagy b\lt a.
Ha a\lt b, akkor ez a rendezési reláció 12.13. Definíciója miatt azt jelenti, hogy létezik olyan k\neq 0 természetes szám, hogy:
a+k=bEzt behelyettesítve az a\cdot c=b\cdot c egyenletbe a következőt kapjuk:
a\cdot c=(\underbrace{a+k}_{=b})\cdot cA Peano-szorzás disztributivitása miatt (12.5. Tétel) az egyenlet jobboldalán lévő zárójel felbontható:
a\cdot c=a\cdot c + k\cdot cAzt viszont tudjuk, hogy egyrészt k\neq 0, másrészt c\neq 0, ezért a 14.1. Lemma alapján a szorzatuk sem lehet 0.
a\cdot c=a\cdot c + \underbrace{k\cdot c}_{\neq 0}Azaz a \lt reláció 12.13. Definíciója alapján lényegében ezt kaptuk:
a\cdot c \lt a\cdot cEz ugye lehetetlen, hiszen semmilyen természetes szám nem lehet kisebb önmagánál. A másik esetben – tehát amikor b\lt a – ugyanilyen módon juthatunk ellentmondásra. Ekkor azt fogjuk kapni, hogy b\cdot c \lt b\cdot c.
Mivel mindkét esetben ellentmondásra jutottunk, ezért csak az eredeti felételezésünk – miszerint a tétel állítása nem igaz – lehetett hibás.
∎Innentől kezdve tehát egy természetes számokon értelmezett egyenlet megoldása során legálisan egyszerűsíthetjük – vagy némiképp helytelenül fogalmazva „oszthatjuk el” – az egyenlet mindkét oldalát egy nemnulla számmal. Azaz a korábbi példaegyenletünk megoldása során a 2\cdot x = 4 állításból a most bizonyított 14.2. Lemma miatt következik, hogy x=2.
Nagyon fontos azonban, hogy csak nemnulla természetes számmal szabad egyszerűsíteni. Például a\cdot 0=b\cdot 0 tetszőleges a és b természetes számokra teljesül, így ebből nem következik, hogy a=b.
A \Z-beli szorzás követelményei
Egy rövid előzetes megjegyzés: eddig a Peano-szorzás jelölésére minden esetben kiírtuk a \cdot műveleti jelet. Mostantól azonban a jobb olvashatóság kedvéért ezt esetenként el fogjuk hagyni. Így például az xy kifejezés ugyanazt fogja jelenteni, mint az x\cdot y kifejezés. Remélhetőleg ez nem fogja összezavarni az Olvasót, hiszen már az általános iskolában is bevett szokás időnként elhagyni a szorzást jelölő \cdot műveleti jelet.
Térjünk most vissza a \Z halmazon értelmezendő \odot művelethez, és intuitív módon alkossuk meg az [(a;b)]\odot [(c;d)] szorzat eredményének képletét. Az eredmény ugye szintén valamilyen egész szám lesz egy betétet és egy adósságot jelző komponenssel.
Az intuíciónk azt mondatja velünk, hogy mindkét komponens valamilyen módon függeni fog az eredeti [(a;b)] és [(c;d)] egész számok mindkét komponensétől. Ennél közelebbit azonban egyelőre nem tudunk mondani, ezért az alábbi viszonylag általános képletből indulunk ki, aztán meglátjuk, jól tippeltünk-e:
\begin{aligned}[(a;b)]\odot [(c;d)] = [(&\overbrace{A\cdot ac + B\cdot ad + C\cdot bc + D\cdot bd}^{\text{1. komponens}}; \\ &\underbrace{E\cdot ac + F\cdot ad + G\cdot bc + H\cdot bd}_{\text{2. komponens}})]\end{aligned}Az eredmény első komponensét tehát úgy kapjuk, hogy képezzük az eredeti két egész szám két-két komponensének összes lehetséges szorzatát, ezeket a szorzatokat ellátjuk valamilyen – egyelőre még ismeretlen – A, B, C és D együtthatókkal, majd az így kapott tagokat összeadjuk. Az eredmény második komponensét ugyanígy kapjuk, csak ott az E, F, G és H – egyelőre szintén ismeretlen – együtthatókat használjuk. Ez a folyamat látható az alábbi ábrán:
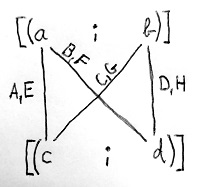
A feladatunk tehát az A, B, C és D, valamint az E, F, G és H természetes számok, mint együtthatók meghatározása oly módon, hogy érvényben maradjanak a szokásos számolási szabályok.
Az első és legfontosabb követelményünk, hogy az f(n)=[(n;0)] legyen egy szorzattartó leképezés a „régi” \N_1 és az „új” \N_2 halmaz között. Azaz ha tetszőleges a és b természetes számoknak képezzük az a\cdot b Peano-szorzatát az \N_1 halmazban, majd vesszük ennek f szerinti képét az \N_2 halmazban, akkor ugyanazt kapjuk, mintha az a és b elemek f(a) és f(b) képeit \odot-oznánk össze az \N_2 halmazban. Ez látható az alábbi ábrán:
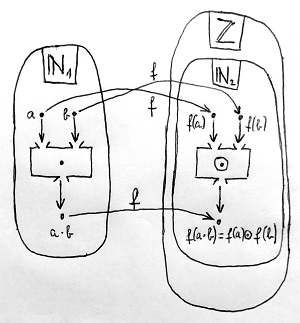
Most nézzük meg, milyen megkötést kell tennünk a keresett 8 együtthatóra ahhoz, hogy ez teljesüljön.
I. követelmény: Az f leképezés legyen szorzattartó
Ezt képlettel így írhatjuk fel:
\underbrace{[(n;0)]}_{=f(n)} \odot \underbrace{[(k;0)]}_{=f(k)} = \underbrace{[(n\cdot k;0)]}_{=f(n\cdot k)}Az egyenlet baloldalára felírva a fentebbi általános képletünket – és persze a 0 tagokat elhagyva – a következőt kapjuk:
[(A\cdot nk;E\cdot nk)]=[(nk;0)]Azt kaptuk tehát, hogy az (A\cdot nk;E\cdot nk) természetes számpárnak ugyanabba a \sim reláció (lásd a 13.1. Definíciót) szerinti ekvivalencia-osztályba kell esnie, mint az (nk;0) számpárnak. Ez viszont az előző részben bizonyított 13.2. Tétel miatt épp azt jelenti, hogy:
A\cdot nk + 0=E\cdot nk + nkA baloldalt 0-val egyszerűsítve, a jobboldalon pedig a Peano-szorzás disztributivitását (12.5. Tétel) kihasználva ez így írható fel:
A\cdot nk=(E+1)\cdot nkItt feltételezhetjük, hogy nk\neq 0, máskülönben ez az egyenlet A és E megválasztásától függetlenül teljesülne. Ha viszont nk\neq 0, akkor az imént bizonyított 14.2. Lemma miatt következik, hogy:
A=E+1A keresett 8 együtthatóról tehát azt már tudjuk, hogy az A együtthatónak E-nél egy 1-gyel nagyobb természetes számot kell választanunk. Ha így teszünk, akkor a fentiek alapján az f leképezés biztosan tartani fogja a Peano-szorzást. Tudományosabban fogalmazva ekkor f egy injektív homomorfizmus (lásd a 13.8. Definíciót) lesz az (\N_1 , \cdot ) és a (\Z , \odot ) algebrai struktúrák között.
Mondhatnánk, hogy készen is vagyunk. Hiszen ez alapján ha az A=1 választással élünk, a másik 7 együtthatót pedig 0-nak választjuk, akkor megvan a művelettartás. Igenám, de mi szeretnénk egyéb megkötéseket is tenni az \odot műveletre annak érdekében, hogy a szokásos számolási szabályok érvényben maradjanak ne csak az \N_2-n belül, hanem a \Z halmaz többi részén is.
II. követelmény: Adósság szorzása pozitív egész számmal
Emlékezzünk vissza, hogy mi motiválta a természetes számok szorzásának bevezetését a 12. részben. Ugye szerettük volna lerövidíteni az olyan kifejezéseket, amikor egy számot önmagával kell sokszor összeadni. Például az a+a+a+a+a kifejezést így rövidíthettük: a\cdot 5. Érdemes lenne megtartani ezt a tulajdonságot a \odot művelet esetén is.
A pozitív egész számokra ezt már biztosítottuk az I. követelménnyel. Most nézzük meg, mi a helyzet akkor, ha egy adósságot reprezentáló egész számot kell önmagával sokszor összeadni. Tekintsük például a [(0;n)] \oplus [(0;n)] \oplus [(0;n)] kifejezést. Ez egyrészt az \oplus művelet 13.12. Definíciója miatt így írható fel:
[(0;n+n+n)]=[(0;n\cdot 3)]Másrészt viszont itt tulajdonképpen arról van szó, hogy a [(0;n)] adósságot reprezentáló negatív egész számot \odot-ozzuk össze a 3 természetes szám f szerinti képével, azaz a [(3;0)] pozitív egész számmal. Azaz lényegében:
[(0;n)]\odot [(3;0)]=[(0;n\cdot 3)]Általánosságban tehát a \odot művelettel szembeni második követelményünk, hogy tetszőleges n és k természetes számok esetén teljesüljön az alábbi:
[(0;n)]\odot \underbrace{[(k;0)]}_{=f(k)}=[(0;n\cdot k)]Az egyenlet baloldalára felírva az általános képletünket – és persze a 0 tagokat elhagyva – a következőt kapjuk:
[(C\cdot nk;G\cdot nk)]=[(0;nk)]Azt kaptuk tehát, hogy a (C\cdot nk;G\cdot nk) természetes számpárnak ugyanabba a \sim reláció (lásd a 13.1. Definíciót) szerinti ekvivalencia-osztályba kell esnie, mint a (0;nk) számpárnak. Ez viszont az előző részben bizonyított 13.2. Tétel miatt épp azt jelenti, hogy:
C\cdot nk + nk=G\cdot nk + 0A jobboldalt 0-val egyszerűsítve, a baloldalon pedig a Peano-szorzás disztributivitását (12.5. Tétel) kihasználva ez így írható fel:
(C+1)\cdot nk=G\cdot nkItt feltételezhetjük, hogy nk\neq 0, máskülönben ez az egyenlet C és G megválasztásától függetlenül teljesülne. Ha viszont nk\neq 0, akkor ismételten a 14.2. Lemma miatt következik, hogy:
C+1=GA keresett 8 együtthatóról most tehát már azt is tudjuk, hogy a G együtthatónak C-nél egy 1-gyel nagyobb természetes számot kell választanunk. Ha így teszünk, akkor a fentiek alapján egy adósságot jobbról megszorozva egy k természetes számnak megfelelő pozitív egész számmal, lényegében az adósság k-szorosát kapjuk.
Most nézzük, milyen megkötéseket lenne érdemes még tenni a \odot műveletre.
III. követelmény: Pozitív egész szám szorzása adóssággal
Szeretnénk, ha a Peano-szorzáshoz hasonlóan a \odot művelet is kommutatív lenne. A pozitív egész számokra ezt már biztosítottuk az I. követelménnyel. Jó volna azonban, ha a kommutativitás a II. követelmény kapcsán felvázolt szituációban is teljesülne, tehát amikor az egyik tényező adósságot, a másik pedig betétet reprezentál.
Általánosságban tehát a \odot művelettel szembeni harmadik követelményünk, hogy tetszőleges n és k természetes számok esetén teljesüljön az alábbi:
[(0;n)] \odot [(k;0)] = [(k;0)] \odot [(0;n)]Az egyenlet mindkét oldalára felírva az általános képletünket – és persze a 0 tagokat elhagyva – a következőt kapjuk:
[(C\cdot nk;G\cdot nk)] = [(B\cdot nk;F\cdot nk)]Azt kaptuk tehát, hogy a (C\cdot nk;G\cdot nk) természetes számpárnak ugyanabba a \sim reláció (lásd a 13.1. Definíciót) szerinti ekvivalencia-osztályba kell esnie, mint a (B\cdot nk;F\cdot nk) számpárnak. Ez viszont az előző részben bizonyított 13.2. Tétel miatt épp azt jelenti, hogy:
C\cdot nk + F\cdot nk=G\cdot nk + B\cdot nkMindkét oldalon a Peano-szorzás disztributivitását (12.5. Tétel) kihasználva ez így írható fel:
(C+F)\cdot nk=(G+B)\cdot nkItt feltételezhetjük, hogy nk\neq 0, máskülönben ez az egyenlet C, F, G és B megválasztásától függetlenül teljesülne. Ha viszont nk\neq 0, akkor ismételten a 14.2. Lemma miatt következik, hogy:
C+F=G+BA II. követelmény kapcsán viszont már megállapítottuk, hogy G=C+1, emiatt:
C+F=\underbrace{C+1}_{=G}+BEzt az egyenletet viszont a 12.16. Lemma miatt egyszerűsíthetjük C-vel:
F=1+BVégül nézzük az utolsó, \odot műveletre vonatkozó megkötésünket.
IV. követelmény: Adósság szorzása adóssággal
Az előző három pontban felvázolt szituációk esetén legalább az egyik tényező lényegében egy természetes szám, pontosabban annak az f leképezés szerinti képe volt. Ezeket az eseteket viszonylag könnyű volt a valósághoz kötni, most azonban kénytelenek leszünk ettől némiképp elvonatkoztatni. Ha ugyanis a \odot műveletet a teljes \Z halmazon szeretnénk értelmezni, akkor muszáj kezelnünk azokat az eseteket is, amikor mindkét tényező egy-egy adósságot reprezentáló negatív egész szám.
Vonatkoztassunk most el attól az apróságtól, hogy ennek látszólag nincs értelme, és tegyük fel, hogy a [(0;n)] \odot [(0;k)] szorzás eredménye is egy valamilyen egész szám. Azt még nem tudjuk, hogy pontosan melyik, az azonban biztos, hogy a \odot műveletnek jóldefiniáltnak kell lennie. Mit is jelent ez pontosan?
Az előző részben definiált \oplus művelet (13.12. Definíció) esetén mindkét tag egy-egy ekvivalencia-osztály volt. Felmerült tehát a kérdés, hogy vajon mindegy-e, hogy a definícióban szereplő képletet e két ekvivalencia-osztály mely elemeire alkalmazzuk. A 13.11. Tétel épp arról szólt, hogy e választástól függetlenül az eredményül kapott számpárok mindig ugyanabból az ekvivalencia-osztályból kerülnek ki. Erre mondtuk azt, hogy a \oplus művelet jóldefiniált a \Z halmazon.
Valami hasonlóra volna szükségünk a \odot művelet kapcsán is. A \sim-vel jelölt „ugyanazt a vagyont jelöli”-reláció 13.1. Definíciója alapján a [(0;n)] és az [(a;n+a)] kifejezések ugyanazt az egész számot jelölik tetszőleges a természetes szám esetén. Elvárjuk tehát, hogy amennyiben ezt egy tetszőleges [(0;k)] negatív egész számmal megszorozzuk, akkor a képletünk által szolgáltatott eredmény mindig ugyabból az ekvivalencia-osztályból kerüljön ki függetlenül attól, hogy a baloldali tényezőt a [(0;n)] vagy az [(a;n+a)] kifejezéssel írtuk-e le. Mint ahogyan törtszámok esetén is teljesen mindegy, hogy \frac{1}{2}-et vagy \frac{2}{4}-et írunk-e egy kifejezésbe.
A fentiek fényében mostmár megfogalmazhatjuk a \odot művelettel szemben támasztott utolsó követelményünket is, miszerint tetszőleges n, k és a természetes számokra teljesülnie kell a következőnek:
[(0;n)] \odot [(0;k)] = [(a;n+a)] \odot [(0;k)]Az egyenlet mindkét oldalára felírva az általános képletünket – és persze a 0 tagokat elhagyva – a következőt kapjuk:
[(D\cdot nk;H\cdot nk)] = [(B\cdot ak + D\cdot (n+a)k;F\cdot ak + H\cdot (n+a)k)]Azt kaptuk tehát, hogy a (D\cdot nk;H\cdot nk) természetes számpárnak ugyanabba a \sim reláció (lásd a 13.1. Definíciót) szerinti ekvivalencia-osztályba kell esnie, mint a (B\cdot ak + D\cdot (n+a)k;F\cdot ak + H\cdot (n+a)k) számpárnak. Ez viszont az előző részben bizonyított 13.2. Tétel miatt épp azt jelenti, hogy:
D\cdot nk + F\cdot ak + H\cdot (n+a)k = H\cdot nk + B\cdot ak + D\cdot (n+a)kMindkét oldalon a Peano-szorzás disztributivitását (12.5. Tétel) kihasználva ez így írható fel:
D\cdot nk + F\cdot ak + H\cdot nk + H\cdot ak = H\cdot nk + B\cdot ak + D\cdot nk + D\cdot akA 12.16. Lemma miatt az egyenlet mindkét oldalát egyszerűsíthetjük D\cdot nk-val és H\cdot nk-val:
F\cdot ak + H\cdot ak = B\cdot ak + D\cdot akIsmételten a Peano-szorzás disztributivitása miatt ez így is írható:
(F+H)\cdot ak = (B+D)\cdot akItt feltételezhetjük, hogy ak\neq 0, máskülönben ez az egyenlet F, H, B és D megválasztásától függetlenül teljesülne. Ha viszont ak\neq 0, akkor a 14.2. Lemma miatt következik, hogy:
F+H = B+DA III. követelmény kapcsán viszont már megállapítottuk, hogy F=B+1, emiatt:
\underbrace{B+1}_{=F} + H=B+DEzt az egyenletet viszont a 12.16. Lemma miatt egyszerűsíthetjük B-vel:
1+H=DA \Z-beli szorzás definíciója
Foglaljuk össze, mire jutottunk eddig. A \odot művelet képletének meghatározására az alábbi általánosnak tekinthető képletből indultunk ki (amelyben tehát ismeretlennek tekintettük az A, B, C és D, valamint az E, F, G és H együtthatóhat):
\begin{aligned}[(a;b)]\odot [(c;d)] = [(&A\cdot ac + B\cdot ad + C\cdot bc + D\cdot bd; \\ &E\cdot ac + F\cdot ad + G\cdot bc + H\cdot bd)]\end{aligned}Az előző szakaszban meghatároztunk 4 olyan követelményt, amelyet elvárunk egy „normálisan viselkedő” szorzástól, mint művelettől. Habár a 8 együttható továbbra is ismeretlen, azt azonban már tudjuk, hogy e 4 követelménynek ez a képlet eleget fog tenni, amennyiben az együtthatókra igazak az alábbiak:
\begin{aligned}A&=E+1 \\ D&=H+1 \\ F&=B+1 \\ G&=C+1 \\ \end{aligned}Mondhatnánk, hogy ezzel nem vagyunk sokkal előrébb, hiszen a B, C, E és H együtthatókat még mindig nem ismerjük. Ez igaz ugyan, azonban a fenti okfejtésből az következik, hogy a kívánt tulajdonságok teljesülése nem függ ennek a 4 együtthatónak az értékétől. Így azokat tulajdonképpen szabadon megválaszthatjuk. Annak érdekében, hogy minél egyszerűbb legyen a végleges képletünk, célszerű ezeket önkényesen 0-nak választani – feltéve, ha nem vagyunk mazochisták.
Így ezeket az együtthatókat kapjuk:
\begin{array}{cc} \begin{aligned}E&=0 \\ H&=0 \\ B&=0 \\ C&= 0 \end{aligned} & \begin{aligned} A=E+1&=1 \\ D=H+1&=1 \\ F=B+1&=1 \\ G=C+1&=1 \end{aligned} \end{array}Ezek alapján már definiálhatjuk az egész számok szorzásának műveletét.
14.3. Definíció (Egész számok szorzása):
A \Z halmazon az alábbi képlet szerint értelmezett \odot-tal jelölt kétváltozós műveletet szorzásnak nevezzük:
[(a;b)] \odot [(c;d)] = [(ac+bd; ad+bc)]A fentiekben + a 11.4. Definíció szerinti Peano-összeadást, az egymás után írás a 12.1. Definíció szerinti Peano-szorzást, [(x;y)] pedig a \Z halmaznak azon elemét jelöli, amelynek – mint ekvivalencia-osztálynak – eleme az (x;y) természetes számpár.
♣Először megmutatjuk, hogy a \odot művelet nemcsak az előző szakaszban megfogalmazott IV. követelmény szerinti esetekben jóldefiniált – tehát amikor adósságot szorzunk adóssággal –, hanem a teljes \Z halmazon:
Bizonyítás:
A 13.9. Tétel tétel szerint minden egész szám felírható [(x;0)] vagy [(0;x)] alakban – ahol x valamilyen természetes szám. Ezért elegendő ellenőrizni, hogy tetszőleges n, k és a természetes számok esetén teljesülnek az alábbiak:
\begin{aligned}\underbrace{[(n;0)]}_{\text{pozitív}} \odot \underbrace{[(k;0)]}_{\text{pozitív}} &= [(n+a;a)] \odot [(k;0)] \\ \underbrace{[(n;0)]}_{\text{pozitív}} \odot \underbrace{[(0;k)]}_{\text{negatív}} &= [(n+a;a)] \odot [(0;k)] \\ \underbrace{[(0;n)]}_{\text{negatív}} \odot \underbrace{[(k;0)]}_{\text{pozitív}} &= [(a;n+a)] \odot [(k;0)] \\ \underbrace{[(0;n)]}_{\text{negatív}} \odot \underbrace{[(0;k)]}_{\text{negatív}} &= [(a;n+a)] \odot [(0;k)] \end{aligned}Ez a 4 egyenlet a 14.3. Definíció miatt rendre így írható fel:
\begin{aligned}[(nk;0)]&=[(nk +ak;ak)] \\ [(0;nk)]&=[(ak;nk +ak)] \\ [(0;nk)]&=[(ak;nk +ak)] \\ [(nk;0)]&=[(nk +ak;ak)] \end{aligned}Mivel a \sim reláció 13.1. Definíciójának 1. pontja miatt egyrészt (nk;0)\sim (nk+ak;ak), másrészt (0;nk)\sim (ak;nk+ak), ezért az egyenletek bal- és jobboldalai valóban ugyanazokat az egész számokat reprezentálják.
A \odot művelet eredménye tehát valóban nem függ attól, hogy a tényezők, mint ekvivalencia-osztályok mely elemeire alkalmazzuk a képletet. Azaz a \odot művelet jóldefiniált ezen ekvivalencia-osztályok halmazán, tehát végsősoron a \Z halmazon.
∎Most vizsgáljuk meg, hogy tényleg minden szükséges tulajdonságot teljesít-e ez a művelet. Az biztos, hogy az f(n)=[(n;0)] beágyazófüggvény – amellyel tehát a Peano-axiómák szerinti \N_1 halmazt ágyazzuk be a \Z halmazba – tartja a Peano-szorzást, hiszen épp ez volt az I. követelményünk az előző szakaszban. Ezért ezt most tételként is kimondhatjuk:
14.5. Tétel:
Tegyük fel, hogy \N_1 a Peano-axiómarendszer (11.1. Definíció) szerint definiált természetes számok halmaza, valamint adva van egy f:\N_1 \to \Z függvény az alábbiak szerint:
f(n)=[(n;0)]Ekkor tetszőleges a és b természetes számokra teljesül, hogy f(a\cdot b)=f(a)\odot f(b). Más szavakkal f egy injektív homomorfizmus az (\N_1, \cdot) és a (\Z ,\odot ) algebrai struktúrák között.
♣Bizonyítás:
A \Z halmazon értelmezett \odot művelet képletének megalkotásakor épp ez volt az I. követelmény, így ez nyilvánvalóan teljesül.
∎Végül megmutatjuk, hogy a \odot művelet teljesíti az iskolából jól ismert számolási szabályokat.
14.6. Tétel:
A \Z halmaz tetszőleges [(a;b)], [(c;d)] és [(e;f)] elemeire igazak az alábbi összefüggések:
[(a;b)] \odot [(c;d)] = [(c;d)] \odot [(a;b)] ([(a;b)] \odot [(c;d)]) \odot [(e;f)] = [(a;b)] \odot ([(c;d)] \odot [(e;f)]) [(a;b)] \odot ([(c;d)] \oplus [(e;f)]) = [(a;b)] \odot [(c;d)] \oplus [(a;b)] \odot [(e;f)]Más szavakkal a \odot művelet kommutatív és asszociatív, valamint disztributív a \oplus műveletre nézve.
♣Bizonyítás:
Először a kommutativitást vizsgáljuk. Az első egyenlet baloldala a \odot művelet 14.3. Definíciója miatt így írható:
[(a;b)] \odot [(c;d)] = [(ac+bd;ad+bc)]Az egyenlet jobboldala ugyanilyen okok miatt így írható:
[(c;d)] \odot [(a;b)] = [(ca+db;cb+da)]Mivel ugyanazt a kifejezést kaptuk mindkét esetben, ezért a \odot művelet valóban kommutatív.
Most nézzük az asszociativitást. A második egyenlet baloldala így írható:
\begin{aligned}&([(a;b)] \odot [(c;d)]) \odot [(e;f)] = \\ = &[(ac+bd;ad+bc)] \odot [(e;f)] = \\ = &[((ac+bd)e + (ad+bc)f; (ac+bd)f + (ad+bc)e)] = \\ = &[(ace+bde+adf+bcf;acf+bdf+ade+bce)]\end{aligned}Az egyenlet jobboldala:
\begin{aligned}&[(a;b)] \odot ([(c;d)] \odot [(e;f)]) = \\ = &[(a;b)] \odot [(ce+df;cf+de)] = \\ = &[(a(ce+df) + b(cf+de); a(cf+de) + b(ce+df))] = \\ = &[(ace+adf+bcf+bde;acf+ade+bce+bdf)]\end{aligned}Mivel ugyanazt a kifejezést kaptuk mindkét esetben, ezért a \odot művelet valóban asszociatív.
Végül ellenőrizzük a disztributivitást. A harmadik egyenlet baloldala:
\begin{aligned}&[(a;b)] \odot ([(c;d)] \oplus [(e;f)]) = \\ = &[(a;b)] \odot [(c+e;d+f)] = \\ = &[(a(c+e) + b(d+f);a(d+f) + b(c+e))] = \\ = &[(ac+ae+bd+bf;ad+af+bc+be)]\end{aligned}Az egyenlet jobboldala:
\begin{aligned}&[(a;b)] \odot [(c;d)] \oplus [(a;b)] \odot [(e;f)] = \\ = &[(ac+bd;ad+bc)] \oplus [(ae+bf;af+be)] = \\ = &[(ac+bd+ae+bf;ad+bc+af+be)]\end{aligned}Mivel ugyanazt a kifejezést kaptuk mindkét esetben, ezért a \odot művelet valóban disztributív a \oplus műveletre nézve.
∎A szokásos számolási szabályok általánosságban
Ebben és az előző részekben többször is beszéltünk már valamiféle „szokásos számolási szabályokról”. Elsőként akkor, amikor a Peano-összeadás és a Peano-szorzás tulajdonságait vizsgáltuk, majd a \Z halmazon értelmezett két művelet kapcsán is. Ez még sokszor elő fog kerülni a következő részekben is, amikor különböző matematikai objektumok – amelyek nem feltétlenül számok – körében értelmezett műveletek tulajdonságait fogjuk vizsgálni. Ezért jó volna egy általánosan használható és tömör fogalomrendszert használni az ilyen esetekben.
A kétváltozós művelet fogalmát a 11.3. Definícióból már ismerjük. Fontos, hogy egy műveletet mindig valamilyen alaphalmazon értelmezünk. Önmagában például nincs értelme összeadásról beszélni. Összeadás hol? A természetes számok \N halmazán? Vagy az egész számok \Z halmazán? Nem mindegy, ugyanis adott esetben más-más tulajdonságai lehetnek egy műveletnek az alaphalmaztól függően. Például a 12.17. Lemma szerint egy összeg csak akkor lehet „nulla”, ha mindkét tagja „nulla”. Ez nyilvánvalóan csak az \N halmazon értelmezett összeadásra igaz, a \Z halmazon már nem. Például [(3;0)]\oplus [(0;3)] = [(3;3)] = [(0;0)]. Eredményül a „nulla” egész számot kaptuk, holott sem a [(3;0)] sem pedig a [(0;3)] nem a „nulla” egész szám. Egyáltalán mit jelent az egy halmazban, hogy „nulla”? Vizsgáljuk meg először ezt a kérdést általánosságban.
Neutrális elem
Tegyük fel, hogy adva van egy tetszőleges R halmaz, valamint egy kétváltozós művelet ezen a halmazon, amelyet jelöljünk most *-gal. Előfordulhat, hogy létezik az R halmazban egy olyan kitüntetett n elem, amellyel bármilyen halmazbeli x elemet össze-*-ozva x-et kapjuk vissza eredményül. Ez látható az alábbi ábrán:
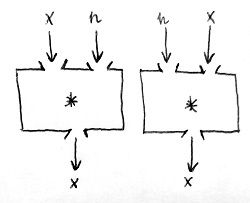
Néhány példa:
- Az \N halmazon értelmezett +-szal jelölt Peano-összeadás esetén a 0 természetes szám.
- Az \N halmazon értelmezett \cdot-tal jelölt Peano-szorzás esetén az 1 természetes szám.
- A \Z halmazon értelmezett \oplus-szal jelölt művelet esetén a [(0;0)] – vagy az iskolában megszokott jelöléssel a 0 – egész szám.
- A \Z halmazon értelmezett \odot-tal jelölt művelet esetén az [(1;0)] – vagy az iskolában megszokott jelöléssel az 1 vagy +1 – egész szám.
Egy adott művelet alaphalmazában egy ilyen tulajdonságú elemnek külön neve van:
14.7. Definíció (Neutrális elem):
Legyen adott egy R halmaz és egy ezen értelmezett *-gal jelölt kétváltozós művelet, valamint legyen n az R halmaz egy eleme.
Az n elemet jobboldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
a*n=aAz n elemet baloldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
n*a=aHa egy n elem egyszerre jobb- és baloldali neutrális elem, akkor őt kétoldali neutrális elemnek, vagy egyszerűen csak neutrális elemnek nevezzük.
A szakirodalomban sok helyen találkozhatunk még a semleges elem, a nullelem, a zéruselem vagy az egységelem kifejezésekkel, valamint a 0 illetve az 1 jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
♣Természetesen kommutatív művelet esetén nincs értelme külön jobb- vagy baloldali neutrális elemről beszélni, hiszen ott minden jobboldali neutrális elem egyben baloldali is, és fordítva. Rögtön felmerülhet a kérdés, hogyha egy halmazban egy adott műveletre nézve létezik neutrális elem, akkor vajon az egyértelmű-e. Ezt válaszolja meg az alábbi tétel:
14.8. Tétel:
Egy tetszőleges R alaphalmazon értelmezett bármilyen * műveletre nézve legfeljebb egy neutrális elem létezik. Más szavakkal a neutrális elem egyértelmű, amennyiben létezik.
♣Bizonyítás:
Tegyük fel, hogy két neutrális elem is létezik a * műveletre nézve. Jelöljük ezeket n-nel és m-mel. Egyrészt, mivel n neutrális, ezért egyben baloldali neutrális is. Így igaz az alábbi:
n*m = mMásrész, mivel m is neutrális, ezért egyben jobboldali neutrális is. Így igaz az alábbi is:
n*m = nAzt kaptuk tehát, hogy n=m, vagyis a neutrális elem egyértelmű, amennyiben létezik.
∎Megjegyezzük, hogy az egyértelműség csak a kétoldali neutrális elemre igaz, a csak jobboldali vagy csak baloldali neutrális elemre nem feltétlenül.
Most, hogy van már neutrális elemünk, ismerkedjünk meg egy másik fontos fogalommal.
Inverz elem, művelet invertálhatósága
Maradjunk továbbra is az R halmaznál és a rajta értelmezett * műveletnél, és tegyük fel, hogy létezik erre a műveletre nézve neutrális elem, amelyet jelöljünk n-nel. A példa kedvéért átmenetileg azt is feltételezzük, hogy a * művelet asszociatív. Tegyük fel, hogy elvégeztük az a*b műveletet, melynek eredményeképp kaptunk egy c elemet. Elképzelhető, hogy szeretnénk megfordítani, vagy tudományosabban fogalmazva invertálni a b-vel való *-ozás folyamatát. Azaz szeretnénk találni egy olyan elemet b-hez, amellyel ha össze-*-ozzuk a c-t, akkor visszakapjuk az eredeti a elemet. Jelöljük ezt a keresett elemet b^{-1}-gyel. Az invertálás folyamata látható az alábbi ábrán:
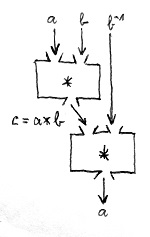
Mivel átmenetileg feltételeztük, hogy a * művelet asszociatív, ezért lényegében egy olyan b^{-1} elemet keresünk, amelyre teljesül, hogy b*b^{-1}=n. Így valóban meg tudjuk fordítani a b-vel való műveletvégzést, hiszen az asszociativitás miatt:
(\underbrace{a*b}_{=c})*b^{-1} = a*(\underbrace{b*b^{-1}}_{=n}) = aAzt szeretnénk tehát, hogy a b*b^{-1} művelet eredménye épp az n neutrális elem legyen. A * művelet asszociativitását mindössze azért feltételeztük átmenetileg, hogy a fenti átzárójelezést meg tudjuk lépni. Így a b^{-1}-gyel való *-ozás valóban visszaszolgáltatja nekünk az eredeti a elemet. Nem asszociatív esetben ez nem feltétlenül van így, ám a most következő fogalom enélkül a „képesség” nélkül is fontos:
14.9. Definíció (Inverz elem, invertálhatóság):
Legyen adott egy R halmaz egy rajta értelmezett * művelettel. Létezzen továbbá neutrális elem erre a műveletre nézve, amelyet jelöljünk n-nel.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b*b^{-1}=n, akkor b^{-1}-et a b elem jobboldali inverzének nevezzük a * műveletre nézve.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b^{-1}*b=n, akkor b^{-1}-et a b elem baloldali inverzének nevezzük a * műveletre nézve.
Ha b^{-1} egyszerre jobb- és baloldali inverz, akkor őt a b elem kétoldali inverzének, vagy egyszerűen csak inverzének nevezzük a * műveletre nézve. Azt mondjuk, hogy a b elem invertálható, amennyiben létezik hozzá inverz elem a * műveletre nézve. Azt mondjuk, hogy a * művelet invertálható, ha minden R-beli elemhez létezik inverz erre a műveletre nézve.
A szakirodalomban sok helyen találkozhatunk még az ellentett elem vagy a reciprok kifejezésekkel, valamint a -b illetve az \frac{1}{b} jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
♣Természetesen kommutatív művelet esetén nincs értelme külön jobb- vagy baloldali inverz elemről beszélni, hiszen ott minden jobboldali inverz elem egyben baloldali is, és fordítva. Megjegyezzük még, hogy a neutrális elem fogalmával ellentétben itt nem egyetlen, az R halmazra nézve globális elemről van szó, amely rendelkezik az „inverzséggel”, mint tulajdonsággal. Inverz elemről beszélni csak akkor van értelme, ha megmondjuk azt is, hogy melyik R-beli elemnek keressük az inverzét.
Rögtön felmerülhet a kérdés, hogyha egy adott elemhez egy műveletre nézve létezik inverz, akkor vajon az egyértelmű-e. Ezt válaszolja meg az alábbi tétel:
14.10. Tétel:
Tegyük fel, hogy * egy valamilyen R halmazon értelmezett asszociatív kétváltozós művelet. Ekkor tetszőleges R-beli a elemhez legfeljebb egy inverz elem létezik erre a műveletre nézve. Más szavakkal minden a elem inverze egyértelmű, amennyiben létezik.
♣Bizonyítás:
Tegyük fel, hogy egy a elemnek két inverze is létezik a * műveletre nézve. Jelöljük ezeket x-szel és y-nal. Egyrészt mivel x inverz, ezért egyben baloldali inverz is. Így igaz az alábbi:
(x*a)*y = n*y = yMásrészt, mivel y is inverz, ezért egyben jobboldali inverz is. Így igaz az alábbi is:
x*(a*y) = x*n = xTekintve, hogy a * művelet asszociatív, ezért a fenti két egyenlet baloldalai megegyeznek, így tulajdonképpen x=y. Az a elem inverze tehát valóban egyértelmű, amennyiben létezik.
∎A neutrális elemmel ellentétben tehát egy adott elem inverze csak akkor egyértelmű, ha a művelet asszociatív, általánosságban azonban ez nem feltétlenül van így.
A kivonás művelete
Most gondoljuk végig, tudunk-e példákat mutatni az inverz fogalmára az eddig tanultakból. A természetes számok \N halmazán ugye nem, hiszen épp azért kezdtük el a számfogalom bővítését és vezettük be a negatív számokat, mert sem a Peano-összeadás, sem pedig a Peano-szorzás nem invertálható. Ezzel szemben a \Z halmazon értelmezett \oplus művelet invertálható, hiszen egy tetszőleges [(a;b)]-vel jelölt egész számnak az ellentettje erre a műveletre nézve épp a [(b;a)]-val jelölt egész szám. Ezek összege ugyanis a 13.12. Definíció értelmében az [(a+b;a+b)] egész szám, amely a 13.10. Definíció alapján megegyezik a [(0;0)] egész számmal, azaz a \oplus művelet neutrális elemével.
A hagyományos jelölésekkel tehát egy n egész szám \oplus műveletre vonatkozó ellentettje a -n egész szám, és fordítva. Ezt a tényt – tehát, hogy minden egész számnak létezik ellentettje – kihasználva mostmár értelmezhetjük a harmadik alapműveletünket, vagyis a kivonást:
14.11. Definíció (Egész számok kivonása):
A \Z halmazon az alábbi képlet szerint értelmezett \ominus-szal jelölt kétváltozós műveletet kivonásnak nevezzük:
[(a;b)] \ominus [(c;d)] = [(a;b)] \oplus [(d;c)]Vagy a hagyományos jelölésekkel:
n - k = n + (-k)Ez tehát azt jelenti, hogy egy n egész számból egy k egész számot úgy vonunk ki, hogy hozzáadjuk az ellentettjét.
♣Sajnos azonban az osztás fogalmát még mindig nem tudjuk értelmezni a \Z halmazon, mivel a \odot művelet nem invertálható ebben a számkörben. Ehhez tovább kéne bővítenünk a szám fogalmát, és bevezetni az úgynevezett racionális (vagy tört-) számokat, ahol már ez a művelet is invertálható. Ezt egyelőre nem fogjuk megtenni, így általánosságban nem fogjuk tudni elvégezni az egész számok közötti osztást. Hamarosan azonban bevezetjük majd az oszthatóság fogalmát, amely bizonyos esetekben mégis lehetővé teszi, hogy egy egész számot „elosszunk” egy másik egész számmal. Ez az „osztás” azonban algebrai értelemben nem lesz művelet, hiszen nem végezhető el általánosságban bármely két egész szám között.
Gyűrűk és testek
Most az eddig tanult fogalmakkal felvértezve ismerkedjünk meg azokkal az algebrai fogalmakkal, amelyekre további számelméleti vizsgálataink során gyakran fogunk hivatkozni.
14.12. Definíció (Gyűrű, test):
Tegyük fel, hogy adva van egy valamilyen R halmaz, amelyen értelmezve van két darab kétváltozós művelet. Az egyiket nevezzük összeadásnak és jelöljük +-szal. A másikat nevezzük szorzásnak és jelöljük \cdot-tal. Az így kapott (R,+,\cdot ) algebrai struktúrát gyűrűnek nevezzük, amennyiben teljesülnek rá az alábbi tulajdonságok – az úgynevezett gyűrűaxiómák:
- A + művelet kommutatív és asszociatív.
- A + műveletre nézve létezik neutrális elem. Ezt a gyűrű nullelemének nevezzük és 0-val jelöljük.
- A + művelet invertálható. Egy tetszőleges a elem +-ra vonatkozó inverzét -a-val jelöljük és a additív inverzének vagy ellentettjének nevezzük.
- A \cdot művelet asszociatív.
- Tetszőleges R-beli a, b és c elemekre teljesülnek az alábbi disztributivitási szabályok:
Amennyiben a \cdot művelet is kommutatív, úgy (R,+,\cdot )-et kommutatív gyűrűnek nevezzük.
Amennyiben a \cdot műveletre nézve is létezik neutrális elem, úgy ezt az elemet a gyűrű egységelemének nevezzük és 1-gyel jelöljük, (R,+,\cdot )-et pedig egységelemes gyűrűnek nevezzük.
Azt a gyűrűt, amely kizárólag a 0 elemet (azaz a gyűrű nullelemét) tartalmazza, nullgyűrűnek nevezzük. Ezt definíció szerint nem tekintjük egységelemes gyűrűnek annak ellenére, hogy a 0 ebben az elfajult esetben nyilvánvalóan neutrális elem az összeadáson kívül a szorzásra nézve is.
Ferdetestnek nevezzük azokat az egységelemes gyűrűket, amelyekben a \cdot műveletre nézve a gyűrű nullelemén kívül minden elemnek létezik inverze. Ha emellett a \cdot művelet még kommutatív is, akkor (R,+,\cdot )-et kommutatív ferdetestnek vagy egyszerűen csak testnek nevezzük (a nullgyűrű tehát nem test, mivel nem is egységelemes a definíció szerint). Egy tetszőleges a elem \cdot-ra vonatkozó inverzét ebben az esetben \frac{1}{a}-val vagy a^{-1}-gyel jelöljük és a multiplikatív inverzének nevezzük.
♣Felhívnánk a figyelmet arra, hogy a fenti definícióban semmit nem tételeztünk fel az R halmazról és a két műveletről azon kívül, hogy teljesülnek rájuk a definícióban szereplő gyűrűaxiómák. Az, hogy „összeadásnak” és „szorzásnak” neveztük a két műveletet, egyáltalán nem azt jelenti, hogy ezeknek adott esetben bármiféle közük van az ebben és az előző részben bevezetett egész számok közötti összeadáshoz és szorzáshoz. Az R halmaz elemei még csak nem is feltétlenül számok.
A gyűrűk és a testek vizsgáltával az absztrakt algebra foglalkozik. Ezek a fejünkben élő számfogalom egyfajta általánosításai, absztrakciói. Célszerű azonban a jól megszokott (\Z ,\oplus , \odot ) algebrai struktúrára gondolni, amikor például gyűrűkre vonatkozó általános összefüggésekről beszélünk. Mint látni fogjuk, ezek az összefüggések bármilyen más gyűrűre ugyanúgy érvényesek lesznek. Ilyen értelemben az absztrakt algebra igen hatékony fegyverként bevethető lesz konkrét – azaz nem absztrakt – problémák megoldására is. Éppen ezért a tágabb értelemben vett számelmélet főként a gyűrűket, illeve azok szerkezetét vizsgálja. A továbbiakban ezért mi is általános gyűrűkre vonatkozó összefüggéseket fogunk bizonyítani, amennyire csak lehetséges.
Visszatérés a megszokott jelölésekhez
A 13.7. Definícióval az előző részben bevezettük az egész számok \Z halmazát, amelynek elemeit természetes számpárok ekvivalencia-osztályaiként határoztuk meg. Ezekre a szokatlan [(a;b)] jelölésmódot alkalmaztuk, és definiáltunk közöttük egy „összeadásnak” és „szorzásnak” nevezett műveletet, amelyeket a szintén szokatlan \oplus és \odot szimbólumokkal jelöltünk. Erre a szokatlan jelölésmódra azért volt szükség, mert szerettük volna kihangsúlyozni, hogy a (\Z , \oplus , \odot ) algebrai struktúrának látszólag semmi köze nincs a 11. és 12. részben bevezetett, a Peano-axiómarendszer által meghatározott (\N ,+,\cdot ) algebrai struktúrához, azaz a természetes számok halmazához.
Mostanra azonban már kiderült, hogy ez utóbbi struktúra beágyazható a \Z halmazba, méghozzá az f(n)=[(n;0)] beágyazófüggvénnyel, amelyről bizonyítottuk, hogy algebrai értelemben tartja a Peano-összeadást és a Peano-szorzást. Ez azt jelenti számunkra, hogy a természetes számok eredeti halmazán – amelyet átmenetileg \N_1-gyel jelöltünk – és annak f szerinti képén – amelyet átmenetileg \N_2-vel jelöltünk, és amely már a \Z halmaz része – az „összeadás” és „szorzás” műveletek gyakorlatilag ugyanúgy viselkednek, leszámítva a jelölésbeli különbséget.
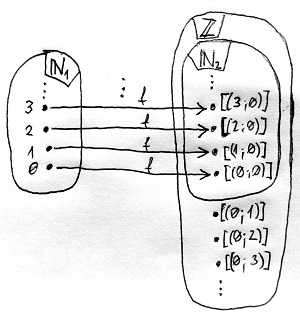
A továbbiakban tehát nyugodtan elfelejthetjük a régi (\N_1 ,+,\cdot ) algebrai struktúrát, és tekinthetjük az új (\N_2 ,\oplus ,\odot ) algebrai struktúrát a természetes számoknak, amely így már az általánosabb (\Z , \oplus, \odot ) algebrai struktúra része. Amint az az alábbi tételből kiderül, ez az algebrai struktúra előnyösebb tulajdonságokkal rendelkezik az elődjéhez képest.
14.13. Tétel (Az egész számok gyűrűje):
A 13.7. Definícióban bevezetett \Z halmaz egy kommutatív, egységelemes gyűrűt alkot a 13.12. Definíció szerinti \oplus és a 14.3. Definíció szerinti \odot műveletekkel.
♣Bizonyítás:
Nincs más dolgunk, mint sorra leellenőrizni a 14.12. Definícióban felsorolt gyűrűaxiómák teljesülését.
- A \oplus művelet a 13.14. Tétel alapján kommutatív és asszociatív.
- A \oplus művelet 13.12. Definíciója alapján a [(0;0)] egész szám neutrális elem erre a műveletre nézve, hiszen tetszőleges a és b természetes számok esetén [(a;b)] \oplus [(0;0)] = [(a+0;b+0)] = [(a;b)].
- Ugyanezen definíció alapján tetszőleges a és b természetes számok esetén [(a;b)] \oplus [(b;a)] = [(a+b;b+a)] = [(0;0)]. Más szavakkal a \oplus művelet invertálható a teljes \Z halmazon.
- A \odot művelet a 14.6. Tétel értelmében asszociatív.
- Ugyanezen tétel miatt teljesülnek a disztributivitási szabályok is.
A (\Z , \oplus , \odot ) algebrai struktúra tehát valóban gyűrű.
Ezen felül a 14.6. Tétel az asszociativitás mellett kimondja a \odot művelet kommutativitását is.
Igaz továbbá, hogy a \odot műveletre nézve az [(1;0)] egész szám neutrális elem, ugyanis tetszőleges a és b természetes számok esetén [(a;b)] \odot [(1;0)] = [(a\cdot 1 + b\cdot 0;a\cdot 0 + b\cdot 1)] = [(a;b)].
A (\Z , \oplus , \odot ) algebrai struktúra tehát valóban egy kommutatív, egységelemes gyűrű, ahogyan a tétel állítja.
∎A továbbiakban tehát a fura \oplus, \odot és \ominus jelölések helyett rendre a +, a \cdot (vagy egymás után írás) és a - szimbólumokat fogjuk használni a \Z halmazon értelmezett műveleteinkhez. Ezen kívül az egész számokat a továbbiakban nem a szintén szokatlan [(a;b)] alakban fogjuk jelölni, hanem a 13.10. Definícióban szereplő, az általános iskolából jól ismert jelöléseket használjuk mostantól. Végül a természetes számok \N halmaza alatt a továbbiakban a \Z-nek azt a részhalmazát fogjuk érteni, amely a pozitív egész számokat és a 0 egész számot tartalmazza.
Ebben a részben tehát intuitív módon értelmeztük a szorzás műveletét is az egész számok halmazán. Ezután megmutattuk róla, hogy teljesíti a megszokott azonosságokat, valamint ugyanúgy viselkedik, mint a Peano-szorzás az \N halmazon. Végül megismerkedtünk néhány hasznos absztrakt algebrai fogalommal, és megmutattuk, hogy a \Z halmaz egy úgynevezett kommutatív, egységelemes gyűrűt alkot az új műveleteinkkel, emiatt a kivonás korlátlanul elvégezhető rajta. Így már tulajdonképpen teljessé vált \N beágyazása \Z-be a \leq rendezési reláció kiterjesztésétől eltekintve, amelyet a következő részben fogunk elvégezni. Megemlítettük azonban, hogy az osztás még a \Z halmazon sem végezhető el korlátlanul. Ez rövidesen elvezet minket az egyik legfontosabb számelméleti fogalomhoz, méghozzá az oszthatóság kérdéséhez.
A következő részt itt találod…



