Az előző részben megismerkedtünk a digitális aláírások és a kriptográfiai hash függvények fogalmával. Láttuk, hogy hogyan építhetünk fel e kriptográfiai primitívekből egy olyan rendszert, amelyben a résztvevők az úgynevezett tanúsítványok segítségével ellenőrizni tudják egymás hitelességét. Az ilyen rendszereket összefoglaló néven publikus kulcs infrastruktúrának neveztük. Megemlítettük, hogy az 1977-ben publikált RSA-algoritmus esetén a publikus és titkos kulcsok szerepe felcserélhető, amely így alkalmas rejtjelezésen kívül digitális aláírások előállítására is. Az RSA működésének megértéséhez azonban tisztában kell lennünk a mögötte meghúzódó számelméleti összefüggésekkel, és úgy általában a matematika alapvető működésével. De vajon hogyan építhető fel egy matematikai elmélet gyakorlatilag a semmiből? Mit nevezünk axiómáknak, amelyek egy ilyen elmélet kiindulópontjai? Mi az a 4 axióma, amelyből következik minden, amit az egész számokról tudunk – és az is, amit még nem tudunk? Hogyan lesz egy állításból tétel? Ebben a részben erről lesz szó…
Az emberek többsége minden bizonnyal nincs elragadtatva a matematikától. Ennek főként az lehet az oka, hogy sok esetben olyan absztrakt dolgokkal foglalkozik, amelyeket nehéz a valósághoz kötni. Rejtvényeket fejteni viszont talán sokkal többen szeretnek. Ez azért jó hír, mivel a modern kriptográfia a matematikának épp egy olyan ágára – nevezetesen a számelméletre – épül, amely tele van a rejtvényekhez hasonló érdekes problémákkal. Ezek a problémák bizonyos esetekben a laikusok számára is könnyen érthetők. Megoldásuk azonban még a legnagyobb elméknek is komoly, sőt sokszor szinte megoldhatatlan kihívást jelentett – és jelent mind a mai napig. Talán épp ez adta a vonzerőt ahhoz, hogy az évszázadok során a matematikusokon kívül rengeteg laikus is szívesen foglalkozzon ezzel a területtel pusztán kedvtelésből.
Ez ahhoz hasonló, mint amikor valaki szeret Sudoku rejtvényeket megoldani. Az ilyen rejtvényeknek önmagukban a szórakoztatáson kívül nem sok hasznuk van. Azonban általános tulajdonságaik vizsgálata elvezethet bennünket igen mély összefüggésekhez, amelyeknek a kutatók szerint lehetnek különböző ipari és tudományos alkalmazásuk is. Hasonló dolog történt a számelmélettel is, amely egészen a közelmúltig a matematikának egy haszontalan ága volt több ezer éven keresztül. A 20. század második felére azonban a számítógépek és az Internet megjelenésével a kódelmélet és azon belül is a kriptográfia fejlődése miatt egy csapásra alapvetően fontossá vált.
Mik azok az axiómák?
Minden logikai játéknak vannak bizonyos alapfogalmai és az ezekre épülő játékszabályai, amelyeket meg kell ismernünk ahhoz, hogy játszani tudjunk. Ezeket az alapfogalmakat és játékszabályokat nincs értelme kétségbe vonnunk, mivel azokat a játék megalkotója hozta létre – mondhatni önkényesen – abból a célból, hogy a játék épp olyan legyen, amilyen. Például kérdezhetnénk, hogy a sakkban a vezér miért nem tud lóugrásban lépni, csak vízszintesen, függőlegesen és átlósan? Erre nagyon egyszerű a válasz: azért mert ez a szabály. Lehetne persze az is a szabály, hogy a vezér lóugrásban is tudjon lépni. Minden bizonnyal az is egy nagyszerű játék lenne, de konkrétan a sakkban ez a lépés meg van tiltva.
A matematika összes területe – így például a számelmélet is – ugyanígy épül fel azzal a különbséggel, hogy itt az alapfogalmakat és a játékszabályokat definícióknak és/vagy axiómáknak nevezik, mert így tudományosabban hangzik. Egy matematikai elmélet axiómáiban ugyanúgy nincs értelme kételkednünk, mint a sakk játékszabályaiban. És nem azért nincs értelme, mert ezek abszolút igazságok lennének, hanem azért, mert ha valamelyik axiómát nem tekintenénk igaznak, akkor az vagy ellentmondáshoz vezetne, vagy pedig egy teljesen más elméletet kapnánk teljesen más logikai következményekkel. Lehet-e egy ilyen módosított elmélet ugyanúgy hasznos, mint az eredeti? „Mi az, hogy! Nagyon is!” – hogy egy klasszikust idézzek.
Erre az egyik legszemléletesebb példát a geometriában találhatjuk. A geometria alapfogalmai közül nézzük a következő hármat: pont, egyenes, egyenesek metszése. Az, hogy ezek lényegét köznyelven hogyan lehet megfogalmazni alapjában véve csak azért fontos, hogy valahogy el tudjuk őket képzelni. Biztos vagyok benne, hogy minden olvasónak él is valamilyen kép a fejében ezekről a fogalmakról. De mégis mi alapján képzelünk el egy egyenest vagy egy pontot épp úgy, ahogy? Habár a megszokás miatt sokan nincsenek ennek tudatában, de ezeket a képeket e geometriai fogalmak alaptulajdonságait leíró axiómák, vagy ha úgy tetszik, a geometria játékszabályai okozzák.
Az egyik ilyen axióma a geometriában az úgynevezett párhuzamossági axióma, amely a következőt mondja ki. Ha van egy e egyenes és egy ezen kívüli P pont, akkor pontosan egy olyan f egyenes létezik, amely átmegy a P ponton, de nem metszi az e egyenest. És valóban: egy papírlapon kipróbálva a fenti axiómát tényleg pontosan egyféleképpen tudunk egy adott egyenessel párhuzamos másik egyenest rajzolni, amely egy adott ponton áthalad:
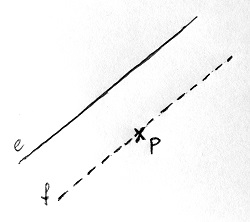
De vajon miért van ez így? Hogyan lehetne erre matematikai bizonyítást adni? A meglepő válasz a következő: ezt nem kell bizonyítani, ez ugyanis egy axióma. A sakkos példa analógiájával élve azért lehet egy adott egyeneshez egy adott ponton keresztül pontosan 1 (azaz se nem több, se nem kevesebb) párhuzamos másik egyenest rajzolni, mert egész egyszerűen ez a szabály. Lehetne persze az is a szabály, hogy ne lehessen egyáltalán párhuzamost rajzolni, vagy hogy éppenséggel végtelen sok párhuzamost lehessen rajzolni. Minden bizonnyal ezek is nagyszerű geometriák lennének… Valóban így van? Nézzük is meg gyorsan egy gondolatkísérlettel!
A játékszabályok megváltoztatása
Önkényesen változtassuk meg a párhuzamossági axiómát – azaz az egyik játékszabályt – a következőképpen. Ha van egy e egyenes, és egy ezen kívüli P pont, akkor nem létezik olyan egyenes, amely átmegy a P ponton, és nem metszi az e egyenest. Vagy ami ennek közvetlen logikai következménye: nem léteznek párhuzamos egyenesek. Mi a gond ezzel? Első olvasatra butaságnak tűnik? Már hogyne léteznének párhuzamosok? Hiszen az előbb próbáltuk ki a papírlapon – mondhatnánk, de meglepő módon tévedünk.
Sokaknak nem tűnik fel, de az előző mondatban a „papírlap” szó kulcsfontosságú volt. Méghozzá azért, mert a papírlapra rajzolt vonalak valójában nem maguk az egyenesek, mint absztrakt geometriai objektumok, hanem azoknak csak a modelljei. Sőt az egész papírlap maga is csak egy modell. Méghozzá annak a geometriának a modellje, amelyben szerepel a párhuzamossági axióma, mint játékszabály. Nem modellje viszont ennek a nagyon furcsának tűnő másik geometriának, amelyből önkényesen kihajítottuk a párhuzamossági axiómát, és felvettünk helyette egy, a párhuzamosságot megtiltó új axiómát. Ha jobban belegondolunk, modellekre csakis nekünk embereknek van szükségünk ahhoz, hogy el tudjuk képzelni a matematikát. A matematika azonban köszöni szépen, de e nélkül is nagyon jól működik. Mi lehet hát a modellje ennek az új geometriának, és vajon hasznos-e egyáltalán?
A válasz az, hogy e nélkül nem létezne hajózás, repülőzés, űrhajózás, és valószínűleg műholdakat sem tudnánk Föld körüli pályára állítani. E geometria ugyanis nem más, mint az úgynevezett gömbi geometria. Ennek egyik – de nem az egyetlen – modellje egy sík papírlap helyett egy gömbfelület. Az „egyenesek” pedig az e gömbfelületen elhelyezkedő úgynevezett főköröknek feleltethetők meg. Főkörnek nevezzük a gömbfelület és egy tetszőleges, a gömb középpontjára illeszkedő sík metszésvonalát. Ha belegondolunk, az „egyenes” fogalmának ilyen módon történő definíciója esetén valóban nem léteznek párhuzamos „egyenesek”, azaz olyanok, amelyek ne metszenék egymást. Ez látható az alábbi ábrán:
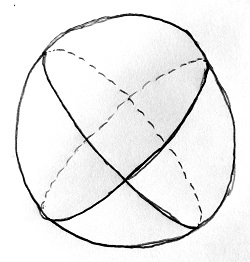
Mondhatnánk, hogy jó-jó, de milyen butaság már „egyeneseknek” hívni a főköröket, amikor a nevükben is benne van, hogy „kör”. Ez azonban pusztán fogalomalkotás kérdése, hiszen nem a neve határozza meg egy adott matematikai objektum tulajdonságait, hanem a rá kimondott axiómák. Az „egyenes” kifejezés használata mellett szól például az, hogy gömbi geometria esetén is igaz marad az a szokásos megállapítás, miszerint 2 pont között a legrövidebb út az őket összekötő „egyenes” mentén helyezkedik el.
Gondoljunk csak mondjuk a repülésre. Biztosan mindenki elgondolkozott már azon, hogy vajon miért tesznek akkora kerülőt Grönland felé az Európából az USA-ba tartó repülőgépek, holott mehetnének nyugat felé is, ami a térképeken látszólag rövidebb út lenne? A válasz nagyon egyszerű. Azért mert a látszat ellenére, ha a kapitány Európában Grönland felé irányítja a gép orrát, és csak egyenesen halad előre irányváltoztatás nélkül, akkor az USA nyugati partján fog kikötni. Mindenki fogjon a kezébe egy földgolyót, és azonnal látni fogja, hogy ez valóban így van.
De akkor miért tűnik mégis kerülőútnak a világtérképen a Grönland felé vezető útvonal? Ennek pusztán az az oka, hogy egy világtérkép a valódi gömbfelületnek csak egy sík felületre történő vetítése, amelyen a távolságok szükségszerűen torzulnak az útvonal mentén. Attól függően, hogy milyen vetítéssel készült az adott térkép, a gömbi geometriának más és más modelljét kapjuk, és ezekben az „egyenesek” modelljei is más és más görbék lesznek. Egy szokásos világtérképen például az „egyenesek” modelljei szinuszhullámok lesznek. Biztos sokan láttak már űrhajós filmet, ahol az irányítóközpont falára volt kivetítve az űrhajó pályája, amely a világtérképen egy szabályos szinuszhullámhoz hasonló görbeként jelent meg.
Az alábbi ábrán például a fehér görbe a Nemzetközi Űrállomás (ISS) földfelszínre vetített pályájának 2 periódusát jelzi. Itt a dolog még annyiban bonyolódik, hogy mivel az ISS másfél óra alatt kerüli meg a Földet, amely ezidő alatt elfordul valamennyit, ezért az egyes periódusok nem ugyanott végződnek a térképen, mint ahol kezdődtek. A térképen ezen kívül látszik még a nappali és az éjszakai oldal határvonala is (világosabb és sötétebb rész):

Most, hogy van már kétféle geometriánk, felmerül a kérdés, hogy melyik a jobb, melyiket használjuk? Egy ilyen kérdést feltenni önmagában nincs értelme, hiszen a válaszhoz tudnunk kell, hogy mihez akarjuk használni. Amennyiben például házat tervezünk, vagy ki akarjuk számolni, hogy mennyi festéket vegyünk egy adott falfelületre, akkor bőven elég a hagyományos síkgeometriát használnunk, hiszen ebben jóval egyszerűbb számolni. Ha viszont egy világkörüli hajóutat kell megterveznünk adott állomásokkal a Föld különböző pontjain, akkor nem árt, ha meg tudjuk mérni az állomások közti távolságokat a szükséges üzemanyagmennyiségek kiszámításához. Erre nyilvánvalóan a síkgeometria nem alkalmas, lévén hogy egy gömbfelületen fogunk hajózni.
Egyszóval a matematika mindössze eszközöket ad a kezünkbe a világ dolgainak modellezésére. Azt azonban mi döntjük el, hogy mennyire pontos modellre van szükségünk az adott feladathoz. A többi „sallangra” nem vagyunk kíváncsiak, ezért ezeket kizárjuk a vizsgálatainkból. Ezt nevezik absztrakciónak.
De mi köze ennek a geometriai példának a kriptográfiához? Közvetlenül természetesen az égvilágon semmi, közvetetten viszont igen fontos látni azt a mechanizmust, amely alapján egy-egy matematikai elmélet felépül. Ezekkel a példákkal remélhetőleg világossá vált, hogy mit értünk axiómák alatt, amik a kiindulópontot adják ehhez az építkezéshez – csakúgy, mint egy valódi ház alapja.
Most az előző részekben megismert kriptográfiai eljárások alapjait jelentő számelmélet „játékszabályait” fogjuk rögzíteni. Ez az axiómarendszer Giuseppe Peano olasz matematikustól származik 1889-ből.
A Peano-féle axiómarendszer
Vélhetően mindenkinek van valamilyen intuitív elképzelése a számokról, azon belül is az úgynevezett természetes számokról. Ezek a pozitív egész számok és a 0. Megjegyezzük, hogy évszázadok óta megy a hitvita arról, hogy a 0-t is természetes számnak kell-e tekinteni vagy nem. Mi ebben a vitában az igenlők pártjára helyezkedünk – azaz természetes számnak tekintjük a 0-t –, ennek azonban pusztán praktikussági okai vannak. Sokak fejében él egy kép valamiféle egyik irányban végtelen – a negatív számokkal egyelőre nem foglalkozunk – számegyenesről, amely a 0-val kezdődik, és a többi természetes szám ettől jobbra helyezkedik el szép sorban, egymástól egyenlő távolságokra. Talán még összeadni és szorozni is tudunk ezen a számegyenesen egy valamely korábbi részben leírtakhoz hasonló módon.
Azonban ne feledjük: egy matematikai objektum tulajdonságait csak és kizárólag a rá kimondott axiómák határozzák meg, nem holmi intuitív kép, ami a fejünkben van. Mivel most a természetes számokra vonatkozó axiómákat fogjuk ismertetni, ezért átmenetileg töröljünk ki mindent a fejünkből, amit ezekről az objektumokról eddig gondoltunk. Tekintsük őket pusztán „valamiknek”, amelyekről ezen a ponton csak annyit tudunk, hogy egy valamilyen halmaz („összesség” vagy „sokaság”) elemei. Ezt a természetes számok halmazának nevezzük, és \N-nel jelöljük. Az, hogy pontosan miként lehet ezeket a „valamiket” elképzelni, igazából ezen a ponton nem is fontos. Minket pusztán a tulajdonságaik érdekelnek, ezeket pedig kizárólag a rájuk kimondott axiómák fogják meghatározni. És mint azt hamarosan látni fogjuk, ezek pontosan összeegyeztethetők lesznek azzal az intuitív képpel, amit az imént átmenetileg kitöröltünk a fejünkből (ugye?!).
Az alábbi definíció ezeket az axiómákat ismerteti szigorúan matematikailag megfogalmazva, az ehhez kapcsolódó intuitív magyarázat a definíció után következik. A definíciók végét a ♣ karakterrel fogjuk jelölni mostantól.
11.1. Definíció (Peano-axiómarendszer):
Legyen adott egy \N-nel jelölt halmaz, valamint egy s:\N \to \N függvény. Az \N halmaz elemeit természetes számoknak nevezzük, amennyiben teljesülnek a következő axiómák:
- Az s függvény az \N halmaz minden x eleméhez rendeljen hozzá valamilyen szintén \N-beli elemet, azaz létezzen az s(x) elem. Ezt az elemet az x rákövetkezőjének nevezzük.
- Ha x és y az \N halmaz két tetszőleges eleme, és s(x)=s(y), akkor x=y. Ilyenkor azt mondjuk, hogy a két elem egyenlő egymással.
- Az \N halmazban létezik pontosan egy olyan 0-val jelölt elem, amelyhez nem található olyan x elem, amelyre teljesül, hogy s(x)=0. Ezt az elemet nullának nevezzük.
- Tegyük fel, hogy a P halmaz az \N halmaznak egy valamilyen részhalmaza. Ha a 0 a P halmazban van, valamint ha abból, hogy egy tetszőleges x elem a P halmazban van következik, hogy s(x) is a P halmazban van, akkor \N összes eleme a P halmazban van – azaz P=\N.
Most vizsgáljuk meg ezeket az axiómákat egyesével.
Az első axióma tulajdonképpen azt követeli meg, hogy minden x természetes számhoz létezzen egy olyan természetes szám is, amely x „rákövetkezője”. Ez azt jelenti, hogy bármelyik természetes számból indulunk ki, a „rákövetkezésen” keresztül mindig tovább tudunk lépni egy másik természetes számhoz, azaz utunk soha nem szakad meg.
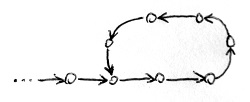
A második axióma lényegében azt mondja ki, hogy egy adott természetes számhoz a „rákövetkezésen” keresztül nem érkezhetünk meg két különböző irányból, bárhonnan is indulunk. Ez tehát megakadályozza egy ehhez hasonló „hurok” kialakulását:
A harmadik axióma kimondja egy és csakis egy olyan speciális természetes szám létezését, amely nem rákövetkezője semmilyen más természetes számnak sem. Ezzel lényegében két nagyon fontos dolgot kapunk. Egyrészt megtudjuk, hogy a „számegyenes” valóban egy egyik irányban végtelen egyenes, amely elkezdődik valahol. Másrészt pedig tulajdonképpen ez az axióma biztosítja, hogy természetes számok egyáltalán léteznek. A másik három axióma ugyanis a szigorúan vett matematikai logika szerint abban az esetben is teljesülne, ha az \N halmaz történetesen üres lenne. Például furcsamód a „minden ismert egyszarvú fehér” állítás igaz. Az persze más kérdés, hogy a „minden” jelen esetben épp 0 darabot jelent, de ettől még az állítás igaz. Akárcsak az az állítás, miszerint „minden ismert egyszarvú fekete”. Általánosságban is elmondható, hogy egy üres halmaz elemeire vonatkozó bármilyen állítás szintén igaz. Furcsa dolog ez a logika, nemde?
Végül a negyedik axióma azt biztosítja, hogy a 0-ból kiindulva a „rákövetkezésen” keresztül minden természetes számhoz eljutunk. Azaz nem léteznek a számegyenestől elszigetelt természetes számok:
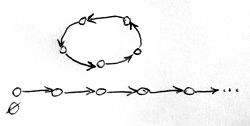
Ezen kívül ez az axióma teszi lehetővé az úgynevezett teljes indukciós bizonyításokat. Erre hamarosan néhány remek példát fogunk látni. Lényegét tekintve arról van szó, hogy ha egy állítás igaz 0-ra – amely alapján őt az axiómában említett P halmazba helyeztük –, továbbá az állítás igazsága a „rákövetkezésen” keresztül öröklődik, akkor igaz lesz minden természetes számra.
Első ránézésre ez egy igencsak szegényesre sikerült axiómarendszer. Azonban lényegében ebből a 4 axiómából következik minden, amit a természetes számokról tudunk. Most vizsgáljuk meg, hogy mennyire sokmindent vagyunk képesek felépíteni ebből a mindössze 4 darab axiómából.
A matematikai bizonyítás fogalma
Az olyan állításokat, amelyek nem axiómák, hanem azoknak valamilyen logikai következményei, tételeknek nevezzük. Ahhoz, hogy egy matematikai állítást tételnek nevezhessünk, bizonyítást kell adnunk rá. Ennek során az állítást szigorú logikai érveléssel vissza kell vezetnünk vagy magukra az axiómákra, vagy pedig korábban már bizonyított tételekre.
Példaként fogalmazzuk meg első tételünket, és nézzük meg, hogyan történik egy bizonyítás. Ez egy roppant magától értetődő állításnak fog tűnni. Azonban ne feledjük, hogy mivel valóban kitöröltünk mindent a fejünkből a természetes számokkal kapcsolatban (ugye?!), ezért most kizárólag a fenti 4 axiómára szorítkozhatunk.
A tételek végét a definíciókéhoz hasonlóan a ♣ karakterrel, a bizonyítások végét pedig a ∎ karakterrel fogjuk jelölni.
11.2. Tétel:
Végtelen sok természetes szám létezik.
♣Bizonyítás:
A 11.1. Definícióban szereplő 3. axióma lényegében kimondja, hogy legalább egy természetes szám létezik, nevezetesen a 0. Felfedeztük tehát az első természetes számot.
Az 1. axióma szerint minden természetes számnak – így nyilván a 0-nak is – létezik rákövetkezője. Jelölje most a 0 rákövetkezőjét s(0). Ez a 0-tól különböző kell legyen, hiszen a 0 szintén a 3. axióma miatt semmilyen természetes számnak sem rákövetkezője – így saját magának sem –, vagyis 0\neq s(0). Felfedeztünk tehát a második természetes számot, nevezetesen az s(0)-t. A tétel bizonyításához azt kell belátni, hogy ezeket az újabb és újabb felfedezéseket vég nélkül folytathatjuk.
Tegyük fel most, hogy a legutóbb felfedezett természetes szám az x. Az 1. axióma miatt minden természetes számnak – így nyilván x-nek is – létezik rákövetkezője, jelöljük ezt s(x)-szel. Ez minden eddig felfedezett természetes számtól különböző kell legyen. A 0-tól a 3. axióma miatt különbözik, amely kimondja, hogy a 0 semmilyen természetes számnak nem lehet rákövetkezője – és így x-nek sem.
De s(x)-nek különböznie kell az összes többi, már felfedezett számtól is, hiszen azokhoz korábban már eljutottunk a 0-ból kiindulva a rákövetkezést követve. Márpedig ha korábban már eljutottunk hozzájuk, akkor a 2. axióma miatt x-ből már nem juthatunk vissza egyikhez sem. Így tehát s(x) egy újabb felfedezett természetes szám. Ugyanezzel a gondolatmenettel újabb és újabb természetes számokat fedezhetünk fel, amelyek mind különbözőek lesznek az addig már felfedezettektől.
Másként fogalmazva a természetes számok \N halmazának végtelen sok eleme van.
∎Látható, hogy a természetes számok végtelensége egyáltalán nem magától értetődő, amennyiben kizárólag a Peano-axiómarendszer 4 darab állítására támaszkodhatunk az érvelésben. Ez a példa jól tükrözi, hogy milyen körültekintően kell eljárni egy logikai érvelés során. Halkan megjegyezzük ugyanakkor, hogy a fenti tétel kimondása előtt tisztáznunk kellett volna, hogy pontosan mit értünk „végtelen sok elemet tartalmazó halmaz” alatt. A szükséges halmazelméleti ismereteket most nem részletezzük, azonban egy rövid példával megpróbálunk rávilágítani a lényegre.
Képzeljünk el egy szállodát végtelen sok szobával, amelyek 0-tól vannak sorszámozva. A kérdés: hogyan tudunk elszállásolni egy újonnan érkező vendéget, ha az összes szoba foglalt? A megoldás roppant egyszerű: megkérünk minden vendéget, hogy költözzön át az 1-gyel nagyobb sorszámú szobába. Ezt minden további nélkül meg tudjuk tenni, következésképp felszabadul a 0-ás sorszámú szoba, ahová az újonnan érkező vendéget elhelyezhetjük. Sőt, ha a vendégeket arra kérjük, hogy költözzenek át a kétszer nagyobb sorszámú szobába, akkor minden páratlan sorszámú szoba felszabadul, így akár végtelen sok új vendég is elhelyezhető.
A költöztetéssel lényegében egy úgynevezett kölcsönösen egyértelmű megfeleltetést létesítettünk az összes szobák A halmazából egy olyan B halmazba, amely nem tartalmazta az összes szobát. A kölcsönösen egyértelműség itt azt jelenti, hogy A minden szobájából elköltöztettük a vendégeket, és B minden szobájába pontosan egy A-beli szobából költöztettünk vendégeket. A matematikában is hasonlóan definiáljuk a végtelen számosságot: egy halmaz számossága akkor végtelen, ha létezik kölcsönösen egyértelmű megfeleltetés saját maga és egy valódi részhalmaza között. A Peano-axiómarendszerben bevezetett s függvény épp egy ilyen megfeleltetést valósít meg.
Most bevezetünk egy általános iskolából is jól ismert műveletet az \N halmazon, azaz a természetes számok között. Ennek a műveletnek a konstrukciójához azonban szintén az axiómáinkat fogjuk csak használni.
Művelet bevezetése az \N halmazon
Először is tisztázzuk, hogy pontosan mit értünk művelet alatt. Minket most speciálisan az olyan műveletek érdekelnek, amelyeknek két bemenetük van, de az alábbi definíció általánosítható lenne tetszőleges számú bemenetre is.
11.3. Definíció (Kétváltozós művelet):
Egy valamilyen H halmazon értelmezett kétváltozós művelet egy olyan függvény, amely H-beli elemekből alkotott párokhoz szintén a H halmaz elemeit rendeli hozzá.
♣Az általános iskolában ezt olyan képzeletbeli gépekkel szokták szemléltetni, amelyeknek a tetején 2, az alján pedig 1 lyuk van. Ha a H halmaz két tetszőleges elemét beledobjuk a gép tetején lévő lyukakba, akkor a gép alján kipottyan az eredmény, amely szintén a H halmaz eleme kell legyen. Ez látható az alábbi ábrán:
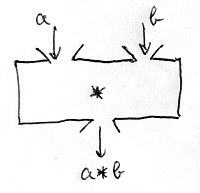
Egy műveletnél tehát meg kell mondanunk azt is, hogy milyen halmazon értelmezzük. Fontos, hogy a művelet „ne vezessen ki” ebből a halmazból. Ez alapján a szokásos összeadás a páratlan számok halmazán nem művelet, mivel például a 3+5 eredménye nem páratlan, azaz nem eleme az alaphalmaznak. A páros számok halmazán azonban az összeadás már művelet, hiszen páros számok összege is páros.
Most definiáljuk, hogy mit értünk összeadás, mint művelet alatt az előzőekben bemutatott \N halmazon, azaz a természetes számok között. Ne feledjük, hogy mivel kitöröltünk a fejünkből mindent (ugye?!), amit a természetes számokról tudni véltünk, ezért csak a Peano-axiómákat használhatjuk ennek az új fogalomnak a bevezetésére:
11.4. Definíció (Peano-összeadás):
Az \N halmazon értelmezett, +-szal jelölt kétváltozós műveletet összeadásnak nevezzük, amennyiben teljesülnek rá a következő tulajdonságok:
- Tetszőleges a számra teljesül, hogy a+0=a.
- Amennyiben valamely a és b számokra az a+b eredménye már ismert, úgy teljesül, hogy a+s(b)=s(a+b).
A fentiekben 0 jelöli az \N halmaznak a Peano-axiómák szerinti, „nullának” nevezett elemét, valamint s jelöli a szintén a Peano-axiómák szerinti „rákövetkezés” függvényt.
♣Ez a definíció tehát két dolgot mond. Egyrészt tetszőleges számhoz 0-t adva az eredmény nem változik. Másrészt pedig ha egy tetszőleges a számhoz egy szintén tetszőleges b szám rákövetkezőjét adjuk hozzá, akkor az eredmény megegyezik annak rákövetkezőjével, mintha a-hoz csak b-t adtunk volna hozzá. Figyeljük meg, hogy semmi mást nem használtunk fel ehhez a definícióhoz, csak a Peano-axiómarendszerben ismertetett 0-val jelölt elemet, valamint az s rákövetkezés függvényt, mint alapfogalmakat.
Ez alapján kiszámítható bármely két természetes szám összege. Amennyiben például \N elemeit a szokásos módon, 10-es számrendszerben jelöljük, akkor a 2+3 összeg az alábbi lépésekben fejthető ki szigorúan a fenti definíció szerint:
\begin{aligned}2+0&=2 \\ 2+1&=2+s(0)=s(2+0)=s(2)=3 \\ 2+2&=2+s(1)=s(2+1)=s(3)=4 \\ 2+3&=2+s(2)=s(2+2)=s(4)=5 \end{aligned}Értelmeztünk tehát egy műveletet az \N halmazon, amelyet önkényesen „összeadásnak” neveztünk, és a + műveleti jellel jelöltünk. Vizsgáljuk hát meg, hogy ez valóban teljesíti-e azokat a jól megszokott tulajdonságokat, amelyeket általános iskolai tanulmányaink alapján elvárnánk tőle.
Az összeadás kommutativitása
Általános iskolában megtanultuk, hogy teljesen mindegy, milyen sorrendben adunk össze két számot, ugyanazt az eredményt kell kapnunk. Megköveteljük tehát, hogy az összeadásban a tagok sorrendje felcserélhető legyen. Az olyan műveleteket, amelyek esetén ez teljesül, kommutatív műveleteknek nevezzük. Első jogos kérdés tehát, hogy vajon a 11.4. Definícióban ismertetett „összeadásnak” nevezett művelet teljesíti-e ezt a kritériumot?
Most meg fogjuk mutatni, hogy ez a tulajdonság bizony teljesül, méghozzá a Peano-axiómák logikai következményeként. Ehhez először egy úgynevezett segédtételt – tudományosabb nevén lemmát – fogunk bizonyítani. Egy lemma semmiben sem különbözik egy sima tételtől. Ezzel az elnevezéssel pusztán azt szeretnénk jelezni, hogy egy olyan állításról van szó, amelynek önmagában nincs jelentősége, viszont felhasználjuk más tételek – jelen esetben például a kommutativitás – bizonyításához. Nézzük is meg ezt a segédtételt:
11.5. Lemma:
Az \N halmaz tetszőleges a és b elemeire igaz az alábbi összefüggés:
a+s(b)=s(a)+b ♣Ennek belátására mutatunk egy remek példát teljes indukciós bizonyításra, amelyet ugye a Peano-axiómarendszer 4. pontja tesz lehetővé. Ez jól szemléltethető egy valamelyik irányban végtelen dominósorral, amelyről belátjuk, hogy bármely dominót felborítva az fel fogja borítani a soron következő dominót is. Ezek után nincs más dolgunk, mint egy laza mozdulattal felborítani az első dominót, és élvezni a – végtelen hosszú – műsort. Most lássuk, hogyan működik ez a gyakorlatban:
Bizonyítás:
A teljes indukciót a b-re fogjuk alkalmazni. Első lépésként feltesszük, hogy az állítás már igaz valamilyen b=n természetes számra, azaz a+s(n)=s(a)+n. Ezt indukciós feltételnek nevezzük. Azt kell bizonyítanunk, hogy ebben az esetben b=s(n)-re is igaz lesz, azaz:
a+s(\underbrace{s(n)}_{=b}) = s(a) + \underbrace{s(n)}_{=b}Most nézzük meg, hogy a baloldali kifejezésből milyen lépéseken keresztül tudunk eljutni a jobboldali kifejezéshez. Először is a 11.4. Definíció 2. pontja miatt:
a+s(s(n)) = s(a+s(n)) = \ldotsAz indukciós feltétel miatt:
\ldots =s(s(a) + n)= \ldotsVégül szintén a 11.4. Definíció 2. pontja miatt:
\ldots = s(a) + s(n)Vagyis azt kaptuk, hogy valóban a+s(\underbrace{s(n)}_{=b}) = s(a) + \underbrace{s(n)}_{=b}.
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. De mit sem érnénk ezzel a ténnyel, ha nem borítanánk fel az első dominót. Ezért most azt igazoljuk, hogy az állítás igaz b=0-ra, azaz:
a+s(0) = s(a) + 0Az 11.4. Definíció 2. pontja miatt:
a + s(0) = s(a+0) = \ldotsUgyanezen definíció 1. pontja miatt:
\ldots = s(a) = \ldotsÉs ismét ugyanezen definíció 1. pontja miatt:
\ldots = s(a) + 0Vagyis azt kaptuk, hogy valóban a+s(0) = s(a) + 0, borul tehát az első dominó, és vele együtt a teljes dominósor.
Ha ugyanis az állítás igaz b=0-ra, akkor igaz lesz b=1. De ha igaz b=1-re, akkor igaz lesz b=2-re is. És így tovább, mivel láttuk, hogy ha igaz b=n-re, akkor igaz lesz b=s(n)-re is, ezért ez az igazság a rákövetkezésen keresztül tovább öröklődik egészen a végtelenségig.
∎Az imént bizonyított segédtételt fogjuk felhasználni az összeadás kommutativitásának bizonyításához. Ezt két lépésben fogjuk megtenni ismét a teljes indukciót alkalmazva. Egyrészt bizonyítjuk, hogy ha tetszőleges a számra valamilyen n esetén teljesül, hogy a + n = n + a, akkor teljesülni fog a+s(n)=s(n)+a is, azaz felállítjuk a dominósort. Másrészt felborítjuk az első dominót, azaz bizonyítjuk, hogy konkrétan n=0 esetén valóban teljesül a kommutativitás. Kezdjük ez utóbbival.
11.6. Lemma:
Az \N halmaz tetszőleges a elemére igaz az alábbi összefüggés:
a+0=0+a ♣Bizonyítás:
Most is teljes indukciót alkalmazunk. Tegyük fel, hogy az állítás igaz valamilyen a=n természetes számra. Az tehát az indukciós feltétel, hogy n+0=0+n. Azt kell bizonyítanunk, hogy ekkor a=s(n)-re is igaz lesz, azaz:
\underbrace{s(n)}_{=a}+0=0+\underbrace{s(n)}_{=a}A korábban bizonyított 11.5. Lemma miatt:
s(n)+0=n+s(0)= \ldotsA 11.4. Definíció 2. pontja miatt:
\ldots =s(n+0)= \ldotsAz indukciós feltétel miatt:
\ldots =s(0+n)= \ldotsVégül szintén a 11.4. Definíció 2. pontja miatt:
\ldots =0+s(n)Vagyis azt kaptuk, hogy valóban \underbrace{s(n)}_{=a} + 0 = 0 + \underbrace{s(n)}_{=a}.
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Ezért most felborítjuk az első dominót, azaz igazoljuk, hogy az állítás igaz a=0-ra. Ez viszont nyilvánvalóan teljesül:
\underbrace{0}_{=a}+0=0+\underbrace{0}_{=a}Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a számra igaz, hogy a+0=0+a.
∎Most tehát rendelkezésünkre áll a 11.5. Lemma és a 11.6. Lemma. Ezek segítségével már be tudjuk látni az összeadás kommutativitását:
11.7. Tétel (Peano-összeadás kommutativitása):
Az \N tetszőleges a és b elemeire igaz az alábbi összefüggés:
a+b = b+a ♣Bizonyítás:
Ismételten teljes indukciót alkalmazunk, ám ezúttal a b-re vonatkozóan. Tegyük fel, hogy az állítás igaz valamilyen b=n természetes számra. Az tehát az indukciós feltétel, hogy a+n=n+a. Azt kell bizonyítanunk, hogy ebben az esetben b=s(n)-re is igaz lesz, azaz:
a+\underbrace{s(n)}_{=b} = \underbrace{s(n)}_{=b}+aA 11.4. Definíció 2. pontja miatt:
a+s(n) = s(a+n) = \ldotsAz indukciós feltétel miatt:
\ldots =s(n+a)= \ldotsIsmételten a 11.4. Definíció 2. pontja miatt:
\ldots = n + s(a) = \ldotsVégül a korábban már bizonyított 11.5. Lemma miatt:
\ldots = s(n) + aVagyis azt kaptuk, hogy valóban a + \underbrace{s(n)}_{=b} = \underbrace{s(n)}_{=b} + a.
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Az első dominót pedig már fel is boríttottuk, ugyanis a 11.6. Lemma alapján az állítás igaz b=0-ra.
Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a és b számra igaz, hogy a+b=b+a.
∎Látható tehát, hogy a 11.4. Definícióban értelmezett „összeadásnak” nevezett művelet valóban kommutatív, ahogy azt az általános iskolában már megszokhattuk tőle. Ez azonban csak és kizárólag a Peano-axiómák logikai következménye, nem pedig holmi fejünkben élő intuitív kép miatt van ez így. A bizonyításához két segédtételen keresztül vezetett az út, azaz kicsit sem mondható magától értetődőnek. A továbbiakban azonban egészen nyugodtan felhasználhatjuk majd ezt a tulajdonságot, hiszen az megnyugtató bizonyosságot nyert.
Most nézzük meg az összeadás egy másik nagyon fontos tulajdonságát, amely szintén jól ismert az általános iskolából.
Az összeadás asszociativitása
Az összeadást egy kétváltozós műveletként definiáltuk, de mi van akkor, ha nem kettő, hanem három – vagy akár ennél több – számot szeretnénk összeadni? Nagyon jó lenne, ha nem kéne újabb és újabb 2-nél többváltozós műveletet bevezetni a tagok számától függően. Tegyük fel például, hogy az a+b+c összeget kell kiszámítani. Hogyan fogjunk hozzá?
Számítsuk ki először az első kettő összegét, és ennek eredményéhez adjuk hozzá a harmadikat? Vagy először számítsuk ki az utolsó kettő összegét, és ennek eredményét adjuk hozzá az elsőhöz? Ezt a két lehetőséget mutatja az alábbi két ábra:
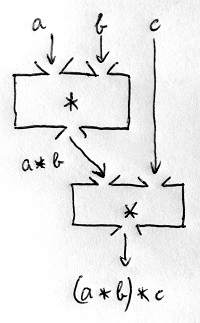
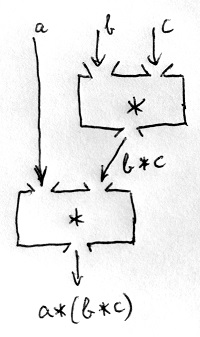
Az olyan műveleteket, amelyek esetén ez mindegy, asszociatív műveleteknek nevezzük. Kérdésünk tehát, hogy vajon a 11.4. Definícióban ismertetett „összeadásnak” nevezett művelet teljesíti-e ezt a kritériumot is? Most megmutatjuk, hogy szintén a Peano-axiómák következménye ennek a teljesülése is.
11.8. Tétel (Peano-összeadás asszociativitása):
Az \N halmaz tetszőleges a, b és c elemeire igaz az alábbi összefüggés:
(a+b)+c = a+(b+c) ♣Bizonyítás:
Ezúttal c-re vonatkozó teljes indukciót alkalmazunk. Tegyük fel, hogy az állítás igaz valamely c=n természetes számra. Az tehát az indukciós feltétel, hogy (a+b)+n = a+(b+n). Azt kell bizonyítanunk, hogy ebben az esetben c=s(n)-re is igaz, azaz:
(a+b)+\underbrace{s(n)}_{=c} = a+(b+\underbrace{s(n)}_{=c})A 11.4. Definíció 2. pontja miatt:
(a+b)+s(n)=s((a+b)+n) = \ldotsAz indukciós feltétel miatt:
\ldots =s(a+(b+n)) = \ldotsIsmételten a 11.4. Definíció 2. pontja miatt:
\ldots = a+s(b+n) = \ldotsÉs végül megint csak a 11.4. Definíció 2. pontja miatt:
\ldots = a+(b+s(n))Vagyis azt kaptuk, hogy valóban (a+b)+\underbrace{s(n)}_{=c} = a+(b+\underbrace{s(n)}_{=c}).
Felállítottuk tehát a dominósort, és beláttuk, hogy bármely dominó felborítása esetén a soron következő dominó is fel fog borulni. Ezért most felborítjuk az első dominót, vagyis igazoljuk, hogy az állítás igaz c=0-ra, azaz:
(a+b)+\underbrace{0}_{=c} = a+(b+\underbrace{0}_{=c})A 11.4. Definíció 1. pontja miatt:
(a+b)+0 = a+b = \ldotsIsmételten a 11.4. Definíció 1. pontja miatt:
\ldots = a+(b+0)Vagyis azt kaptuk, hogy valóban (a+b)+\underbrace{0}_{=c} = a+(b+\underbrace{0}_{=c}).
Borul tehát az első dominó, és vele együtt a teljes dominósor, azaz minden a, b és c számra igaz, hogy (a+b)+c=a+(b+c).
∎Látható tehát, hogy a 11.4. Definícióban értelmezett „összeadásnak” nevezett művelet azon kívül, hogy kommutatív, teljesíti az asszociativitást is, ahogy azt az általános iskolában már megszokhattuk tőle.
Megjegyezzük ugyanakkor, hogy a fentiekben a kommutativitást csak 2 tagú, míg az asszociativitást csak 3 tagú összegekre bizonyítottuk. Nem jelent túl nagy kihívást azonban annak belátása sem, hogy tetszőleges számú tagból álló összegek is hasonló tulajdonsággal rendelkeznek. Sőt, általánosságban érvényes az alábbi állítás, amelynek belátását azonban az Olvasóra bízom.
11.9. Állítás:
Tegyük fel, hogy adott egy H halmaz és egy rajta értelmezett asszociatív és kommutatív kétváltozós művelet. Jelöljük ezt a műveletet *-gal. Mutassuk meg, hogy ekkor az
a_1 * a_2 * \dots * a_nkifejezést akárhogyan is zárójelezzük, illetve akármilyen sorrendben is írjuk fel, az eredmény mindig ugyanaz lesz.
♣Ebben a részben tehát ízelítőt mutattunk abból, hogy hogyan történik egy matematikai elmélet felépítése. Egy ilyen építménynek az alapja mindig egy úgynevezett axiómarendszer, amely néhány olyan állításból áll, amelyeket igaznak fogadunk el. Ezekből kiindulva aztán újabb fogalmak definiálhatók, és újabb állítások eredeztethetők a matematikai logika szigorú szabályai szerint. Példaként bemutattuk a Peano-axiómarendszert, amely mindössze 4 állítást fogalmaz meg. Ebből következik minden, amit a természetes számokkal kapcsolatban jelenleg tudunk, de az is, amit majd csak az utókor fog felfedezni a jövőben. A Peano-axiómák segítségével bevezettünk egy műveletet is a természetes számok között, amelyet összeadásnak neveztünk el. Végül a teljes indukciós bizonyításra mutattunk példákat, amelyekkel bizonyítottuk, hogy az összeadás jól megszokott tulajdonságai valóban teljesülnek, mint az axiómák logikai következményei.
A következő részben egy másik műveletet is be fogunk vezetni, amelyet szorzásnak fogunk nevezni. Erre a műveletre is hasonló tulajdonságokat fogunk bizonyítani az axiómákból, valamint megmutatunk egy nagyon fontos kapcsolatot a két művelet között. Ezután végre rátérhetünk azokra a kérdésekre, amelyek lehetővé teszik az előző részekben bemutatott kriptográfiai primitívek működését, és amelyek nélkül ma nem létezne információs társadalom.
A következő részt itt találod…



