Az előző részben elkezdtük felvázolni a modern kriptográfiai eljárások mögött meghúzódó alapvető számelméleti gondolatokat. Olyan alapfogalmakat ismertünk meg, mint egyirányú függvények, moduláris összeadás, szorzás és hatványozás, valamint a diszkrét logaritmus problémája. Ezután részletesen megvizsgáltuk a Diffie-Hellman kulcscsere protokoll működését. Láttuk ugyanakkor, hogy megfelelő partnerhitelesítés hiányában egy aktív támadó könnyedén kijátszhatja ezt a rendszert. Ezért elkezdtük bemutatni az úgynevezett aszimmetrikus kulcsú titkosítás alapötletét. Végül megemlítettük az erre az ötletre épülő RSA-algoritmust. Ez – mint látni fogjuk – a digitális aláírások és tanúsítványok segítségével választ ad a partnerhitelesítés kérdésére is. De vajon mik azok a digitális aláírások és tanúsítványok? Hogyan tud meggyőződni Alice és Bob arról, hogy valóban egymással kommunikálnak, nem pedig egy rosszindulatú támadóval? Mik azok a bizalmi modellek és hogyan épülnek fel? Ebben a részben erről lesz szó…
Figyelem! Erősen ajánlott elolvasni az 5. és 9. részt az alábbiak megértéséhez. A teljes cikksorozat elejét itt találod.
Az aszimmetrikus kulcsú rejtjelezés kapcsán láthattuk, hogy ebben az esetben Alice nem ugyanazt a kulcsot használja a Bob-nak szánt üzenet rejtjelezésére, mint amivel Bob az üzenetet dekódolja. Ebben a felállásban minden résztvevő rendelkezik egy kulcspárral, amelynek egyik felét nyilvános (publikus), másik felét pedig titkos (privát) kulcsnak nevezzük. Egy adott résztvevő – például Bob – a saját nyilvános kulcsát nyugodtan elérhetővé teheti bárki számára. Az ugyanis csak a neki küldött üzenetek rejtjelezéséhez használható. A dekódolás kizárólag a kulcspár másik részével, a titkos kulccsal lehetséges, amelyet viszont Bob sosem ad ki a kezéből, azt titokban tartja.
Ez önmagában még nem biztosít partnerhitelesítést, mivel egy aktív támadó – például Mallory – könnyedén kijátszhatja a rendszert, méghozzá a következőképpen. Tegyük fel, hogy Alice szeretne Bob-nak rejtjelezett üzenetet küldeni. Ezért megszólítja Bob-ot és elkéri tőle a nyilvános kulcsát. A csaló Mallory azonban eltéríti ezt az üzenetet és beékelődik Alice és Bob közé, pontosan ugyanúgy, mint ahogy a Diffie-Hellman kulcscsere protokoll támadásakor tette. Válaszol Bob-nak kiadva magát, és visszaküldi a saját K_M nyilvános kulcsát Alice-nak. Ezzel párhuzamosan megszólítja Bob-ot, és elkéri az ő K_B nyilvános kulcsát, neki viszont azt hazudja, hogy ő Alice. Ezen a ponton Alice azt hiszi, hogy Bob nyilvános kulcsát kapta meg, Bob pedig azt hiszi, hogy Alice kérte el az ő nyilvános kulcsát. A támadásnak ez a része látható az alábbi ábrán:
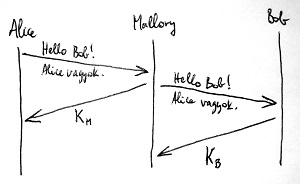
Ezután Alice egy bizalmas x üzenetet küld Bob-nak, amelyet rejtjelez a K_M kulccsal. Alice erről a kulcsról azt hiszi, hogy Bob nyilvános kulcsa, de valójában a csaló Mallory-é. Így amikor Mallory elfogja a rejtjelezett y üzenetet, azt könnyedén dekódolni tudja a saját k_M titkos kulcsával, megismerve ezáltal a bizalmas információt. Annak érdekében, hogy Alice és Bob ne fogjon gyanút, Mallory gyorsan újból rejtjelezi az üzenetet, de ezúttal Bob K_B nyilvános kulcsával, és továbbküldi azt Bob-nak. Végül Bob megkapja a z rejtjelezett üzenetet, és dekódolja azt a saját k_B titkos kulcsával, mit sem sejtve erről az egész disznóságról. Ez a folyamat látható az alábbi ábrán:

Ennek a problémának a kiküszöbölését teszik lehetővé az úgynevezett digitális tanúsítványok, amelynek alapvető építőelemei a digitális aláírások.
Digitális aláírások
Láthattuk, hogy egy aszimmetrikus kulcsú rejtjelező esetén a kulcspár nyilvános részével kódolt üzeneteket kizárólag ugyanezen kulcspár titkos részével lehet dekódolni. Igen hasznos eszközt kapunk a kezünkbe, amennyiben a kulcsok szerepe ilyen értelemben felcserélhető. Nevezetesen, ha a kulcspár titkos részével kódolt üzeneteket viszont kizárólag a kulcspár nyilvános részével lehet dekódolni. Nem minden aszimmetrikus kulcsú rejtjelező teljesíti ezt a kritériumot, de történetesen a már sokszor említett RSA-algoritmus igen. De vajon miért olyan hasznos ez?
Rejtjelezésre nyilván nem használható. Ha ugyanis Alice kódol egy üzenetet a saját titkos kulcsával, akkor azt a fentiek alapján bárki dekódolni tudja Alice nyilvános kulcsával, hiszen az bárki számára elérhető. Vegyük észre azonban, miszerint az a tény, hogy egy üzenet dekódolható Alice nyilvános kulcsával egyben azt is jelenti, hogy azt csak egy olyan résztvevő kódolhatta, aki Alice titkos kulcsának birtokában volt. Márpedig ha Alice nem teljesen bolond, és valóban sosem adja ki a kezéből a titkos kulcsát, akkor ez bizonyíték arra, hogy az üzenetet kizárólag ő küldhette. Ily módon Bob könnyedén meggyőződhet arról, hogy Mallory vagy más belekontárkodott-e az üzenetbe az átvitel során vagy nem.
Tegyük fel ugyanis, hogy Alice szeretne egy x üzenetet küldeni Bob számára, de azt is szeretné, ha Bob ellenőrizni tudná, hogy valóban az az üzenet érkezik-e meg hozzá, amelyet ő elküldött. Alice-nak nincs más dolga, mint kódolni az üzenetet, de ezúttal nem Bob nyilvános kulcsát, hanem a saját k_A titkos kulcsát használva. Az így kapott y kódszöveget ezután Alice az elküldeni kívánt x üzenethez fűzi, és az így keletkezett (x,y) összetett üzenetet küldi el Bob-nak. Ez látható az alábbi ábrán:
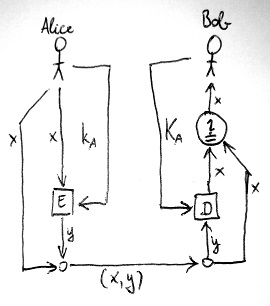
Bob a vételi oldalon szétszedi a megérkező (x,y) összetett üzenetet, de mielőtt annak x komponensét felhasználná, szeretne meggyőződni róla, hogy az sértetlenül érkezett-e meg hozzá. Ezt könnyen megteheti, hiszen csak vennie kell Alice K_A nyilvános kulcsát, azzal dekódolni a kapott összetett üzenet y komponensét, és az eredményt összehasonlítani x-szel. Amennyiben ez a kettő megegyezik, úgy Bob biztos lehet benne, hogy az üzenet küldője Alice titkos kulcsának birtokában volt. Következésképp a küldő csak Alice lehetett.
Amennyiben viszont Bob különbséget észlel, akkor ez azt bizonyítja számára, hogy egy aktív támadó garázdálkodik a kommunikációs csatornán. Hiszen Mallory hiába próbálja meg korrumpálni az x üzenetet, a megváltoztatott üzenethez tartozó y komponenst nem fogja tudni előállítani, mivel nem ismeri Alice titkos kulcsát. Az y komponens tehát tulajdonképpen hitelesíti az x komponens eredetét Bob számára, így azt szemléletesen Alice digitális aláírásának nevezzük.
Ez mind szép és jó, van azonban három probléma, amit mindenképpen meg kéne oldani. Az első, és legkisebb probléma az, hogy az (x,y) összetett üzenet x komponense teljesen nyílt szövegként halad át a kommunikációs csatornán. Így annak tartalmát egy támadó – habár módosítani nem tudja az y digitális aláírás miatt – minden erőfeszítés nélkül megismerheti. Ez a probléma könnyen kiküszöbölhető, ha Alice először rejtjelezi az x üzenetet Bob K_B nyilvános kulcsával, és az így kapott s kódszöveget látja el a saját digitális aláírásával x helyett.
Bob ebben az esetben ugyanúgy ellenőrizni tudja az s kódszöveg hitelességét az előbb ismertetett módon, csak ezután még dekódolnia kell azt a saját k_B titkos kulcsával annak érdekében, hogy megkapja az eredeti x üzenetet. Ilyen módon tehát az üzenet eredetiségének védelme mellett a tartalmának elrejtése is biztosítható. Ez látható az alábbi ábrán:
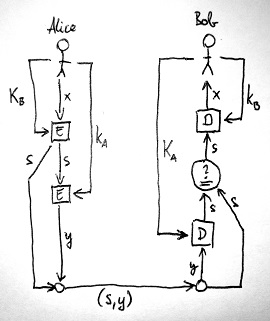
A második probléma a digitális aláírás méretével függ össze. Vegyük észre, hogy a digitális aláírás nem más, mint az aláírni kívánt bitsorozat Alice titkos kulcsával kódolt változata. Következésképp ugyanolyan hosszú, mint maga az üzenet. Ezt a problémát a következő szakaszban tárgyalt úgynevezett kriptográfiai hash függvényekkel iktathatjuk ki.
Végül a harmadik probléma Bobnak az Alice nyilvános kulcsába vetett bizalmával függ össze. Nevezetesen, amikor Bob ellenőrzi egy üzenet digitális aláírását Alice nyilvános kulcsával, hogyan győződhet meg arról, hogy az valóban Alice nyilvános kulcsa, nem pedig Mallory-é, aki csak azt hazudja a kulcsról, hogy Alice-é? Bob vagy egy nyilvános kulcstárból kérdezi le Alice kulcsát, vagy pedig maga Alice küldi el neki. De gondoljunk bele, hogy Mallory kontrollálni tudja a résztvevők teljes kommunikációját. Így azt is elérheti, hogy Bob-hoz már egy olyan nyilvános kulcs jut el, ami valójában Mallory titkos kulcsának a párja. Mallory tehát ebben az esetben képes digitálisan aláírni egy meghamisított üzenetet oly módon, hogy Bob rendben találja az aláírást, mivel azt hiszi, hogy Alice nyilvános kulcsát használta az ellenőrzéshez. Ennek kivédésére szolgálnak a digitális tanúsítványok, amelyekről szintén ebben a részben lesz szó.
Kriptográfiai hash függvények
Egy hash függvény egy olyan művelet, amely egy tetszőleges hosszúságú bemeneti bitsorozatból egy fix méretű – tipikusan 256 vagy 512 bit hosszúságú – kimeneti bitsorozatot állít elő. Ezt a kimeneti bitsorozatot a bemenet hash értékének nevezzük. Amennyiben egy hash függvény teljesít bizonyos kritériumokat, akkor az általa előállított hash értéket a bemeneti bitsorozat eredetiségének ellenőrzésére használhatjuk. Ezeket kriptográfiai hash függvényeknek nevezzük.
Ahhoz hasonlóan, ahogy minket azonosít az ujjlenyomatunk, az adatok hash értéke is egy, az adott adatra jellemző mennyiség. Ha úgy tetszik, egyfajta „digitális ujjlenyomat”. Mivel függvényről van szó, ezért ugyanazt a jelölést alkalmazhatjuk, mint amit az előző részben a függvényeknél tanultunk. Például legyen adott egy x üzenet és egy h hash függvény. Ekkor az x üzenet hash értékét – vagy „lenyomatát” így jelöljük: h(x). Az alábbi ábrán egy hash függvény látható:
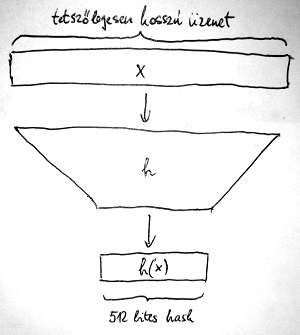
Vegyük észre, hogy egy hash függvény lehetséges bemeneteinek halmaza végtelen – hiszen a bemenet bármilyen tetszőleges hosszúságú bitsorozat lehet –, a lehetséges hash értékek halmaza viszont véges számosságú – hiszen a kimenet egy fix (például 512 bit) méretű bitsorozat. Emiatt nyilvánvalóan végtelen sok olyan bitsorozat létezik, amelyeknek ugyanaz a hash értéke. Az ilyen eseteket ütközéseknek (collision) nevezzük. A kriptográfiai alkalmazások esetén fontos, hogy minél kisebb valószínűséggel következzen be ütközés egy adott hash függvény és a szóba jövő üzenetek esetén. Egy jó kriptográfiai hash függvénynek ezért az alábbi kritériumokat kell teljesítenie:
- Őskép ellenállóság (pre-image resistance): Tetszőleges x üzenet h(x) hash értékét algoritmikusan „könnyű” legyen kiszámítani, de egy adott y hash értékhez algoritmikusan „nehéz” legyen olyan x üzenetet találni, amelynek épp y a hash értéke – azaz amelyre y=h(x) teljesül. Ez a kritérium lényegében azt követeli meg, hogy a h hash függvény legyen egyirányú függvény. Arról, hogy mit nevezünk algoritmikusan „könnyű” vagy „nehéz” feladatnak, a 7. részben volt szó részletesen. Az ilyen tulajdonságú hash függvényeket őskép ellenálló hash függvényeknek nevezzük.
- Második őskép ellenállóság (second pre-image resistance): Egy adott x_1 üzenethez algoritmikusan „nehéz” legyen olyan x_2 üzenetet találni, amelynek ugyanaz a hash értéke – azaz amelyre h(x_1)=h(x_2) teljesül. Az ilyen tulajdonságú hash függvényeket gyengén ütközésmentes hash függvényeknek nevezzük.
- Ütközésellenállóság (collision resistance): Algoritmikusan „nehéz” legyen két olyan tetszőleges x_1 és x_2 egymástól különböző üzenetet találni, amelyeknek ugyanaz a hash értéke – azaz amelyre h(x_1)=h(x_2) teljesül. Az ilyen tulajdonságú hash függvényeket erősen ütközésmentes hash függvényeknek nevezzük.
A fenti kritériumok miatt egy hash függvényre érvényesülnie kell az úgynevezett lavinahatásnak. Ez lényegében azt jelenti, hogy a bemenet egyetlen bitjének megváltoztatása hatására a „lenyomat” minden bitjének 50-50% eséllyel kell megváltoznia. Ha egy hash függvény nem mutat erőteljes lavinahatást – azaz gyengén véletlenszerűsít – akkor nem tekinthető erősnek. Innen ered egyébként a „hash” kifejezés is, amely angolul „zagyvalékot” jelent.
Napjainkban kriptográfiai hash függvényt megvalósító eljárásként az MD5 (Message-Digest algorithm 5) és az SHA (Secure Hash Algorithm) különböző változatai terjedtek el a legjobban. Ezek részleteire itt nem térünk ki, ám megemlítjük, hogy az MD5 hash algoritmus ma már nem tekinthető biztonságosnak. Ennek okait lentebb fogjuk részletezni. Sőt, 2005 óta már az SHA-1 algoritmus támadhatósága is ismert, ezért rengeteg szervezet az SHA család későbbi változatait ajánlja kriptográfiai alkalmazásra.
Előbb azonban vizsgáljuk meg, hogy a kriptográfiai hash függvények hogyan kapcsolódnak a fentebb már említett digitális aláírásokhoz.
Kriptográfiai hash függvények alkalmazása
Említettük, hogy a digitális aláírás kedvéért nem szeretnénk megduplázni a kommunikációs csatornán átküldött adat mennyiségét. Márpedig ha Alice a Bob-nak szánt üzenetet egy az egyben kódolja a saját titkos kulcsával, akkor az így kapott digitális aláírás hossza az aláírt eredeti üzenet hosszával fog megegyezni.
Ehelyett egy valódi digitális aláírásnál a következő történik. Tegyük fel, hogy Alice digitális aláírással kívánja ellátni az x bitsorozatot. Az most lényegtelen számunkra, hogy ez az eredeti üzenet-e, vagy annak Bob nyilvános kulcsával titkosított változata. A lényeg, hogy ez az a bitsorozat, amelyről Alice bizonyítani szeretné Bob számára, hogy valóban ő küldte azt.
Ennek érdekében Alice először egy h hash függvényt alkalmaz az aláírni kívánt x bitsorozatra, amelynek eredményként előáll az x bitsorozat h(x) „ujjlenyomata”. Ezután Alice ezt a h(x) „lenyomatot” kódolja a saját k_A titkos kulcsával. Valójában ennek a kódolásnak az eredményét nevezzük az x üzenet digitális aláírásának, amelyet \text{sig}(x)-szel jelölünk. Alice ezt a bitsorozatot fűzi hozzá az eredeti üzenethez, és az így kapott (x, \text{sig}(x)) összetett üzenetet küldi el Bob-nak. Ez az aláírási folyamat látható az alábbi ábrán:
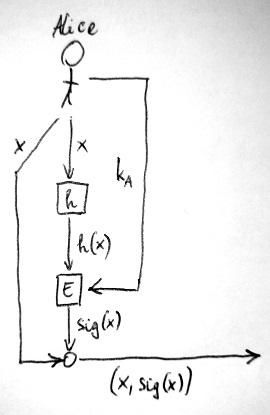
A vételi oldalon az aláírás ellenőrzése – egy kis különbséggel – ugyanúgy történik, mint a fentebb már említett esetben. Bob szétszedi a megérkező (x,\text{sig}(x)) összetett üzenetet, de mielőtt annak x komponensét felhasználná, szeretne meggyőződni róla, hogy az sértetlenül érkezett-e meg hozzá. Ehhez egyrészt veszi Alice K_A nyilvános kulcsát, azzal dekódolja a kapott összetett üzenet \text{sig}(x) komponensét, így megkap egy bitsorozatot. Ennek x sértetlensége esetén meg kell egyeznie a h(x) hash értékkel. Azaz Bob-nak is ki kell számolnia a h(x) lenyomatot, és összehasonlítania a \text{sig}(x) dekódolása során kapott bitsorozattal. Az alábbi ábrán az aláírás ellenőrzésének folyamata látható:
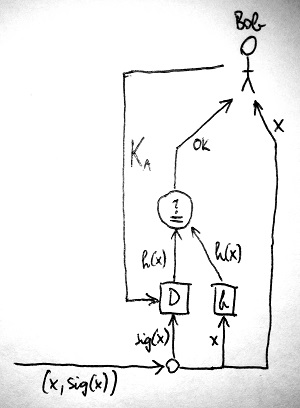
Amennyiben az ellenőrzés sikeres volt, úgy Bob biztos lehet benne, hogy az x üzenet küldője Alice titkos kulcsának birtokában volt, következésképp az csak Alice lehetett. Amennyiben viszont Bob különbséget észlel, akkor ez azt bizonyítja számára, hogy egy aktív támadó garázdálkodik a kommunikációs csatornán. Hiszen Mallory hiába próbálja meg korrumpálni az eredeti x üzenetet, az ugyanis nagy valószínűséggel már egy teljesen különböző hash értéket fog eredményezni a hash függvény lavinahatása miatt. Ezt viszont Mallory nem fogja tudni aláírni Alice nevében, mivel nem ismeri Alice titkos kulcsát.
Mallory egyetlen esélye, ha sikerül találnia egy olyan meghamisított x' üzenetet, amelynek ugyanaz a lenyomata, mint x-nek – azaz h(x')=h(x) teljesül –, ekkor ugyanis a digitális aláírás is egyezni fog, és Bob nem fog gyanút. Ez azonban gyakorlatilag lehetetlen Mallory számára, amennyiben a használt hash függvény ütközésellenálló.
Most megvizsgálunk egy valószínűségszámításból származó érdekes jelenséget, amelyre a kriptográfiai hash függvények elleni úgynevezett ütközéses támadások épülnek.
A születésnap paradoxon
A születésnap paradoxon egy érdekes furcsaság, amely matematikai értelemben nem, csak a szó hétköznapi értelmében nevezhető paradoxonnak. Azért hívják mégis így, mivel némileg ellentmond a „józan észnek”.
Tegyük fel, hogy egy szobában véletlenül választott emberek egy csoportja tartózkodik. Ezen kívül feltesszük, hogy ha valakinek nem ismerjük a születésnapját, akkor az a 365 napos év minden napján azonos valószínűséggel születhetett. A kérdés az, hogy mennyi a valószínűsége, hogy legalább két személynek megegyezik a születésnapja. A meglepő válasz az, hogy ennek esélye több mint 50%, ha a csoport létszáma legalább 23. Sőt, legalább 58 személy esetén ez a valószínűség már 99% felett van. A legtöbb ember valószínűleg sokkal kisebb esélyt mondana erre, ha tippelnie kéne, ezért nevezzük paradoxonnak.
A jelenség megértéséhez kulcsfontosságú az az észrevétel, hogy noha viszonylag kevés ember van a szobában, már így is nagyon sok párt alkotnak, melyeknél egyenként kell vizsgálni a születésnap egyezést. Nem az a kérdés tehát, hogy a szobában tartózkodó emberek közül legalább az egyiknek a születésnapja egybeesik-e egy konkrét emberével – például a miénkével. A születésnap paradoxon esetén ehelyett azt vizsgáljuk, hogy bármely két embernek egyezik-e a születésnapja. A szóbanforgó valószínűség kiszámításának pontos módja most nem érdekes. Az azonban igen, hogy mit jelent ez a jelenség a kriptográfiai hash függvények esetén.
Tegyük fel, hogy egy hash függvény N bit hosszú lenyomatokat állít elő tetszőleges hosszúságú üzenetekből. Az összes létező lenyomatok száma tehát 2^N. Tegyük fel továbbá, hogy bármilyen üzenetre is alkalmazzuk a hash függvényt, teljesen véletlenszerű, hogy végül melyik lesz az üzenet lenyomata ebből a 2^N lehetőségből. Ez a feltételezés lényegében azt mondja ki, hogy a hash függvényünkre erőteljesen érvényesül a fentebb már említett lavinahatás.
A születésnap paradoxon terminológiájában az üzenetek a szobában tartózkodó embereknek, a véges számú lehetséges lenyomatok pedig a különböző születésnapoknak felelnek meg. A kérdés tehát az, hogy egy támadónak hány üzenetpárt kell megvizsgálnia ahhoz, hogy elegendően nagy valószínűséggel találjon két olyan üzenetet, amelynek ugyanaz a hash értéke. A születésnap paradoxon-hoz hasonló gondolatmenet miatt előfordulhat, hogy egy megfelelő számítási kapacitással rendelkező támadó számára egy ilyen üzenetpár megtalálása belátható időn belül kivitelezhető, amennyiben a használt hash értékek nem elegendően hosszúak. A fentebb már említett MD5 hash függvény 128 bit hosszúságú lenyomatokat képez, amely már több, mint 10 éve – a mai számítási kapacitásokról már nem is beszélve – egyáltalán nem nevezhető biztonságosnak.
Például 2004 márciusában indult az MD5CRK nevű projekt, amelynek célja az MD5 gyengeségeinek demonstrálása volt. Végül 2004 augusztusának második felében mutatták be a módszert, amellyel egy óra alatt sikerült ütközést találni. Az ehhez használt hardver konfiguráció 32 darab 1.90 GHz-es processzorral és 1 TB memóriával volt felszerelve. Ez akkoriban erősnek számított ugyan, de annyira azért nem volt a valóságtól elrugaszkodott számítási kapacitás. 2006-ban egy olyan módszert publikáltak, amely már mindössze néhány perc alatt képes volt MD5 ütközést előállítani egy akkori átlagos laptopon (1.6 GHz Intel Pentium).
Vegyük észre, hogy egy születésnap paradoxonra épülő támadás nem egy adott hash értékhez keres egy üzenetet. Az ugyanis még MD5 esetén is kivitelezhetetlen volna. Ehelyett a támadó olyan üzenet-párokat keres, amelyeknek ugyanaz a hash értéke. Most nézzük meg, hogyan tud ebből anyagi előnyt kovácsolni?
A születésnapi támadás
Tegyük fel, hogy a csaló Mallory és Bob adásvételi szerződést kötnek Bob autójára. Mallory kézségesen vállalja, hogy megírja a szerződés szövegét. Az adásvételi szerződésen kívül azonban Mallory egy másik, hamis szerződést is ír, miszerint kölcsönadott Bob-nak 10 millió forintot, amelynek visszafizetését Bob egy adott határidőig vállalja. Mallory kezében tehát van két szerződés, egy valódi és egy hamis. Azt szeretné elérni, hogy a hamis szerződés is el legyen látva Bob digitális aláírásával. A valódi szerződésre azért van szüksége, hogy megszerezze Bob digitális aláírását, mivel azt ő maga – Bob titkos kulcsának hiányában – nem tudja előállítani. Az így megszerzett digitális aláírást ezután a hamis szerződés hitelesítéséhez akarja felhasználni.
Van azonban egy probléma, amit Mallory-nek még meg kell oldania a csaláshoz. Mivel a digitális aláírás nem az íráshordozóhoz, hanem a tartalomhoz kötött, ezért a valódi és a hamis szerződés digitális aláírása nagy valószínűséggel nem fog megegyezni. Ez csak egyetlen módon lehetséges: ha történetesen ugyanaz a két szerződést leíró bitsorozat hash értéke.
Mallory ezért elkezdi módosítgatni mind a valódi, mind pedig a hamis szerződést. Csak olyan módosításokat hajt végre rajta, amelyek a két szöveg lényegi részét nem érintik. Például extra szóközöket helyez el, kihagy egy-egy vesszőt, máshogy tördeli a szöveget, átfogalmaz néhány mondatot, stb. Egy adásvételi vagy egy kölcsönszerződés már elegendően hosszú ahhoz, hogy az ilyen láthatatlan változtatások összes lehetséges kombinációinak száma meglehetősen nagy legyen. Például, hogy összemérhető legyen a lehetséges hash értékek számának nagyságrendjével. A valódi szerződés módosított változatait jelölje x_1, x_2, x_3, \dots, a hamis szerződés módosított változatait pedig y_1, y_2, y_3, \dots.
Ugyan apró módosításokról van szó, azonban a hash függvény lavinahatása miatt már ezek is gyakorlatilag véletlenszerű hash értékeket fognak eredményezni. Mallory mindkét sorozatból veszi az első változatot – azaz x_1-et és y_1-et –, mindkettőnek kiszámítja a hash értékét – azaz h(x_1)-et és h(y_1)-et –, és összehasonlítja őket. Amennyiben ezek különböznek, akkor a két sorozat következő elemére hajtja végre ugyanezt, és így tovább mindaddig, amíg nem talál egy olyan x_i, y_i valódi-hamis szerződéspárt, amelyek hash értéke megegyezik.
Amennyiben valamilyen elavult hash függvényről van szó, akkor a születésnap paradoxon miatt Mallory belátható időn belül ütközést fog találni. Legyen tehát x_i az a valódi, y_i pedig az a hamis szerződésváltozat, amelyeknél ez az ütközés bekövetkezik, azaz amelyekre h(x_i)=h(y_i). Ezután Mallory odaadja a mit sem sejtő Bob-nak a valódi x_i szerződést aláírásra, az így megszerzett \text{sig}(x_i) digitális aláírást pedig a hash értékek egyezősége miatt nyugodtan felhasználhatja a hamis y_i szerződés digitális aláírásaként is.
Mallory és Bob a megkötött valódi szerződésnek megfelelően lezavarják az adásvételt, elbúcsúznak egymástól, és mindenki megy szépen haza. Telik-múlik az idő, és elérkezik a hamis kölcsönszerződés szerinti fizetési határidő, amely szerződés létezéséről Bob nem is tud. Mallory felszólítja Bob-ot, hogy adja vissza neki a nem létező kölcsönt. Bob tiltakozik, miszerint ő soha nem kötött kölcsönszerződést Mallory-vel. Mallory ezért a bírósághoz fordul, és bemutatja a hamis szerződést, amelyen ott virít Bob digitális aláírása. A bíróság pedig az aláírás ellenőrzése után Mallory-nek fog igazat adni, és kötelezni fogja Bob-ot a nem létező kölcsön visszafizetésére. Mallory pedig jót röhög a markába, mivel így tulajdonképpen ingyen megszerezte Bob autóját, és még némi pénzt is sikerült tőle kicsalnia.
Az ilyen jellegű csalásokat a megfelelő minőségű és elegendően hosszú lenyomatokat előállító hash függvények alkalmazásával lehet kivédeni. Ilyenkor ugyanis egy ütközés megtalálása Mallory számára algoritmikusan kivitelezhetetlen lesz.
Digitális tanúsítványok
Ennek a résznek az elején megemlítettünk egy még megoldásra váró problémát, amely a nyilvános kulcsokba vetett bizalommal függ össze. Nevezetesen ahhoz, hogy Alice biztonsággal használhassa Bob nyilvános kulcsát – akár egy neki szánt bizalmas üzenet titkosításához, akár egy tőle származó digitális aláírás ellenőrzéséhez – mindenekelőtt meg kell bíznia abban, hogy az valóban Bob nyilvános kulcsa, nem pedig a csaló Mallory-é.
Ezt a problémát Alice és Bob egy olyan harmadik résztvevő bevonásával tudják megoldani, akiben mindketten megbíznak. E résztvevő feladata tanúsítani, hogy egy adott publikus kulcs valóban a tulajdonosként megjelölt résztvevőhöz tartozik. Őt ezért tanúsító hatóságnak vagy szervezetnek (certificate authority – CA) nevezzük.
Tegyük fel például, hogy Bob egy új felhasználó a rendszerben. Generál magának egy nyilvános és titkos kulcspárt. A titkos kulcsot szépen elzárja a széfjébe, majd a nyilvános kulcsával elballag a CA-hoz. Itt igazolja a személyazonosságát, és megkéri a CA-t, hogy állítson ki számára egy úgynevezett digitális tanúsítványt arról, hogy a bemutatott publikus kulcs valóban az övé. Itt megjegyezzük, hogy sok esetben a kulcspárt maga a CA generálja a résztvevők számára, ám ez a lényegen nem változtat. A CA által kiállított tanúsítvány nagyjából a következőket tartalmazza:
- A tanúsítvány tulajdonosának (jelen esetben Bob) adatai
- A tanúsítvány tulajdonosának publikus kulcsa
- A tanúsítvány érvényességi ideje
- A tanúsítvány kiállítója
- A tanúsítvány kiállítójának digitális aláírása
Tegyük most fel, hogy Alice bizalmas üzenetet szeretne küldeni Bob-nak, előbb azonban meg akar győződni róla, hogy valóban Bob van-e a „vonal” túloldalán. Megkéri tehát a „vonal” túloldalán lévő résztvevőt, hogy igazolja magát egy tanúsítvánnyal, amelyet egy olyan CA állított ki, akiben Alice megbízik. Bob elküldi tehát Alice-nak a fenti tanúsítványt. Alice ezután ellenőrzi a tanúsítványon szereplő digitális aláírás hitelességét. Ezt a CA nyilvános kulcsával tudja megtenni a fentebb már ismertetett módon. Itt feltételezzük, hogy a CA nyilvános kulcsát Alice ismeri, és megbízik annak hitelességében. Például azért, mert a rendszeradminisztrátor elhelyezte azt Alice számítógépén, mint megbízható nyilvános kulcsot. Miután Alice ellenőrizte a tanúsítványon szereplő aláírást, már nyugodtan megbízhat a kommunikációs partnere hitelességében – azaz, hogy ő valóban Bob.
A bizalom továbbítása – chain of trust
Térjünk most vissza a 7. részben már említett Kompánia országába. Tegyük fel, hogy a kormány teljesen át akar térni az elektronikus ügyintézésre a hagyományos papíralapú helyett. A bíróságok, a rendőrség, a kormányhivatalok és az egész közigazgatás mind mind elektronikus iratokkal dolgozik és az állampolgároknak lehetőségük van teljesen elektronikusan intézni az ügyeiket.
Egy ilyen bonyolult és sokrésztvevős rendszerben nyilvánvalóan rengeteg tanúsítványt kell kibocsájtani. Nem lenne túl szerencsés, ha ezt a hatalmas feladatot egyetlen CA-ra bíznánk. Ehelyett több CA van a rendszerben, amelyek egy hierarchikusan felépülő fastruktúrába szerveződnek. A hierarchia csúcsán álló hitelesítő szervezetet gyökér CA-nak (root CA) vagy másnéven bizalmi horgonynak nevezzük. E bizalmi modell alapja, hogy minden résztvevő megbízzon legalább a gyökérben, és birtokában legyen a gyökér CA saját maga által aláírt tanúsítványának, az úgynevezett gyökér tanúsítványnak (root certificate). Ebből indul ki a bizalom továbbadása az úgynevezett tanúsítványláncon vagy bizalmi láncon (chain of trust) keresztül. Most Kompánia közigazgatásának példáján keresztül nézzük meg, hogyan kell elképzelni egy ilyen tanúsítványláncot.
Tegyük fel, hogy Kompánia esetén mindenki megbízik a Belügyminisztériumban, ezért ebben az elektronikus közigazgatási rendszerben ő fogja betölteni a bizalmi horgony, azaz a gyökér CA szerepét. Feltételezzük tehát, hogy azok az állampolgárok, akik elektronikusan szeretnék ügyeiket intézni, rendelkeznek egy tanúsítvánnyal, amelyet a Belügyminisztérium állított ki. Ez a tanúsítvány tartalmazza a Belügyminisztérium saját publikus kulcsát, és digitálisan alá van írva a Belügyminisztérium saját titkos kulcsával. Kompániában a törvények értelmében ez a tanúsítvány kötelezően telepítve kell legyen minden olyan számítógépen, amelyet Kompániában értékesítenek.
Tegyük fel, hogy egy állampolgár – például Alice – úgy dönt, hogy mostantól ügyeit elektronikusan fogja intézni a Kompániai Ügyfélkapu nevű internetes szolgáltatáson keresztül. Ehhez először el kell mennie a legközelebbi kormányhivatalba, amely – miután Alice igazolta személyazonosságát – kiállít egy digitális tanúsítványt igazolandó, hogy Alice publikus kulcsának valóban Alice a tulajdonosa. A kormányhivatal ezt a tanúsítványt digitálisan aláírja a saját titkos kulcsával. Ezt végfelhasználói tanúsítványnak (end-user certificate) nevezzük.
Ezen kívül a kiállított tanúsítvány meghivatkozik egy másik, magasabb szintű tanúsítványt, amelyet viszont maga a Belügyminisztérium állított ki. Ez azt igazolja, hogy bárki, aki megbízik a helyi kormányhivatalban, az egyúttal megbízhat azokban a tanúsítványokban is, amelyeket ő állít ki. Ezt a tanúsítványt köztes tanúsítványnak (intermediate certificate) nevezzük. Végül ez a köztes tanúsítvány meghivatkozza a Belügyminisztérium gyökértanúsítványát. Ez azt igazolja, hogy bárki, aki megbízik a Belügyminisztériumban, az megbízhat a köztes tanúsítvány tulajdonosában is, azaz a helyi kormányhivatalban.
Tegyük fel, hogy Alice-on kívül Bob is csatlakozik ehhez a rendszerhez. Az ő számára azonban egy másik kormányhivatal állít ki tanúsítványt, amely azonban szintén a kompániai Belügyminisztérium fennhatósága alá tartozik. A tanúsítványoknak ez a hierarchiája látható az alábbi ábrán:
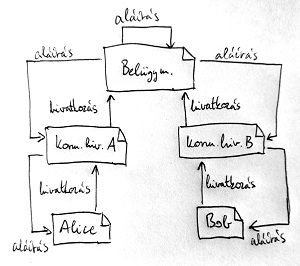
Ezután Alice az fentebb leírtakhoz hasonlóan bizalmas üzenetet szeretne küldeni Bob-nak. Előbb azonban meg akar győződni róla, hogy valóban Bob van-e a „vonal” túloldalán. Bob a saját végfelhasználói tanúsítványával válaszol, amelyet a saját helyi kormányhivatala állított ki. Most Alice-nak arról kell meggyőződnie, hogy megbízhat-e ennek a tanúsítványnak a hitelességében. Ennek érdekében ellenőrzi a meghivatkozott köztes tanúsítványt, és azt látja, hogy azt egy olyan valaki állította ki, aki a Belügyminisztériumnak mondja magát. Végül a gyökér tanúsítvány segítségével Alice azt is ellenőrizni tudja, hogy a köztes tanúsítványt valóban a Belügyminisztérium állította ki. Alice mostmár nyugodtan megbízhat a kommunikációs partnere hitelességében, hiszen sikeresen lezajlott a tanúsítványlánc ellenőrzése Bob tanúsítványától kiindulva egészen a gyökér tanúsítványig.
Megjegyezzük, hogy a fentebb leírt fastruktúrájú bizalmi modellnek léteznek módosított változatai. Az úgynevezett elosztott bizalmi modell például lehetővé teszi a szereplők hitelesítését több különböző bizalmi hierarchia esetén is. Ilyenkor több különböző gyökér CA van jelen, és közvetlenül mindegyikük a rendszernek csak a saját fastruktúrájába tartozó részét tudja hitelesíteni. Az egyes szereplők alaphelyzetben csak a saját gyökér CA-juk tanúsítványában bíznak meg. A teljes körű hitelesítés megvalósításához tehát szükség van valamilyen módszerre, amivel a bizalmat az egyes bizalmi horgonyok között továbbítani lehet. Erre a legelterjedtebb megoldás az úgynevezett kereszthitelesítés, amikoris a gyökér CA-k egymás számára is kiállítanak tanúsítványokat. Ennek – és az egyéb változatoknak – a részleteit itt mellőzzük, az ilyen bizalmi rendszereket általánosságban publikus kulcs infrastruktúrának (public key infrastructure – PKI) nevezzük.
Ebben a részben tehát megismerkedtünk a kriptográfiai hash függvények és a digitális aláírások működésének alapjaival. Láttuk, hogy egy nem megfelelő körültekintéssel megválasztott hash függvény esetén milyen agyafúrt módon lehet meghamisítani ezeket az aláírásokat. Végül a bizalmi modellek bemutatásán keresztül képet kaptunk arról, hogy hogyan történik egy ilyen rendszer résztvevőinek hitelesítése. A következő részben azokat a számelméleti összefüggéseket kezdjük el áttekinteni, amelyek mindezt valóban lehetővé teszik, és amelyeken például az RSA-eljárás is alapul.
A következő részt itt találod…



