Az előző részben megismerkedtünk a rosszminőségű kommunikációs csatornák okozta problémákkal. E problémák kezelésére tettünk egy kitérőt a csatornakódolás, és azon belül is a hibajavító kódok elméletének irányába. Megismertük a csatornakódolási tételt, amely ezek elvi korlátaival kapcsolatban tesz egy igen meglepő állítást. Információátviteli modellünk így már képes arra, hogy Alice és Bob adatait megvédje az átviteli csatorna zaja által okozott sérülésektől. De vajon milyen egyéb veszélyek fenyegetik ezeket az adatokat? A kriptográfia tudománya hol kapcsolódik be ebbe a játszmába annak érdekében, hogy az adatok ezektől a veszélyektől is védve legyenek? Mikre kell felkészülnünk a potenciális támadók képességeit illetően? Mit jelent a feltétel nélküli, illetve az algoritmikus biztonság? Létezik-e az előbbi? Ha igen, annak mik a limitációi? Ebben a részben ezekről a kérdésekről lesz szó…
Az adatokat a fizikai sérüléseken kívül egyéb veszélyek is fenyegetik, amelyeket rosszindulatú támadók okoznak. Az ő motivációjuk főként az anyagi haszonszerzés, amely Alice és Bob számára a legtöbbször anyagi kárként jelentkezik. Fontos leszögezni, hogy a kriptográfusok – és általában a mérnökök – hozzáállása alapvetően pesszimista. Ez azt jelenti, hogy próbálnak az adott alkalmazás esetén elképzelhető legrosszabb esetre felkészülni. Feltételezhető ugyanis, hogyha a tervezett rendszer ilyen szélsőséges körülményeknek ellenáll, akkor ellen fog állni a gyakorlatban bekövetkező eseteknek is.
A támadók célja, hogy információkat szerezzenek meg a legális felektől. A példáinkban a legális feleket két fiktív személlyel, a már jól ismert Alice-szal és Bob-bal azonosítjuk. A támadók a megszerzett információkat azután a saját céljaikra szeretnék felhasználni. A továbbiakban csak az algoritmikus típusú támadási módszerekkel foglalkozunk. Ezeken kívül elképzelhetők további támadási módszerek is. Ilyenek például a betörés, megvesztegetés, szabotázs, stb. Az ezek elleni védekezés azonban nem a kriptográfia feladata.
A rejtjelező komponens
Alice és Bob az adataik támadókkal szembeni védelme érdekében tehát kénytelenek egy úgynevezett rejtjelező komponenst használni. Az alábbi ábrán látható ennek a komponensnek az elhelyezkedése az előző részekből már ismert információátviteli modellben:

Látható, hogy az egyetlen praktikus rejtjelezési pont a csatornakódoló és a forráskódoló között helyezkedik el. Ha a forráskódoló elé építenénk be, akkor jó esetben a forrásból érkező információ jellegétől függően különböző rejtjelezési eljárásokat kéne kitalálnunk. Rosszabb esetben a rejtjelezés egyáltalán nem volna lehetséges, mivel sokszor magát a forráskódolót tekintjük az információátviteli rendszer belépési pontjának. A csatornakódoló után szintén nem célszerű rejtjelezőt elhelyezni. Ebben az esetben ugyanis a kódszöveget (a rejtjelezett bitsorozatot) semmi nem védené a csatorna zaja által okozott sérülésektől. Ezzel kapcsolatban lásd az előző részt.
A támadóval szemben mindig feltételezni kell, hogy teljes részletességgel ismeri az alkalmazott forrás- és csatornakódolási eljárásokat. Például mert ő is birtokában van az ehhez használt eszközöknek vagy szoftver megoldásoknak, amelyeket egyébként bárki megvásárolhat a boltban. Amennyiben nem alkalmazunk rejtjelezést, és a támadó hozzá tud férni a csatornán áthaladó bitekhez, úgy a csatorna- és forráskódolási eljárások ismeretében lényegében a Bob-nak küldött információhoz is hozzá tud férni.
A továbbiakban kriptográfiai szempontból fogjuk vizsgálni az információátviteli rendszerünket, ezért a fenti modellünket egyszerűsíteni fogjuk az alábbiak szerint:
- A forráskódolót a forrás részének tekintjük.
- A forrásdekódolót a nyelő részének tekintjük.
- A csatornakódolót és -dekódolót a csatorna részének tekintjük.
- Végül feltételezzük, hogy a támadó ugyanúgy megkapja a csatornára küldött bitsorozatot, mint Bob (mert például lehallgatja a csatonát).
Ha tehát Alice és Bob biztonságosan szeretnének kommunikálni egymással, a rejtjelezőt a következőképpen kell használniuk ebben az egyszerűsített modellben:
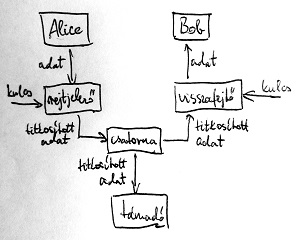
Alice a csatornára küldés előtt a rejtjelező segítségével végrehajt egy kódoló transzformációt a Bob-nak szánt adaton, azaz a nyílt szövegen (plaintext). Ez a transzformáció előállítja a titkosított adatot, azaz a kódszöveget (ciphertext). A kódszöveg ezek után a csatornán keresztül megérkezik Bob-hoz, aki a visszafejtő segítségével a kódoló transzformáció inverzét (megfordítását) hajtja végre rajta. Ezt dekódoló transzformációnak nevezzük, amely tehát visszaállítja Bob számára az eredeti adatot. A támadó a csatorna lehallgatásával szintén hozzájut a kódszöveghez, célja pedig ebből a nyílt szöveg előállítása és tartalmának megismerése.
Az első részben közölt súlyos történelmi példákból láttuk, hogy a támadóval szemben mindig feltételezni kell, hogy részletesen ismeri az Alice és Bob által használt rejtjelezési eljárást. Például mert ő is megvásárolta a boltban az ezt megvalósító szoftver- vagy hardvereszközt. Éppen ezért a kódoló és dekódoló eljárásokat úgy kell megtervezni, hogy egy kulcsnak nevezett adattal paraméterezhető legyen, és a rejtjelezés biztonsága kizárólag az Alice és Bob által paraméterként használt kulcsnak, ne pedig magának az eljárásnak a titokban tartásától függjön. Ez alatt azt értjük, hogy a kulcs ismeretében „könnyű”, míg annak hiányában „nehéz” feladat legyen a nyílt szöveg előállítása a kódszövegből. A cikksorozat következő részeiben lesz szó arról, hogy algoritmikus szempontból mit értünk „könnyű” illetve „nehéz” feladat alatt.
A passzív támadó
Képességei szerint a támadókat kétféle típusra oszthatjuk. Az első típus az úgynevezett passzív támadó. Ő a csatornára kerülő bitsorozatot ugyanúgy képes megfigyelni, mint Bob, azonban módosítani nem tudja azt. Egy ilyen támadó valamilyen módon lehallgatja a fizikai csatornát. Ezért őt a „lehallgatás” angol megfelelője (eavesdropping) után általában Eve néven szoktuk emlegetni. Eve-ről feltételezzük továbbá, hogy hallgatózó tevékenységét képes Alice és Bob előtt titokban tartani, és hogy nem ismeri az Alice és Bob által használt kulcsot. Azt mondjuk, hogy Eve feltörte a rejtjelezési eljárást, ha „gyorsan” képes meghatározni a lehallgatott kódszöveg alapján a nyílt szöveget függetlenül attól, hogy Alice és Bob éppen melyik kulcsot használta. A „gyorsaság” itt olyan időintervallumot jelent, amelyen belül Eve sikeresen használhatja céljaira a megszerzett információt.
Az Eve által végrehajtott törési kísérleteket azok növekvő ereje alapján a következő kategóriákba sorolhatjuk:
- Rejtett szövegű támadás (ciphertext only attack): Ebben a leggyengébb esetben Eve-nek csupán nagyszámú azonos kulccsal kódolt kódszöveg áll rendelkezésére (mert például lehallgatta a csatornát), és ezekből az információkból próbál meg eljárást kidolgozni további üzenetek megfejtésére, vagy akár a kulcs kiszámítására.
- Nyílt szövegű támadás (known plaintext attack): Ilyenkor Eve-nek az azonos kulccsal kódolt elfogott kódszövegeken kívül rendelkezésére állnak azok nyílt szöveg párjai is (mert például valamilyen sunyi módon megszerezte azokat).
- Választott szövegű támadás (chosen text attack): Ebben a legerősebb esetben Eve saját maga választhatja ki azokat a kódszövegeket, amelyeknek a nyílt párját látni szeretné a törési eljárás kidolgozásához. A gyakorlatban ez persze ritkán fordul elő, azonban célszerű egy rendszert erre a „legrosszabb esetre” felkészíteni.
A rejtjelezés célja alapvetően a passzív támadások elleni védekezés. Azt mondjuk, hogy egy rejtjelező rendszer algoritmikusan biztonságos, ha a támadó nem képes olyan gyorsan kinyerni a rejtett információt a kódszövegből, hogy azt céljaira felhasználhassa, feltéve hogy a rendelkezésére álló számítási kapacitás egy adott ésszerű korlát alatt marad. Nyilvánvalóan minden gyakorlatban használt rejtjelező rendszer elméletben feltörhető az úgynevezett kimerítő kulcskereséssel. Kimerítő kulcskeresés esetén Eve az összes lehetséges kulcsot végigpróbálja. Ezt elméletben megteheti, mivel a lehetséges kulcsok száma véges. Ha azonban ez a szám elegendően nagy, akkor ez beláthatatlanul sok ideig eltarthat még a világ összes számítógépének is.
A feltörhetetlen rejtjelező
Ezzel szemben azt mondjuk, hogy egy rejtjelező rendszer feltétel nélkül biztonságos, ha a támadó korlátlan számítási kapacitás mellett sem tudja feltörni azt. A jó hír az, hogy ilyen rejtjelező eljárás létezik, a neve: one-time pad. Mielőtt rátérnénk a rossz hírre, ismertetjük az eljárás lényegét. A one-time pad lényegét tekintve megegyezik az első részben már ismertetett Vigenére-kóddal, ezért először felfrissítjük az ezzel kapcsolatos emlékeinket. Vigenére-kód esetén a nyílt szöveg egyes betűit betűnként váltakozó értékekkel toljuk el az ábécében. A kulcs egy számsorozat, amely meghatározza, hogy melyik betűre mekkora eltolást kell alkalmazni. Például a 26 elemű ABCDEFGHIJKLMNOPQRSTUVWXYZ ábécé használata esetén a (14, 19, 15) kulcsot használva a SZIABOB üzenet kódolása a következő:
S Z I A B O B
14 19 15 14 19 15 14
G S X O U D P
A nyílt szöveg első betűjére tehát 14, a másodikra 19, a harmadikra pedig 15 eltolást alkalmaztunk. A további betűkre ezeket az eltolásokat ismételgettük periodikusan. Ennek eredményeként állt elő a GSXOUDP kódszöveg. Mielőtt rátérnénk a one-time pad leírására, röviden egy hasznos trükköt fogunk ismertetni a kódolás és dekódolás megkönnyítésére.
Könnyebben megjegyezhetővé tehetjük a kulcsot, ha az őt alkotó számok helyett az ábécé megfelelő sorszámú betűit jegyezzük meg (ahol a 0 sorszámú betű az A, az 1 sorszámú betű a B, stb.). Eszerint a hozzárendelés szerint tehát a (14, 19, 15) kulcs helyett elég az OTP kulcsszót megjegyeznünk. Ezek után készíthetünk egy táblázatot oly módon, hogy felírjuk az ábécé összes eltolt változatát egymás alá (beleértve a 0 eltolást, azaz az eredeti ábécét is). Ebből nyilván 26 féle van, azonban a számunkra most csak az eredeti, illetve a kulcsszó betűivel kezdődő ábécék az érdekesek. Ezek ugye a következők:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
OPQRSTUVWXYZABCDEFGHIJKLMN
TUVWXYZABCDEFGHIJKLMNOPQRS
PQRSTUVWXYZABCDEFGHIJKLMNO
Kódoláskor a kulcsot alkotó számok helyett a kulcsszó betűit írjuk az üzenet betűi alá. A kódszöveget ezután úgy állítjuk elő, hogy a fenti táblázatból kikeressük azt a sort és oszlopot, amelyek rendre a kulcsszó és a nyílt szöveg aktuális betűivel kezdődnek. A kódszöveg aktuális betűje ekkor épp a kiválasztott sor és oszlop metszéspontjában lévő betű lesz (a fenti táblázatban az aláhúzott betűk). Ezek alapján a SZIABOB üzenet kódolása:
SZIABOB
OTPOTPO
GSXOUDP
Dekódoláskor ennek az eljárásnak a megfordítását hajtjuk végre. Ilyenkor a kódszöveg betűi alá írjuk a kulcsszó betűit. Ezek minden betűhöz kijelölik azt a sort a táblázatban, amely alapján az adott betű kódolva lett. Ebben a sorban megkeressük a kódszöveg aktuális betűjét, és megnézzük, hogy az eredeti ábécében ez melyik betűnek felel meg (azaz melyik oszlopban van). Ez lesz a nyílt szöveg aktuális betűje. Ezek alapján a GSXOUDP kódszöveg dekódolása az OTP kulcsot használva:
GSXOUDP
OTPOTPO
SZIABOB
Most nézzük meg, hogy ebből az eljárásból hogyan nyerhetünk valóban feltörhetetlen rejtjelezőt. A Vigenére-kód esetén a kulcs általában rövidebb, mint a nyílt szöveg, és ezért periodikusan ismételgetni kell az eltolások sorozatát. Ez lehetőséget adhat egy passzív támadónak arra, hogy a kódszöveg statisztikai elemzésével információkat nyerhessen (feltéve persze, hogy elegendő mennyiségű azonos kulccsal kódolt kódszöveg áll rendelkezésére).
Ezzel szemben a one-time pad esetén a kulcsra az alábbi megkötéseket tesszük:
- Hossza a nyílt szöveg hosszával egyezik meg.
- Tökéletesen véletlenszerű.
- Minden egyes üzenethez új kulcsot használnak.
A már sokat emlegetett Claude Shannon bizonyította be, hogy a one-time pad valóban feltörhetetlen. Ennek oka az, hogy a véletlenszerűen előállított kulcs olyan szinten függetleníti a kódszöveget a nyílt szövegtől, hogy közöttük semmilyen statisztikai összefüggés nem tárható fel. Azaz Eve gyakorlatilag egy „pénzfeldobás sorozatot” fog látni statisztikai értelemben. A feltörhetetlenséget ténylegesen abszolút értelemben kell érteni. Ez azt jelenti, hogy Eve még akkor sem fogja tudni megfejteni a nyílt szöveget, ha az összes lehetséges kulcsot végigpróbálgatja. Az alábbiakban egy egyszerű példán keresztül megmutatjuk, hogy miért.
Tegyük fel, hogy háború van. Alice és Bob a maximális biztonság érdekében úgy dönt, hogy one-time paddel fogják rejtjelezni katonai üzeneteiket. Megállapodnak abban, hogy az angol ábécé 26 betűjét fogják használni ékezetek, írásjelek és szavak közti szünetek nélkül. Végül megegyeznek, hogy minden esetben pontosan 20 karakter hosszú üzenetekkel fognak kommunikálni. Az ennél hosszabb üzeneteket felszeletelik több üzenetre, míg az ennél rövidebb üzeneteket kiegészítik X betűkkel úgy, hogy éppen 20 betű hosszúak legyenek. Például a SZIABOB üzenet helyett a SZIABOBXXXXXXXXXXXXX üzenetet fogják kódolni. Ennek értelme hamarosan világos lesz.
Ezek után előállítanak egy könyvnyi teljesen véletlenszerű betűsorozatot, amelyet kulcsként fognak használni. Amikor Alice egy 20 betűs üzenetet szeretne küldeni Bobnak, a kulcskönyv soron következő 20 betűjét felírja a nyílt szöveg alá kulcsként. Ezután alkalmazza a Vigenére-kódolást, majd a felhasznált 20 betűt kihúzza a kulcskönyvből. Alice, miután megkapta a 20 betűs kódszöveget, a kulcskönyv nála lévő példányából szintén felírja a soron következő 20 betűt a kódszöveg alá. Dekódolja az üzenetet, végül ő is kihúzza a felhasznált 20 betűt a saját kulcskönyvéből. Amennyiben Alice és Bob soha nem hibázik, és szinkronban haladnak előre a kulcskönyvben a kommunikáció során, akkor az általuk alkalmazott rejtjelezés feltörhetetlen Eve számára. Most megmutatjuk, hogy miért.
Képzeljük magunkat Eve helyébe, aki az Alice és Bob által használt csatorna lehallgatása során elfogja a 20 betűs AWLJKFHAEIFHWOIJSSBF kódszöveget. Tegyük fel, hogy Eve tudja, hogy Alice és Bob one-time pad rejtjelezést használt, a szintén 20 betűs kulcsot azonban nem ismeri. Nézzük meg hogy mit tehet. Gyakoriságelemzést nem érdemes alkalmaznia még abban az esetben sem, ha esetleg rengeteg korábbi kódszöveg áll a rendelkezésére. Tudja ugyanis, hogy azokat mind más és más kulccsal titkosították. Amelyek ráadásul tökéletesen véletlenszerűek voltak, csakúgy, mint a jelenleg használt kulcs. Eve tehát nem tehet mást, mint szisztematikusan elkezdni végigpróbálgatni az összes lehetséges 20 hosszú kulcsot. Ezekből a 26 betűs angol ábécé használata esetén 2620, azaz egészen pontosan 19928148895209409152340197376 darab van. Most nagyvonalúan lépjünk túl azon, hogy ennyi kulcs végigpróbálgatása az idők végezetéig is eltarthat a világ összes számítási kapacitásával is. Tételezzük fel, hogy az Eve rendelkezésére álló számítási kapacitás valóban korlátlan.
Eve abban reménykedik, hogy valamelyik kipróbált kulcs esetén értelmes szöveget fog kapni. Egy idő után például el fog érkezni a HWZJHFPTQXSHHXEDMOQI kulcshoz. Ekkor a TAMADASHOLNAPREGGELX feltételezett nyílt szöveget kapja. Ez kétségkívül egy értelmes üzenetnek tűnik, de vajon joggal gondolhatja-e Eve, hogy megtalálta az Alice és Bob által használt kulcsot?
A biztonság kedvéért tovább folytatja az összes létező kulcs szisztematikus kipróbálását. Nagy meglepetésére a FOTRLFMMROUHERLMVVEI kulcshoz érve a VISSZAVONULASXXXXXXX feltételezett nyílt szöveget fogja kapni. Látszólag ez is egy értelmes üzenet, aminek jelentése ráadásul épp az ellenkezője az előzőnek. Eve egyre idegesebb, és tovább folytatja a kulcskeresést. Ám döbbenten tapasztalja, hogy egyre több és több értelmesnek látszó potenciális üzenetet kap a visszafejtési kísérletekből. Például a ZSBFTXOWMVHNQOPSEHEI kulcs kipróbálása esetén a BEKERITESNYUGATROLXX üzenetet, a WFXRCMDILYBQCBYMVVEI kulcs esetén az EROSITESTKERUNKXXXXX üzenetet, és a PSFBRFVMYIMHEKRZOTTV kulcs esetén a LEGITAMOGATASERKEZIK üzenetet kapja. Sőt, mire végez az összes kulcs ellenőrzésével, az összes olyan potenciális nyílt szöveg jelöltet megkapja, amely legfeljebb 20 betű hosszú. De megkapja az olyanokat is, amelyek akár egy hosszabb üzenet valamilyen részei lehetnek.
Látható tehát, hogy one-time pad rejtjelezés esetén Eve helyzete reménytelen, hiszen Alice ezek közül bármelyik üzenetet küldhette. Mivel a használt kulcs teljesen véletlenszerű és egyszer használatos volt, ezért Eve semmit sem feltételezhet azzal kapcsolatban, hogy melyik feltételezett nyílt szöveg a legvalószínűbb. Ráadásul mindez független attól, hogy mennyi erőforrást tudott mozgósítani a feltöréshez.
Akkor mi értelme van folytatni?
Hurrá! – mondhatnánk, hiszen úgy tűnik, hogy megtaláltuk a kriptográfia Szent Grálját, tehát mindenki mehet szépen haza. Sajnos nem ez a helyzet, mivel a one-time pad, habár elméletben tökéletes, a gyakorlatban – néhány speciális esettől eltekintve – nem alkalmazható. A legkisebb probléma, hogy az egyszer használatos kulcsoknak valóban „tökéletesen véletlenszerű számokból” kell állniuk. Hogy ez matematikailag pontosan mit jelent, az messzire vezetne, és e problémakör messze nem olyan egyszerű, mint gondolnánk. Léteznek azonban olyan célhardverek, amelyek valamilyen fizikai jelenséget kihasználva állítanak elő valódi véletlenszámokat. Tegyük fel tehát, hogy ezt a problémát megoldottuk.
Ami egy ennél sokkal nagyobb gond, az az első rész végén már felvázolt kulcsmegosztás problémája. Ez a probléma one-time pad esetén hatványozottan jelentkezik. Nevezetesen: hogyan juttassuk el a kommunikáció összes résztvevőjének azt a temérdek mennyiségű kulcsot biztonságosan? Gondoljunk bele, hogy mi történne, ha például egy egész hadsereg szeretne ilyen módon kommunikálni. Az egymással harcoló egységek helyett a csatamező futárokkal lenne tele, akik a kulcsokat szállítják. Azon logisztikai problémáról már nem is beszélve, hogy mindenki mindig a megfelelő egyszer használatos kulcsot használja. Ha bárki hibázna, az a rendszer teljes összeomlásához vezetne.
Persze megemlítettük az első rész végén, hogy a kulcsmegosztás problémája megoldható biztonságos csatorna használata nélkül is, hiszen az egész cikksorozatnak ez a központi témája. Ez a megoldás azonban „csupán” algoritmikus biztonságot nyújt. Azaz feltételezi, hogy az Eve rendelkezésére álló számítási kapacitás bizonyos korlát alatt marad, még ha ez a korlát nagyon nagy is. A one-time paddel azonban éppenséggel egy korlátlan erőforrásokkal rendelkező támadó ellen akarunk védekezni. Botorság lenne tehát pont a kulcsokat egy olyan rendszeren keresztül továbbítani, amely nem garantálja a feltétel nélküli biztonságot.
A one-time pad alkalmazása tehát iszonyatosan drága, ezért csak néhány nagyon speciális és különleges esetben használják. Csak hogy egyet említsünk: one-time pad rejtjelezést használnak az USA és Oroszország között a kubai rakétaválság apropóján 1963-ban létrehozott forródrót titkosítására, az egyszeri kulcsokat pedig a lehető legszigorúbb biztonsági intézkedések mellett osztják meg egymás között.
Vegyük észre, hogy a one-time pad főként a kulcsmegosztás problémája miatt használhatatlan a gyakorlatban. Ha azonban ezt is meg tudnánk oldani feltétel nélkül biztonságos módon, akkor valóban megtalálnánk a Szent Grált, és a kriptográfia tudományának fejlődése véget érne. A jó hír az, hogy a kvantumfizika törvényei ezt elvileg lehetővé teszik, és – habár ez a technológia még gyerekcipőben jár – már vannak nagyon bíztató eredmények, sőt bizonyos gyakorlati alkalmazások is. A kvantumkriptográfiáról majd egy későbbi részben lesz szó bővebben. Ez azonban még csak a jövő, a titkaink védelmét a jelenben az algoritmikus biztonságra bízzuk, ezért most visszatérünk ehhez a témakörhöz.
Az aktív támadó
Ismerkedjünk hát meg történetünk leggonoszabb szereplőjével. Ő Eve-vel ellentétben nem csak passzívan figyeli a kommunikációt, hanem aktív támadóként be is avatkozik abba.
Az ő neve Mallory, amely név a „rosszindulatú támadó” angol megfelelőjére (malicious attacker) rímel. Mallory azért nagyon veszélyes, mert nemcsak megfigyelni képes a csatornán áthaladó üzeneteket, hanem képes azokat részben vagy teljes egészében megváltoztatni Alice és Bob számára észrevétlenül. Ezenkívül Mallory olykor arra is vetemedik, hogy megpróbálja eljátszani egy vagy több legális fél szerepét azért, hogy valamely másik legális résztvevőktől információt csaljon ki. Ezt megszemélyesítésnek (impersonating) nevezzük.
Az aktív támadásokat algoritmikus eszközökkel nem tudjuk megakadályozni, de úgynevezett kriptoprotokollok alkalmazásával a támadást detektálhatóvá tehetjük Alice és Bob (tehát a legális résztvevők) számára. A protokollok általánosságban véve egy előre meghatározott üzenetcsere folyamatot jelentenek, amelyet kettő vagy több legális fél bonyolít le kooperatívan valamilyen feladat végrehajtására. A kriptoprotokollok építőelemként használják a rejtjelezőt és egyéb kriptográfiai építőelemeket (ezeket összefoglaló néven kriptográfiai primitíveknek nevezzük), s biztosítják a védett kapcsolat felépülését és a kommunikáció alatti aktív támadások észlelhetőségét. Ezen kívül garantálják a kommunikációban résztvevő felek és üzenetfolyamataik hitelességének ellenőrizhetőségét.
Egy üzenet hitelessége azt jelenti Alice vagy Bob számára, hogy majdnem biztos lehet benne, hogy az módosítatlanul, eredeti állapotában érkezett meg hozzá. Egy partner hitelessége Alice vagy Bob számára azt jelenti, hogy majdnem biztos lehet benne, hogy egy üzenetet valóban a tartalmából kiderülő partner küldte, nem pedig Mallory vagy egy hozzá hasonló gazember. A „majdnem biztos benne” itt azt jelenti, hogy a tévedés esélye nagyságrendileg megegyezik annak az esélyével, hogy valaki egymás után ötször megnyeri a főnyereményt az 5-ös lottón.
A mérnöki pesszimizmus a Mallory elleni védekezés kapcsán is megjelenik azáltal, hogy a várhatónál nagyobb hatalmat biztosít neki, azaz feltételezi, hogy Mallory a legálisan résztvevő felek teljes kommunikációját kontrollálni tudja. Ez alatt egyrészt azt értjük, hogy Mallory minden üzenetet képes lehallgatni, módosítani és törölni, másrészt képes olyan hamis üzenetek generálására is, amit a rendelkezésére álló információk lehetővé tesznek. Például képes üzeneteket megfigyelni, megjegyezni és később visszajátszani is. Lényegében tehát a legális résztvevők Mallory-n keresztül kommunikálnak egymással, azaz üzeneteiket neki küldik és tőle is kapják. Ezen kívül Mallory képes bármelyik résztvevőt bevonni egy protokoll végrehajtásába, sőt még arra is rá tud venni egy becsületes résztvevőt, hogy az kezdeményezze egy protokoll végrehajtását Mallory-vel vagy egy másik becsületes résztvevővel.
Mallory tehát egy igazi csaló, aki ellen sokkal nehezebb védekezni, mint Eve-vel szemben. Átalában azonban feltételezzük Mallory-ről, hogy nem elsősorban a protokollok által használt kriptográfiai primitívek feltörésével próbálkozik, hanem abban keresi a gyengeséget, ahogyan a protokoll ezeket az építőelemeket egymással kombinálja. A kriptoprotokollok alapvetően 3 féle kriptográfiai primitívből építkeznek, ezek a következők: rejtjelezők, digitális aláírások és az úgynevezett kriptográfiai hash függvények. Ebben a cikksorozatban főként e primitívek bemutatása fog megtörténni, de ki fogunk térni néhány olyan példára is, amely azt szemlélteti, hogy hogyan lehet ezeket kombinálva egy aktív támadások elleni kriptoprotokollt (vagy egy ilyen elleni támadást) létrehozni. Első körben a rejtjelezőt, mint primitívet vesszük górcső alá, a digitális aláírásokról és a hash függvényekről pedig későbbi részekben lesz szó bővebben.
Blokkrejtjelezők
Rejtjelezőkre számos példát láttunk a korábbi részekben, de általánosságban a következő ábrával lehet összefoglalni őket:
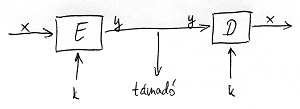
Itt x jelöli a nyílt szöveget, y a kódszöveget, k pedig az Alice és Bob által használt kulcsot. Az E-vel jelölt doboz a kódolási, a D-vel jelölt doboz pedig a dekódolási transzformációnak felel meg. A támadó a két transzformáció közé ékelődik be, és feltételezzük róla, hogy csak az y kódszöveget látja, a nyílt szöveget és a kulcsot nem ismeri.
Egy valódi „boltban kapható” rejtjelező szoftver- vagy hardvereszköz n bit hosszú nyílt szöveg blokkokat kódol n bit hosszú rejtjelezett blokkokba (n értéke tipikusan 128, 256, vagy 512 bit). Ezeket blokkrejtjelezőknek nevezzük. A gyakorlati alkalmazásokban azonban általában ennél jóval hosszabb (vagy rövidebb) üzeneteket szeretnénk titkosítani, ezért szükségünk van olyan eljárásokra, amelyek lehetővé teszik tetszőleges hosszúságú üzenetek titkosítását egy n bites blokkrejtjelező ismételt alkalmazásával. Ezeket az eljárásokat blokkrejtjelezési módoknak nevezzük.
Az első kézenfekvő gondolatunk az lehetne, hogy a nyílt szöveget n bit hosszú blokkokra szeleteljük, ezeket egyenként rejtjelezzük, és az így kapott szintén n bit hosszú rejtjelezett blokkokat egymás után fűzve kapjuk a kódszöveget. A vételi oldalon ehhez hasonlóan a kódszöveget n bit hosszú blokkokra szeleteljük, ezeket egyenként dekódoljuk, és az így kapott n bit hosszú nyílt blokkokat egymás után fűzve visszakapjuk a nyílt szöveget. Ennek a módszernek hátránya, hogy a blokkok rejtjelezése egymástól függetlenül történik, lehetőséget adva Eve-nek a gyakoriságelemzésre. Ez ugyan ilyen blokkméretek esetén eléggé reménytelen vállalkozásnak tűnik, de nem lehetetlen.
Ezért több blokkból álló üzenetek rejtjelezését célszerű úgy végezni, hogy egy rejtjelezett blokk ne csak az azonos pozícióban lévő nyílt blokktól, hanem az előző rejtjelezett blokktól – és így áttételesen az összes korábbi nyílt blokktól – is függjön. Ezen kívül előfordulhat, hogy az üzenet hossza nem n többszöröse, így az utolsó nyílt blokk hossza kisebb lenne, mint n. Ilyen esetben az utolsó nyílt blokkot ki kell egészíteni oly módon, hogy a vételi oldalon a dekódolás után a kiegészítés egyértelműen felismerhető és eldobható legyen (a one-time pad fentebbi bemutatásánál az üzenet X betűkkel való feltöltésekor ugyanez történt).
A fenti problémákat a különböző blokkrejtjelezési módok különbözőképpen oldják meg, ezeket azonban nem részletezzük. Számunkra most csak az a fontos, hogy a blokkrejtjelező egy olyan eszköz, amelyet ha felparaméterezünk egy k kulccsal, a bemenetére pedig egy n bites nyílt bitsorozatot küldünk, akkor a kimenetén elő fog állítani egy szintén n bites rejtjelezett bitsorozatot. Hasonlóképpen a blokkdekódoló egy olyan eszköz, amelyet ha felparaméterezzük ugyanazzal a k kulccsal, a bemenetére pedig a rejtjelező által előállított n bites rejtjelezett bitsorozatot küldjük, akkor a kimenetén elő fogja állítani az eredeti n bites nyílt bitsorozatot.
A 3. részben a számábrázolási módok kapcsán láthattuk, hogy bitsorozatokat lehet egész számokként értelmezni. Ez alapján tehát a rejtjelezőt és a dekódolót felfoghatjuk matematikai függvényekként is. Ha a nyílt blokknak megfelelő számot x-szel, a rejtjelezett blokknak megfelelőt y-nal, a k kulccsal paraméterezett rejtjelező és dekódoló függvényeket pedig Ek-val és Dk-val jelöljük, akkor a rejtjelezés és dekódolás tulajdonképpen az alábbi két összefüggést valósítja meg:
\begin{aligned}y &= E_k(x) \\ x &= D_k(y)\end{aligned}Egy szemléletes példával élve ez olyan, mintha Alice a Bob-nak szánt x üzenetet betenné egy lakattal ellátott ládába, majd a lakatot lezárná a k kulccsal és a lezárt ládát elküldené Bob-nak. Ha Bob-nak van egy másolata a k kulcsról, akkor ki tudja nyitni a ládán lévő lakatot, és ki tudja venni a ládából az x üzenetet. Eve-nek ezzel szemben nincs másolata a k kulcsról, ezért ő nem tudja kinyitni a ládát. A kulcsmegosztás problémája ebben az esetben azt jelenti, hogy Alice és Bob hogyan tudja elérni, hogy mindketten rendelkezzenek egy-egy kulcsmásolattal anélkül, hogy egy ilyen másolatnak a birtokába kerüljön Eve is. Alice persze megtehetné, hogy a kulcs másolatát beteszi egy másik ládába, amelyet egy másik kulccsal lezár, és ezt elküldi Bob-nak. Ekkor azonban visszatértünk az előző problémára, mivel ebben az esetben Bob-nak szüksége van egy másolatra erről a második kulcsról.
Háromutas kulcsforgalom
Egy remek megoldás lehetne azonban a következő: tegyük fel, hogy Alice-nak és Bob-nak is van egy-egy lakatja a hozzá tartozó kulcsokkal. Amikor Alice üzenetet szeretne küldeni Bob-nak, akkor azt beteszi egy ládába, ráteszi a saját lakatját, és elküldi a lezárt ládát Bob-nak, de a kulcsot megtartja magának. Bob ezt a lezárt ládát nem tudja ugyan kinyitni, mivel nem rendelkezik az Alice lakatját nyitó kulccsal, azt azonban megteheti, hogy ő is ráteszi a saját lakatját, és így visszaküldi a ládát Alice-nak, de a kulcsot ő is megtartja magának. Alice ezután leveszi a saját lakatját a ládáról, amelyen így már csak Bob lakatja marad, és megint visszaküldi a ládát Bob-nak. Végül Bob is leveszi a saját lakatját, kinyitja a ládát, és elolvassa az üzenetet.
Figyeljük meg, hogy ebben az esetben nem történt semmiféle kulcs küldözgetés Alice és Bob között, és Eve sem tud hozzáférni a láda tartalmához, mivel akárhányszor elfogja a ládát, azon minden alkalommal van legalább egy lakat. A lakatokat nyitó kulcsok pedig mindvégig Alice-nál és Bob-nál maradtak biztonságban. Ezt a folyamatot szemlélteti az alábbi ábra:
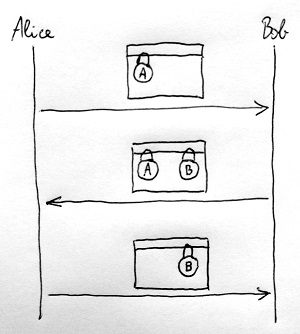
Kérdés azonban, hogy ami működik lakatokkal, az vajon működik-e matematikai függvényekkel. Tegyük fel, hogy Alice kulcsa a, Bob kulcsa pedig b. Ennek megfelelően Alice kódoló és dekódoló függvényei Ea és Da, míg Bob kódoló és dekódoló függvényei Eb és Db. Miután mindketten rátették a „lakatot” az x üzenetre, az Eb(Ea(x)) üzenet érkezik vissza Alice-hoz. Alice leveszi a „lakatot”, azaz erre az üzenetre alkalmazza a Da dekódoló függvényt, és az eredményül kapott Da(Eb(Ea(x))) üzenetet visszaküldi Bob-nak. Amennyiben ez megegyezik az Eb(x) értékkel – azaz amikor már csak Bob „lakatja” van rajta az x üzeneten –, akkor Bob gond nélkül leveheti erről a saját „lakatját” és visszakapja az x üzenetet. A feltétel tehát, hogy tetszőleges x üzenetre és a, b kulcsokra teljesüljön az alábbi összefüggés:
D_a(E_b(E_a(x))) = E_b(x)Az ilyen rejtjelezőket kommutatív rejtjelezőknek nevezzük. A „kommutatív” kifejezés általánosságban a felcserélhetőséget jelenti, ami ebben az esetben arra utal, hogy a „lakatok” felhelyezési és levételi sorrendje ilyen rejtjelező függvények használata esetén felcserélhető.
A 20. század második felében tehát megindult a kutatás az ilyen tulajdonságú függvények keresésére. Ez ugyan nem oldja meg a kulcsmegosztás problémáját, viszont megkerüli azt, ami hatalmas előrelépés. Az első kommutatív rejtjelezőt Adi Shamir izraeli kriptográfus találta meg 1980-ban. Ennek az alapja egy nagyon fontos számelméleti összefüggés, az 1636-ban – tehát sokkal korábban – felfedezett úgynevezett kis Fermat-tétel. E tételre egy későbbi részben még részletesen vissza fogunk térni, amikor már kellő eszköztárunk lesz a megértéséhez. Ezen kívül Adi Shamir nevét se felejtsük el, hiszen hamarosan nagyon fontos szerephez fog jutni ebben a cikksorozatban.
A fenti „lakatos” megoldást háromutas kulcsforgalomnak nevezzük, ami egy kicsit megtévesztő, hiszen valójában nem a kulcsok utaznak, hanem a „lezárt ládák”. Van azonban két probléma ezzel a megoldással. Az első egy gyakorlati probléma, nevezetesen: Alice-nak és Bob-nak online kell lenniük, hiszen oda-vissza kell üzengetniük egymásnak ahhoz, hogy egy üzenet biztonságosan megérkezzen Bob-hoz. Ezért például titkosított email-ek küldésére a módszer nem igazán alkalmas, mivel egy email elküldése és annak a címzetthez való megérkezése között hosszabb idő is eltelhet. A másik – és egyben nagyobb – probléma az, hogy Mallory ellen nem alkalmazható. Ugyanis sem Alice, sem pedig Bob nem lehet biztos abban, hogy egymással, és nem pedig a közéjük beékelődött Mallory-vel kommunikálnak. Vagyis a partner- és üzenethitelesítés nincs biztosítva.
Ebben a részben tehát rátértünk a cikksorozat fő témájára, és megnéztük, hogy a kriptográfia hol foglal helyet az információátviteli modellünkben. Felmértük, hogy milyen jellegű támadások ellen kell megvédenie magát Alice-nak és Bob-nak, ha nem akarnak csalások áldozatává válni. Bemutattunk egy abszolút biztonságos rejtjelezési módszert, ugyanakkor rámutattunk annak gyakorlati korlátjaira is, amelyek miatt kénytelenek vagyunk megelégedni az algoritmikus biztonsággal. Végül elkezdtük matematikai alapokra helyezni a rejtjelezés és dekódolás folyamatát, és bemutattuk a kommutatív rejtjelező fogalmát, amellyel megkerülhető a kulcsmegosztás problémája, de megemlítettük ennek hiányosságait is. A következő néhány részben részletesebben körbejárjuk azt a kérdéskört, hogy pontosan mit értünk algoritmikus biztonság alatt. Ennek keretében megismerkedünk néhány algoritmuselméleti alapfogalommal. Ezek után fogjuk részletesen bemutatni egy olyan rejtjelező rendszer működését, amely kiküszöböli a háromutas kulcsforgalom módszerének hiányosságait, és partner- illetve üzenethitelesítést is biztosít.
A következő részt itt találod…



