Az előző részben leírtak fényében az Alice és Bob közötti kommunikáció konkrét tartalmától a továbbiakban teljesen elvonatkoztatunk. Azt egy 1-esekből és 0-ákból álló bináris sorozatnak fogjuk tekinteni. Most folytatjuk információelméleti kitérőnket, és megismerkedünk az átviteli csatornával, amelynek feladata ezt a sorozatot eljuttatni Alice-tól Bob-hoz. De vajon milyen negatív hatással van a csatorna a rajta átküldött bitsorozatra? Hogyan védekezhetünk e negatív hatás ellen? Ennek mik az elvi korlátai? Miért lehet elolvasni egy CD-t akkor is, ha megkarcolódott? Mi az a hibajavító kódolás és hogyan működik? Ebben a részben erről lesz szó…

Az eddig megismert információátviteli modellünk eddig két komponenst tartalmazott. Az információforrásról és a forráskódolóról a 2. részben volt szó bővebben. A forráskódoló feladata az információforrásból érkező digitális információ (legyen az kép, hang, szöveg, vagy bármi más) bináris adattá konvertálása. Ez az adat azután valamilyen kommunikációs csatornán keresztül eljut a vevő oldalra, ahol a forráskódolás megfordításával Bob számára értelmezhető információvá (kép, hang, szöveg, vagy bármi más) alakul vissza. Az alábbi ábrán a kommunikációs csatornával kibővített modell látható:

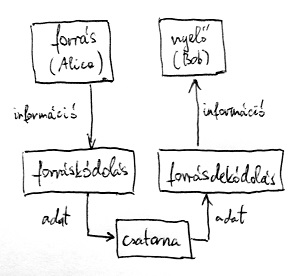
Megjegyezzük, hogy matematikai szempontból irreleváns a csatorna jellege, az információ átvitelének időbeli lefolyása, mint ahogyan az is, hogy az információ Bob-hoz való megérkezését mennyi idővel előzi meg ennek az információnak az Alice általi előállítása és elküldése. Gondoljunk csak például valamilyen CD-re írt adatokra. De bármilyen jellegű médiumot is reprezentál a modellünkben a „csatorna” feliratú doboz, nem árt felkészülnünk egy jelentős problémára, amely a csatorna fizikai jellege miatt sajnos elkerülhetetlen. Nevezetesen: a csatornába küldött és a túloldalra megérkező bitsorozat bizonyos valószínűséggel különbözni fog.

Ennek az oka egész egyszerűen az, hogy a biteknek bármilyen valós csatornában mindig van valamilyen fizikai reprezentációja. Ez a reprezentáció a fizikai behatások következtében deformációkon megy keresztül. Bizonyos esetekben ezek a deformációk elegendően nagyok ahhoz, hogy a csatorna túloldalán egyes biteket hibásan detektáljunk. Az ilyen eseteket bithibáknak nevezzük. Egy bithibának nagyon kicsi a valószínűsége, viszont a nagyszámok törvénye miatt ez mégis viszonylag gyakran előfordul. Ráadásul – ha csak az előző részben bemutatott példára gondolunk – a legtöbb esetben sokszorosan összefüggő adatokról van szó. Ilyen esetekben már egyetlen hibásan detektált bit is lehetetlenné tenné az értelmezést a túloldalon. Ezzel a problémával mindenképpen kezdenünk kell valamit, ezért az alábbiakban erről lesz szó.

A csatorna negatív hatása

Nézzünk először egy életszerű példát. Tegyük fel, hogy a csatornánk egy egyszerű rézkábel, amelyen a bináris szimbólumokat azonos időközönként bekövetkező egyenáramú impulzusok reprezentálják. Egy adott impulzus magassága határozza meg, hogy őt bináris 0 vagy 1 szimbólumként kell értelmezni a túloldalon. Például a 0.8V és 1.2V közötti magasságú impulzusok jelentsék a 0 biteket, az 1.8V és 2.2V közötti magasságú impulzusok pedig jelentsék az 1 biteket. Így a vételi oldalon egyértelműen eldönthető, hogy hol vannak a bithatárok, illetve hogy milyen bitről van szó. Például a 011001 bitsorozatot reprezentáló elektronikus jel alakja az adó oldalon valahogy így nézne ki:

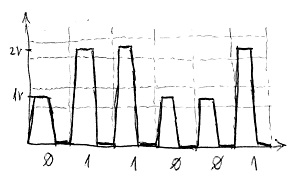
Nyilván az a célunk, hogy minél rövidebb idő alatt minél több bit, azaz végsősoron minél több ilyen impulzus haladjon át a csatornán. Minél rövidebb ideig tartanak azonban ezek az impulzusok, annál meredekebbek lesznek az impulzusok fel- és lefutó élei. Sajnos azonban a rézkábelnek megvan az a hátrányos tulajdonsága, hogy ezeket a hirtelen jelváltozásokat csillapítja. Ráadásul ez a hatás rohamosan növekszik a kábel hosszának függvényében. Ezért előfordulhat, hogy a vételi oldalhoz már az alábbi deformált jel fog érkezni:

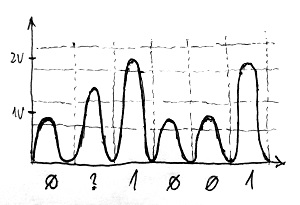
Sajnos ebben az esetben a második bitnek megfelelő impulzus olyan mértékben deformálódott, hogy a vételi oldalon már nem lehet megállapítani, hogy a magassága melyik bináris szimbólumnak megfelelő sávba esik. Ezáltal nem lehet eldönteni, hogy az Alice által küldött bináris sorozat a 011001, vagy pedig a 001001 volt. Nem kell hangsúlyoznunk, hogy ez mekkora félreértésekhez vezethet egy Alice és Bob közötti kommunikációban.

A fenti egy tipikus példája az úgynevezett törléses bithibáknak. Ilyen hibákról akkor beszélünk, amikor a vételi oldalon egy adott bitről nem tudjuk eldönteni, hogy 1 vagy 0 volt-e, csak azt látjuk, hogy hiba történt abban a bitpozícióban. Ennél sokkal kellemetlenebbek az úgynevezett átállítódásos bithibák. Ilyenkor egész egyszerűen 0 helyett 1-et vagy 1 helyett 0-át detektálunk, vagyis a vételi oldal a hiba tényéről sem szerez tudomást, az rejtve marad a számára. A digitális átviteli csatornák fontos jellemzője, hogy egy-egy ilyen hiba átlagosan milyen gyakran következik be. Ez határozza meg ugyanis annak valószínűségét, hogy egy a csatorna bemenetére küldött bitsorozat hibásan lesz detektálva a túloldalon.

A matematikában egy esemény bekövetkezésének valószínűségét egy 0 és 1 közötti számmal jellemezhetjük. Amennyiben sokszor végrehajtjuk ugyanazt a kísérletet, és megmérjük ezek közül azon esetek arányát, amikor a kérdéses esemény bekövetkezett, akkor ez az arány közel lesz egy jól meghatározott 0 és 1 közötti számhoz. Minél több kísérletet végzünk, annál közelebb. Ezt a számot nevezzük az adott esemény valószínűségének. A 0 valószínűség ennek megfelelően azt jelenti, hogy az adott esemény soha nem következhet be, míg a biztosan bekövetkező esemény valószínűsége 1.

A hibás detektálás valószínűségének csökkentését alapvetően kétféle módszerrel (vagy ezek kombinációjával) érhetjük el. Egyrészt használhatunk jobb minőségű csatornát. Ennek nyilván gátat szab a csatornára elkölthető pénz mennyisége. Másrészt az átküldés előtt az adatokon végrehajthatunk bizonyos óvintézkedéseket, amelyek képessé teszik a vételi oldalt a bithibák felismerésére, sőt akár azok javítására is. Az ilyen jellegű óvintézkedéseket összefoglaló néven csatornakódolásnak nevezzük. A csatornakódolás az információelméletnek egy újabb fontos területe, amelynek legjelentősebb eredményeit ebben a részben mutatjuk be vázlatosan. Ehhez bevezetjük a diszkrét memóriamentes csatorna absztrakt modelljét, amely matematikailag kezelhetővé teszi a fentiekben leírt kellemetlen jelenségeket függetlenül attól, hogy milyen konkrét fizikai csatornáról van szó.

Csatornamodellek

A gyakorlatban előforduló csatornákat jól leírja az úgynevezett diszkrét memóriamentes csatorna modellje. Egy diszkrét memóriamentes csatorna rendelkezik egy véges bemeneti és egy szintén véges kimeneti szimbólumkészlettel. Ezt a végességet jelenti a diszkrét elnevezés. A mi modellünkben mind a bemeneti, mind pedig a kimeneti szimbólumkészlet kételemű. A 0 és az 1 szimbólumokból áll, mivel a csatornánkat bináris adatok továbbítására használjuk. Esetenként a kimeneti szimbólumkészlethez hozzávehetjük még a ? szimbólumot is, amennyiben a fentihez hasonló törléses bithibákat is modellezni szeretnénk. A csatornáról ebben a modellben feltételezzük továbbá a szinkron működést. Ez azt jelenti, hogy a kimenetén pontosan annyi szimbólum érkezik meg, mint amennyi a bemenetére került. Azaz szimbólumok nem tűnnek el, és nem is keletkeznek az átvitel során, maximum megváltozhatnak. Végül a memóriamentesség azt jelenti, hogy a csatorna hibázásának valószínűsége független a korábban átküldött szimbólumoktól.

Egy ilyen csatorna jól modellezhető egy úgynevezett irányított élsúlyozott gráffal. Egy gráf bizonyos dolgokat és az ezek közötti kapcsolatokat írja le. A dolgokat a gráf csúcsai, míg a közöttük lévő kapcsolatokat az őket összekötő élek reprezentálják. Egy gráfot vizuálisan többféleképpen is megjeleníthetünk. Nem a konkrét megjelenítés számít ugyanis, hanem az, hogy mely csúcsok vannak összekötve éllel és melyek nincsenek. Az alábbi ábrán például ugyanannak a gráfnak két különböző vizuális megjelenítése látható:

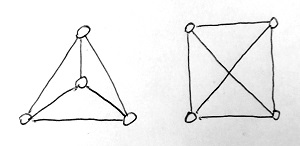
Irányított gráfokat akkor használunk, ha a leírni kívánt kapcsolatok nem szimmetrikusak. Ha például valakinek szimpatikus valaki más, attól még nem biztos, hogy ez a szimpátia kölcsönös. Ezt az adott gráf éleinek lerajzolásakor egyszerű vonalak helyett nyilakkal szemléltetjük. Az alábbi ábrán például egy 5 ember közötti szimpátiagráfot láthatunk:

Végül élsúlyozott gráfokat akkor használunk, ha a kapcsolatokat valamilyen számértékekkel is szeretnénk jellemezni. Ilyenkor ezeket a számokat az adott él fölé írjuk. Például egy várostérképet reprezentáló gráf éleihez rendelt értékek jelenthetik az adott élnek megfelelő útszakasz pillanatnyi leterheltségét. Ez alapján egy útvonaltervező szoftver például el tudja kerülni a dugókat.

A diszkrét memóriamentes csatornák modelljét is felfoghatjuk egy olyan irányított élsúlyozott gráfnak, amelynek csúcspontjai két csoportra oszthatók. Az egyik csoport csúcspontjai a bemeneti, a másik csoport csúcspontjai pedig a kimeneti szimbólumoknak felelnek meg. A gráf élei a bemeneti szimbólumokat kötik össze egy vagy több kimeneti szimbólummal. Egy-egy ilyen él azt jelzi, hogy az adott bemeneti szimbólum esetén milyen kimeneti szimbólumok jelenhetnek meg a túloldalon. Végül az élekhez rendelt súlyok azt jelzik, hogy mely „átmenet” milyen valószínűséggel következhet be az adott csatornán. Az alábbi ábrán egy ilyen csatornamodell látható:

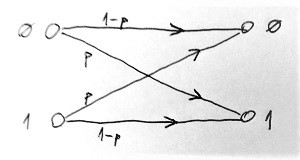
Ezt bináris szimmetrikus csatornának (BSC) nevezzük. A BSC esetén csak átállítódásos hibák fordulhatnak elő, azaz valamilyen p valószínűséggel kapunk a bemenethez képest ellentétes bitet a kimeneten. Egy másik gyakori csatornamodellt láthatunk az alábbi ábrán:

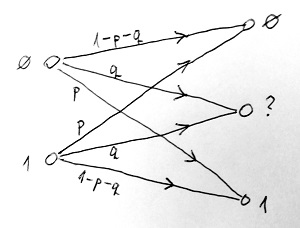
Ezt bináris törléses csatornának nevezzük, és ilyenkor a p valószínűségű átállítódásokon kívül a kimeneten a ? szimbólum is előfordulhat valamilyen q valószínűséggel. Ez azokat az eseteket modellezi, amikor az adott bit a vételi oldalon felismerhetetlen lett, de a hiba ténye nem maradt rejtve.

A továbbiakban az egyszerűség kedvéért a BSC modellt fogjuk használni, mivel ez viszonylag jól leírja a gyakorlatban előforduló csatornákat.

Csatornakapacitás

Bármilyen csatornamodellt is alkalmazunk, az érezhető, hogy a csatorna „zaját” tulajdonképpen az éleken lévő valószínűségekkel jellemezhetjük. A gyakorlatban ezeket mérésekkel lehet meghatározni. Ha a csatornán nincs zaj, akkor a bemeneti szimbólum egyértelműen meghatározza a kimeneti szimbólumot. Ekkor minden átmenetvalószínűség 0 vagy 1 értékű. Ahogy a zaj növekszik, a valószínűségek ettől egyre jobban eltérnek, azaz a kimeneti szimbólumsorozatból egyre kisebb bizonyossággal tudjuk meghatározni a bemeneti sorozatot. Végsősoron tehát egyre kevesebb a csatornán átvihető információ mennyisége átlagosan.

Ha az átvitt információ mennyiségét nem kötjük egy konkrét bemeneti szimbólumsorozathoz, akkor definiálhatjuk az úgynevezett csatornakapacitást. Ez a szimbólumonként átlagosan átvihető maximális információmennyiséget méri tetszőleges bemeneti valószínűségeloszlás esetén. A matematikai részleteket itt mellőzzük, de egy hasonlattal élve a csatorna kapacitása hasonló egy út szélességéhez. Csak a csatorna műszaki konstrukciójától függ, nem pedig az éppen rajta továbbított információ jellegétől. Ugyanígy egy út szélessége sem függ attól, hogy éppen milyen forgalom halad rajta keresztül, a maximális áteresztőképességét azonban meghatározza.

A csatornakapacitás elméleti meghatározása az átmenetvalószínűségek ismeretében általában nem egyszerű feladat, de létezik rá tetszőlegesen pontos eredményt szolgáltató numerikus eljárás. A csatornakapacitás mértékegysége bit/szimbólum, ami azt fejezi ki, hogy a csatorna bemeneti szimbólumonként hány bit információt képes továbbitani átlagosan. A fentebbi BSC modell csatornakapacitása látható az alábbi ábrán a p átállítódásos bithibavalószínűség függvényében:

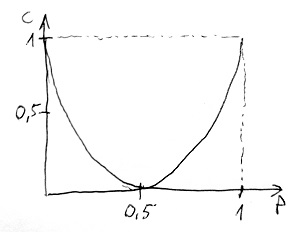
Látható, hogy a legrosszabb eset az, amikor a csatorna 50-50% valószínűséggel hibázik. Ilyenkor a kimeneti szimbólumsorozat statisztikailag teljesen független a bemeneti szimbólumsorozattól, azaz a csatornakapacitás 0, információ nem vihető át rajta. Ezzel szemben a soha nem hibázó, illetve a mindig hibázó csatorna egyaránt zajmentesnek tekinthető. Ilyenkor ugyanis a kimeneti szimbólumból mindig egyértelműen meghatározható a bemeneti szimbólum. Az utóbbi eset hasonló a mindig hazudozó politikushoz: bármit is mond, annak mindig az ellenkezője lesz az igazság. A valódi csatornák kapacitása a teljesen zajmentes, illetve a teljesen zajos végletek között helyezkedik el valahol.

Hogyan védekezzünk a csatorna zaja ellen?

Most nézzünk egy rendkívül egyszerű példát annak illusztrálására, hogy algoritmikus úton – azaz csatornakódolást alkalmazva – hogyan növelhetjük meg az átvitel biztonságát. Tegyük fel, hogy egy p=0.1 hibavalószínűségű BSC-vel állunk szemben, azaz a csatornánk átlagosan minden tizedik bitet az ellentettjére változtat a rajta lévő zaj miatt. Tegyük fel továbbá, hogy 2 bites üzeneteket szeretnénk átküldeni a csatornán. Először vizsgáljuk meg a hibás üzenetvétel valószínűségét abban az esetben, ha nem alkalmazunk semmiféle csatornakódolást. Ekkor a csatorna bemenetére 4 féle közlemény kerülhet: 00, 01, 10 vagy 11. Ezek közül bármely üzenetet adjuk a bemenetre, azokban az esetekben történik hibás detektálás a vételi oldalon, amikor vagy az első, vagy a második, vagy pedig mindkettő bit elromlik a csatornán. Ennek az összetett eseménynek a valószínűségét az alábbi képlettel lehet kiszámítani a p bithitbavalószínűségből:

\begin{aligned}\overbrace{p\cdot (1-p)}^{\text{első bit hibás}} + \overbrace{(1-p)\cdot p}^{\text{második bit hibás}} &+ \\ + \underbrace{p\cdot p}_{\text{mindkét bit hibás}} = 2p-p^2\end{aligned}

Ez p=0.1 bithibavalószínűség esetén 0.19, azaz átlagosan a leadott 2 bites közlemények ötöde hibás lesz a vételi oldalon.

Ez elfogadhatatlan, ezért most alkalmazzuk a következő egyszerű csatornakódolást: a közlemények minden bitjét triplázzuk meg a küldés előtt. Például a 01 közlemény helyett a 000111 kódszót küldjük a csatornára. Ezek után a vételi oldalra érkező biteket hármasával dolgozzuk fel, és minden három bitet többségi döntés alapján dekódolunk. Azaz pontosan akkor detektálunk 1-es szimbólumot, ha a vett három bit között legalább két darab 1-es érkezik a csatornán. Ha például a vételi oldalra a 010110 bitsorozat érkezik meg, akkor a vett közlemény többségi döntés alapján – helyesen – a 01 lesz. Látható, hogy annak ellenére, hogy 2 bit is elromlott a csatornán, az eredeti közleményt kaptuk vissza. Most nézzük meg, hogy mi a hibás közleménydetektálás valószínűsége ebben az esetben.

Egyszerűbb kiszámítani a helyes detektálás valószínűségét, majd ezt 1-ből levonva megkapjuk a hibázás valószínűségét. Helyes a detektálás akkor, ha a két bemeneti szimbólumból kapott mindkét 3 bites blokk esetén a többségi döntés helyes volt. Egy darab 3 bites blokk esetén akkor helyes a döntés, ha a csatorna legfeljebb 1 bitet rontott el a 3-ból. Ennek valószínűsége p = 0.1 esetén:

\begin{aligned}\overbrace{(1-p)\cdot (1-p)\cdot (1-p)}^{\text{nincs bithiba}} &+ \\ + \overbrace{p\cdot (1-p)\cdot (1-p)}^{\text{első bit hibás}} &+ \\ + \overbrace{(1-p)\cdot p\cdot (1-p)}^{\text{második bit hibás}} &+ \\ + \overbrace{(1-p)\cdot (1-p)\cdot p}^{\text{harmadik bit hibás}} &= 0.972\end{aligned}

Mivel ennek mindkét blokkra teljesülnie kell, ezért a helyes detektálás valószínűsége ennek négyzete. A hibázás valószínűsége tehát

1-0.972^2=0.055216

Látható, hogy a fenti egyszerű csatornakódolást alkalmazva csaknem a negyedére sikerült lecsökkentenünk a hibásan detektált közlemények átlagos számát, pedig ugyanazt a rosszminőségű csatornát használtuk. A probléma az, hogy ezért hatalmas árat fizettünk: nevezetesen 3-szor annyi idő alatt sikerült átvinnünk a kívánt információt, hiszen minden bitet meg kellett tripláznunk.

Az alkalmazott csatornakódolásnak tehát a hibavalószínűségen kívül további fontos tulajdonsága az úgynevezett kódsebesség. Ez azt adja meg, hogy a csatorna bemenetére adott szimbólumok átlagosan hány bit információt szállítanak. Ennek mértékegysége – a csatornakapacitáshoz hasonlóan – szintén bit/szimbólum. A fenti első példában az átküldendő adatfolyamunkat 2 bites közleményekre szabdaltuk, és ezeket mindenféle kódolás nélkül küldtük a csatorna bemenetére. Ebben az esetben a kódsebesség 1 bit/szimbólum volt. Cserébe viszont meglehetősen magas (0.19) volt a hibavalószínűség. Ezzel szemben a második példában alkalmazott triplázásos kódolás mellett mindössze 0.055-re csökkent a hibavalószínűség, cserébe viszont a kódsebesség a harmadára esett vissza.

Úgy tűnik tehát, hogy egy csatornakód hibavalószínűsége és kódsebessége két egymásnak ellentmondó szempont, amelyek között kénytelenek vagyunk kompromisszumot kötni, amikor csatornakódot tervezünk. A korábbi részekben már többször emlegetett Claude Shannon azonban az információelmélet kidolgozásakor meglepő módon ezzel ellentétes következtetésre jutott az 1940-es évek végén. Ez az eredmény csatornakódolási tétel néven ismeretes, amelynek hatására komoly kutatások indultak meg a csatornakódok – és azon belül is az úgynevezett hibajavító kódok – matematikai elméletében. A csatornakódolási tétel meglepő állítását, és az említett kutatások jelenlegi állását egy rövid kitérő után ismertetjük, előbb azonban nézzük meg a hibajavító kódok működési alapelveit.

A hibajavító kódok működése

Hibajavításról akkor beszélünk, ha az Alice által Bobnak szánt közleményeket úgy juttatjuk át a zajos és megbízhatatlan csatornán, hogy a vételi oldal a csatorna által okozott bithibákat lehetőség szerint képes legyen kijavítani, és ne legyen szükség a közlemények újraküldésére. Hibajelzés esetén ezzel szemben csak jelezni tudjuk, ha volt bithiba, ám azt a vételi oldal kijavítani nem képes, így ilyenkor a közlemények újraküldése szükséges. A gyakorlatban használt hibajavító kódok általában mindkét tulajdonsággal rendelkeznek. Bizonyos mértékig képesek jelezni a bithibákat, egy ennél kisebb mértékben pedig javítani is.

Egy hibajavító kódoló a bemenetére érkező k bit hosszúságú közleményeket valamilyen szabályok alapján k-nál hosszabb, n bit hosszúságú kódszavakba képezi le oly módon, hogy ez a leképezés invertálható (megfordítható) legyen. Invertálhatóság alatt azt értjük, hogy egy kódszóról mindig egyértelműen el lehessen dönteni, hogy az melyik közleményből lett leképezve. A kódsebességet a \frac{k}{n} hányados adja meg. A fenti triplázásos példában a k=2 hosszú közleményeket n=6 hosszú kódszavakra képeztük le az alábbi szabályok alapján:

\begin{aligned}00 &\to 000000 \\ 01 &\to 000111 \\ 10 &\to 111000 \\ 11 &\to 111111\end{aligned}

A hibajavító és hibajelző képességet itt az adja, hogy 6 biten 64 különböző bitsorozat írható le, ám ezek közül itt mindössze csak négyet tekintünk tényleges kódszónak. Ezért ha a vételi oldalra valamilyen ettől a négytől különböző 6-hosszú bitsorozat érkezik meg, Bob azonnal detektálhatja, hogy hiba történt az átvitel során, sőt bizonyos esetekben még javítani is képes ezeket a hibákat. Nézzük meg, mi kell ahhoz, hogy a hibákat javítani is lehessen.

A javításhoz Bobnak valahogyan el kell tudnia dönteni, hogy a hozzá megérkező hibás bitsorozat melyik kódszóhoz áll a „legközelebb”. Két azonos hosszúságú bitsorozat „távolságának” mérésére szolgál az úgynevezett Hamming-távolság, amely azt adja meg, hogy a két bitsorozat hány pozícióban különbözik egymástól. Például a 000000 és a 000111 sorozatok Hamming-távolsága 3, mivel az utolsó 3 pozícióban különböznek. A Hamming-távolság teljesíti a „távolsággal”, mint fogalommal szemben elvárt intuitív követelményeket, azaz tetszőleges a, b és c bitsorozatra igazak az alábbiak:

• Szimmetria: a „távolsága” b-től ugyanannyi, mint b „távolsága” a-tól.
• Egyenlőségi tulajdonság: a és b „távolsága” akkor és csak akkor 0, ha a és b megegyeznek.
• Háromszög-egyenlőtlenség: az a és b közötti, valamint a b és c közötti „távolságok” összege legalább annyi, mint az a és c közötti közvetlen „távolság”.

Ahhoz, hogy Bob minél több hibát tudjon javítani vagy jelezni n bites kódszavak használata esetén, célszerű az összes n hosszú bitsorozat közül azokat kiválasztani kódszavaknak, amelyek minél „távolabb” vannak egymástól a fenti értelemben. Egy hibajavító kódolásnak ezért egy rendkívül fontos paramétere az úgynevezett kódtávolság, amely nem más, mint a két egymáshoz „legközelebb” eső kódszó Hamming-távolsága. Ezt a mennyiséget d_min-nel jelöljük. Az alábbi ábrán egy d_min kódtávolságú hibajavító kód két legközelebbi kódszava (a és b) látható:

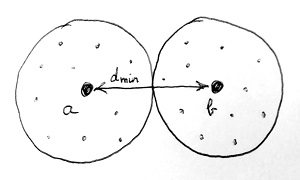
A baloldali (vagy jobboldali) körben lévő kisebb pontok azokat az n hosszú bitsorozatokat jelölik, amelyek nem kódszavak, viszont Hamming-távolságuk alapján a-hoz (vagy b-hez) közelebb vannak, mint bármely más kódszóhoz. Ha Bob a vételi oldalra megérkező n hosszú bitsorozatokat mindig a hozzájuk legközelebbi kódszóra javítja, akkor biztos lehet benne, hogy bármely \frac{d_{min}-1}{2}-nél nem nagyobb számú átállítódásos bithibát képes javítani. Ennél nagyobb számú bithiba esetén azonban előfordulhat, hogy a vett bitsorozat már egy másik kódszóhoz van a legközelebb, mint amit Alice elküldött. Ezen kívül Bob bármely d_{min}-1-nél nem nagyobb számú bithibát képes detektálni. Ennél nagyobb számú bithiba esetén azonban előfordulhat, hogy Bob éppenséggel egy kódszót kapott a vételi oldalon, amely azonban egy másik kódszó, mint amit Alice elküldött.

Elméletben Alice és Bob a fentiek alapján könnyen konstruálhat magának egy adott számú bithibát javítani képes hibajavító kódot, hiszen nincs más dolguk, mint a lehető legmesszebb „elhelyezni” egymástól a kódszavakat. Ezen kívül a dekódolás is elméletben könnyű, hiszen Bob-nak a csatornáról érkező vett bitsorozathoz kell csupán megtalálnia a hozzá legközelebbi kódszót. A problémát az adja, hogy k hosszú közleményekhez 2^k darab kódszót kell ilyen módon „elhelyezni” a hibajavító kód konstrukciójakor, a dekódoláskor pedig Bob-nak a vett bitsorozat ugyancsak 2^k darab kódszótól mért Hamming-távolságait kell kiszámítania ahhoz, hogy megtalálja közöttük a legközelebbit. A 2^k mennyiség nagyon gyorsan növekszik k függvényében, ezért ezzel az elméleti módszerrel adott esetben egyetlen közlemény dekódolása is reménytelenül sokáig tartana még a leggyorsabb számítógépeknek is.

A kódelmélet tudománya azzal foglalkozik, hogy hogyan lehet oly módon elvégezni a hibajavítást, hogy ne kelljen mind a 2^k darab Hamming-távolságot kiszámítani. E kódok műkődési alapelve az, hogy bizonyos követelményeket kielégítő műveleteket értelmezünk a kódszavak halmazán, és az így kialakított matematikai objektumok algebrai tulajdonságait és összefüggéseit próbáljuk meg kihasználni a kódolás és dekódolás során. A legfontosabb polgári életben használt hibajavító kód a Reed-Solomon kódcsalád, amelyet Irving S. Reed és Gustave Solomon fejlesztettek ki az 1950-es években. Ezzel védik többek között a különböző optikai adathordozókon (CD, DVD, Blu-ray) lévő adatokat a fizikai sérülésektől. Ha például egy CD véletlenül megkarcolódik, azzal rengeteg bit olvashatatlanná válik, ennek ellenére a Reed-Solomon hibajavító kódolásnak köszönhetően az adatok továbbra is kinyerhetőek, feltételezve persze, hogy a sérülés mértéke egy bizonyos szint alatt marad. Ezen kívül a manapság szinte minden reklámon megtalálható QR-kódokat is Reed-Solomon kóddal védik a rossz képminőség okozta felismerési hibák ellen.

A csatornakódolási tétel

Most térjünk vissza a már említett csatornakódolási tétel meglepő állítására, amely megcáfolta azt az intuitív elképzelést, miszerint a kódsebesség és a hibavalószínűség közötti kompromisszumra lenne szükség egy csatornakód tervezésekor.

Ezzel szemben a tétel a következőt állítja: ha az elérni kívánt kódsebesség kisebb, mint a csatornakapacitás, akkor létezik tetszőlegesen kicsi hibavalószínűségű csatornakód.

Igaz továbbá a tétel megfordítása is: ha az elérni kívánt kódsebesség a csatornakapacitásnál nagyobb, akkor ilyen kód nem létezik.

Gondoljunk csak bele, hogy ez mennyire ellentmond annak, amit gondolnánk az eddigiek alapján. Tegyük fel, hogy a hibavalószínűséget valamilyen nagyon kicsi érték alá szeretnénk szorítani, és mindemellett azt is szeretnénk elérni, hogy a kódsebesség minél közelebb legyen az elvi maximumhoz, azaz a csatornakapacitáshoz. A tétel állítása szerint ilyen kódnak léteznie kell. Az egyetlen bökkenő az, hogy a csatornakódolási tétel pusztán ilyen kód létezését állítja, nem mond azonban semmit arról, hogy azt hogyan kéne megkonstruálni. Például nem tudjuk azt sem, hogy egy adott hibavalószínűségi korlát eléréséhez milyen hosszú kódszavakat kellene használnunk.

Az ezzel kapcsolatos kutatások napjainkban is tartanak. Ennek nagy lökést adtak az 1960-as években felfedezett úgynevezett konvolúciós kódok. Ezen kívül a kódelméleti kutatások viszonylag új vonalát jelentik az úgynevezett turbó kódok, melyek kódsebessége már megközelíti a csatornakapacitást. Jelenleg úgy tűnik, hogy széleskörű elterjedésüknek csak a kódolás és dekódolás során fellépő nagy késleltetés és komplexitás szab határt. Legfőbb felhasználási területük az űrtávközlés, azon belül is főként a mélyűr kommunikáció. Itt tipikusan nagyon zajos csatornákon, és emiatt rendkívül alacsony csatornakapacitás mellett kell tudni megbízhatóan kommunikálni. Gondoljunk csak például a New Horizons nevű űrszondára, amelynek nemrég a Plútó térségéből kellett képeket és mérési adatokat visszaküldeni a Földre. Olyan távolságból, ahonnan még a rádiójeleknek is 4-5 óráig tart ideérni fénysebességgel. Egy ilyen csatornán rengeteg a bithiba, ugyanakkor a nagy késleltetés miatt szeretnénk elkerülni az üzenetek újraküldését, amennyire csak lehet.

A fentiek alapján az információátviteli modellünket az alábbi ábrán látható módon kell tehát kibővítenünk:

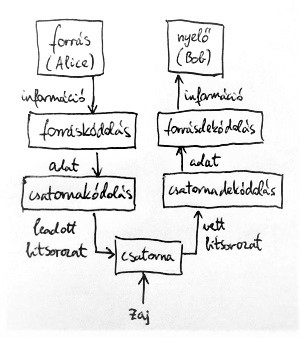
Az adatainkat tehát a rosszminőségű kommunikációs csatornák okozta adatvesztéstől meg kell védenünk. Ezért ebben a részben tettünk egy rövid kitérőt az információelmélet egy másik nagy területe, a csatornakódolás és a hibajavító kódok elmélete irányába. Érintőlegesen bemutattuk ezek működésének alapelveit, illetve a legfontosabb kódelméleti alapfogalmakat. Ezután megemlékeztünk a rendkívül meglepő csatornakódolási tételről, amely optimális csatornakódok létezését igazolja. Végül megemlítettük az ilyen kódok keresésére indított kutatások jelenlegi állását.

A modellünk azonban még nem teljes. Az adatainkat ugyanis nem csak a sérülésektől, hanem a rossz szándékú támadóktól is meg kell védenünk. A következő rész fontos szereplőjévé lép majd elő a korábban már említett Eve, aki a csatorna lehallgatásával bizalmas információkra szeretné rátenni az enyves kezét. Ezen kívül történetünk egy új szereplőjével is meg fogunk ismerkedni, aki még az Eve-énél is gonoszabb tettektől sem riad vissza némi anyagi haszon reményében…

A következő részt itt találod…