Az előző három részben (6., 7. és 8.) egy algoritmuselméleti kitérő keretében eléggé pontosan tisztáztuk, hogy mit értünk „könnyű” illetve „nehéz” algoritmikus feladat alatt. Ezért ebben a részben visszatérünk Alice és Bob fő problémájához, és ott folytatjuk, ahol az 5. részben abbahagytuk. Nevezetesen: ahhoz, hogy biztonságosan tudjanak kommunikálni egymással, Alice-nak és Bob-nak először egy kulcsnak nevezett közös titokban kell megállapodniuk. Ezt neveztük a kulcsmegosztás problémájának. A 20. század végéig tartotta magát az a hittétel, miszerint ez kizárólag biztonságos csatornán keresztül – például személyes találkozó – oldható meg. De vajon mit tehet Alice és Bob, ha ilyen csatorna nem áll rendelkezésükre? Hogyan működik és hogyan támadható a Diffie-Hellmann kulcscsere protokoll? Mi az az aszimmetrikus kulcsú rejtjelezés? Ebben a részben erről lesz szó…

Figyelem! Erősen ajánlott elolvasni az 5. részt az alábbiak megértéséhez. A teljes cikksorozat elejét itt találod.

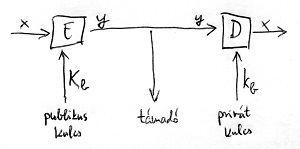
Az összes eddig vizsgált rejtjelezési eljárás nagyon hasonlóan működött. Alice-nak lényegében egy E rejtjelezőt, míg Bob-nak egy D dekódolót kellett paramétereznie egy közös k kulccsal ahhoz, hogy biztonságosan kommunikálni tudjanak egymással. Ez a kommunikációs folyamat látható az alábbi ábrán:

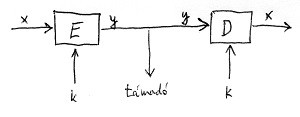
A k-val paraméterezett E rejtjelező az x nyílt szövegből előállítja az y kódszöveget, míg a vételi oldalon a szintén k-val paraméterezett D dekódoló az y kódszövegből visszaállítja az x nyílt szöveget. A biztonság szempontjából megköveteljük, hogy amennyiben a támadó nem ismeri a k kulcsot, akkor számára algoritmikusan nehéz feladat legyen az x nyílt szöveget előállítani pusztán az y kódszöveg ismeretében. Ezt a felállást szimmetrikus kulcsú titkosításnak nevezzük, mivel Alice ugyanazt a k kulcsot használja a rejtjelezéshez, mint amit Bob használ a dekódoláshoz. Ilyenekre a korábbi részekben láttunk pár példát: Caesar-kód, Vigenére-kód, a német Enigma vagy akár az 5. részben bemutatott, ténylegesen feltörhetetlen one-time-pad.

1976-ban azonban megjelent Whitfield Diffie és Martin Hellman Új direktívák a kriptográfiában című írása, amely két forradalmian új ötletet tartalmazott. Egyrészt ez az írás ismerteti az úgynevezett Diffie-Hellman kulcscsere protokollt, amelynek a segítségével Alice és Bob képes megállapodni egy közös kulcsban egy nem biztonságos csatornán keresztül oly módon, hogy az mégis rejtve marad a csatornát lehallgató Eve elől. Másrészt pedig az írásból körvonalazódott az úgynevezett aszimmetrikus kulcsú titkosítás alapgondolata – habár végül a konkrét eljárást nem ők, hanem Ron Rivest, Adi Shamir és Len Adleman fejlesztette ki 1977-ben. Ezt a feltalálók vezetékneveinek kezdőbetűi után RSA-eljárásnak nevezzük, amely napjaink leggyakrabban használt titkosítási eljárása. Ez a rejtjelezésen kívül partner- és üzenethitelesítést is biztosít Alice és Bob számára. Mindkét eljárás működése az úgynevezett egyirányú függvényeken alapszik, ezért először ezzel a fogalommal – és általánosságban a függvény fogalmával – ismerkedünk meg.

Ismét a függvényekről

A 6. részben a Turing-gépek kapcsán már felmerült a függvény fogalma. Ott adva volt egy Turing-gép, amely a bemeneti szalagjára írt jelsorozatból a futása során a kimeneti szalagján előállított egy másik jelsorozatot. Azt mondhatjuk tehát, hogy a Turing-gép valamilyen hozzárendelést valósít meg a szimbólumkészletéből alkotható jelsorozatok között. Ezt a hozzárendelést a Turing-gép által kiszámított függvénynek nevezzük. Az alábbiakban egy ennél általánosabb definíciót adunk a függvény fogalmára.

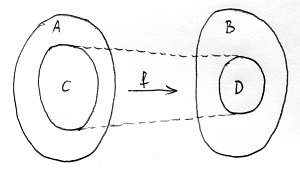
Ehhez hasonlóan általánosságban egy függvény is egy hozzárendelést valósít meg két tetszőleges – nem feltétlenül különböző – halmaz között. Alaphalmaznak nevezzük azt a halmazt, amelyek közül a bemenetek, míg képhalmaznak nevezzük azt a halmazt, amelyek közül a kimenetek kerülhetnek ki. Az alaphalmaz és a képhalmaz lehet különböző, ezt azonban nem követeljük meg. Legyen például A és B két – nem feltétlenül különböző – halmaz. Ekkor egy olyan f hozzárendelést, amely az A halmaz minden eleméhez legfeljebb egy B-beli elemet rendel, az A halmazból a B halmazba képező függvénynek nevezzük és így jelöljük:

f:A \to B

Ha például x az A halmaz egy olyan eleme, amelyhez az f függvény hozzárendel egy B-beli elemet, akkor ezt a B-beli elemet az x képének nevezzük és így jelöljük:

f(x)

Elképzelhető, hogy az alaphalmaz nem minden elemének van képe, azonban fontos megkötés, hogy minden elemnek legfeljebb 1 képe lehet. Az alaphalmaz azon részét, amely a képpel rendelkező elemeket tartalmazza, a függvény értelmezési tartományának nevezzük. Hasonlóan elképzelhető, hogy a képhalmaz nem minden eleme képe az alaphalmaz valamely elemének, itt viszont már nincs megkötés arra vonatkozóan, hogy a képhalmaz egy adott eleme hány alaphalmazbeli elemnek lehet képe. Ha például x és y az alaphalmaz két különböző eleme, akkor elképzelhető, hogy a képük ugyanaz az elem a képhalmazban, azaz f(x)=f(y). A képhalmaz azon részét, amely azokat az elemeket tartalmazza, amelyek képei legalább egy alaphalmazbeli elemnek, a függvény értékkészletének nevezzük. Az alábbi ábrán a most ismertetett fogalmakat szemléltetjük. Itt az f függvény alaphalmaza A, képhalmaza B, értelmezési tartománya C, értékkészlete pedig D:

Jogosan merülhet fel a kérdés az olvasóban, hogy mi értelme van az értelmezési tartományon kívül az ennél – adott esetben – bővebb alaphalmazról beszélni, ha a függvény úgyis csak az értelmezési tartománybeli elemekhez rendel képet. Hasonlóan jogos kérdés, hogy mi értelme van az értékkészleten kívül az ennél – adott esetben – bővebb képhalmazról beszélni, ha a függvény úgyis csak az értékkészletbeli elemeket rendeli hozzá képként az alaphalmazbeli elemekhez. Nos, ennek pusztán praktikussági okai vannak, ugyanis sok esetben nehéz pontosan meghatározni akár az értelmezési tartományt, akár az értékkészletet. Ezért célszerűbb olyan alap- és képhalmazt választani, amelyeket könnyen meg tudunk határozni, ugyanakkor nem túl tágak a tényleges értelmezési tartományhoz és értékkészlethez képest.

Hogy ne csak a levegőbe beszéljünk, nézzük is rögtön egy egyszerű példát. Tekintsük például azt a függvényt, amely tetszőleges n egész számhoz hozzárendeli mondjuk a 2-nek az n-edik hatványát, azaz a 2^n egész számot. Nevezzük ezt a függvényt f-nek. Ekkor az alábbi képlettel adhatjuk meg ezt a függvényt:

f(n)=2^n

Látható, hogy ennek a függvénynek a bemenetei és a kimenetei is ugyanabból a halmazból, nevezetesen az egész számok közül kerülnek ki. Az egész számok halmazát konvencionálisan \Z-vel szokták jelölni, ezért a korábbi jelölésekkel ezt írhatjuk:

f:\Z \to \Z

A fenti f függvény különleges abból a szempontból, hogy le lehet írni csak az n változótól függő explicit képlettel: f(n)=2^n. Ez sok esetben nem, vagy csak nehezen tehető meg. Tekintsük például a híres Fibonacci-függvényt, amely a pozitív egész számokon van értelmezve. Ennek az értéke n=1 és n=2 esetén 1, azaz f(1)=1 és f(2)=1, minden további n-re pedig teljesíti az alábbi úgynevezett függvényegyenletet:

f(n)=f(n-1) + f(n-2)

A Fibonacci-függvény néhány további értékét ennek alapján könnyedén kiszámíthatjuk:

f(3)=f(2)+f(1)=1+1=2 f(4)=f(3)+f(2)=1+2=3 f(5)=f(4)+f(3)=2+3=5 \vdots

Látható, hogy ez az f(n)-re adott kifejezés nem explicit, mivel a függvény két korábbi helyén felvett értékétől függ. Ha például ez alapján az f(100)-at szeretnénk kiszámítani, akkor előbb ki kell számítanunk a függvény 100 alatti számokra adott értékeit is. Érdekességképp megjegyezzük, hogy a Fibonacci-függvény esetén létezik csak n-től függő explicit képlet is:

f(n)=\frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{\sqrt{5} \cdot 2^n}

Az Olvasó behelyettesítésekkel könnyen leellenőrizheti ennek a képletnek a helyességét. Az persze más kérdés, hogy hogyan lehet egy ilyen képletre rájönni. Ennek ismertetését a szükséges absztrakt algebrai ismeretek hiányában mellőzzük. Sok olyan fontos függvény van azonban, amelyre ilyen explicit képlet nem is létezik, ezért általánosságban az értelmezési tartomány és/vagy az értékkészlet meghatározása nem egyszerű feladat.

Egyirányú függvények

Most térjünk vissza az f(n)=2^n függvényhez, és ennek kapcsán vizsgáljuk meg, hogy mit jelent az egyirányú függvény fogalma. A pontos matematikai definíció helyett egy gyakorlati példán keresztül mutatjuk meg a fogalom lényegét. Tekintsük az f(n)=2^n függvénynek azt a megszorítását, amely csak az 1, 2, …, 10 számokra van értelmezve. Ezekre az értékekre algoritmikusan könnyű meghatározni a függvény értékét, hiszen csak hatványozni kell. Az értékek rendre a 2, 4, 8, 16, 32, 64, 128, 256, 512 és 1024 számok lesznek.

Tegyük fel, hogy ennek a függvénynek a megfordítása a feladat, azaz olyan algoritmust kell készítenünk, amely bemenetként kap egy számot ebből az értékkészletből (legyen ez mondjuk 512), és azt kell kiszámítani, hogy ez melyik n értéknek a képe az f függvény szerint. Keressük tehát azt az n kitevőt, amelyre 2-t emelve épp 512-t kapunk. A szemfülesebb olvasók egyből észreveszik, hogy itt az 512-nek a 2-es alapú logaritmusának a kiszámításáról van szó, de tegyük most félre ezt a fogalmat és szorítkozzunk a „józan paraszti eszünkre”.

Jobban megvizsgálva észrevehetjük, hogy a függvényünk ad bizonyos támpontokat. Nevezetesen n értékét növelve (illetve csökkentve) az f(n) mennyiség is határozottan növekszik (illetve csökken). Ezt a tulajdonságot okosan kihasználva igen hatékonyan megtalálhatjuk az 512-höz tartozó n értékét megfelelő szisztéma szerinti próbálgatással.

Végezzünk például egy próbát az értelmezési tartomány közepe táján lévő n=5-re. Ebben az esetben f(5) = 2^5 = 32. Ez ugyan 512-nél kisebb, viszont a függvényünk fenti tulajdonsága miatt egyből következik, hogy a keresett n csak nagyobb lehet 5-nél. Azaz a lehetőségek felét kizárhatjuk, és a továbbiakban elegendő n értékét a 6, 7, 8, 9, 10 halmazban keresnünk. Most végezzünk egy újabb próbát ennek a szűkített halmaznak a közepén lévő n=8-ra. Ebben az esetben f(8) = 2^8 = 256 . Ez még mindig kisebb, mint 512, azaz a keresett n biztos, hogy csak a 9 és 10 számok valamelyike lehet, vagyis újra kizárhattuk a lehetőségek felét. Végül egy utolsó próbával megkapjuk, hogy f(9) = 2^9 = 512, azaz a keresett n értéke 9.

Általánosságban bináris keresésnek hívjuk az olyan módszereket, amikor egy véges halmazban kell keresnünk a megoldást, és minden lépésben ki tudjuk zárni a lehetőségek felét. Ez egy rendkívül hatékony algoritmikus módszer, mivel a szükséges lépések száma a halmaz méretének 2-es alapú logaritmusával arányos. Ha például a megoldást egy ezermilliárdszor milliárdszor milliárd nagyságú halmazban kell is keresnünk, a szükséges lépések száma akkor is nagyságrendileg mindössze 100 körül van. Többek között ezért tudunk megtalálni hamar egy keresett szót egy szótárban. Habár nem tudatosul bennünk, de ilyenkor is lényegében egy bináris keresést hajtunk végre a szavak halmazán, csak ebben az esetben a rendezést az ábécé-sorrend határozza meg.

Az olyan függvényeket, amelyek esetén az alaphalmaz elemeinek képe algoritmikusan könnyen kiszámítható, de a képhalmaz tetszőleges eleméhez algoritmikusan nehéz olyan alaphalmazbeli elemet találni, amelynek épp ő a képe, egyirányú függvényeknek nevezzük.

Az egyirányú függvényeket egy adott irányban nyíló csapóajtóhoz hasonlíthatjuk. Az egyik irányban (az alaphalmazból a képhalmaz irányába) könnyű áthaladni rajta, azonban ha egyszer bezárult mögöttünk az ajtó, akkor nehezen juthatunk vissza rajta a másik irányba (a képhalmazból az alaphalmazba).

A fenti példában szereplő f függvény nyilván nem egyirányú függvény, hiszen a megfordítása egy algoritmikusan könnyű bináris keresési feladathoz vezet, azonban egy aprónak tűnő módosítással ezt a megfordítást reménytelenül nehézzé tehetjük egy potenciális támadó számára. Ehhez teszünk egy kis kitérőt az úgynevezett moduláris aritmetika irányába, amelyet most az egyszerűség kedvéért csak óraaritmetikának fogunk nevezni. Az elnevezés mindjárt világossá válik. A későbbi részekben részletesen ki fogunk térni a moduláris aritmetikára, most azonban az elsődleges cél az alapgondolat megértése.

Számolás az óralapon

Az általános iskolából jól ismert szokásos összeadás és szorzás műveletek a mindkét irányban végtelen számegyenesen vannak értelmezve. Vizsgáljuk meg először, hogy ezen a számegyenesen hogyan adunk össze két számot, például a 8-at és a 4-et. Elindulunk az egyik számtól, mondjuk a 8-tól, és a másik számnak megfelelő számú, azaz jelen esetben 4 lépést teszünk jobbra a számegyenesen. Az összeadás eredménye az a szám lesz, ahová megérkeztünk, ez ugye a 12. A hagyományos összeadás esetén tehát 8+4=12.

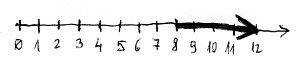
Most átértelmezzük egy kicsit az összeadás műveletét. Vágjunk ki a számegyenesből egy 0-tól kezdődő 11 számból álló szakaszt. Az így kapott szakasz két végét képzeletben ragasszuk össze, így egy óra számlapjához hasonló elrendezést kapunk. A különbség pusztán annyi, hogy itt nem 1-től 12-ig futnak a számok, hanem 0-tól 10-ig. Ez látható az alábbi ábrán:

Ezen az óralapon egy nagyon hasonló műveletet tudunk definiálni, mint amilyen a hagyományos összeadás volt. Ezt a műveletet modulo 11 összeadásnak nevezzük, vagy általánosságban – egy N darab számot tartalmazó óralap esetén – modulo N összeadásról beszélünk. Adjuk össze ismét az előző példában szereplő 8 és 4 számokat, de ezúttal a számegyenes helyett ezen az óralapon végezzük a számolást. Induljunk el a 8-as számtól, és tegyünk meg 4 lépést az óramutató járásával megegyező irányban. Az összeadás eredménye az a szám lesz, ahová megérkeztünk, ami jelen esetben az 1. A modulo 11 összeadás esetén tehát a 8 és a 4 összege 1, amit így jelölünk:

8+4=1 \pmod{11}

Az óralapon számolva ezt az összeadást az alábbi ábra szerint végezzük el:

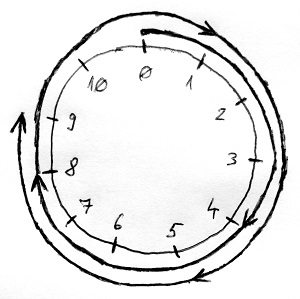
Az összeadáshoz hasonlóan szorzást is értelmezhetünk ebben a furcsa óraaritmetikában. Legyen például a két összeszorzandó szám a 4 és az 5. Ilyenkor a 0-ról indulunk, és annyiszor lépünk az egyik tényezőnek megfelelő lépést, mint amennyi a másik tényező. A hagyományos számegyenesen jobbra kell lépkedni, így a 20-as számhoz jutunk, azaz 4\cdot 5=20. Ezzel szemben az óraaritmetikában ismét az óramutató járásával megegyező irányban kell lépkedni, így nem egész két kör megtétele után a 9-es számhoz jutunk, azaz 4\cdot 5=9 \pmod{11}. Az alábbi ábrákon a 4\cdot 5 szorzás eredményét láthatjuk a kétféle aritmetikában:

Most, hogy van már szorzásunk is, nem lesz nehéz értelmezni a modulo 11 hatványozást sem. Egy x szám n-edik hatványát – hasonlóan a hagyományos hatványozáshoz – úgy kapjuk meg, hogy veszünk egy olyan n darab tényezőből álló szorzatot, amelyben minden tényező x. A különbség annyi a hagyományos hatványozáshoz képest, hogy a hagyományos szorzás helyett az imént bevezetett modulo 11 szorzást alkalmazzuk:

x^n = \underbrace{x \cdot x \cdot \ldots \cdot x}_{\text{n darab}}

Most vizsgáljuk meg, hogy mi történik az előző szakaszban bevezetett f(n) = 2^n függvénnyel, ha a hagyományos számegyenes helyett a modulo 11 óraaritmetikában alkalmazzuk.

A diszkrét logaritmus fogalma

Az alábbi táblázat első oszlopa az n változó, míg a második és harmadik oszlopa az f(n) = 2^n függvény értékét tartalmazza rendre a hagyományos és a modulo 11 hatványozás esetén:

\begin{array}{c}{ \begin{array}{|c|c|c|} \hline n & 2^n & 2^n \pmod{11} \\ \hline \hline 0 & 1 & 1 \\ \hline 1 & 2 & 2\\ \hline 2 & 4 & 4\\ \hline 3 & 8 & 8\\ \hline 4 & 16 & 5 \\ \hline 5 & 32 & 10 \\ \hline 6 & 64 & 9 \\ \hline 7 & 128 & 7 \\ \hline 8 & 256 & 3 \\ \hline 9 & 512 & 6\\ \hline 10 & 1024 & 1\\ \hline 11 & 2048 & 2\\ \hline \end{array}} \\ \vdots \end{array}

Ha megvizsgáljuk a táblázat harmadik oszlopát, akkor láthatjuk, hogy ez a sorozat – a második oszloppal ellentétben – teljesen véletlenszerűen ugrál össze-vissza a függvény értékkészletét alkotó számokon. Itt nem kapunk semmiféle támpontot a függvény megfordításához.

Ennek érzékeltetéséhez képzeljük most magunkat egy potenciális támadó – például Eve – helyébe. Tegyük fel, hogy a támadási kísérlet során Eve-nek ki kell számítania azt az n kitevőt, amely esetén 2^n = 6 \pmod{11}. Ezt a kitevőt a 6-os szám 2-es alapú diszkrét logaritmusának nevezik. Mivel modulo 11 óraaritmetikában számolunk, ezért Eve csak annyit tud, hogy a megoldás az 1, 2, …, 10 számok közül kerülhet ki.

Eve azt megteheti, hogy elkezdi sorban kipróbálni ezeket a kitevőket, ez azonban reménytelenül sokáig tarthat neki, amennyiben nem egy 11 elemű, hanem egy ennél sokkal nagyobb óralapon kell keresgélnie. Sebaj – gondolja magában Eve –, szerencsére a fentebb már ismertetett bináris keresést épp az ilyen esetekre találták ki.

Eve tehát először tesz egy próbát az értelmezési tartomány közepén lévő n=5 értékre. Erre azt kapja, hogy 2^5=10 \pmod{11}. Az így kapott eredmény nagyobb, mint 6, ezért Eve a bináris keresés logikáját követve azt a következtetést vonja le, hogy a keresett kitevő biztosan 5-nél kisebb. Ez azonban hibás feltételezés, hiszen a megoldás ebben az esetben a 9 lenne. A modulo 11 hatványozás tehát nem ad olyan támpontokat, mint a hagyományos, így Eve ezzel a módszerrel nem tudja kizárni minden lépésben a kitevőjelöltek felét.

Sőt, jelenleg nem is ismeretes semmilyen más módszer sem, ami a modulo hatványozás megfordítására lényegesen gyorsabb megoldást szolgáltatna, mint az összes lehetséges kitevőjelölt végigpróbálgatása. Ez viszont egy megfelelően nagy méretű óralap esetén reménytelen feladat elé állítja Eve-et. A modulo hatványozás tehát valóban egy egyirányú függvénynek tűnik, amelyet Alice és Bob kulcsmegosztásra használhatnak. Az előző részben a prímfaktorizációról tett megjegyzéshez hasonlóan azonban itt is kénytelenek vagyunk megjegyezni, hogy a diszkrét logaritmus problémájáról sem bizonyított, hogy NP-teljes lenne.

A Diffie-Hellman kulcscsere protokoll

Tegyük fel, hogy Alice és Bob szeretnének megegyezni egy közös kulcsban, amelyet aztán egy valamilyen szimmetrikus kulcsú titkosításhoz fognak használni. A korábbi részekben már láttuk, hogy az Alice és Bob közötti kommunikáció gyakorlatilag számok küldözgetéséből áll, így a rejtjelező és dekódoló komponensekre nyugodtan tekinthetünk matematikai függvényekként. Alice és Bob feladata tehát megegyezni egy egész számban, amellyel ezeket a függvényeket paraméterezni fogják. Jelen esetben azonban nem tudnak egymással személyesen találkozni, így a kulcsban való megegyezést egy nembiztonságos csatornán keresztül kell megoldaniuk.

Alice ezért felhívja Bob-ot telefonon, és megállapodnak egy egyirányú függvényben. Legyen ez az egyirányú függvény például az előző szakaszból már ismerős modulo 11 hatványozás:

f(n) = 2^n \pmod{11}

Miután ezt megbeszélték, mindketten kiválasztanak maguknak egy-egy titkos kitevőt, ezt azonban titokban tartják még egymás előtt is. Tegyük fel, hogy Alice az a=4, míg Bob a b=8 titkos kitevőt választja magának. Most mindketten alkalmazzák ezekre a kitevőkre a megbeszélt egyirányú függvényt, és az eredményt elküldik egymásnak. Alice tehát elküldi a 5-ös számot Bob-nak – mivel 2^a=2^4=5 \pmod{11} –, Bob pedig elküldi a 3-as számot Alice-nak – mivel 2^b=2^8=3 \pmod{11}.

Végül a kapott számot mindketten a saját titkos kitevőjükre emelik szintén modulo 11 számolva. Alice ugye a 3-es számot kapta Bob-tól, a saját titkos kitevője a=4, ezért ő a 3^4 = 4 \pmod{11} értéket fogja kapni végeredményül. Bob ehhez hasonlóan jár el: ő a 5-ös számot kapta Alice-tól, a saját titkos kitevője b=8, így az általa kiszámított végeredmény a 5^8 = 4\pmod{11} lesz. Láss csodát: mindketten ugyanúgy a 4-es számot kapták végeredményül. Ez lesz tehát a közös k kulcs. A kulcscsere folyamat az alábbi ábrán látható:

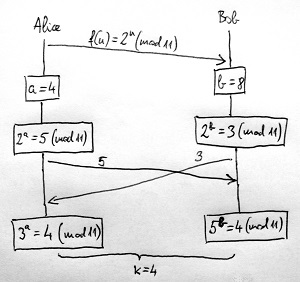
Mielőtt azt a kérdést megválaszolnánk, hogy hogyan kaphatta Alice és Bob is ugyanazt az eredmény, először vizsgáljuk meg, hogy mit lát ebből az egészből Eve. Róla ugye korábbról már tudjuk, hogy minden olyan üzenetnek ő is a birtokába kerül, amely áthalad a kommunikációs csatornán. Az első ilyen alkalom az, amikor Alice telefonon megbeszéli Bob-bal azt az egyirányú függvényt, amely alapján a kulcscserét végre fogják hajtani. Eve tehát megtudja, hogy Alice és Bob az f(n)=2^n \pmod{11} függvényt fogják használni.

Ezután Eve elfogja az Alice által Bob-nak küldött 5-ös és a Bob által Alice-nak küldött 3-as számot, és nyilván szeretné ő is kiszámítani a közös kulcsot. Eve-nek ezen a ponton két választása van: vagy az 5^b \pmod{11} vagy pedig a 3^a \pmod{11} értéket számítja ki. Mindegy melyiket választja, hiszen mindkettő ugyanazt az eredmény – a kulcsot – adja. A probléma csak annyi, hogy Eve nem ismeri sem az a, sem pedig a b kitevőt, hiszen ezeket Alice és Bob nem közölte egymással.

Eve mindössze 2 dolgot tud az a és b kitevőkről. Egyrészt az Alice által Bob-nak küldött 5-ös számból tudja, hogy 2^a=5 \pmod{11}. Másrészt pedig a Bob által Alice-nak küldött 3-as számból tudja, hogy 2^b=3 \pmod{11}. Bármelyik kitevőt is szeretné kiszámítani, kénytelen megoldani a fentebb ismertetett diszkrét logaritmus problémáját. Ez azonban jóval nagyobb számok esetén – mint tudjuk – gyakorlatilag lehetetlen feladat a számára még a világ összes számítógépével is. Ezzel szemben Alice-nak és Bob-nak mindössze két modulo hatványozást kell csak elvégeznie, amely – ahogy azt majd egy későbbi részben látni fogjuk – egy algoritmikusan könnyű feladat számukra.

Most vizsgáljuk meg, hogy miből adódik a Diffie-Hellman protokoll helyessége. Bob ugye megkapja Alice-tól a 2^a \pmod{11} számot, és ezt hatványozza a saját titkos kitevőjével. Azaz végeredményként a (2^a)^b \pmod{11} kulcsot fogja kapni. Ehhez hasonlóan Alice megkapja Bob-tól a 2^b \pmod{11} számot, és ezt hatványozza a saját titkos kitevőjével. Azaz végeredményként a (2^b)^a \pmod{11} kulcsot fogja kapni. A Diffie-Hellman protokoll ezek után nyilván akkor helyes, ha ez a két szám ugyanaz, vagyis:

(2^a)^b = (2^b)^a \pmod{11}

Erre a figyelmetlen olvasó – aki jól megtanulta általános iskolában a hatványozás azonosságait – rögtön rávágná, hogy nyilvánvalóan teljesül. Vigyázzunk azonban, itt ugyanis nem a hagyományos, hanem modulo 11 hatványozás történik. Szerencsére ezek az összefüggések a moduláris aritmetikában is érvényesek, ez azonban korántsem magától értetődő. Ennek részleteiről majd egy későbbi részben lesz szó.

Diffie-Hellman protokoll festékekkel

A fentiek megértéséhez most egy egyszerű analógiát ismertetünk. Ennek ugyan semmi köze nem lesz a kriptográfiához, ám jól szemlélteti az egyirányú függvények működését. Képzeljük el, hogy Alice és Bob most nem számokkal, hanem festékekkel dolgozik. A közös titok, amelyben meg szeretnének egyezni, egy adott színű festékkeverék. Ennek érdekében először megegyeznek egy közös kiinduló színben. Ebben a példában ez legyen mondjuk egy-egy liter fehér festék.

Most mindketten kiválasztanak maguknak egy-egy liter festéket valamilyen titkos színből, és hozzákeverik a náluk lévő fehér festékhez, de nem árulják el még egymásnak sem, hogy mi volt a titkos szín. Ezután az így képződött színkeveréket elküldik egymásnak postán. Bob-hoz kerül tehát Alice, Alice-hoz pedig Bob keveréke. Végül a kapott keverékhez ismét hozzáöntenek mindketten egy-egy liter festéket a saját titkos színükből. Így mindkettejüknél lesz 3 liter festékkeverék, amelyekben 1 liter fehér festék van összekeverve 1-1 literrel Alice és Bob titkos festékéből. Következésképp a végső festékkeverék mindkettejüknél ugyanolyan színű kell legyen, ez lesz tehát a közös titok. Ez a folyamat látható az alábbi ábrán:

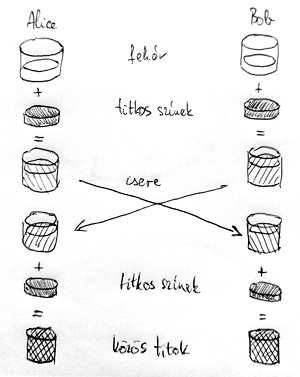
Vegyük észre, hogy Eve megint hasonló szituációban van, mint a modulo hatványozásra épülő példában. Nevezetesen: hiába ismeri a kiinduló fehér színt, és hiába kukkant bele az egymásnak küldött köztes keverékekbe, ezekkel az információkkal nem tud mihez kezdeni, mivel nem ezek alkotják a kulcsot. Ahhoz, hogy Eve is elő tudja állítani a végső színkeveréket, ismernie kéne Alice és Bob titkos színei közül legalább az egyiket. Ehhez azonban külön kéne tudnia választani ezeket a kiinduló fehér színtől, amikor a köztes keverékeket elfogja a kommunikációs csatornán. Ez Eve számára gyakorlatilag lehetetlen feladat, tekintve, hogy a festékkeverés egy egyirányú művelet.

A Diffie-Hellman protokoll támadása

Jelenleg ugyan – mint azt fentebb már említettük – még nincs bizonyítva a diszkrét logaritmus problémájának NP-teljessége, de tegyük fel, hogy ez valóban egy reménytelen feladat. Ezután jogosan merül fel a kérdés, hogy vajon milyen módszerek állnak egy passzív támadó – például Eve – rendelkezésére ahhoz, hogy sikeres támadást hajtson végre a protokoll ellen, és megszerezze Alice és Bob kulcsát.

A protokoll egy gyenge pontja lehet az, amikor Alice és Bob megállapodnak a használt egyirányú függvény paramétereiben. Egy Diffie-Hellman protokollban használt függvény általános alakja így néz ki:

f(n)=g^n \pmod{N}

Itt a g paramétert generátorelemnek, az N paramétert pedig modulusnak nevezzük. A fentebb ismertetett egyszerű példában Alice és Bob a g=2 generátorelemben és az N=11 modulusban egyeztek meg. Ám egy valódi kulcscsere esetén ennél jóval nagyobb számokat használunk. Egy tipikus N modulus például nagyságrendileg 200 számjegyből áll.

Előfordulhat, hogy bizonyos szerencsétlenül megválasztott g generátorelem és N modulus esetén Eve-nek lényegesen könnyebb dolga van egy ilyen függvény megfordításával még akkor is, ha nagy számokat használnak. Azonban eléggé jól ismerjük azokat a számelméleti kritériumokat, amelyeket e paramétereknek teljesíteniük kell a megfelelő biztonság érdekében. Ezekről a későbbiekben még bőven lesz szó, most azonban nyugodtan feltételezhetjük, hogy Alice és Bob ilyen értelemben megfelelő körültekintéssel választja meg a használt paramétereket.

Ilyen feltételezések mellett kimondhatjuk, hogy a Diffie-Hellman protokoll egy passzív támadó – például Eve – számára gyakorlatilag feltörhetetlen. Sajnos azonban egy aktív támadó – például a csaló Mallory – könnyedén ki tud csalni titkos információkat Alice-tól és Bob-tól egy úgynevezett közbeékelődéses támadás (man-in-the-middle attack) segítségével.

Mallory ezt úgy tudja elérni, hogy Alice és Bob közé ékelődik a kommunikációs folyamat során, és elhiteti velük, hogy egymással folytatják le a kulcscsere folyamatot. Valójában azonban Alice és Bob is Mallory-vel kommunikál közvetlenül, nem pedig egymással. Ennek folyamatát az alábbi ábra mutatja:

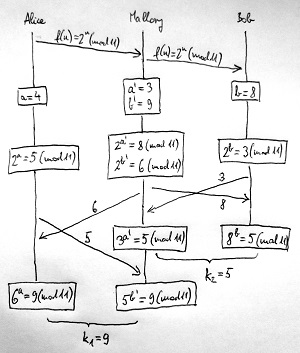
Itt Alice kulcscserét kezdeményez Bob-bal, ez a kezdeményezés azonban nem jut el Bob-hoz, mivel Mallory eltéríti az üzenetet. Bob helyett Mallory folytatja le a kulcscserét Alice-szal Bob-nak kiadva magát. Így Alice azt hiszi, hogy Bob-bal állapodott meg a k_1 = 9 közös kulcsban. Ezzel párhuzamosan Mallory Bob-bal is kezdeményez egy kulcscserét Alice-nak kiadva magát. Így Bob azt hiszi, hogy Alice-szal állapodott meg a k_2 = 5 közös kulcsban.

A kulcscserét követően tehát Alice és Bob is azt hiszi, hogy egymással beszélgetnek közvetlenül. Ám valójában Mallory-n keresztül kommunikálnak, aki így gond nélkül birtokába jut a bizalmas információknak, ráadásul teljesen észrevétlenül.

Ez igen pofátlan dolog, nemde? A kérdés tehát az, hogy Alice hogyan tudja igazolni Bob-nak, hogy ő valóban Alice, és viszont? Erre a következő részben fogjuk megadni a választ, amelyhez most felvázoljuk egy olyan rejtjelező rendszer alapjait, amely ezt lehetővé teszi.

Aszimmetrikus kulcsú rejtjelezés

Ennek a résznek az elején felvázoltuk az eddig ismertetett rejtjelezők közös működési modelljét, amelyet szimmetrikus kulcsú rejtjelezésnek neveztünk. Ebben az esetben Bob ugyanazt a kulcsot használja a dekódoláshoz, amelyet Alice használ a rejtjelezéshez. Diffie és Hellman fentebb már említett forradalmi irásában azonban az úgynevezett aszimmetrikus kulcsú rejtjelezés merőben új alapgondolata körvonalazódott.

Az 5. részben a háromutas kulcsforgalom kapcsán már éltünk egy olyan analógiával, amely ládákat, lakatokat és kulcsokat használt a rejtjelezés szemléltetésére. Ezzel az analógiával élve a szimmetrikus kulcsú rejtjelezés úgy fogható fel, hogy Alice a Bob-nak szánt üzenetet beteszi egy ládába, amelyet lezár egy lakattal. Bob csak akkor tudja kinyitni a ládát, ha neki is van egy másolata a lakatot nyitó kulcsról. A problémát itt az okozza, hogy hogyan tudjuk eljuttatni a kulcsmásolatokat a kommunikáló felekhez biztonságosan.

Az aszimmetrikus kulcsú rejtjelezés egy egészen más gondolatra épül. A kulcsos, lakatos analógiával élve ez kicsit olyan, mintha nem a kulcsról, hanem a lakatról készítenénk másolatokat. Képzeljük el, hogy Bob szeretné, ha bárki tudna neki titkos üzenetet küldeni. Ennek érdekében Bob a saját lakatját minél több példányban publikusan elérhetővé teszi bárki számára. A trükk abban van, hogy a Bob-féle lakatokat mindössze egyetlen kulcs nyitja, amely végig ott lapul Bob zsebében.

Tegyük fel, hogy Alice szeretne Bob-nak egy titkos üzenetet küldeni. Elmegy hát a postára, kér egy Bob-féle lakatot, az üzenetet beleteszi egy ládába, amelyet lezár ezzel a lakattal. Ezt könnyedén megteheti, hiszen a lakatot csak rá kell pattintani a ládára. Innentől kezdve azonban kizárólag Bob fogja tudni kinyitni ezt a lakatot, hiszen csak ő rendelkezik az ehhez szükséges egyetlen kulccsal. Olyannyira, hogy a láda lezárása után még maga Alice sem tudja többé kinyitni azt.

A lakatokat félretéve itt tehát arról van szó, hogy egy üzenet dekódolásához szükség van egy plusz információra ahhoz képest, mint ami a rejtjelezéséhez kell. A dekódoláshoz szükséges plusz információt privát (titkos) kulcsnak, míg a rejtjelezéshez szükséges információt publikus (nyilvános) kulcsnak nevezzük. A rendszerben lévő valamennyi résztvevőhöz tehát nem egy kulcs, hanem egy kulcspár tartozik. E kulcspár privát részét csak az adott résztvevő ismeri, és azt soha nem adja ki a kezéből. Ezzel szemben a kulcspár publikus része bárki számára elérhető egy nyilvános kulcstárban egy telefonkönyvhöz hasonlóan.

Tegyük fel, hogy Alice szeretne Bob-nak elküldeni egy x üzenetet. Ehhez előkeresi a nyilvános kulcstárból Bob K_b publikus kulcsát, és ezzel paraméterezi az E rejtjelező függvényt. Ily módon előáll az y kódszöveg, amelyet elküld Bob-nak. Ezt az üzenetet kizárólag Bob tudja visszafejteni, mivel a K_b publikus kulcshoz tartozó k_b privát kulcsot csak ő ismeri. Bob tehát a k_b privát kulccsal paraméterezve a D dekódoló függvényt könnyedén vissza tudja állítani az eredeti x üzenetet. Ez a folyamat látható az alábbi ábrán:

Ez az alapgondolat forradalmat indított el a kriptográfiában, megindult ugyanis a versenyfutás a dicsőségért, amely a fentieknek megfelelő E és D függvények elsőként való megtalálásáért járt. A dicsőség Ron Rivest-nek, Adi Shamir-nak, és Len Adleman-nak jutott, akik 1977-ben publikálták az úgynevezett RSA-algoritmust, amely alapjaiban változtatta meg világunkat.

Ebben a részben tehát megismerkedtünk a modern kriptográfia két alapvető felfedezésével. Az első a Diffie-Hellman kulcscsere protokoll volt, amely lehetővé teszi, hogy Alice és Bob a pofátlan Eve szeme láttára állapodjanak meg egy közös titkos kulcsban, teljes biztonságban. Láttuk azonban, hogy egy aktív támadó könnyedén kijátszhatja ezt a rendszert, hacsak nem tudjuk kibővíteni a protokollt valamilyen partnerhitelesítéssel. Ezért megismerkedtünk az úgynevezett aszimmetrikus kulcsú rejtjelezés alapgondolatával. A következő részben erre építkezve bemutatjuk a digitális aláírás és partnerhitelesítés működésének alapjait, majd a további részekben elkezdünk megismerkedni az RSA-algoritmus számelméleti hátterével.

A következő részt itt találod…