Az előző részben jobban megismerkedtünk Alice és Bob két fő ellenségével, Eve-vel és Mallory-vel. Megvizsgáltuk, hogy milyen gonosz módokon próbálnak borsot törni főhőseink orra alá. Bemutattuk a one-time pad nevű abszolút biztonságos rejtjelezési rendszert, de láttuk, hogy az a gyakorlatban nagyon limitáltan használható. Ezért az abszolút biztonság helyett a továbbiakban megelégszünk az algoritmikus biztonsággal. Ez olyan módszerek használatát jelenti, hogy Alice és Bob számára egy kulcsnak nevezett plusz információ birtokában algoritmikusan „könnyű” feladat legyen egymással bizalmas információkat közölni, de Eve számára a kulcs ismeretének hiányában algoritmikusan „nehéz” legyen e titkok felfedése. De vajon mit jelent az, hogy egy feladat algoritmikusan „könnyű” vagy „nehéz”? Egyáltalán mit jelent az a szó, hogy „algoritmus”? Vajon minden feladat megoldható algoritmussal? Ebben és a következő részekben erről lesz szó…
Általános iskola alsó tagozatában remélhetőleg mindenki megtanulta, hogyan lehet összeadni vagy összeszorozni két tetszőlegesen nagy egész számot. Összeadás esetén például a két számot egymás alá kell felírni, és számjegyenként végezni az összeadást. Ha pedig valamelyik helyiértéken 9-nél nagyobb számot kapnánk részeredményül, akkor a „túlcsordulást” át kell vinni a következő helyiértékre. Szorzásnál egy kicsit bonyolultabb a helyzet, de az is elvégezhető helyiértékenként végzett szorzásokkal és összeadásokkal.
Ez nem más, mint egy algoritmus, amelynek bemenete a két összeadandó vagy összeszorzandó szám. A végrehajtás során elemi lépéseket végzünk, miközben a papíron először a részeredmények jelennek meg a „munkaterületen”. Végül pedig sorra előállnak a végeredmény számjegyei, mint az algoritmus kimenete. A lépések abban az értelemben elemiek, hogy azok végrehajtása az algoritmus futtatója számára nem igényel további részletezést. Például számítógépek esetén van egy véges utasításkészlet, amelyet a gép áramköri megvalósítása határoz meg, és így adottnak tekinthető. Egy algoritmus leírása ebben az esetben megfelel egy programnak, amely ebből az utasításkészletből gazdálkodhat, ezeket tetszőlegesen kombinálhatja. Például ciklusok, feltételektől függő elágazások, és egyéb, a futás útját vezérlő utasítások segítségével. Az egyetlen kikötés, hogy ennek a leírásnak végesnek kell lennie.
Az algoritmus végrehajtójának nem kell foglalkoznia azzal a kérdéssel, hogy az miért ad helyes eredményt tetszőleges bemenet esetén. Neki mindössze annyi a dolga, hogy „bambán” de pontosan kövesse az algoritmus leírását. Egy számítógép is pontosan ezt csinálja egy program futtatása során. Ráadásul ő valóban „bamba” és nem gondolkozik, ezért az ő számára nagyon pontos leírásra van szükség. Ez az oka annak, hogy egy bonyolult algoritmust nem könnyű leprogramozni. A számítógép ugyanis nem azt csinálja, amit le akartunk írni számára, hanem azt, amit ténylegesen leírtunk. Azt viszont halál pontosan.
Ahhoz, hogy algoritmussal meg tudjunk oldani egy problémát, a probléma példányait valamilyen módon le kell tudnunk írni a számára. Ezen kívül az algoritmus eredményét is valamilyen írott formában fogjuk megkapni. A fenti példában a probléma az egész számok összeadása. Ez az, amire egy általános algoritmust szeretnénk adni. Ennek a problémának egy példánya mondjuk konkrétan a 32, a 11 és a 67 egész számok összeadása. Ha tehát az algoritmus bemenetére ennek a számhármasnak egy olyan leírását adjuk, amit az algoritmus értelmezni képes, akkor a 110 egész számnak szintén valamilyen leírását fogjuk kapni eredményül.
Most megvizsgáljuk azt a kérdést, hogy egy algoritmus bemenetét és kimenetét hogyan tudjuk leírni egy véges szimbólumkészlettel. Ehhez teszünk egy rövid kitérőt az úgynevezett formális nyelvek elmélete felé.
Formális nyelvek
A 3. részben már képet kaptunk arról, hogy számokat – vagy bármi mást – hogyan lehet leírni valamilyen véges szimbólumkészlettel. Például a számítógépek tipikusan 2 elemű szimbólumkészlettel dolgoznak, amelynek elemeit bináris szimbólumoknak nevezzük. Mi kényelmi szempontból egy ennél bővebb készlettel fogunk dolgozni, ám ennek nincs elméleti jelentősége. Rögzítsük tehát először magát a szimbólumkészletet, illetve azokat a szabályokat, amivel az egyes problémapéldányokat és magát az eredményt le fogjuk írni. Csak ezután van ugyanis értelme algoritmusról beszélni.
Kezdjük a szimbólumkészlettel. A mi szimbólumkészletünk összesen 11 elemből fog állni. Legyenek ezek a 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 és a # szimbólumok. Ez a 11 elemű halmaz lesz tehát az az ábécé, amivel az algoritmusunk dolgozni fog. Az ábécét, mint halmazt tipikusan görög nagybetűkkel szoktuk jelölni. Nevezzük például a fenti ábécét \Sigma-nak (ejtsd: „szigma”). Eszerint tehát:
\Sigma = \lbrace 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; \# \rbraceAz algoritmus a \Sigma elemeiből alkotott jelsorozatok formájában fogja megkapni a bemenetét, és a kimenetét is ilyen formában kell előállítania. Azt a halmazt, amely a \Sigma elemeiből alkotott összes lehetséges véges hosszúságú jelsorozatból áll, \Sigma^*-gal (ejtsd: „szigma csillag”) jelöljük.
A \Sigma^* halmaznak az ábécével ellentétben végtelen sok eleme van. Eleme például a 12##986#1##, a ###7#, vagy a 32#11#67 jelsorozat, de ide soroljuk azt a jelsorozatot is, amely 0 darab szimbólumból áll. Ennek a speciális jelsorozatnak a neve üres jelsorozat. Az üres jelsorozatot általában \varepsilon-nal (ejtsd: „epszilon”) jelöljük. Az \varepsilon tehát nem az ábécé egy szimbóluma, hanem azt a jelsorozatot jelöli, amely egyetlen szimbólumot sem tartalmaz.
Most, hogy megállapodtunk a szimbólumkészletben, rögzítsük a bemeneti és a kimeneti jelsorozatokkal szemben támasztott követelményeket. Nyilvánvalóan nem minden \Sigma^*-beli jelsorozat lesz bemenetként értelmezhető az algoritmus számára. Például állapodjunk meg abban, hogy az összeadandó számokat 10-es számrendszerben kell felsorolnunk, és ezeket a számokat a # szimbólummal kell elválasztanunk egymástól. Eszerint a megállapodás szerint például a 32#11#67 jelsorozat egy értelmes bemenet, és azt fogja jelenteni az algoritmus számára, hogy adja össze a 32, a 11 és a 67 számokat. Állapodjunk meg továbbá abban, hogy értelmes bemenet esetén az algoritmus az összeadás eredményét szintén 10-es számrendszerben írja a kimenetre. A 32#11#67 bemeneti jelsorozat esetén tehát az algoritmus kimenetén az 110 jelsorozatnak kell megjelennie a megállapodás szerint.
Mivel „hülyebiztos” algoritmust szeretnénk készíteni, ezért kezdenünk kell valamit azokkal az esetekkel is, amikor a felhasználó a bemenetre nem egy értelmes jelsorozatot adott meg. Például a ###7# nem egy értelmes jelsorozat a fenti értelmezés szerint. Állapodjunk meg abban, hogy az ilyen esetekben az algoritmus kimenete legyen az üres jelsorozat, azaz \varepsilon. Az értelmes jelsorozatok tehát a \Sigma^*-on belül egy részhalmazt alkotnak. Az algoritmusnak nyilván először el kell tudnia dönteni, hogy a bemeneti jelsorozat egyáltalán eleme-e ennek a részhalmaznak, és csak ezután kezdheti elvégezni az összeadást. Ehhez kapcsolódik a most következő definíció.
A \Sigma^* halmaznak egy valamilyen L részhalmazát a \Sigma ábécé feletti formális nyelvnek, az L részhalmaz elemeit pedig e formális nyelv mondatainak nevezzük. Ez a definíció egy kissé szokatlannak tűnik annak fényében, amit eddig a „nyelvről”, mint fogalomról gondoltunk. De igazából semmi meglepő nincs benne. Vegyük például a szokásos magyar ábécét az írásjelekkel és az egyéb, írásban használt szimbólummal együtt. A magyar nyelv tulajdonképpen nem más, mint az ezekből alkotott összes lehetséges jelsorozatok halmazának egy jól meghatározott részhalmaza. Az persze más kérdés, hogy ezt a jól meghatározott – és általában szintén végtelen sok elemet tartalmazó – részhalmazt hogyan jelölhetjük ki az összes jelsorozat tengerében valamilyen véges leírással anélkül, hogy egyenként fel kellene sorolni az elemeit. Erre szolgálnak az úgynevezett nyelvtani szabályok, amelyek meghatározzák, hogy mely jelsorozatokat tekintjük a magyar nyelv mondatainak, és melyeket nem.
Egy formális nyelv ilyen tekintetben semmiben nem különbözik a természetes nyelvektől két dolgot leszámítva. Egyrészt egy formális nyelv a fenti definíció szerint a \Sigma^* halmaz bármely részhalmaza lehet. Még akár egy olyan részhalmaz is, amelynek a kijelölésére nem lehet a nyelvtani szabályokat egy véges leírással megadni. Ennek a résznek egy későbbi szakaszában fogunk ilyenekre példát mutatni. Ilyen nyelvek esetén azt fogjuk mondani, hogy egy jelsorozat nyelvbe tartozása algoritmikusan eldönthetetlen. Másrészt, egy formális nyelvet leíró véges szabályrendszer – amennyiben létezik – egyértelmű, és általában lényegesen egyszerűbb, mint amit a természetes nyelvek esetén megszoktunk.
A formális nyelvek elméletével – és általában a nyelvtudománnyal – kapcsolatos úttörő munkássága miatt érdemes megismerni Noam Chomsky nevét. Chomsky eredményei rettentő fontos szerepet játszanak az informatikában is, hiszen az ember és gép, illetve a gép és gép közötti kommunikáció is minden esetben formális nyelvek segítségével történik. Gondoljunk csak például a programozási nyelvekre, vagy akár arra az egyszerű nyelvre, amelyet az imént definiáltunk az összeadó algoritmusunk bemeneteinek és kimeneteinek leírására.
Látható, hogy a formális nyelvek fenti definíciója önmagában nem túl használható. Ezért most megismerkedünk egy olyan matematikai objektummal, amelynek a segítségével el tudjuk dönteni, hogy egy jelsorozat egy adott nyelv mondata-e. Egy ilyen objektumra tehát tekinthetünk az adott nyelv szabályainak egyfajta véges leírásaként. Ezen kívül pedig ez az objektum a fenti, egész számok összeadásával kapcsolatos problémánkat is képes lesz megoldani.
A Turing-gép
A Turing-gép fogalmát az első részben már említett Alan Turing dolgozta ki. A név kissé félrevezető, mivel a Turing-gép, mint matematikai objektum nem elsősorban a valódi számítógépek működését, hanem az általuk végrehajtott számítási folyamatot modellezi. Ezért a számítógépek absztrakciójaként érdemes rá tekinteni a továbbiakban. Most nézzük meg, hogy tulajdonképpen mit tudunk leírni egy Turing-gép segítségével.
Az előző összeadásos példában igazából arról van szó, hogy adva van egy \Sigma ábécé, és az ennek elemeiből alkotott jelsorozatok között szeretnénk egyfajta hozzárendelést leírni valahogyan. Például a 32#11#67 jelsorozathoz az 110 jelsorozatot szeretnénk hozzárendelni. Vagy például azt szeretnénk, hogy az „értelmetlen” ###7# jelsorozat párja az \varepsilon, azaz az üres jelsorozat legyen eszerint a hozzárendelés szerint. Vegyük észre, hogy ez matematikailag nem más, mint egy függvény. Épp csak annyi a szokatlan benne, hogy ez a függvény nem számhalmazok között teremt kapcsolatot, hanem a \Sigma^* halmaz bizonyos elemeihez szintén a \Sigma^* halmaz bizonyos más elemeit rendeli hozzá. Az alábbi ábra néhány ilyen hozzárendelést mutat:
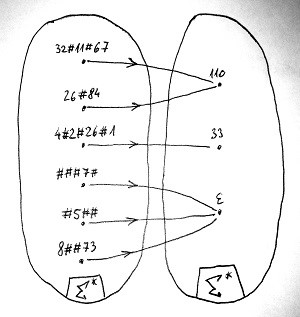
Az összes ilyen hozzárendelést nyilvánvalóan nem tudjuk felsorolni, mégis szeretnénk valamilyen véges leírást adni erre a függvényre – amennyiben az lehetséges. Egy olyan leírást, amely alapján bárki tetszőleges \Sigma^*-beli jelsorozathoz meg tudja találni a függvény által hozzárendelt párját. A Turing-gép nem más, mint egy ilyen leírás. Most nézzük meg, mit tud. Elsőre meglehetősen primitívnek fog tűnni, azonban hamarosan látni fogjuk, hogy a látszat ellenére mennyire erős számítási potenciált képvisel.
Egy Turing-gép rendelkezik egy vagy több szalaggal, amelyek az egyik irányban végtelenek és cellákra vannak osztva. Egy adott cella lehet üres, vagy szerepelhet benne a \Sigma ábécé valamilyen szimbóluma. Ezen kívül a Turing-gép rendelkezik egy író-olvasófejekkel ellátott vezérlőegységgel. Ez a fejeken keresztül képes írni és olvasni a szalagok celláit, valamint azokon jobbra-balra lépkedni. Végül a vezérlőegységnek van véges sok állapota, amelyek közül mindig pontosan az egyikben tartózkodik. Kezdetben a Turing-gép vezérlőegysége egy adott kezdőállapotból indul, az első szalag elején a Turing-gép bemenete helyezkedik el az üres cellák óceánja előtt, a többi szalag üres, és a vezérlőegység író-olvasó fejei a szalagok legelső celláira mutatnak.
Az alábbi ábrán a mi kis összeadó Turing-gépünk vázlata látható. Tegyük fel, hogy a gép összesen 3 szalaggal rendelkezik, valamint a lehetséges állapotainak száma 5. Tegyük fel továbbá, hogy kezdetben az 1-es számú állapotból indul, és épp most kapta meg a 32#11#67 jelsorozatot bemenetként. Ez a jelsorozat tehát ott virít az első szalag elején, a többi szalag pedig üres:
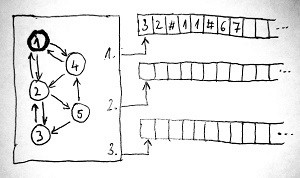
A Turing-gép a futása során elemi lépéseket végez. Azt, hogy a soron következő elemi lépésben mi történjen, egy hatalmas – de véges – szabályokból álló lista írja le. Ezeket állapotváltási szabályoknak nevezzük, amelyek tehát lényegében a Turing-gép programját írják le. Egy állapotváltási szabály akkor hajtható végre, ha teljesül annak előfeltétele. Egy állapotváltási szabály előfeltétele akkor teljesül, ha a fejek által aktuálisan mutatott cellákban az előfeltételben meghatározott tartalom van, és a vezérlőegység az előfeltételben meghatározott állapotban van.
Amennyiben legalább egy állapotváltási szabály előfeltétele teljesül, úgy a Turing-gép önkényesen választ közülük pontosan egyet, amelyet végrehajt. A szabály végrehajtása során a Turing-gép a szabályban leírtaknak megfelelően a fejek által mutatott cellák tartalmát felülírhatja vagy törölheti, a fejeket elmozdíthatja 1-1 pozícióval jobbra vagy balra, valamint a vezérlőegységet új állapotba léptetheti.
Ezek után az egész folyamat kezdődik elölről. A Turing-gép újra megvizsgálja, hogy mely szabályok hajthatók végre, ezek közül választ pontosan egyet, majd az abban leírtakat végrehajtja. És így tovább mindaddig, amíg talál legalább 1 végrehajtható szabályt. Amennyiben ilyen szabályt már nem talál, úgy a Turing-gép megáll, és a futása véget ér. Ilyenkor azt mondjuk, hogy a Turing-gép kiszámította a bemenethez tartozó kimenetet (vagy választ), amely az utolsó szalag tartalma lesz. Előfordulhat azonban, hogy a Turing-gép soha nem áll meg, mert mindig talál legalább 1 végrehajtható szabályt. Ilyenkor azt mondjuk, hogy a Turing-gép végtelen ciklusba került.
Az alábbi ábrán az összeadó Turing-gépünk látható közvetlenül azután, hogy megállt – jelen esetben mondjuk a 3-as számú állapotban. Épp most írta ki a 110 jelsorozat, azaz az eredmény utolsó szimbólumát az utolsó szalagra. Ezt tekintjük tehát a számítás eredményének. A többi szalag tartalma minket most nem érdekel, azok csupán valamilyen részeredmények, amelyeket a Turing-gép a futása során „odaszemetelt”:
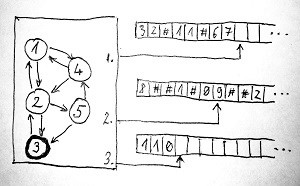
Érezhető, hogy az állapotváltási szabálylista már egy ilyen egyszerű feladat esetén is vélhetően roppant sok szabályt tartalmaz. Példaként nézzünk meg közelebbről egy állapotváltási szabályt:
HA
\begin{array}{|c|c|c|c|}\hline \text{állapot} & \text{szalag 1} & \text{szalag 2} & \text{szalag 3} \\ \hline 2 & \# & \text{üres} & \text{mindegy} \\ \hline\end{array}AKKOR
\begin{array}{|c|c|c|c|}\hline \text{állapot} & \text{szalag 1} & \text{szalag 2} & \text{szalag 3} \\ \hline 4 & \larr & (\text{üres},\larr) & (8,\larr) \\ \hline\end{array}Ennek a konkrét szabálynak – bármilyen célt is szolgáljon az összeadási feladat szempontjából – az előfeltétele akkor teljesül, ha a vezérlőegység a 2-es számú állapotban van, az 1-es szalagra mutató fej alatti cellában a # szimbólum van, a 2-es szalagra mutató fej alatti cella pedig üres. A szabály a 3-as szalag tartalmáról nem nyilatkozik, így attól nem függ az előfeltétel teljesülése. Ha az előfeltétel teljesül, akkor a szabály végrehajthatóvá válik. Ha ez az egyetlen végrehajtható szabály, akkor a Turing-gép köteles azt végrehajtani. Ha több másik szabály is végrehajtható ezen kívül, akkor a Turing-gép választhat, hogy ezek közül melyiket hajtja végre (de egyet mindenképpen választania kell). Ha pedig egyetlen szabály sem végrehajtható, akkor a Turing-gép futása megáll. Tegyük fel, hogy a Turing-gép végrehajtja ezt a szabályt. Nézzük meg, mi történik.
A szabály arra utasítja a Turing-gépet, hogy menjen át a 4-es számú állapotba, írja felül a 3-as szalagra mutató fej alatti cellát a 8-as szimbólummal, törölje a 2-es szalagra mutató fej alatti cella tartalmát, és léptesse mindhárom fejet balra – jelentsen ez bármit is az összeadási feladat szempontjából. Jogosan merülhet fel az Olvasóban a kérdés, hogy egy ennyire alacsonyszintű leírással hogyan tudunk megoldani akár egyetlen gyakorlati problémát is. Egyáltalán mi köze ennek egy valódi számítógép által végrehajtott számítási folyamathoz? Vegyük észre azonban, hogy ez csupán technikai – de semmiképpen sem elméleti – nehézséget jelent.
A legalacsonyabb szinten ugyanis egy számítógép processzora sem csinál ennél többet. Van neki egy memóriája, amely a 3. részben leírtak alapján véges sok 8-bites rekeszből áll. Következésképp a memória tartalma véges sokféle lehet a futás során, még ha ez a szám nagyon nagy is. A memória aktuális tartalmát tehát elméleti síkon tekinthetjük a Turing-gép aktuális állapotának. Amennyiben a gépünk a véges memóriába nem férne bele valamilyen ok miatt, úgy használhatja a háttértárat (ami a legtöbbször a merevlemez) is a részeredmények tárolására. A háttértár tehát szintén elméleti síkon tekinthető a Turing-gép szalagjának vagy szalagjainak.
Az egyetlen különbség a kettő között, hogy egy Turing-gép szalagjai végtelen hosszúak, míg egy valódi számítógép háttértára nem. Ez azonban nem jelent elméleti megszorítást. Ha ugyanis egy feladat megoldható Turing-géppel véges sok lépésben, akkor a futás során a szalagokra is véges sok szimbólum fog kerülni a megállásig. Következésképp mindig található olyan háttértár méret, amely elegendő e szimbólumok tárolására, ha a fix méretű memóriába a részeredmények esetleg nem férnének bele. Egy valódi háttértár tehát tekinthető potenciálisan végtelen méretűnek.
Egy valódi számítógép által végrehajtandó program a legalacsonyabb szinten – amelyet gépi kódnak nevezünk – a Turing-gépünk szabályrendszeréhez nagyon hasonló módon írja le a gép számára, hogy mit kell csinálnia. Az, hogy a programozóknak mégsem kell ennyire alacsonyszintű programkódot írniuk, pusztán az úgynevezett magasszintű programozási nyelveknek, és a fordítóprogramoknak köszönhető. A programozási nyelvek ugyanis lehetővé teszik, hogy a végrehajtandó feladatot az emberi nyelvekhez sokkal közelebb – de azért attól még mindig viszonylag távol – álló módon „fogalmazhassuk meg” a gép számára. A fordítóprogramok feladata pedig ennek az elkészült magasszintű leírásnak a lefordítása olyan alacsonyszintű gépi kódra, amely már közvetlenül értelmezhető a processzor számára.
A nemdeterminisztikus Turing-gép
Az előző szakasz elején azt mondtuk, hogy egy probléma matematikai értelemben nem más, mint egy függvény. Méghozzá egy olyan függvény, amely az adott \Sigma ábécé feletti jelsorozatokhoz hozzárendel valamilyen szintén \Sigma feletti jelsorozatot. Elképzelhető, hogy a függvény bizonyos bemeneti jelsorozatokra egyáltalán nincs értelmezve, azaz ezekhez a jelsorozatokhoz nem rendel hozzá semmit. Azonban azokon a helyeken, ahol értelmezve van, egyértelmű kell legyen. Ez azt jelenti, hogy egy adott bemeneti jelsorozathoz a függvény minden esetben legfeljebb egy kimeneti jelsorozatot rendelhet hozzá.
Máskülönben nem függvényről, hanem egy úgynevezett relációról beszélnénk. A relációk mindössze annyiban különböznek a függvényektől, hogy egy bemeneti jelsorozathoz tetszőleges számú – tehát akár végtelen sok – kimeneti jelsorozatot is hozzárendelhetnek. Ilyen értelemben egy függvény egy olyan speciális relációként fogható fel, amelynél ez a „tetszőleges szám” legfeljebb 1.
Az alábbi ábrán a függvény és a reláció fogalma közötti különbség látható:
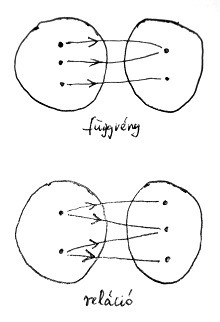
De mi köze ennek a két fogalomnak a Turing-gépekhez? Az előző szakaszban említettük, hogy egy Turing-gépnél előfordulhat, hogy egy adott helyzetben egynél több állapotváltási szabály is végrehajtható. Ilyenkor a Turing-gépnek ugye választania kell, hogy ezek közül konkrétan melyiket hajtja végre a következő lépésben. Arra azonban nem tettünk semmilyen megkötést, hogy mi alapján válasszon. Ilyen helyzetekben azt mondjuk, hogy a Turing-gép következő lépése nem determinált. Az olyan Turing-gépeket, amelyek a szabályrendszerük alapján ilyen választási helyzetbe kényszerülhetnek, nemdeterminisztikus Turing-gépeknek nevezzük. Ezzel szemben ha minden esetben legfeljebb 1 szabály hajtható végre, akkor determinisztikus Turing-gépekről beszélünk.
Vegyük észre, hogy a függvény és reláció fogalma közötti különbség párhuzamba hozható a determinisztikus és nemdeterminisztikus Turing-gépek lehetséges számítási útvonalai közötti különbséggel. Egy determinisztikus Turing-gépnek egy adott bemenetre egyetlen lehetséges számítási útvonala létezik, hiszen minden helyzetben legfeljebb 1 szabály lesz végrehajtható. Ez az egyetlen számítási útvonal vagy végtelen hosszú lesz, vagy pedig véges attól függően, hogy az adott bemenetre a gép végtelen ciklusba kerül-e vagy nem. Előbbi esetben a bemenetre nem érkezik semmilyen kimenet (azaz válasz), utóbbi esetben pedig a megállás után a kimenet ott lesz az utolsó szalagon. Az alábbi ábra mutatja ezt a két lehetőséget determinisztikus Turing-gép esetén:
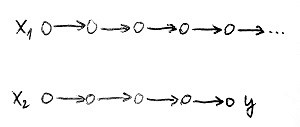
Az első esetben az x_1 bemenetre nem kaptunk kimenet, míg a második esetben az x_2 bemenetre megkaptuk az egyértelmű y kimenetet. Épp úgy, mintha egy függvény az x_1 jelsorozathoz nem rendelt volna hozzá semmit, de az x_2 jelsorozathoz az y jelsorozatot rendelte volna hozzá.
Ezzel szemben egy nemdeterminisztikus Turing-gépnek egy adott bemenetre 1-nél több – amely lehet akár végtelen sok – számítási útvonala létezik, hiszen bizonyos helyzetekben 1-nél több szabály lesz végrehajtható. E végtelen sok számítási útvonal között bizonyára lesznek végtelen és véges hosszúak is attól függően, hogy az adott bemenetre az adott útvonalon a gép végtelen ciklusba kerül-e vagy nem. Amennyiben minden lehetséges számítási útvonal végtelen hosszú, akkor a bemenetre nem érkezik semmilyen kimenet (azaz válasz). Amennyiben léteznek véges hosszú útvonalak is, akkor ezeknek az útvonalaknak a kimenete a megállás után ott lesz az utolsó szalagon. Az alábbi ábra mutatja ezt a két lehetőséget nemdeterminisztikus Turing-gép esetén:
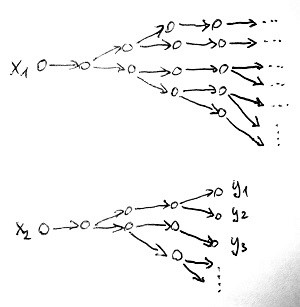
Az első esetben az x_1 bemenetre nem kaptunk kimenet, míg a második esetben az x_2 bemenetre megkaptuk az y_1, y_2, y_3, \dots kimeneteket. Épp úgy, mintha egy reláció az x_1 jelsorozathoz nem rendelt volna hozzá semmit, de az x_2 jelsorozathoz az y_1, y_2, y_3, \dots jelsorozatokat rendelte volna hozzá.
A determinisztikus és nemdeterminisztikus Turing-gépek által reprezentált számítási modellek közötti viszonynak érezhetően köze van a függvények és relációk fogalma közötti viszonyhoz.
A Turing-gép által kiszámított függvény
Legyen adott egy M determinisztikus Turing-gép, valamint egy \Sigma ábécé, amellyel ez a gép dolgozik. Ekkor a \Sigma feletti jelsorozatok két részre oszthatók. Egyrészt lesznek olyanok, amelyekre – mint bemenetekre – az M Turing-gép véges sok lépés után megáll és ad valamilyen kimenetet. Másrészt lesznek olyanok, amelyekre végtelen ciklusba kerül, azaz nem ad kimenetet. Definiálhatunk tehát egy függvényt, amely épp azokra a jelsorozatokra van értelmezve, amelyekre M megáll, és minden ilyen jelsorozathoz épp azt a jelsorozatot rendeli hozzá, amely a megállás után a kimeneti szalagon van. Ezt a függvényt az M Turing-gép által kiszámított függvénynek nevezzük, és f_M-mel jelöljük.
Ehhez hasonlóan legyen adott egy N nemdeterminisztikus Turing-gép, valamint szintén egy \Sigma ábécé, amellyel ez a gép dolgozik. Ekkor a \Sigma feletti jelsorozatok két részre oszthatók. Lesznek olyanok, amelyekre – mint bemenetekre – az N Turing-gép legalább 1 számítási útvonalon véges sok lépés után megáll, és minden ilyen számítási útvonal végén ad valamilyen kimenetet, és lesznek olyan bemenetek is, amelyekre a gép mindegyik számítási útvonalon végtelen ciklusba kerül, azaz nem ad semmilyen kimenetet. Definiálhatunk tehát egy relációt, amely épp azokra a jelsorozatokra van értelmezve, amelyekre N legalább 1 számítási útvonalon megáll, és minden ilyen bemenethez épp azokat a jelsorozatokat rendeli hozzá, amelyek a megálló számítási útvonalak végén a kimeneti szalagon vannak. Ezt a relációt az N Turing-gép által kiszámított relációnak nevezzük, és R_N-nel jelöljük.
Látható, hogy a nemdeterminisztikus Turing-gépek a determinisztikus Turing-gépek általánosításának tekinthetők hasonlóan ahhoz, mint ahogy a relációk a függvények általánosításai. A továbbiakban függvényekkel fogunk foglalkozni, és ennek megfelelően Turing-gép alatt mindig determinisztikus Turing-gépet fogunk érteni, hacsak külön nem jelezzük ennek ellentettjét. A most következő definíciók egyfajta alapvető osztályozását adják az összes lehetséges \Sigma feletti jelsorozatokon értelmezett függvénynek.
Egy f függvényt parciálisan rekurzív függvénynek nevezzük, ha létezik olyan Turing-gép, amely által kiszámított függvény épp f. A „parciális” elnevezés arra utal, hogy az f függvénynek nem feltétlenül kell minden bemeneti jelsorozatra értelmezve lennie, de azt elvárjuk, hogy létezzen olyan Turing-gép, amely minden olyan jelsorozatra véges sok lépésben megáll és kiszámolja a függvény értékét, amelyre a függvény értelmezve van. A „rekurzív” elnevezés a matematika egy másik területéről ered, ezt most nem részletezzük.
Az olyan parciálisan rekurzív függvényeket, amelyek minden bemeneti jelsorozatra értelmezve vannak, rekurzív függvényeknek nevezzük. A rekurzív függvényeket fogjuk algoritmikus szempontból kezelhető függvényeknek tekinteni, mivel ezek azok, amelyeknél a kiszámításukat végző Turing-gép soha nem keveredik végtelen ciklusba. Erre egy remek példa a fenti összeadó Turing-gépünk, amely az összeadás szempontjából értelmezhetetlen bemenetekre is megáll, és az üres jelsorozatot, mint kimenetet produkálja. Kérdés, hogy nem túl szűk-e ez a meghatározás? Nincsenek-e esetleg olyan algoritmusok, amelyek nem valósíthatók meg Turing-géppel? Nem lehet-e valamilyen „hiper-szuper” számítógéppel olyan függvényt is kiszámítani, amit Turing-géppel nem? Most ezekre a kérdésekre adjuk meg a választ.
A Church-Turing tézis
Az úgynevezett Church-Turing tézis állítása a következő: minden olyan probléma, amely algoritmussal megoldható, arra szerkeszthető alkalmas Turing-gép is. Vegyük észre, hogy ez nem egy matematikai tétel, hanem egy tapasztalati kijelentés, de felfoghatjuk magának az „algoritmus” fogalom matematikai definíciójának is. Az olyan problémamegoldási módszereket tekintjük tehát algoritmusnak, amelyekre készíthető Turing-gép. Ennek oka mindössze annyi, hogy számos kísérlet ellenére eddig még senki sem adott meg olyan algoritmus-fogalmat, amely a gyakorlatban megvalósítható lenne, és a Turing-kiszámíthatóságnál erősebb képességű. Természetesen, ha majd a jövőben képesek leszünk építeni olyan számítógépeket, amelyek működése alapjaiban különbözik a jelenlegi gépektől, akkor ezt a paradigmát át kell majd értékelnünk. Ilyenek lesznek például az úgynevezett kvantumszámítógépek. Az elméleti számítástudomány fejlődése természetesen már elindult ilyen irányokba is, ám ez még csak a jövő. A jelen valóságában a Church-Turing tézist kell elfogadnunk igaznak.
Elméleti értelemben mindegy, hogy a gép hány szalaggal rendelkezik. Sőt, elképzelhető, hogy esetleg szalagok helyett négyzetrácsos füzethez hasonló síkokon dolgozik, a fejek pedig nem csak jobbra és balra, hanem fel és lefelé, vagy akár tetszőleges helyre mozoghatnak. Ezekről mind-mind bebizonyítható, hogy ugyanazt a számítási potenciált képviselik. Ami tehát megoldható az egyikkel, az megoldható az összes többivel is. Maximum nagyobb – de még mindig véges – szabályrendszerrel tudjuk leírni a gépet. Elméleti szempontból tehát teljesen mindegy, hogy melyiket tekintjük „a Turing-gép” definíciójának, maximum „kényelmi” szempontból használjuk hol az egyik, hol a másik definíciót. Mi a továbbiakban a fenti többszalagos változatot fogjuk Turing-gépnek tekinteni, hacsak ennek ellenkezőjét nem állítjuk.
Most nézzük meg, hogy függvények kiszámításán kívül mire lehet még használni a Turing-gépet.
A Turing-gép által felismert nyelv
Algoritmussal általában optimalizálási feladatokat oldunk meg, azaz egy megoldáshalmazból olyan megoldást keresünk, amely bizonyos szempontok szerint a „legjobb”. Például legrövidebb vagy leggyorsabb útvonal keresése egy térképen.
Amikor azonban egy optimalizálási feladat „nehézségéről” szeretnénk képet kapni, akkor célszerű azt egy úgynevezett döntési problémára visszavezetni. Például létezik-e olyan útvonal, amely egy adott küszöbértéknél rövidebb vagy gyorsabb. Ha ugyanis az optimalizálási feladat „könnyű”, akkor a belőle képzett döntési feladat is „könnyű”, hiszen csak a kapott eredményt kell összehasonlítani a küszöbértékkel. Másként fogalmazva: ha egy döntési feladat „nehéz”, akkor a hozzátartozó optimalizálási feladat is „nehéz”. A döntési problémák lényegében olyan függvények, amelyek a bemeneti jelsorozatokhoz kétféle kimeneti jelsorozatot rendelhetnek, amelyek egy „igen” vagy egy „nem” választ reprezentálnak. Ezeket döntőfüggvényeknek nevezzük.
Az alábbi ábrán egy olyan döntőfüggvény látható, amely nem minden bemeneti jelsorozatra van értelmezve. De amelyekre értelmezve van, azok esetén a kimenet kétféle lehet: az egyik az „igen”, míg a másik a „nem” választ jelenti:
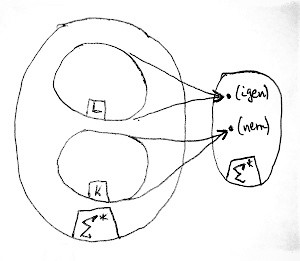
Mivel egy döntőfüggvény is épp olyan függvény, mint amikről eddig szó volt, ezért ő is lehet parciálisan rekurzív. Ebben az esetben tehát létezik olyan M Turing-gép, amely őt kiszámolja. Ilyenkor 3 eset lehetséges erre a Turing-gépre vonatkozólag:
- A fenti ábrán az L részhalmazba tartozó bemenetekre a Turing-gép megáll, és az „igen” választ adja.
- Az ábrán a K részhalmazba tartozó bemenetekre a Turing-gép megáll, és a „nem” választ adja.
- A többi bemenetre a Turing-gép végtelen ciklusba kerül.
Ilyen esetekben tehát a Turing-gép egy döntési problémát old meg. A probléma példányai ebben az esetben valamilyen eldöntendő kérdések. Ezeket reprezentálják a bemeneti jelsorozatok a Turing-gép számára, amelytől választ várunk a kérdésre. Azok a bemeneti jelsorozatok, amelyekre a Turing-gép az „igen” választ adja, egy részhalmazt alkotnak az összes bemeneti jelsorozat között. Ezt a részhalmazt a Turing-gép által felismert nyelvnek nevezzük és L_M-mel jelöljük. A most következő definíciók egyfajta alapvető osztályozását adják az összes lehetséges \Sigma feletti formális nyelvnek – hasonlóan ahhoz, mint ahogy a függvényeket osztályoztuk.
Egy L nyelvet rekurzívan felsorolható, vagy algoritmikusan felismerhető nyelvnek nevezzük, ha létezik olyan Turing-gép, amely által felismert nyelv épp L. Az elnevezés ismét a matematika egy másik területéről ered, ennek részleteit most mellőzzük. Egy rekurzívan felsorolható nyelv mondatait tehát tulajdonképpen egy olyan döntőfüggvény jelöli ki, amely parciálisan rekurzív. Az ilyen nyelvek osztályát RE-vel jelöljük.
Egy nyelv rekurzívan felsorolhatósága azonban önmagában még kevés, mivel az csak annyit garantál, hogy a nyelvbe tartozó jelsorozatokra a Turing-gép mindig megáll, és az „igen” választ adja. Ha azonban véletlenül egy olyan jelsorozat kerül a bemenetre, amely nem mondata a nyelvnek, akkor nem garantált, hogy a Turing-gép valaha is megáll, és megkapjuk a „nem” választ. Azokat a nyelveket, amelyek esetén még ez utóbbi is garantált, rekurzív, vagy más néven algoritmikusan eldönthető nyelveknek nevezzük, az ilyen nyelvek osztályát pedig R-rel jelöljük.
Vegyük észre, hogy a döntési problémák és egy adott \Sigma ábécé feletti nyelvek között megfeleltetés létesíthető. Minden döntési probléma ugyanis kijelöl egy \Sigma feletti formális nyelvet. Ennek épp azok a \Sigma feletti jelsorozatok lesznek a mondatai, amelyek a döntési probléma igenpéldányait reprezentálják. Megfordítva, tetszőleges \Sigma feletti formális nyelvnek megfeleltethető egy olyan döntési probléma, amelynek igenpéldányai épp a nyelv mondataival reprezentálhatók.
Azokat a döntési problémákat tekintjük tehát algoritmikusan eldönthető problémáknak, amelyeket reprezentáló nyelvek az R osztályban vannak, azaz rekurzívak. Az R nyilvánvalóan részhalmaza RE-nek, azaz minden rekurzív nyelv egyben rekurzívan felsorolható is. Az olvasó jól érzékeli, hogy most az algoritmikus eldönthetőség határait feszegetjük, ezért természetesen adódik a kérdés, hogy vajon valódi részhalmazról van-e szó? Esetleg létezik-e olyan \Sigma feletti nyelv, amely rekurzívan felsorolható ugyan, de nem rekurzív? Sőt továbbmegyek: vajon létezik-e olyan nyelv, amely még csak nem is rekurzívan felsorolható? A továbbiakban ezekre a kérdésekre adjuk meg a választ.
Az univerzális Turing-gép
Képzeljünk most el egy olyan Turing-gépet, amely képes bármilyen más Turing-gép működését szimulálni tetszőleges bemenetre. Az ilyen Turing-gépet logikus módon univerzális Turing-gépnek nevezzük. Az univerzális Turing-gép bemenete két részből áll: az első rész a szimulálni kívánt Turing-gép valamilyen w leírását (amely ugye véges), míg a második rész a szimulálni kívánt Turing-gép x bemenetét tartalmazza. Az univerzális Turing-gép ezután pontosan úgy viselkedik erre az összetett bemenetre, mint ahogyan a w „betűsorozat” által leírt szimulált Turing-gép viselkedne az x bemenetre. Kérdés, hogy egyáltalán létezik-e univerzális Turing-gép?
A válasz igen, ám ennek konkrét konstrukciójától most eltekintünk, mivel ez inkább technikai jellegű probléma, mintsem elméleti. Az univerzális Turing-gép létezése egyébként nem meglepő, hiszen ha belegondolunk, tulajdonképpen minden valódi számítógép tekinthető ilyen konstrukciónak. A szimulált gépek w leírásai valódi számítógépek esetén a különböző programoknak felelnek meg, maga a szimuláció pedig nem más, mint a w „betűsorozat” által leírt program futtatása. Az, hogy egy tetszőleges Turing-gépet hogyan tudunk leírni egy w „betűsorozattal” szintén technikai jellegű kérdés, de ez nyilván megoldható valamilyen szabványos módon.
Ennyi bevezető után végre rátérhetünk az algoritmikus eldönthetőség kérdésére.
Algoritmikusan eldönthetetlen problémák
A 19. század végéig mindenki úgy gondolta, hogy egy kellőképpen pontosan megfogalmazott döntési problémára mindig létezik olyan algoritmus (azaz Turing-gép) amely a probléma tetszőleges konkrét példányára (azaz tetszőleges bemenetre) megadja az „igen” vagy „nem” választ. Maximum túl sokáig, de mindenképpen véges ideig tart ennek az algoritmusnak a végrehajtása. Vagy esetleg az algoritmus létezik ugyan, de a tudomány jelenlegi állása alapján azt még nem találtuk meg, így az az utókor feladata lesz. A századforduló megdöbbentő felfedezése az, hogy ez egyszerűen nem így van: feltehetünk olyan kérdést, amely algoritmikusan eldönthetetlen. Sőt, olyan kérdés is megfogalmazható, amelynek az algoritmikus eldönthetetlensége is eldönthetetlen, és így tovább, ez az eldönthetetlenségi láncolat vég nélkül folytatható.
Most demonstrálunk egy olyan nyelvet, amely nemhogy nem rekurzív, de még csak nem is rekurzívan felsorolható, azaz nem létezik olyan Turing-gép, amely a nyelvhez tartozó „szavakat” egyáltalán felismeri. Ennek a nyelvnek a neve diagonális nyelv, és főként elméleti jelentőségű, mivel demonstrálja rekurzívan nem felsorolható nyelvek létezését.
Figyelem! Logikai tandemugrás következik.
A diagonális nyelv olyan \Sigma feletti jelsorozatokból áll, amelyek Turing-gép leírások, és az általuk leírt Turing-gép nem fogadja el őket, azaz vagy a „nem” választ adja, vagy nem is áll meg. A diagonális nyelv jele L_d. Itt a nyelv egy elemét egyszerre tekintjük bemenetnek és algoritmusnak is. Ráadásul azzal a nyakatekert tulajdonsággal, hogy saját magára, mint bemenetre az algoritmus „nem”-et mond, vagy nem áll meg. Most megvizsgáljuk, milyen furcsa tulajdonsággal rendelkezik ez a nyelv.
Az L_d nyelv nem rekurzívan felsorolható. Ha ugyanis az lenne, akkor létezne olyan M Turing-gép, amely épp L_d-t ismeri fel. Ha létezne ilyen M Turing-gép, akkor azt le lehetne írni egy valamilyen w „betűsorozattal”. De vajon mit tenne M, ha ráküldenénk w-t (azaz a saját leírását), mint bemenetet? Az alábbi két eset lehetséges:
- Ha M elfogadná w-t (azaz „igen” választ adna rá), akkor az azt jelentené, hogy w eleme az L_d nyelvnek (hiszen M éppen az L_d elemeit fogadja el). Ha w eleme az L_d nyelvnek, akkor ő egy olyan Turing-gép leírása, amely nem fogadja el a saját leírását (hiszen L_d épp az ilyen Turing-gép leírások nyelve). De w épp M leírása, tehát M nem fogadhatja el w-t.
- Ha M nem fogadná el w-t (azaz „nem” választ adna rá, vagy végtelen ciklusba kerülne), akkor az azt jelentené, hogy w nem eleme az L_d nyelvnek (hiszen M éppen az L_d elemeit fogadja el). Ha w nem eleme az L_d nyelvnek, akkor ő egy olyan Turing-gép leírása, amely elfogadja a saját leírását. De mivel w épp M leírása, ezért M-nek el kell fogadnia w-t.
Teljes logikai paradoxonba kerülnénk, ha feltételeznénk M létezését, vagyis azt, hogy L_d rekurzívan felsorolható. L_d tehát nem lehet rekurzívan felsorolható. Persze az L_d egy nagyon elborult nyelv, és mondhatnánk, hogy ilyen nyelvet konstruálni nagyon nem egyszerű feladat, pláne ha még gyakorlati hasznot is megkövetelünk tőle. Ez így is van, azonban az az érdekes, hogy halmazelméleti szempontból egy adott \Sigma ábécé feletti nyelvek közül „majdnem mindegyik” ilyen, és csak „elvétve” fordulnak elő közöttük RE-beli (azaz algoritmikusan felismerhető) nyelvek. Az összes \Sigma feletti nyelvek számossága ugyanis kontinuum számosságú, míg az RE-beli nyelvek „csak” megszámlálhatóan végtelen sokan vannak. A pontos matematikai definíciót mellőzzük, de e kétféle végtelen nagyjából úgy viszonyul egymáshoz, mint ahogyan az egész számok végtelensége viszonyul a számegyenesen lévő összes szám végtelenségéhez. Az összes szám folytonosan tölti fel a számegyenest (innen a „kontinuum” elnevezés), míg közöttük az egész számok „csak” elvétve fordulnak elő.
De térjünk vissza a Földre, és foglalkozzunk mostantól csak az RE-beli nyelvekkel, hiszen a többivel nem sok mindent tudunk kezdeni. A kérdés ezek után az, hogy létezik-e olyan nyelv, amely rekurzívan felsorolható ugyan, de nem rekurzív (azaz algoritmikusan eldönthetetlen)?
A megállási probléma
Gyakorlati szempontból hasznos volna, ha egy algoritmusról el tudnánk dönteni, hogy létezik-e olyan bemenet, amelyre végtelen ciklusba kerülne. Gondoljunk csak bele: egy csomó teszteléstől meg tudnák magukat kímélni a szoftverfejlesztők, ha lenne egy olyan „szuperalgoritmusuk”, amely bármilyen programról ítéletet tudna mondani ilyen tekintetben. Legyünk szerények: vizsgáljuk csak azt a kérdést, hogy egy algoritmus egy adott konkrét bemenettel kerülhet-e végtelen ciklusba. Ezt megállási problémának nevezik, ahol az eldöntendő kérdés tehát az, hogy egy w jelsorozattal leírt Turing-gép egy adott x bemenetre megáll-e vagy sem. Az ilyen tulajdonságú (w,x) párokat leíró mondatokat tartalmazó nyelvet megállási nyelvnek nevezzük és L_h-val jelöljük.
Sajnos az a helyzet, hogy az L_h nyelv ugyan rekurzívan felsorolható, de nem rekurzív. A bizonyításnak csak a vázlatát ismertetjük, annak részleteit mellőzzük. A rekurzívan felsorolhatóság könnyen adódik: bütyköljük meg az univerzális Turing-gépet úgy, hogy ha megáll valamilyen (w,x) bemenetre, akkor mindig „igen” választ adjon. Az így megbütykölt gép nyilván felismeri az L_h nyelvet, tehát az rekurzívan felsorolható. Ezután azt kell megvizsgálni, hogy mi lenne, ha ezen felül még rekurzív is lenne. Ebben az esetben lenne olyan M Turing-gép, amely L_h-t ismeri fel és mindig megáll. Ekkor azonban – itt nem részletezett módon – tudnánk konstruálni M segítségével egy olyan „szuperokos” Turing-gépet is, amely a fentebb ismertetett diagonális nyelvet ismerné fel. De ez ugye – mint láttuk – képtelenség, hiszen a diagonális nyelv nem rekurzívan felsorolható. Nem létezhet tehát a „szuperokos” Turing-gép alapjául szolgáló M Turing-gép sem, amely mindig megáll és L_h-t ismeri fel, azaz L_h nem lehet rekurzív.
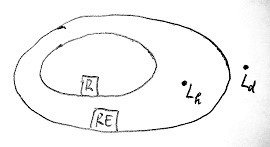
Az alábbi ábrán az eddig megismert RE és R nyelvosztályok egymáshoz való viszonya, valamint az eddig megismert 2 nyelv (a diagonális és a megállási nyelv) elhelyezkedése látható:
Hilbert 10. problémája
Végül bemutatunk egy igazán érdekes döntési problémát, amely a Turing-gépek formalizmusától függetlenül, természetesen is megfogalmazható. 1900-ban Párizsban a világ matematikusainak kongresszusán David Hilbert egy azóta legendás hírűvé vált előadást tartott, amelyen a jövő fontos kutatási területeit próbálta meg kijelölni. Huszonhárom olyan kérdést fogalmazott meg, amelyről úgy vélte, hogy megoldásuk lényeges előrelépést jelentene sok területen.
Ezek közül a 10. probléma szól az úgynevezett diofantoszi egyenletek megoldásáról. Ehhez előbb szükségünk van egy fontos fogalomra. Egész együtthatós polinom alatt olyan kifejezéseket értünk, amelyek változókból és egész számokból építhetők fel az összeadás, kivonás és szorzás segítségével. Például az x^2\cdot y - z - 1 kifejezés az x, y és z változók egy egész együtthatós polinomja. Egy egész együtthatós polinomból képzett diofantoszi egyenlet megoldásakor az egész számok között keressük a változók olyan értékeit, melyeket a polinomba helyettesítve az eredmény 0. Egy diofantoszi egyenletet megoldhatónak mondunk, ha létezik ilyen értelemben vett megoldás. Például a fenti diofantoszi egyenletnek egy lehetséges egészekből álló megoldása:
\begin{aligned}x &= 1 \\ y &=2 \\ z&=1 \end{aligned}A David Hilbert által felvázolt 10. probléma így hangzik: adjunk algoritmust, amely tetszőleges diofantoszi egyenletre eldönti, hogy létezik-e megoldása vagy nem. A kérdést végül 1970-ben Martin Davis, Julia Robinson és mások munkáira építve Jurij Matyijaszevics válaszolta meg, amikor bizonyította, hogy a diofantoszi egyenletek megoldhatóságának kérdése algoritmikusan eldönthetetlen. Ez persze nem azt jelenti, hogy egy-egy konkrét diofantoszi egyenletről ezt ne lehetne eldönteni annak valamilyen speciális tulajdonságát felhasználva, hanem azt, hogy nincs olyan általános döntési algoritmus, amely ezt tetszőleges egyenletről képes eldönteni.
Ebben a részben megismerkedtünk a Turing-gépnek nevezett elméleti konstrukcióval, amely lényegében az „algoritmus” matematikai definíciója, és amellyel döntési és optimalizálási problémákat lehet megoldani. A döntési problémákat formális nyelvekkel reprezentáltuk, ahol a Turing-gép feladata felismerni egy adott jelsorozatról, hogy egy adott nyelv mondata-e vagy sem. Ennek kapcsán a formális nyelveket az RE és R nyelvosztályokba soroltuk aszerint, hogy létezik-e a nyelvet felismerő Turing-gép (RE osztály) és ez a Turing-gép vajon olyan jelsorozatokra is mindig megáll-e, amelyek nem mondatai a nyelvnek (R osztály). Az utóbbi osztályba tartozó nyelveket (és az általuk reprezentált problémákat) tekintjük algoritmikusan eldönthető nyelveknek. Az algoritmikus eldönthetőség határait feszegetve mutattunk pár algoritmikusan eldönthetetlen problémát, köztük a komoly gyakorlati jelentőséggel bíró megállási problémát és Hilbert híres 10. problémáját is.
A következő részben az algoritmikusan eldönthető problémákat (azaz a rekurzív nyelveket) osztályozzuk tovább aszerint, hogy mennyire hatékonyan található meg rájuk az „igen” vagy a „nem” válasz. Ezután már látni fogjuk, hogy mit jelent Alice, Bob és Eve számára egy feladat „nehézsége”.
A következő részt itt találod…



