Az előző részben megismerkedtünk a formális nyelvek és a Turing-gép fogalmával és láttuk, hogy a Turing-gépeket hogyan lehet optimalizálási vagy döntési problémák megoldására használni. A továbbiakban döntési problémákról, illetve azok „nehézségéről” lesz szó. Az előző részben láttuk, hogy minden döntési problémának megfeleltethető egy valamilyen véges ábécé feletti formális nyelv. Amennyiben a probléma egyes példányait (azaz az eldöntendő kérdéseket) ezen ábécé elemeiből alkotott jelsorozatokkal reprezentáljuk, úgy az algoritmikus feladat annak eldöntése, hogy egy adott jelsorozat mondata-e egy adott nyelvnek vagy sem. Azokat neveztük algoritmikusan eldönthető problémáknak, amelyek esetén a nyelvbe tartozás kérdése eldönthető Turing-géppel anélkül, hogy az végtelen ciklusba keveredne. A továbbiakban csak ilyen problémákkal foglalkozunk. De vajon mikor tekinthető egy döntési probléma „nehéznek” vagy „könnyűnek”? Mi számít vízválasztónak ilyen tekintetben? Valóban léteznek igazán „nehéz” problémák, vagy csupán ügyetlenek vagyunk? Mit mond erről a számítástudomány – és talán az egész matematika – egyik legfontosabb megoldatlan sejtése? Ebben a részben erről lesz szó…
Figyelem! Erősen ajánlott elolvasni az előző részt az alábbiak megértéséhez. A teljes cikksorozat elejét itt találod.
Egy adott feladat esetén nem egyszerűen az a cél, hogy találjunk rá egy algoritmust. Az is fontos, hogy az algoritmus bizonyos szempontból minél jobb legyen. Az algoritmust megvalósító Turing-gép szempontjából a „jóságot” kétféleképpen mérhetjük. Mérhetjük egyrészt, hogy a Turing-gép a végrehajtás során mennyi cellát használ fel a szalagjaiból, azaz hogy legalább mekkora tárolókapacitásra van szüksége ahhoz, hogy a döntést meghozza. Ezt a Turing-gép tárkomplexitásának nevezzük. Másrészt mérhetjük azt is, hogy a Turing-gépnek a döntésig hány elemi lépést kell megtennie. Ezt a Turing-gép időkomplexitásának nevezzük.
Igazából az érdekel minket, hogy a bemenet méretének függvényében e két mennyiség milyen gyorsan növekszik. Habár adott esetben mindkét érték fontos lehet, mi az egyszerűség kedvéért a továbbiakban elsősorban az időkomplexitást fogjuk vizsgálni. Nézzünk először egy példát, hogy lássuk, pontosan miről is van szó.
Gráfok színezése
A távoli Kompánia ország lakói között vannak, akik utálják egymást, és vannak, akik nem. Ez az állítás persze minden országra igaz, de mi most szorítkozzunk Kompániára. Feltételezzük, hogy két ember közötti utálat vagy nem utálat kölcsönös, azaz vagy mindkettő utálja a másikat, vagy egyik sem. Az algoritmikus döntési feladat annak eldöntése, hogy felosztható-e az egész ország két pártra úgy, hogy az azonos pártban lévők ne utálják egymást.
Ezt ábrázolhatjuk egy úgynevezett „utálatgráffal”, amely csúcsokból és élekből áll. A gráfokról bővebben már volt szó korábban a csatornamodellek kapcsán. Ebben a példában a gráf minden csúcsa egy-egy embert jelképez, és két csúcs akkor van összekötve éllel, ha a nekik megfelelő két ember utálja egymást. Jelöljük az egyik pártot 0-val, a másikat pedig 1-gyel. Ekkor a feladat annak eldöntése, hogy az „utálatgráf” csúcsai megjelölhetők-e 1-gyel vagy 0-val úgy, hogy két szomszédos csúcs soha ne kapjon ugyanolyan jelölést. Ezt a gráfelméletben szemléletesen színezésnek nevezzük. A kérdés tehát így hangzik: kiszínezhetőek-e egy adott gráf csúcsai 2 színnel úgy, hogy a szomszédos csúcsok ne legyenek azonos színűek? Amennyiben ez megtehető egy adott gráfra, akkor azt mondjuk, hogy a gráf 2-színezhető.
Az alábbi gráf például nem 2-színezhető:
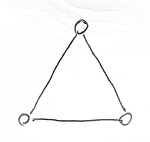
Ezzel szemben az alábbi gráf 2-színezhető, a csúcsokhoz rendelt számok pedig egy helyes 2-színezést jelölnek:

Most próbáljunk meg algoritmust adni a 2-színezhetőség eldöntésére. A könnyebb érthetőség miatt az algoritmust nem egy Turing-gép szabályrendszerének szintjén, hanem természetes nyelven fogjuk leírni. Elemi lépéseknek az alábbiakat fogjuk tekinteni:
- Tetszőleges csúcs színének olvasása és írása.
- Tetszőleges csúcs szomszédainak lekérdezése.
Első ötletünk az lehet, hogy szisztematikusan végigpróbálgatjuk az összes lehetséges színezést. Ha egy színezéssel megvagyunk, akkor leellenőrizzük, hogy a kapott színezés helyes-e, vagy nem. Ezt úgy tudjuk megtenni, hogy minden csúcs színére megvizsgáljuk, hogy különbözik-e a szomszédos csúcsok színeitől. Amennyiben egy adott színezés esetén ez minden csúcsra teljesül, akkor nyilván találtunk egy helyes 2-színezést. Ekkor a döntési algoritmus kimenete „igen”. Amennyiben ilyen színezést nem találtunk, úgy a kimenet „nem”. Ez az algoritmus nyilvánvalóan tetszőleges bemeneti gráf esetén véges sok lépés alatt eldönti a kérdést. A gráf csúcsainak száma ugyanis véges, ezért a lehetséges színezések száma – amelyeket ugye egyenként ellenőrizni kell – is véges.
Ha most az előző részben ismertetett Turing-gép szintjén vizsgáljuk a kérdést, akkor a bemeneti gráfot egy valamilyen véges ábécé szimbólumaiból alkotott jelsorozat formájában kell a Turing-gép bemeneti szalagjára írni. Miután a Turing-gép végzett, a kimeneti szalagon ott lesz az „igen” vagy „nem” választ reprezentáló jelsorozat. Nyilvánvalóan szerkeszthető olyan Turing-gép erre a döntési feladatra, amely soha nem kerül végtelen ciklusba. Például a fenti, minden lehetséges színezést kipróbáló buta algoritmusunk „Turing-gépesített” változata. Az előző rész alapján elmondhatjuk tehát, hogy a 2-színezhető gráfok leírásaiból alkotott formális nyelv rekurzív, vagy más néven algoritmikusan eldönthető.
Ez mind szép és jó, a gond csak az, hogy viszonylag sokáig tart. Ha például Kompánia lakosainak száma 100 (ami azért nem túl sok), akkor 2100 lehetséges színezés van. Ha brutálisan gyors számítógépünk van, ami másodpercenként 100 milliárd színezést tud megvizsgálni, akkor is több, mint 400 milliárd évig tartana az algoritmus futása. Ennyi időt még akkor sem vagyunk hajlandók várni, ha nagyon nem szeretnénk egypártrendszert. Az algoritmusunk tehát hiába működik elméletben, a gyakorlatban használhatatlan.
Egy ennél némileg hatékonyabb eljárást ismertetünk az alábbiakban. Válasszunk ki egy tetszőleges csúcsot, és színezzük ki 0-val. Az már biztos, hogy a kiszínezett csúcs szomszédait 1-gyel kell színeznünk, ezért színezzük is ki őket. És így tovább, az eddig már kiszínezett csúcsok összes, eddig még ki nem színezett szomszédját színezzük mindig ellenkező színnel. Folytassuk ezt az eljárást addig, ameddig minden csúcsot ki nem színeztünk. Ekkor az algoritmus eredménye legyen „igen”. Előfordulhat, hogy menet közben találunk egy olyan csúcsot, amelyet ha kiszíneznénk az épp soron következő színnel, akkor megsértenénk a színezési szabályt. Ekkor az algoritmus eredménye legyen „nem”. Könnyen belátható, hogy ez az algoritmus is helyes eredményt fog adni. Vizsgáljuk meg az időkomplexitását, amely ugye a szükséges lépések számát jelenti.
Az eljárás lépésszáma arányos a gráfban lévő élek számával. A legrosszabb eset nyilván az, amikor minden csúcs minden más csúccsal össze van kötve. Ekkor van ugyanis a gráfban a lehető legtöbb él. Ebben a legrosszabb esetben tehát egy n csúcsú gráfnak egészen pontosan
\dfrac{n\cdot (n-1)}{2}darab éle van. Azaz az eljárásunk a 100 lakosú Kompánia utálatgráfjára legfeljebb 4950 lépés alatt végez. Egy számítógéppel ez egy pillanat alatt elvégezhető, ezért ez már valóban egy használható algoritmus. Most hasonlítsuk össze az előbbi „buta” és az utóbbi „okos” algoritmus időkomplexitását általánosságban.
Az algoritmusok időkomplexitásának mérése
Vegyük észre, hogy gyakorlatilag lényegtelen, hogy a két algoritmust egy primitív Turing-gép leírásának szintjén, vagy a fenti magasabbszintű leírások alapján vizsgáljuk. A kettő között csak annyi a különbség, hogy mit tekintünk elemi lépésnek. Elképzelhető, hogy egy Turing-gép primitív lépéseiben számolva az előző szakaszban kiszámolt lépésszámoknak a többszörösét kapnánk. Az azonban elmondható, hogy ez a szorzó tényező nem, vagy csak elhanyagolható mértékben függ a bemeneti gráf méretétől. Feltéve persze, hogy értelmes formában írtuk le a Turing-gép bemeneti szalagján a gráfot a használt ábécé szimbólumaival.
Egy algoritmus komplexitásának mérésekor tehát elsősorban nem konkrét lépésszámokra vagyunk kíváncsiak. Ilyenkor alapvetően az a lényeges számunkra, hogy a bemenet méretének növelésével milyen gyorsan növekszik a végrehajtáshoz szükséges lépésszám. Ezt az algoritmus skálázódásának nevezzük. Egy olyan „vízválasztót” keresünk tehát, amely elválasztja egymástól a „gyors” és a „lassú” algoritmusokat.
Jelöljük a bemenet méretét n-nel. Azt, hogy n adott esetben pontosan mire vonatkozik az határozza meg, hogy milyen szinten vizsgáljuk az algoritmust. Egy Turing-gép primitív szintjén például jelölheti a bemeneti jelsorozat szimbólumainak számát. Mi most egy ennél absztraktabb szinten vizsgáljuk a fenti két algoritmust. Gráfalgoritmusokról lévén szó, célszerű az n mennyiséget valamilyen módon a bemeneti gráf méretéhez kötni. Jelölje például n a gráf csúcsainak számát.
Célunk, hogy találjunk egy olyan n-től függő f(n) mennyiséget, amelyet a tényleges lépésszám biztosan nem fog meghaladni „elegendően nagy” n értékektől kezdve. Más szavakkal valamilyen módon felső becslést szeretnénk adni a szükséges lépésszámra a bemenet méretének függvényében.
Az első, „buta” algoritmusnál láttuk, hogy a lépésszám n csúcsú gráf esetén egy olyan mennyiséggel becsülhető felülről, amely 2^n-nel arányos. Az olyan függvényeket, ahol a változó mennyiség (amely jelen esetben n) a kitevőben is előfordul, exponenciális függvényeknek nevezzük. Ezzel szemben a második, „okos” algoritmus esetén a lépésszám egy n^2-tel arányos mennyiséggel becsülhető felülről. Az olyan függvényeket, ahol a változónak csak valamilyen rögzített kitevőjű hatványai fordulnak elő, polinomiális függvényeknek nevezzük. Mindkét függvénycsaládnak megvan az a tulajdonsága, hogy zárt a négy alapműveletre. Például két tetszőleges polinomiális függvény összege és szorzata is polinomiális, és ugyanez a zártság igaz az exponenciális függvényekre is.
Ezen kívül igaz az is, hogy bármilyen exponenciális függvény – feltéve, hogy az alapja 1-nél nagyobb – előbb-utóbb minden polinomiális függvénynél gyorsabban kezd el növekedni. Vegyük például az 1.1^n és az n^5 függvényeket. Az első egy 1-hez közeli alapú (tehát relatíve lassan növekvő) exponenciális függvény, a második pedig egy viszonylag magas kitevőjű (tehát relatíve gyorsan növekvő) polinomiális függvény. Az alábbi ábrán e két függvény grafikonja látható:
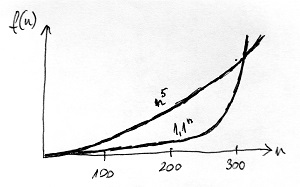
Látható, hogy kezdetben ugyan az exponenciális függvény a polinomiális függvény alatt marad, n\approx 300 körül azonban végül „beelőzi” azt, és onnantól már sokkal nagyobb sebességgel növekszik. De választhattunk volna egy még lassabban növekvő exponenciális függvényt (például 1.001^n) és egy még gyorsabban növekvő polinomiális függvényt (például n^{100}). Azokra ugyanúgy igaz lenne, hogy az előbbi „beelőzi” az utóbbit, maximum ez n magasabb értékénél következik be.
Ezek után a Turing-gép fogalmára lefordítva meg tudjuk adni egy algoritmus „hatékonyságát”. Tegyük fel, hogy egy probléma megoldására alkottunk egy Turing-gépet. Ha a probléma egy példányának reprezentációja (a fenti példában egy konkrét gráf leírása) a Turing-gép bemeneti szalagján n „betűből” áll, és a Turing-gép legfeljebb f(n) lépésben be tudja fejezni a számolást tetszőleges bemenetre, de ennél gyorsabban nem, akkor azt mondjuk, hogy a Turing-gép időkomplexitása f(n). Ha f(n) egy valamilyen polinomiális függvénnyel felülről becsülhető, akkor azt mondjuk, hogy a Turing-gép polinomiális időkomplexitású. Ha f(n) polinomiális függvénnyel nem, csak exponenciális függvénnyel becsülhető felülről, akkor a Turing-gép exponenciális időkomplexitású. A továbbiakban a „probléma” és a „formális nyelv” szavakat, valamint az „algoritmus” és a „Turing-gép” szavakat szinonimaként fogjuk használni. Az előző részben ugyanis láttuk, hogy ezek gyakorlatilag ugyanazt jelentik.
A gyakorlatban felmerülő problémák esetén egy algoritmus hatékonyságának általában egy jó vízválasztója az, hogy polinomiális vagy exponenciális időkomplexitású-e. Elképzelhető azonban, hogy a szóba jövő bemenet-méretek esetén jobb egy exponenciális időkomplexitású algoritmus, mint egy polinomiális. Az előző grafikonon például láthattuk, hogy egy relatíve lassan növő exponenciális függvény értéke egy ideig alatta maradhat egy relatíve gyorsan növő polinomiális függvény értékének. Amennyiben ez a két függvény két különböző algoritmus időkomplexitását jelöli, úgy elmondható, hogy az exponenciális algoritmus mindaddig hatékonyabb a polinomiálisnál, ameddig n értéke 300 alatt marad (bármit is jelentsen n a bemenet méretére vonatkozóan).
Amennyiben tudható, hogy a bemenet mérete biztosan az n<300 értéktartomány alatt fog maradni az algoritmus használata során, úgy nyilvánvalóan ebben a konkrét esetben sokkal jobban megéri az exponenciális algoritmust alkalmazni. Ettől függetlenül nagy általánosságban elmondható, hogy a polinomiális algoritmusokat tekinthetjük „hatékony”, míg az exponenciálisakat „rossz” algoritmusoknak.
A P problémaosztály
Most módosítsuk egy kicsit a Kompániára vonatkozó feladatunkat. Ezúttal ne 2, hanem 3 pártra próbáljuk meg szétosztani a lakosságot úgy, hogy az egy pártba kerülők ne utálják egymást. Az ide tartozó döntési probléma: kiszínezhetők-e egy adott gráf csúcsai 3 színnel úgy, hogy az azonos színű csúcsok között ne legyen él? Amennyiben ez megtehető egy adott gráfra, akkor azt mondjuk, hogy a gráf 3-színezhető.
Az alábbi gráf például nem színezhető ki 3 színnel:
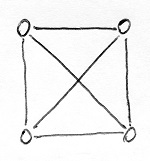
Ezzel szemben az alábbi gráf 3-színezhető, a csúcsokhoz rendelt számok pedig egy helyes 3-színezést jelölnek:

A korábbi, 2-színezhetőségre vonatkozó döntési problémára lehetett exponenciális és polinomiális időkomplexitású algoritmust is találni. A 3-színezhetőség eldöntésére azonban sajnos nem ismerünk exponenciálisnál gyorsabb algoritmust. Nem tudjuk, hogy létezik-e egyáltalán – csak esetleg még nem találta meg senki –, vagy pedig elméletileg sem létezhet ilyen algoritmus. Ha ez utóbbi a helyzet, akkor nem csak a jelenleg ismert algoritmusok „rosszak”, hanem maga a probléma is „nehéz”. Ezt jelenleg azonban csak sejtjük. Ezzel szemben a 2-színezhetőség eldöntése „könnyű”, mert létezik rá polinomiális algoritmus.
Egy másik gráfelméletből ismert fontos probléma az úgynevezett független csúcsok problémája. Elhelyezhető-e a sakktáblán 8 vezér úgy, hogy ne üssék egymást? Az alábbi ábra mutatja, hogy ez lehetséges, de aki maga próbálta ezt a rejtvényt megfejteni, tudja, hogy nem olyan könnyű egy ilyen elhelyezést megtalálni:

Ez a feladat is megfogalmazható a gráfok nyelvén. A sakktábla mezői legyenek a gráf csúcsai, és két csúcsot akkor kössünk össze éllel, ha az egyik mezőről a vezér egy lépéssel el tud jutni a másikba, azaz a másik mezőt „ütni” tudja. Az általános, már gráfokra vonatkozó probléma így szól: adott egy gráf és egy k egész szám, a kérdés pedig az, hogy ki lehet-e választani a gráfból k darab csúcsot úgy, hogy ezek között a csúcsok között ne legyen él. Ezt úgy mondjuk, hogy található-e a gráfban k darab független csúcs. Azokat a gráfokat, amelyekre ez teljesül, k-független gráfoknak nevezzük. A k-függetlenség eldöntésére sem ismert exponenciálisnál gyorsabb algoritmus, tehát ez is egy „nehéz” probléma, legalábbis annak tűnik.
Azokat a rekurzív nyelveket, amelyek eldöntésére létezik polinomiális időkomplexitású determinisztikus Turing-gép, egy osztályba soroljuk, amelyet P-vel jelölünk, és a polinomiális időben eldönthető nyelvek osztályának nevezünk. Lényegében az összes hatékonyan kezelhető döntési problémához tartozó nyelv P-beli. Ilyen volt például a 2-színezhetőségről szóló probléma. A 3-színezhetőség és a k-függetlenség problémájáról azonban nem tudjuk, hogy vajon P-ben vannak-e.
Amit viszont tudunk róluk, hogy – sok más rendkívül fontos algoritmikus problémával együtt – egy P-nél általánosabb problémaosztályba tartoznak. Ezért most ezzel a problémaosztállyal ismerkedünk meg. Ennek keretében felfrissítjük emlékeinket a 6. részben már említett nemdeterminisztikus Turing-gépekkel kapcsolatban.
Az NP problémaosztály
A nemdeterminisztikus Turing-gépek mindössze abban különböznek a determinisztikus Turing-gépektől, hogy ezek kerülhetnek olyan helyzetbe, amikor egynél több állapotváltási szabály előfeltétele is teljesül. Így ezekben a helyzetekben a gépünk választhat, hogy melyik szabályt fogja alkalmazni. Innen ered a neve is, ugyanis a gép további sorsa ezekben a helyzetekben nem determinált (nem egyértelműen meghatározott). Az alábbi ábrákon egy-egy olyan determinisztikus és nemdeterminisztikus Turing-gép futása látható, amelyek egy-egy x bemeneti jelsorozat adott nyelvbe tartozását döntik el (azaz az eredményük egy „igen” vagy egy „nem” válasz):
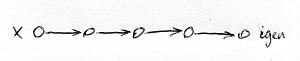
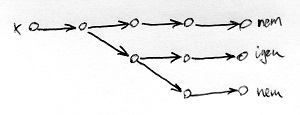
Az egyes csúcsok az adott Turing-gép különböző helyzeteit jelölik, amelyekbe a döntés meghozatala során kerül. Látható, hogy a determinisztikus Turing-gép mindig csak egy szabályt alkalmazhat, ezért a döntéshez vezető út egyértelmű. A nemdeterminisztikus testvére azonban a fenti példában 2 helyen is kétféle számítási úton folytathatja a futását. Tekintve, hogy a kimeneti szalagon megjelenő „igen” vagy egy „nem” válasz függhet attól, hogy végül melyik útvonalat választotta, a nemdeterminisztikus Turing-gépeket látszólag nem igazán lehet nyelvek felismerésére használni. Legalábbis nem abban az értelemben, ahogyan az előző részben definiáltuk a Turing-gép által felismert nyelvet. Az ott szereplő definíció determinisztikus Turing-gépekre vonatkozott, ezért most általánosítjuk ezt a definíciót a nemdeterminisztikus esetre is.
Tekintsünk most egy M nemdeterminisztikus Turing-gépet. Ha M összes lehetséges számítási útvonalát egyszerre vizsgáljuk, akkor kétféle eset lehetséges:
- Van legalább 1 olyan számítási útvonal, amely mentén a Turing-gép nem kerül végtelen ciklusba, és az eredmény „igen”.
- Ilyen számítási útvonal nincs, azaz a Turing-gép minden számítási útvonala vagy a „nem” válasszal végződik, vagy végtelen ciklusba kerül.
Az első esetben azt mondjuk, hogy a nemdeterminisztikus Turing-gép elfogadta az x jelsorozatot, míg a második esetben elutasította azt. Hasonlóan a determinisztikus Turing-gépek esetéhez, azok a bemeneti jelsorozatok, amelyeket a nemdeterminisztikus Turing-gép a fenti értelemben elfogad, egy részhalmazt alkotnak az összes bemeneti jelsorozat között. Ezt a részhalmazt a nemdeterminisztikus Turing-gép által felismert nyelvnek nevezzük és L_M-mel jelöljük.
Nyilván a nemdeterminisztikus esetben is csak azokkal a Turing-gépekkel érdemes foglalkoznunk, amelyek nem keverednek végtelen ciklusba egyetlen lehetséges számítási útvonalon sem. Másként fogalmazva ez azt jelenti, hogy a leghosszabb számítási útvonal hossza is felülről becsülhető valamilyen, a bemenet n hosszától függő véges f(n) mennyiséggel. Amennyiben ilyen felső becslésnek megadható egy polinomiális függvény, akkor azt mondjuk, hogy a nemdeterminisztikus Turing-gép polinomiális időkomplexitású.
Azokat a rekurzív nyelveket, amelyek eldöntésére létezik polinomiális időkomplexitású nemdeterminisztikus Turing-gép, egy osztályba soroljuk, amelyet NP-vel jelölünk, és a nemdeterminisztikusan polinomiális időben eldönthető nyelvek osztályának nevezzük (innen ered tehát az NP rövidítés). A P nyelvosztály nyilván része NP-nek, ha ugyanis egy nyelv determinisztikus Turing-géppel eldönthető polinomiális időben, akkor nemdeterminisztikus Turing-géppel „méginkább” eldönthető.
Jogosan vetődhet fel az Olvasóban a kérdés, hogy mi értelme nemdeterminisztikus döntési algoritmusokkal foglalkozni, amikor ez nem egy realisztikus számítási modell. Hiszen a számítási útvonalakat úgyis csak egyenként tudnánk „bejárni” egy valódi számítógéppel?
Emlékezzünk azonban, hogy az előző részben a Church-Turing tézis kapcsán már megemlítettük a kvantumszámítógépeket. Ezek egy olyan – most még többnyire csak elméletben létező – számítási modellt valósítanak meg, amely kihasználja az elemi részecskék szintjén jelentkező nagyon furcsa jelenségeket. Ezeket a kvantumfizika írja le, és nagyjából arról van szó, hogy egy elemi részecske nem feltétlenül van mindig egy adott állapotban, hanem bizonyos körülmények között egy úgynevezett szuperpozíciós állapotba kerülhet. Tegyük fel például, hogy egy ilyen részecske valamilyen irányú „pörgése” a bináris 1, a fordított irányú „pörgése” pedig a bináris 0 szimbólumot jelenti. Ezeket a „kvantumbit” kifejezés alapján qubit-eknek nevezzük. Amennyiben több qubit-et is sikerül szuperpozíciós állapotba hozni, úgy egy ilyen rendszer párhuzamosan tud számításokat végezni a qubit-állapotok összes lehetséges kombinációján.
Egy ilyen gép tehát nagyon hasonló számítási modellt valósítana meg, mint a nemdeterminisztikus Turing-gép, amelynek rengeteg párhuzamos számítási útvonalat kell egyszerre vizsgálnia. A fő technikai problémát az okozza, hogy a szuperpozíció egy nagyon érzékeny állapot, és a rendszer a legapróbb külső behatásra egy konkrét állapotba „zuhanhat”, véget vetve a kvantumszámításnak. Vannak egészen ígéretes eredmények, azonban ez a technológia még igencsak gyerekcipőben jár.
A P problémaosztályról szóló előző szakaszban megemlítettük, hogy a 3-színezhetőség és a k-függetlenség problémájáról – sok egyéb más, a gyakorlatban rendkívül fontos probléma mellett – nem tudjuk, hogy vajon P-beliek-e. Azt viszont nemsokára látni fogjuk, hogy ha P-be nem is tartoznak bele feltétlenül, az NP problémaosztályba azonban igen. Kérdés, hogy hogyan tudjuk bizonyítani egy döntési problémáról – pontosabban az őt reprezentáló formális nyelvről –, hogy NP-beli. Ez ugyanis igen nehézkesnek tűnik a fenti, nemdeterminisztikus számítási modellre építő definíció alapján. Ezért most megismerkedünk az NP nyelvosztály egy másik definíciójával, amely a sokkal könnyebben kezelhető determinisztikus Turing-gépekre épít.
A tanú-tétel
Képzeljük el, hogy a 3-színezhetőség eldöntését próbáljuk megoldani egy konkrét, viszonylag nagy gráfra. Hatékony algoritmus hiányában helyzetünk reménytelennek tűnik. Tegyük fel azonban, hogy valahonnan hozzájutunk egy olyan plusz információhoz, amelynek helyességét már hatékonyan le tudjuk ellenőrizni. Például támad egy sejtésünk, vagy valaki megsúg nekünk bizonyos információkat a megoldásról. Ezt a plusz információt tanúnak (vagy súgásnak) nevezzük. A tanúval szemben két fontos követelményünk van:
- Ne legyen túl hosszú az eredeti bemenet méretéhez képest. Ez pontosabban fogalmazva azt jelenti, hogy ha az eredeti bemeneti jelsorozat x, a tanút leíró jelsorozat pedig t, akkor megköveteljük, hogy t hossza x hosszának legfeljebb polinomiális függvénye legyen.
- Megköveteljük továbbá, hogy a tanú helyessége legyen leellenőrizhető polinomiális időkomplexitású DETERMINISZTIKUS Turing-géppel.
A „súgás” elnevezés arra utal, hogy e plusz információnak csak a létezése a feltétel. Annak eredetével kapcsolatosan azonban nincs semmilyen kiszámíthatósági feltételezésünk. Az olyan döntési problémák osztályát szintén NP-vel jelöljük, amelyek esetén az „igen” válasznak létezik hatékonyan ellenőrizhető tanúja.
A tanú-tétel azt állítja, hogy a NEMDETERMINISZTIKUSAN polinomiális eldönthetőségre, és a DETERMINISZTIKUSAN polinomiális ellenőrizhetőségre épülő két látszólag teljesen különböző definíció ugyanazt a nyelvosztályt határozza meg, így mindegy, hogy melyiket nevezzük NP-nek. Mielőtt a bizonyítás vázlatára rátérnénk, nézzük meg egy konkrét példán, hogy hogyan kell értelmezni a tanú fogalmára épülő definíciót.
A már említett 3-színezhetőség eldöntése reménytelenül nehéz feladatnak tűnik, ha csak a bemeneti gráf áll rendelkezésre. Ha azonban kapunk hozzá egy konkrét színezést, mint tanút (vagy más néven súgást), annak helyessége már könnyen leellenőrizhető. Továbbá az is nyilvánvaló, hogy csak a 3-színezhető gráfokhoz létezik helyes színezés, azaz tanú. Végezetül, egy színezés leírható a bemeneti gráf méretéhez képest „nem túl hosszan”, hiszen csak az egyes csúcsokhoz rendelt színeket kell felsorolni. Ehhez hasonlóan a k-függetlenség problémája esetén k darab független csúcs felsorolása szintén megfelelő tanú, hiszen könnyen leellenőrizhető, hogy azok valóban függetlenek-e. A 3-színezhetőség és a k-függetlenség problémája tehát a második definíció alapján mindketten az NP problémaosztályba tartoznak.
Egy NP-beli L nyelv esetén egy adott x bemeneti jelsorozat L-be tartozásának eldöntése felfogható egy bírósági analógiával is. Képzeljünk el egy bírót, aki elé oda kerül az x jelsorozat, mint vádlott. A vád az, hogy x mondata az L nyelvnek. A kérdés eldöntésére a bírónak polinomiális időkorlátja van, azaz kissé türelmetlen, és segítségre van szüksége, hogy időben meg tudja hozni az ítéletet. Ekkor jelentkezik egy rejtélyes tanú, aki terhelő vallomást tesz az x vádlottra. A bírónak így csak ellenőriznie kell, hogy a vallomás tényleg bizonyítja-e a vádat. Nem kell azonban foglalkoznia a tanú megkeresésével, amely mai tudásunk szerint sok fontos esetben nem is tehető meg polinomiális időben.
Látható, hogy ez a tanú fogalmára építő második definíció igen hasznos, hiszen segítségével lényegesen könnyebben tudjuk bizonyítani adott nyelvekre, hogy NP-beliek, mintha a nemdeterminisztikus Turing-gépekkel kellene szórakoznunk. Ahhoz azonban, hogy ezt a piszkos kis trükköt legálisan használhassuk, még bizonyítanunk kell a tanú-tételt.
Először azonban fogalmazzuk meg újra a tanú-tétel állítását, de ezúttal a matematika nyelvén. Bonyolultnak fog tűnni, de valójában ugyanarról van szó, mint amiről eddig beszéltünk. Érdemes végigkövetni, hogy szokjuk egy kicsit ezt a szigorú nyelvezetet.
Tegyük fel, hogy adva van egy L nyelv, és azt szeretnénk bizonyítani, hogy ez a nyelv NP-ben van-e vagy nem. Az NP nyelvosztály első definíciója alapján tehát keresnünk kellene egy olyan polinomiális időkomplexitású NEMDETERMINISZTIKUS Turing-gépet, amely eldönti az L-be tartozást, vagy pedig bizonyítani, hogy ilyen Turing-gép nem létezik. Mi nem ezt az utat fogjuk választani az NP-beliség eldöntésére, ugyanis nem szeretnénk nemdeterminisztikus Turing-gépekkel bajlódni.
Ehelyett L-ből konstruálni fogunk egy másik K nyelvet, és azt fogjuk vizsgálni, hogy ez a K nyelv eldönthető-e polinomiális időkomplexitású DETERMINISZTIKUS Turing-géppel (azaz, hogy P-beli-e). Most nézzük meg, hogy milyen jelsorozatokat tartalmazzon ez a K nyelv.
Tartalmazzon K olyan x és t jelsorozatokból álló párokat, amelyeknél t hossza az x hosszának legfeljebb polinomiális függvénye, azaz t ne legyen „túl hosszú” x-hez képest. Hogy az éppen használt ábécé segítségével hogyan lehet ilyen párokat leírni, az most részletkérdés. A lényeg, hogy a pár összetevőit (tehát az x és t jelsorozatokat) egyértelműen be lehessen azonosítani a K-beli szavakban. Mi a továbbiakban az (x,t) jelölést fogjuk használni ezekre a párokra, függetlenül attól, hogy ez konkrétan hogyan néz ki a K nyelv ábécéjével leírva. A t jelsorozatot az x jelsorozat tanújának fogjuk nevezni.
Teljesüljön ezen kívül a K és L nyelvekre a következő: egy tetszőleges x jelsorozat akkor és csak akkor tartozzon L-be, ha létezik olyan t tanú, amely esetén az (x,t) jelsorozat K-ba tartozik. Amennyiben ilyen tanú nem létezik egy adott x-hez, akkor x ne tartozzon L-be. Mégegyszer hangsúlyozzuk, hogy a tanúnak csak a létezése a feltétel. A megtalálásának mikéntjéről nem feltételezünk semmit, de azt gondoljuk, hogy az „nehéz”.
A tanú-tétel ezek után a következőt állítja: az L nyelv akkor és csak akkor van NP-ben, ha a K nyelv P-ben van. Vegyük észre, hogy ha ez igaz, akkor egy nemdeterminisztikus Turing-gép létezésének bizonyítása helyett egy determinisztikus Turing-gép létezését kell bizonyítanunk egy nyelv NP-beliségének eldöntéséhez, ami sok esetben jóval egyszerűbb. Most vizsgáljuk meg, hogy miért igaz ez a tétel.
A tanú-tétel bizonyítása (vázlat)
Itt csak a tanú-tétel bizonyításának alapötletét ismertetjük, a részletek ugyanis főként technikai jellegűek, és csak elterelnék a figyelmet a gondolatmenetről.
Tekintve, hogy ez egy „akkor és csak akkor” típusú állítás, ezért a bizonyítás két részből fog állni. Egyrész bizonyítani kell, hogy ha a K nyelv P-ben van, akkor az L nyelv NP-beli. Másrészt azt is bizonyítani kell, hogy az L nyelv NP-belisége semmilyen más esetben nem fordulhat elő, csak akkor, ha a K nyelv P-beli. Másként fogalmazva bizonyítani kell a másik irányú következtetést is, azaz azt, hogy ha az L nyelv NP-ben van, akkor a K nyelv P-beli.
Kezdjük ez utóbbival, azaz tegyük fel az L nyelvről, hogy NP-ben van. Ez azt jelenti, hogy polinomiális időkomplexitású nemdeterminisztikus Turing-géppel eldönthető, ezért bármely, a nyelvbe tartozó x jelsorozathoz (de csak azokhoz) létezik legalább 1 olyan számítási útvonal, amelyet követve a számolás végeredménye az „igen” válasz. Az alábbi ábrán egy ilyen útvonal látható:
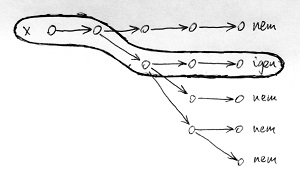
Építsünk most egy olyan determinisztikus Turing-gépet, amely az x bemeneten kívül megkapja még ennek az útvonalnak a leírását is valamilyen formában. Jelöljük ezt a gépet M-mel. Az M gép legyen olyan, hogy szimulálja a nemdeterminisztikus testvérének működését, de minden olyan szituációban, ahol a nemdeterminisztikus gép számítási útvonala elágazik, M a kapott útvonal-leírás szerinti úton haladjon tovább a számítással. A technikai részleteket az Olvasóra bízom, de viszonylag könnyen belátható, hogy egyrészt az útvonal leírható „nem túl hosszan”, azaz úgy, hogy hossza az x bemenet hosszának polinomiális függvénye legyen. Másrészt szintén viszonylag könnyen belátható, hogy az M determinisztikus Turing-gép időkomplexitása szintén polinomiális, tekintve hogy az eredeti nemdeterminisztikus gép időkomplexitása is polinomiális volt.
Ez azt jelenti, hogy az útvonal leírása megfelel a tanúval szemben támasztott követelményeknek. Ezen kívül az is igaz, hogy csak azokra az x jelsorozatokhoz van ilyen tanú, amelyek L-ben vannak. Az eredeti nemdeterminisztikus Turing-gép ugyanis az egyéb jelsorozatokat nem fogadja el, így az ilyen jelsorozatokra nincs „igen” végződésű számítási útvonal, következésképp az azt leíró tanú sem létezhet.
A tanú tétel másik felének bizonyításához azt kell belátni, hogy ha az L nyelvhez tartozó jelsorozatokhoz (de csak azokhoz) létezik tanú a fenti értelemben, akkor az L nyelv polinomiális időkomplexitású nemdeterminisztikus Turing-géppel eldönthető. Vegyünk tehát egy tetszőleges x bemeneti jelsorozatot, és építsünk egy olyan nemdeterminisztikus gépet, amely x-et elfogadja, ha az L nyelvhez tartozik, és elutasítja, ha nem.
Azt mondtuk, hogy az x jelsorozat akkor és csak akkor tartozik L-hez, ha létezik hozzá egy ezt bizonyító tanú. Ha tehát a készülő gépünk végig tudná vizsgálni az összes olyan jelsorozatot, amely tanúként szóba jöhet, akkor el tudná dönteni az x jelsorozat L-be tartozását is. Szerencsére az ilyen lehetséges tanúkból véges sok van, mivel azt mondtuk, hogy a tanú „nem túl hosszú” x-hez képest. Ha például az x jelsorozat hossza n szimbólum, akkor a keresett tanú – ha egyáltalán létezik – maximum f(n) darab szimbólummal leírható, ahol f egy valamilyen rögzített polinomiális függvény.
A készülő nemdeterminisztikus gépünknek tehát nincs más dolga, mint különböző számítási útvonalakon előállítani az összes lehetséges tanújelöltet, és mindegyik számítási útvonalon leellenőrizni, hogy az adott tanújelölt bizonyítja-e az x jelsorozat L-be tartozását. Ehhez az ellenőrzéshez pedig használhatja a feltételünk szerint létező polinomiális időkomplexitású determinisztikus Turing-gépet. Tegyük fel például, hogy a bináris ábécét használjuk, és az x jelsorozat hosszúsága alapján maximum 3 szimbólum hosszú tanújelöltek jöhetnek szóba. Ekkor a nemdeterminisztikus gépünk számítási útvonalai a következőképpen alakulnak:
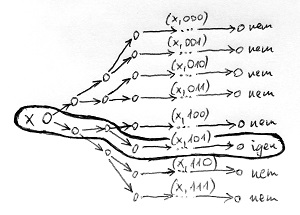
A működés első felében annyiszor ágazik el minden útvonal, ahány szimbólumból a lehetséges tanújelöltek állnak. Erről ugye tudjuk, hogy az x bemenet hosszának polinomiális függvénye. A működés második felében – miután minden lehetséges tanújelölt előállt valamelyik útvonalon – le kell futtatni mindegyik számítási ágon az adott t tanút ellenőrző polinomiális időkomplexitású determinisztikus Turing-gépet, azaz innentől kezdve már nem fognak tovább ágazni az útvonalak. Ennek a szakasznak a hossza ugye az (x,t) összetett jelsorozat hosszának polinomiális függvénye.
Az így megkonstruált nemdeterminisztikus Turing-gépnek az összlépésszáma tehát végsősoron szintén az eredeti x bemenet hosszának polinomiális függvénye az összes lehetséges számítási útvonalon. Az is igaz továbbá, hogy ez a gép akkor és csak akkor fogja elfogadni az x bemenetet, ha van „igen” végződésű számítási útvonala. Ez viszont akkor és csak akkor lehetséges, ha az x jelsorozathoz létezik az ő L-be tartozását bizonyító tanú.
Ezzel bizonyítottuk az NP nyelvosztály kétféle definíciójának ekvivalenciáját. A továbbiakban tehát nyugodtan használhatjuk a tanú létezését megkövetelő definíciót, amikor egy adott nyelv NP-be tartozását akarjuk igazolni.
Most pedig rátérhetünk a számítástudomány egyik legfontosabb megoldatlan problémájára.
Az egymillió dolláros megoldatlan probléma
Az nyilvánvaló, hogy a P problémaosztály mind az első, mind pedig a második definíció alapján is része az NP problémaosztálynak. Ha ugyanis a bíró maga is meg tudja oldani a feladatot polinomiális időben, akkor nincs más dolga, mint a kapott megoldást összehasonlítani a tanú „vallomásával”, és „igen”-t ítélni egyezés esetén.
Érdekes kérdés viszont, hogy vajon valódi tartalmazásról van-e szó, vagy a két problémaosztály valójában egy és ugyanaz lenne? Vajon ha egy feladat megoldásának az ellenőrzésére van hatékony eljárás, akkor szükségképpen létezik-e hatékony eljárás magának a megoldásnak a megtalálására is? Amennyiben ez igaz lenne, annak rendkívül messzemenő következményei lennének nemcsak a matematika számos területén, hanem más tudományokban is.
A választ nem tudjuk, de alapos okunk van feltételezni, hogy P \neq NP, azaz vannak nemcsak nehéznek tűnő, hanem valóban nehezen megoldható, viszont hatékonyan ellenőrizhető feladatok. Ez jelenleg a számítástudomány, de talán az egész matematika egyik legfontosabb megválaszolatlan kérdése. A P \neq NP-sejtés egyike az úgynevezett Millenniumi Problémáknak is. Ez hét olyan matematikai problémát takar, amelyek megoldására 2000-ben magas pénzjutalommal járó díjat alapított az amerikai Clay Matematikai Intézet. Ezek közül hat még mindig megfejtésre vár – köztük a P \neq NP-sejtés is –, amelyekért a dicsőségen túl egyenként egymillió amerikai dollár is jár.
Az alábbi két ábrán az eddig megismert „bonyolultságtérképünk”, valamint az ebben a részben bemutatott 2-színezhetőség, 3-színezhetőség és k-függetlenség problémájának elhelyezkedése látható ezen a térképen a P \neq NP sejtésre adható két lehetséges válasz esetére:
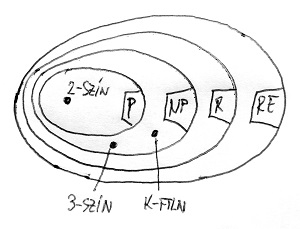
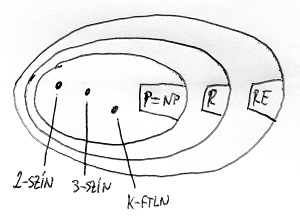
A következő részben megismerkedünk egy fontos fogalommal, amelynek a segítségével az algoritmikus problémákat össze tudjuk majd hasonlítani „nehézség” szempontjából. Ennek kapcsán megismerkedünk az NP problémaosztály „krémjével”, azokkal a problémákkal, amelyek bizonyos tekintetben a legnehezebb NP-beli feladatoknak tűnnek. Ekkor fog világossá válni, hogy miért valószínűsítjük annyira, hogy P nem azonos NP-vel, még ha egzakt bizonyításunk nincs is erre. A kérdés többek között azért is rendkívül fontos, mivel a modern információbiztonsági és rejtjelezési eljárások 5. részben említett algoritmikus biztonsága alapvetően ezen áll vagy bukik.
A következő részt itt találod…



