Az előző részben tovább osztályoztuk az algoritmikusan eldönthető problémákat aszerint, hogy a döntés milyen hatékonysággal hozható meg. Azt mondtuk, hogy hatékonyság szempontjából az a vízválasztó, hogy egy problémára létezik-e polinomiális időkomplexitású algoritmus vagy nem. Mutattunk néhány problémát, amelyekre jelenleg nem ismeretes ebben az értelemben hatékony algoritmus. Megismerkedtünk a P és NP problémaosztályokkal. Előbbibe azokat a problémákat soroltuk, amelyek eldönthetőek polinomiális időkomplexitású determinisztikus Turing-géppel. Utóbbiba pedig azokat, amelyekkel ugyanez megtehető nemdeterminisztikus Turing-géppel.

A tanú-tételt ismertetve megmutattuk, hogy ez utóbbi ekvivalens azoknak a problémáknak az osztályával, amelyek esetén az „igen” válasznak létezik polinomiális időben ellenőrizhető bizonyítéka. Végül megemlítettük a számítástudomány legjelentősebb megválaszolatlan kérdését, miszerint vajon e két problémaosztály megegyezik-e, vagy az általunk nehéznek gondolt problémák valóban nehezek. Ennek megválaszolása ugyanis kulcsfontosságú a kriptográfia szempontjából. De még ha nem is tudjuk ezt a kérdést jelenleg megválaszolni, miért lehetünk majdnem biztosak abban, hogy P \neq NP? Hogyan tudjuk az algoritmikus problémák nehézségét összehasonlítani egymással? Melyek azok a problémák, amelyek minden más NP-beli problémánál nehezebbek ilyen értelemben? Ebben a részben erről lesz szó…

Figyelem! Erősen ajánlott elolvasni a 6. és a 7. részt az alábbiak megértéséhez. A teljes cikksorozat elejét itt találod.

Most visszanyúlunk az előző részben ismertetett két nehéznek gondolt döntési problémához. A 3-színezhetőség problémája így hangzott: adott egy gráf, amelyről el kell dönteni, hogy a csúcsai kiszínezhetők-e legfeljebb 3 színnel úgy, hogy a szomszédos csúcsok különböző színűek legyenek. Azokat a gráfokat, amelyekre ez teljesül, 3-színezhető gráfoknak neveztük. A k-függetlenség problémája pedig így hangzott: adott egy gráf és egy k egész szám, és azt kell eldönteni, hogy ki lehet-e választani a gráfból k darab csúcsot úgy, hogy ezek között a csúcsok között ne legyen él. Ezt úgy is mondhatjuk, hogy található-e a gráfban k darab független csúcs. Azokat a gráfokat, amelyekre ez teljesül, k-független gráfoknak neveztük.

Mivel mindkét fenti probléma igencsak fontos az informatikában, ezért eléggé fájó, hogy egyikre sem ismeretes polinomiális időkomplexitású – azaz hatékony – algoritmus. E két döntési probléma között azonban algoritmikus komplexitási kapcsolat mutatható ki. Nevezetesen: bizonyítható, hogy az egyik „legalább olyan nehéz”, mint a másik. Ez azt jelenti, hogyha a „nehezebbre” található polinomiális algoritmus, akkor a „könnyebbre” is. Megfordítva, ha a „könnyebbre” nem található polinomiális algoritmus, akkor a „nehezebbre” sem. De mit jelent pontosan, hogy egy döntési probléma „legalább olyan nehéz”, mint egy másik?

Problémák nehézségének összehasonlítása

Ennek megértéséhez döntési problémák helyett ismét az őket reprezentáló nyelvekre koncentrálunk, és bevezetjük az úgynevezett Karp-redukció fogalmát. Képzeljük el, hogy van két rekurzív nyelvünk, nevezzük őket L-nek és K-nak. Ezen kívül tegyük fel, hogy f egy olyan rekurzív függvény, amely az összes L-beli jelsorozathoz K-beli jelsorozatot, míg az összes L-en kívüli jelsorozathoz K-n kívüli jelsorozatot rendel. Az előző részben a tanú-tétel bizonyításánál alkalmazott „akkor és csak akkor” típusú mondatszerkezettel ez így fogalmazható meg: egy tetszőleges x jelsorozat akkor és csak akkor mondata az L nyelvnek, ha az f(x) jelsorozat mondata a K nyelvnek. Az alábbi ábrán egy ilyen tulajdonságú függvény által megvalósított hozzárendelés látható két konkrét jelsorozatra:

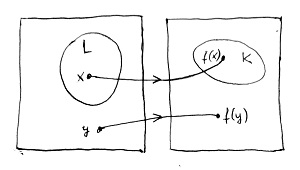
Az alábbi ábrán viszont egy olyan függvény látható, amely megsérti ezt a szabályt, mivel egy olyan y jelsorozatot is a K nyelvbe képez, amely nem mondata az L nyelvnek:

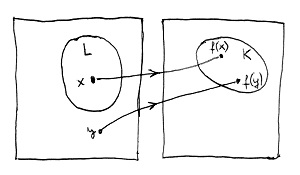
Mint ahogyan azt az előző részben már láttuk, az „akkor és csak akkor” a matematikában egy igen szigorú mondatszerkezet, és sokkal többet jelent annál, mint egy sima „ha … akkor” típusú mondat. A fenti „akkor és csak akkor” típusú állítás egyrészt azt jelenti, hogy ha egy x jelsorozat eleme az L nyelvnek, akkor az f(x) jelsorozat eleme a K nyelvnek. Ezen túlmenően azonban azt is jelenti, hogy ha egy x jelsorozat nem eleme az L nyelvnek, akkor az f(x) jelsorozat sem eleme a K nyelvnek (ez utóbbi tulajdonságot sérti meg a második ábrán látható függvény). Azaz vagy egyszerre mindkettő állítás teljesül, vagy egyik sem, de olyan nincs, hogy az egyik igen, a másik pedig nem. De miért is olyan jó dolog ilyen függvényt találni?

Képzeljük el azt a szituációt, hogy egy olyan algoritmust szeretnénk készíteni, amely eldönti az L nyelvbe tartozást, de sehogyan sem jövünk rá a megoldásra. Van viszont algoritmusunk a K nyelvbe tartozás eldöntésére. Ha sikerülne találnunk egy olyan rekurzív f függvényt, amely teljesíti a fenti tulajdonságot, akkor tulajdonképpen meglenne az algoritmusunk L eldöntésére is. Ha ugyanis egy x jelsorozatra el kell dönteni, hogy L-be tartozik-e, nincs más dolgunk, mint kiszámítani az f(x) jelsorozatot, majd erre a jelsorozatra lefuttatni a már létező, K-ba tartozást eldöntő algoritmust. Ennek „igen” vagy „nem” válasza egyben megválaszolja az x jelsorozat L-be tartozásának kérdését is az f függvény fenti tulajdonsága miatt. Ráadásul minden x jelsorozatra véges időn belül megkapjuk a választ, hiszen az f függvény rekurzív, tehát létezik olyan őt kiszámító Turing-gép, amely soha nem keveredik végtelen ciklusba.

Ha a fentieken kívül az f függvényre még az is teljesül, hogy polinomiális időkomplexitású Turing-géppel kiszámítható, akkor azt mondjuk, hogy az f függvény az L nyelv Karp-redukciója a K nyelvre. Ennek a fogalomnak a segítségével lényegében összehasonlíthatóvá válnak a döntési problémák a nehézségük szempontjából. Egy ilyen Karp-redukció létezése ugyanis azt jelenti, hogy az L nyelv felismerése nem lényegesen nehezebb, mint a K nyelv felismerése, leszámítva egy polinomiális időkomplexitású kis extra munkát, amit az f függvény kiszámítása jelent. Az L nyelv Karp-redukcióját a K nyelvre így jelöljük: L \prec K. Most példaként megadunk egy Karp-redukciót a 3-színezhetőség és a k-függetlenség eldöntésének problémája között.

Karp-redukció (példa)

Ehhez egy olyan polinomiális időkomplexitású algoritmust kell találnunk, amely egy tetszőleges G gráfból (azaz a 3-színezhetőség problémájának egy példányából) előállít egy H gráfot és egy k egész számot (azaz a k-függetlenség problémájának egy példányát), méghozzá úgy, hogy a H gráf akkor és csak akkor legyen k-független, ha a G gráf 3-színezhető. Az „akkor és csak akkor” mondatszerkezetet ismét a fentebb már említett szigorú értelemben kell venni.

A H gráf és a k egész szám előállítása G-ből (tehát maga a Karp-redukció) a következő: másoljuk le a G gráfot 3 példányban, és kössük össze azokat a csúcsokat éllel, amelyek ugyanannak az eredeti G-beli csúcsnak a másolatai. Az így kapott „nagy” gráf legyen a H, valamint k értéke legyen az eredeti G gráf csúcsainak száma. Az alábbi ábrán egy konkrét 5 csúcsú problémapéldány konverziója látható:

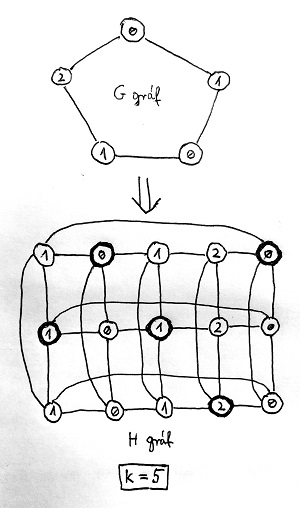
A fenti G gráf a 3-színezhetőség problémának egy konkrét példánya, a csúcsokhoz rendelt 0, 1 és 2 számok a G gráf egy konkrét színezését jelölik. Ebből a fenti Karp-redukció szerint képeztük a lenti H gráfot és a k egész számot, mint a k-függetlenség problémájának egy példányát. A H gráf vízszintes szintjei a G gráf kiterített másolatai, míg a függőleges irányítású élek azokat a csúcsokat kötik össze, amelyek ugyanannak a G-beli csúcsnak a másolatai.

Most kezdjünk el végigmenni a G gráf csúcsain szép sorban, és mindegyikhez jelöljük meg az ő G-beli színének megfelelő szinten lévő másolatát a H gráfban. A 0, 1 és 2 színeknek rendre a felső, a középső és az alsó szintek feleljenek meg. A fenti ábrán a megjelölt csúcsokat vastagított körökkel jelöltük. Ha tehát például egy G-beli csúcs színe 2, akkor jelöljük meg az ő H-beli másolatát az alsó szinten. Vegyük észre, hogy ebből épp k=5 darab van (hiszen a G gráfnak k=5 darab csúcsa volt).

Igaz továbbá, hogy a megjelölt csúcsok között nincs él a H gráfban, azaz függetlenek. Az adott szinten belüli él azért nincs közöttük, mivel ha lenne, akkor a G-beli megfelelőjük között is lenne, és így nem kaphatták volna ugyanazt a színt. Függőleges irányú él pedig azért nincs, mert mindegyik oszlopból csak egy csúcsot jelöltünk meg H-ban. Ez a gondolatmenet tetszőleges 3-színezhető G gráf tetszőleges színezésére működik. Azt tehát már tudjuk, hogy ha a G gráf 3-színezhető, akkor a H gráf k-független.

Vegyük észre továbbá, hogy a H gráf nem is lehet másként k-független, azaz a k-függetlenség valóban csak akkor teljesül, ha a G gráf 3-színezhető. Tegyük fel ugyanis, hogy a G gráf nem 3-színezhető (azaz minimum 4 szín kell a kiszínezéséhez). Ekkor a H gráfban sem lehet k darab független csúcs, hiszen ha lenne, akkor végigmehetnénk rajtuk, és mindegyikük G-beli eredetijét kiszínezhetnénk annak a H-beli szintnek megfelelő színnel, amelyben helyet foglalnak. Így viszont G-nek egy jó 3-színezését kapnánk, tehát G mégiscsak 3-színezhető lenne, és ez ellentmondana a feltételezésünknek.

Természetesen egy Turing-gép vagy valódi számítógép számára ennél jóval pontosabb leírást kéne adnunk a fenti „átalakító” algoritmusra. A lényegen azonban ez nem változtatna. Most vizsgáljuk meg ennek az „átalakító” algoritmusnak a lépésszámát. Könnyen látható, hogy az a bemeneti G gráf méretének polinomiális függvénye. Hiszen ha G csúcsainak száma n, éleinek száma pedig e, akkor a belőle létrehozott H gráf 3n darab csúcsot és 3n+3e darab élet fog tartalmazni. Másrészt k értéke is könnyen számítható, hiszen csak meg kell számolni G csúcsait. A fenti „átalakító” algoritmus tehát valóban egy a Karp-redukció a 3-színezhetőségről a k-függetlenség problémájára.

Az NP problémaosztály krémje

A Karp-redukció fogalmának segítségével tehát egy adott L nyelv felismerésének feladatát vissza lehet vezetni egy másik K nyelv felismerésének feladatára. Egy L \prec K Karp-redukció létezése azt jelenti számunkra, hogy az L nyelv felismerése nem lényegesen nehezebb a K nyelv felismerésénél, leszámítva egy polinomiális időkomplexitású extra munkát. Ebből következik, hogy ha K felismerésére van polinomiális idejű algoritmusunk, akkor L-re is van. Fordítva: ha L-re nincs polinomiális algoritmus, akkor K-ra sincs. Az NP nyelvosztály érdekes tulajdonsága, hogy léteznek benne ilyen értelemben „legnehezebb” nyelvek (döntési feladatok). Ezt világítjuk meg a következő definícióval.

Tegyük fel, hogy K egy NP-beli nyelv. Amennyiben tetszőleges, szintén NP-beli L nyelv esetén létezik L \prec K Karp-redukció, akkor azt mondjuk, hogy a K nyelv NP-teljes. Az NP-teljes nyelvek felismerése tehát „legalább olyan nehéz”, mint bármilyen más NP-beli nyelv felismerése. Amennyiben a kérdéses K nyelvtől nem követeljük meg, hogy maga is NP-ben legyen, úgy a K nyelvet NP-nehéznek nevezzük. Az NP-teljes nyelvek tehát olyan speciális NP-nehéz nyelvek, amelyek maguk is NP-ben vannak.

A fenti definíció egyszerű következménye, hogy amennyiben akár egyetlen NP-teljes nyelv eldöntésére is találnánk polinomiális algoritmust, abból következne, hogy P=NP. Ha ugyanis akár egyetlen egy NP-teljes K nyelv is a P osztályban lenne (azaz felismerhető lenne polinomiális időkomplexitású algoritmussal), úgy minden NP-beli L nyelv szintén a P osztályban lenne, hiszen az L \prec K Karp-redukció létezése miatt ebben az esetben az L nyelvet is fel tudnánk ismerni polinomiális algoritmussal. De megfordítva is igaz: amennyiben akár egyetlen NP-teljes nyelvről is kiderülne, hogy nem létezik őt felismerő polinomiális algoritmus, abból következne – azon kívül, hogy nyilván P \neq NP lenne –, hogy egyetlen NP-teljes nyelv felismerésére sem létezik polinomiális algoritmus. Ha ugyanis egy NP-teljes L nyelvről bebizonyosodna, hogy a P osztályon kívül van, akkor nem létezhet olyan NP-teljes K nyelv, ami P-ben van, hiszen különben az L \prec K Karp-redukció létezése miatt az L nyelvet is fel tudnánk ismerni polinomiális algoritmussal.

Vagyis minden NP-teljes nyelv vagy egyszerre polinomiális vagy egyszerre exponenciális időkomplexitású. Rendkívül sok algoritmikus probléma vezethető vissza NP-teljes nyelvek felismerésének feladatára. Éppen ezért eléggé bosszantó, hogy eddig – számtalan próbálkozás ellenére – egyetlen ilyen nyelvről sem tudtuk bizonyítani egyik eshetőséget sem. Az alábbi ábrán az eddig megismert bonyolultsági osztályok egymáshoz való viszonya látható a P \neq NP sejtésre adható két lehetséges válasz esetére:

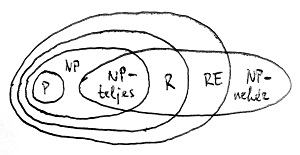
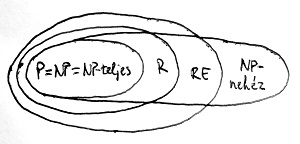
E két eshetőség közül a legtöbb matematikus az első elrendezést valószínűsíti. A gyakorlatban is előforduló algoritmikus feladatok között ugyanis nagyon gyakoriak az NP-teljes problémák. A szakirodalomban dokumentált NP-teljes feladatok száma jóval ezer felett van. Azonban ezek intenzív vizsgálata ellenére sem tapasztalható a polinomiális algoritmusok irányába történő legcsekélyebb előrehaladás. Így meglehetősen furcsa lenne, ha kiderülne, hogy ezek mindegyikére létezik hatékony algoritmus. Most mutatunk néhány, a gyakorlatban fontos algoritmikus optimalizálási feladatot, amelyek mind NP-teljes döntési problémákhoz vezetnek.

NP-teljes és NP-nehéz problémák

Az alábbiakban néhány olyan, az informatikában is gyakran felmerülő optimalizálási feladatot ismertetünk, amelyek NP-teljes döntési problémákra vezethetők vissza.

Maximális méretű klikk keresése gráfokban

Gráfokról az előző részben már volt szó. Egy gráfban klikknek nevezünk egy olyan csúcshalmazt, amelyen belül bármely két csúcs között van él. A feladat egy adott gráfban megtalálni a legnagyobb klikket. Például az alábbi gráfban a legnagyobb klikk 4 csúcsból áll. Ezeket tele körökkel jelöltük:

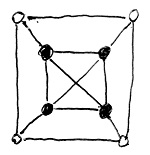
Az ehhez a feladathoz tartozó döntési probléma így hangzik: adott egy G gráf és egy k egész szám. Az eldöntendő kérdés: létezik-e G-ben k-nál nagyobb méretű klikk?

Leghosszabb útvonal keresése gráfokban

Adott egy gráf és annak két csúcspontja, amelyek között a lehető leghosszabb (legtöbb élből álló) útvonalat kell megtalálni. Fontos kikötés, hogy az útvonal során a gráf minden csúcsát legfeljebb 1-szer érinthetjük. Azaz egy már bejárt csúcshoz nem térhetünk vissza mégegyszer. Ez a kikötés érthető is, hiszen különben egy így kialakuló kör mentén haladva tetszőlegesen hosszú útvonal is létezne. Az alábbi ábrán látható példa gráfon vastagított vonallal jelöltük az a és b csúcsok közötti leghosszabb útvonalat:

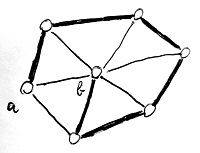
Az ehhez a feladathoz tartozó döntési probléma így hangzik: adott egy G gráf és egy k egész szám. Az eldöntendő kérdés: létezik-e G-ben k-nál hosszabb útvonal?

Ez a döntési probléma NP-teljes, érdekes ugyanakkor, hogy a legrövidebb útvonal megtalálására viszont léteznek polinomiális időkomplexitású algoritmusok. A legismertebb példák a használatukra a különböző navigációs alkalmazások útvonalkeresői. Az egyik legismertebb ilyen eljárás a Dijkstra-algoritmus.

Gráfok színezése

Gráfok színezéséről az előző részben már volt szó. A feladat egy adott gráf csúcsait a lehető legkevesebb szín felhasználásával kiszínezni oly módon, hogy bármely két szomszédos csúcs különböző színű legyen.

Az ehhez a feladathoz tartozó döntési probléma így hangzik: adott egy G gráf és egy k egész szám. Az eldöntendő kérdés: kiszínezhető-e G legfeljebb k darab szín felhasználásával?

Az előző részben már említettük, hogy k=3 esetén ennek eldöntésére jelenleg nem ismert polinomiális időkomplexitású algoritmus. Ráadásul nem is várható, hogy bárki felfedez ilyen algoritmust, ugyanis k>2 esetén ez a döntési probléma is NP-teljes.

Független csúcshalmaz keresése gráfokban

A független csúcsok problémájáról szintén az előző részben volt szó. A feladat egy adott gráf csúcsai közül kiválasztani a lehető legtöbbet úgy, hogy ezek között ne legyen két egymással szomszédos csúcs.

Az ehhez a feladathoz tartozó döntési probléma így hangzik: adott egy G gráf és egy k egész szám. Az eldöntendő kérdés: létezik-e G-ben legalább k darab csúcsot tartalmazó független csúcshalmaz?

Az előző részben már említettük, hogy k>1 esetén ennek eldöntésére sem ismert polinomiális időkomplexitású algoritmus. Valószínű, hogy nem is létezik, ugyanis ez a döntési probléma is NP-teljes.

Az utazóügynök-probléma (egyszerűsített változat)

A feladat egy adott gráfban olyan útvonal keresése, amely minden csúcson pontosan egyszer halad keresztül, és végül a kiindulópontba jut vissza. Az ilyen útvonalakat Hamilton-köröknek nevezzük.

Az ehhez a feladathoz tartozó döntési probléma így hangzik: adott egy gráf, és el kell dönteni, hogy létezik-e benne Hamilton-kör. Ez a döntési probléma is NP-teljes.

Az utazóügynök-probléma a logisztikai problémákon túl nagy gyakorlati jelentőséggel bír például a nyomtatott áramkörök gyártása során alkalmazott fúrórobotok ideális mozgásának megtervezésében. De ezen kívül is rengeteg optimalizálási feladat vezethető vissza rá.

A hátizsák-probléma

Adott valahány darab tárgy, mindegyiknek meg van adva a súlya és az értéke, valamint adott egy valamilyen teherbírású hátizsák. A feladat a tárgyakból minél nagyobb összeértékű részhalmazt belepakolni a hátizsákba úgy, hogy ne lépjük át a súlyhatárt. Ezzel rokon probléma, amikor különböző méretű dobozokat kell bepakolni egy adott méretű szekrénybe úgy, hogy minél jobban kihasználjuk a rendelkezésre álló helyet. Ki ne bosszankodott volna például, amikor nyaralás előtt minél több mindent szeretett volna bepakolni a csomagtartóba? Most már tudjuk, hogy a bosszankodás oka az volt, hogy ez is egy NP-teljes döntési problémához vezet.

Az NP-nehéz problémák kezelése

Jogosan merül fel a kérdés, hogy mitévők legyünk akkor, ha munkánk során olyan problémába ütközünk, amely bizonyítottan NP-nehéz. Ez ugyanis viszonylag gyakran előfordul, mégsem kell ezen problémák megoldásáról teljesen lemondanunk.

Az egyik lehetőség, hogy megvizsgáljuk, milyen méretű bemenetek várhatók a gyakorlati alkalmazás során, és olyan exponenciális időkomplexitású algoritmust keresünk, amely e bemenetméretek esetén is elfogadható idő alatt lefut.

Előfordulhat az is, hogy egy, a gyakorlatban felmerülő NP-nehéz problémáról kiderül, hogy valójában csak egy speciális esetét kell kezelnünk, amire már elképzelhető, hogy létezik polinomiális algoritmus.

Bevett módszer az is, hogy a problémára optimális, de lassú eljárás helyett az optimumnál rosszabb eredményt produkáló, de gyors algoritmust próbálunk keresni. Amennyiben bizonyítani tudjuk, hogy a gyors algoritmus eredményének az optimálistól való eltérése adott korlát alatt marad, úgy közelítő algoritmusról beszélünk.

Végül előfordulhat, hogy sikerül gyors algoritmust találnunk, amely közelíti ugyan az optimumot, de nem tudjuk bizonyítani azt, hogy a közelítés hibája adott korlát alatt marad, azonban a tapasztalat azt mutatja, hogy megfelelő eredményt ad a legtöbb esetben. Ezeket heurisztikus algoritmusoknak nevezzük.

A Cook-Levin tétel

A most következő egyszerű tétel hasznos eszköz, ha egy nyelv NP-teljességét szeretnénk bizonyítani. Ha egy L nyelv NP-teljes, egy K nyelv pedig NP-ben van, valamint létezik egy L \prec K Karp-redukció, akkor a K nyelv is NP-teljes. Az NP-teljesség tehát a Karp-redukción keresztül „öröklődik”.

Ez azt jelenti, hogy egy K nyelv NP-teljességének bizonyításához nem szükséges, hogy redukáljuk az összes NP-beli nyelvet K-ra, elegendő ezt megtenni egyetlen NP-teljes nyelvvel. Vegyünk ugyanis egy tetszőleges NP-beli X nyelvet. Mivel a fenti tételbeli L nyelv NP-teljes, ezért az X nyelv felismerését polinomiális idejű extra munkával redukálni tudjuk az L nyelv felismerésére. Ha az L nyelv felismerését szintén polinomiális időben tovább tudjuk redukálni a K nyelv felismerésére, akkor e két redukció egymás utáni alkalmazásával tulajdonképpen az X nyelvet is redukálni tudjuk K-ra polinomiálisan, azaz K valóban NP-teljes.

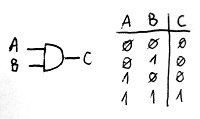
A fenti tétel alkalmazásához azonban szükségünk van legalább egy NP-teljes nyelvre, amiről tovább örökíthetnénk ezt a tulajdonságot más nyelvekre. Kiemelt jelentőségű volt emiatt Stephen Cook és Leonid Levin 1971-es eredménye, amely az első NP-teljes nyelvet mutatta meg. Ez az eredmény Cook-Levin tétel néven ismeretes. Ez a nyelv az úgynevezett kielégíthető logikai hálózatok nyelve. Egy logikai hálózat úgynevezett logikai kapukból és a közöttük lévő összeköttetésekből épül fel. A kapuknak vannak bemenetei, amelyek kétféle logikai értéket vehetnek fel – 1 vagy 0 (igaz vagy hamis). Ezenkívül van egy kimenete, amelyen a kapu szintén egy logikai értéket állít elő a típusának és a bemenetein lévő logikai értékeknek a függvényében. Egy hálózat építéséhez 3 féle logikai kaput használhatunk:

• ÉS-kapu: két bemenete van, a kimenetén pedig akkor és csak akkor állít elő 1-et, ha mindkét bemenetének értéke 1.
• VAGY-kapu: szintén két bemenete van, a kimenetén pedig akkor és csak akkor állít elő 1-et, ha legalább az egyik bemenetének értéke 1.
• NEM-kapu: egy bemenete van, a kimenetén pedig akkor és csak akkor állít elő 1-et, ha a bemenetének értéke 0.

E három féle kapu működését az igazságtáblázatukkal adhatjuk meg, amely minden lehetséges bemeneti kombinációra megadja, hogy mi lesz a kimeneten. Az alábbi ábrákon a három féle kapu igazságtáblázata és jelölése látható:

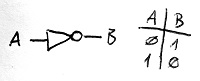
Egy logikai hálózat e kapuk segítségével a hálózat n darab bemenetéből egy kimenetet állít elő. Egy kapu bármely bemenetére akármelyik másik kapu kimenetét, vagy közvetlenül a logikai hálózat valamely bemenetét köthetjük. Hasonlóan egy kapu kimenetét akármelyik másik kapu (vagy kapuk) bemenetére, vagy közvetlenül a logikai hálózat kimenetére köthetjük. Mindössze két megkötés van. Egyrészt minden kapu-bemenetre illetve a hálózat kimenetére is pontosan egy jel lehet kötve. Másrészt a hálózat tetszőleges bemenetétől a hálózat kimenetéhez vezető útvonalak mentén minden kapu legfeljebb egyszer fordulhat elő. Azaz nem lehetnek „hurkok” a hálózatban. Akkor beszélünk kielégíthető logikai hálózatról, ha létezik a bemeneteinek olyan kombinációja, amelyre a hálózat a kimenetén a logikai 1 értéket állítja elő. Az alábbi ábrán egy 3 bemenetű logikai hálózatot láthatunk egy ilyen „kielégítő” bemeneti kombinációval:

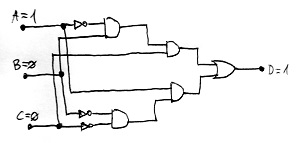
Javasoljuk az olvasónak, hogy kövesse végig, hogy ez a bemeneti kombináció valóban a D=1 kimenetet eredményezi. Ezek után a döntési feladatunk egy tetszőleges logikai hálózatról eldönteni, hogy kielégíthető-e a fenti értelemben. Formális nyelvekre átfogalmazva: nevezzük SAT-nak az olyan jelsorozatokat tartalmazó nyelvet, amely jelsorozatok egyrészt valamilyen logikai hálózat leírásai, másrészt az általuk leírt logikai hálózat a fenti értelemben kielégíthető. A feladatunk pedig egy olyan Turing-gép létrehozása, amely tetszőleges x jelsorozatra eldönti, hogy a SAT nyelvbe tartozik-e. A Cook-Levin tétel állítása a következő: a SAT nyelv NP-teljes.

Annak bizonyítása viszonylag egyszerű, hogy a SAT nyelv NP-ben van, hiszen egy helyes kiértékelés – mint tanú – ellenőrzése hatékonyan megoldható, ahogy azt az olvasó a fenti példából érzékelhette. Az NP-teljességhez azonban azt is bizonyítani kell, hogy tetszőleges NP-beli L nyelvről létezik Karp-redukció a SAT nyelvre. A Cook-Levin tétel bizonyítása lényegében egy olyan polinomiális időkomplexitású algoritmus leírása, amely egy tetszőleges NP-beli L nyelvhez és tetszőleges x jelsorozathoz konstruál egy y jelsorozatot (azaz az általa leírt logikai hálózatot) úgy, hogy az x jelsorozat akkor és csak akkor tartozik L-be, ha az y jelsorozat SAT-ba tartozik (azaz az általa leírt logikai hálózat kielégíthető).

A bizonyítás leírása hosszadalmas és erősen technikai jellegű, ezért ettől most eltekintünk. Arra azonban érdemes felhívni a figyelmet, hogy ezek szerint tetszőleges NP-beli döntési probléma egy adott példányát le lehet írni egyetlen logikai kifejezéssel, vagy egy azt reprezentáló logikai hálózattal. Ez jól mutatja a logika kifejező erejét.

Ezen túlmenően a SAT nyelv NP-teljességének önmagában is komoly jelentősége van. A valódi számítógépek integrált áramkörei ugyanis szintén a fentihez hasonló – persze annál lényegesen bonyolultabb – logikai hálózatokat valósítanak meg. Ezek optimalizálása épp az NP-teljesség miatt általában nem egyszerű. Optimalizálás alatt ebben az esetben ugyanannak a logikai hálózatnak a minél kevesebb logikai kapu használatával történő megvalósítását értjük.

A Cook-Levin tétel fontossága azonban elsősorban abban nyilvánul meg, hogy szinte az összes többi NP-teljességi bizonyítás – például a fentebb már említett említett 3-színezhetőség vagy k-függetlenség NP-teljessége is – közvetetten vagy közvetlenül a SAT nyelv NP-teljességén alapszik.

Egy meglepő fordulat

2015 novemberében Babai László, a Chicagoi Egyetem professzora bejelentette, hogy egy úgynevezett kvázipolinomiális időkomplexitású algoritmust talált a matematikusokat évtizedek óta foglalkoztató gráf-izomorfizmus problémára. A „kvázipolinomiális” fogalmát itt most nem részletezzük, azonban megpróbáljuk érzékeltetni a felfedezés jelentőségét.

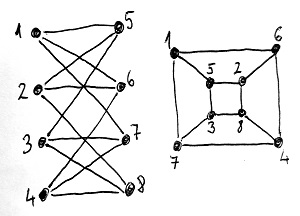
Egy G és H gráfra akkor mondjuk, hogy izomorfak egymással, ha a csúcshalmazaik között létezik olyan kölcsönösen egyértelmű megfeleltetés, amely megőrzi az éleket illetve azok hiányát is. Ha tehát G-ben veszünk két szomszédos csúcsot, akkor a nekik megfeleltetett csúcsok szintén szomszédosak lesznek H-ban. Ugyanígy ha a két csúcs nem volt szomszédos G-ben, akkor a nekik megfeleltetett csúcsok szintén nem szomszédosak H-ban. A kölcsönösen egyértelműség pedig azt jelenti, hogy G minden csúcsához pontosan egy csúcs van hozzárendelve H-ban, és H minden csúcsa pontosan egy G-beli csúcshoz van hozzárendelve. Ilyenkor azt mondjuk, hogy a két gráf lényegében ugyanaz, maximum máshogyan lettek felrajzolva, vagy máshogyan neveztük el a csúcsaikat. Ilyenkor ezt a két csúcshalmaz közötti strúktúratartó megfeleltetést (vagy ha úgy tetszik, függvényt) izomorfizmusnak nevezzük.

Az alábbi ábrán látható két gráf például izomorf egymással, még ha ez nem is látszik elsőre. Az izomorfizmus alapján egymáshoz rendelt csúcsokat azonos számokkal láttuk el:

Az alábbi ábrán látható két gráf viszont nem izomorf egymással:

A gráf-izomorfizmus probléma ezek után így fogalmazható meg: adott két gráf, és el kell dönteni, hogy izomorfak-e vagy sem. Mindezidáig nagyon úgy tűnt, hogy ez egy rendkívül nehéz algoritmikus feladat nagy gráfok esetén. Ilyen esetekben korábban mindig az történt, hogy egy nehéznek tűnő problémáról vagy bebizonyosodott, hogy mégis hatékonyan kezelhető (azaz P-beli), vagy pedig az, hogy NP-teljes.

Sokáig nyitott volt például az a kérdés, hogy egy egész számról eldönthető-e hatékonyan, hogy prímszám-e vagy összetett. 2002-ben azonban 3 indiai matematikus, Manindra Agrawal, Neeraj Kayal és Nitin Saxena felfedeztek egy polinomiális algoritmust ennek eldöntésére. Ennek neve a felfedezők neveinek kezdőbetűi után AKS-algoritmus. Eddig is voltak természetesen prímtesztelő algoritmusok, hiszen – mint azt később látni fogjuk – fontos jelentőségük van a rejtjelezésben. De ezek mind csak bizonyos valószínűséggel adják meg a választ, azonban ritkán előfordulhat, hogy tévednek. A gyakorlatban továbbra is ezeket a potenciálisan tévedő eljárásokat használjuk prímtesztelésre, mivel jóval gyorsabbak, mint az AKS-algoritmus, és a tévedés valószínűsége az alkalmazás szempontjából elhanyagolható. Az AKS-algoritmusnak inkább elméleti jelentősége van, mivel megmutatta, hogy egy addig nehéznek tartott probléma nemhogy nem NP-teljes, de egyenesen P-beli. Jóval gyakoribbak azonban azok az esetek, amikor egy nehéznek gondolt problémáról kiderül, hogy valóban NP-teljes.

Babai publikációját éppen ezért a matematikus társadalom, mint az évtized legnagyobb számítástudományi áttörését ünnepelte. Ebből az eredményből ugyanis nagyon úgy tűnik – még ha egyértelműen nem is következik belőle –, hogy a gráf-izomorfizmus problémája se nem NP-teljes, se nem P-beli, azaz valahol a kettő között helyezkedhet el. Ha ez valóban így van, akkor ez lenne az első ilyen tulajdonságú probléma, amit felfedeztek, ráadásul a P \neq NP sejtésre is megadná végre a választ. Erre azonban egyelőre még várni kell.

De hogy jön ide a kriptográfia?

Ahhoz, hogy Alice és Bob biztonságosan tudjanak egymással kommunikálni egy olyan csatornán keresztül, amelyet a gonosz Eve képes lehallgatni, szükségük van valamilyen rejtjelezési eljárásra. Ezen kívül szükségük van egy kulcsnak nevezett közös titokra is, amellyel az alkalmazott rejtjelezési eljárást paraméterezni fogják. A rejtjelezési eljárással szembeni legfontosabb követelmény, hogy a kulcs ismeretében „könnyű”, annak hiányában viszont „nehéz” algoritmikus feladat legyen a rejtjelezett üzenetek dekódolása. Az utóbbi 3 részben felvázolt bonyolultságelméleti fogalmak ismeretében az Olvasónak mostmár remélhetőleg világos, hogy pontosan mit értünk „könnyű” illetve „nehéz” algoritmikus feladat alatt.

Ezen túlmenően Alice-nak és Bob-nak azt a problémát is meg kell oldania, hogy hogyan tudnak megállapodni ebben a kulcsnak nevezett közös titokban anélkül, hogy személyesen találkozniuk kellene egymással. Ezt a kulcsmegosztás problémájának nevezzük. Ehhez a megállapodáshoz nyilván csak a nembiztonságos csatornát használhatják. De mégis hogyan lehetséges az, hogy a kulcsban való megállapodás érdekében küldött üzeneteket Eve ugyanúgy el tudja olvasni, mint Alice és Bob, mégsem tudja megfejteni magát a kulcsot (pontosabban fogalmazva az egy algoritmikusan roppant „nehéz” feladat a számára)?

Erre a látszólagos paradoxonra a számelmélet fogja megadni a választ a következő részekben. A számelmélet évezredekig a matematikának látszólag egy haszontalan területe volt. A 20. század második felére azonban az információs társadalom alapjává vált. Már most megemlítjük azonban, hogy ebben kulcsfontosságú szerepet játszik az úgynevezett prímfaktorizáció feladatának látszólagos algoritmikus nehézsége. Ezen áll vagy bukik ugyanis az egész. A prímszámokról és a prímfaktorizációról bőven lesz még szó a következő részekben. Azt azonban mindenképpen fontosnak tartom megemlíteni ezen a ponton, hogy a prímfaktorizáció feladatáról még nem bizonyított, hogy NP-teljes lenne.

Babai eredménye után jogosan vetődik fel a kérdés: lehetséges, hogy a prímfaktorizáció problémája is a P és az NP-teljes problémaosztály között helyezkedik el valahol? Netán egyenesen P-beli? A választ nem tudjuk, de nagyon reméljük, hogy nem így van. Egy ilyen felfedezés ugyanis alapjaiban változtatná meg a jelenleg használt rejtjelezési eljárások biztonságába vetett hitünket. Ezen a ponton érdemes feltenni a kérdést, hogy vajon valóban senki nem tudja a választ? Vajon ha igenlő lenne a válasz és valaki rájönne egy hatékony prímfaktorizációs algoritmusra, biztosan publikálná-e a tudományos közösség számára? Vagy megpróbálna inkább titokban hasznot húzni belőle? Döntse el az Olvasó…

Ebben a részben tehát megismertük a Karp-redukció fogalmát, amelynek segítségével összehasonlíthatóvá válnak az algoritmikus problémák a nehézségük szempontjából. Definiáltuk az NP-teljes problémák osztályát, amelyekről ugyan nem tudjuk biztosan, hogy valóban olyan nehezek, mint amilyennek látszanak, de megmutattuk, hogy miért lenne rendkívül meglepő, ha mégsem ez lenne a helyzet. Most már van egy átfogó képünk arról, hogy mit tekintünk algoritmikusan „nehéz” vagy „könnyű” feladatnak. A következő részekben felvázoljuk egy olyan rejtjelező rendszer alapjait, amellyel Alice és Bob meg tudja oldani a kulcsmegosztás problémáját anélkül, hogy személyesen találkozniuk kéne. Ez az eljárás továbbá az 5. részben bemutatott Mallory, mint aktív támadó elleni védelemben is komoly szerepet játszik, mint azt látni fogjuk.

A következő részt itt találod…