Az előző részben azt vizsgáltuk meg, hogy a 18. részben bevezetett kongruencia, maradékosztály és maradékosztálygyűrű fogalmai mit jelentenek az egész számok esetében. Láthattuk, hogy a kongruenciákkal nagyjából ugyanúgy kell számolni, mint a hagyományos egyenletekkel, de azért bizonyos esetekben vigyázni kell. Ezután megismerkedtünk az Euler-féle \varphi-függvénnyel, amely a modulo m redukált maradékosztályok számát adja meg. Végül az úgynevezett lineáris kongruenciák megoldhatóságának feltételeit, valamint az Euler-Fermat tételt ismertük meg. Ugyanis az ebben a részben ismertetett RSA-eljárás esetén ezek teremtik meg a nyilvános és titkos kulcsok közötti számelméleti kapcsolatot.
De vajon hogyan lehet a legnagyobb közös osztó kiszámítására szolgáló euklidészi algoritmust lineáris kongruenciák megoldásához is használni? Hogyan kell kiszámítani az Euler-féle \varphi-függvény értékét egy adott számra, és milyen információra van ehhez szükség? Hogyan működik az RSA nevű aszimmetrikus kulcsú rejtjelező eljárás? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 17., 19. és 20. részekben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Tegyük fel, hogy R elemein értelmezve van egy olyan f:R\to \N függvény, amely eleget tesz az alábbi követelményeknek:
- Tetszőleges a elem esetén f(a)=0 akkor és csak akkor teljesül, ha a=0_R, ahol 0_R az R gyűrű nullelemét, míg 0 a „nullának” nevezett természetes számot jelöli.
- Tetszőleges a és b\neq 0_R elemek esetén létezik olyan k hányados és r maradék az R gyűrűben, hogy a=k\cdot b + r és f(r)<f(b). Ezt a „műveletet” az a és b elemek közötti maradékos osztásnak vagy euklidészi osztásnak nevezzük.
Ekkor az f függvényt az R integritástartományon értelmezett euklidészi normának nevezzük. Amennyiben az R integritástartományon létezik (definiálható) euklidészi norma, úgy R-et euklidészi gyűrűnek nevezzük.
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Amennyiben R minden ideálja főideál (azaz generálható egyetlen elemmel), akkor R-t főideálgyűrűnek nevezzük.
Legyenek a, b két tetszőleges, valamint m\geq 0 nemnegatív egész szám, és legyen I az m által generált főideál, azaz I=(m). Ekkor teljesülnek az alábbiak:
- Amennyiben m\gt 0, úgy a 18.20. Definíció szerinti a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha a és b ugyanazt a nemnegatív maradékot adja m-mel osztva.
- Amennyiben m=0, úgy az a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha a=b.
- Általánosságban az a\equiv b\pod I kongruencia akkor és csak akkor teljesül, ha fennáll az m|a-b oszthatóság.
- Speciálisan amennyiben m=1, úgy az a\equiv b\pod I kongruencia mindig teljesül.
Az a és b egész számok közötti, I=(m) főideál szerinti kongruenciát illetve inkongruenciát speciálisan így is jelölhetjük:
\begin{aligned}&a\equiv b\pmod m \\ &a\ \cancel{\equiv}\ b\pmod m \end{aligned}Ilyenkor azt mondjuk, hogy az a egész szám kongruens a b egész számmal az m modulus szerint, vagy modulo m.
Legyen adva egy tetszőleges m\geq 0 nemnegatív egész szám. A 20.1. Tételben bevezetett modulo m kongruencia egy ekvivalenciareláció az egész számok \Z gyűrűjén. Az ehhez tartozó ekvivalencia-osztályokat modulo m kongruenciaosztályoknak vagy modulo m maradékosztályoknak nevezzük.
Ha m\gt 0, akkor pontosan m darab modulo m maradékosztály létezik. Legyen a egy tetszőleges egész szám. Ekkor az a-t tartalmazó modulo m maradékosztály bármely eleme felírható km + a alakban valamilyen alkalmas k egész számmal. Visszafelé: Minden k egész szám esetén a km + a egész szám benne van az a-t tartalmazó modulo m maradékosztályban.
Ha m=0, akkor végtelen sok modulo m maradékosztály létezik, és minden ilyen maradékosztályban pontosan egy egész szám van.
Legyen m\gt 0 egy tetszőleges pozitív egész szám. Ekkor a \Z/m\Z-vel jelölt modulo m maradékosztálygyűrű (lásd a 20.5. Tételt) invertálható elemeit modulo m redukált maradékosztályoknak nevezzük.
Legyen m\gt 0 tetszőleges pozitív egész szám. Ekkor a modulo m redukált maradékosztályok számát a \varphi(m)-mel jelölt függvény értéke adja meg. Ezt a függvényt Euler-féle \varphi-függvénynek (ejtsd: „fi”) nevezzük.
Legyen a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám. Ekkor az alábbi kongruenciaegyenletet lineáris kongruenciának nevezzük:
a\cdot x\equiv b\pmod mEgy lineáris kongruencia egy megoldásán egy olyan modulo m maradékosztályt értünk, amelynek tetszőleges elemét x helyére behelyettesítve a kongruencia teljesül.
Egy lineáris kongurencia megoldásszáma alatt azon modulo m maradékosztályok számát értjük, amelyek megoldásai az adott lineáris kongruenciának.
Legyen R főideálgyűrű, továbbá legyenek a és b az R tetszőleges elemei. Ekkor az a és b elemek kitüntetett közös osztója kifejezhető u\cdot a+v\cdot b alakban az R gyűrű alkalmasan választott u és v elemeinek segítségével. Ezt az összeget az a és b elemek u és v elemekkel vett lineáris kombinációjának nevezzük.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 17., 19. és 20. részeket, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Kezdjük tehát a lineáris kongruenciák megoldásával. Rögzítsünk egy m\gt 0 pozitív modulust. A 20.8. Definíció és az utána lévő megjegyzés alapján egy ax\equiv b\pmod m lineáris kongruencia egy megoldása alatt egy olyan modulo m maradékosztályt értünk, amelynek bármely elemét behelyettesítve x helyére a kongruencia fennáll. A 20.12. Tétel alapján a fenti lineáris kongruencia akkor és csak akkor oldható meg – azaz létezik ilyen maradékosztály –, ha megoldható az alábbi úgynevezett lineáris diofantoszi egyenlet:
ax+my=bEbben az esetben tehát megoldás alatt olyan EGÉSZ számpárt értünk, amelyet a fenti egyenletbe x és y helyére behelyettesítve fennáll az egyenlet. Ha tehát egy ilyen egyenletet meg tudunk oldani, akkor bármilyen lineáris kongruenciát is meg tudunk oldani. Azok mindegyike ugyanis egy-egy ilyen egyenletre vezethető vissza. Nézzünk is egy gyors példát egy lineáris diofantoszi egyenlethez vezető egyszerű problémára.
A 7., 10. és 13. részekben szó volt már a messzi-messzi Kompánia országáról. Tegyük fel, hogy ebben az országban az emberek aranytallérokon kívül bankjegyeket is használnak fizetőeszközként. Igenám, csakhogy ebben a furcsa országban mindössze kétféle címlet létezik: 79 és 47 aranytallér névértékű bankjegy. Tegyük fel, hogy Alice kinézett valamilyen ajándékot Bob-nak, amely 10000 aranytallérba kerül, viszont csak bankjegyek vannak nála. Kérdés, hogy Alice ki tudja-e fizetni pontosan az összeget ezen bankjegyek segítségével, és ha igen, akkor hányféleképpen? Keressük tehát az alábbi lineáris diofantoszi egyenlet megoldásait:
\underbrace{79}_{=a}\cdot x+\underbrace{47}_{=m}\cdot y=\underbrace{10000}_{=b}Ne feledjük, hogy x-nek és y-nak is EGÉSZ számnak kell lennie, ráadásul NEMNEGATÍV egésznek, mivel a kifizetendő bankjegyek számáról van szó. A 20.12. Tétel alapján a fenti egyenlet akkor és csak akkor oldható meg, ha az (a,m)=(79,47) kitüntetett közös osztó osztója az egyenlet jobboldalának, azaz b=10000-nek. Előszöris tehát ki kell számítanunk a (79,47) kitüntetett közös osztót annak érdekében, hogy eldöntsük, egyáltalán létezik-e megoldás.
A 17. részben ismertettük az euklidészi algoritmus alapgondolatát, amely pontosan erre való. Azt is megmutattuk, hogy ez az eljárás minden olyan gyűrűn végrehajtható, amelynek elemei között valamilyen absztrakt értelemben elvégezhető a maradékos osztás. Ezeket a 17.16. Definícióban euklidészi gyűrűknek neveztük el, és a 17.17. Tétel bizonyításában általánosságban is ismertettük az euklidészi algoritmus menetét. Eszerint bármely a és b gyűrűelem kitüntetett közös osztóját megkapjuk az alábbi maradékos osztások során kapott utolsó nemnulla maradékként:
\begin{aligned}a&=k_1b+r_1\\b&=k_2r_1+r_2\\r_1&=k_3r_2+r_3\\r_2&=k_4r_3+r_4\\&\vdots\\r_{n-2}&=k_nr_{n-1}+r_n\\r_{n-1}&=k_{n+1}r_n+0\end{aligned}Ez jelen esetben tehát r_n lesz:
\begin{aligned}(a,b)&=(b,r_1)=(r_1,r_2)=\ldots\\\ldots&=(r_{n-1},r_n)=(r_n,0)=r_n\end{aligned}Azt is megmutattuk, hogy az eljárás garantáltan végetér véges számú lépés után, mivel a kapott maradékok euklidészi normája egy szigorúan monoton csökkenő sorozatot alkot a természetes számok halmazán, és így a 17.14. Tétel miatt előbb-utóbb biztosan eléri a 0-t.
Az egész számok \Z gyűrűjében a 17.18. Definíció szerinti abszolútérték-függvény a 17.19. Tétel értelmében egy euklidészi norma – azaz \Z euklidészi gyűrű –, és így ezen a gyűrűn alkalmazható az euklidészi algoritmus. Végrehajtva az algoritmus lépéseit a 79 és 47 bemeneti számokon, az alábbi maradékos osztásokat kapjuk:
\begin{aligned}79&=1\cdot 47+32 \\ 47&=1\cdot 32+15 \\ 32&=2\cdot 15+2 \\ 15&=7\cdot 2+1 \\ 2&=2\cdot 1+0\end{aligned}Az utolsó nemnulla maradék lesz a két bemeneti szám kitüntetett közös osztója, azaz jelen esetben (79,47)=1. Ez a szám természetesen osztója a 79x+47y=10000 diofantoszi egyenlet jobboldalának, következésképp ennek az egyenletnek a 20.12. Tétel értelmében létezik megoldása. A következő szakaszokban megmutatjuk, hogy egyrészt hogyan található meg egy megoldás az euklidészi algoritmus segítségével, másrészt, hogy ebből hogyan számítható ki az összes többi.
A kibővített euklidészi algoritmus
A 20.12. Tételben igazoltuk, hogy az ax+my=b lineáris diofantoszi egyenlet megolhatóságának szükséges és elégséges feltétele, hogy az egyenlet jobboldala – azaz b – osztható legyen az (a,m) kitüntetett közös osztóval. Az elégségesség bizonyításához az előző részben bemutatott Bézout-lemma (20.11. Tétel) volt a kulcs, amely kimondja, hogy ez a kitüntetett közös osztó minden főideálgyűrűben kifejezhető (a,m)=au+mv alakban alkalmasan választott u és v gyűrűelemek segítségével. Amennyiben tehát fennáll az (a,m)|b oszthatóság, az azt jelenti, hogy létezik olyan t gyűrűelem, hogy teljesül az alábbi:
(a,m)\cdot t=bEzt összevetve a Bézout-lemmával a következőt kapjuk:
(\underbrace{au+mv}_{=(a,m)})\cdot t=bFelbontva a zárójelet végsősoron megkapjuk az ax+my=b lineáris diofantoszi egyenlet egy megoldását:
a\cdot \underbrace{(ut)}_{=x}+m\cdot \underbrace{(vt)}_{=y}=bElőször tehát meg kell határoznunk az u és v együtthatókat. A Bézout-lemma (20.11. Tétel) főideálgyűrűk esetén ugyan garantálja ezek létezését, azonban a bizonyítás nem konstruktív abban az értelemben, hogy nem mutat eljárást ezek kiszámítására. Szerencsére az eulidészi gyűrűk esetén – amelyek ugye a 19.16. Tétel értelmében mindannyian főideálgyűrűk – egy ilyen eljárást is kapunk a kezünkbe, amennyiben a 17. részben ismertetett euklidészi algoritmust egy kicsit kibővítjük.
Ezért most két bizonyítást mutatunk a Bézout-lemma euklidészi gyűrűkre vonatkoztatott változatára. Az első bizonyítás automatikusan adódik a már említett 20.11. Tételből, ez azonban tehát csak a keresett u és v együtthatók létezését garantálja. Ezzel szemben a második bizonyítás konstruktív, mivel ismerteti a kibővített euklidészi algoritmust, amelynek segítségével ezeket az együtthatókat ki is számíthatjuk. Cserébe viszont nem minden főideálgyűrűn, hanem csak euklidészi gyűrűkön működik.
21.1. Tétel (Bézout-lemma euklidészi gyűrűkben):
Legyen R euklidészi gyűrű (lásd a 17.16. Definíciót), továbbá legyenek a és b az R tetszőleges elemei. Ekkor az (a,b) kitüntetett közös osztó kifejezhető (a,b)=au+bv alakban az R gyűrű alkalmasan választott u és v elemeinek segítségével. Ezt az összeget az a és b elemek u és v elemekkel vett lineáris kombinációjának nevezzük.
♣Bizonyítás:
A 20.11. Tétel alapján az állítás teljesül minden főideálgyűrűben. Minthogy a 19.16. Tétel értelmében minden euklidészi gyűrű főideálgyűrű, ezért az állítás nyilvánvalóan teljesül speciálisan az euklidészi gyűrűkben is.
∎Bizonyítás a kibővített euklidészi algoritmussal:
Legyen a és b az R integritástartomány két tetszőleges eleme, és jelöljük 0_R-rel a nullelemet, 1_R-rel pedig az egységelemet – amely ugye létezik, hiszen a 17.16. Definíció alapján minden euklidészi gyűrű egységelemes.
Ha a és b közül mindkettő 0_R, akkor a 17.5. Tétel 1. pontja miatt a kitüntetett közös osztójuk 0_R, amely nyilvánvalóan kifejezhető a kívánt alakban, méghozzá tetszőleges u és v gyűrűelemekkel:
\underbrace{0_R}_{=a}\cdot u+\underbrace{0_R}_{=b}\cdot v=\underbrace{0_R}_{=(a,b)}Ha a és b közül csak az egyikük 0_R, akkor viszont ugyanezen tétel 4. pontja miatt a kitüntetett közös osztójuk a másik elem lesz. Ha például a\neq 0_R és b=0_R, akkor (a,b)=(a,0_R)=a. Ez nyilván kifejezhető a kívánt alakban u=1_R és tetszőleges v gyűrűelemekkel:
a\cdot \underbrace{1_R}_{=u}+\underbrace{0_R}_{=b}\cdot v=\underbrace{(a,b)}_{=a}Értelemszerűen ha a=0_R és b\neq 0_R, akkor pedig v=1_R és u tetszőleges.
Feltételezhetjük tehát, hogy a\neq 0_R és b\neq 0_R. Ekkor lefuttathatjuk erre a két gyűrűelemre, mint bemenetre a 17.17. Tétel bizonyításában ismertetett euklidészi algoritmust. Ez ugye garantáltan befejeződik véges számú lépés után. Tegyük fel, hogy az algoritmus futtatásakor az n-edik maradékos osztás során kapjuk meg az utolsó nemnulla maradékot, amely ugye az (a,b) kitüntetett közös osztó lesz. Ez tehát az alábbi n darab maradékos osztást jelenti. Az (n+1)-edik maradékos osztást itt nem tüntettük fel, amelynek során végül a 0_R maradékot megkapjuk és amely terminálja az algoritmust:
\begin{aligned}a&=k_1b+r_1\\b&=k_2r_1+r_2\\r_1&=k_3r_2+r_3\\r_2&=k_4r_3+r_4\\&\vdots\\r_{n-2}&=k_nr_{n-1}+\underbrace{r_n}_{=(a,b)}\end{aligned}Célunk tehát, hogy az n-edik lépésben megkapott r_n maradékot kifejezzük r_n=au+bv alakban valamilyen u és v gyűrűelemek segítségével.
Vegyük észre, hogy az első maradékos osztást leíró egyenlet mindkét oldalából k_1b-t kivonva kapunk egy ehhez hasonló kifejezést az r_1 maradékra. Jelöljük az így kapott együtthatókat u_1-gyel és v_1-gyel:
r_1=a-k_1b=a\cdot \underbrace{1}_{=u_1}+b\cdot \underbrace{(-k_1)}_{=v_1}Az első lépésben kapott r_1 maradékot tehát ilymódon kifejeztük az a és b lineáris kombinációjaként az u_1=1 és a v_1=-k_1 együtthatók segítségével. Most tegyük meg ugyanezt a második lépésben kapott r_2 maradékkal is. Ehhez semmi mást nem kell tennünk, mint a második maradékos osztást leíró egyenlet mindkét oldalából levonnunk k_2r_1-et, majd r_1 helyére behelyettesíteni az előző lépésben kapott kifejezést. Jelöljük az így kapott együtthatókat u_2-vel és v_2-vel:
\begin{aligned}r_2&=b-k_2r_1=b-k_2(\overbrace{a-k_1b}^{=r_1})=\\&=a\cdot \underbrace{(-k_2)}_{=u_2} + b\cdot \underbrace{(1+k_1k_2)}_{=v_2}\end{aligned}A második lépésben kapott r_2 maradékot tehát szintén kifejeztük az a és b lineáris kombinációjaként az u_2=-k_2 és a v_2=1+k_1k_2 együtthatók segítségével.
Ezt a bizonyítást persze folytathatnánk egészen az n-edik lépésig, amikor végül az r_n=(a,b) kitüntetett közös osztót is megkapnánk a és b lineáris kombinációjaként. Mi azonban lusták vagyunk, ezért adunk egy általános képletet, amely megadja, hogy a soron következő r_i maradékot hogyan lehet előállítani a és b lineáris kombinációjaként, ha egyébként az r_{i-2} és r_{i-1} maradékokra ez az előállítás már ismert. Tegyük fel tehát, hogy az alábbi lineáris kombinációs előállításokat már ismerjük, azaz az alábbi kifejezésekben szereplő u_{i-2} és v_{i-2} valamint u_{i-1} és v_{i-1} együtthatókat már kiszámítottuk:
\begin{aligned}r_{i-2}&=a\cdot u_{i-2} + b\cdot v_{i-2} \\ r_{i-1}&=a\cdot u_{i-1} + b\cdot v_{i-1}\end{aligned}Feladatunk tehát előállítani az r_i maradékot az a és b elemek lineáris kombinációjaként. Ehhez először is tekintsük az euklidészi algoritmus futtatása során kapott i-edik maradékos osztást leíró egyenletet:
r_{i-2}=k_ir_{i-1}+r_iMindkét oldalából vonjunk le k_ir_{i-1}-et:
r_i=r_{i-2}-k_ir_{i-1}Az i-edik lépésben kapott r_i maradékot tehát kifejeztük az r_{i-2} és r_{i-1} lineáris kombinációjaként. Ez utóbbi kettőről viszont azt mondtuk, hogy már előállítottuk őket a és b lineáris kombinációjaként. Helyettesítsük is be a fenti egyenletbe ezeket az előállításokat:
r_i=(\underbrace{au_{i-2} + bv_{i-2}}_{=r_{i-2}})-k_i\cdot (\underbrace{au_{i-1} + bv_{i-1}}_{=r_{i-1}})Ezt a gyűrűaxiómáknak megfelelően (14.12. Definíció) átrendezve megkapjuk r_i-t is a és b lineáris kombinációjaként. Jelöljük az így kapott együtthatókat u_i-vel és v_i-vel:
r_i=a\cdot (\underbrace{u_{i-2}-k_iu_{i-1}}_{=u_i}) + b\cdot (\underbrace{v_{i-2}-k_iv_{i-1}}_{=v_i})Ezzel a bizonyításunk teljes, mivel az első két lépésben kapott r_1 és r_2 maradékokat előállítottuk a és b lineáris kombinációjaként, az imént látott indukció alapján pedig elő tudjuk állítani a további maradékokat is. Ezek közül ugye az n-edik lépés során kapott r_n=au_n+bv_n előállítás épp az (a,b) kitüntetett közös osztó előállítása az a és b lineáris kombinációjaként.
∎Az iménti bizonyításban látott kibővitett euklidészi algoritmus tehát abban különbözik a 17. részben ismertetett eredeti algoritmustól, hogy itt nem csak a futás során kapott r_1, r_2, …, r_n maradékokat számítjuk ki, hanem a k_1, k_2, …, k_n hányadosokat is felhasználjuk e maradékok lineáris kombinációs előállításához.
Hogy ne csak a levegőbe beszéljünk, térjünk most vissza a 17. részben bemutatott példához, és futtassuk le ezúttal a kibővített euklidészi algoritmust a 12\space 439\space 705\space 049 és a 15\space 828\space 713\space 003 egész számokra. A feladat ismét e két szám kitüntetett közös osztójának kiszámítása. Jelöljük ezt most d-vel. Ezúttal azonban ki is szeretnénk fejezni a d kitüntetett közös osztót e két szám lineáris kombinációjaként. Azaz keressük az alábbi egyenletben szereplő u és v együtthatókat:
d=15\space 828\space 713\space 003\cdot u + 12\space 439\space 705\space 049\cdot vEhhez megint használhatunk bármilyen kalkulátort, csak most az osztási maradékokon kívül a hányadosokat is ki kell számolnunk. Ehhez a két számot egyszerűen elosztjuk egymással, és az eredményből a tizedesjegyeket levágva kapjuk meg a keresett hányadost. Ez az egész osztásnak nevezett művelet – itt nem részletezett digitális áramköri okok miatt – az osztási maradék kiszámításához hasonlóan egy számítógép számára rendkívül gyorsan elvégezhető. Ezek után az u_i és v_i együtthatókat az iménti bizonyításban szereplő módon számíthatjuk ki. Az első két lépés együtthatóit tehát az alábbi képletekkel:
\begin{array}{ll}u_1=1 & u_2=-k_2 \\ v_1=-k_1 & v_2=1+k_1k_2\end{array}A további lépések együtthatóit pedig a megelőző két lépés együtthatóiból az alábbi képlettel:
\begin{aligned}u_i&=u_{i-2}-k_iu_{i-1} \\ v_i&=v_{i-2}-k_iv_{i-1}\end{aligned}Ezek alapján az alábbi táblázat mutatja az algoritmus futását:
\begin{array}{c|c|c|c|c|c|c}i & r_{i-2} & r_{i-1} & r_i & k_i & u_i & v_i \\ \hline 1 & 15828713003 & 12439705049 & 3389007954 & 1 & 1 & -1 \\ \hline 2 & 12439705049 & 3389007954 & 2272681187 & 3 & -3 & 4 \\ \hline 3 & 3389007954 & 2272681187 & 1116326767 & 1 & 4 & -5 \\ \hline 4 & 2272681187 & 1116326767 & 40027653 & 2 & -11 & 14 \\ \hline 5 & 1116326767 & 40027653 & 35580136 & 27 & 301 & -383 \\ \hline 6 & 40027653 & 35580136 & 4447517 & 1 & -312 & 397 \\ \hline 7 & 35580136 & 4447517 & 0 & - & - & -\end{array}A kitüntetett közös osztó az utolsó nemnulla maradék lett a 6. sorban – 4\space 447\space 517 –, ennek lineáris kombinációs együtthatói pedig ugyanebben a sorban találhatók:
4\space 447\space 517 = \overbrace{(-312)}^{=u}\cdot 15\space 828\space 713\space 003 + \overbrace{397}^{=v}\cdot 12\space 439\space 705\space 049Lineáris diofantoszi egyenlet megoldásai
Most vizsgáljuk meg, hogy a kibővített euklidészi algoritmus segítségével hogyan kapható meg egy lineáris diofantoszi egyenlet összes megoldása. Az alábbi tételben ezt a kérdést válaszoljuk meg.
21.2. Tétel:
Legyenek a, b és m tetszőleges egész számok, és tegyük fel, hogy a és m közül legalább az egyik nemnulla. Tegyük fel továbbá, hogy az alábbi lineáris diofantoszi egyenlet megoldható:
ax+my=bEkkor igazak az alábbiak:
1. Az egyenlet egyik megoldását magkaphatjuk a 21.1. Tétel bizonyításában ismertetett kibővített euklidészi algoritmus segítségével.
2. Ha az x=s, y=t számpár egy megoldás, akkor minden k egész szám esetén az alábbi számpár is egy megoldás:
\begin{aligned}x&=s+k\cdot \frac{m}{(a,m)} \\ y&=t-k\cdot \frac{a}{(a,m)}\end{aligned}3. Ha az x=s_1, y=t_1 számpár valamint az x=s_2, y=t_2 számpár két tetszőleges megoldás, akkor létezik olyan k egész szám, amelyre igaz az alábbi:
\begin{aligned}s_2&=s_1+k\cdot \frac{m}{(a,m)} \\ t_2&=t_1-k\cdot \frac{a}{(a,m)}\end{aligned}Itt \frac{m}{(a,m)} illetve \frac{a}{(a,m)} alatt azokat az egész számokat értjük, amelyeket az (a,m) kitüntetett közös osztóval megszorozva rendre az m illetve az a egész számot kapjuk eredményül.
♣Bizonyítás:
Az általánosság megsértése nélkül feltehetjük, hogy az m\neq 0 feltétel teljesül. Ha ugyanis mégsem így lenne, akkor a tétel szövege alapján szükségképpen teljesül az a\neq 0 feltétel, és az alábbi gondolatmenet az a és m együtthatók szerepének felcserélésével ugyanígy végigjátszható. Először az m\gt 0 esetet igazoljuk.
Az 1. állítás az m\gt 0 esetben: Mivel az egyenlet megoldható, ezért a 20.12. Tétel alapján teljesül az (a,m)|b oszthatóság. Vagyis létezik olyan egész szám, amellyel az (a,m) kitüntetett közös osztót megszorozva b-t kapunk. Jelöljük ezt az egész számot \frac{b}{(a,m)}-mel, azaz:
(a,m)\cdot \frac{b}{(a,m)} = bA 21.1. Tétel alapján az (a,m) kitüntetett közös osztó felírható az a és m egész számok lineáris kombinációjaként. Azaz léteznek olyan u és v egész együtthatók, hogy teljesül az alábbi:
(a,m)=au+mvEzt összevetve az előző egyenlettel:
(\underbrace{au+mv}_{=(a,m)})\cdot \frac{b}{(a,m)} = a\cdot (\underbrace{u\cdot \frac{b}{(a,m)}}_{=x}) + m\cdot (\underbrace{v\cdot \frac{b}{(a,m)}}_{=y}) = bAzaz megkaptuk az ax+my=b lineáris diofantoszi egyenlet egy megoldását:
\begin{aligned}x&=u\frac{b}{(a,m)} \\ y&=v\frac{b}{(a,m)}\end{aligned}Az u és v együtthatók a 21.1. Tétel bizonyításában szereplő kibővített euklidészi algoritmussal hatékonyan kiszámíthatók.
A 2. állítás az m\gt 0 esetben: Tegyük fel, hogy az x=s, y=t számpár egy megoldása az ax+my=b egyenletnek, és helyettesítsük be ugyanebbe az egyenletbe az állításban szereplő számpárt:
a\cdot(\underbrace{s+k\cdot \frac{m}{(a,m)}}_{=x})+m\cdot (\underbrace{t-k\cdot \frac{a}{(a,m)}}_{=y})=bA zárójeleket felbontva az alábbit kapjuk:
as+ka\cdot \frac{m}{(a,m)}+mt-km\cdot \frac{a}{(a,m)}=bSzorozzuk meg mindkét oldalt az (a,m) kitüntetett közös osztóval:
as\cdot (a,m)+ka\cdot \frac{m}{(a,m)}\cdot (a,m)+mt\cdot (a,m)-km\cdot \frac{a}{(a,m)}\cdot (a,m)=b\cdot (a,m)A tétel szövege alapján \frac{m}{(a,m)}\cdot (a,m)=m és \frac{a}{(a,m)}\cdot (a,m)=a, ezért az alábbit kapjuk:
as\cdot (a,m)+\cancel{kam}+mt\cdot (a,m)-\cancel{kma}=b\cdot (a,m)Mivel m\neq 0, és teljesül az (a,m)|m oszthatóság – hiszen (a,m) közös osztó –, ezért az oszthatóság tulajdonságairól szóló 16.2. Tétel 4. pontja miatt (a,m)\neq 0, és így a 15.4. Tétel alapján az egyenlet mindkét oldalát lehet egyszerűsíteni vele:
as+mt=bEz viszont teljesül, mivel az x=s, y=t számpárról tudjuk, hogy megoldása az ax+my=b egyenletnek.
A 3. állítás az m\gt 0 esetben: Tegyük fel, hogy az x=s_1, y=t_1 számpár, valamint az x=s_2, y=t_2 számpár is megoldása az ax+my=b egyenletnek. Ez a 20.12. Tétel alapján azt jelenti, hogy az [s_1]_m és az [s_2]_m maradékosztály is megoldása az ax\equiv b\pmod m lineáris kongruenciának, azaz tejesülnek az alábbi kongurenciák:
\begin{aligned}as_1&\equiv b\pmod m \\ as_2&\equiv b\pmod m\end{aligned}A 20.2. Tétel 4. pontja miatt ez a két kongruencia kivonható egymásból. A másodikat az elsőből kivonva ezt kapjuk:
a\cdot (s_2-s_1)\equiv 0\pmod mA kongruenciák egyszerűsítéséről szóló 20.3. Tétel alapján mindkét oldalt egyszerűsíthetjük a-val, amennyiben az m modulust is egyszerűsítjük az (a,m) kitüntetett közös osztóval. Ezt végrehajtva a következőt kapjuk:
s_2-s_1\equiv 0\pmod{\frac{m}{(a,m)}}Ez a kongruencia a 20.1. Tétel 3. pontja alapján épp azt jelenti, hogy teljesül az alábbi oszthatóság:
\frac{m}{(a,m)}|s_2-s_1Az oszthatóság 16.1. Definíció definíciója alapján ez épp azt jelenti, hogy létezik olyan k egész szám, amelyre teljesül az alábbi egyenlet:
k\cdot \frac{m}{(a,m)}=s_2-s_1Mindkét oldalhoz s_1-et adva megkapjuk a tételben szereplő képletet s_2-re:
s_2=s_1+k\cdot \frac{m}{(a,m)}Mostmár csak a t_2-t kellene valahogy kifejezni t_1-ből. Azt ugye tudjuk, hogy az x=s_1, y=t_1 számpár, valamint az x=s_2, y=t_2 számpár is megoldása az ax+my=b egyenletnek, azaz:
\begin{aligned}as_1+mt_1&=b \\ as_2+mt_2&=b\end{aligned}A második egyenletből az elsőt kivonva az alábbit kapjuk:
a(s_2-s_1)+m(t_2-t_1)=0Az s_2-re fentebb megkapott képletet behelyettesíthetjük:
a(\underbrace{s_1+k\cdot \frac{m}{(a,m)}}_{=s_2}-s_1)+m(t_2-t_1)=0Azaz:
\cancel{as_1}+ak\cdot \frac{m}{(a,m)}-\cancel{as_1}+m(t_2-t_1)=0A tétel szövege alapján \frac{m}{(a,m)}\cdot (a,m)=m, ezért mindkét oldalt az (a,m) kitüntetett közös osztóval megszorozva ezt kapjuk:
akm+m\cdot (a,m)\cdot (t_2-t_1)=0Mivel m\neq 0, ezért a 15.4. Tétel alapján az egyenlet mindkét oldalát lehet egyszerűsíteni vele:
ak+(a,m)\cdot (t_2-t_1)=0Mindkét oldalból ak-t levonva ezt kapjuk:
(a,m)\cdot (t_2-t_1)=-akA tétel szövege alapján \frac{a}{(a,m)}\cdot (a,m)=a, így:
(a,m)\cdot (t_2-t_1)=-k\cdot \underbrace{\frac{a}{(a,m)}\cdot (a,m)}_{=a}Mivel m\neq 0, és teljesül az (a,m)|m oszthatóság – hiszen (a,m) közös osztó –, ezért az oszthatóság tulajdonságairól szóló 16.2. Tétel 4. pontja miatt (a,m)\neq 0, és így a 15.4. Tétel alapján az egyenlet mindkét oldalát lehet egyszerűsíteni vele:
t_2-t_1=-k\cdot \frac{a}{(a,m)}Mindkét oldalhoz t_1-et adva megkapjuk a tételben szereplő képletet t_2-re:
t_2=t_1-k\cdot \frac{a}{(a,m)}A tételt tehát igazoltuk m\gt 0 esetben, ezért most vizsgáljuk meg az m\lt 0 esetet. Ilyenkor a 15.12. Definíció utáni megjegyzés alapján -m\gt 0, amit a továbbiakban erősen ki fogunk használni.
Az 1. állítás az m\lt 0 esetben: Mivel -m\gt 0, ezért az ax+(-m)y=b egyenlet egy megoldását az 1. állítás eddigi bizonyítása alapján kiszámíthatjuk a kibővített euklidészi algoritmus segítségével. Tegyük fel, hogy eredményként az x=s, y=t számpárt kapjuk, azaz teljesül az alábbi:
as+(-m)t=bA 15.1. Tétel 3. pontja alapján az egyenlet baloldala átírható a következőképpen:
as+m(-t)=bAzaz megkaptuk az eredeti ax+my=b egyenlet egy megoldását: x=s és y=-t.
A 2. állítás az m\lt 0 esetben: Tegyük fel, hogy az x=s, y=t számpár megoldása az ax+my=b egyenletnek. Ekkor az előbbihez hasonló módon az x=s, y=-t számpár megoldása az ax+(-m)y=b egyenletnek. Mivel -m\gt 0, ezért a 2. állítás eddigi bizonyítása alapján tetszőleges k egész szám esetén az alábbi számpár is megoldása az ax+(-m)y=b egyenletnek:
\begin{aligned}x&=s+k\cdot \frac{-m}{(a,-m)}=s-k\cdot \frac{m}{(a,-m)} \\ y&=-t-k\cdot \frac{a}{(a,-m)}\end{aligned}A 16.8. Tétel 1. pontja alapján m és az ellentettje asszociáltak – azaz pontosan ugyanazok az osztóik és a többszöröseik –, emiatt teljesül az (a,-m)=(a,m) egyenlőség, vagyis az ax+(-m)y=b egyenlet iménti megoldása átírható így:
\begin{aligned}x&=s-k\cdot \frac{m}{(a,m)} \\ y&=-t-k\cdot \frac{a}{(a,m)}\end{aligned}Ekkor azonban az alábbi számpár megoldása az eredeti ax+my=b egyenletnek:
\begin{aligned}x&=s-k\cdot \frac{m}{(a,m)} \\ y&=t+k\cdot \frac{a}{(a,m)}\end{aligned}Ha tehát kiválasztunk egy tetszőleges l egész számot, akkor az iménti gondolatmenetet a k=-l helyettesítéssel végigjátszva az eredeti ax+my=b egyenlet egy x=s, y=t megoldásából valóban egy újabb megoldást kapunk a tételben szereplő képlettel:
\begin{aligned}x&=s+l\cdot \frac{m}{(a,m)} \\ y&=t-l\cdot \frac{a}{(a,m)}\end{aligned}Végül a 3. állítás az m\lt 0 esetben: Tegyük fel, hogy az x=s_1, y=t_1 számpár és az x=s_2, y=t_2 számpár két tetszőleges megoldása az ax+my=b egyenletnek. Ekkor az előbbihez hasonló módon az x=s_1, y=-t_1 számpár és az x=s_2, y=-t_2 számpár megoldása az ax+(-m)y=b egyenletnek. Mivel -m\gt 0, ezért a 3. állítás eddigi bizonyítása alapján létezik olyan k egész szám, amelyre teljesülnek az alábbiak:
\begin{aligned}s_2&=s_1+k\cdot \frac{-m}{(a,-m)}=s_1-k\cdot \frac{m}{(a,-m)} \\ -t_2&=-t_1-k\cdot \frac{a}{(a,-m)}\end{aligned}Továbbra is érvényes marad a második egyenlet, ha vesszük mindkét oldal ellentettjét. Továbbá igaz, hogy a 16.8. Tétel 1. pontja alapján m és az ellentettje asszociáltak – azaz pontosan ugyanazok az osztóik és a többszöröseik –, emiatt teljesül az (a,-m)=(a,m) egyenlőség. Vagyis a fenti egyenletek átírhatók így:
\begin{aligned}s_2&=s_1-k\cdot \frac{m}{(a,m)} \\ t_2&=t_1+k\cdot \frac{a}{(a,m)}\end{aligned}Az l=-k választással élve tehát valóban találtunk olyan egész számot, amely esetén az eredeti ax+my=b egyenlet bármely két x=s_1, y=t_1 és x=s_2, y=t_2 megoldásai között fennáll a tételben szereplő alábbi összefüggés:
\begin{aligned}s_2&=s_1+l\cdot \frac{m}{(a,m)} \\ t_2&=t_1-l\cdot \frac{a}{(a,m)}\end{aligned} ∎Megjegyzés:
A tételben szereplő 2. és 3. állítást egyben is megfogalmazhatjuk az alábbi módon:
Ha az ax+my=b lineáris diofantoszi egyenlet valamelyik x=s, y=t megoldását már ismerjük, akkor az alábbi képlet segítségével megkaphatjuk az összes megoldást, amennyiben a k paraméterrel végigszaladunk az összes létező egész számon:
\begin{aligned}x&=s+k\cdot \frac{m}{(a,m)} \\ y&=t-k\cdot \frac{a}{(a,m)}\end{aligned} ♣Most térjünk vissza a kompániai példánkhoz, és az iménti tétel alapján határozzuk meg, hogy hányféleképpen tudja Alice kifizetni a Bob-nak szánt 10000 aranytalléros ajándékot, amennyiben csak 79 és 47 aranytallér névértékű bankjegyek állnak rendelkezésére. Keressük tehát a nemnegatív egész megoldásait az alábbi lineáris diofantoszi egyenletnek:
\underbrace{79}_{=a}\cdot x + \underbrace{47}_{=m}\cdot y=\underbrace{10000}_{=b}Azt már az euklidészi algoritmus segítségével kiszámítottuk, hogy a (79,47) kitüntetett közös osztó 1, aminek nyilván többszöröse az egyenlet jobboldalán szereplő 10000. Így tehát ennek az egyenletnek létezik egész megoldása. Kérdés, hogy vajon nemnegatív egész megoldás is létezik-e, és ha igen, akkor mennyi?
Az imént bizonyított 21.2. Tétel 1. pontja alapján az egyik megoldást a kibővített euklidészi algoritmus segítségével határozhatjuk meg, amelyből aztán a 2. és 3. pont értelmében könnyedén előállíthatjuk az összes megoldást. Ezekből már látni fogjuk, hogy van-e közöttük olyan, amely esetén x is és y is nemnegatív. Futtassuk hát le a két együtthatón a kibővített euklidészi algoritmust, és állítsuk elő a kitüntetett közös osztójukat a lineáris kombinációjukként:
\begin{array}{c|c|c|c|c|c|c}i & r_{i-2} & r_{i-1} & r_i & k_i & u_i & v_i \\ \hline 1 & 79 & 47 & 32 & 1 & 1 & -1 \\ \hline 2 & 47 & 32 & 15 & 1 & -1 & 2 \\ \hline 3 & 32 & 15 & 2 & 2 & 3 & -5 \\ \hline 4 & 15 & 2 & 1 & 7 & -22 & 37 \\ \hline 5 & 2 & 1 & 0 & - & - & -\end{array}A megkapott lineáris kombináció tehát az alábbi:
(79,47) = \underbrace{(-22)}_{=u}\cdot 79 + \underbrace{37}_{=v}\cdot 47=1Minthogy fennáll az oszthatóság a (79,47) kitüntetett közös osztó és az egyenlet jobboldala – azaz 10000 – között, ezért létezik a \frac{10000}{(79,47)} hányados, amelyre teljesül az alábbi:
(79,47)\cdot \frac{10000}{(79,47)}=10000A hányadost egy egész osztással kiszámítva, valamint felhasználva az imént előállított lineáris kombinációt, az alábbit kapjuk:
(\underbrace{79\cdot (-22)+47\cdot 37}_{=(79,47)})\cdot \underbrace{10000}_{=\frac{10000}{(79,47)}}=10000A baloldalon lévő zárójelet felbontva tulajdonképpen megkaptuk a 79x+47y=10000 egyenlet egyik megoldását:
\underbrace{79}_{=a}\cdot \underbrace{(-220000)}_{=x} + \underbrace{47}_{=m}\cdot \underbrace{370000}_{=y}=\underbrace{10000}_{=b}Ebben a megoldásban az x sajnos negatív, így ez nem egy jó megoldás számunkra. A 21.2. Tétel 2. és 3. pontjai alapján azonban az alábbi képlet segítségével megkapjuk az összes megoldást, amennyiben a k paraméterrel végigszaladunk az összes létező egész számon:
\begin{aligned}x&=-220000+47k \\ y&=370000-79k\end{aligned}Mi alapvetően lusták vagyunk, így nem szeretnénk a k paraméter végtelen sok lehetséges értékét végigvizsgálni azért, hogy megtudjuk, mikor kapunk nemnegatív számot x-re és y-ra egyaránt. Ehelyett az alábbi egyenlőtlenségeket írjuk fel:
\begin{aligned}0\leq \overbrace{-220000+47k}^{=x} \\ 0\leq \underbrace{370000-79k}_{=y}\end{aligned}Ezeket megoldva azt kapjuk, hogy mindössze a k=4681, k=4682 és a k=4683 esetekben kapunk nemnegatív megoldást.
Alice tehát háromféleképpen tudja kifizetni a 10000 aranytallért a Bobnak szánt ajándékra, amennyiben csak 79 és 47 aranytallér névértékű bankjegyek vannak nála:
\begin{aligned}10000&=7\cdot 79+201\cdot 47=\\&=54\cdot 79+122\cdot 47=\\&=101\cdot 79+43\cdot 47\end{aligned}Félretéve a szöveges feladatot, most próbáljuk meg a 79x+47y=10000 diofantoszi egyenlet összes megoldását – amelyekbe tehát mostmár a negatívakat is beleértjük – egy kétdimenziós koordináta-rendszerben ábrázolni, ahol a két tengely a megoldásokhoz tartozó x és y értékeket jelenti. A megoldásokat szolgáltató fentebbi képletből látható, hogy ha egy adott megoldásból kiindulva a k értékét 1-gyel megnöveljük, akkor az így kapott új megoldáshoz tartozó x értéke 47-tel nő, míg az y értéke 79-cel csökken.
Így tehát a megoldások mindannyian egy ferdén lefelé tartó egyenes mentén fognak elhelyezkedni. Az alábbi ábrán a k paraméternek az adott megoldásokhoz tartozó értékeit is feltüntettük:

Ebből szépen látható, hogy mindössze a k=4681, k=4682 és a k=4683 értékekhez tartozó megoldások esnek a jobb-felső síknegyedbe – amikoris mindkét koordináta pozitív.
Az ebben a szakaszban ismertetett módszerrel tehát bármilyen lineáris diofantoszi egyenletet, és így a 20.12. Tétel alapján bármilyen lineáris kongruenciát meg tudunk oldani. Így az RSA kriptográfiai eljárás egyik fontos összetevője már a kezünkben van. Most ismerkedjünk meg egy másik fontos összetevővel.
Az Euler-féle \varphi-függvény kiszámítása
Az RSA-algoritmus másik fontos összetevőjeként ebben a szakaszban megtanuljuk, hogy hogyan lehet kiszámítani a 20.7. Definícióban ismertetett Euler-féle \varphi-függvény értékét bármilyen tetszőleges pozitív egész számra. A definíció szerint egy m pozitív egész szám esetén ez a függvény a modulo m redukált maradékosztályok számát adja meg. A 20.6. Definíció alapján ezek épp a 20.5. Tételben definiált \Z/m\Z maradékosztálygyűrű azon elemei, amelyek invertálhatók a maradékosztályok közötti szorzásra nézve.
Az előző részben a 20.17. Következményben megmutattuk, hogy ez a szám éppenséggel megegyezik a 0 és m közötti, m-hez relatív prímek számával, amely tehát az Euler-féle \varphi-függvénynek egy alternatív definícióját adja. Például a 0 és 18 közötti, 18-hoz relatív prímek halmaza az alábbi számhalmaz:
\{1; 5; 7; 11; 13; 17\}Ezek száma 6, így tehát \varphi(18)=6. Az alábbi tételben a \varphi-függvény egy fontos tulajdonságát igazoljuk.
21.3. Tétel:
Legyen a és b két tetszőleges pozitív egész szám. Tegyük fel továbbá, hogy a és b egymáshoz relatív prímek (lásd a 17.10. Definíciót). Ekkor teljesül az alábbi:
\varphi(ab)=\varphi(a) \cdot \varphi(b) ♣Bizonyítás:
A \varphi(ab) tehát azon ab-nél nemnagyobb pozitív egészeknek a számával egyezik meg, amelyek ab-hez relatív prímek. Vegyük észre, hogy tetszőleges egész szám akkor és csak akkor relatív prím ab-hez, ha relatív prím a-hoz is és b-hez is.
Tegyük fel ugyanis indirekt, hogy egy valamilyen c egész szám relatív prím ab-hez, de nem relatív prím a-hoz. Ez azt jelentené, hogy létezik olyan n egész szám, amely közös osztója a-nak és c-nek, de nem egység. Ekkor a 16.2. Tétel 7. pontja miatt n közös osztója lenne ab-nek és c-nek, és mivel nem egység, ezért c nem lehetne relatív prím az ab szorzathoz. Ilyen n közös osztó tehát nem létezhet, következésképp minden ab-hez relatív prím egész egyben relatív prím a-hoz. Ehhez hasonlóan igazolható, hogy minden ab-hez relatív prím egész egyben relatív prím b-hez is.
Visszafelé: Tegyük fel, hogy egy valamilyen c egész szám relatív prím a-hoz is és b-hez is. Ez azt jelenti, hogy sem a-nak, sem pedig b-nek nincs c-vel közös osztója az egységeken kívül. Mivel a 17.22. Tétel szerint az egész számok \Z gyűrűjében teljesül a számelmélet alaptétele, ezért ez azt is jelenti, hogy a és b prímtényezői mind különböznek c prímtényezőitől, és így a szorzatuknak sincs c-vel közös prímtényezője, tehát osztója sem az egységeken kívül. Azaz c valóban relatív prím ab-hez.
Eddig tehát azt igazoltuk, hogy a \varphi(ab) érték kiszámításához azokat az ab-nél nemnagyobb pozitív egészeket kell megszámlálnunk, amelyek relatív prímek a-hoz is és b-hez is. Ezt a következő lépésekben fogjuk megtenni:
- Összegyűjtjük az összes a-hoz relatív prím egész számot.
- Ezek közül kiválasztjuk azokat, amelyek 0 és ab közé esnek.
- Végül a maradékból kiválogatjuk azokat, amelyek b-hez is relatív prímek.
Az 1. lépés: A 20.14. Tétel alapján az a-hoz relatív prímek pontosan a modulo a redukált maradékosztályok elemei lesznek. Ilyen maradékosztályból épp \varphi(a) darab van. E \varphi(a) darab modulo a redukált maradékosztály mindegyikéből válasszuk ki a legkisebb pozitív elemet. Az így kapott r_1, r_2, ..., r_{\varphi(a)} számok tehát reprezentálják az összes modulo a redukált maradékosztályt. A 20.4. Tétel alapján e maradékosztályok elemei (és csak azok) kifejezhetők az r_1, r_2, ..., r_{\varphi(a)} reprezentánselemek segítségével az alábbi táblázat szerint (minden oszlop egy-egy redukált maradékosztálynak felel meg):
\begin{array}{c|c|c|c}[r_1]_a & [r_2]_a & \cdots & [r_{\varphi(a)}]_a \\ \hline \vdots & \vdots & & \vdots \\ r_1-2a & r_2-2a & \cdots & r_{\varphi(a)}-2a \\ r_1-1a & r_2-1a & \cdots & r_{\varphi(a)}-1a \\ r_1+0a & r_2+0a & \cdots & r_{\varphi(a)}+0a \\ r_1+1a & r_2+1a & \cdots & r_{\varphi(a)}+1a \\ r_1+2a & r_2+2a & \cdots & r_{\varphi(a)}+2a \\ r_1+3a & r_2+3a & \cdots & r_{\varphi(a)}+3a \\ \vdots & \vdots & & \vdots \end{array}A 2. lépés: Most minden olyan számot kidobálunk ebből a táblázatból, amely nem 0 és ab közé esik. Mivel az r_1, r_2, ..., r_{\varphi(a)} reprezentánselemeket úgy választottuk ki, hogy minden oszlopban ők legyenek a legkisebb pozitív egészek, ezért a táblázat ezek fölötti részét ki is hajíthatjuk, hiszen ott már csupa negatív szám szerepel. Kérdés, hogy lefelé meddig mehetünk el a k paraméterrel úgy, hogy bármely i-edik oszlopban az r_i+ka\lt ab egyenlőtlenség még éppen teljesüljön? A határvonal épp a k=b-1 érték lesz. Ezt ugyanis behelyettesítve az egyenlőtlenségbe, valamint kihasználva a 15.11. Definíció szerinti 1. rendezési axiómát, az alábbi adódik:
\begin{aligned}r_i+\overbrace{(b-1)}^{=k}a&\lt ab \\ r_i+\cancel{ba}-a&\lt \cancel{ab}\\r_i\lt a\end{aligned}Ez viszont nyilvánvalóan teljesül, hiszen r_i az egyik modulo a maradékosztály legkisebb pozitív eleme. Minthogy a 0, 1, 2, ..., a-1 számok az összes létező modulo a maradékosztályt reprezentálják, ezért r_i is szükségképpen közöttük van.
Másrészt viszont a k=b érték már nem megfelelő, ha ugyanis ezt helyettesítjük be az egyenlőtlenségbe, akkor az alábbit kapjuk:
\begin{aligned}r_i+\overbrace{b}^{=k}\cdot a&\lt ab \\ r_i&\lt 0\end{aligned}Ez az egyenlőtlenség már nem teljesül, hiszen az r_i-t pozitívnak választottuk. Az 1. lépésben keletkezett táblázatból tehát az alábbi rész maradt meg, a többit kidobáltuk:
\begin{array}{c|c|c|c}[r_1]_a & [r_2]_a & \cdots & [r_{\varphi(a)}]_a \\ \hline r_1+0a & r_2+0a & \cdots & r_{\varphi(a)}+0a \\ r_1+1a & r_2+1a & \cdots & r_{\varphi(a)}+1a \\ r_1+2a & r_2+2a & \cdots & r_{\varphi(a)}+2a \\ \vdots & \vdots & & \vdots \\ r_1+(b-1)a & r_2+(b-1)a & \cdots & r_{\varphi(a)}+(b-1)a \end{array}Ez a táblázat tehát tartalmazza az összes olyan 0 és ab közé eső egész számot, amely relatív prím a-hoz.
A 3. lépés: Ez tehát egy \varphi(a) oszlopból álló táblázat, és minden oszlopban b darab szám van. Tekintsük például az i-edik oszlopot. Ennek elemei a következők:
\begin{aligned}r_i&+0a\\r_i&+1a\\r_i&+2a\\&\vdots\\r_i&+(b-1)a\end{aligned}Vegyük észre, hogy ezt a számhalmazt úgy kaptuk, hogy a \{0;1;2;\ldots;b-1\} számhalmaz minden elemét megszoroztuk a-val – ami ugye a tétel szövege alapján relatív prím b-hez –, majd az így kapott számokhoz hozzáadtunk r_i-t. Mivel azonban a \{0;1;2;\ldots;b-1\} számhalmaz nem más, mint egy modulo b teljes maradékrendszer, ezért a 20.18. Tétel alapján az újonnan kapott számhalmaz is az.
Mivel a táblázat minden oszlopa ugyanígy képződött, ezért a táblázat minden oszlopában tulajdonképpen egy-egy modulo b teljes maradékrendszer áll. Minden oszlopban képviselve van tehát az összes modulo b maradékosztály. Mivel ezek közül a redukált maradékosztályok száma az Euler-függvény 20.7. Definíciója alapján \varphi(b), ezért ez egyben azt is jelenti a 20.17. Következmény alapján, hogy minden oszlopban \varphi(b) darab olyan elem van, amely relatív prím b-hez. Minthogy a táblázatban az oszlopok száma \varphi(a), így a táblázatnak összesen \varphi(a)\cdot \varphi(b) eleme relatív prím b-hez is.
Összefoglalva: Összesen tehát \varphi(a)\cdot \varphi(b) darab olyan 0 és ab közötti egész szám létezik, amely relatív prím a-hoz is és b-hez is. Ezek száma a bizonyítás elején közölt észrevétel alapján megegyezik azon 0 és ab közötti egészek számával, amelyek relatív prímek ab-hez. Ezek száma viszont \varphi(ab), így tehát valóban teljesül a tétel állítása:
\varphi(ab)=\varphi(a)\cdot \varphi(b) ∎Például próbáljuk ez alapján meghatározni a \varphi(77) értékét. Ehhez a 77 prímtényezős felbontását, valamint az iménti tételt használva az alábbi adódik:
\varphi(77)=\varphi(7\cdot 11)=\varphi(7)\cdot \varphi(11)Ha feltételezzük, hogy a \varphi(7)=6 és a \varphi(11)=10 értékeket valahogyan kiszámítottuk, akkor a \varphi(77)=60 végeredmény már könnyen adódik. Az alábbiakban ezt a „valahogyan”-t vizsgáljuk meg. Ehhez azonban szükségünk lesz az alábbi segédtételre.
21.4. Lemma:
Legyen a tetszőleges, k\gt 0 pedig valamilyen pozitív egész szám. Ekkor tetszőleges p prímszám esetén az a egész akkor és csak akkor relatív prím a p^k hatványhoz, ha nem osztható p-vel, azaz NEM teljesül a p|a oszthatóság.
♣Bizonyítás:
Tegyük fel ugyanis, hogy teljesül a p|a oszthatóság. Ekkor – mivel a p|p^k oszthatóság nyilvánvalóan teljesül – p egy közös osztója lesz p^k-nak és a-nak. Mivel a tétel szövege szerint p prím – és így a 16.13. Definíció szerint nem egység –, az a és p^k számok valóban nem lehetnek egymáshoz relatív prímek. Másként fogalmazva ha a és p^k egymáshoz relatív prímek, akkor valóban nem teljesülhet a p|a oszthatóság.
Visszafelé: Ha a és p^k egymáshoz nem relatív prímek, akkor létezik olyan d közös osztó, amely nem egység, és amely esetén fennáll az alábbi két oszthatóság:
\begin{aligned}d&|a \\ d&|p^k\end{aligned}Mivel p prím, ezért a második oszthatóság alapján d az alábbi számok közül kerülhet ki:
p,p^2,p^3,p^4,\ldots, p^{k-1}, p^kTegyük fel például, hogy d=p^i valamilyen 1\leq i\leq k kitevőre, azaz:
\begin{aligned}\overbrace{p^i}^{=d}&|a \\ \underbrace{p^i}_{=d}&|p^k\end{aligned}Ám mivel a p|p^i oszthatóság nyilvánvalóan teljesül, ezért a 16.2. Tétel 5. pontja miatt valóban fennáll a p|a oszthatóság.
∎Ennek segítségével mostmár tetszőleges prímszámra – vagy még általánosabban tetszőleges prímhatványra – könnyedén ki tudjuk számítani az Euler-féle \varphi-függvény értékét
21.5. Tétel:
Legyen p\gt 0 valamilyen pozitív prímszám, k\gt 1 pedig tetszőleges, 1-nél nagyobb pozitív egész. Ekkor teljesül az alábbi:
\varphi(p^k)=p^k-p^{k-1}Speciálisan prímszámokra az Euler-féle \varphi-függvény értéke:
\varphi(p)=p-1 ♣Bizonyítás:
Nézzük először az 1. állítást! A \varphi(p^k) a 20.17. Következmény alapján a 0, 1, 2, ..., p^k-1 közül a p^k-hoz relatív prím egészek számát adja meg. Nincs más dolgunk tehát, mint ezeket megszámlálni. A 21.4. Lemma alapján egy tetszőleges a egész szám akkor és csak akkor relatív prím p^k-hoz, ha nem osztható p-vel, azaz NEM teljesül a p|a oszthatóság.
Ahhoz tehát, hogy megkapjuk \varphi(p^k) értékét, meg kell számolnunk, hogy összesen hány p-vel osztható egész szám van az első p^k darab pozitív egész szám között. A fentiek alapján ugyanis épp az ezeken kívüli számok lesznek relatív prímek p^k-hoz. A p-vel osztható számok az alábbiak lesznek:
\begin{aligned}1&\cdot p \\ 2&\cdot p \\ 3&\cdot p \\ &\vdots \\ p^{k-1}&\cdot p\end{aligned}Ezek száma összesen p^{k-1}. Ezt levonva p^k-ból valóban \varphi(p^k) értékét kapjuk, ahogyan a tétel állítja:
\varphi(p^k)=p^k-p^{k-1}Végül nézzük a 2. állítást! Ebben az esetben tehát a 0, 1, 2, ... p-1 közül a p-hez relatív prím egészek számát kéne meghatározni. Vegyük észre, hogy ezek közül egyedül a 0 nem relatív prím p-hez. Egyrészt ugyanis a 17.5. Tétel 4. pontja alapján (p,0)=p\neq 1, azaz a 0 valóban nem relatív prím p-hez. Másrészt viszont minden egyéb a esetén szükségképpen (a,p)=1, máskülönben p-nek lenne az 1-en és önmagán kívül más pozitív osztója, és így nem lehetne prím. A 0, 1, 2, ..., p-1 számok között tehát valóban p-1 darab olyan szám van, amely p-hez relatív prím.
∎Ennek és a 21.3. Tételnek a segítségével mostmár bármilyen m\gt 0 pozitív egész szám esetén könnyedén ki tudjuk számítani a \varphi(m) értéket. Ehhez „mindössze” az m egész szám prímtényezős felbontására van szükségünk.
Tegyük fel például, hogy szeretnénk kiszámítani a \varphi(93\ 372\ 871) értéket. Tegyük fel továbbá, hogy ismerjük a 93\ 372\ 871 prímtényezős felbontását:
93\ 372\ 871=5387\cdot 17333Ezután alkalmazhatjuk a fenti két tételt:
\begin{aligned}\varphi(93\ 372\ 871)&=\varphi(5387)\cdot \varphi(17333)=\\&=5386\cdot 17332=93\ 350\ 152\end{aligned}Ha tehát ismerjük a bemeneti m egész szám prímtényezős felbontását, akkor könnyedén ki tudjuk számítani a \varphi(m) értéket. Ami viszont kriptográfiai szempontból hasonlóan fontos: Ha nem ismerjük m prímtényezős felbontását, akkor nem ismeretes hatékony algoritmus \varphi(m) kiszámításához. Ez lényeges szerepet játszik az RSA rejtjelező eljárás esetén. Mielőtt azonban ezt ismertetnénk, szükségünk van egy harmadik összetevőre is.
Az ismételt négyzetreemelések módszere
A 18. részben többek között a Diffie-Hellman kulcscsere protokoll kapcsán merült fel – ebben a részben pedig az RSA eljárás kapcsán fog felmerülni – az igény arra, hogy hatékonyan tudjunk hatványozni az úgynevezett óraaritmetikában. Egy ott szereplő példa volt annak meghatározása, hogy a 2^{328} hatvány mennyi maradékot ad 11-gyel osztva. Megmutattuk, hogy ez tulajdonképpen a 18.3. Definíció szerinti \Z_{11} gyűrűben elvégzett hatványozásnak felel meg, méghozzá a \bmod_{11} maradékképző függvény művelettartó tulajdonságai miatt.
Eszerint tehát ahelyett, hogy először a \Z gyűrűben számítanánk ki a 2^{328} hatványt, és vennénk ennek a bődületesen nagy számnak a 11-gyel való osztási maradékát, a \Z_{11} gyűrűben végezzük el az alábbi 328 tényezős moduláris szorzást. Ezt képlettel kifejezve:
\bmod_{11}(\underbrace{2\cdot 2\cdot \ldots \cdot 2}_{\text{328 darab}})=\underbrace{\bmod_{11}(2)\odot \bmod_{11}(2)\odot \ldots \odot \bmod_{11}(2)}_{\text{328 darab}}Ez azért szerencsés, mert így számolgatás közben nem fogunk olyan óriási részeredményeket kapni, amelyek túllépik a számítógép számábrázolási határait. A gyakorlatban azonban a kitevő nagyságrendje a többszázjegyű számok körében mozog, így ez a módszer beláthatatlanul sok moduláris szorzást igényel. Most egy olyan módszert fogunk mutatni, amelynek a segítségével még ezek az óriási kitevős moduláris hatványok is pillanatok alatt kiszámíthatók. Ez az ismételt négyzetre emelések módszere néven ismeretes, és a moduláris hatványozás 18.8. Tétel szerinti azonosságait használja ki igen trükkös módon.
Maradjunk továbbra is a \bmod_{11}(2^{328}) moduláris hatvány kiszámításának példájánál. Első lépésként a 328-as kitevőt felírjuk kettes számrendszerben:
328 \to 101001000A különböző számrendszerekről részletesen a 3. részben volt szó. Az ott leírtaknak megfelelően ez tulajdonképpen a 328 felírása bizonyos 2-hatványok összegeként. Ebben az összegben épp azok a 2-hatványok szerepelnek, amelyeknek megfelelő helyiértéken 1-es áll a fenti bináris számábrázolásban. Azaz:
328=2^8+2^6+2^3Ennek az összegnek a tagjaiból a 14.12. Definíció 5. pontjának megfelelő disztributivitási szabályt alkalmazva kiemelhetjük a 2^3 hatványt:
328=(2^5+2^3+1)\cdot 2^3Ehhez hasonlóan a zárójelben maradt összeg első két tagjából ismételten kiemelhető a 2^3 hatvány:
328=((2^2+1)\cdot 2^3+1)\cdot 2^3Így tehát az eredeti \bmod_{11}(2^{328}) moduláris hatvány felírható a következőképpen:
\bmod_{11}(2^{328})=\bmod_{11}(2^{((2\cdot 2+1)\cdot 2\cdot 2\cdot 2+1)\cdot 2\cdot 2\cdot 2})A hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontjai alapján ez így írható fel:
\bmod_{11}(2^{328})=\bmod_{11}((((((((2^2)^2\cdot 2)^2)^2)^2\cdot 2)^2)^2)^2)Azaz egy olyan műveletsorozatot kell elvégeznünk, amelynek minden lépésében az előző lépésben kapott részeredményt vagy négyzetre emeljük, vagy pedig megszorozzuk a 2 alappal. Ebben a konkrét példában egy dupla négyzetreemelés után először szorozni kell. Ezután következik egy tripla négyzetreemelés, aztán ismét egy szorzás, végül megint egy tripla négyzetreemelés.
Minthogy a \bmod_{11} maradékképző függvény a 18.7. Tétel alapján egy gyűrűhomomorfizmus az egész számok \Z gyűrűje és a \Z_{11} gyűrű között, ezért ez a műveletsorozat a \Z_{11} gyűrűben is elvégezhető. Ezt az alábbiakban el is végezzük lépésenként:
\begin{aligned}\bmod_{11}&(2^2)=4 \\ \bmod_{11}&(4^2)=5 \\ \bmod_{11}&(5\cdot 2)=10 \\ \bmod_{11}&(10^2)=1 \\ \bmod_{11}&(1^2)=1 \\ \bmod_{11}&(1^2)=1 \\ \bmod_{11}&(1\cdot 2)=2 \\ \bmod_{11}&(2^2)=4 \\ \bmod_{11}&(4^2)=5 \\ \bmod_{11}&(5^2)=3 \end{aligned}Azaz a \bmod_{11}(2^{328})=3 végeredményt 327 helyett megkaptuk mindössze 10 darab moduláris szorzásból.
Most vizsgáljuk meg az imént leírt módszer lépésszámát általánosságban is. Tegyük fel, hogy a \bmod_{m}(a^x) moduláris hatványt szeretnénk meghatározni. Lépésszám alatt most értelemszerűen a szükséges moduláris szorzások számát értjük. Ezt az x kitevő nagysága határozza meg, amelyről most tegyük fel, hogy n darab számjeggyel írható le a kettes számrendszerben. A legrosszabb eset nyilván az, amikor minden bináris számjegy értéke 1, hiszen ekkor az összes neki megfelelő 2-hatvány szerepel az összegben:
x=2^{n-1}+2^{n-2}+2^{n-3}+\ldots +2^3+2^2+2^1+1A sorozatos kiemelések hatására egy olyan kifejezést kapunk, amely n-2 darab egymásba ágyazott zárójelet tartalmaz:
\begin{aligned}x&=(2^{n-2}+2^{n-3}+\ldots +2^2+2^1+1)\cdot 2+1=\\&=((2^{n-3}+2^{n-4}+\ldots +2^1+1)\cdot 2+1)\cdot 2+1=\\&\vdots \\&=\underbrace{((\ldots (}_{n-2 \text{ darab}}2+1)\cdot 2 + 1)\cdot 2 +\ldots +1)\cdot 2 + 1\end{aligned}Azaz mind az n-2 darab zárójel esetén az addigi részeredményhez hozzá kell adni 1-et, majd az egészet megszorozni 2-vel. Végül az utolsó lépésben mégegyszer hozzá kell adni az egészhez 1-et. Mivel ez a kifejezés a \bmod_m(a^x) moduláris hatvány kitevőjében szerepel, ezért a 18.8. Tétel 2. és 3. pontjai alapján ennek a hatványnak a kiszámítása összesen 2n-1 darab moduláris szorzásból megúszható. Ráadásul ez a lehető legrosszabb eset, amikor a kitevő bináris számábrázolásában minden bit értéke 1.
Ez tehát azt jelenti, hogy mind a Diffie-Hellman kulcscsere protokoll, mind pedig a következő szakaszban bemutatott RSA-eljárás során előforduló moduláris hatványokat rendkívül gyorsan ki tudjuk számítani még abban az esetben is, ha több ezer bites számokról van szó. Ugyanis legrosszabb esetben is a kitevő bináris számjegyei számának duplája lesz az elvégzendő moduláris szorzások száma.
Az itt lévő oldalon egy hasznos kis kalkulátor található, amelynek a segítségével a további numerikus példákban szereplő moduláris hatványokat tudjuk majd kiszámítani a most ismertetett módszerrel.
Eddig tehát megismertük a továbbiakban fontos 3 összetevőt:
- lineáris kongruenciák megoldása
- az Euler-féle \varphi-függvény kiszámítása
- az ismételt négyzetreemelések módszere
Ezek után minden készen áll arra, hogy megismerkedjünk az emberiség egyik legfontosabb találmányával.
A Rivest-Shamir-Adleman (RSA) aszimmetrikus kulcsú rejtjelező eljárás
A 9. részben mutattuk be az aszimmetrikus kulcsú rejtjelezés forradalmian új gondolatát. Ezt most pár mondatban átismételjük, ám javasoljuk az Olvasónak a hivatkozott rész átolvasását. A nagy ötlet ugye az volt, hogy a fogadó oldalon az üzenet visszafejtéséhez más kulcsot kelljen használni, mint amivel a küldő oldal titkosította azt. Ekkor ugyanis nincs szükség arra, hogy a fogadó és a küldő oldal előzetesen megállapodjon egy közös kulcsban.
Ezt sok esetben egyébként nem is tudnák megtenni. Gondoljunk csak például arra, amikor valamilyen külföldi webáruházban vásárolunk. Ez a vásárlás végén átirányít minket egy olyan bank fizetőoldalára, amelynek nem is vagyunk az ügyfelei. Ilyenkor a böngészőnknek a begépelt bankkártyaadatokat titkosítva kell elküldenie a bank szerverére, hiszen rendkívül érzékeny adatokról van szó. Amennyiben nem létezne aszimmetrikus kulcsú titkosítás, akkor a folyamat itt meg is akadna. Szükség lenne ugyanis egy közös kulcsra a vásárló és a bank közötti kommunikáció titkosításához. Az RSA-eljárásnak köszönhetően azonban ilyenre nincs szükség, mivel a böngésző a bank publikus kulcsával – amely tehát bárki számára elérhető – titkosíthatja az elküldendő bankkártyaadatokat, amelyet azután csak a bank fog tudni visszafejteni a saját titkos kulcsával.
Visszatérve főszereplőinkhez: Tegyük fel, hogy Alice szeretne Bob-nak elküldeni egy x üzenetet. Ehhez előkeresi a nyilvános kulcstárból Bob K_b publikus kulcsát, és ezzel paraméterezi az E rejtjelező függvényt. Ily módon előáll az y kódszöveg, amelyet elküld Bob-nak. Ezt az üzenetet kizárólag Bob tudja visszafejteni, mivel a K_b publikus kulcshoz tartozó k_b privát kulcsot csak ő ismeri. Bob tehát a k_b privát kulccsal paraméterezve a D dekódoló függvényt könnyedén vissza tudja állítani az eredeti x üzenetet, míg a privát kulcsot nem ismerő támadó számára ez gyakorlatilag lehetetlen. Ez a folyamat látható az alábbi ábrán:
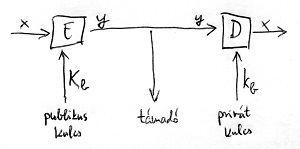
Az 1970-es évek nagy kérdése volt, hogy vajon mik lehetnek az ábrán szereplő E és D függvények – ha egyáltalán léteznek ilyenek. Az úttörő eredmény az alábbi képen látható Ronald Linn Rivest, Adi Shamir és Leonard Max Adleman érdeme, akik 1977-ben publikálták az úgynevezett Rivest-Shamir-Adleman (RSA) algoritmust, amely talán az emberiség egyik legnagyobb horderejű felfedezése volt – legalábbis a társadalmunkra gyakorolt hatását tekintve mindenképpen.

Az alábbiakban – mostmár a szükséges számelméleti ismeretekkel felvértezve – ismertetjük ennek az eljárásnak a részleteit, majd az egészet egy egyszerű példán szemléltetjük.
RSA-kulcspár generálása
Előszöris Bobnak szüksége lesz egy publikus és egy privát részből álló kulcspárra. Ezek előállítását kulcsgenerálásnak nevezzük. Ehhez Bob keres magának két különböző, elegendően nagy prímszámot. Az „elegendően nagy” manapság tipikusan 1024 vagy 2048 bináris számjeggyel ábrázolható prímeket jelent. Ez tízes számrendszerben körülbelül a 300-600 számjegyű számok nagyságrendje. Arról egy következő részben lesz szó, hogy Bob hogyan képes ilyen nagyságrendű prímeket találni viszonylag hamar, ezért ezt a problémát egyelőre tegyük félre. Jelöljük a Bob által talált, és persze a lehető legnagyobb titokban tartott két prímet p-vel és q-val. Bob ezután összeszorozza ezt a két prímszámot. Az így kapott m=p\cdot q egész számot modulusnak fogjuk nevezni a továbbiakban, amelyet nem szükséges titokban tartani, az ugyanis a publikus kulcs része lesz.
Második lépésként Bob kiszámítja az Euler-féle \varphi-függvény értékét az m modulusra, azaz kiszámítja a \varphi(m) értéket. A p és q prímszámok ismeretében ezt a 21.3. Tétel, valamint a 21.5. Tétel alapján könnyen meg tudja tenni:
\varphi(m)=(p-1)\cdot (q-1)Bob az így kiszámolt \varphi(m) értéket szintén a lehető legnagyobb titokban tartja.
Harmadik lépésként Bob választ egy tetszőleges 0 és \varphi(m) közötti e egész számot, amely relatív prím \varphi(m)-hez. A 20.14. Tétel alapján ez tehát azt jelenti, hogy Bob választ egy modulo \varphi(m) redukált maradékosztályt, a keresett e szám pedig ennek a legkisebb pozitív reprezentánseleme lesz. Megint más megfogalmazásban a gyűrűk homomorfizmustétele (18.25. Tétel) miatt a keresett e szám tulajdonképpen a \Z_{\varphi(m)} gyűrű valamelyik invertálható eleme lesz.
Ezt Bob szintén hatékonyan ki tudja választani, mivel szerencsére – itt nem részletezett analitikus számelméleti okok miatt – viszonylag gyakori, hogy két tetszőlegesen kiválasztott egész szám egymáshoz relatív prím. Így Bob megteheti, hogy véletlenszerűen választ a 0 és \varphi(m) közötti számok közül, majd az euklidészi algoritmus segítségével kiszámítja a kiválasztott szám és \varphi(m) kitüntetett közös osztóját. Ha ez egy egység – azaz a választott szám relatív prím \varphi(m)-hez –, akkor megvan a keresett e, ha pedig nem, akkor Bob megismétli az eljárást egy másik véletlenszerűen választott számmal mindaddig, amíg nem talál egy \varphi(m)-hez relatív prím számot. Az említett analitikus számelméleti összefüggések miatt ez majdnem biztosan már néhány lépés után megtörténik. Az így kapott e számot nem szükséges titokban tartani, az ugyanis a publikus kulcs része lesz.
Negyedik lépésként Bob kiszámítja az előző lépésben kiválasztott e szám multiplikatív inverzét a \Z_{\varphi(m)} gyűrűben. Ehhez meg kell oldania az alábbi lineáris kongruenciát:
e\cdot x\equiv 1\pmod{\varphi(m)}A 20.8. Definíció alapján a kongruencia megoldása egy modulo \varphi(m) maradékosztály lesz, amely – lévén, hogy e relatív prím \varphi(m)-hez – a 20.13. Tétel miatt egyértelmű lesz. Az e szám \Z_{\varphi(m)}-beli multiplikatív inverze ennek az eredményül kapott maradékosztálynak a legkisebb pozitív eleme lesz, amelyet a továbbiakban d-vel fogunk jelölni.
A d kiszámításához a 20.12. Tétel szerint Bobnak tulajdonképpen az ex+\varphi(m)y=1 lineáris diofantoszi egyenletet kell megoldania, amelyhez a 21.2. Tétel 1. pontja alapján a kibővített euklidészi algoritmust használhatja. Bob a kapott d számot titokban tartja, az ugyanis a privát kulcs része lesz.
A kulcsgenerálás ezzel befejeződött. Bob kulcspárja a következő lesz:
- Bob publikus kulcsa: Az m modulusból és az e egész számból álló (m;e) számpár.
- Bob privát kulcsa: Az m modulusból és a d egész számból álló (m;d) számpár.
Bob mostmár akár meg is semmisítheti az eredetileg választott p és q prímszámokat, valamint a belőlük kiszámított \varphi(m) értéket, azokra ugyanis a továbbiakban nem feltétlenül van szüksége. A következő részben látni fogjuk azonban, hogy a p és q számok segítségével Bob hogyan tudja jelentősen felgyorsítani a dekódolás folyamatát. Mindenesetre biztonságos helyen kell ezeket tárolnia, ugyanis a segítségükkel a publikus kulcsból a fentiek alapján hatékonyan kiszámítható a privát kulcs, így nem lenne jó, ha illetéktelen kezekbe kerülnének. Nélkülük azonban jelenlegi számelméleti ismereteink alapján ez egy belátható időn belül nem kivitelezhető feladat még a világ összes számítási kapacitásával sem. Ehhez ugyanis prímtényezőire kéne bontani a publikus kulcsban szereplő m modulust, vagy valamilyen más módon kiszámítani a \varphi(m) értéket, ami ugye a d szám meghatározásához kell.
Bob a kulcspárjának publikus részét – azaz az (m;e) számpárt – nyilvánosságra hozhatja, ugyanis ennek segítségével lehet majd a neki szánt bizalmas üzeneteket titkosítani. Ezzel szemben a kulcspár titkos részét – azaz az (m;d) számpárt – a lehető legnagyobb titokban kell tartania, ugyanis a titkosított üzeneteket kizárólag ezzel lehet majd visszafejteni.
RSA-kódolás és dekódolás
Az RSA esetén mind a rejtjelezés, mind pedig a visszafejtés során tulajdonképpen egy-egy moduláris hatványozást kell elvégezni. Ennek módjáról az ismételt négyzetreemelések módszerének kapcsán egy fentebbi szakaszban volt szó bővebben. Ha Alice valamilyen üzenetet vagy adathalmazt szeretne küldeni Bob-nak, akkor előszöris kikeresi a nyilvános kulcstárból Bob publikus kulcsát. Az ebben szereplő m modulus fogja kijelölni a \Z_m gyűrűt, amiben majd moduláris hatványozást el kell végezni, az e szám pedig a kódoláshoz használandó kitevő lesz.
A rejtjelezni kívánt üzenetet Alice valamilyen egyezményes vagy szabványos módon egy, a \Z_m gyűrű elemeiből álló számsorozattá alakítja át, amelyet előkódolásnak nevezünk. Ez sokféleképpen történhet, a technikai részletekre itt nem térünk ki, ám a következő szakaszban fogunk mutatni erre egy egyszerű példát. A lényeg, hogy Bob ebből a számsorozatból egyértelműen tudja majd rekonstruálni az eredeti üzenetet. Az RSA szempontjából tehát a nyílt szöveg tulajdonképpen egy x_1, x_2, x_3, \ldots számsorozat, amelynek tagjai a \Z_m gyűrű elemei, azaz m-nél kisebb nemnegatív egész számok. Az Alice által használt E rejtjelező függvény tehát az alábbi moduláris hatványozás lesz:
E(x)=\bmod_m(x^e)Itt x jelöli a nyílt szöveget alkotó számsorozat soron következő tagját, az e kitevő és az m modulus pedig Bob publikus kulcsát alkotják. Alice tehát a bemeneti x_1, x_2, x_3, \ldots nyílt számsorozatból (nyíltszövegből) a Bob (m;e) publikus kulcsával paraméterezett E rejtjelező függvény segítségével előállítja az y_1, y_2, y_3, \ldots rejtjelezett számsorozatot (kódszöveget):
\begin{aligned}y_1&=\bmod_m({x_1}^e) \\ y_2&=\bmod_m({x_2}^e) \\ y_3&=\bmod_m({x_3}^e) \\ &\vdots \end{aligned}Az így kapott y_1, y_2, y_3, \ldots számsorozatot Alice átküldi a nembiztonságos kommunikációs csatornán Bob-nak. A Bob által használt D dekódolófüggvény nagyon hasonlít a rejtjelező függvényhez. Az egyetlen különbség, hogy ezúttal Bob (m;d) privát kulcsával kell paraméterezni a moduláris hatványozást:
D(y)=\bmod_m(y^d)Bob tehát a bemeneti y_1, y_2, y_3, \ldots rejtjelezett számsorozatból (kódszövegből) a saját (m;d) privát kulcsával paraméterezett D visszafejtő függvény segítségével „varázslatos módon” visszakapja az Alice által közölni kívánt x_1, x_2, x_3, \ldots nyílt számsorozatot (nyíltszöveget):
\begin{aligned}x_1&=\bmod_m({y_1}^d) \\ x_2&=\bmod_m({y_2}^d) \\ x_3&=\bmod_m({y_3}^d) \\ &\vdots \end{aligned}A visszakapott számsorozatból végül Bob az egyezmény vagy szabvány szerinti előkódolás megfordításával megkapja az eredeti üzenetet vagy adathalmazt.
A következő részben fogjuk igazolni, hogy az imént említett „varázslat” valójában nem a véletlen műve, hanem az eddig megismert számelméleti összefüggések következménye. Most azonban nézzünk egy egyszerű példát az RSA-rejtjelező használatára.
Példa RSA-rejtjelezésre
Tegyük fel, hogy Alice egy bizalmas üzenetet szeretne elküldeni Bob-nak. Az egyszerűség kedvéért Alice és Bob megegyeznek, hogy a kommunikációhoz az angol ábécé betűit használják írásjelek és szóközök nélkül, az üzenet végét pedig a # karakter fogja jelezni. A bizalmas üzenet ezek alapján a következő:
sziabobmiahelyzet#
Ahhoz, hogy Alice ezt az üzenetet egy digitális kommunikációs csatornán átküldhesse, valamilyen módon egy bináris jelsorozattá kell alakítania azt. Ez történhet például az ASCII kódrendszer alapján, amelyről bővebben a 2. részben volt szó. Mi most az egyszerűség kedvéért egy ennél egyszerűbb kódrendszert fogunk használni, amely csak az angol ábécé kisbetűit és az üzenet végét jelző # karaktert tartalmazza. Ez összesen 27 szimbólum, amely 5 bites szavakkal ábrázolható. Az alábbi táblázat első oszlopa a kódolandó szimbólumokat, a második és harmadik oszlop pedig a hozzájuk rendelt számokat tartalmazza tizes és kettes számrendszerben. A számrendszerekről bővebben a 3. részben volt szó:
\begin{array}{c|c|c} \text{symbol} & \text{decimal} & \text{binary} \\ \hline a & 0 & 00000 \\ b & 1 & 00001 \\ c & 2 & 00010 \\ d & 3 & 00011 \\ e & 4 & 00100 \\ f & 5 & 00101 \\ g & 6 & 00110 \\ h & 7 & 00111 \\ i & 8 & 01000 \\ j & 9 & 01001 \\ k & 10 & 01010 \\ l & 11 & 01011 \\ m & 12 & 01100 \\ n & 13 & 01101 \\ o & 14 & 01110 \\ p & 15 & 01111 \\ q & 16 & 10000 \\ r & 17 & 10001 \\ s & 18 & 10010 \\ t & 19 & 10011 \\ u & 20 & 10100 \\ v & 21 & 10101 \\ w & 22 & 10110 \\ x & 23 & 10111 \\ y & 24 & 11000 \\ z & 25 & 11001 \\ \# & 26 & 11010 \end{array}Ezek alapján a sziabobmiahelyzet# üzenetből az alábbi 90 bit hosszú bináris jelsorozat lesz:
\begin{aligned}&\underbrace{10010}_{\text{s}} \underbrace{11001}_{\text{z}} \underbrace{01000}_{\text{i}} \underbrace{00000}_{\text{a}} \underbrace{00001}_{\text{b}} \underbrace{01110}_{\text{o}} \underbrace{00001}_{\text{b}} \\ &\underbrace{01100}_{\text{m}} \underbrace{01000}_{\text{i}} \underbrace{00000}_{\text{a}} \underbrace{00111}_{\text{h}} \underbrace{00100}_{\text{e}} \underbrace{01011}_{\text{l}} \underbrace{11000}_{\text{y}} \\ &\underbrace{11001}_{\text{z}} \underbrace{00100}_{\text{e}} \underbrace{10011}_{\text{t}} \underbrace{11010}_{\#} \end{aligned}Mivel a kommunikációs csatornát a szemtelen Eve lehallgatja, ezért Alice kénytelen titkosítani ezt a jelsorozatot. Sajnos azonban ezúttal Alice-nak és Bob-nak nincs módja személyes találkozót megbeszélni annak érdekében, hogy valamilyen közös szimmetrikus kulcsban meg tudjanak állapodni, ahogy tették azt az 1. részben. De ez nem is jelent problémát, hiszen ismerik a fentebb leírt aszimmetrikus kulcsú RSA eljárást. Alice ezért megkéri Bob-ot, hogy generáljon magának egy aszimmetrikus kulcspárt, és annak publikus részét küldje el neki a kommunikációs csatornán keresztül, hogy azzal titkosítani tudja számára a fenti bizalmas üzenetet.
Bob ezért választ magának két különböző prímszámot. Tegyük fel, hogy Bob a p=211 és q=139 prímszámokat választotta. A gyakorlatban persze a választott prímszámoknak többszázjegyűeknek kell lenniük a megfelelő biztonság érdekében, azonban most a példa kedvéért maradjunk ezeknél. Bob e két prímszám összeszorzásával meghatározza az m modulust és a \varphi(m) értéket:
\begin{aligned}m&=p\cdot q=211\cdot 139=29329 \\ \varphi(m)&=(p-1)\cdot (q-1)=210\cdot 138=28980\end{aligned}Bob választ továbbá egy \varphi(m)-hez relatív prím e számot. Ezt a leírtaknak megfelelően úgy tudja megtenni, hogy választ egy véletlen számot 0 és \varphi(m) között, majd az euklidészi algoritmus segítségével leellenőrzi, hogy a választott szám valóban relatív prím-e \varphi(m)-hez. Ez majdnem biztosan teljesülni fog már elsőre. Ha esetleg mégsem, akkor újabb véletlenszámokkal próbálkozik mindaddig, amíg nem talál egy megfelelőt. Tegyük fel, hogy Bob az e=187 számot választotta.
Ha e valóban relatív prím \varphi(m)-hez, akkor ki kell számítani a multiplikatív inverzét a \Z_{\varphi(m)} gyűrűben, azaz meg kell oldani az alábbi lineáris kongruenciát:
\underbrace{187}_{=e} \cdot d\equiv 1\pmod {\underbrace{28980}_{=\varphi(m)}}Ennek a kongruenciának a 20.12. Tétel alapján az alábbi lineáris diofantoszi egyenlet felel meg:
\underbrace{187}_{=e}\cdot d+\underbrace{28980}_{=\varphi(m)}\cdot y=1Szerencsére a kibővített euklidészi algoritmus egyszerre számítja ki az (e,\varphi(m)) kitüntetett közös osztót, és állítja elő azt e és \varphi(m) lineáris kombinációjaként. Bob tehát lefuttatja a kibővitett euklidészi algoritmust:
\begin{array}{c|c|c|c|c|c|c}i & r_{i-2} & r_{i-1} & r_i & k_i & u_i & v_i \\ \hline 1 & 28980 & 187 & 182 & 154 & 1 & -154 \\ \hline 2 & 187 & 182 & 5 & 1 & -1 & 155 \\ \hline 3 & 182 & 5 & 2 & 36 & 37 & -5734 \\ \hline 4 & 5 & 2 & 1 & 2 & -75 & 11623 \\ \hline 5 & 2 & 1 & 0 & - & - & -\end{array}Az utolsó nemnulla maradék 1, így e=187 valóban relatív prím \varphi(m)=28980-hoz, továbbá Bob megkapta a Bézout-lemma szerinti lineáris kombinációs együtthatókat is (lásd a 21.1. Tételt), azaz lényegében a fenti lineáris diofantoszi egyenlet egy megoldását:
\underbrace{28980}_{=\varphi(m)}\cdot \underbrace{(-75)}_{=y} + \underbrace{187}_{=e}\cdot \underbrace{11623}_{=d}=1Megvan tehát a keresett d=11623. A kulcsgenerálás ezzel befejeződött. Bob kulcspárja a következő:
- Bob publikus kulcsa: Az m=29329 modulus és az e=187 egész szám.
- Bob privát (titkos) kulcsa: Az m=29329 modulus és a d=11623 egész szám.
Ezek után Bob elküldi Alice-nak a kulcspár publikus részét – vagy akár elérhetővé teszi azt bárki számára egy nyilvános kulcstárban –, a titkos részét azonban szigorúan titokban tartja.
Alice-nak tehát az elküldendő bináris jelsorozatot a \Z_m=\Z_{29329} gyűrű elemeinek sorozatává kell alakítania. Ez egy olyan számsorozatot jelent, amelynek minden tagja nemnegatív és kisebb az m=29329 modulusnál. Egy rövid számolgatás után azt kapja, hogy a 14 bites számok biztosan megfelelnek ennek a kritériumnak, hiszen 2^{14}=16384. Ezzel szemben a 15 bites számok között már előfordulhatnának a modulusnál esetleg nagyobb számok is, mivel 2^{15}=32768. Így tehát Alice az üzenetet 14 bit hosszú részekre darabolja.
Az elküldendő bitsorozat 90 bit hosszú, így az utolsó darab 6 bitből fog állni. A fennmaradó 8 bitet Alice nyugodtan kitöltheti véletlenszerűen választott bitekkel, mivel a vételi oldalon Bob az üzenet végét jelző # karakterből egyértelműen azonosítani tudja majd ezeket az eldobható biteket. Így tehát az Alice által titkosítandó számsorozat a következő:
\begin{aligned}10010110010100 &\to x_1=9620 \\ 00000000001011 &\to x_2=11 \\ 10000010110001 &\to x_3=8369 \\ 00000000001110 &\to x_4=14 \\ 01000101111000 &\to x_5=4472 \\ 11001001001001 &\to x_6=12873 \\ 111010\overbrace{01101001}^{\text{kitöltés}} &\to x_7=14953\end{aligned}Alice ezután a Bob publikus kulcsát alkotó m=29329 modulus és e=187 kitevő segítségével kiszámítja a titkosított számsorozatot. Ezeket a moduláris hatványokat Alice a fentebb ismertetett ismételt négyzetreemelés módszerének segítségével hatékonyan tudja kiszámítani. Az Olvasó ezeket a számításokat maga is elvégezheti az itt található kalkulátor segítségével:
\begin{aligned}y_1&=\bmod_{29329}({9620}^{187})=7812 \\ y_2&=\bmod_{29329}({11}^{187})=869 \\ y_3&=\bmod_{29329}({8369}^{187})=445 \\ y_4&=\bmod_{29329}({14}^{187})=25123 \\ y_5&=\bmod_{29329}({4472}^{187})=2090 \\ y_6&=\bmod_{29329}({12873}^{187})=24726 \\ y_7&=\bmod_{29329}({14953}^{187})=9793 \\ \end{aligned}Ezután Alice az így kapott y_1,y_2,\ldots,y_7 számokat kettes számrendszerben ábrázolja az eredeti számsorozathoz hasonlóan. Most azonban már előfordulhat bármilyen szám 0 és m=29329 között, így Alice kénytelen 15 bitet használni:
\begin{aligned}001111010000100 &\gets y_1=7812 \\ 000001101100101 &\gets y_2=869 \\ 000000110111101 &\gets y_3=445 \\ 110001000100011 &\gets y_4=25123 \\ 000100000101010 &\gets y_5=2090 \\ 110000010010110 &\gets y_6=24726 \\ 010011001000001 &\gets y_7=9793\end{aligned}Ezeket a 15 bites darabokat Alice szépen egymás után fűzi, és az így kapott 105 bites titkosított bitsorozatot elküldi Bob-nak a kommunikációs csatornán keresztül. Ne feledjük, hogy az Alice által használt, Bob-hoz tartozó publikus kulcs csak a titkosításhoz elegendő. A kulcs titkos része nélkül maga Alice sem tudná visszafejteni ezt az üzenetet.
Példa RSA-dekódolásra
Most nézzük meg, hogy mit tud kezdeni ezzel a titkosított bitsorozattal a vételi oldalon lévő Bob, illetve a kommunikációs csatornát pofátlanul lehallgató Eve.
Bob publikus kulcsát mindketten ismerik. Bob nyilván, hiszen ő maga generálta azt az előző szakaszban. Eve pedig akkor értesül róla, amikor Bob közli azt Alice-szal a kommunikációs csatornán keresztül, vagy pedig közvetlenül letölti a nyilvános kulcstárból. Így tehát mindketten ismerik az m=29329 modulust, azaz tudják, hogy az Alice által elküldött titkosított bitsorozatot 15 bites részekre kell darabolni ahhoz, hogy megkapják a 0 és 29329 közötti számokból álló y_1,y_2,\ldots,y_7 sorozatot, amely tehát a következő:
\begin{aligned}001111010000100 &\to y_1=7812 \\ 000001101100101 &\to y_2=869 \\ 000000110111101 &\to y_3=445 \\ 110001000100011 &\to y_4=25123 \\ 000100000101010 &\to y_5=2090 \\ 110000010010110 &\to y_6=24726 \\ 010011001000001 &\to y_7=9793\end{aligned}Ebből a Bob titkos kulcsát alkotó m=29329 modulus és d=11623 kitevő segítségével lehet kiszámítani az eredeti számsorozatot. Ezeket a moduláris hatványokat Bob a fentebb ismertetett ismételt négyzetreemelés módszerének segítségével hatékonyan tudja kiszámítani, az Olvasó pedig az itt található kalkulátorral ellenőrizheti:
\begin{aligned}x_1&=\bmod_{29329}({7812}^{11623})=9620 \\ x_2&=\bmod_{29329}({869}^{11623})=11 \\ x_3&=\bmod_{29329}({445}^{11623})=8369 \\ x_4&=\bmod_{29329}({25123}^{11623})=14 \\ x_5&=\bmod_{29329}({2090}^{11623})=4472 \\ x_6&=\bmod_{29329}({24726}^{11623})=12873 \\ x_7&=\bmod_{29329}({9793}^{11623})=14953 \\ \end{aligned}Bob tehát valóban visszakapta az Alice által küldött eredeti számsorozatot. Eve azonban ezen a ponton bajba kerül, mivel nem ismeri a d=11623 kitevőt, hiszen azt Bob mindvégig titokban tartotta. Sebaj, gondolja Eve, és megkísérli kiszámítani a publikus kulcsból a titkos kulcsot, pontosan úgy, ahogyan Bob tette a kulcsgenerálás során. Ehhez Eve-nek meg kéne tudnia határozni az e=187 egész szám multiplikatív inverzét a \Z_{\varphi(m)} gyűrűben, hiszen ez épp a keresett d kitevő lesz.
Igenám, csakhogy a \varphi(m) értékének meghatározásához Eve-nek a 21.3. Tétel és a 21.5. Tétel alapján szüksége volna az m=29329 modulus prímtényezős felbontására. Nem ismeretes ugyanis olyan algoritmikus módszer, amellyel a \varphi(m) értéke hatékonyan kiszámítható m prímtényezőinek ismerete nélkül. Ezért Eve sajnos (szerencsére) kénytelen megkeresni m prímtényezőit, amelyre szintén nem ismert hatékony algoritmus. Így ez a feladat az idők végezetéig is eltarthat neki a világ összes számítógépével, amennyiben a Bob által választott prímszámok megfelelően nagyok.
Ezzel szemben Bob azért volt képes olyan gyorsan meghatározni \varphi(m)-et, és így a d titkos kitevőt, mivel ő ismerte a p=211 és q=139 prímtényezőket. Nyilván, hiszen azokat ő maga választotta, és a kulcsgenerálás során ezek szorzatából képezte az m=29329 modulust. Természetesen – mint már említettük – a gyakorlatban a választott prímszámoknak többszázjegyűeknek kell lenniük a megfelelő biztonsági szint eléréséhez.
Bob tehát minden gond nélkül ki tudta számítani az x_1, x_2, \ldots, x_7 számsorozatot. És ami még fontosabb: mivel kizárólag ő ismeri a d=11623 titkos kitevőt, ezért rajta kívül bárki más, aki az üzenet megfejtésével próbálkozik Eve-vel azonos helyzetben találja magát.
Az x_1, x_2, \ldots, x_7 számsorozatból már viszonylag egyszerűen megkapható az Alice által elküldött karaktersorozat. A modulusból ugyanis tudható, hogy Alice 14 bites számokat használt, amikor előállította ezt a sorozatot:
\begin{aligned}10010110010100 &\gets x_1=9620 \\ 00000000001011 &\gets x_2=11 \\ 10000010110001 &\gets x_3=8369 \\ 00000000001110 &\gets x_4=14 \\ 01000101111000 &\gets x_5=4472 \\ 11001001001001 &\gets x_6=12873 \\ 11101001101001 &\gets x_7=14953\end{aligned}Bob ezeket a biteket összefűzi, és az így kapott bitsorozatból a kódábécé alapján dekódolja az üzenetet. Amikor az üzenet végét jelző # karakterhez ér, a fennmaradó kitöltő biteket eldobja:
\begin{aligned}&\underbrace{10010}_{\text{s}} \underbrace{11001}_{\text{z}} \underbrace{01000}_{\text{i}} \underbrace{00000}_{\text{a}} \underbrace{00001}_{\text{b}} \underbrace{01110}_{\text{o}} \underbrace{00001}_{\text{b}} \\ &\underbrace{01100}_{\text{m}} \underbrace{01000}_{\text{i}} \underbrace{00000}_{\text{a}} \underbrace{00111}_{\text{h}} \underbrace{00100}_{\text{e}} \underbrace{01011}_{\text{l}} \underbrace{11000}_{\text{y}} \\ &\underbrace{11001}_{\text{z}} \underbrace{00100}_{\text{e}} \underbrace{10011}_{\text{t}} \underbrace{11010}_{\#} \underbrace{01101001}_{\text{eldobható}} \end{aligned}Ezután pedig válaszolhat Alice-nak ugyanezen a módon. Ekkor azonban Alice publikus kulcsával kell rejtjeleznie a választ, amelyet viszont csak Alice fog tudni visszafejteni a saját titkos kulcsával. Alice-nak és Bob-nak tehát nincs szükségük biztonságos csatornára – például személyes találkozó – ahhoz, hogy egy közös kulcsban megegyezzenek, amelyet aztán egy valamilyen szimmetrikus kulcsú rejtjelező eljáráshoz használhatnak. Az 1. részben ismertetett kulcsmegosztás problémája tehát megoldódni látszik. Van azonban még egy probléma, amelyet meg kell oldani.
RSA partnerhitelesítés és digitális aláírás
Korábban volt szó bővebben arról, hogy egy aktív támadó – például Mallory – ezt a rendszert könnyedén kijátszhatja. Ő ugyanis képes elérni, hogy Alice a Bob-nak szánt üzenetek kódolásához Mallory publikus kulcsát használja, miközben azt gondolja, hogy az valójában Bob publikus kulcsa. Alice-nak emiatt meg kell tudnia győződnie arról, hogy a kódoláshoz használt publikus kulcs valóban Bob publikus kulcsa, és nem pedig Mallory-é, aki csak azt hazudja magáról, hogy ő Bob. Ezt partnerhitelesítésnek nevezzük, és a hozzá kapcsolódó problémakört részletesen kifejtettük a 10. részben. A megoldást a digitális aláírások jelentik, amelynek lényegét most röviden átismételjük.
Egy aszimmetrikus kulcsú rejtjelezési eljárás esetén a kulcspár nyilvános részével kódolt üzeneteket kizárólag ugyanezen kulcspár titkos részével lehet dekódolni. Most igazolni fogjuk, hogy az RSA esetében a kulcsok szerepe felcserélhető. Nevezetesen: a kulcspár titkos részével kódolt üzeneteket kizárólag a kulcspár nyilvános részével lehet dekódolni. Az alábbi egyenlet a publikus kulcscsal való kódolás, majd a privát kulcscsal való dekódolás műveletének egymás után való alkalmazását írja le. Tegyük fel, hogy ennek eredményeként valóban az eredeti x üzenetet kapjuk vissza – ezt természetesen a következő részben igazolni fogjuk:
\bmod_m((\underbrace{\bmod_m(x^e)}_{=y})^d)=xMinthogy a \bmod_m maradékképző függvény a 18.7. Tétel alapján egy gyűrűhomomorfizmus az egész számok \Z gyűrűje és a \Z_m gyűrű között, ezért a zárójelen belüli y=\bmod_m(x^e) hatványozás a \Z_m gyűrűben is elvégezhető. Ugyanezen okok miatt a d kitevővel való külső x=\bmod_m(y^d) hatványozás szintén elvégezhető a \Z_m gyűrűben.
Ha tehát ezt a két egymás utáni hatványozást a \Z_m gyűrűben értjük, akkor az alábbi egyenlet írható fel:
\underbrace{(x^e)^d}_{\Z_m \text{ gyűrűben}}=xA hatványozás azonosságairól szóló 18.8. Tétel bármilyen kommutatív gyűrű esetén alkalmazható, így nyilván a \Z_m gyűrű esetén is. Ennek 2. pontja alapján az alábbit kapjuk:
(x^e)^d=x^{e\cdot d}=x^{d\cdot e}=(x^d)^e = xVagyis valóban, ha először kódolunk egy üzenetet egy kulcspár titkos részével, majd ezt dekódoljuk ugyanazon kulcspár publikus részével, akkor szintén az eredeti üzenetet kapjuk vissza. Ez alkalmassá teszi az RSA eljárást digitális aláírások képzéséhez is. Ha ugyanis egy bitsorozat dekódolható például Bob publikus kulcsával, akkor azt csak egy olyan résztvevő kódolhatta, aki Bob titkos kulcsának birtokában volt. Márpedig ha Bob nem teljesen bolond, és valóban sosem adja ki a kezéből a titkos kulcsát, akkor ez bizonyíték arra, hogy az adott üzenetet kizárólag ő küldhette. A digitális aláíráson alapuló partnerhitelesítésről a 10. részben volt szó részletesen, így azt itt nem ismételjük meg.
Ebben a részben tehát megtanultunk lineáris diofantoszi egyenleteket megoldani a kibővített euklidészi algoritmus segítségével. Ezután az Euler-féle \varphi-függvény kiszámításához szükséges összefüggéseket tisztáztuk. Végül a moduláris hatványozáshoz mutattunk egy igen hatékony módszert, az úgynevezett ismételt négyzetreemelések módszerét. Ezután ismertettük az RSA-algoritmus részleteit, amelyet egy konkrét példán ki is próbáltunk.
Ebből úgy tűnik, hogyha egy üzenetet egy kulcspár valamelyik tagjával – legyen az akár a publikus, akár a titkos kulcs – kódolunk, majd az így kapott eredményt dekódoljuk a kulcspár másik tagjával, akkor varázslatos módon az eredeti üzenetet kapjuk vissza. A következő részben matematikai bizonyítást adunk arra, hogy ez az összefüggés valóban bármilyen, az ismertetett kritériumoknak megfelelő kulcspár, továbbá bármilyen üzenet esetén fennáll. Ezután megismerjük azokat a módszereket, amelyek segítségével viszonylag könnyedén találhatunk többszázjegyű prímszámokat az RSA kulcsok generálásához.
A következő részt itt találod…



