Az előző részben megvizsgáltuk, hogyan kell osztási maradékokkal műveleteket végezni. Ezeket a műveleteket moduláris összeadásnak és moduláris szorzásnak neveztük, és igazoltuk, hogy az osztási maradékok halmaza ezzel a két művelettel gyűrűt alkot. Ennek során megmutattuk a 9. részben ismertetett Diffie-Hellman kulcscsere protokoll helyességét. Ezután általánosságban is megvizsgáltuk a gyűrűk közötti művelettartó leképezések, azaz a gyűrűhomomorfizmusok tulajdonságait. Ez adta a motivációt a kongruencia fogalmának bevezetéséhez. Megmutattuk, hogy a kongruencia nem függ egy konkrét f gyűrűhomomorfizmustól, hanem csak azoktól az elemektől, amelyekhez f a célgyűrű nullelemét rendeli hozzá. Ezt a részhalmazt f magjának neveztük. Ezzel párhuzamosan definiáltuk az ideál fogalmát, és megmutattuk, hogy egy gyűrűben pontosan az ideálok lehetnek gyűrűhomomorfizmusok magjai. Ehhez meg kellett ismerkednünk a maradékosztálygyűrű (vagy faktorgyűrű) fogalmával. Végül egy egyszerű következményként adódott az úgynevezett homomorfizmustétel.
De vajon hogyan néznek ki az egész számok gyűrűjének ideáljai? Mi a kapcsolat az ideálok és a 16. részben bevezetett oszthatósági alapfogalmak között? Mik azok a főideálgyűrűk, és ezeknek milyen jó tulajdonságaik vannak? Mi közük az euklidészi gyűrűkhöz? Hogyan zárható le a számelmélet alaptételének kérdése végérvényesen az ideálok segítségével? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 12., 16., 17. és 18. részekben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, antiszimmetrikus és tranzitív, úgy R-et H feletti részbenrendezésnek hívjuk, vagy pedig azt mondjuk, hogy a H egy részbenrendezett halmaz az R relációval.
Az R relációt teljes rendezésnek nevezzük H felett, ha a fentieken kívül a trichotómia is teljesül rá. Ilyenkor azt mondjuk, hogy a H egy rendezett halmaz az R relációval.
Tegyük fel, hogy R egy kommutatív gyűrű, valamint a és b a gyűrű két eleme. Amennyiben létezik olyan k gyűrűelem, hogy ak=b, akkor azt mondjuk, hogy a osztója b-nek az R gyűrűben. Ezzel egyenértékű megfogalmazások: b osztható a-val vagy b többszöröse a-nak.
Az oszthatóság tehát egy kétváltozós reláció az R gyűrűben. Azt a relációt, hogy „a osztója b-nek R-ben”, így jelöljük: a|_R b.
Amennyiben a és b között nem áll fenn az oszthatósági reláció – azaz a nem osztója b-nek az R gyűrűben –, azt így jelöljük: a{\nmid}_R b.
Ha a kontextusból egyértelmű, hogy melyik gyűrűben vizsgáljuk az oszthatóságot, akkor a relációt jelölő szimbólumból elhagyhatjuk a gyűrűre való hivatkozást. Ilyenkor például a|_R b helyett egyszerűen a|b-t írhatunk.
Legyen R egy tetszőleges kommutatív gyűrű. Ha egy adott e gyűrűelem esetén minden a gyűrűelemre teljesül az e|a oszthatósági reláció, akkor az e elemet egységnek nevezzük.
Egy kommutatív gyűrű valamely a és b elemeire akkor mondjuk, hogy egymás asszociáltjai, ha pontosan ugyanazok a többszöröseik és az osztóik is. Pontosabban fogalmazva, ha tetszőleges r gyűrűelem esetén a|r akkor és csak akkor teljesül, amikor b|r is teljesül, valamint r|a akkor és csak akkor teljesül, amikor r|b is teljesül.
Azt, hogy a és b egymás asszociáltjai így jelöljük: a\sim b.
Legyen R egy tetszőleges integritástartomány. Azt mondjuk, hogy R-ben érvényes a számelmélet alaptétele, ha R minden nemnulla és nem egység eleme egyértelműen felbontható R felbonthatatlan elemeinek szorzatára. Egy felbonthatatlan elem „felbontása” alatt önmagát, mint „egytényezős szorzatot” értjük.
A felbontás egyértelműsége a következőt jelenti. Tekintsük valamely r elem két tetszőleges felbontását:
\begin{aligned}r&=p_1\cdot p_2\cdot \ldots \cdot p_n = \\ &= q_1\cdot q_2\cdot \ldots \cdot q_k\end{aligned}Ekkor a tényezők száma ugyanannyi (azaz n=k), és a két felbontás tényezői egymással párba állíthatók úgy, hogy a párok tagjai egymásnak asszociáltjai legyenek.
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Tegyük fel, hogy R elemein értelmezve van egy olyan f:R\to \N függvény, amely eleget tesz az alábbi követelményeknek:
- Tetszőleges a elem esetén f(a)=0 akkor és csak akkor teljesül, ha a=0_R, ahol 0_R az R gyűrű nullelemét, míg 0 a „nullának” nevezett természetes számot jelöli.
- Tetszőleges a és b\neq 0_R elemek esetén létezik olyan k hányados és r maradék az R gyűrűben, hogy a=k\cdot b + r és f(r)<f(b). Ezt a „műveletet” az a és b elemek közötti maradékos osztásnak vagy euklidészi osztásnak nevezzük.
Ekkor az f függvényt az R integritástartományon értelmezett euklidészi normának nevezzük. Amennyiben az R integritástartományon létezik (definiálható) euklidészi norma, úgy R-et euklidészi gyűrűnek nevezzük.
Ha egy R gyűrű valamely S részhalmaza maga is gyűrű az R műveleteire nézve, akkor azt mondjuk, hogy S részgyűrű R-ben. Ezt így jelöljük: S\leq R.
A nullgyűrű és maga a teljes R nyilvánvalóan részgyűrűk R-ben. Ezeket triviális részgyűrűknek nevezzük. Azt, hogy S részgyűrű R-ben, de S\neq R így jelöljük: S\lt R. Ilyenkor azt mondjuk, hogy S valódi részgyűrű R-ben.
Legyen adva egy R gyűrű, valamint annak egy I részhalmaza, amely részgyűrű R-ben. Tegyük fel továbbá, hogy r az R gyűrű egy tetszőleges – tehát nem feltétlenül I-beli – eleme.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az r\cdot a szorzat is I-ben van, akkor azt mondjuk, hogy I balideál R-ben.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az a\cdot r szorzat is I-ben van, akkor azt mondjuk, hogy I jobbideál R-ben.
Amennyiben egy I részgyűrű egyszerre bal- és jobbideál, akkor azt mondjuk, hogy I kétoldali ideál, vagy egyszerűen csak ideál R-ben. Ezt így jelöljük: I\triangleleft R.
A nullgyűrű és maga a teljes R nyilvánvalóan ideálok R-ben. Ezeket triviális ideáloknak nevezzük.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 12., 16., 17. és 18. részeket, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Az oszthatósági alapfogalmak kapcsán a 16. részben ismerkedtünk meg a felbonthatatlan (vagy prím-) számokkal, és láttuk, hogy ezek bizonyos értelemben az építőkövek szerepét töltik be a számok között. A 17. részben ugyanis igazoltuk, hogy egyrészt minden egész szám előállítható prímszámok szorzataként, másrészt pedig azt, hogy ez lényegében csak egyféleképpen tehető meg. Ezt a két állítást – tehát a prímtényezős felbontás létezését és egyértelműségét – együttesen a számelmélet alaptételének neveztük. Mi azonban nem kimondottan az egész számok körében, hanem ennél általánosabban, a gyűrűk – pontosabban az integritástartományok – absztrakciós szintjén vizsgáltuk a kérdést. Ezen a szinten általánosságban már különválik a felbonthatatlan (16.11. Definíció) és a prím fogalma (16.13. Definíció). Láttuk, hogy a számelmélet alaptétele bizony nem teljesül minden integritástartományban, ezért megpróbáltuk meghatározni ennek feltételeit. Először ismételjük át ennek főbb lépéseit.
A keresett feltételek megtalálása mindeddig felemásan sikerült. Elsőként a 16.18. Tétel és a 16.16. Tétel fogalmazott meg egy-egy szükséges feltételt. E két tétel alapján a számelmélet alaptétele csak egységelemes integritástartományokban teljesülhet, és azok közül is csak azokban, amelyekben minden felbonthatatlan elem prímtulajdonságú. Itt egyrészt megemlítettük, hogy ez a két feltétel szükséges ugyan, de önmagában még nem elégséges az alaptételhez. Másrészt viszont azt is megemlítettük, hogy „nem hiányzik sok”, mivel a második feltétel az alaptétel egyértelműségi állításához már elégséges (azaz a prímtényezős felbontás létezését ugyan nem garantálja, ám ha az mégis létezik, akkor egyértelmű).
Ezután a 17. részben megismerkedtünk az úgynevezett euklidészi gyűrűkkel (17.16. Definíció), amelyekben bizonyos absztrakt értelemben elvégezhető a maradékos osztás. Ennek két fontos következménye volt. Egyrészt a 17.17. Tétel értelmében bármely két elemnek létezik a kitüntetett közös osztója (17.4. Definíció), amelyből a 17.12. Tétel alapján következik, hogy minden felbonthatatlan elem prímtulajdonságú (azaz az alaptétel egyértelműségi állítása).
Másrészt viszont a 17.20. Tétel és a 17.21. Tétel alapján ha egy integritástartományon létezik bármilyen euklidészi norma, akkor létezik olyan is, amely szigorúan nagyobb értéket ad bármilyen kéttényezős szorzatra, mint a tényezőkre külön-külön (kivéve ha valamelyik tényező egység, amikoris egyenlőség áll fenn). Ebből a 17.22. Tétel alapján már viszonylag egyszerűen következik a prímtényezős felbontás létezéséről szóló állítás.
A maradékos osztás elvégezhetősége tehát egy elégséges feltétel az alaptétel tejesüléséhez, megemlítettük ugyanakkor, hogy sajnos nem szükséges. Léteznek ugyanis olyan integritástartományok, amelyek nem euklidészi gyűrűk, mégis teljesül bennük az alaptétel. Van már tehát szükséges (de nem elégséges), és elégséges (de nem szükséges) feltételünk. Jó volna mostmár végleg lezárni ezt a kérdést, és találni egy olyan feltételrendszert, amely egyszerre szükséges és elégséges is. Szerencsére az előző részben bevezetett ideálok segítségével ebben a részben képesek leszünk megfogalmazni egy ilyen feltételrendszert.
Ez szoros összefüggésben fog állni bizonyos ideálok egymáshoz való viszonyával. Minthogy egy gyűrű ideáljai tulajdonképpen halmazok, ezért nem árt először megismerkedni néhány halmazokkal kapcsolatos alapfogalommal és jelöléssel.
Halmazelméleti gyorstalpaló
A halmaz a matematika egyik legalapvetőbb fogalma, melyet leginkább az „összesség” illetve „sokaság” szavakkal tudunk körülírni. Ezt a fogalmat nem definiáljuk, mivel alapfogalom. Ez ahhoz hasonlatos, mint ahogyan a természetes számokat bevezettük a 11. részben. Ha visszaemlékszünk, ott sem mondtuk meg, hogy konkrétan mik azok a természetes számok. Pusztán annyit állítottunk róluk, hogy egy \N-nel jelölt halmaz elemei, amelyek eleget tesznek 4 egyszerű tulajdonságnak. Ezeket a tulajdonságokat Peano-axiómáknak neveztük és a 11.1. Definícióban soroltuk fel őket. Minden, amit az elmúlt részekben tárgyaltunk, ennek a mindössze 4 axiómának a következménye, vagy legalábbis abból eredeztethető.
Míg a természetes és az általánosabb egész számokkal a számelmélet, addig a halmazok tulajdonságaival a halmazelmélet foglalkozik. Végsősoron minden, a matematika által vizsgált objektum halmaz, de legalábbis megadható olyan modellje, amely kizárólag a halmazelmélet alapfogalmait használja. Így annak ellenére, hogy csak a 19. századra fejlődött ki, a halmazelmélet mára a modern matematika minden ágának – a matematikai logika mellett – az alapja lett.
A halmazelmélet korai változatát, az úgynevezett naív halmazelméletet Georg Cantor és Richard Dedekind úttörő munkásságának köszönhetjük. Mi ebben a részben elsősorban ezzel fogunk foglalkozni a könnyebb érthetőség kedvéért. Ugyanakkor megemlítjük, hogy a 20. század elején a naív halmazelméletben bizonyos szélsőséges esetekben komoly logikai ellentmondásokat fedeztek fel, amely az egész matematikát megrengette, így szükségessé vált a halmazelméletet is axiomatikus alapokra helyezni. Ebben a cikksorozatban azonban erre nem fogunk kitérni bővebben. Az általunk használt halmazelméleti eszköztár ugyanis az axiomatikus halmazelméletben is ugyanaz lenne.
Minden matematikai elmélet valamilyen objektumokkal, illetve azok tulajdonságaival foglalkozik. Például a számelméletben ezek az objektumok lehetnek mondjuk az egész számok, egy tulajdonság pedig a 2-vel való oszthatóság. A halmazelmélet ennél absztraktabb módon tekint a világra: számára csak objektumok és tulajdonságok vannak. Halmaznak nevezzük azon objektumok összességét, amelyekre teljesül valamilyen közös tulajdonság. Ám azzal, hogy konkrétan mik ezek az objektumok és a szóban forgó tulajdonság, a halmazelmélet szintjén már nem foglalkozunk. Ezt úgy is meg lehet fogalmazni, hogy magát a tulajdonságot – bármi legyen is az – egy halmazként, azokat az objektumokat pedig – bármik legyenek is azok –, amelyekre az e halmaz által reprezentált tulajdonság teljesül, a halmaz elemeiként képzeljük el.
Az alábbi definíció nem határozza meg a most ismertetett „halmaz” és „eleme lenni” fogalmak jelentését, mivel azok formális logikai szempontból alapfogalmak, így ez lehetetlen lenne. Ehelyett csak az ezekre vonatkozó jelöléseket ismerteti, valamint definiál néhány kapcsolódó fogalmat is, amelyek viszont már nem alapfogalmak:
19.1. Definíció (Halmazelméleti alapfogalmak):
A halmazelmélet mindössze két alapfogalmat használ. Ezek: a „halmaz” és az „eleme lenni” reláció. A halmazokat konvencionálisan nyomtatott nagybetűkkel jelöljük. Például: A.
Azt, hogy egy vizsgált a objektum eleme az A halmaznak, így jelöljük: a\in A. Azt, hogy a nem eleme A-nak, így jelöljük: a\notin A. E két állítás közül minden esetben pontosan az egyik teljesül.
Két halmazra akkor mondjuk, hogy egyenlőek egymással, ha pontosan ugyanazok az elemeik. Ha tehát A és B halmazok, akkor az A=B kifejezés azt jelenti, hogy minden a objektum esetén a\in A akkor és csak akkor teljesül, ha a\in B is teljesül.
Azt a halmazt, amelynek egyetlen eleme sincsen, üres halmaznak nevezzük, és így jelöljük: \empty. Ha tehát A=\empty, akkor minden a objektum esetén a\notin A.
Ezzel szemben azt a halmazt, amelynek minden vizsgált objektum eleme, univerzális halmaznak, tárgyalási univerzumnak, vagy egyszerűen csak univerzumnak nevezzük, és így jelöljük: U. Tehát minden a objektum esetén a\in U.
Egy halmaz (elemeinek) megadása kapcsos zárójelek között történik. Erre néhány példa látható a definíció utáni megjegyzésben. Bármilyen leírást is használunk, akkor mondjuk, hogy megadtunk egy halmazt, ha a tárgyalási univerzum minden objektumáról el lehet dönteni, hogy eleme-e vagy nem.
♣Megjegyzés:
Például ha P a páros számok halmaza, akkor ezt leírhatjuk az alábbi módokon:
- Az elemek felsorolása intuitív módon: A=\{\ldots ;-4;-2;0;2;4;\ldots\}
- Leírás eldöntési szabállyal („olyan x-ek, amelyek oszthatók 2-vel”): A=\{x:2|x\}
- Szöveges leírás: A=\{\text{páros egészek}\}
A definícióval kapcsolatban megjegyezzük az alábbiakat:
- Az üres halmaz egyértelmű, azaz csak egy üres halmaz létezik. Tegyük fel ugyanis indirekt, hogy két üres halmaz is létezik, amelyek különbözőek. Jelöljük ezeket \empty_1-gyel és \empty_2-vel. Ezek különbözősége a definíció szerint azt jelenti, hogy van olyan a objektum, amely esetén a\notin \empty_1, de a\in \empty_2, vagy pedig a\in \empty_1, de a\notin \empty_2. De ez ellentmond annak a ténynek, hogy a \empty_1 és a \empty_2 halmazoknak nincs egyetlen eleme sem.
- Hasonló okok miatt az U univerzális halmaz is egyértelmű. Tegyük fel ugyanis indirekt, hogy két univerzális halmaz is létezik, amelyek különbözőek. Jelöljük ezeket U_1-gyel és U_2-vel. Ezek különbözősége a definíció szerint azt jelenti, hogy van olyan a objektum, amely esetén a\notin U_1, de a\in U_2, vagy pedig a\in U_1, de a\notin U_2. De ez ellentmond annak a ténynek, hogy az U_1 és az U_2 halmazoknak minden objektum eleme.
- A fenti definícióban a „halmaz” és az „eleme lenni” kifejezések az alapfogalmak szerepét töltik be ugyanúgy, mint a 11.1. Definíció szerinti Peano-axiómarendszerben szereplő „nulla” és „rákövetkező” szavak. Ezeket nem definiáljuk, hanem helyette az axiómákban fogalmazzuk meg a velük szemben támasztott követelményeket.
- A fenti definícióban implicit módon csak egyetlen axióma szerepel, amely azt fogalmazza meg, hogy mikor nevezünk egyenlőnek két halmazt. Ezt meghatározottsági (vagy extenzionalitási) axiómának nevezzük. A naív halmazelméletben nincsenek további axiómák.
Az univerzális halmaz definíciójában szerepelő, kissé homályos „minden vizsgált objektum” megfogalmazás talán zavaró lehet. Az, hogy ezalatt pontosan mit értünk, mindig attól függ, hogy pontosan milyen matematikai objektumokat vizsgálunk a halmazelmélet eszközeivel. Vizsgálhatjuk például az egész számokat, amikoris az univerzális halmaz az egész számok \Z halmaza lesz. De vizsgálhatjuk például egy valamilyen H halmaz bizonyos részhalmazait is. Ebben az esetben az univerzális halmaz H-nak a vizsgált részhalmazaiból fog állni. Ilyen úgynevezett halmazrendszerekről lesz szó a következő szakaszban, azután pedig az ott szerzett ismereteket gyűrűk ideáljainak vizsgálatához fogjuk felhasználni.
Az imént bevezetett halmazelméleti alapfogalmak segítségével most bevezetünk egy fontos relációt két halmaz között.
19.2. Definíció (Részhalmaz):
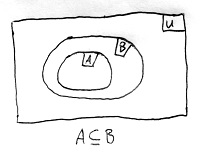
Legyenek A és B valamilyen halmazok. Tegyük fel továbbá, hogy minden olyan esetben, amikor a\in A teljesül, egyúttal teljesül a\in B is. Ekkor azt mondjuk, hogy az A halmaz részhalmaza a B halmaznak, vagy más szavakkal a B halmaz tartalmazza az A halmazt. Ezt így jelöljük: A\sube B.
Ha A\neq \empty és A\neq B, akkor azt mondjuk, hogy A valódi részhalmaza B-nek. Ezzel szemben az üres halmaz és maga B is nemvalódi részhalmazai B-nek.
Ha A\sube B, de A\neq B, akkor azt mondjuk, hogy szigorú tartalmazás áll fenn B és A között. Ezt így jelöljük: A\sub B.
♣Például az egész számok \Z halmazának egy valódi részhalmazát alkotják a páros számok. Részhalmaz, mert minden páros szám egyben egész szám is, és valódi részhalmaz, mert van olyan egész szám, amely nem páros.
Megjegyzés:
- Az imént bevezetett \sube szimbólummal jelölt tartalmazási relációt ne keverjük össze a 19.1. Definícióban bevezetett \in relációval. Nagyon nem ugyanaz a két fogalom! Ha például A és B két halmaz, akkor A\sube B azt fejezi ki, hogy A összes eleme egyúttal B-nek is eleme. Ezzel szemben A\in B azt fejezi ki, hogy B egy olyan halmaz, amelynek elemei maguk is halmazok, és ezek közül az A halmaz az egyik. Az előző részben a 18.23. Tételben bevezetett maradékosztálygyűrűknek például az elemei maradékosztályok, amelyek ugye maguk is halmazok. Gyakran fogjuk ugyanakkor használni az „A tartalmazza B-t elemként” kifejezést. Ilyenkor értelemszerűen mindig a B\in A „eleme”-relációra, és nem pedig a B\sube A tartalmazási relációra gondolunk.
- Az üres halmaz részhalmaza tetszőleges A halmaznak, hiszen nyilván igaz az a kijelentés, hogy az üres halmaz minden eleme egyben A-nak is eleme. Az persze más kérdés, hogy ez a „minden eleme” jelen esetben 0 darab elemet jelent. Ezt a furcsa logikai jelenséget a 17.22. Tétel bizonyítása utáni megjegyzésben fejtettük ki részletesen.
- Minden A halmaz részhalmaza önmagának (azaz A\sube A), máskülönben létezne olyan a objektum, amelyre a\in A és a\notin A egyszerre teljesül, ami nyilvánvaló ellentmondás.
- Minden A halmaz részhalmaza továbbá az U univerzális halmaznak. Máskülönben létezne olyan a objektum, amelyre a\in A teljesül ugyan, azonban a\notin U. Ez nyilvánvaló ellentmondás, mivel a 19.1. Definíció alapján U-nak eleme minden objektum.
- Két halmaz akkor és csak akkor egyenlő egymással, ha részhalmazai egymásnak. Ha ugyanis A=B, akkor a fenti 3. megjegyzés miatt A\sube B és B\sube A teljesül. Visszafelé: Egyrészt, ha A\sube B teljesül, akkor a\in A-ból következik a\in B. Másrészt ha B\sube A is teljesül, akkor a\in B-ből is következik a\in A. Ebben az esetben tehát a\in A akkor és csak akkor, ha a\in B, azaz a két halmaznak pontosan ugyanazok az elemei, és így a 19.1. Definíció alapján egyenlőek egymással.
Halmazok között értelmezhetünk kétváltozós műveleteket (lásd a 11.3. Definíciót). Ezek tehát két tetszőleges halmazból képeznek egy újabb halmazt, méghozzá az alábbiak szerint.
19.3. Definíció (Halmazműveletek):
Legyen A és B két tetszőleges halmaz. Ekkor az A és B halmazok uniójának (vagy egyesítésének) nevezett halmaznak azok az objektumok az elemei, amelyek elemei az A és B közül legalább az egyiknek. Ezt a halmazt A\cup B-vel jelöljök.
Az A és B halmazok metszetének (vagy közös részének) nevezett halmaznak azok az objektumok az elemei, amelyek elemei az A halmaznak is és a B halmaznak is. Ezt a halmazt A\cap B-vel jelöljük. Ha A és B közös részének egyáltalán nincsenek elemei – azaz A\cap B=\empty –, akkor őket diszjunkt halmazoknak nevezzük.
Végül az A és B halmazok különbségének nevezett halmaznak azok az objektumok az elemei, amelyek elemei az A halmaznak, de nem elemei a B halmaznak. Ezt a halmazt A\setminus B-vel jelöljük. Amennyiben B\sube A, akkor az A\setminus B halmazt a B halmaz A-ra vonatkozó komplementerének is nevezzük. Beszélhetünk egy valamilyen A halmaznak egyszerűen csak a komplementeréről, amely alatt az U\setminus A halmazt értjük, ahol U jelöli a 19.1. Definíció szerinti univerzális halmazt. Az A halmaz komplementerét \overline{A}-val jelöljük.
♣Ha például A=\{1;2;3\}, B=\{3;4;5\}, és az U univerzumnak a pozitív egész számokat tekintjük, akkor az imént definiált halmazműveletek az alábbi halmazokat adják:
\begin{aligned}A\cup B&=\{1;2;3;4;5\} \\ A\cap B&=\{3\} \\ A\setminus B&=\{1;2\} \\ B\setminus A&=\{4;5\} \\ \overline{A}&=\{4;5;6;\ldots\} \\ \overline{B}&=\{1;2;6;7;8;\ldots\}\end{aligned}A halmazokat, illetve azok viszonyait az úgynevezett Venn-diagramok segítségével ábrázolhatjuk. Itt a halmazokat különböző síkidomok (körök, téglalapok, ellipszisek), míg a halmazok elemeit pontok reprezentálják. Az univerzális halmazt legtöbbször az ábrát körülvevő tégalalappal jelöljük. A Venn-diagram általában csak néhány halmaz szemléltetésére alkalmas, mivel sok egymást kölcsönösen metsző halmaz esetén az ábra elbonyolódik, vagy nem is lehetséges az összes metszetet ábrázolni. Az alábbi Venn-diagramokon a fenti példában szereplő halmazműveleteket és a 19.2. Definíció szerinti tartalmazási relációt szemléltettük:

A 19.3. Definíció szerinti halmazműveletekre érvényesek az alábbi tulajdonságok.
19.4. Tétel (Halmazműveletek tulajdonságai):
Legyenek A, B és C tetszőleges halmazok, valamint jelölje U az univerzális, \empty pedig az üres halmazt. Ekkor teljesülnek az alábbiak:
- Az üres halmaz az unióképzés, az univerzális halmaz pedig a metszetképzés műveletére nézve neutrális elem (lásd a 14.7. Definíciót), azaz A\cup \empty=A és A\cap U=A.
- Mindkét műveletre teljesül az úgynevezet idempotencia, azaz A\cup A=A és A\cap A=A.
- Mindkét művelet kommutatív, azaz A\cup B=B\cup A és A\cap B=B\cap A.
- Mindkét művelet asszociatív, azaz (A\cup B)\cup C=A\cup (B\cup C) és (A\cap B)\cap C=A\cap (B\cap C).
- A két művelet kölcsönösen disztributív egymásra nézve, azaz A\cup (B\cap C)=(A\cup B)\cap (A\cup C) és A\cap (B\cup C)=(A\cap B)\cup (A\cap C).
- Mindkét műveletre teljesül az úgynevezett elnyelési tulajdonság (abszorptivitás), azaz A\cup (A\cap B)=A és A\cap (A\cup B)=A.
- Az üres halmaz és az univerzális halmaz egymás komplementerei, azaz \overline{\empty}=U és \overline{U}=\empty.
- A komplementerképzést duplán elvégezve az eredeti halmazt kapjuk vissza, azaz \overline{\overline{A}}=A.
- Egy halmaz és komplementerének uniója az univerzális halmaz, metszetük pedig az üres halmaz, azaz A\cup \overline{A}=U és A\cap \overline{A}=\empty.
- Teljesülnek az úgynevezett de Morgan-azonosságok, azaz \overline{A\cup B}=\overline{A}\cap \overline{B} és \overline{A\cap B}=\overline{A}\cup \overline{B}.
Az alábbi bizonyítás gondolatmeneteinek könnyebb megértése érdekében javasoljuk az Olvasónak a fentebb már említett Venn-diagramok használatát.
Bizonyítás:
Az 1. tulajdonság: Ez nyilvánvalóan következik az üres halmaz és az univerzális halmaz definíciójából. Az üres halmaznak ugyanis nincs egyetlen eleme sem, így a vele végzett unióképzés nem ad hozzá elemeket semmilyen halmazhoz. Ehhez hasonlóan az univerzális halmaznak minden objektum az eleme, így a vele végzett metszetképzés nem vesz el elemeket semmilyen halmazból.
A 2. tulajdonság: Ez is teljesen nyilvánvalóan adódik az unió- és a metszetképzés 19.3. Definíciójából.
A 3. tulajdonság: Ha a\in A vagy a\in B közül legalább az egyik teljesül, akkor ez nyilván nem változik a két feltétel megcserélésével sem. Így tehát az A\cup B halmaz pontosan meg fog egyezni a B\cup A halmazzal. Ugyanez a gondolatmenet a metszetképzéssel is végigjátszható.
A 4. tulajdonság: Az unióképzésre vonatkozó asszociativitás mindkét oldalán az a halmaz szerepel, amelynek minden a elemére a\in A, a\in B vagy a\in C közül legalább az egyik teljesül, hiszen teljesen mindegy, hogy ezt a 3 feltételt milyen sorrendben ellenőrizzük le. A metszetképzésre vonatkozó asszociativitásra ugyanez a gondolatmenet végigjátszható.
Az 5. tulajdonság: Csak az első disztributivitási szabályt fogjuk igazolni, a másik nagyon hasonló gondolatmenettel igazolható. Tegyük fel, hogy egy x objektum benne van a disztributivitási szabály baloldalán lévő halmazban, azaz az A\cup (B\cap C) unióhalmazban. Itt az unió miatt két eset lehetséges. Első esetben x\in A, és ekkor nyilván x\in A\cup B és x\in A\cup C is teljesül, tehát x\in (A\cup B)\cap (A\cup C) is. Második esetben x\notin A, de ekkor viszont az unió miatt x\in B\cap C, tehát x\in B és x\in C egyszerre teljesül. Ilyenkor megintcsak teljesülnek az x\in A\cup B és x\in A\cup C relációk, azaz x\in (A\cup B)\cap (A\cup C) is. Mindkét esetben azt kaptuk, hogyha x eleme a disztributivitási szabály baloldalának, akkor eleme a jobboldalának is, tehát a baloldal részhalmaza a jobboldalnak.
Most tegyük fel, hogy x benne van a disztributivitási szabály jobboldalán lévő halmazban, azaz az (A\cup B)\cap (A\cup C) metszethalmazban. Itt a metszet miatt tehát x\in A\cup B és x\in A\cup C is teljesül. Ez két ok miatt teljesülhet. Egyrészt, ha x\in A, akkor jók vagyunk, mert ekkor x benne van minkét unióban, és így ezek metszetében is. Ha x\notin A, akkor viszont x\in B és x\in C kell teljesüljön, ami azt jelenti, hogy x\in B\cap C. Azt kaptuk, hogy x\in A vagy x\in B\cap C közül legalább az egyik teljesül, azaz x\in A\cup (B\cap C) is. Ha tehát x eleme a disztributivitási szabály jobboldalának, akkor eleme a baloldalnak is, tehát a jobboldal is részhalmaza a baloldalnak.
Minthogy a szabály két oldalán álló halmazokról megmutattuk, hogy kölcsönösen részhalmazai egymásnak, ezért a 19.2. Definíció utáni 5. megjegyzés alapján szükségképpen megegyeznek. A másik disztributivitási szabály ugyanilyen módon igazolható.
A 6. tulajdonság: Nézzük először az A\cup (A\cap B) kifejezést. Mivel a metszetképzés 19.3. Definíciója miatt bármilyen x objektum esetén ha x\in A\cap B, akkor x\in A, ezért ez egyben azt is jelenti, hogy a zárójelben lévő metszet részhalmaza A-nak (lásd a 19.2. Definíciót). A fenti kifejezésben tehát tulajdonképpen az A halmaznak egy X részhalmazával vett uniója szerepel. Az A\cup X unió viszont nyilvánvalóan A-val egyezik meg, mivel X-nek nincs olyan eleme, ami ne lenne magának A-nak is eleme (hiszen azt mondtuk, hogy X\sube A). Valóban igaz tehát, hogy A\cup (A\cap B)=A, azaz teljesül az unióképzésre vonatkozó elnyelési tulajdonság. A metszetképzésre vonatkozó elnyelési tulajdonság a disztributivitásból és az idempotenciából következik:
A\cap (A\cup B)=(\underbrace{A\cap A}_{=A})\cup (A\cap B)=A\cup (A\cap B)=AA 7. tulajdonság: Az üres halmaz komplementere az U\setminus \empty különbséghalmaz, amely a 19.3. Definíció alapján azokat az elemeket tartalmazza, amelyek benne vannak U-ban, de nincsenek benne az üreshalmazban. Tekintve, hogy az üres halmazban egyáltalán nincsenek elemek, ezért ez a különbséghalmaz magával U-val egyezik meg. Ehhez hasonlóan az univerzális halmaz komplementere az U\setminus U különbséghalmaz, amely tehát azokat az elemeket tartalmazza, amelyek benne is vannak és nincsenek is benne U-ban. Ilyen elem létezése nyilvánvaló ellentmondás lenne, ezért ez a különbséghalmaz csak az üres halmaz lehet.
A 8. tulajdonság: Az \overline{A} komplementerhalmaz azokat az elemeket tartalmazza, amelyekre nem igaz az, hogy elemei A-nak. Ennek a komplementere pedig azokat, amelyekre nem igaz az, hogy nem elemei A-nak. Ezek viszont a dupla tagadás miatt épp A elemei, azaz valóban \overline{\overline{A}}=A.
A 9. tulajdonság: Az A halmaz és komplementerének úniója azokat az x elemeket tartalmazza, amelyekre x\in A vagy x\notin A közül legalább az egyik teljesül. Ez viszont minden létező x igaz, hiszen valami vagy benne van egy halmazban, vagy nincs. Így tehát valóban A\cup \overline{A}=U. Ehhez hasonlóan az A halmaz és komplementerének metszete az üres halmaz, máskülönben létezne olyan x, amelyre x\in A és x\notin A egyszerre teljesülne, ami nyilvánvaló ellentmondás. Így tehát valóban A\cap \overline{A}=\empty.
Végül a 10. tulajdonság: Az A\cup B komplementerébe azok az x elemek tartoznak, amelyekre nem igaz az, hogy x\in A vagy x\in B közül legalább az egyik teljesül. Másként fogalmazva ezek az elemek sem A-ban, sem pedig B-ben nincsenek benne, azaz ezekre x\notin A és x\notin B egyszerre teljesül. Ez viszont épp A és B komplementerhalmazainak a metszete. Ehhez hasonlóan az A\cap B komplementerébe azok az x elemek tartoznak, amelyekre nem igaz az, hogy x\in A és x\in B egyszerre teljesül. Másként fogalmazva ezek az elemek A és B közül legalább az egyikben nincsenek benne, azaz ezekre x\notin A vagy x\notin B közül legalább az egyik teljesül. Ez viszont épp A és B komplementerhalmazainak az uniója.
∎Halmazrendszerek
E rövid halmazelméleti gyorstalpaló után ebben a szakaszban olyan halmazokkal fogunk megismerkedni, amelyeknek az elemei maguk is halmazok. Ezeknek az első hallásra furcsa halmazoknak külön nevük is van, és kontextustól függően általában jelölésben is megkülönböztetjük őket.
19.5. Definíció (Halmazrendszerek):
Legyen H egy tetszőleges halmaz, valamint jelöljük \mathcal{H}-val azt a halmazt, amelynek elemei H-nak bizonyos részhalmazai – de nem feltétlenül az összes. Ekkor a \mathcal{H} halmazt egy H feletti halmazrendszernek, magát a H halmazt pedig e halmazrendszer alaphalmazának nevezzük.
Speciálisan azt a H feletti halmazrendszert, amely a H összes részhalmazaiból áll – beleértve a két nemvalódi részhalmazt is –, a H halmaz hatványhalmazának nevezzük, és így jelöljük: \mathcal{P}(H). A H feletti halmazrendszerek tehát pontosan a \mathcal{P}(H) hatványhalmaz részhalmazai.
♣Tegyük fel például, hogy az alaphalmazunk az alábbi:
H=\{1;2;3\}Ekkor a \mathcal{P}(H) hatványhalmaznak összesen 8 eleme lesz, méghozzá a H halmaz összes lehetséges részhalmaza:
\mathcal{P}(H)=\{ \empty; \{1\};\{2\};\{3\}; \{1;2\}; \{1;3\}; \{2;3\}; \{1;2;3\}\}Jól vigyázzunk a jelölésekre! Először is a \empty itt nem a „nulla” egész számot, hanem az üres halmazt jelöli. Nagyon nem mindegy továbbá, hogy 1-et, vagy pedig \{1\}-et írunk. Az 1 ugyanis NEM a \mathcal{P}(H) hatványhalmaznak, hanem magának a H alaphalmaznak egy eleme. Ezzel szemben az egyetlen elemből álló \{1\} halmaz már a \mathcal{P}(H) hatványhalmaznak egy eleme. Látható, hogy a \mathcal{P}(H) halmazban valóban benne van H összes részhalmaza elemként. Még a \empty-val jelölt üres halmaz, sőt, maga a H=\{1;2;3\} alaphalmaz is.
A definíció szerint tehát \mathcal{P}(H) maga is egy halmazrendszer H felett, méghozzá a lehető legbővebb, ami csak létezik. De tegyük fel, hogy mi H-nak csak a valódi részhalmazait szeretnénk vizsgálni. Ezek szintén egy halmazrendszert alkotnak H felett, amelyet jelöljünk most \mathcal{H}-val. Ekkor a \mathcal{H} halmazrendszer az alábbi 6 elemből fog állni:
\mathcal{H}=\{ \{1\};\{2\};\{3\}; \{1;2\}; \{1;3\}; \{2;3\}\}Mint ahogyan a definícióban már említettük, a \mathcal{H} halmazrendszer \mathcal{P}(H)-nak egy részhalmaza lesz, azaz \mathcal{H}\sube \mathcal{P}(H). Nyilván, hiszen minden \mathcal{H}-beli elem egyúttal eleme a \mathcal{P}(H) hatványhalmaznak is. Előbbi ugyanis a H alaphalmaznak csak a valódi részhalmazait tartalmazza elemként, utóbbi pedig az összeset.
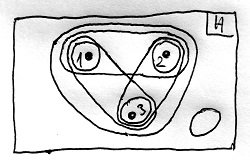
Ha esetleg az Olvasó megpróbálta magát a H alaphalmazt, illetve a fenti \mathcal{H} halmazrendszert ugyanazon a Venn-diagramon ábrázolni, akkor ez a kísérlet minden bizonnyal sikertelenül zárult. Ennek az a nagyon egyszerű oka, hogy teljesen más jellegű matematikai objektumokról van szó. Első esetben ugyanis a vizsgált objektumok tulajdonképpen a H halmaz elemei, azaz az 1, 2, és 3 egész számok, így a tárgyalási univerzumnak a H halmazt tekinthetjük. Ennek megfelelően az alábbi Venn-diagramon a H halmaz részhalmazait ellipszisekkel ábrázolhatjuk, míg a H feletti halmazrendszereket ezen az ábrán nem tudjuk megjeleníteni:
Ezzel szemben a második esetben a vizsgált objektumok a H részhalmazai, a tárgyalási univerzum pedig ebben az esetben a \mathcal{P}(H) hatványhalmaz lesz. Ennek megfelelően az alábbi Venn-diagramon a H halmaz részhalmazait pontokkal jelöljük, és így a H feletti halmazrendszerek már láthatóvá válnak:
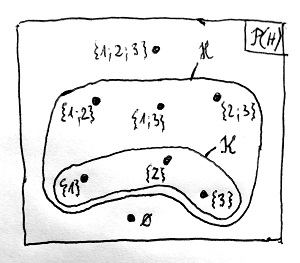
Itt például a példában szereplő \mathcal{H} halmazrendszer mellett egy másik, \mathcal{K}-val jelölt halmazrendszert is ábrázoltunk, amely a H alaphalmaznak a pontosan egyelemű részhalmazait tartalmazza elemként.
Halmazrendszerek részbenrendezése
A 12. részben a természetes számok \leq szimbólummal jelölt rendezési relációjának kapcsán általánosságban is szó volt az úgynevezett részbenrendezésekről és részbenrendezett halmazokról. Javasoljuk az Olvasónak, hogy a továbbolvasás előtt ismételje át az ott tanult fogalmakat. A 12.12. Definícióban részbenrendezésnek hívtuk azokat a relációkat, amelyek egyszerre reflexívek (12.8. Definíció), antiszimmetrikusak (12.9. Definíció) és tranzitívak (12.10. Definíció).
Az alábbi tétel alapján bármilyen \mathcal{H} halmazrendszer is tulajdonképpen nem más, mint egy részbenrendezett halmaz.
19.6. Tétel:
Legyen H egy tetszőleges halmaz, \mathcal{H} pedig egy H feletti halmazrendszer. Ekkor a H hamaz részhalmazai közötti \sube reláció egy részbenrendezés a \mathcal{H} halmazrendszer elemei között. Azaz a \sube reláció reflexív, antiszimmetrikus és tranzitív.
A \sub szigorú tartalmazási reláció ezzel szemben nem részbenrendezés, mivel nem reflexív és nem antiszimmetrikus. A tranzitivitást viszont ez a reláció is teljesíti.
♣Bizonyítás:
A 19.2. Definíció utáni megjegyzés 3. és 5. pontjai alapján a \sube reláció reflexív és antiszimmetrikus. Így már csak azt kell megmutatni, hogy teljesül a tranzitivitás is, azaz a halmazrendszer tetszőleges A, B és C elemei esetén ha A\sube B és B\sube C, akkor A\sube C. Ez viszont könnyedén adódik a részhalmaz 19.2. Definíciójából.
Legyen ugyanis x egy tetszőleges elem a H alaphalmazban. Mivel A\sube B, ezért ha x\in A teljesül, akkor x\in B is teljesül. Ugyanakkor B\sube C is igaz, ezért egyúttal x\in C is teljesül. Mivel azt kaptuk, hogy x\in A-ból következik x\in C, ezért valóban A\sube C.
Most térjünk át a \sub relációra vonatkozó állításokra. Ez nyilvánvalóan nem reflexív, ugyanis A\sub A a 19.2. Definíció alapján azt jelentené, hogy A\sube A és A\neq A. Ez utóbbi nyilván lehetetlen, mivel minden halmaz azonos önmagával. De antiszimmetrikus sem lehet, hiszen akkor a 12.9. Definíció miatt A\sub B és B\sub A esetén A=B következne. Ez ugye lehetetlen, mert például A\sub B azt jelenti, hogy A\sube B és A\neq B.
Végül megmutatjuk, hogy \sub tranzitív. Tegyük fel, hogy A\sub B és B\sub C. Ezek a feltételek a 19.2. Definíció alapján azt jelentik, hogy egyrészt A\sube B és B\sube C, másrészt pedig A\neq B és B\neq C. Az első két feltételből a \sube reláció tranzitivitása miatt A\sube C következik, tehát a \sub reláció tranzitivitásához elegendő azt megmutatni, hogy A\neq C. A B\sube C tartalmazás miatt egyrészt tudjuk, hogy B minden eleme C-nek is eleme. Másrészt B\neq C miatt azt is tudjuk, hogy C-nek van olyan x eleme, ami viszont nem eleme B-nek, azaz x\in B nem teljesül. Azt kell igazolni, hogy x\in A sem teljesül. Ez viszont nyilvánvaló, máskülönben A\sube B miatt x\in B mégiscsak teljesülne, ami ellentmondás. A \sub-val jelölt szigorú tartalmazási reláció tehát valóban tranzitív.
∎A részbenrendezett halmazok ábrázolására szolgál az úgynevezett Hasse-diagram. Egy ilyen diagramon a halmaz elemeit pontok reprezentálják, és két pont között pontosan akkor megy él, ha ők „közvetlenül egymás után vannak” a vizsgált részbenrendezés szerinti „nagyságrendi sorban”. Azt, hogy melyikük a „kisebb” vagy „nagyobb” úgy ábrázoljuk, hogy a „nagyobb” elemet feljebb rajzoljuk az ábrán. Ez az ábrázolásmód azért működik, mert a részbenrendezés „irányát” követve annak tranzitivitása miatt soha nem fordulhat elő, hogy egy pontból kiindulva oda visszatérnénk.
Tekintsük például az előző szakaszban fehozott H=\{1;2;3\} alaphalmazt, és képezzük ennek a \mathcal{P}(H) hatványhalmazát. Ez ugye egy halmazrendszer H felett, amelynek a Hasse-diagramja az alábbi ábrán látható:
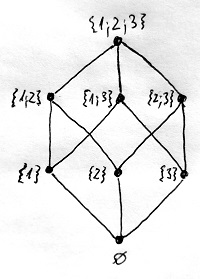
A diagramon az is jól látszik, hogy a \sube rendezési relációra nem teljesül a trichotómia (12.11. Definíció). A trichotómia ugye azt követeli meg, hogy bármely két elem összehasonlítható legyen egymással. Az egész számok \Z gyűrűjének vagy a természetes számok \N halmazának rendezése teljesíti ezt az extra tulajdonságot is, ezért neveztük őket teljes rendezésnek. Ezzel szemben a \sube reláció nem egy teljes rendezés, hiszen például az \{1;2\} és a \{2;3\} részhalmazok között egyik irányban sem teljesül a tartalmazás, így ők nem összehasonlíthatók. A fenti diagramon ez úgy mutatkozik meg, hogy egyikből sem tudunk eljutni a másikba az éleken keresztül, amennyiben csak lentről felfelé haladhatunk. De például a \{2\} és az \{1;2;3\} részhalmazok között fennáll a tartalmazási reláció, hiszen \{2\}-ből felfelé kiindulva két lépés után az \{1;2;3\}-hoz érkezünk.
A \mathcal{P}(H) halmazrendszer Hasse-diagramját vizsgálva feltűnhet, hogy az egész számok \Z gyűrűjének rendezésével ellentétben itt létezik „legkisebb” és „legnagyobb” elem. A „legkisebb” elem szerepét itt az üres halmaz tölti be, hiszen nincs másik olyan halmaz, amely „szűkebb” lenne nála. Ehhez hasonlóan a „legnagyobb” elem maga a H alaphalmaz, hiszen nincs másik olyan halmaz, amely „bővebb” lenne nála. Az alábbi definíció ezeket a fogalmakat tisztázza.
19.7. Definíció:
Legyen H egy tetszőleges halmaz, \mathcal{H} pedig egy tetszőleges halmazrendszer H felett. A \mathcal{H} halmazrendszer egy A elemét \mathcal{H}-ban minimális elemnek nevezzük, ha nem létezik olyan X elem a halmazrendszerben, amelyre X\sub A teljesülne, és \mathcal{H}-ban legszűkebb (vagy legkisebb) elemnek nevezzük, ha a halmazrendszer tetszőleges X elemére A\sube X teljesül.
Ehhez hasonlóan a \mathcal{H} halmazrendszer egy A elemét \mathcal{H}-ban maximális elemnek nevezzük, ha nem létezik olyan X elem a halmazrendszerben, amelyre A\sub X teljesülne, és \mathcal{H}-ban legbővebb (vagy legnagyobb) elemnek nevezzük, ha a halmazrendszer tetszőleges X elemére X\sube A teljesül.
♣Talán egy kicsit furcsa lehet, hogy a definíció megkülönbözteti a „minimális” és a „legkisebb”, valamint a „maximális” és a „legnagyobb” fogalmát. Ennek személtetéséhez vizsgáljunk most két halmazrendszert a H=\{1;2;3;4\} halmaz felett. Az egyik legyen a teljes \mathcal{P}(H) hatványhalmaz, a másikat pedig jelöljük \mathcal{H}-val, és tartalmazza H-nak csak a valódi részhalmazait. Az alábbi ábrákon egymás alatt láthatjuk e két halmazrendszer Hasse-diagramjait.
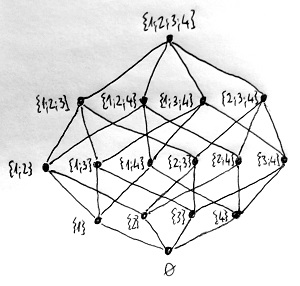
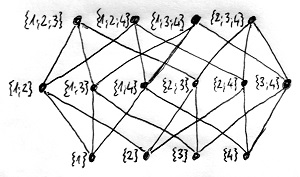
Látható, hogy minimuma és maximuma mindkét halmazrendszernek van. A \mathcal{P}(H) halmazrendszer minimuma a \empty-val jelölt üres halmaz, maximuma pedig a teljes H=\{1;2;3;4\} alaphalmaz. A \mathcal{H} halmazrendszernek szintén van minimuma és maximuma is, ráadásul több is. Minimuma például az összes egyelemű részhalmaz, hiszen nincs olyan halmaz \mathcal{H}-ban, amely ezek bármelyikének valódi részhalmaza lenne. Ehhez hasonlóan maximuma az összes háromelemű részhalmaz, hiszen nincs olyan halmaz \mathcal{H}-ban, amelynek ezek bármelyike valódi részhalmaza lenne.
Ezzel szemben legszűkebb illetve legbővebb eleme csak a \mathcal{P}(H) halmazrendszernek van, méghozzá szintén az üres halmaz és a teljes H alaphalmaz. Előbbi ugyanis a halmazrendszer minden elemének részhalmaza, utóbbinak pedig a halmazrendszer minden eleme részhalmaza. Ezzel szemben a \mathcal{H} halmazrendszerben nem találunk ilyen értelemben legszűkebb és legbővebb elemeket.
A minimum (illetve maximum) esetén tehát csak annyit követelünk meg, hogy ne legyen náluk szűkebb (vagy bővebb) halmaz a rendszerben. De mivel létezhetnek olyan halmazok, amelyek egymással nem összehasonlíthatók a \sube reláció szerint, ezért létezhet több minimum (illetve maximum) is a rendszerben, ahogyan azt a fenti példa mutatja. A legszűkebb (illetve legbővebb) halmaz fogalma ennél szigorúbb feltételt határoz meg, ezektől ugyanis megköveteljük, hogy bármelyik másik halmazzal összehasonlíthatóak legyenek. Most megmutatjuk, hogy ha egyáltalán létezik legszűkebb (illetve legbővebb) halmaz egy rendszerben, akkor az egyértelmű.
19.8. Tétel:
Legyen H egy tetszőleges halmaz, \mathcal{H} pedig egy tetszőleges halmazrendszer H felett. Ekkor \mathcal{H}-ban legfeljebb egy legszűkebb (illetve legbővebb) elem létezhet.
Ezen túlmenően, ha A a legszűkebb (illetve legbővebb) elem \mathcal{H}-ban, akkor egyrészt A minimális (illetve maximális) elem \mathcal{H}-ban, másrészt ilyenkor ő az egyetlen minimális (illetve maximális) elem.
♣Bizonyítás:
Tegyük fel, hogy A és B is legszűkebb elem \mathcal{H}-ban. Mivel A legszűkebb elem, ezért ő tetszőleges halmaznak részhalmaza, többek között például B-nek is, azaz A\sube B. Másrészt, mivel B is legszűkebb elem, ezért ő is részhalmaza tetszőleges halmaznak, többek között például A-nak is, azaz B\sube A. Így tehát A és B kölcsönösen részhalmazai egymásnak, vagyis a 19.2. Definíció utáni megjegyzés 5. pontja miatt megegyeznek, azaz A=B. Egy halmazrendszer legszűkebb eleme tehát – amennyiben egyáltalán létezik – egyértelmű. Ugyanilyen gondolatmenettel belátható, hogy egy halmazrendszer legbővebb eleme is egyértelmű.
Tegyük fel most indirekt, hogy A a \mathcal{H} halmazrendszer legszűkebb eleme, azonban mégsem minimális. Ez egyrészt azt jelentené, hogy létezik olyan X halmaz \mathcal{H}-ban, amelyre X\sub A teljesül. Másrészt, mivel A a legszűkebb \mathcal{H}-ban, ezért A\sube X-nek is teljesülnie kéne. De X\sub A és A\sube X egyszerre nem teljesülhet, hiszen ekkor X\sub A alapján létezne olyan a, amely eleme A-nak, de nem eleme X-nek, ugyanakkor A\sube X miatt mindenképpen eleme kéne legyen X-nek. Egy halmazrendszer legszűkebb eleme tehát – amennyiben egyáltalán létezik – mindenképpen minimális. Ugyanilyen gondolatmenettel belátható egy halmazrendszer legbővebb eleméről, hogy – amennyiben egyáltalán létezik – mindenképpen maximális.
Végül tegyük fel, hogy A a \mathcal{H} halmazrendszer legszűkebb eleme, amely tehát minimális, de létezik egy másik minimális elem is, amelyet jelöljünk most B-vel. Mivel A a legszűkebb elem, ezért A\sube B teljesül. Ugyanakkor, mivel B minimális, ezért nem állhat fenn az A\sub B szigorú tartalmazás. Ez a 19.2. Definíció alapján A\sube B mellett csak A=B esetén lehetséges. Tehát valóban A az egyetlen minimális elem. Ugyanilyen gondolatmenettel belátható, hogy amennyiben A a legbővebb elem \mathcal{H}-ban, akkor egyúttal ő az egyetlen maximális elem.
∎Az iménti tétel szerint tehát egy halmazrendszerben legfeljebb egy legszűkebb, illetve legfeljebb egy legbővebb elem létezhet. Jogosan teheti fel a kérdést az Olvasó, hogy miféle elvetemült halmazrendszer lehet az, amelyben egyáltalán nem léteznek ilyen tulajdonságú halmazok. Azt még csak-csak el lehet képzelni, hogy nincs legbővebb halmaz. Például az egész számok \Z halmaza felett könnyen találhatunk olyan halmazrendszert, amelynek nincs legbővebb eleme. Ilyen például az alábbi halmazokból álló rendszer:
\begin{aligned}A_0&=\empty \\ A_1&=\{1\} \\ A_2&=\{1;2\} \\ A_3&=\{1;2;3\} \\ A_4&=\{1;2;3;4\} \\ &\vdots \end{aligned}Látható, hogy ebben a halmazsorozatban minden elem valódi részhalmaza a rákövetkező elemnek, így ebben a \Z feletti halmazrendszerben nem létezik legbővebb elem. Ezzel szemben elsőre nehéz elképzelni egy olyan halmazrendszert \Z felett, amelynek ne lenne legszűkebb eleme. Meglepő módon azonban ilyen is létezik. Vegyük például az alábbi konstrukciót:
\begin{aligned}A_0 &=\Z \\ A_1&=\Z\setminus \{1\} \\ A_2&=\Z\setminus\{1;2\} \\ A_3&=\Z\setminus \{1;2;3\} \\ A_4&=\Z\setminus \{1;2;3;4\} \\ &\vdots \end{aligned}Ennek a sorozatnak az első eleme tehát a teljes \Z halmaz, amelyből szép sorban elkezdünk kidobálni egyre több, de mindig véges számú egész számot. Nyilvánvalóan ebben a sorozatban minden elem valódi részhalmaza a sorozatban előtte lévő elemnek, így ebben a \Z feletti halmazrendszerben nem létezik legszűkebb elem.
De elképzelhetünk egy olyan halmazrendszert is, amelynek alaphalmazát egy síkra rajzolt szakasz pontjai alkotják, és amely az alábbi A_0, A_1, A_2, A_3, … halmazsorozatból áll:
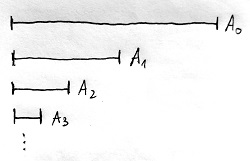
Ennek a sorozatnak minden eleme az eredeti szakasz feleakkora részéből áll, mint az őt megelőző elem. Azaz a sorozatban minden elem valódi részhalmaza a sorozatban előtte lévő elemnek, így ebben a rendszerben sincs legszűkebb elem.
A további szakaszokban az eddig szerzett halmazelméleti ismereteinket gyűrűk ideáljainak vizsgálatához fogjuk felhasználni.
Ideálok generálása
Egy gyűrű tulajdonképpen nem más, mint egy R alaphalmaz, amelyen értelmezve van két művelet. Ennek megfelelően R részgyűrűi és ideáljai is halmazok, méghozzá R részhalmazai. Előszöris megmutatjuk, hogy milyen hatása van a metszetképzésnek egy tetszőleges gyűrű részgyűrűi és ideáljai között.
19.9. Tétel:
Legyen R egy tetszőleges gyűrű, valamint legyen \mathcal{S} egy olyan R feletti halmazrendszer, amely R valahány – akár végtelen számú – részgyűrűjét tartalmazza elemként. Ekkor az \mathcal{S}-ben lévő halmazok metszete is részgyűrű R-ben.
Ehhez hasonlóan ha az \mathcal{I} egy olyan halmazrendszer, amely R valahány – akár végtelen számú – balideálját (illetve jobbideálját) tartalmazza elemként, akkor az \mathcal{I}-ben lévő halmazok metszete is balideál (illetve jobbideál) R-ben.
Végül ha \mathcal{J} az R gyűrű valahány – akár végtelen számú – (kétoldali) ideálját tartalmazza elemként, akkor a \mathcal{J}-ben lévő halmazok metszete is (kétoldali) ideál R-ben.
♣Például az egész számok \Z gyűrűjében a 2-vel és 3-mal osztható számok egy-egy ideált alkotnak. Ezeket az előző részben ismertetett komplexusszorzás ismeretében 2\Z-vel és 3\Z-vel jelölhetjük (lásd a 18.19. Definíció utáni megjegyzés 1. pontját). E két ideál metszetét azok a számok alkotják, amelyek 2-vel is és 3-mal is oszthatók. Ezek épp a 6-tal osztható számok lesznek, azaz 2\Z \cap 3\Z=6\Z, ami szintén ideál \Z-ben, épp ahogyan a tétel állítja. Nézzük meg, hogy miért igaz ez általánosságban is.
Bizonyítás:
Nézzük először a részgyűrűk metszetére vonatkozó állítást! Jelöljük S-sel az \mathcal{S} halmazrendszerben lévő részgyűrűk metszetét. Azt kell megmutatni, hogy S részgyűrű R-ben. Ez a 18.15. Tétel szerint pontosan akkor teljesül, ha S zárt az R-beli összeadásra, szorzásra és ellentettképzésre, valamint tartalmazza az R gyűrű nullelemét.
Mivel \mathcal{S} minden eleme részgyűrű, így a 18.15. Tétel miatt mindegyik tartalmazza az R gyűrű nullelemét. A nullelem tehát valóban benne van ezek metszetében, azaz S-ben.
Legyen most x az S halmaz egy tetszőleges eleme. Mivel S az \mathcal{S}-beli részgyűrűk metszete, így x e részgyűrűk mindegyikének szintén eleme, amelyek viszont ismét a 18.15. Tétel miatt zártak az ellentettképzésre. Így -x is eleme az összes \mathcal{S}-beli részgyűrűnek, vagyis valóban benne van ezek metszetében, azaz S-ben.
Végül legyen x és y az S halmaz két tetszőleges eleme. Mivel S az \mathcal{S}-beli részgyűrűk metszete, így x és y e részgyűrűk mindegyikének szintén eleme, amelyek viszont ismét a 18.15. Tétel miatt zártak az összeadásra és szorzásra. Így az x+y összeg, valamint az x\cdot y szorzat is eleme az összes \mathcal{S}-beli részgyűrűnek, vagyis valóban benne vannak ezek metszetében, azaz S-ben. Az S tehát valóban részgyűrű R-ben, ahogyan a tétel állítja.
Most nézzük a balideálok metszetére vonatkozó állítást! Jelöljük I-vel az \mathcal{I} halmazrendszerben lévő balideálok metszetét. Azt kell megmutatni, hogy I balideál R-ben. Ez a 18.18. Definíció szerint azt jelenti, hogy egyrészt I részgyűrű R-ben, másrészt akármelyik a\in I elemet balról megszorozva akármelyik r\in R elemmel, az így kapott r\cdot a szorzat szintén benne van I-ben. Minthogy \mathcal{I} minden eleme részgyűrű R-ben (hiszen balideál), ezért a fentiek alapján I is részgyűrű R-ben. Elegendő tehát csak a baloldali szorzásra vonatkozó feltételt ellenőrizni.
Tegyük fel, hogy a az I részgyűrű, r pedig az R gyűrű egy tetszőleges eleme. Mivel I az \mathcal{I}-beli balideálok metszete, így a e balideálok mindegyikének szintén eleme. Emiatt az r\cdot a szorzat is benne van az összes \mathcal{I}-beli balideálban, tehát ezek metszetében is, azaz I-ben. Emiatt I valóban balideál R-ben.
A jobbideálok metszetére vonatkozó állítás értelemszerűen ugyanezzel a gondolatmenettel igazolható azzal a különbséggel, hogy ekkor az r\cdot a szorzat helyett az a\cdot r szorzatot kell tekinteni.
Végül a (kétoldali) ideálok metszetére vonatkozó állítás triviálisan adódik, hiszen minden (kétoldali) ideál egyszerre bal- és jobbideál.
∎Most egy R gyűrűben azokat a részgyűrűket (vagy ideálokat) fogjuk megvizsgálni, amelyek R-nek egy adott X részhalmazát tartalmazzák. Ezek a részgyűrűk (vagy ideálok) szintén egy halmazrendszert alkotnak R felett, amelynek egy fontos tulajdonságát mondja ki az alábbi tétel.
19.10. Tétel (Generált részgyűrű és ideál):
Legyen R egy tetszőleges gyűrű, továbbá X az R gyűrűnek egy tetszőleges részhalmaza. Jelöljük \mathcal{X}-szel azt az R fölötti halmazrendszert, amelynek elemei pontosan azok a részgyűrűk R-ben, amelyek tartalmazzák X-et.
Ekkor \mathcal{X}-ben létezik pontosan egy legszűkebb elem, amelyet az X által generált részgyűrűnek nevezünk, és \lang X\rang-szel jelölünk. Ilyenkor azt mondjuk, hogy az X részhalmaz generálja ezt a bizonyos részgyűrűt – amely természetesen lehet maga a teljes R is, mint triviális részgyűrű.
Ugyanilyen értelemben beszélhetünk az X által generált bal-, jobb- vagy kétoldali ideálról is.
♣Bizonyítás:
A 19.8. Tétel alapján egy halmazrendszerben legfeljebb egy legszűkebb elem létezhet. Így elegendő megmutatni, hogy létezik legszűkebb elem, az ugyanis garantáltan az egyetlen legszűkebb elem lesz.
Mivel X az R gyűrű tetszőleges részhalmaza lehet, ezért előszöris kérdés, hogy létezik-e egyáltalán olyan részgyűrű, amely tartalmazza X-et? Erre természetesen igen a válasz, hiszen „legrosszabb esetben” maga a teljes R egy ilyen részgyűrű. Az \mathcal{X} halmazrendszer tehát biztosan nem üres.
Most képezzük az \mathcal{X} halmazrendszer összes elemének metszetét, és jelöljük ezt a halmazt S-sel. Minthogy \mathcal{X} elemei részgyűrűk R-ben, így a 19.9. Tétel alapján S is részgyűrű R-ben. Továbbá az X-ről azt mondtuk, hogy ő részhalmaza minden \mathcal{X}-beli részgyűrűnek, emiatt részhalmaza ezek metszetének, azaz S-nek is.
Ez viszont azt jelenti, hogy S maga is az \mathcal{X} halmazrendszer eleme, hiszen ő is egy X-et tartalmazó részgyűrű R-ben. Ráadásul mivel ő a metszete \mathcal{X} összes elemének, ezért egyben részhalmaza is azoknak. Másként fogalmazva bármilyen T\in \mathcal{X} részgyűrűre teljesül, hogy S\sube T. Ez a 19.7. Definíció szerint viszont épp azt jelenti, hogy S nem más, mint az \mathcal{X} halmazrendszer legszűkebb eleme. Más szavakkal S a legszűkebb olyan részgyűrű R-ben, amely tartalmazza az X részhalmazt, azaz a tételbeli jelölést használva S=\lang X\rang.
A legszűkebb X-et tartalmazó bal-, jobb-, illetve kétoldali ideál létezésére és egyértelműségére vonatkozó állítás a fentiekhez teljesen hasonló módon igazolható.
∎Ez alapján tehát egy adott R gyűrű bármely X részhalmaza egyértelműen meghatároz egy ideált. Ez lesz az X-et tartalmazó legszűkebb ideál. Ugyanakkor ez a tétel semmit nem mond arról, hogy az X által generált \lang X\rang ideált lehet-e generálni egy X-nél szűkebb részhalmazzal is vagy nem. Amikor tehát azt mondjuk, hogy egy ideál „generálható X-szel”, ez még nem jelenti azt, hogy az adott ideál kizárólag X-szel generálható. Számelméleti szempontból rendkívül fontosak azok az ideálok, amelyek a gyűrű kevés számú – speciálisan akár egyetlen – eleméből alkotott részhalmazaival generálhatók.
19.11. Definíció (Végesen generált ideálok és főidálok):
Legyen R tetszőleges gyűrű, I pedig valamilyen ideál R-ben. Amennyiben R-nek létezik olyan véges számú elemet tartalmazó X=\{a_1;a_2;\ldots;a_n\} részhalmaza, amely esetén \lang X\rang =I, akkor azt mondjuk, hogy az I ideál végesen generált. Ezt így jelöljük: I=(a_1,a_2,\ldots,a_n).
Speciálisan ha I generálható az R gyűrű egyetlen eleméből álló részhalmazával, akkor I-t főidálnak nevezzük. Az a\in R által generált I főideált így jelöljük: I=(a).
♣A főideálok kapcsolata az oszthatósággal
A továbbiakban elsősorban kommutatív és nullosztómentes gyűrűket, más szóval integritástartományokat fogunk vizsgálni. Az ilyen gyűrűk esetén fontos kapcsolat van a 16. részben tárgyalt oszthatóság (16.1. Definíció), valamint a gyűrű főideáljai között. Ebben a tekintetben egy kicsit másként viselkednek az egységelemes és a nem egységelemes gyűrűk. Az alábbi tétel az egységelemes esettel foglalkozik. Itt nem használjuk ki a nullosztómentességet, ezért ez a tétel nem csak integritástartományokra, hanem bármilyen kommutatív és egységelemes gyűrűre működik.
19.12. Tétel:
Legyen R tetszőleges kommutatív és egységelemes gyűrű, valamint legyenek a\neq 0 és b az R tetszőleges elemei. Ekkor teljesülnek az alábbiak:
- Az a|b oszthatóság akkor és csak akkor teljesül, ha teljesül a (b)\sube (a) tartalmazási reláció.
- Az (a)=(b) egyenlőség akkor és csak akkor teljesül, ha a és b asszociáltak, azaz a\sim b.
Bizonyítás:
Előszöris vizsgáljuk meg az (a) főideál szerkezetét. A 19.11. Definíció alapján az (a) főideál az a legszűkebb ideál, amely tartalmazza az a elemet. Mivel a\in (a), ezért a 18.18. Definíció szerint tetszőleges r\in R elem esetén szükségképpen ra\in (a) is teljesül. Azaz az (a) ideál biztosan tartalmazza az a elemen kívül annak összes többszörösét is. Egyéb elemet viszont nem tartalmaz, hiszen úgy már nem ő lenne az a elemet tartalmazó legszűkebb ideál. Ugyanezen okok miatt a (b) főideál a b elemet és annak többszöröseit tartalmazza, és ezeken kívül nincs más eleme. Ezek után már igazolhatjuk a tétel állításait.
Az 1. állítás: Egyrészt azt kell bizonyítani, hogy ha teljesül az a|b oszthatóság, akkor bármilyen c\in (b) esetén c\in (a) is teljesül. A c\in (b) a fentiek alapján azt jelenti, hogy c vagy megegyezik b-vel, vagy pedig annak többszöröse. Egységelemes gyűrűben mindkét feltétel azt jelenti, hogy teljesül a b|c oszthatóság. De mivel azt mondtuk, hogy teljesül az a|b oszthatóság, ezért az oszthatóság tranzitivitása miatt (16.2. Tétel 5. pont) teljesül az a|c oszthatóság is. Ez viszont azt jelenti, hogy c egyike az a elem többszöröseinek is, azaz c\in (a). Mivel megmutattuk, hogy a (b) főideál bármely eleme egyúttal eleme az (a) főideálnak is, így a 19.2. Definíció alapján valóban (b)\sube (a).
Másrészt azt is bizonyítani kell, hogy ha (b)\sube (a), akkor teljesül az a|b oszthatóság. A (b)\sube (a) tartalmazási reláció a 19.2. Definíció alapján azt jelenti, hogy a (b) főideál bármely eleme egyúttal eleme az (a) főideálnak is. Ez természetesen magára b-re is igaz, azaz b\in (a). Így tehát b vagy megegyezik a-val, vagy pedig egyike az a elem többszöröseinek. Egységelemes gyűrűben mindkét feltétel azt jelenti, hogy teljesül az a|b oszthatóság.
A 2. állítás könnyen adódik az 1. állításból. A 19.2. Definíció utáni megjegyzés 5. pontja alapján ugyanis az (a)=(b) halmazegyenlőség akkor és csak akkor teljesül, ha (a) és (b) kölcsönösen egymás részhalmazai. Ez az 1. állítás miatt azzal ekvivalens, hogy egyszerre teljesülnek az a|b, valamint a b|a oszthatóságok. A 16.9. Tétel miatt azonban a kölcsönös oszthatóság kommutatív és egységelemes gyűrűkben akkor és csak akkor teljesül, ha a és b egymásnak asszociáltjai.
∎A most következő tétel az előbbihez hasonló, de nem teljesen azonos kapcsolatot mond ki az oszthatóság és a főideálok között, ám ezúttal a NEM egységelemes esetben. Itt már kihasználjuk a nullosztómentességet is, ezért ez a tétel csak integritástartományokra működik.
19.13. Tétel:
Legyen R tetszőleges kommutatív és nullosztómentes, de NEM egységelemes gyűrű, valamint legyenek a\neq 0 és b az R tetszőleges elemei. Ekkor teljesülnek az alábbiak:
- Az a|b oszthatóság akkor és csak akkor teljesül, ha teljesül a (b)\sub (a) szigorú tartalmazási reláció.
- Az (a)=(b) egyenlőség akkor és csak akkor teljesül, ha a=b.
A NEM egységelemes esetben tehát már nem elegendő a sima tartalmazási reláció és a sima asszociáció. Ehelyett az ezeknél speciálisabb szigorú tartalmazásra van szükség az 1. ponthoz, míg konkrétan egyenlőségre a 2. ponthoz.
Bizonyítás:
Ennek a tételnek a bizonyítása nagyon fog hasonlítani a 19.12. Tétel bizonyításához. Arra azonban figyelnünk kell, hogy az egységelem hiánya miatt ezúttal nem teljesül az a|a oszthatóság, mivel a nullosztómentesség miatt ez ellentmondana a 16.2. Tétel 2. pontjának.
Az 1. állítás: Egyrészt azt kell bizonyítani, hogy ha teljesül az a|b oszthatóság, akkor bármilyen c\in (b) esetén c\in (a) is teljesül, azaz fennáll a (b)\sube (a) tartalmazási reláció. A c\in (b) ugye azt jelenti, hogy c vagy megegyezik b-vel – és ekkor nyilván teljesül az a|\underbrace{c}_{=b} oszthatóság –, vagy pedig annak többszöröse – és ekkor pedig a b|c oszthatóság teljesül. De mivel azt mondtuk, hogy teljesül az a|b oszthatóság, ezért ez utóbbi esetben az oszthatóság tranzitivitása miatt (16.2. Tétel 5. pont) ugyancsak teljesül az a|c oszthatóság. Mindkét eset azt jelenti, hogy c egyike az a elem többszöröseinek is, azaz c\in (a). Mivel megmutattuk, hogy a (b) főideál bármely eleme egyúttal eleme az (a) főideálnak is, így a 19.2. Definíció alapján valóban (b)\sube (a).
Másrészt azt kell még megmutatni, hogy NEM egységelemes gyűrű esetén ez valójában egy szigorú tartalmazási reláció. Mutatnunk kell tehát egy olyan elemet, amely benne van az (a) főideálban, viszont nincs benne a (b) főideálban. Vegyük észre, hogy az a elem pont ilyen, hiszen egyrészt ő nyilvánvalóan benne van a saját maga által generált (a) főideálban. Másrészt viszont a (b) főideálban nem lehet benne, máskülönben vagy a b=a egyenlőség, vagy pedig a b|a oszthatóság teljesülne. De mivel azt mondtuk, hogy teljesül az a|b oszthatóság, ezért b=a esetén nyilvánvalóan, míg b|a esetén pedig az oszthatóság tranzitivitása miatt (16.2. Tétel 5. pont) teljesülne az a|a oszthatóság is, ami ugye ellentmondás.
Visszafelé: Tegyük most fel, hogy teljesül a (b)\sub (a) szigorú tartalmazási reláció. A (b)\sub (a) tartalmazás többek között azt jelenti, hogy a (b) főideál bármely eleme egyúttal eleme az (a) főideálnak is. Ez természetesen magára b-re is igaz, azaz b\in (a). Így tehát b vagy a-nak többszöröse (azaz teljesül az a|b oszthatóság), vagy pedig megegyezik vele. De ez utóbbi lehetetlen, hiszen ebben az esetben az (a) és (b) főideálok megegyeznének, és így a közöttük lévő tartalmazási reláció nem lehetne szigorú. Így tehát valóban csak a|b lehet a helyzet.
A 2. állítás: Az (a)=(b) azt jelenti, hogy a két főideálnak pontosan ugyanazok az elemeik. Mivel a nyilván benne van a saját maga által generált főideálban, ezért ő a (b) főideálnak is eleme. Ugyanezen okok miatt b is eleme az (a) főideálnak. Így tehát ők vagy megegyeznek egymással, vagy pedig egymás osztói, azaz a|b és b|a is teljesül. Ez utóbbi esetben azonban az oszthatóság tranzitivitása miatt teljesülne az a|a oszthatóság is, ami ugye nem egységelemes gyűrűk esetén lehetetlen. Így tehát (a)=(b)-ből valóban csak a=b következhet. Visszafelé: ha a=b, akkor az általuk generált főideálok nyilvánvalóan megegyeznek.
∎A következő szakaszban az iménti két tételt felhasználva a főideálok segítségével mutatni fogunk egy olyan feltételrendszert, amely egyszerre szükséges és elégséges is ahhoz, hogy egy integritástartományban teljesüljön a számelmélet alaptétele. Ezzel végre lezárhatjuk ezt a kérdést, előtte azonban a könnyebb érthetőség kedvéért vizsgáljunk meg egy egyszerű példát.
A halmazrendszerek kapcsán szó volt arról, hogy a \sube szimbólummal jelölt tartalmazási reláció tulajdonképpen egy részbenrendezés bármilyen halmazrendszer elemei között. Mutattunk néhány példát is arra, hogy egy ilyen részbenrendezés hogyan ábrázolható az úgynevezett Hasse-diagramokon. Ezeket a diagramokat azonban nemcsak konkrétan halmazrendszerek tartalmazási relációjának, hanem tetszőleges halmaz részbenrendezési relációjának megjelenítésére is használhatjuk.
Most felvázolunk egy szép párhuzamot egy R integritástartomány főideáljai – mint egy R fölötti halmazrendszer elemei – közötti tartalmazási reláció, valamint magának az R-nek az elemei közötti oszthatósági reláció között.
Az egyszerűség kedvéért szorítkozzunk most arra az esetre, amikor R egységelemes. Ebben az esetben az oszthatósági reláció reflexív, azaz tetszőleges a elem esetén teljesül az a|a oszthatóság (lásd a 16.2. Tétel 1. pontját). Ezenkívül ugyanezen tétel 5. pontja alapján tranzitív is, így már csak az antiszimmetria (12.9. Definíció) hiányzik ahhoz, hogy részbenrendezés lehessen. Ez ugye azt jelentené, hogy ha valamilyen a és b elemek között mindkét irányban teljesül az oszthatóság, akkor abból a=b-nek kéne következnie. A 16. részben megemlítettük ugyanakkor, hogy sajnos az egyenlőség nem, hanem csak az ennél valamivel gyengébb a\sim b asszociáció teljesül, az viszont minden esetben (lásd a 16.8. Tétel 4. pontját).
Ezt a problémát azonban egy trükkel megkerülhetjük. Minthogy az asszociáció a 16.7. Tétel alapján egy ekvivalenciareláció, így az az R gyűrűt a 13.5. Tétel alapján ekvivalencia-osztályokra bontja. Ha mármost minden ilyen ekvivalencia-osztályból legfeljebb egy elemet választunk ki, akkor ilymódon R-nek egy olyan S részhalmazára térhetünk át, amelyen már az oszthatóság is antiszimmetrikus lesz. Ebben az esetben ugyanis bármely S-beli a és b elemek közötti kölcsönös oszthatóságból a=b következik, hiszen S konstrukciója miatt csak ebben az esetben teljesülhet az a\sim b asszociáció.
Például az egész számok \Z gyűrűjéből válasszuk ki a 60 nemnegatív osztóit, és nevezzük ezt a halmazt D-nek. A 16.10. Tétel alapján egyik D-beli elempár sem asszociált. Ezen a halmazon tehát az oszthatóság egy részbenrendezési reláció, és így felrajzolhatjuk a Hasse-diagramját:
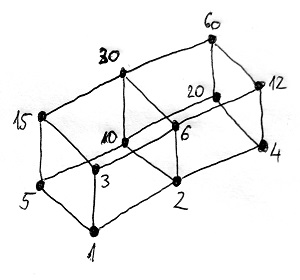
Most tekintsük azt a \Z fölötti halmazrendszert, amely a D-ben lévő elemek által generált főideálokból áll. Ezen a halmazrendszeren a főideálok közötti tartalmazási reláció szintén egy részbenrendezési reláció lesz, amelynek a Hasse-diagramja viszont így néz ki:
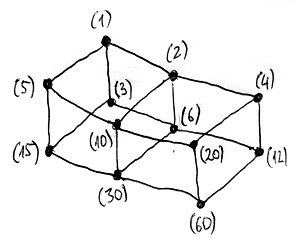
Mint látható, a két Hasse-diagram gyakorlatilag megegyezik. Mindössze abban különböznek egymástól, hogy az egyik a másiknak a feje tetejére állított változata. Nos ez nem véletlenül van így, hanem a 19.12. Tétel miatt. Ez ugye kimondja, hogy az a|b reláció pontosan akkor teljesül, amikor a (b)\sube (a) reláció is teljesül. A részbenrendezett halmazok nyelvén ezt úgy is meg lehet fogalmazni, hogy az a elem pontosan akkor „kisebb” b-nél az oszthatósági reláció szerint, amikor az (a) főideál „nagyobb” a (b) főideálnál a tartalmazási reláció szerint. A két részbenrendezési reláció tehát épp egymás fordítottja, és mivel a D halmaz elemei kölcsönösen egyértelműen megfeleltethetők az általuk generált főideálokkal, ezért a két Hasse-diagram csak az irányításban különbözik egymástól.
A főideálok és a számelmélet alaptétele
Most vizsgáljuk meg, hogy az iménti észrevételeknek mi köze van a számelmélet alaptételéhez. Ahhoz, hogy a számelmélet alaptétele teljesüljön egy integritástartományon alapvetően két dolog kell: a prímtényezős felbontás létezése, illetve annak egyértelműsége. Ezt precízen a 16.15. Definícióban fogalmaztuk meg.
Az egyértelműségi állításra már mutattunk egy olyan feltételt, amely szükséges és egyben elégséges is. A 16.16. Tétel és a 16.17. Tétel alapján az egyértelműségi állítás akkor és csak akkor teljesül egy R integritástartományon, ha R minden felbonthatatlan eleme prímtulajdonságú. Ez tehát biztosan része lesz annak a feltételrendszernek, amely pontosan meghatározza, hogy mikor teljesül az alaptétel és mikor nem. Nem érünk azonban sokat az egyértelműségi garanciával, ha magának a prímtényezős felbontásnak a létezése nem garantált. Ebben a szakaszban arról lesz szó, hogy a létezéshez mire van szükség pontosan.
Ehhez elevenítsük fel egy kicsit a 17. részben definiált euklidészi gyűrű fogalmát. Ezeknek az integritástartományoknak az volt a speciális tulajdonságuk, hogy minden elemükhöz hozzá tudtunk rendelni egy nemnegatív egész mérőszámot, az úgynevezett euklidészi normát. Méghozzá olymódon, hogy egyrészt bármely kéttényezős szorzat tényezőinek a normája legfeljebb akkora legyen, mint magának a szorzatnak normája (17.20. Tétel), másrészt egyenlőség akkor és csak akkor teljesüljön, ha valamelyik tényező egység (17.21. Tétel). Tulajdonképpen ez garantálja a prímtényezős felbontás létezését, hiszen bármely a elem esetén az alábbi 3 eset lehetséges:
- Az a elem egyáltalán nem bontható szorzatra.
- Az a elemnek csak triviális felbontása létezik.
- Az a elemnek létezik nemtriviális a=bc felbontása.
Az 1. és a 2. esetben a-t felbonthatatlan elemnek neveztük (16.11. Definíció), amelynek a prímtényezős felbontása alatt a 16.15. Definíció szerint önmagát, mint egytényezős szorzatot értjük. A probléma a 3. esettel lehet, méghozzá akkor, ha a bc szorzat tényezői a végtelenségig bonthatók tovább nemtriviális módon. A 16.18. Tétel bizonyításában mutattunk is egy ilyen példát.
Az euklidészi gyűrűkben azonban az euklidészi norma említett tulajdonságai szerencsére ezt megakadályozzák. Ez ugyanis azt jelentené, hogy a „felbontási fában” lefelé haladva egy olyan, gyűrűelemekből álló végtelen sorozatot tudnánk mutatni, amelyben az elemeknek egyre kisebb és kisebb az euklidészi normájuk. Ez viszont lehetetlen, hiszen az euklidészi norma értékkészlete a természetes számok \N halmaza, márpedig a 17.14. Tételben megmutattuk, hogy \N bármely részhalmazának létezik minimuma. Egy idő után tehát a „felbontási fa” minden ágán garantáltan „bele kell ütköznünk” egy olyan elembe, amely tovább már nem bontható nemtriviálisan. Habár megemlítettük, hogy létezik olyan alaptételes gyűrű is, amely nem euklidészi, ám a „felbonthatatlan elembe ütközés garanciájának” alapgondolata talán átmenthető erre az általános esetre is.
Ehhez a főideálok jelentik a kulcsot. Ugye azt szeretnénk, hogy bármely elem felbontási fájának minden ágán előbb-utóbb garantáltan beleütközzünk egy felbonthatatlan elembe. Ehhez az kell, hogy a gyűrű bármely részhalmazában létezzen „minimális” elem oszthatósági reláció szerint. Az előző szakaszban felvázolt példa alapján ez pontosan akkor fog teljesülni, ha létezik „maximális” főideál a tartalmazási reláció szerint.
Ezt fogalmazza meg precízen az alábbi tétel, amely tehát egy szükséges és elégséges feltételrendszert ad a számelmélet alaptételére bármilyen integritástartomány esetén.
19.14. Tétel:
Legyen R tetszőleges integritástartomány, \mathcal{R} pedig az R összes főideáljából álló halmazrendszer R fölött. A számelmélet alaptétele akkor és csak akkor teljesül R-ben, ha fennállnak az alábbi feltételek:
- A főideálokból álló \mathcal{R} halmazrendszer bármely nemüres részhalmazában létezik maximális elem a 19.7. Definíció szerinti értelemben.
- Az R integritástartomány minden felbonthatatlan eleme prímtulajdonságú.
Bizonyítás:
Nézzük először az elégségességet! Azaz egyrészt tegyük fel, hogy R-ben minden felbonthatatlan elem prímtulajdonságú, másrészt pedig azt, hogy a főideálokból álló \mathcal{R} halmazrendszer bármely nemüres részhalmazának létezik maximuma. Ez utóbbi azt jelenti, hogy akárhogyan is választunk ki akár végtelen sok főideált az \mathcal{R} halmazrendszerből, azok között mindig lesz maximális elem a 19.7. Definíció szerinti értelemben. Ezt röviden úgy fogjuk mondani, hogy az \mathcal{R} halmazrendszerre teljesül maximumfeltétel. Tegyük fel továbbá indirekt, hogy ennek ellenére léteznek olyan, a nullelemtől és egységektől különböző elemek, amelyek nem bonthatók fel felbonthatatlanok szorzatára. Minden ilyen elemhez készítsük el az általa generált főideált, és legyen \mathcal{H} az összes ilyen főideál halmaza, amely tehát az \mathcal{R} halmazrendszer egy részhalmaza. Mivel \mathcal{R}-re teljesül a maximumfeltétel, ezért \mathcal{H}-ban van maximális elem. Jelöljük ezt a főideált (m)-mel, amely tehát az m elemet és annak többszöröseit tartalmazza.
Az indirekt feltevésünk alapján ugye m-nek nem létezik prímtényezős felbontása. Emiatt az m elem maga nem lehet felbonthatatlan, máskülönben ő saját magának az egytényezős felbontása lenne a 16.15. Definíció értelmében. Mivel m nem felbonthatatlan, ezért a 16.11. Definíció alapján ő felírható m=a\cdot b alakban, méghozzá olymódon, hogy sem a, sem pedig b nem egység, és nem is asszociáltja m-nek. Teljesülnek tehát az a|m és a b|m oszthatóságok. Emiatt ha R egységelemes, akkor a 19.12. Tétel, ha pedig R nem egységelemes, akkor a 19.13. Tétel alapján teljesülnek az (m)\sub (a) és az (m)\sub (b) szigorú tartalmazási relációk.
Mivel az (m) főideálról azt mondtuk, hogy a \mathcal{H} halmazrendszer maximális eleme, így sem az (a), sem pedig a (b) főideálok nem lehetnek benne \mathcal{H}-ban. Ezért nekik már létezik prímtényezős felbontásuk:
\begin{aligned}a&=p_1p_2\ldots p_k \\ b&=q_1q_2\ldots q_n\end{aligned}Ám ekkor m=ab miatt e tényezők szorzata valójában m-nek lenne egy prímtényezős felbontása, amiről ugye azt mondtuk, hogy nem létezik. A \mathcal{H} halmazrendszer tehát szükségképpen üres, azaz – indirekt feltevésünkkel ellentétben – mégiscsak minden elemnek létezik prímtényezős felbontása. Továbbá, mivel minden felbonthatatlan elem prímtulajdonságú, ezért a 16.17. Tétel értelmében egy ilyen prímtényezős felbontás – a tényezők sorrendjétől és asszociáltságtól eltekintve – szükségképpen egyértelmű.
A tételben szereplő feltételek tehát valóban elégségesek az alaptételhez. Most vizsgáljuk meg, hogy vajon tényleg szükségesek-e? Tételezzük fel tehát, hogy R-ben teljesül az alaptétel. Ebben az esetben egyrészt a 16.18. Tétel miatt R biztosan egységelemes. Másrészt a 16.16. Tétel miatt valóban minden felbonthatatlan elem prímtulajdonságú, így már csak a tételben szereplő 1. feltétel teljesülését kell ellenőrizni. Tegyük fel indirekt, hogy nem teljesül az 1. feltétel, azaz a főideálokból álló \mathcal{R} halmazrendszernek van olyan nemüres részhalmaza, amelyben nincs maximális elem. Ez a 19.7. Definíció, valamint a \sub reláció tranzitivitása (19.6. Tétel) miatt azt jelenti, hogy létezik olyan végtelen, főideálokból álló sorozat, amelyben minden főideál szigorúan tartalmazza a sorozatban előtte lévőt:
(a_1)\sub (a_2)\sub (a_3)\sub \ldotsMivel R egységelemes, ezért a 19.12. Tétel miatt az a_1, a_2, a_3, \ldots elemek közül semelyik sem asszociáltja semelyik másiknak, továbbá teljesülnek az alábbi oszthatóságok:
\begin{aligned}a_2&|a_1 \\ a_3&|a_2 \\ a_4&|a_3 \\ &\vdots\end{aligned}Ebből egyrészt következik, hogy legkésőbb a_2-től kezdve a sorozat egyik tagja sem lehet a nullelem. Máskülönben ugyanis az általa generált főideál csak a nullelemet tartalmazná, és így a 18.15. Tétel 3. pontja miatt nem létezhetne nála szűkebb főideál. Másrészt viszont a sorozat egyetlen tagja sem lehet egység, máskülönben ugyanis az általa generált főideál a teljes R gyűrű lenne – hiszen a 16.3. Definíció alapján egy egységnek minden gyűrűelem többszöröse –, és így nem létezhetne nála bővebb főideál.
Az a_2 tehát egy olyan elem, amely nem a nullelem és nem is egység, továbbá az oszthatóság tranzitivitása miatt végtelen sok olyan osztója van, amelyek közül egyik sem egység, és egyik sem asszociáltja a_2-nek. Így tehát a_2-nek nem létezik prímtényezős felbontása, ami viszont lehetetlen, hiszen azt mondtuk, hogy R-ben teljesül a számelmélet alaptétele. Csak az indirekt feltevésünk lehetett hibás, azaz a főideálokból álló \mathcal{R} halmazrendszernek valóban nem létezhet olyan nemüres részhalmaza, amelyben ne lenne maximális elem.
∎Ezzel végérvényesen lezárthatjuk a számelmélet alaptételének kérdését, hiszen az iménti tétel segítségével már bármilyen integritástartományról egyértelműen eldönthető, hogy alaptételes-e vagy sem.
Főideálgyűrűk
Végül megismerkedünk egy számunkra nagyon fontos gyűrűosztállyal, amelybe – mint látni fogjuk – az egész számok \Z gyűrűje is beletartozik. Ezeknek a speciális gyűrűknek fontos tulajdonságaik vannak a következő részekben tárgyalt kriptográfiai eljárások szempontjából. Előszöris nézzük meg, mik ezek a speciális gyűrűk.
19.15. Definíció (Főideálgyűrűk):
Legyen R tetszőleges integritástartomány, melyben létezik egységelem. Amennyiben R minden ideálja főideál (azaz generálható egyetlen elemmel), akkor R-t főideálgyűrűnek nevezzük.
♣Egy főideálgyűrűben tehát minden ideál valamelyik gyűrűelemből, illetve annak többszöröseiből áll. Minket elsősorban az egész számok \Z gyűrűje fog érdekelni a további részekben. Minden bizonnyal nem túl meglepő, hogy \Z is egy főideálgyűrű. A most következő tételben egy ennél erősebb állítást igazolunk.
19.16. Tétel:
Minden euklidészi gyűrű – és így a 17.19. Tétel miatt az egész számok \Z gyűrűje is – főideálgyűrű.
♣Bizonyítás:
Legyen R egy tetszőleges euklidészi gyűrű, I pedig egy tetszőleges ideál R-ben. Azt kell megmutatnunk, hogy létezik olyan r\in R elem, amely generálja I-t, azaz amelyre I=(r) teljesül. Jelöljük az R euklidészi gyűrű nullelmét 0_R-rel. Ha I csak a nullelemből áll, akkor I=(0) nyilván teljesül. Feltehetjük tehát, hogy I nem csak a nullelemből áll.
Mivel R euklidészi gyűrű, ezért ennek elemein értelmezhető egy f:R\to\N euklidészi norma, amely eleget tesz a 17.16. Definícióban szereplő feltételeknek. Az f euklidészi norma tehát az I ideál minden nemnulla eleméhez hozzárendel valamilyen pozitív egész számot. A 17.14. Tétel alapján ennek a számhalmaznak mindenképpen van minimuma függetlenül attól, hogy I végtelen sok elemet tartalmaz-e vagy sem. Legyen b az I ideál egy olyan nemnulla eleme, amelyhez az f euklidészi norma épp ezt a minimumot rendeli hozzá. Azt kell megmutatni, hogy b generálja az I ideált, azaz I=(b).
Az egyrészt nyilvánvaló, hogy mivel b\in I, ezért b-nek bármilyen többszöröse is I-ben van. Ez az ideál definíciójából következik (18.18. Definíció). Másrészt azt kell még igazolnunk, hogy I-nek ezeken kívül nincs is más eleme. Tegyük fel tehát, hogy a\in I, és mutassuk meg, hogy a szükségképpen többszöröse b-nek. Mivel b\neq 0_R, és R euklidészi gyűrű, ezért a és b között a 17.16. Definíció 2. pontja alapján elvégezhető a maradékos osztás. Azaz létezik olyan k hányados és r maradék, amelyekre teljesülnek az alábbi feltételek:
\begin{aligned}a&=k\cdot b+r \\ f(r)&\lt f(b)\end{aligned}Az egyenletből az r maradékot kifejezve ezt kapjuk:
r=a-k\cdot bMivel I ideál és b\in I, ezért a 18.18. Definíció alapján kb\in I is teljesül. Másrészt tudjuk, hogy a\in I, és így a 18.15. Tétel 1. és 4. pontja alapján az r=a-kb maradék szintén benne van I-ben.
Vegyük észre, hogy a maradékos osztás f(r)\lt f(b) feltétele miatt az r egy olyan eleme az I ideálnak, amelynek euklidészi normája szigorúan kisebb b euklidészi normájánál. Márpedig azt mondtuk, hogy I-ben nincs olyan elem, amelynek euklidészi normája a b euklidészi normájánál kisebb, de még mindig pozitív. Ezért kizárólag f(r)=0 lehetséges, ami a 17.16. Definíció 1. pontja alapján azt jelenti, hogy r=0_R.
Az a és b közötti maradékos osztást elvégezve tehát a maradék csak a nullelem lehet, azaz valójában teljesül a b|a oszthatóság. Az a elem tehát többszöröse b-nek, és így a\in (b) teljesül. Más szavakkal a b elem tényleg generálja az I ideált, azaz I=(b). Minthogy ez a gondolatmenet tetszőleges ideállal végigjátszható, ezért R valóban főideálgyűrű, ahogyan a tétel állítja.
∎Felhívnánk a figyelmet arra, hogy az iménti tétel megfordítása nem igaz. Létezik olyan főideálgyűrű, amely nem euklidészi. Ilyenek bizonyos úgynevezett algebrai egész számokból alkotott gyűrűk, ám ennek a témakörnek a részleteire a szükséges algebrai ismeretek hiányában egyelőre nem tudunk bővebben kitérni.
Az euklidészi gyűrűkről szóló 17. részben már igazoltuk, hogy teljesül bennük a számelmélet alaptétele. Most ugyanezt fogjuk igazolni az ennél általánosabb főideálgyűrűkre is, azaz megmutatjuk, hogy minden főideálgyűrű teljesíti az előző szakaszban bizonyított 19.14. Tétel szerinti feltételeket.
Az 1. feltétel ugye azt követeli meg, hogy a főideálokból álló halmazrendszer bármely nemüres részhalmazában legyen maximális elem. Ehhez először igazolni fogunk egy segédtételt. A 19.9. Tételben már megmutattuk, hogy ideálok metszete is ideál. De vajon mi a helyzet az olyan halmazokkal, amelyek ideálok uniójaként állnak elő? Az ilyen halmazok általában nem ideálok. Tekintsük például az egész számok \Z gyűrűjében lévő (2) és (3) főideálokat. Ezek uniója azokból a számokból áll, amelyek 2-vel VAGY 3-mal oszthatók.
Ez a halmaz könnyen láthatóan nem ideál, hiszen még csak nem is részgyűrű, mivel nem zárt az összeadásra. Például a 2 és a 3 benne van ebben az unióban, de az összegük nem, mivel az 5 nem többszöröse sem 2-nek, sem pedig 3-nak. Az alábbi segédtétel egy olyan speciális esetről szól, amikor bizonyos ideálok uniója mégis ideál. Felhívjuk a figyelmet, hogy a tétel nem kizárólag integritástartományokra, hanem bármilyen gyűrűre alkalmazható.
19.17. Lemma:
Legyen R egy tetszőleges gyűrű, valamint legyen \mathcal{S} egy olyan, részgyűrűkből álló halmazrendszer R fölött, amelyben bármely két részgyűrű között legalább az egyik irányban fennáll a \sube szimbólummal jelölt tartalmazási reláció. Ekkor az \mathcal{S}-ben lévő halmazok uniója is részgyűrű R-ben.
Ehhez hasonlóan legyen \mathcal{I} egy olyan, balideálokból (illetve jobbideálokból) álló halmazrendszer R fölött, amelyben bármely két balideál (illetve jobbideál) között legalább az egyik irányban fennáll a \sube szimbólummal jelölt tartalmazási reláció. Ekkor az \mathcal{I}-ben lévő halmazok uniója is balideál (illetve jobbideál) R-ben.
Végül ha \mathcal{J} egy olyan, ideálokból álló halmazrendszer R fölött, amelyben bármely két ideál között legalább az egyik irányban fennáll a \sube szimbólummal jelölt tartalmazási reláció, akkor a \mathcal{J}-ben lévő halmazok uniója is ideál R-ben.
♣Például az imént említett (2) és (3) főideálokra nem alkalmazható a tétel, mert sem (2)\sube (3), sem pedig (3)\sube (2) nem teljesül. Ezzel szemben a (8)\sube (4)\sube (2) főideálokból álló sorozatra teljesül a feltétel, így a tétel alapján a (8)\cup (4)\cup (2) unióhalmaz is ideál \Z-ben. Ez végülis nyilvánvaló, hiszen a (8) és a (4) főideál is részhalmaza a (2) főideálnak, így ezek uniója valójában maga a (2) főideál.
Ami már kevésbé nyilvánvaló, hogy a tétel végtelen sok ideálból álló halmazrendszerekre is működik. Sőt, még akkor is, ha ezek között esetleg nincs is a 19.7. Definíció szerinti értelemben vett legbővebb ideál. Ilyen lehet például egy ideálokból álló végtelen I_1\sube I_2\sube I_3\sube \ldots sorozat. Nézzük meg, hogy miért.
Bizonyítás:
Nézzük először a részgyűrűk uniójára vonatkozó állítást! Jelöljük S-sel az \mathcal{S} halmazrendszerben lévő részgyűrűk unióját. Azt kell megmutatni, hogy S részgyűrű R-ben. Ez a 18.15. Tétel szerint pontosan akkor teljesül, ha S zárt az R-beli összeadásra, szorzásra és ellentettképzésre, valamint tartalmazza az R gyűrű nullelemét.
Mivel \mathcal{S} minden eleme részgyűrű, így a 18.15. Tétel miatt mindegyik tartalmazza az R gyűrű nullelemét. A nullelem tehát valóban benne van ezek uniójában, azaz S-ben.
Legyen most x az S halmaz egy tetszőleges eleme. Mivel S az \mathcal{S}-beli részgyűrűk uniója, így ezek között biztosan létezik olyan X részgyűrű, amelynek x szintén eleme. Az X viszont ismét a 18.15. Tétel miatt zárt az ellentettképzésre. Így -x is eleme X-nek, és emiatt S-nek is.
Végül legyen x és y az S halmaz két tetszőleges eleme. Mivel S az \mathcal{S}-beli részgyűrűk uniója, így ezek között biztosan léteznek olyan X és Y részgyűrűk, hogy x\in X és y\in Y teljesül. Mivel az \mathcal{S} halmazrendszerben bármely két részgyűrű között legalább az egyik irányban fennáll a tartalmazási reláció, ezért X\sube Y vagy Y\sube X közül legalább az egyik teljesül.
Ha például X\sube Y a helyzet, akkor x\in X miatt x\in Y is teljesül, azaz x és y mindketten benne vannak a Y-ban. De ekkor az összegük és a szorzatuk is benne van Y-ban – mivel Y részgyűrű –, és így S-ben is.
Ha X\sube Y nem teljesül, akkor teljesül Y\sube X, és ekkor a fentivel megegyező gondolatmenet alapján x és y összege és szorzata X-ben lesz benne, és így megintcsak S-ben is. Az S unióhalmaz tehát valóban részgyűrű R-ben, ahogyan a tétel állítja.
Most nézzük a balideálok uniójára vonatkozó állítást! Jelöljük I-vel az \mathcal{I} halmazrendszerben lévő balideálok unióját. Azt kell megmutatni, hogy I balideál R-ben. Ez a 18.18. Definíció szerint azt jelenti, hogy egyrészt I részgyűrű R-ben, másrészt akármelyik a\in I elemet balról megszorozva akármelyik r\in R elemmel, az így kapott r\cdot a szorzat szintén benne van I-ben. Minthogy \mathcal{I} minden eleme részgyűrű R-ben (hiszen balideál), ezért a fentiek alapján I is részgyűrű R-ben. Elegendő tehát csak a baloldali szorzásra vonatkozó feltételt ellenőrizni.
Tegyük fel, hogy a az I részgyűrű, r pedig az R gyűrű egy tetszőleges eleme. Mivel I az \mathcal{I}-beli balideálok uniója, így e balideálok között biztosan létezik olyan X balideál, amelynek a szintén eleme. Minthogy X balideál, emiatt az r\cdot a szorzat is benne van X-ben, és így I-ben is. Emiatt I valóban balideál R-ben.
A jobbideálok uniójára vonatkozó állítás értelemszerűen ugyanezzel a gondolatmenettel igazolható azzal a különbséggel, hogy ekkor az r\cdot a szorzat helyett az a\cdot r szorzatot kell tekinteni.
Végül a (kétoldali) ideálok uniójára vonatkozó állítás triviálisan adódik, hiszen minden (kétoldali) ideál egyszerre bal- és jobbideál.
∎Most rátérünk annak igazolására, hogy minden főideálgyűrű teljesíti a 19.14. Tétel szerinti 1. feltételt. Az alábbi tétel valójában egy ennél erősebb állítást mond ki, és az előző tételhez hasonlóan nem csak integritástartományokra, hanem bármilyen gyűrűre működik.
19.18. Tétel:
Legyen R tetszőleges gyűrű. Ha R minden ideálja végesen generált, akkor az ezekből álló \mathcal{R} halmazrendszer bármely nemüres részhalmazában létezik maximális elem a 19.7. Definíció szerinti értelemben.
♣Eszerint tehát ahhoz, hogy egy gyűrű főideáljaira teljesüljön a 19.14. Tétel szerinti 1. feltétel, elegendő, ha az ideálok végesen generáltak. Ez speciálisan főideálgyűrűkre nyilván teljesül, hiszen az ezekben lévő ideálok szintén végesen generáltak – konkrétan egyetlen elem által.
Bizonyítás:
Tegyük fel indirekt, hogy R minden ideálja végesen generált, ám ennek ellenére az \mathcal{R} halmazrendszernek létezik egy olyan nemüres \mathcal{S} részhalmaza, amelynek nincs maximális eleme. Ez a 19.7. Definíció alapján azt jelenti, hogy bármilyen X ideált választunk is ki \mathcal{S}-ből, biztosan létezni fog egy Y\in \mathcal{S} ideál is, amely X-nél bővebb, azaz amelyre teljesül az X\sub Y szigorú tartalmazási reláció. Eszerint tehát \mathcal{S} elemeiből alkotható egy olyan végtelen, ideálokból álló sorozat, amelyben minden ideál szigorúan tartalmazza a sorozatban előtte lévőt:
I_1\sub I_2\sub I_3\sub \ldotsKépezzük ennek a végtelen sok ideálnak az unióját, és nevezzük az így kapott halmazt U-nak. A 19.17. Lemma alapján ekkor U is ideál az R gyűrűben. Mivel R minden ideálja végesen generált, így U is. Léteznek tehát az R gyűrűben olyan a_1,a_2,\ldots,a_n elemek, amelyek generálják az U ideált, azaz:
U=(a_1,a_2,\ldots,a_n)Mivel e generátorelemek benne vannak az U unióhalmazban, ezért minden generátorelemnek benne kell lennie az I_1, I_2, I_3,\ldots ideálok közül is legalább az egyikben. Mivel ezen ideálok közül mindegyik szigorúan tartalmazza a sorozatban előtte lévőt, ezért kell lennie közöttük egy olyan I_k ideálnak, amely már minden generátorelemet tartalmaz.
Tehát egyrészt teljesül az U\sube I_k tartalmazási reláció, hiszen a 19.10. Tétel miatt U a legszűkebb olyan ideál, amely az a_1, a_2, \ldots, a_n generátorelemeket tartalmazza. Másrészt a fenti ideálokból álló sorozat következő elemére, azaz I_{k+1}-re ugye teljesül az I_k\sub I_{k+1} szigorú tartalmazási reláció, továbbá az I_{k+1}\sube U tartalmazási reláció is, hiszen I_{k+1} egyike azon ideáloknak, amelyek uniójából állítottuk elő az U ideált. Ezeket összevetve tehát az alábbit kaptuk:
U\sube I_k\sub I_{k+1}\sube UMivel a \sube és a \sub relációk tranzitívak (19.6. Tétel), ezért ez azt jelenti, hogy teljesül az U\sub U szigorú tartalmazási reláció. Ez viszont lehetetlen, hiszen ez azt jelentené, hogy létezik olyan x gyűrűelem, amelyre x\in U és x\notin U egyaránt teljesül.
Ha tehát R minden ideálja végesen generált, akkor az ezekből álló \mathcal{R} halmazrendszer bármely nemüres részhalmazának szükségképpen kell legyen maximuma.
∎Ahhoz, hogy főideálgyűrűkre is igazoljuk az alaptétel teljesülését, hátravan még a 19.14. Tétel szerinti 2. feltétel. Ez azt követeli meg, hogy minden felbonthatatlan elem prímtulajdonságú legyen. Szerencsére ehhez a 17.12. Tétel alapján elegendő azt igazolni, hogy egy főideálgyűrűben bármely két elemnek létezik kitüntetett közös osztója (17.4. Definíció).
Nézzük hát meg, hogy milyen összefüggés van a kitüntetett közös osztó, és a gyűrű ideáljai között.
19.19. Tétel:
Legyen R tetszőleges integritástartomány, amelyben létezik egységelem. Legyenek továbbá a, b és d az R tetszőleges elemei, és tegyük fel, hogy (a,b)=(d) teljesül. Ekkor d kitüntetett közös osztója a-nak és b-nek.
♣Megjegyzés:
Az Olvasót eddig esetleg zavarhatta, hogy az a és b elemeket tartalmazó legszűkebb ideált ugyanúgy (a,b)-vel jelöljük, mint e két elem kitüntetett közös osztóját. Ez a tétel pontosan ennek az okára világít rá.
♣Bizonyítás:
Az a elem nyilván benne van az (a,b) ideálban, ami a feltétel alapján a (d) főideállal egyezik meg. Emiatt az a elem összes többszöröse is (d)-ben van. Ezek viszont épp az (a) főideál elemei, azaz (a)\sube (d), és így a 19.12. Tétel alapján teljesül a d|a oszthatóság. Hasonló okok miatt teljesül a d|b oszthatóság is, így d közös osztója a-nak és b-nek. Azt kell még megmutatni, hogy d rendelkezik a 17.4. Definíció szerinti kitüntetett tulajdonsággal.
Ehhez tegyük fel, hogy c szintén valamilyen közös osztó, azaz c|a és c|b. Ekkor a 19.12. Tétel miatt teljesülnek az (a)\sube (c) és a (b)\sube (c) tartalmazási relációk. Ez azt jelenti, hogy minden, ami az (a) vagy a (b) főideálok közül legalább az egyiknek eleme, az eleme egyúttal a (c) főideálnak is. Ez nyilván igaz magára az a és b elemekre is, azaz a\in (c) és b\in (c). Minthogy az (a,b) ideál a 19.10. Tétel alapján a legszűkebb olyan ideál, amely tartalmazza az a és b elemeket, ezért az ugyanilyen tulajdonsággal rendelkező (c) főideál biztosan nem lehet nála szűkebb, azaz (a,b)\sube (c). A tételben szereplő (a,b)=(d) feltétel miatt tehát (d)\sube (c) teljesül, azaz a 19.12. Tétel miatt fennáll a c|d oszthatóság.
Ugyanezzel a gondolatmenettel bármilyen közös osztóról igazolható, hogy osztója a d közös osztónak, amely emiatt valóban kitüntetett közös osztó.
∎Mostmár könnyedén igazolhatjuk az alaptétel teljesülését minden főideálgyűrűre.
19.20. Tétel:
Minden főideálgyűrűben teljesül a számelmélet alaptétele.
♣Bizonyítás:
Azt kell megmutatni, hogy a 19.14. Tétel szerinti mindkét feltétel teljesül. Mivel egy R főideálgyűrű minden ideálja generálható egyetlen elemmel, ezért alkalmazható a 19.18. Tétel. Eszerint a főideálok bármely nemüres részhalmazának van maximuma, így teljesül az 1. feltétel.
Legyen a és b az R főideálgyűrű két tetszőleges eleme, és képezzük belőlük az (a,b) ideált, ami ugye a 19.10. Tétel alapján létezik. Minthogy R főideálgyűrű, ezért az (a,b) ideál generálható egyetlen elemmel is. Legyen ez az elem d, azaz (a,b)=(d). A 19.19. Tétel alapján d kitüntetett közös osztója a-nak és b-nek. Ugyanilyen gondolatmenettel bármely két elemre megmutatható, hogy létezik a kitüntetett közös osztójuk, és így a 17.12. Tétel alapján minden felbonthatatlan elem prímtulajdonságú. Azaz teljesül a 2. feltétel is, tehát R-ben valóban érvényes a számelmélet alaptétele.
∎Összefoglalás
Most tehát már van egy átfogó képünk a különböző típusú gyűrűkről. Az alábbi ábrán az eddig megismert összes gyűrűosztály, és ezek egymáshoz való viszonya látható:

Az összes gyűrű között 3 nagy gyűrűosztályt határolhatunk el. Ezek az alábbiak:
- Kommutatív gyűrűk: ezekben az összeadáshoz hasonlóan a szorzás is kommutatív, azaz a tényezők sorrendje felcserélhető.
- Egységelemes gyűrűk: ezekben az összeadáshoz hasonlóan a szorzásra nézve is létezik neutrális elem.
- Nullosztómentes gyűrűk: ezekben két elem szorzata garantáltan csak akkor lehet a nullelem, ha legalább az egyik tényező szintén a nullelem.
Azokat a gyűrűket neveztük integritástartományoknak, amelyek egyszerre kommutatívak és nullosztómentesek. Ez a fenti ábrán a zsúfoltság elkerülése érdekében nincs külön megjelenítve. Külön osztályt alkotnak azok az integritástartományok, amelyekben teljesül a számelmélet alaptétele. Ezeket az ábrán alaptételes gyűrűknek neveztük el. Minthogy a 16.18. Tétel alapján az ilyen gyűrűkben biztosan létezik egységelem, ezért ezek a fenti 3 nagy gyűrűosztály metszetében helyezkednek el.
Az alaptételes gyűrűk alosztályát alkotják az ebben a részben megismert főideálgyűrűk. Ezekben az integritástartományokban bármely két elemnek garantáltan létezik kitüntetett közös osztója, és ez igen fontos lesz számunkra a további részekben. Fontos megjegyezni, hogy léteznek olyan alaptételes gyűrűk, amelyek nem főideálgyűrűk. Ám ilyen példákra a szükséges algebrai ismeretek hiányában egyelőre szintén nem tudunk kitérni.
Végül a 17. részben volt szó az euklidészi gyűrűkről, amelyekben nemcsak a kitüntetett közös osztó létezése garantált, hanem a maradékos osztás elvégezhetősége révén egy gyors algoritmust is kaptunk a kezünkbe ennek kiszámítására. Ezt az eljárást euklidészi algoritmusnak neveztük el, amely szintén egy fontos összetevője a hamarosan terítékre kerülő kriptográfiai eljárásoknak. A 17.19. Tételben igazoltuk, hogy az egész számok \Z gyűrűje is ehhez a gyűrűosztályhoz tartozik.
Ebben a részben tehát végérvényesen lezártuk a számelmélet alaptételének kérdését azáltal, hogy egyszerre szükséges és elégséges feltételrendszert mutattunk a teljesülésére. Ehhez egy rövid halmazelméleti gyorstalpaló után az ideálok elméletének néhány alapvető összefüggésével ismerkedtünk meg. Végül bevezettük az euklidészi gyűrűknél általánosabb főideálgyűrűk fogalmát, és igazoltuk, hogy ezekben is mindig teljesül az alaptétel.
A következő részekben elsősorban a főideálgyűrűk – és speciálisan az egész számok \Z gyűrűjének – ideáljaival, valamint az ezek szerinti kongruenciákkal és faktorgyűrűkkel fogunk foglalkozni. Ennek során az RSA-algoritmus és a különböző prímtesztelő eljárások számelméleti összetevőivel ismerkedünk meg.
A következő részt itt találod…



