Az előző részben megismerkedtünk az úgynevezett csoportelmélet néhány alapfogalmával és összefüggésével, amely az absztrakt algebra egy igen hatékony eszköze. Bevezettük a csoport, a részcsoport fogalmát, valamint definiáltuk, hogy mit értünk egy csoport illetve egy csoportelem rendje alatt. Ezután a mellékosztály fogalmának bevezetésével igazoltuk Lagrange tételét, amely egy fontos oszthatósági kapcsolatot mond ki egy csoport és a részcsoportok illetve csoportelemek rendjei között. Végül ezt felhasználva megmutattuk, hogy bármilyen páratlan összetett szám esetén a redukált maradékosztályoknak legalább a fele Miller-Rabin-tanú, így gyakorlatilag szinte nincs esélye annak, hogy a Miller-Rabin-prímteszt tévedjen. Meg fogjuk azonban mutatni, hogy még ennél is jobb a helyzet, és a redukált maradékosztályoknak nemhogy a fele, de legalább a háromnegyede Miller-Rabin-tanú. Ehhez azonban ebben a részben megismerkedünk néhány újabb, fontos csoportelméleti összefüggéssel.
Mik azok a csoporthomomorfizmusok, normálosztók és faktorcsoportok? Milyen párhuzam mutatható ki ezek és a korábban már ismertetett gyűrűhomorfizmusok, ideálok és maradékosztálygyűrűk között? Milyen szép struktúratartó tulajdonságai vannak egy csoporthomomorfizmusnak? Mik azok a ciklikus csoportok, és összesen hány ilyen létezik? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 18. és a 24. részben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy adva van egy (R,+,\cdot) és egy (S,\oplus,\odot) gyűrű. Ekkor egy f:R\to S függvényt gyűrűhomomorfizmusnak nevezünk, amennyiben tetszőleges R-beli a és b elemekre teljesülnek az alábbi követelmények:
\begin{aligned}f(a+b)&=f(a)\oplus f(b)\\f(a\cdot b)&=f(a)\odot f(b)\end{aligned}Amennyiben S minden eleme legalább egy R-beli elemhez hozzá van rendelve, akkor f-et szürjektív gyűrűhomomorfizmusnak vagy gyűrűráképzésnek nevezzük.
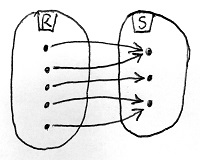
Amennyiben S minden eleme legfeljebb egy R-beli elemhez van hozzárendelve, akkor f-et injektív gyűrűhomomorfizmusnak vagy gyűrűbeágyazásnak nevezzük.
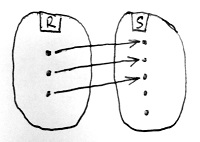
Amennyiben S minden eleme pontosan egy R-beli elemhez van hozzárendelve, akkor f-et bijektív gyűrűhomomorfizmusnak vagy gyűrűizomorfizmusnak nevezzük.
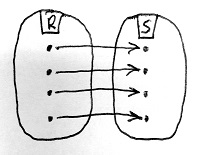
Ilyenkor azt mondjuk, hogy az R és az S gyűrű izomorf egymással. Ezt így jelöljük: R\simeq S.
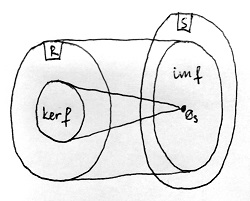
Legyenek R és S tetszőleges gyűrűk, valamint legyen adva közöttük egy f:R\to S gyűrűhomomorfizmus. Ekkor az f gyűrűhomomorfizmus magjának nevezzük azon R-beli elemek halmazát, melyeknek f szerinti képe az S gyűrű nulleleme. Az f magját – az angol „kernel” szóból eredeztetve – így jelöljük: \ker f.
Az f gyűrűhomomorfizmus képének nevezzük azoknak az S-beli elemeknek a halmazát, amelyek képei legalább egy R-beli elemnek. Az f képét – az angol „image” szóból eredeztetve – így jelöljük: \text{im} f.
Az alábbi ábra szemlélteti a fenti fogalmakat:
Legyen adva egy R gyűrű, valamint annak egy I részhalmaza, amely részgyűrű R-ben. Tegyük fel továbbá, hogy r az R gyűrű egy tetszőleges – tehát nem feltétlenül I-beli – eleme.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az r\cdot a szorzat is I-ben van, akkor azt mondjuk, hogy I balideál R-ben.
Amennyiben az I részgyűrű tetszőleges a eleme esetén az a\cdot r szorzat is I-ben van, akkor azt mondjuk, hogy I jobbideál R-ben.
Amennyiben egy I részgyűrű egyszerre bal- és jobbideál, akkor azt mondjuk, hogy I kétoldali ideál, vagy egyszerűen csak ideál R-ben. Ezt így jelöljük: I\triangleleft R.
A nullgyűrű és maga a teljes R nyilvánvalóan ideálok R-ben. Ezeket triviális ideáloknak nevezzük.
Legyen R egy tetszőleges gyűrű, és tegyük fel, hogy I ideál R-ben. Jelöljük R/I-vel azt a halmazt, amelynek elemei a 18.21. Tételben definiált I ideál szerinti maradékosztályok. Vezessünk be ezek között két műveletet az alábbiak szerint:
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek összege legyen az A\oplus B=(a+b)+I maradékosztály.
- Ha A=a+I és B=b+I két maradékosztály, akkor ezek szorzata legyen az A\odot B=(a\cdot b)+I maradékosztály.
Ekkor az R/I halmaz ezzel a két művelettel gyűrűt alkot, amelyet az R gyűrű I ideál szerinti maradékosztálygyűrűjének vagy faktorgyűrűjének nevezünk.
Ha 0_R jelöli az R gyűrű nullelemét, akkor az R/I gyűrű nulleleme a 0_R+I maradékosztály.
Ha -a jelöli az R gyűrű egy a elemének ellentettjét, akkor az R/I gyűrű a+I elemének ellentettje a (-a)+I maradékosztály.
Ha R egységelemes, és 1_R jelöli az egységelemét, akkor R/I is egységelemes, az egységelem pedig az 1_R+I maradékosztály.
Ha R kommutatív, akkor R/I is az.
Tekintsük továbbá azt az f:R\to R/I függvényt, amely minden R-beli r elemhez az r+I maradékosztályt rendeli hozzá az R/I gyűrűből. Ekkor f egy gyűrűhomomorfizmus R és R/I között, melynek magja I. Ennek a neve természetes gyűrűhomomorfizmus.
Tegyük fel, hogy adva van egy valamilyen G halmaz, amelyen értelmezve van egy kétváltozós művelet. Nevezzük ezt a műveletet szorzásnak és jelöljük \cdot-tal, vagy egymás után írással. Például egy a és egy b elem szorzatát jelöljük a\cdot b-vel vagy ab-vel.
Az így kapott (G,\cdot ) algebrai struktúrát félcsoportnak nevezzük, amennyiben az említett művelet asszociatív. Azaz tetszőleges a, b és c elemek esetén teljesül az alábbi:
(a\cdot b)\cdot c = a\cdot (b\cdot c)Csoportnak nevezzük az olyan félcsoportokat, amelyek esetén az asszociativitáson kívül a műveletre nézve létezik neutrális elem is (14.7. Definíció), továbbá a művelet invertálható (14.9. Definíció). Egy csoport esetén a neutrális elemet általában e-vel vagy 1-gyel szoktuk jelölni, és ilyenkor egységelemről beszélünk. Egy a elem inverzét a^{-1}-gyel szoktuk jelölni. Tetszőleges a elem esetén teljesülnek tehát az alábbiak:
\begin{aligned}a\cdot e &= e\cdot a = a \\ a\cdot a^{-1} &= a^{-1}\cdot a = e\end{aligned}Amennyiben a művelet a fentieken felül még kommutatív is, úgy Abel-csoportról vagy kommutatív csoportról beszélünk. Abel-csoportok esetén a csoportműveletet tipikusan a + szimbólummal, a neutrális elemet 0-val, egy a elem inverzét pedig -a-val szoktuk jelölni. Ilyenkor a neutrális elemet nullelemnek, az a elem inverzét pedig a ellentettjének nevezzük.
Ha egy G csoport valamely H részhalmaza maga is csoport a G műveletére nézve, akkor azt mondjuk, hogy H részcsoport G-ben. Ezt így jelöljük: H\leq G.
Ha H részcsoport G-ben, de H\neq G, akkor azt mondjuk, hogy H valódi részcsoport G-ben. Ezt így jelöljük: H\lt G.
Legyen G tetszőleges csoport, H pedig valamilyen részcsoport G-ben. Definiáljunk egy \sim szimbólummal jelölt relációt a G csoport elemei között a következőképpen: a\sim b akkor és csak akkor, ha a^{-1}b\in H.
Ekkor a \sim reláció egy ekvivalenciareláció a G csoport elemei között. Az ehhez tartozó ekvivalencia-osztályokat a G csoport H részcsoportja szerinti baloldali mellékosztályoknak nevezzük. Ha g egy tetszőleges elem a G csoportban, akkor a g elemet tartalmazó H szerinti baloldali mellékosztály épp a 18.19. Definícióban bevezetett komplexusszorzással képzett gH halmaz lesz.
Ehhez hasonlóan, ha az a\sim b relációt úgy definiáljuk, hogy akkor és csak akkor teljesüljön, ha ba^{-1}\in H, akkor ugyanígy egy ekvivalenciarelációt kapunk. Ebben az esetben az ekvivalencia-osztályokat a H részcsoport szerinti jobboldali mellékosztályoknak nevezzük, a g elemet tartalmazó jobboldali mellékosztály pedig a Hg halmaz lesz.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 18. és a 24. részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
A 18. részben ismertettük az úgynevezett moduláris aritmetika, azaz a maradékokkal való számolás absztrakt algebrai hátterét. Mint ahogyan azt az Olvasó is látni fogja, az ennek kapcsán felépített fogalmak és tételek szinte egytől egyig párhuzamba állíthatók lesznek az ebben a részben leírtakkal. Ezekre a szép párhuzamokra a tárgyalás során folyamatosan rá fogunk mutatni annak érdekében, hogy lehessen mihez kötni az itt bevezetett, sok esetben meglehetősen absztrakt csoportelméleti fogalmakat. Ettől függetlenül azt javasoljuk az Olvasónak, hogy gyakran lapozzon vissza az említett 18. részhez, mivel ezek a párhuzamok adott esetben egészen más megvilágításba helyezhetik az eddig tanultakat.
A 18. részben elsőként egy nagyon fontos, az egész számok \Z gyűrűjén értelmezett függvénnyel, az úgynevezett modulo m maradékképző függvénnyel ismerkedtünk meg (18.3. Definíció). Ez a \bmod_m-mel jelölt függvény minden egész számhoz az m egész számmal való nemnegatív osztási maradékát rendeli hozzá. Ennek a függvénynek az értékkészletét \Z_m-mel jelöltük, amelyen egy összeadásnak és egy szorzásnak nevezett műveletet is értelmeztünk a 18.3. Definícióban leírtaknak megfelelően.
Ezután igazoltuk, hogy a \Z_m halmaz ezzel a két művelettel egy kommutatív gyűrűt alkot. Ám ami talán még fontosabb volt számunkra, hogy a \bmod_m maradékképző függvény egy szoros kapcsolatot létesített a \Z és a \Z_m gyűrűk között.
Csoporthomomorfizmusok
A már említett \bmod_m függvényről a 18.7. Tételben megmutattuk, hogy ő egy úgynevezett gyűrűhomomorfizmus \Z és \Z_m között. Ez a 18.6. Definíció alapján azt jelentette, hogy a \bmod_m függvény tartja a \Z gyűrű összeadását és szorzását. Azaz teljesen mindegy, hogy két számot először a \Z gyűrűben adunk vagy szorzunk össze, az eredmény \bmod_m szerinti képe a \Z_m gyűrűben ugyanaz lesz, mintha először képeztük volna a két szám maradékát, és ezeket adtuk vagy szoroztuk volna össze a \Z_m gyűrűn értelmezett műveletekkel.
Most bevezetünk egy nagyon hasonló fogalmat, amely tehát két gyűrű helyett két csoport között létesít ehhez hasonló szoros kapcsolatot.
25.1. Definíció (Csoporthomomorfizmus):
Tegyük fel, hogy adva van egy (G,\cdot) és egy (H,\odot) csoport. Ekkor egy f:G\to H függvényt csoporthomomorfizmusnak nevezünk, amennyiben tetszőleges G-beli a és b elemekre teljesül az alábbi művelettartó tulajdonság:
f(a\cdot b)=f(a)\odot f(b)Amennyiben H minden eleme legalább egy G-beli elemhez hozzá van rendelve, akkor f-et szürjektív csoporthomomorfizmusnak vagy csoportráképzésnek nevezzük.
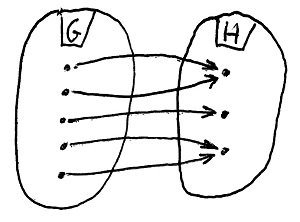
Amennyiben H minden eleme legfeljebb egy G-beli elemhez van hozzárendelve, akkor f-et injektív csoporthomomorfizmusnak vagy csoportbeágyazásnak nevezzük.
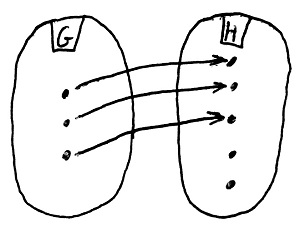
Amennyiben H minden eleme pontosan egy G-beli elemhez van hozzárendelve, akkor f-et bijektív csoporthomomorfizmusnak vagy csoportizomorfizmusnak nevezzük.
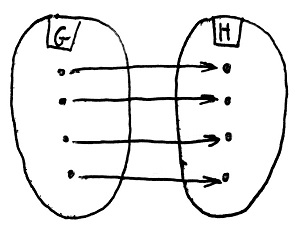
Ilyenkor azt mondjuk, hogy a G és a H csoport izomorf egymással. Ezt így jelöljük: G\simeq H.
♣Megjegyzés:
A csoportizomorfizmusokra a gyűrűizomorfizmusokhoz hasonlóan teljesül a szimmetria, a tranzitivitás és a reflexivitás. Azaz ha G, H és K tetszőleges csoportok, akkor teljesülnek az alábbiak:
- Szimmetria: Ha G\simeq H, akkor H\simeq G.
- Tranzitivitás: Ha G\simeq H és H\simeq K, akkor G\simeq K.
- Reflexivitás: G\simeq G.
Ezek igazolása a gyűrűhomomorfizmusokról szóló 18.6. Definíció utáni megjegyzésben foglaltakkal szinte szó szerint megegyezik azzal a különbséggel, hogy itt kettő helyett csak egy művelet van.
♣A gyűrűhomomorfizmus fogalmának bevezetése után egy fontos segédtételt bizonyítottunk, amely demonstrálta az ilyen leképezések struktúratartó tulajdonságait. Ez a 18.11. Lemma volt, amelyben azt mutattuk meg, hogy a gyűrűhomomorfizmusok tartják a kiindulási gyűrű nullelemét, továbbá az ott értelmezett ellentettképzést is. Azaz nullelem képe a célgyűrű nulleleme, illetve ellentett képe a kép ellentettje lesz a célgyűrűben.
Most a csoporthomomorfizmusok kapcsán igazolunk egy nagyon hasonló segédtételt. Az egyetlen különbség mindössze annyi, hogy csoportok esetén nullelem helyett általában egységelemről, míg ellentett helyett inverzről szoktunk beszélni.
25.2. Lemma:
Legyen adva egy (G,\cdot) és egy (H,\odot) csoport, valamint egy közöttük lévő f:G\to H csoporthomomorfizmus. Ekkor igazak az alábbiak:
- Ha rendre e_G és e_H jelöli a G és H csoportok egységelemét, akkor f(e_G)=e_H.
- Ha a -1 kitevő az inverzképzést jelöli a megfelelő csoportban, akkor tetszőleges G-beli a elem esetén f(a^{-1})=(f(a))^{-1}.
Szavakkal: egy csoporthomomorfizmus az inverzképzést és az egységelemet is tartja. Azaz egyrészt a G csoport egységelemének képe a H csoport egységeleme, másrészt bármely G-beli elem G-beli inverzének képe az elem képének H-beli inverze.
♣Bizonyítás:
Az 1. állítás: Mivel egyrészt e_G a G csoport egységeleme, valamint f tartja a csoportműveletet, ezért a G csoport tetszőleges a elemére felírhatók az alábbiak:
\begin{aligned}f(a)&=f(a\cdot e_G)=f(a)\odot f(e_G) \\ f(a)&=f(e_G\cdot a)=f(e_G)\odot f(a)\end{aligned}Másrészt, mivel e_H a H csoport egységeleme, ezért f(a)=f(a)\odot e_H és f(a)=e_H\odot f(a) is igaz. Ezt az előző egyenletekkel összevetve az alábbit kapjuk:
\begin{aligned}\underbrace{f(a)\odot f(e_G)}_{=f(a)}&=f(a)\odot e_H \\ \underbrace{f(e_G)\odot f(a)}_{=f(a)}&=e_H\odot f(a)\end{aligned}Ha az első egyenlet mindkét oldalát balról, vagy a második egyenlet mindkét oldalát jobbról megszorozzuk a H csoportban az f(a) elem H-beli inverzével, akkor megkapjuk a tétel 1. állítását:
f(e_G)=e_HA 2. állítás: Legyen a a G csoport valamely tetszőleges eleme, amelynek G-beli ellentettjét jelöljük a^{-1}-gyel. Ekkor az 1. állítás miatt:
\begin{aligned}f(a\cdot a^{-1})=f(e_G)&=e_H \\ f(a^{-1}\cdot a)=f(e_G)&=e_H\end{aligned}Másrészt viszont f tartja a csoportműveletet, így igaz az alábbi is:
\begin{aligned}f(a\cdot a^{-1})&=f(a)\odot f(a^{-1}) \\ f(a^{-1}\cdot a)&=f(a^{-1})\odot f(a)\end{aligned}A két-két egyenletet egymással összevetve ezt kapjuk:
\begin{aligned}f(a)\odot f(a^{-1})&=e_H \\ f(a^{-1})\odot f(a)&=e_H\end{aligned}Mivel f(a) és f(a^{-1}) szorzata mindkét sorrendben épp a H csoport egységeleme, valamint az inverzképzés a 14.10. Tétel alapján egyértelmű, ezért f(a^{-1}) valóban az f(a) elem H-beli inverzével egyezik meg.
∎Csoporthomomorfizmus magja és képe
A 18. részben a gyűrűhomomorfizmusok jellemzéséhez megismerkedtünk a gyűrűhomomorfizmus magjának és képének fogalmával (18.12. Definíció). Egy f:R\to S gyűrűhomomorfizmus magjának neveztük azon R-beli elemek halmazát, amelyekhez az f függvény épp az S gyűrű nullelemét rendeli hozzá, míg f képének azoknak az S-beli elemeknek a halmazát neveztük, amelyeket f legalább egy R-beli elemhez hozzárendel. Ennek mintájára az alábbiakban definiáljuk a csoporthomomorfizmusok magjának és képének fogalmát. A különbség pusztán annyi, hogy most a célgyűrű nullelemének szerepét a célcsoport egységeleme veszi át.
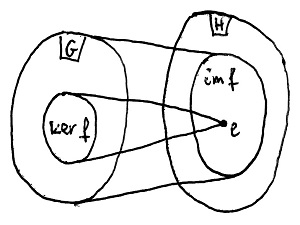
25.3. Definíció (Csoporthomomorfizmus magja és képe):
Legyenek G és H tetszőleges csoportok, valamint legyen adva közöttük egy f:G\to H csoporthomomorfizmus. Ekkor az f csoporthomomorfizmus magjának nevezzük azon G-beli elemek halmazát, melyeknek f szerinti képe a H csoport egységeleme. Az f magját – az angol „kernel” szóból eredeztetve – így jelöljük: \ker f.
Az f csoporthomomorfizmus képének nevezzük azoknak a H-beli elemeknek a halmazát, amelyek képei legalább egy G-beli elemnek. Az f képét – az angol „image” szóból eredeztetve – így jelöljük: \text{im} f.
Az alábbi ábra szemlélteti a fenti fogalmakat:
Ezek után bevezettük a részgyűrű fogalmát (18.14. Definíció) és megmutattuk, hogy egy f gyűrűhomomorfizmus képe minden esetben részgyűrű abban az S gyűrűben, ahová f képez (lásd a 18.16. Tételt). Ezen túlmenően ebben a tételben azt is megemlítettük, hogy ennél többet nem is tudunk elmondani az S-be képező gyűrűhomomorfizmusok képeiről. Ez másként fogalmazva azt jelenti, hogy S bármely részgyűrűje képe valamilyen S-be mutató gyűrűhomomorfizmusnak.
A részcsoport fogalmát a 24.4. Definícióban már bevezettük, és most az említett 18.16. Tétel mintájára egy nagyon hasonló állítást fogunk igazolni a csoporthomomorfizmusok képeivel kapcsolatban.
25.4. Tétel:
Legyen adva egy H csoport, és annak egy T részhalmaza. A T részhalmaz akkor és csak akkor képe egy H-ba mutató csoporthomomorfizmusnak, ha részcsoport H-ban.
♣Bizonyítás:
Tekintsük azt az f csoporthomomorfizmust, amelynek képe T. Ez egy valamilyen, számunkra ismeretlen X csoport elemein van értelmezve, amelynek egységelemét jelöljük most e_X-szel, míg a H csoport egységelemét jelöljük e_H-val. Azt kell megmutatnunk, hogy T-re teljesülnek a 24.5. Tételben felsorolt feltételek.
A 25.2. Lemma 1. pontja alapján f(e_X)=e_H, így tehát a H csoport egységeleme valóban benne van T-ben.
Ha valamilyen a és b elemek benne vannak T-ben, akkor léteznek olyan x_a és x_b elemek X-ben, amelyeknek épp ő a képük, azaz f(x_a)=a és f(x_b)=b. A két egyenletet összeszorozva H-ban, valamint kihasználva f művelettartó tulajdonságait az alábbit kapjuk:
f(x_a)\cdot f(x_b)=f(x_a\cdot x_b)=a\cdot bLétezik tehát olyan elem X-ben, amelynek a\cdot b a képe (nevezetesen x_a\cdot x_b), emiatt az a\cdot b szorzat is benne van T-ben, ami így valóban zárt a H csoport szorzására nézve.
Végül ha valamilyen a elem benne van T-ben, akkor létezik olyan x_a elem X-ben, amelynek épp a a képe, azaz f(x_a)=a. A 25.2. Lemma 2. pontja alapján azonban f tartja az inverzképzést is, így teljesül az alábbi:
f(x_a^{-1})=(f(x_a))^{-1}=a^{-1}Létezik tehát olyan elem X-ben, amelynek a^{-1} a képe (nevezetesen x_a^{-1}), emiatt a^{-1} is benne van T-ben, ami így zárt az inverzképzésre nézve is. Minthogy a 24.5. Tételben felsorolt minden feltétel teljesül, ezért T valóban részcsoport H-ban.
Visszafelé: Tegyük most fel, hogy T részcsoport H-ban. Azt kell megmutatnunk, hogy van olyan H-ba mutató csoporthomomorfizmus, amelynek képe T. Tekintsük például azt az f:T\to H függvényt, amely T minden eleméhez önmagát rendeli hozzá. Ez kétségkívül nem egy izgalmas függvény, viszont nyilvánvalóan csoporthomomorfizmus, aminek a képe ráadásul épp a T halmaz.
∎Egy H csoportban tehát az odamutató csoporthomomorfizmusok képeiről mindössze annyit tudunk mondani, hogy azok pontosan H részcsoportjai lesznek. Ezzel szemben egy G csoport azon részhalmazairól, amelyek valamilyen G-ből kiinduló csoporthomomorfizmusok magjai lehetnek, ennél többet is fogunk tudni mondani.
Ez párhuzamba állítható azzal, ahogyan a gyűrűhomomorfizmusok magjait jellemeztük. Először a 18.17. Tételben adtunk erre egy szükséges feltételt. E tétel szerint ha egy R gyűrű valamely I részhalmaza egy R-ből kiinduló gyűrűhomomorfizmus magja, akkor I egy olyan speciális részgyűrű R-ben, amely nem csak az I-beli elemekkel, hanem tetszőleges R-beli elemmel való szorzásra is zárt. Az ilyen speciális részgyűrűket a 18.18. Definícióban ideáloknak neveztük.
Most ehhez hasonlóan arra mutatunk szükséges feltételt, hogy egy G csoport valamely részhalmaza mikor lehet valamilyen G-ből induló csoporthomomorfizmus magja. Nem meglepő módon ezek a részhalmazok is bizonyos értelemben speciális részcsoportok lesznek G-ben. Nézzük is meg, hogy mi az a speciális extra tulajdonság, amit még – azon felül, hogy részcsoportok – teljesítenek.
25.5. Tétel:
Tegyük fel, hogy egy G csoport valamely N részhalmaza egy G-ből kiinduló csoporthomomorfizmus magja. Ekkor teljesülnek az alábbiak:
- Az N halmaz egy részcsoport G-ben.
- Tetszőleges a\in G és b\in G elemek esetén f(a)=f(b) akkor és csak akkor, ha a és b ugyanabban az N részcsoport szerinti baloldali mellékosztályban van, azaz b\in aN.
- Tetszőleges a\in G és b\in G elemek esetén f(a)=f(b) akkor és csak akkor, ha a és b ugyanabban az N részcsoport szerinti jobboldali mellékosztályban van, azaz b\in Na.
- A G csoport N részcsoportja szerinti bal- és jobboldali mellékosztályok megegyeznek, azaz tetszőleges a\in G elem esetén aN=Na.
Bizonyítás:
Tekintsük azt az f csoporthomomorfizmust, amelynek N a magja. Ez egy valamilyen, számunkra ismeretlen X csoportba képez, amelynek egységelemét jelöljük most e_X-szel, míg a G csoport egységelemét jelöljük e_G-vel. Az f függvény tehát N minden eleméhez e_X-et rendeli hozzá, hiszen \ker f=N. Ezt a szituációt mutatja az alábbi ábra.
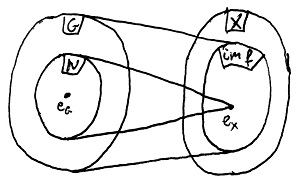
Az 1. állítás igazolásához azt kell megmutatni, hogy N részcsoport G-ben. Ez a 24.5. Tétel alapján pontosan akkor teljesül, ha N tartalmazza e_G-t, valamint zárt a G csoport műveletére és a G-beli inverzképzésre.
Mivel f csoporthomomorfizmus, ezért a 25.2. Lemma értelmében tartja az egységelemet és az inverzképzést. Azaz egyrészt f(e_G)=e_X, és így e_G valóban benne van f magjában, vagyis N-ben. Másrészt ha valamilyen a benne van N-ben, akkor f(a)=e_X, és így az inverzképzés tartása miatt f(a^{-1})=(f(a))^{-1}=e_X^{-1}=e_X. Azaz a inverzének is e_X a képe, következésképp ő is benne van N-ben.
A G csoport műveletére való zártság szintén f művelettartó tulajdonságából ered. Ha ugyanis a és b az N két tetszőleges eleme, akkor egyrészt f(a)=e_X és f(b)=e_X. Másrészt viszont a művelettartás miatt az ő szorzatukra teljesül az alábbi:
f(a\cdot b)=f(a)\cdot f(b)=\underbrace{e_X}_{=f(a)}\cdot \underbrace{e_X}_{=f(b)}=e_XTehát az a\cdot b szorzat is az X csoport egységelemére képeződik, következésképp ő is benne van N-ben. Mivel teljesül a 24.5. Tétel minden feltétele, ezért N valóban részcsoport G-ben.
A 2. állítás igazolásához tegyük fel tehát, hogy f(a)=f(b) valamilyen a\in G és b\in G elemek esetén. Vizsgáljuk meg, hogy mi lesz az a^{-1}b szorzat f szerinti képe X-ben. Ehhez kihasználjuk egyrészt f művelettartó és inverzképzéstartó (lásd a 25.2. Lemma 2. pontját) tulajdonságát, másrészt pedig azt a tényt, hogy jelen esetben ugye f(a)=f(b):
f(a^{-1}b)=f(a^{-1})\cdot f(b)=\underbrace{(f(a))^{-1}}_{=f(a^{-1})}\cdot \underbrace{f(a)}_{=f(b)}=e_XMivel tehát az a^{-1}b szorzat épp az X csoport egységelemére képződött, ezért ez a szorzat benne van f magjában, azaz a^{-1}b\in N. Ez viszont azt jelenti, hogy a és b között fennáll a 24.7. Tételben definiált \sim-vel jelölt ekvivalenciareláció, azaz a és b ugyanabban az ekvivalencia-osztályban vannak. Minthogy az említett tétel alapján ezek az ekvivalencia-osztályok tulajdonképpen az N szerinti baloldali mellékosztályok, ezért valóban b\in aN.
Visszafelé: Tegyük most fel, hogy a és b ugyanabban az N szerinti baloldali mellékosztályban vannak. Ez a 24.7. Tétel alapján azt jelenti, hogy a^{-1}b\in N. De mivel N az f csoporthomomorfizmus magja, ezért ez a szorzat az X csoport egységelemére képződik, azaz f(a^{-1}b)=e_X. Ebből viszont – ismét kihasználva f művelettartó és inverzképzéstartó tulajdonságát – az alábbi következik:
f(a^{-1}b)=f(a^{-1})\cdot f(b)=(f(a))^{-1}\cdot f(b)=e_XHa most az utolsó egyenlőségjel által leírt egyenlet mindkét oldalát balról megszorozzuk f(a)-val, akkor az alábbit kapjuk:
\underbrace{f(a)\cdot (f(a))^{-1}}_{=e_X}\cdot f(b)=f(a)\cdot e_XAzaz – az egységelemeket elhagyva – valóban f(b)=f(a), és ezzel igazoltuk a tétel 2. állítását.
A 3. állítás ugyanígy igazolható, csak ebben az esetben az a^{-1}b szorzat helyett a ba^{-1} szorzatot kell tekinteni, és f(a)-val nem balról, hanem jobbról kell szorozni.
Végül a 4. állításhoz most tekintsünk egy tetszőleges a\in G elemet, és mutassuk meg, hogy az aN mellékosztály, mint halmaz megegyezik az Na mellékosztállyal. Ehhez a 19.2. Definíció utáni megjegyzés 5. pontja alapján azt kell igazolni, hogy az alábbi mindkét tartalmazási reláció fennáll:
\begin{aligned}aN&\sube Na \\ Na&\sube aN\end{aligned}Az első tartalmazáshoz azt kell megmutatni, hogy tetszőleges b\in aN esetén b\in Na is teljesül. Mivel b\in aN, ezért ez azt jelenti, hogy b ugyanabban a baloldali mellékosztályban van, mint a. Ez viszont a már bizonyított 2. állítás alapján azt jelenti, hogy f(a)=f(b), ami azonban a szintén már bizonyított 3. állítás miatt azt is jelenti, hogy b ugyanabban a jobboldali mellékosztályban van, mint a, azaz valóban b\in Na. A másik irányú tartalmazást ugyanilyen módon lehet megmutatni a 2. és 3. állítások felhasználásával.
Ezzel igazoltuk a tétel 4. állítását, miszerint az N szerinti bal- és jobboldali mellékosztályok valóban megegyeznek.
∎Megjegyzés a bizonyításhoz:
Megjegyezzük, hogy az iménti bizonyítás gondolatmenete alapján a tételben az 1. állítás mellett elegendő lett volna kizárólag a 4. állítást megfogalmazni, hiszen az ekvivalens a 2. és 3. állítások együttes teljesülésével.
Tegyük fel ugyanis, hogy teljesül a 4. állítás. Ekkor ha valamilyen a és b elemek ugyanabban a baloldali mellékosztályban vannak, akkor a 4. állítás miatt egyúttal ugyanabban a jobboldali mellékosztályban is vannak – hiszen ezek ugye megegyeznek –, és ebben az esetben a 2. és 3. állítások bizonyításának „visszafele”-irányú gondolatmenete ugyanúgy működik. Megfordítva: ha teljesülnek a 2. és 3. állítások, akkor az iménti bizonyításban már megmutattuk, hogy teljesül a 4. állítás is.
♣A 24.7. Tétel utáni megjegyzésben már megemlítettük, hogy általában egy részcsoport szerinti bal- illetve jobboldali mellékosztályok különböző halmazok lesznek. Az iménti tétel alapján azonban ha egy részcsoport egy valamilyen csoporthomomorfizmus magja, akkor ezek a mellékosztályok szükségképpen megegyeznek. Csoportok esetén ez tehát az a keresett extra feltétel, amely szükséges ahhoz, hogy egy részcsoport egy csoporthomomorfizmus magja lehessen. Most megmutatjuk, hogy ez egyben elégséges is.
Normálosztók és faktorcsoportok
A gyűrűk esetén ideáloknak neveztük el azokat a speciális részgyűrűket, amelyek gyűrűhomomorfizmusok magjai lehetnek. Úgy tűnik, hogy az előző szakaszban egy csoport részcsoportjaira is sikerült azonosítanunk egy olyan speciális tulajdonságot, ami – legalábbis – szükséges ahhoz, hogy ők csoporthomomorfizmusok magjai lehessenek. Most az ilyen speciális részcsoportokat nevezzük el, majd megmutatjuk, hogy ezeken kívül más részcsoport nem is lehet csoporthomomorfizmus magja (azaz az említett speciális tulajdonság egyben elégséges is).
25.6. Definíció (Normálosztó):
Legyen adva egy G csoport, valamint egy N részcsoport G-ben. Tegyük fel továbbá, hogy az N részcsoport szerinti bal- és jobboldali mellékosztályok megegyeznek, azaz minden a\in G esetén teljesül az alábbi:
aN=NaEkkor azt mondjuk, hogy az N részcsoport normálosztó G-ben. Ezt így jelöljük: N\triangleleft G.
Az a részcsoport, amely csak G egységeleméből áll, illetve maga a teljes G nyilvánvalóan normálosztók G-ben. Ezeket triviális normálosztóknak nevezzük.
♣Megjegyzés:
Figyelem! A definíció NEM azt mondja, hogy tetszőleges n\in N esetén a\cdot n=n\cdot a. EHELYETT mindössze annyit állít, hogyha elvégezzük a 18.19. Definíció szerint értelmezett aN és Na komplexusszorzásokat, akkor ugyanazt a két HALMAZT kapjuk eredményül. Ez az elemek szintjén pusztán annyit jelent, hogy minden n\in N-hez létezik olyan m_1 és m_2 elem az N részcsoportban, hogy egyrészt a\cdot n=m_1\cdot a, másrészt n\cdot a=a\cdot m_2.
Természetesen Abel-csoportok esetén (24.1. Definíció) a részcsoport és a normálosztó fogalma egybeesik, hiszen ezekben a csoportokban bármely g és h elemek esetén g\cdot h=h\cdot g teljesül.
♣E speciális tulajdonság elégségességének bizonyításához a 18. részben látott módon fogunk eljárni. Azaz mutatunk egy olyan konstrukciót, amely tetszőleges G csoportból annak valamely N normálosztójának segítségével létrehoz egy új csoportot, továbbá egy G-ből ebbe az új csoportba mutató olyan csoporthomomorfizmust, amelynek magja épp N. Ehhez előszöris értelmezni fogunk egy műveletet az N normálosztó, mint speciális részcsoport szerinti baloldali (vagy a velük azonos jobboldali) mellékosztályok között.
Az ideál szerinti maradékosztályok között a 18.23. Tételben definiált műveletek mintájára ezt a műveletet is a reprezentánselemek segítségével kell majd elvégezni. Kicsit bővebben: két mellékosztályt úgy fogunk „összeszorozni” egymással, hogy kiválasztunk belőlük egy-egy tetszőleges elemet, amelyeket összeszorzunk az eredeti G csoport műveletével, majd azt a mellékosztályt választjuk „végeredménynek”, amelybe az így kapott elem esik. Egy ilyen mellékosztályok közötti műveletnek nyilvánvalóan akkor van csak értelme, ha az eredményül kapott mellékosztály nem függ attól, hogy a két bemeneti mellékosztályból mely elemeket választottuk ki a művelet elvégzéséhez.
Az alábbi ábrán például az A és B mellékosztályok „összeszorzása” látható, amit két különböző elempár segítségével elvégezve ugyanaz az eredmény adódik:
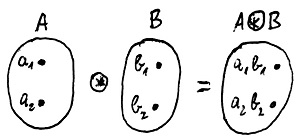
Megköveteljük tehát, hogy függetlenül attól, hogy az a_1\cdot b_1 vagy az a_2\cdot b_2 szorzatot számítjuk-e ki, az eredménynek mindkét esetben ugyanabba a mellékosztályba kell esnie. Ilyenkor mondjuk azt, hogy a művelet jóldefiniált.
Egy gyűrűben a maradékosztályok közötti műveletek jóldefiniáltsága a 18.22. Tétel alapján azon múlott, hogy az a részgyűrű, amelynek a segítségével ezeket a maradékosztályokat képeztük speciálisan egy ideál volt. Most megmutatjuk, hogy ehhez hasonlóan egy csoport esetén egy N részcsoport szerinti mellékosztályok közötti művelet akkor lesz jóldefiniált, ha N speciálisan egy normálosztó.
25.7. Tétel:
Legyen G tetszőleges csoport, N pedig normálosztó G-ben. Tegyük fel továbbá, hogy a G csoport valamilyen a_1 és a_2 valamint b_1 és b_2 elemeire teljesülnek az alábbiak:
- Az a_1 elem ugyanabban az N szerinti baloldali mellékosztályban van, mint az a_2 elem.
- A b_1 elem ugyanabban az N szerinti baloldali mellékosztályban van, mint a b_2 elem.
Ekkor az a_1\cdot b_1 szorzat is ugyanabban az N szerinti baloldali mellékosztályban van, mint az a_2\cdot b_2 szorzat.
Minthogy a 25.6. Definíció alapján az N szerinti bal- és jobboldali mellékosztályok megegyeznek, ezért ugyanez az állítás természetesen a jobboldali mellékosztályokra is érvényes.
♣Bizonyítás:
Előzetesen felhívjuk az Olvasó figyelmét, hogy a bizonyítás leírásában a 18.19. Definícióban szereplő komplexusszorzást és a G csoport szorzásnak nevezett műveletét jelölésben is élesen meg fogjuk különböztetni egymástól, mivel ki szeretnénk hangsúlyozni, hogy nagyon nem ugyanarról van szó. Míg előbbit simán egymás után írással, addig utóbbit a \cdot szimbólummal fogjuk jelölni.
Egyrészt az 1. feltétel – miszerint a_1 ugyanabban az N szerinti baloldali mellékosztályban van, mint a_2 – a 24.7. Tétel alapján azt jelenti, hogy az a_1N és az a_2N halmazok megegyeznek, azaz:
a_1N=a_2NEhhez hasonlóan a 2. feltétel az alábbi halmazegyenlőséget jelenti:
b_1N=b_2NEzek alapján tehát azt kell bizonyítanunk, hogy az (a_1\cdot b_1)N és az (a_2\cdot b_2)N halmazok is megegyeznek. Az (a_1\cdot b_1)N halmaz elemeit ugye a 18.19. Definíció alapján úgy kapjuk meg, hogy az (a_1\cdot b_1)\cdot x kifejezésbe x helyére az N normálosztó összes elemét behelyettesítjük. Ez a kifejezés viszont a 24.1. Definíció alapján a csoportművelet asszociativitása miatt átzárójelezhető:
a_1\cdot (b_1\cdot x)Ha most itt csak a zárójelben lévő kifejezést tekintjük, és ebbe helyettesítjük be N összes elemét, akkor tulajdonképpen a b_1N baloldali mellékosztályt, mint halmazt kapjuk. Ebből következően az (a_1\cdot b_1)N halmaz elemeit úgy is megkaphatjuk, hogy az a_1\cdot y kifejezésbe y helyére a b_1N baloldali mellékosztály elemeit helyettesítjük be. Vagyis fennáll az alábbi halmazegyenlőség:
(a_1\cdot b_1)N=a_1(b_1N)=\ldotsA 2. feltételből következően viszont a b_1N halmaz megegyezik a b_2N halmazzal, ami viszont – lévén, hogy N normálosztó – a 25.6. Definíció alapján megegyezik az Nb_2 halmazzal, azaz:
\ldots=a_1(Nb_2)=\ldotsEnnek a halmaznak az elemeit tehát úgy kapjuk meg, hogy az a_1\cdot y kifejezésbe y helyére az Nb_2 jobboldali mellékosztály elemeit helyettesítjük be, amelynek az elemeit viszont úgy kapjuk, hogy az x\cdot b_2 kifejezésbe x helyére az N normálosztó elemeit helyettesítjük be. Azaz lényegében az a_1\cdot (x\cdot b_2) kifejezésbe helyettesítettük be N elemeit, amely kifejezés viszont ismét az asszociativitás miatt átzárójelezhető, tehát ugyanazt a halmazt kapjuk, ha az (a_1\cdot x)\cdot b_2 kifejezésbe helyettesítjük be N elemeit.
Ha most itt ismét csak a zárójelben lévő kifejezést tekintjük, és ebbe helyettesítjük be N összes elemét, akkor tulajdonképpen az a_1N baloldali mellékosztályt, mint halmazt kapjuk. Ebből következően az a_1(Nb_2) halmaz elemeit úgy is megkaphatjuk, hogy az y\cdot b_2 kifejezésbe y helyére az a_1N baloldali mellékosztály elemeit helyettesítjük be. Vagyis a fenti halmazegyenlőségi sorozatot tovább folytathatjuk:
\ldots=(a_1N)b_2=\ldotsA 2. feltételből következően viszont az a_1N halmaz megegyezik az a_2N halmazzal, ami viszont – lévén, hogy N normálosztó – a 25.6. Definíció alapján megegyezik az Na_2 halmazzal, azaz:
\ldots=(Na_2)b_2=\ldotsA fenti, a csoportművelet asszociativitására építő gondolatmenetet megismételve ez viszont az N(a_2\cdot b_2) jobboldali mellékosztállyal lesz azonos, ami viszont meg fog egyezni az (a_2\cdot b_2)N baloldali mellékosztállyal, hiszen N ugye normálosztó:
\ldots=N(a_2\cdot b_2)=(a_2\cdot b_2)NTehát valóban megkaptuk a tétel állítását, miszerint az (a_1\cdot b_1)N és az (a_2\cdot b_2)N baloldali mellékosztályok megegyeznek, vagy másként fogalmazva az a_1\cdot b_1 szorzat valóban ugyanabban a baloldali mellékosztályban van, mint az a_2\cdot b_2 szorzat.
∎Ez tehát azt jelenti, hogy a normálosztók szerinti mellékosztályok közötti művelet valóban jóldefiniált, azaz művelet a szó algebrai értelmében is (lásd a 11.3. Definíciót). Most e művelet segítségével a 18.23. Tételben definiált faktorgyűrűk (vagy az eddig használt nevükön: maradékosztálygyűrűk) mintájára az alábbi tételben definiáljuk a faktorcsoport fogalmát. Végül e tétel közvetlen következményeként megmutatjuk, hogy tetszőleges G csoport esetén a G-ből kiinduló csoporthomomorfizmusok magjai pontosan a G-beli normálosztók lesznek.
25.8. Tétel (Faktorcsoport):
Legyen G egy tetszőleges csoport, és tegyük fel, hogy N normálosztó G-ben. Jelöljük G/N-nel azt a halmazt, amelynek elemei a 24.7. Tételben definiált N szerinti baloldali mellékosztályok.
Vezessük be ezek között az alábbi műveletet: Ha A=aN és B=bN két baloldali mellékosztály, akkor ezek szorzata legyen az A\odot B=(a\cdot b)N baloldali mellékosztály.
Ekkor a G/N halmaz ezzel a művelettel csoportot alkot, amelyet a G csoport N normálosztó szerinti faktorcsoportjának nevezünk.
Ha e_G jelöli a G csoport egységelemét, akkor a G/N faktorcsoport egységeleme az e_GN baloldali mellékosztály.
Ha a^{-1} jelöli a G csoport egy a elemének inverzét, akkor a G/N faktorcsoport aN elemének inverze az (a^{-1})N baloldali mellékosztály.
Ha G kommutatív csoport (vagy más néven Abel-csoport), akkor G/N is az.
Tekintsük továbbá azt az f:G\to G/N függvényt, amely minden G-beli a elemhez az aN baloldali mellékosztályt rendeli hozzá a G/N faktorcsoportból. Ekkor f egy csoporthomomorfizmus G és G/N között, melynek magja N. Ennek a neve természetes csoporthomomorfizmus.
♣Bizonyítás:
A 25.7. Tétel alapján a baloldali mellékosztályok közötti \odot műveletek jóldefiniáltak, azaz az eredményként kapott baloldali mellékosztály nem függ az a és b reprezentánselemek megválasztásától. Így G/N-re elegendő a 24.1. Definíció szerinti csoportaxiómákat ellenőrizni.
Az asszociativitási tulajdonság: Azt kell megmutatni, hogy tetszőleges A=aN, B=bN és C=cN baloldali mellékosztályok esetén teljesül az alábbi:
(A\odot B)\odot C=A\odot (B\odot C)A \odot tételben szereplő definíciója alapján ez így írható fel az a, b és c reprezentánselemek segítségével:
((a\cdot b)\cdot c)N=(a\cdot (b\cdot c))NA reprezentánselemek között viszont teljesül az asszociativitás, hiszen ők a G csoport elemei.
Egységelem létezése: A G/N faktorcsoportban kell egy olyan E baloldali mellékosztályt mutatni, amelyre tetszőleges A=aN baloldali mellékosztály esetén teljesül az alábbi:
A\odot E=E\odot A=AHa a G csoport egységeleme e_G, akkor az E=e_GN baloldali mellékosztály épp megfelelő lesz egységelemnek a G/N faktorcsoportban, hiszen:
\begin{aligned}(\underbrace{aN}_{=A})\odot (\underbrace{e_GN}_{=E})&=(a\cdot e_G)N=aN=A \\ (\underbrace{e_GN}_{=E})\odot (\underbrace{aN}_{=A})&=(e_G\cdot a)N=aN=A\end{aligned}Inverz elem létezése: Itt azt kell megmutatni, hogy amennyiben E=e_GN a G/N faktorcsoport egységeleme, úgy tetszőleges A=aN elemhez létezik olyan A^{-1}-gyel jelölt elem, amelyre teljesül az alábbi:
A\odot A^{-1}=A^{-1}\odot A=EAz A^{-1}=(a^{-1})N baloldali mellékosztály épp megfelelő lesz inverz elemnek a G/N faktorcsoportban, hiszen:
\begin{aligned}(\underbrace{aN}_{=A})\odot (\underbrace{(a^{-1})N}_{=A^{-1}})&=(a\cdot a^{-1})N=e_GN=E \\ (\underbrace{(a^{-1})N}_{=A^{-1}})\odot (\underbrace{aN}_{=A})&=(a^{-1}\cdot a)N=e_GN=E\end{aligned}A G/N halmaz tehát valóban csoportot alkot a tételben szereplő művelettel. Tegyük most fel, hogy G kommutatív, és legyen az A=aN valamint a B=bN két tetszőleges baloldali mellékosztály a G/N faktorcsoportban. Ekkor G kommutativitása miatt teljesül az alábbi, azaz G/N is valóban kommutatív:
\begin{aligned}A\odot B&=(aN)\odot (bN)=(a\cdot b)N=\\&=(b\cdot a)N=(bN)\odot (aN)=B\odot A\end{aligned}Végezetül meg kell mutatni, hogy a tételben szereplő f:G\to G/N függvény egy csoporthomomorfizmus az eredeti és a G/N faktorcsoport között. Az f függvény tehát minden G-beli a elemhez az aN baloldali mellékosztályt rendeli hozzá. Tegyük fel, hogy g és h a G csoport tetszőleges elemei. Ekkor a művelettartó tulajdonság az alábbi alapján valóban teljesül:
f(g)\odot f(h)=(gN)\odot (hN)=(g\cdot h)N=f(g\cdot h)Végül azt kell megmutatni, hogy f magja épp az N normálosztó. Egy tetszőleges G-beli g elemhez az f csoporthomomorfizmus pontosan akkor rendeli hozzá a G/N faktorcsoport egységelemét, azaz az e_GN baloldali mellékosztályt, ha f(g)=gN=e_GN. Minthogy N egy részcsoport G-ben (hiszen normálosztó), ezért a 24.5. Tétel 2. pontja alapján ő az, aki tartalmazza e_G-t, azaz e_GN=N. Az f(g)=e_GN tehát akkor és csak akkor teljesül, ha g benne van N-ben. Az N normálosztó tehát valóban magja az f csoporthomomorfizmusnak.
∎Az imént bizonyított és a 25.5. Tétel következményeként mostmár egyértelműen azonosítani tudjuk egy csoport azon részhalmazait, amelyek valamilyen csoporthomomorfizmusok magjai lehetnek. Erről szól az alábbi következmény.
25.9. Következmény:
Legyen adva egy G csoport és annak egy N részhalmaza. Az N részhalmaz akkor és csak akkor magja egy valamilyen G-ből kiinduló csoporthomomorfizmusnak, ha normálosztó G-ben.
♣Bizonyítás:
Ha N magja egy csoporthomomorfizmusnak, akkor a 25.5. Tétel alapján normálosztó G-ben, azaz N\triangleleft G. Megfordítva: Ha N normálosztó G-ben, akkor a 25.8. Tétel alapján a G-ből kiinduló és a G/N faktorcsoportba mutató természetes csoporthomomorfizmusnak éppen N a magja.
∎Csoportok homomorfizmustétele
A 18. részben ezek után igazoltuk az úgynevezett homomorfizmustételt gyűrűk esetén (lásd a 18.25. Tételt). Ez abban volt a segítségünkre, hogy felfedjük egy R gyűrűből egy S gyűrűbe mutató f gyűrűhomomorfizmus képének pontos szerkezetét. A furcsa az, hogy ezt még akkor is meg tudjuk tenni, ha csupán f magját ismerjük, de sem magáról f-ről, sem pedig az S gyűrűről nincs semmi egyéb információnk. Másként fogalmazva f magja minden információt tartalmaz ezekről.
Ezen az alapon tehettük meg az elmúlt részekben, hogy gyakorlatilag felváltva használtuk a 18.3. Definícióban ismertetett \Z_m gyűrűt, valamint a 20.5. Tételben bevezetett \Z/m\Z faktorgyűrűt. E két gyűrűnek látszólag semmi köze egymáshoz. A \Z_m gyűrű ugyanis az egész számok \Z gyűrűjén értelmezett, szintén a 18.3. Definícióban bevezetett \bmod_m maradékképző függvény, mint gyűrűhomomorfizmus képe, melynek elemei ugye a 0, 1, 2, …, |m-1| egész számok. Ezzel szemben a \Z/m\Z gyűrű az (m)=m\Z ideállal képzett faktorgyűrű, amelynek az elemei maradékosztályok, azaz halmazok.
A homomorfizmustétel azonban nagyon szorosan összeköti e két gyűrűt, sőt nem kevesebbet állít, mint hogy a két gyűrű izomorf egymással – azaz az elemek és a műveletek jelölésétől eltekintve megegyezik. A \bmod_m maradékképző függvény, mint gyűrűhomomorfizmus magja ugyanis épp az (m)=m\Z ideál. Így az ezzel az ideállal képzett \Z/m\Z faktorgyűrű izomorf \bmod_m képével, ami jelen esetben nem más, mint a \Z_m gyűrű.
Most ennek mintájára kimondjuk és bizonyítjuk a csoportok homomorfizmustételét, amely egy ugyanilyen összefüggést mond ki csoportok esetére.
25.10. Tétel (Csoportok homomorfizmustétele):
Legyenek G és H tetszőleges csoportok, valamint tegyük fel, hogy adva van egy f:G\to H csoporthomomorfizmus. Ekkor G/\ker f \simeq \text{im} f, azaz a G-ből képzett f magja szerinti faktorcsoport izomorf f képével.
♣Bizonyítás:
Előszöris megjegyezzük, hogy a 25.5. Tétel 4. pontja alapján \ker f normálosztó G-ben, így a baloldalon álló G/\ker f faktorcsoport valóban értelmes. Igaz továbbá, hogy a 25.4. Tétel alapján \text{im} f részcsoport abban a csoportban, ahová f mutat, így a tételben szereplő csoportizomorfia jobboldala is értelmes. Most megmutatjuk, hogy az izomorfia valóban teljesül.
Az átláthatóság érdekében vezessük be az N=\ker f jelölést. A G/N faktorcsoport elemei tehát az N=\ker f, mint normálosztó szerinti baloldali mellékosztályok. A 25.5. Tétel 2. pontja alapján minden ilyen baloldali mellékosztályban az ott lévő elemeknek ugyanaz lesz az f szerinti képe H-ban, tehát abban a csoportban, ahová f mutat.
Ez alapján definiálhatunk egy g:G/N\to \text{im} f leképezést a tételben szereplő faktorcsoport és az f csoporthomomorfizmus képe között. Ennek a leképezésnek a képletét a G csoport elemeinek és az f csoporthomomomorfizmusnak a segítségével adjuk meg. Az alábbi képlet azt fejezi ki, hogy minden a elem esetén a g leképezés az a elemet tartalmazó BALOLDALI MELLÉKOSZTÁLYhoz épp azt az elemet rendeli hozzá a H csoportból, amelyet az f csoporthomomorfizmus is hozzárendel magához az a ELEMhez:
g(aN)=f(a)Az alábbi ábra mutatja a g leképezés iménti konstrukcióját.

Ez egy értelmes leképezés, ha ugyanis valamely a és b elemek ugyanabban a baloldali mellékosztályban vannak, akkor a 25.5. Tétel 2. pontja alapján az ő f szerinti képük megegyezik. Így tehát a g leképezés eredménye nem függ attól, hogy a bemeneti baloldali mellékosztály mely reprezentánselemének segítségével számítottuk azt ki a fenti képlettel.
Most igazoljuk, hogy a g leképezés kölcsönösen egyértelmű. Előszöris azt mutatjuk meg, hogy két különböző baloldali mellékosztály g szerinti képe is különbözik. Tegyük fel ezért indirekt, hogy a G csoport a és b elemei két különböző baloldali mellékosztályban vannak, ám e két mellékosztálynak ennek ellenére ugyanaz a g szerinti képe, azaz g(aN)=g(bN). Ez a g leképezés definíciója alapján azt jelentené, hogy f(a)=f(b). De ez ellentmondás, hiszen ez azt jelentené, hogy a és b mégis ugyanabban a baloldali mellékosztályban van. Azt tehát már tudjuk, hogy a H-beli \text{im} f részcsoport minden eleme legfeljebb egy baloldali mellékosztálynak lehet a g szerinti képe, azaz g injektív.
A kölcsönös egyértelműséghez azt kell még igazolni, hogy \text{im} f-ben nincs olyan elem, amely ne lenne képe valamely baloldali mellékosztálynak a g függvény szerint (azaz, hogy g szürjektív). Ez viszont természetesen teljesül, hiszen \text{im} f nem más, mint az f csoporthomomorfizmus képe. Következésképp minden itt lévő a elemhez létezik olyan x elem a G csoportban, amelynek épp a a képe az f függvény szerint (azaz f(x)=a). Ez az x elem viszont benne van az xN baloldali mellékosztályban, amelyhez viszont a g függvény rendeli hozzá az a elemet H-ban. A g függvény tehát valóban kölcsönösen egyértelmű.
A g művelettartási tulajdonsága a fenti képletből már könnyen adódik. Felhívjuk az Olvasó figyelmét, hogy az alábbi levezetésben három különböző csoport is érintett, ennek megfelelően az ezekben értelmezett műveletek között jelölésbeli különbséget is tettünk. A G/N faktorcsoport műveletét a \odot, a G csoport műveletét a \cdot, míg a H csoport műveletét a \boxdot szimbólumokkal jelöltük:
\begin{aligned}g(aN\odot bN)&=g((a\cdot b)N)=\\&=f(a\cdot b)=f(a)\boxdot f(b)=\\&=g(aN)\boxdot g(bN)\end{aligned}Így tehát g valóban csoportizomorfizmus a G/N faktorcsoport és f képe között.
∎Csoporthomomorfizmusok struktúratartó tulajdonságai
Ebben a szakaszban azt fogjuk megmutatni, hogy egy f:G\to H csoporthomomorfizmuson keresztül a H csoport milyen fontos strukturális tulajdonságokat örököl meg a G csoporttól. Főként ezekre a kulcsfontosságú észrevételekre fogjuk építeni a Miller-Rabin-tanúk számára vonatkozó alsó becslésünk lényeges javítását. Ezek megfogalmazásához előbb azonban ismerkedjünk meg néhány függvényekkel kapcsolatos további fogalommal.
25.11. Definíció (Kép, teljes inverz kép):
Legyenek A és B tetszőleges halmazok, továbbá tegyük fel, hogy értelmezve van egy f:A\to B függvény, amely tehát az A halmaz minden eleméhez hozzárendel egy elemet a B halmazból.
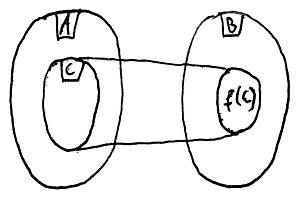
Legyen adott egy C\sube A halmaz. Ekkor B-nek azt a – 19.7. Definíció szerinti értelemben vett – legszűkebb részhalmazát, amely minden C-beli elem f szerinti képét tartalmazza, a C halmaz f szerinti képének (vagy értékkészletének) nevezzük és f(C)-vel jelöljük. Ezt az elrendezést mutatja az alábbi ábra:
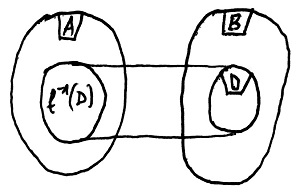
Legyen adott egy D\sube B halmaz. Ekkor A-nak azt a – 19.7. Definíció szerinti értelemben vett – legbővebb részhalmazát, amelynek f szerinti képe D, a D halmaz f szerinti teljes inverz képének nevezzük és f^{-1}(D)-vel jelöljük. Ezt az elrendezést mutatja az alábbi ábra:
Megjegyzés:
Vigyázat! Az f(C) kifejezés ebben az esetben nem valamiféle matematikai objektumot jelöl, amelyet az f függvény a C halmazhoz hozzárendel. Ehelyett azt a halmazt jelöli, amely pontosan a C-beli elemek f szerinti képeit tartalmazza. Ehhez hasonlóan az f^{-1}(D) nem egy olyan matematikai objektumot jelöl, amelyhez az f függvény épp a D halmazt rendeli hozzá. Ehelyett azt a halmazt jelöli, amely pontosan azokat az A-beli elemeket tartalmazza, amelyeknek f szerinti képe D-ben van.
A definícióból következik, hogy ha f^{-1}(D)=C teljesül, akkor f(C)=D is teljesül. Nyilván, hiszen a definíció szerint C is egy olyan részhalmaz A-ban, amelynek f szerinti képe D – történetesen a legbővebb.
Vigyázzunk azonban, ugyanis ez utóbbi állítás megfordítása nem igaz! Azaz f(C)=D-ből a C=f^{-1}(D) állítás még nem, csupán az ennél gyengébb C\sube f^{-1}(D) állítás következik. Elképzelhető ugyanis, hogy létezik egy C-nél bővebb E\sube A halmaz is, amelynek szintén D a képe. Ezt a szitációt mutatja az alábbi ábra:
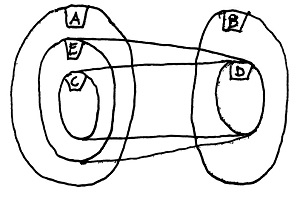
Végül megjegyezzük, hogy az f(C) halmaz tetszőleges C esetén létezik, mivel az f egy függvény, amely A minden eleméhez, és így speciálisan az összes C-beli elemhez is szükségképpen hozzárendel valamit a B halmazból. Így f(C) legrosszabb esetben legalább egy elemet mindenképpen tartalmaz – kivéve persze ha C az üreshalmaz, amikoris f(C) is az üreshalmaz.
Ezzel szemben az f^{-1}(D) teljes inverz kép adott D esetén nem biztos, hogy létezik. Sőt, még csak az sem biztos, hogy létezik egyáltalán olyan részhalmaz A-ban, amelynek D az f szerinti képe. Elképzelhető ugyanis, hogy D-ben van olyan elem, amely egyetlen A-beli elemhez sincs hozzárendelve. Természetesen most is igaz, hogy ha D az üreshalmaz, akkor f^{-1}(D) létezik, és szintén az üreshalmaz.
♣Most azt vizsgáljuk meg, hogy egy f:G\to H csoporthomomorfizmus esetén mik lesznek a G csoport részcsoportjainak képei.
25.12. Tétel:
Legyenek G és H tetszőleges csoportok, f:G\to H pedig egy csoporthomomorfizmus e két csoport között. Ekkor tetszőleges K\leq G esetén f(K)\leq H, azaz G minden részcsoportjának f szerinti képe részcsoport H-ban.
♣Bizonyítás:
Az f(K) halmaz a 25.11. Definíció alapján nyilván részhalmaza H-nak, ezért csak a 24.5. Tétel feltételeinek teljesülését kell ellenőrizni f(K)-ra.
1. feltétel: f(K) zárt a H csoport műveletére nézve
Legyenek a és b az f(K) halmaz két tetszőleges eleme. A 25.11. Definíció alapján minden f(K)-beli elemhez létezik olyan elem K-ban, amelynek épp ő az f szerinti képe. Így a-hoz és b-hez is léteznek olyan x_a\in K és x_b\in K elemek, amelyekre teljesülnek az alábbiak:
\begin{aligned}f(x_a)&=a \\ f(x_b)&=b\end{aligned}Ám ekkor – mivel K részcsoport G-ben – a 24.5. Tétel 1. pontja alapján az x_ax_b szorzat is benne van K-ban. Ez viszont ugyancsak a 25.11. Definíció alapján azt jelenti, hogy e szorzat f szerinti képe viszont benne van f(K)-ban, azaz:
f(x_ax_b)\in f(K)Mivel azonban f csoporthomomorfizmus, ezért igaz az alábbi:
f(x_ax_b)=f(x_a)\cdot f(x_b)=a\cdot b\in f(K)Tehát az a és b elemek szorzata is f(K)-ban van, ami így valóban zárt a H csoport műveletére nézve.
2. feltétel: f(K) tartalmazza a H csoport egységelemét
Mivel K részcsoport G-ben, ezért a 24.5. Tétel 2. pontja alapján tartalmazza G egységelemét, amelyet most jelöljünk e_G-vel. A 25.2. Lemma 1. pontja szerint az e_G egységelem f szerinti képe a H csoport egységeleme, amelyet most jelöljünk e_H-val. De mivel e_H egy K-beli elem – nevezetesen e_G – képe, ezért a 25.11. Definíció szerint szükségképpen benne van f(K)-ban.
3. feltétel: f(K) zárt a H-beli inverzképzésre
Legyen a az f(K) halmaz tetszőleges eleme. A 25.11. Definíció alapján minden f(K)-beli elemhez létezik olyan elem K-ban, amelynek épp ő az f szerinti képe. Így a-hoz is létezik olyan x_a\in K elem, amelyre teljesül az alábbi:
f(x_a)=aÁm ekkor – mivel K részcsoport G-ben – a 24.5. Tétel 3. pontja alapján az x_a^{-1} inverz is benne van K-ban. Ez viszont ugyancsak a 25.11. Definíció alapján azt jelenti, hogy ennek f szerinti képe viszont benne van f(K)-ban, azaz:
f(x_a^{-1})\in f(K)Mivel azonban f csoporthomomorfizmus, ezért a 25.2. Lemma 2. pontja igaz az alábbi:
f(x_a^{-1})=(f(x_a))^{-1}=a^{-1}\in f(K)Tehát az a elem H-beli inverze is f(K)-ban van, ami így valóban zárt a H-beli inverzképzésre nézve.
∎Azt tehát már tudjuk, hogy egy f:G\to H csoporthomomorfizmus esetén minden G-beli részcsoportnak valamilyen H-beli részcsoport lesz az f szerinti képe. Most nézzük meg, hogy mi a helyzet a másik irányban, azaz mik lesznek a H-beli részcsoportok teljes inverz képei G-ben. Ezekről egy fokkal többet tudunk mondani.
25.13. Tétel:
Legyenek G és H tetszőleges csoportok, f:G\to H pedig egy csoporthomomorfizmus e két csoport között. Ekkor tetszőleges L\leq H esetén f^{-1}(L)\leq G és \ker f\sube f^{-1}(L) – amennyiben persze létezik az f^{-1}(L) teljes inverz kép (lásd a 25.11. Definíció utáni megjegyzést).
Szavakkal: H minden részcsoportjának f szerinti teljes inverz képe – amennyiben egyáltalán létezik – egy olyan részcsoport G-ben, amely tartalmazza f magját.
♣Bizonyítás:
Tegyük fel tehát, hogy L-nek létezik teljes inverz képe G-ben – hiszen a tétel úgyis csak ezekről az esetekről nyilatkozik –, és vezessük be a K=f^{-1}(L) jelölést. A K halmaz a 25.11. Definíció alapján nyilván részhalmaza G-nek. Ezért csak a 24.5. Tétel feltételeinek teljesülését kell ellenőrizni K-ra, továbbá igazolni a \ker f\sube K tartalmazást.
1. feltétel: K zárt a G csoport műveletére nézve
Legyenek a és b a K halmaz két tetszőleges eleme. Mivel K=f^{-1}(L), ezért a 25.11. Definíció utáni megjegyzés alapján f(K)=L, és így ugyanezen definíció alapján f(a) és f(b) is benne van L-ben. Ekkor azonban a 24.5. Tétel 1. pontja miatt az ő f(a)\cdot f(b) szorzatuk is L-ben van, hiszen a tétel szövege alapján L részcsoport H-ban, azaz zárt a H-beli műveletre nézve. Ez a szorzat azonban f művelettartó tulajdonsága alapján átírható az alábbi módon:
f(a)\cdot f(b)=f(ab)\in LVagyis az ab szorzat f szerinti képe L-ben van. Mivel azonban K=f^{-1}(L), ezért ez a 25.11. Definíció szerint azt is jelenti, hogy az ab szorzat csak K-ban lehet. A K halmaz tehát valóban zárt a G-beli műveletre nézve.
2. feltétel: K tartalmazza a G csoport egységelemét
Mivel L részcsoport H-ban, ezért a 24.5. Tétel 2. pontja miatt tartalmazza annak egységelemét, amelyet most jelöljünk e_H-val. A 25.2. Lemma 1. pontja alapján azonban tudjuk, hogy a G csoport egységelemének – amelyet most jelöljünk e_G-vel – f szerinti képe e_H, azaz f(e_G)=e_H. Mivel azonban K az L halmaz f szerinti teljes inverz képe, ezért a 25.11. Definíció miatt e_G csak K-ban lehet. Így tehát K valóban tartalmazza a G csoport egységelemét.
3. feltétel: K zárt a G-beli inverzképzésre
Legyen a tetszőleges K-beli elem. Ekkor az 1. feltétel bizonyításánál már látott f(K)=L miatt f(a) benne van L-ben. Mivel azonban L részcsoport H-ban, így a 24.5. Tétel 3. pontja miatt az (f(a))^{-1} inverz is benne van L-ben. A 25.2. Lemma 2. pontja alapján azonban tudjuk, hogy f tartja a G-beli inverzképzést, így teljesül az alábbi:
(f(a))^{-1}=f(a^{-1})\in LVagyis az a^{-1} inverz f szerinti képe L-ben van. Mivel azonban K=f^{-1}(L), ezért ez a 25.11. Definíció szerint azt is jelenti, hogy maga az a^{-1} inverz csak K-ban lehet. A K halmaz tehát valóban zárt a G-beli inverzképzésre nézve.
Végül a \ker f\sube K tartalmazást igazoljuk.
Legyen a tetszőleges elem f magjában, azaz a\in \ker f. Azt kell megmutatni, hogy ekkor a\in K is teljesül. Mivel a benne van f magjában, így az ő f szerinti képe a H csoport egységeleme, amelyet jelöljünk továbbra is e_H-val. Azaz:
f(a)=e_HAz e_H-ról azonban tudjuk, hogy benne van L-ben, hiszen L ugye részcsoport H-ban. Mivel azonban e_H az a elem f szerinti képe, ezért f^{-1}(L)=K miatt a 25.11. Definíció alapján maga a szükségképpen benne van K-ban.
∎Az imént bizonyított tétel alapján tehát az körvonalazódik, hogy a G csoport bizonyos strukturális tulajdonságai egy f:G\to H csoporthomomorfizmus által átöröklődnek H-ra. A mostani tételben ezeket összegezzük.
25.14. Tétel (Csoporthomomorfizmusok struktúratartó tulajdonságai):
Legyenek G és H tetszőleges csoportok, f:G\to H pedig egy szürjektív csoporthomomorfizmus e két csoport között, és vezessük be az N=\ker f jelölést. Ekkor teljesülnek az alábbiak:
- A H részcsoportjai kölcsönösen egyértelmű megfeleltetésben állnak G azon részcsoportjaival, amelyek N-et teljes egészében tartalmazzák. Egy L\leq H részcsoporthoz az f^{-1}(L) teljes inverz kép, mint G-beli, N-et tartalmazó részcsoport tartozik. A továbbiakban legyenek K\leq G és L\leq H ebben az értelemben egymásnak megfelelő részcsoportok.
- A K szerinti baloldali mellékosztályok az L szerinti baloldali mellékosztályok teljes inverz képei f szerint, és ez a megfeleltetés szintén kölcsönösen egyértelmű.
- Ugyanez mondható el a jobboldali mellékosztályokról is.
- Az L részcsoport akkor és csak akkor normálosztó H-ban, ha K normálosztó G-ben, és ilyenkor a G/K és H/L faktorcsoportok izomorfak.
Bizonyítás:
Az 1. állítás: Itt tulajdonképpen két halmazrendszer (lásd a 19.5. Definíciót) elemei között kell kölcsönösen egyértelmű megfeleltetést létesíteni. Az első halmazrendszer tehát a G csoport azon részcsoportjaiból áll, amelyek tartalmazzák N-t, mint az f csoporthomomorfizmus magját. Ezt jelöljük \mathcal{G}-vel. A második halmazrendszer pedig H összes részcsoportjaiból áll. Ezt jelöljük \mathcal{H}-val.
A 25.12. Tételben már láttuk, hogy tetszőleges G-beli K részcsoport f szerinti képe részcsoport H-ban, azaz f(K)\leq H. A 25.11. Definíció alapján f(K) a legszűkebb olyan részcsoport H-ban, amely K minden elemének képét tartalmazza, és így a 19.8. Tétel értelmében f(K) egyértelműen meghatározott. Mindez természetesen speciálisan igaz az N-et tartalmazó G-beli részcsoportokra is. Az a leképezés tehát, amely tetszőleges K\in \mathcal{G} részcsoportból képzi az f(K)\in \mathcal{H} részcsoportot, tekinthető egy \mathcal{G}-ből \mathcal{H}-ba mutató függvénynek is.
Visszafelé: Mivel f most szürjektív csoporthomomorfizmus, ezért minden H-beli elem legalább egy G-beli elem képe, és így H tetszőleges L részcsoportjának létezik teljes inverz képe G-ben (vesd össze a 25.11. Definíció utáni megjegyzéssel). A 25.13. Tétel alapján ez a bizonyos f^{-1}(L)-lel jelölt teljes inverz kép részcsoport G-ben. Ezenkívül f^{-1}(L) a legbővebb olyan részcsoport, amelynek minden elemének képe L-ben van, és így egyrészt a 19.8. Tétel értelmében egyértelműen meghatározott. Másrészt pedig mivel L tartalmazza H egységelemét – hiszen részcsoport H-ban –, ezért f^{-1}(L) szükségképpen tartalmaz minden olyan G-beli elemet, amelyek erre az egységelemre képződnek. Ezek viszont épp az N homomorfizmus-magot alkotják, azaz f^{-1}(L) tartalmazza N-et, és így benne van a \mathcal{G} halmazrendszerben. Így tehát az előző gondolatmenethez hasonlóan a teljes inverz kép képzése tekinthető egy \mathcal{H}-ból \mathcal{G}-be mutató függvénynek.
Most már tehát van egy g:\mathcal{G}\to \mathcal{H}, valamint egy h:\mathcal{H}\to \mathcal{G} függvényünk a két halmazrendszer között. A kölcsönösen egyértelműséghez azt kell megmutatni, hogy e két függvény épp egymás megfordítása. Ez azt jelenti, hogy bármilyen sorrendben is alkalmazzuk őket egymás után, pontosan a kiinduló részcsoportot kell kapnunk eredményül. Azaz tetszőleges K\in \mathcal{G} és L\in \mathcal{H} esetén igazolnunk kell az alábbi hozzárendelések érvényességét:
\begin{aligned}K&\xmapsto{g} f(K)\xmapsto{h} f^{-1}(f(K))=K \\ L&\xmapsto{h} f^{-1}(L) \xmapsto{g} f(f^{-1}(L))=L\end{aligned}A második megfeleltetés nyilvánvalóan teljesül, hiszen a 25.11. Definíció utáni megjegyzés alapján tetszőleges L\in \mathcal{H} részcsoport teljes inverz képének képe maga L.
Ezzel szemben az első megfeleltetés igazolásánál egy picit nehezebb dolgunk van, ugyanis a 25.11. Definíció utáni megjegyzés szerint alapból nem mindig teljesül, hogy tetszőleges K\leq G részcsoport képének teljes inverz képe maga K. Most viszont tudjuk, hogy K\in \mathcal{G}, azaz ő nem akármilyen részcsoport, hanem olyan, amely tartalmazza az f csoporthomomorfizmus N-nel jelölt magját. Vezessük be az L=f(K) jelölést. Ezek után azt kell tehát megmutatni, hogy ebben a speciális esetben mégis fennáll a K=f^{-1}(L) halmazegyenlőség, ami a 19.2. Definíció utáni megjegyzés 5. pontja alapján azt jelenti, hogy e két halmaz kölcsönösen tartalmazza egymást.
A K\sube f^{-1}(L) tartalmazás a 25.11. Definíció utáni megjegyzésből következik, hiszen f(K)=L, amiből e megjegyzés alapján K\sube f^{-1}(L) következik.
Most nézzük az f^{-1}(L)\sube K tartalmazást. Legyen a az f^{-1}(L) tetszőleges eleme. Ekkor egyrészt a 25.11. Definíció alapján az a elem f szerinti képe benne van L-ben, azaz f(a)\in L. Másrészt L=f(K) miatt a 25.11. Definíció alapján minden L-beli elem legalább egy K-beli elemnek a képe. Ez speciálisan igaz az f(a)\in L elemre is, azaz léteznie kell K-ban egy olyan k elemnek, amelyre f(k)=f(a) teljesül.
Ez viszont a 25.5. Tétel 2. pontja alapján azt jelenti, hogy a ugyanabban az N szerinti baloldali mellékosztályban van, mint k, azaz a\in kN. Ezek szerint létezik olyan n\in N, hogy a=k\cdot n. Most viszont tudjuk, hogy N\sube K, így ez a bizonyos n benne van egyúttal a K részcsoportban is, következésképp az a=k\cdot n szorzat is benne van K-ban, hiszen ő zárt a szorzásra nézve. Vagyis valóban teljesül az f^{-1}(L)\sube K tartalmazás, és így az f^{-1}(L)=K halmazegyenlőség is.
A 2. állítás: Az 1. állításhoz hasonlóan itt is két halmazrendszer elemei között kell kölcsönösen egyértelmű megfeleltetést létesíteni. Az első halmazrendszer tehát a K\leq G részcsoport szerinti baloldali mellékosztályokból áll. Ezt jelöljük \mathcal{K}-val. A második halmazrendszer pedig az L\leq H részcsoport szerinti baloldali mellékosztályokból áll. Ezt jelöljük \mathcal{L}-lel. Mutatnunk kell egy \mathcal{K} és \mathcal{L} közötti kölcsönösen egyértelmű megfeleltetést. Ehhez azt a 24.7. Tételben szereplő ekvivalenciarelációt fogjuk használni, amely a baloldali mellékosztályokat kijelöli a G és a H csoportokban.
Legyen ezért a és b két tetszőleges elem G-ben. Ez a két elem a 24.7. Tétel szerint akkor és csak akkor van ugyanabban a K részcsoport szerinti mellékosztályban, ha az a^{-1}b szorzat benne van magában a K részcsoportban. Minthogy a K részcsoport az L részcsoport teljes inverz képe, ezért az a^{-1}b szorzat akkor és csak akkor van benne K-ban, ha f(a^{-1}b) benne van L-ben. Az f csoporthomomorfizmus művelet- és inverzképzéstartó tulajdonságai miatt az f(a^{-1}b)\in L állítás ekvivalens az (f(a))^{-1}f(b)\in L állítással. Ez viszont szintén a 24.7. Tétel alapján akkor és csak akkor teljesül, ha f(a) ugyanabban az L részcsoport szerinti baloldali mellékosztályban van, mint f(b).
Egyrészt tehát azt kaptuk, hogy egy adott K szerinti baloldali mellékosztály összes elemének ugyanabban az L szerinti baloldali mellékosztályban lesz az f szerinti képe. Az f csoporthomomorfizmus tehát ilymódon minden \mathcal{K}-beli baloldali mellékosztályhoz egyértelműen kijelöl egy \mathcal{L}-beli baloldali mellékosztályt. Ez tekinthető egy k:\mathcal{K} \to \mathcal{L} függvénynek is. Ha például g\in G egy tetszőleges elem, akkor ez a függvény a gK baloldali mellékosztályhoz az f(gK) halmazt rendeli hozzá, amely tehát épp az f(g)L baloldali mellékosztály lesz, azaz k(gK)=f(g)L.
Továbbá a k függvényről elmondható, hogy injektív, hiszen azt is megkaptuk, hogy különböző K szerinti baloldali mellékosztályba eső elemek f szerinti képei különböző L szerinti baloldali mellékosztályokban lesznek. Ha tehát valamilyen a és b elemek esetén k(aK)=k(bK), akkor ebből aK=bK következik. Ez egyben azt is jelenti, hogy a K szerinti mellékosztályok a hozzájuk tartozó L szerinti mellékosztályoknak valóban a teljes inverz képei.
Végül a k függvény szürjektív is. Ugyanis a tétel szövege alapján az f csoporthomomorfizmus is az, és így bármely h\in H elemhez van olyan g\in G, amelyre f(g)=h teljesül. Így viszont a hL=f(g)L baloldali mellékosztályt épp a gK baloldali mellékosztályhoz rendeli hozzá a k függvény. Vagyis valóban minden L szerinti mellékosztály párja valamelyik K szerinti mellékosztálynak, és így k egy kölcsönösen egyértelmű megfeleltetés.
A 3. állítás: Ugyanígy igazolható, csak ekkor a 24.7. Tételben szereplő másik ekvivalenciarelációt kell használni, amely a jobboldali mellékosztályokat jelöli ki.
A 4. állítás: Tegyük fel, hogy K normálosztó G-ben. Ez a 25.6. Definíció alapján azt jelenti, hogy a K szerinti bal- és jobboldali mellékosztályok megegyeznek, azaz tetszőleges g\in G esetén gK=Kg. Ám ekkor a 2. és 3. állítás bizonyításában szereplő k megfeleltetés őhozzájuk az f(g)L=Lf(g) mellékosztályokat rendeli, amelyek szintén megegyeznek. A k függvény szürjektivitása miatt ilymódon minden L szerinti baloldali mellékosztályról megkaptuk, hogy megegyezik a megfelelő jobboldali mellékosztállyal, azaz L is normálosztó H-ban.
Most tegyük fel, hogy K nem normálosztó G-ben. Azaz létezik olyan g\in G, hogy gK\neq Kg. Ekkor viszont f(g)L\neq Lf(g) is igaz, máskülönben az ő teljes inverz képük, azaz gK és Kg mégiscsak megegyezne. Így tehát L sem normálosztó H-ban.
Végül tegyük fel, hogy K és L normálosztók, és tekintsük a G/K és a H/L faktorcsoportokat. Ezek elemei rendere a K és az L szerinti bal- illetve a velük megegyező jobboldali mellékosztályok. A 2. és 3. állítás bizonyításában szereplő, közöttük lévő k megfeleltetésről már láttuk, hogy kölcsönösen egyértelmű, ezért már csak azt kell megmutatni, hogy művelettartó is. Legyen tehát aK és bK két tetszőleges baloldali mellékosztály a G/K faktorcsoportban. Azt kell megmutatni, hogy az ő k szerinti megfelelőik szorzata a H/L faktorcsoportban ugyanaz, mint a G/K faktorcsoportban vett szorzatuk k szerinti megfelelője.
Az egyértelműség érdekében az alábbiakban a különböző csoportok műveleteit különböző szimbólumokkal jelöltük. Így \odot jelöli a G/K faktorcsoport, \boxdot a H/L faktorcsoport, \cdot a G csoport, végül \bullet a H csoport szorzását:
\begin{aligned}k(aK) \boxdot k(bK)&=f(a)L \boxdot f(b)L=(f(a)\bullet f(b))L \\ k(aK \odot bK)&=k((a\cdot b)K)=f(a\cdot b)L=(f(a)\bullet f(b))L\end{aligned}Mindkét esetben azonos végeredményt kaptunk, tehát a k leképezés művelettartó, és így valóban egy izomorfizmus a G/K és H/L faktorcsoportok között.
∎Az imént bizonyított tételnek a következő részben lesz kulcsfontosságú szerepe, amikoris a Miller-Rabin-tanúk számának alsó becslését fogjuk lényegesen megjavítani az előző részben szereplő 24.20. Következményhez képest.
Csoportok direkt szorzata
A 22. részben a kínai maradéktétel kapcsán került elő egy szorzatgyűrűnek nevezett konstrukció, amelynek a segítségével kettő vagy több gyűrűből egy további gyűrűt lehet képezni. A 22.7. Tételben definiáltuk is, hogy pontosan mit értünk szorzatgyűrű alatt, és igazoltuk, hogy ez a konstrukció valóban teljesíti a 14.12. Definícióben felsorolt gyűrűaxiómákat. Most egy ehhez nagyon hasonló konstrukciót mutatunk be a csoportok esetére is, amelynek szintén a következő részben fogjuk hasznát venni.
25.15. Tétel (Csoportok direkt szorzata, szorzatcsoport):
Legyenek G_1, G_2, ..., G_n tetszőleges csoportok, és értelmezzünk egy műveletet a G_1\times G_2\times \ldots \times G_n halmaz tetszőleges (g_1;g_2;\ldots;g_n) és (h_1;h_2;\ldots;h_n) elemei között az alábbi módon:
(g_1;g_2;\ldots;g_n)\odot (h_1;h_2;\ldots;h_n)=(g_1\cdot h_1;g_2\cdot h_2;\ldots;g_n\cdot h_n)Azaz a \odot műveletet úgy kell elvégezni, hogy az azonos pozícióban lévő komponensek szorzatait képezzük a megfelelő csoportokban.
Ekkor a G_1\times G_2\times \ldots \times G_n halmaz szintén egy csoportot alkot ezzel a művelettel. Ezt a csoportot a G_1, G_2, ..., G_n csoportok direkt szorzatának, vagy szorzatcsoportjának nevezzük.
A szorzatcsoport egységeleme egy olyan rendezett n-es, amelynek minden komponensében a megfelelő csoport egységeleme áll. Azaz:
e_{G_1\times G_2\times \ldots \times G_n}=(e_{G_1};e_{G_2};\ldots;e_{G_n})A szorzatcsoport egy tetszőleges (g_1;g_2;\ldots;g_n) elemének (g_1;g_2;\ldots;g_n)^{-1}-gyel jelölt inverzét úgy kapjuk meg, hogy vesszük minden komponens inverzét a megfelelő csoportban. Azaz:
(g_1;g_2;\ldots;g_n)^{-1}=(g_1^{-1};g_2^{-1};\ldots;g_n^{-1}) ♣Bizonyítás:
A 24.1. Definícióban felsorolt csoportaxiómákat kell ellenőrizni:
A \odot művelet asszociativitása könnyedén adódik a G_1, G_2, ..., G_n csoportokon értelmezett műveletek ugyanezen tulajdonságából:
\begin{aligned}((&a_1;\ldots;a_n)\odot(b_1;\ldots;b_n))\odot(c_1;\ldots;c_n) =\\&= (a_1\cdot b_1;\ldots;a_n\cdot b_n)\odot(c_1;\ldots;c_n) =\\&=((a_1\cdot b_1)\cdot c_1;\ldots;(a_n\cdot b_n)\cdot c_n) =\\&= (a_1\cdot (b_1\cdot c_1);\ldots;a_n\cdot (b_n\cdot c_n)) =\\&=(a_1;\ldots;a_n)\odot(b_1\cdot c_1;\ldots;b_n\cdot c_n)=\\&=(a_1;\ldots;a_n)\odot((b_1;\ldots;b_n)\odot(c_1;\ldots;c_n))\end{aligned}Most igazoljuk az egységelemre vonatkozó állítást. Legyen (g_1;\ldots;g_n) a G_1\times \ldots \times G_n halmaz egy tetszőleges eleme. Ezt az (e_{G_1};\ldots;e_{G_n}) elemmel összeszorozva bármely oldalról az eredmény valóban nem változik, hiszen minden komponensben a megfelelő csoport egységelemével való szorzás fog szerepelni. Az alábbiakban a jobbról való szorzás esetét igazoltuk, a másik irányú szorzás esete ehhez nagyon hasonló:
\begin{aligned}(&g_1;\ldots;g_n)\odot(e_{G_1};\ldots;e_{G_n})=\\&=(g_1\cdot e_{G_1};\ldots;g_n\cdot e_{G_n})=\\&=(g_1;\ldots;g_n)\end{aligned}Ehhez hasonlóan igazoljuk az inverzképzésre vonatkozó állítást is. A (g_1;\ldots;g_n) elemet a (g_1^{-1};\ldots;g_n^{-1}) elemmel jobbról szorozva az eredmény valóban az (e_{G_1};\ldots;e_{G_n}) elem lesz, hiszen minden komponensben az adott komponens és annak a megfelelő csoportban vett inverzével való jobbról szorzás fog szerepelni:
\begin{aligned}(&g_1;\ldots;g_n)\odot(g_1^{-1};\ldots;g_n^{-1})=\\&=(g_1\cdot g_1^{-1};\ldots;g_n\cdot g_n^{-1})=\\&=(e_{G_1};\ldots;e_{G_n})\end{aligned}A (g_1^{-1};\ldots;g_n^{-1}) elemmel való balról szorzás esete ehhez nagyon hasonlóan igazolható.
∎Részcsoportok generálása
A 19. részben a részgyűrűkkel és ideálokkal kapcsolatban vezettük be a generálás fogalmát. Ott azt mondtuk, hogy egy gyűrű tetszőleges nemüres X részhalmazához mindig egyértelműen létezik egy legszűkebb olyan részgyűrű (vagy ideál), amely X-et tartalmazza. Ezt az X által generált részgyűrűnek (vagy ideálnak) neveztük és \lang X\rang-szel jelöltük.
Ugyanilyen értelemben bármely csoport részcsoportjaira (vagy normálosztóira) is bevezethető a generálás fogalma. A gyűrűknél ennek feltétele az volt, hogy részgyűrűk (vagy ideálok) metszete is részgyűrű (vagy ideál) legyen, amelyet a 19.9. Tételben igazoltunk is. Most a részcsoportokra (vagy normálosztókra) mondunk ki egy ugyanilyen tulajdonságot, előbb azonban igazolnunk kell egy segédtételt, amely lényegében a normálosztókra ad egy alternatív definíciót.
25.16. Tétel:
Egy G csoport valamely N részcsoportja akkor és csak akkor normálosztó, ha minden n\in N és g\in G esetén a gng^{-1} szorzat benne van N-ben.
Az állítás a g^{-1}ng szorzatra is ugyanígy kimondható.
♣Bizonyítás:
Ha N normálosztó, akkor az a 25.6. Definíció alapján azt jelenti, hogy az N szerinti bal- és jobboldali mellékosztályok megegyeznek. Ez az említett definíció utáni megjegyzés alapján az elemek szintjén azt jelenti, hogy tetszőleges g\in G és n\in N esetén létezik olyan m_1\in N és m_2\in N, hogy teljesülnek az alábbiak:
\begin{aligned}g\cdot n&=m_1\cdot g \\ n\cdot g&=g\cdot m_2\end{aligned}Az első egyenletet jobbról, a másodikat pedig balról szorozva g^{-1}-gyel az alábbiakat kapjuk:
\begin{aligned}g\cdot n\cdot g^{-1}&=m_1 \\ g^{-1}\cdot n\cdot g&=m_2\end{aligned}Vagyis a gng^{-1} és a g^{-1}ng szorzatok valóban benne vannak N-ben, hiszen előbbi m_1-gyel, utóbbi pedig m_2-vel egyezik meg.
Megfordítva: Tegyük fel, hogy minden g\in G és n\in N esetén a gng^{-1} szorzat benne van N-ben. Ez természetesen g inverzére is igaz, azaz g^{-1}n(g^{-1})^{-1}=g^{-1}ng is benne van N-ben. Léteznek tehát olyan m_1 és m_2 elemek N-ben, hogy teljesülnek az alábbiak:
\begin{aligned}g\cdot n\cdot g^{-1}&=m_1 \\ g^{-1}\cdot n\cdot g&=m_2\end{aligned}Az első egyenletet jobbról, a másodikat pedig balról szorozva g-vel az alábbiakat kapjuk:
\begin{aligned}g\cdot n&=m_1\cdot g \\ n\cdot g&=g\cdot m_2\end{aligned}Ez a 25.6. Definíció utáni megjegyzés alapján épp azt jelenti, hogy az N szerinti bal- és jobboldali mellékosztályok megegyeznek, azaz N valóban normálosztó.
∎Ezután már könnyedén kimondhatjuk a 19.9. Tételhez hasonló állításunkat egy csoport részcsoportjainak (vagy normálosztóinak) metszetéről.
25.17. Tétel:
Legyen G egy tetszőleges csoport, valamint legyen \mathcal{H} egy olyan G feletti halmazrendszer, amely G valahány – akár végtelen számú – részcsoportját tartalmazza elemként. Ekkor a \mathcal{H}-ban lévő halmazok metszete is részcsoport G-ben.
Ehhez hasonlóan ha \mathcal{N} egy olyan halmazrendszer, amely G valahány – akár végtelen számú – normálosztóját tartalmazza elemként, akkor az \mathcal{N}-ben lévő halmazok metszete is normálosztó G-ben.
♣Bizonyítás:
Nézzük először a részcsoportok metszetére vonatkozó állítást! Jelöljük H-val a \mathcal{H} halmazrendszerben lévő részcsoportok metszetét. Azt kell megmutatni, hogy H részcsoport G-ben. Ez a 24.5. Tétel szerint pontosan akkor teljesül, ha H zárt a G-beli műveletre és inverzképzésre nézve, valamint tartalmazza G egységelemét.
Mivel \mathcal{H} minden eleme részcsoport, így a 24.5. Tétel miatt mindegyik tartalmazza G egységelemét, amely tehát valóban benne van ezek metszetében, azaz H-ban.
Legyen most x a H halmaz egy tetszőleges eleme. Mivel H a \mathcal{H}-beli részcsoportok metszete, így x e részcsoportok mindegyikének szintén eleme, amelyek viszont ismét a 24.5. Tétel miatt zártak az inverzképzésre. Így x^{-1} is eleme az összes \mathcal{H}-beli részcsoportnak, vagyis valóban benne van ezek metszetében, azaz H-ban.
Végül legyen x és y a H halmaz két tetszőleges eleme. Mivel H a \mathcal{H}-beli részcsoportok metszete, így x és y e részcsoportok mindegyikének szintén eleme, amelyek viszont ismét a 24.5. Tétel miatt zártak a G-beli műveletre nézve. Így az xy szorzat is eleme az összes \mathcal{H}-beli részcsoportnak, vagyis valóban benne van ezek metszetében, azaz H-ban. A H halmaz tehát valóban részcsoport G-ben, ahogyan a tétel állítja.
Most nézzük a normálosztók metszetére vonatkozó állítást! Jelöljük N-nel az \mathcal{N} halmazrendszerben lévő normálosztók metszetét. Azt kell megmutatni, hogy N normálosztó G-ben. Ez a 25.16. Tétel szerint azt jelenti, hogy egyrészt N részcsoport G-ben, másrészt minden n\in N és g\in G esetén a gng^{-1} szorzat benne van N-ben. Minthogy \mathcal{N} minden eleme részcsoport G-ben (hiszen normálosztó), ezért ezek metszete, azaz N is részcsoport G-ben. Elegendő tehát csak a második feltételt ellenőrizni.
Legyen g tetszőleges G-beli, n pedig tetszőleges N-beli elem. Mivel N az \mathcal{N} halmazrendszerben lévő halmazok metszete, ezért \mathcal{N} minden eleme szintén tartalmazza n-et. Továbbá mivel ezek normálosztók, ezért a 25.16. Tétel alapján a gng^{-1} szorzat mindegyiküknek eleme. Ám ekkor ezek metszetének, azaz N-nek is eleme a gng^{-1} szorzat. Ez viszont ismét a 25.16. Tétel alapján azt jelenti, hogy N is normálosztó G-ben.
∎Mostmár a generált részgyűrűhöz illetve generált ideálhoz hasonlóan (lásd a 19.10. Tételt) bevezethetjük a generált részcsoport illetve generált normálosztó fogalmát.
25.18. Tétel (Generált részcsoport és normálosztó):
Legyen G egy tetszőleges csoport, továbbá X a G csoportnak egy tetszőleges részhalmaza. Jelöljük \mathcal{X}-szel azt a G fölötti halmazrendszert, amelynek elemei pontosan azok a részcsoportok G-ben, amelyek tartalmazzák X-et.
Ekkor \mathcal{X}-ben létezik pontosan egy legszűkebb elem, amelyet az X által generált részcsoportnak nevezünk, és \lang X\rang-szel jelölünk.
Ugyanilyen értelemben beszélhetünk az X által generált normálosztóról is.
♣Bizonyítás:
A 19.8. Tétel alapján egy halmazrendszerben legfeljebb egy legszűkebb elem létezhet. Így elegendő megmutatni, hogy létezik legszűkebb elem, az ugyanis garantáltan az egyetlen legszűkebb elem lesz.
Mivel X a G csoport tetszőleges részhalmaza lehet, ezért előszöris kérdés, hogy létezik-e egyáltalán olyan részcsoport, amely tartalmazza X-et? Erre természetesen igen a válasz, hiszen „legrosszabb esetben” maga a teljes G egy ilyen részcsoport. Az \mathcal{X} halmazrendszer tehát biztosan nem üres.
Most képezzük az \mathcal{X} halmazrendszer összes elemének metszetét, és jelöljük ezt a halmazt H-val. Minthogy \mathcal{X} elemei részcsoportok G-ben, így a 25.17. Tétel alapján H is részcsoport G-ben. Továbbá az X-ről azt mondtuk, hogy ő részhalmaza minden \mathcal{X}-beli részcsoportnak, emiatt részhalmaza ezek metszetének, azaz H-nak is.
Ez viszont azt jelenti, hogy H maga is az \mathcal{X} halmazrendszer eleme, hiszen ő is egy X-et tartalmazó részcsoport G-ben. Ráadásul mivel ő a metszete \mathcal{X} összes elemének, ezért egyben részhalmaza is azoknak. Másként fogalmazva bármilyen K\in \mathcal{X} részcsoportra teljesül, hogy H\sube K. Ez a 19.7. Definíció szerint viszont épp azt jelenti, hogy H nem más, mint az \mathcal{X} halmazrendszer legszűkebb eleme. Más szavakkal H a legszűkebb olyan részcsoport G-ben, amely tartalmazza az X részhalmazt, azaz a tételbeli jelölést használva H=\lang X\rang.
A legszűkebb X-et tartalmazó normálosztó létezésére és egyértelműségére vonatkozó állítás a fentiekhez teljesen hasonló módon igazolható.
∎Ahhoz hasonlóan, ahogyan a részgyűrűk és ideálok generálása kapcsán a 19. részben már kifejtettük, egy adott G csoport bármely X részhalmaza egyértelműen meghatároz egy részcsoportot (vagy speciális esetben egy normálosztót). Ez lesz az X-et tartalmazó legszűkebb részcsoport (vagy normálosztó). Ugyanakkor elképzelhető, hogy az \lang X\rang részcsoportot (vagy normálosztót) lehet generálni egy X-nél szűkebb részhalmazzal is. Amikor tehát azt mondjuk, hogy egy részcsoport „generálható X-szel”, ez még nem jelenti azt, hogy az adott részcsoport kizárólag X-szel generálható.
Ciklikus csoportok
Végül ebben a szakaszban megismerkedünk a csoportok legegyszerűbb osztályával, az úgynevezett ciklikus csoportokkal, és – legalábbis izomorfia erejéig – meg is adjuk az összes, ebbe az osztályba tartozó csoportot. Az ideálok generálása kapcsán a 19.11. Definícióban külön jelentőséget tulajdonítottunk az olyan ideáloknak, amelyek a szóbanforgó gyűrű kevés számú – sőt a főideálok esetén mindössze egyetlen – elemével generálhatók. Ez csoportok esetén elvezet minket egy, a továbbiakban számunkra fontos fogalomhoz.
25.19. Definíció (Ciklikus csoportok):
Legyen G tetszőleges csoport, H pedig valamilyen részcsoport G-ben. Amennyiben G-ben létezik olyan g elem, hogy az egyelemű X=\{g\} halmaz generálja H-t – azaz \lang X\rang = H –, akkor azt mondjuk, hogy H ciklikus részcsoport G-ben, amelynek generátoreleme (vagy primitív eleme) g.
Amennyiben maga a teljes G – mint triviális részcsoport – generálható egyetlen elemmel, akkor G-t ciklikus csoportnak nevezzük.
♣Megjegyzés:
Az, hogy G ciklikus, amelynek generátoreleme g, pontosan azt jelenti, hogy G összes eleme kifejezhető ennek az egyetlen g elemnek az egész kitevős hatványaiként (lásd a 24.9. Definíciót). A G csoport e egységeleme és g inverze ugyanis a 24.9. Definíció alapján g-nek rendre a nulladik és a -1-edik hatványaként írható fel, továbbá minden egyéb elem kifejezhető a g valamint a g^{-1} elemek valamilyen sorrendben felírt szorzataként – máskülönben g nem lenne generátorelem. Például:
ggg^{-1}gg^{-1}g^{-1}ggEgy ilyen szorzatban az egymás mellett álló g és g^{-1} tényezők nyilván elhagyhatók. Vagyis végeredményben vagy magát az egységelemet, vagy egy olyan szorzatot kapunk, amely már csak g vagy csak g^{-1} tényezőket tartalmaz. A 24.9. Definíció alapján a végeredmény tehát első esetben g^0-ként, míg második esetben g^n-ként írható fel valamilyen pozitív vagy negatív n kitevővel.
Ebből az is következik, hogy minden G ciklikus csoport Abel-csoport. Legyenek ugyanis a és b a G csoport tetszőleges elemei. Mivel G ciklikus, ezért a és b felírhatók valamilyen g\in G generátorelem egész kitevős hatványaiként:
\begin{aligned}a&=g^n \\ b&=g^k\end{aligned}Ám ekkor e két elem szorzata a 24.10. Tétel 3. pontja alapján felcserélhető, hiszen:
a\cdot b=g^n\cdot g^k=g^{n+k}=g^{k+n}=g^k\cdot g^n=b\cdot a ♣Kézenfekvő példaként megmutatjuk, hogy az egész számok \Z gyűrűjének additív csoportja, továbbá bármilyen nemnegatív m\geq 0 esetén a \Z/m\Z maradékosztálygyűrű additív csoportja, azaz a 24.3. Definíció alapján \Z^+-szal illetve (\Z/n\Z)^+-szal jelölt csoportok ciklikusak.
25.20. Tétel:
A \Z^+ additív csoport továbbá tetszőleges m\geq 0 esetén a (\Z/m\Z)^+ additív csoportok ciklikus csoportok. Előbbi generátoreleme az 1 egész szám, utóbbi generátoreleme pedig az [1]_m maradékosztály.
♣Bizonyítás:
Mivel a \Z^+ és a (\Z/m\Z)^+ csoportok esetén a csoportműveletet + jelöli, ezért a 24.1. Definíciónak megfelelően az „egységelem” és „inverz” helyett a „nullelem” és „ellentett” kifejezéseket használjuk, továbbá a 24.9. Definíció utáni megjegyzés alapján a szokásos x^n helyett az nx írásmódot követjük és hatvány helyett többszörösről beszélünk.
A \Z^+ csoportban az 1 egész szám ellentettje a -1 egész szám. A pozitív egész számok ennek megfelelően n1, míg a negatív számok n(-1) alakban fejezhetők ki. Végül a 0 egész szám a \Z^+ csoport nulleleme, így a 24.9. Definíció alapján ő 0\cdot 1-ként fejezhető ki, mint az 1 egész szám többszöröse. A \Z^+ csoport tehát valóban ciklikus, melynek generátoreleme 1.
Ehhez hasonlóan a (\Z/m\Z)^+ csoportban az [1]_m maradékosztály ellentettje a [-1]_n maradékosztály. Ebben a csoportban a + műveletet a 20.5. Tételben leírtaknak megfelelően a reprezentánselemeken kell elvégezni. Így az n[1]_m többszörös tulajdonképpen az [n1]_m maradékosztály lesz, ahol n1 a fentiekhez hasonlóan az 1 egész szám valamilyen többszörösét jelöli. Minthogy fentebb már bizonyítottuk, hogy bármely egész szám felírható az 1 többszöröseként – hiszen ugye \Z^+ ciklikus – ezért ez azt jelenti, hogy az [1]_m maradékosztály többszöröseiként is minden létező modulo m maradékosztályt megkaphatunk. A (\Z/m\Z)^+ csoport tehát valóban ciklikus, melynek generátoreleme az [1]_m maradékosztály.
∎Hamarosan egy fontos csoportelméleti struktúratételt fogunk bizonyítani a ciklikus csoportokra vonatkozóan, amely azt mondja ki, hogy a fenti tételben szereplő \Z^+ és (\Z/m\Z)^+ csoportokon kívül – izomorfiától eltekintve – nem is létezik más ciklikus csoport. Ehhez azonban szükségünk lesz az alábbi segédtételre.
25.21. Lemma:
Legyenek G és H tetszőleges csoportok, továbbá legyen adott egy f:G\to H szürjektív csoporthomomorfizmus. Ebben az esetben ha G ciklikus, melynek generátoreleme g, akkor H is ciklikus, melynek generátoreleme f(g).
♣Bizonyítás:
Azt kell megmutatni, hogy f(g) valóban H generátoreleme. Legyen ezért h a H csoport tetszőleges eleme. Mivel az f csoporthomomorfizmus szürjektív, ezért biztosan létezik olyan x elem G-ben, amelynek épp h az f szerinti képe, azaz:
f(x)=hMivel G ciklikus, ezért ez a bizonyos x kifejezhető a g generátorelem egész kitevős hatványaként, azaz létezik olyan n egész szám, hogy teljesül az alábbi:
f(\underbrace{g^n}_{=x})=hHa n pozitív, akkor ez a kifejezés a 24.9. Definíció alapján így írható fel:
f(\underbrace{g\cdot g\cdot \ldots g}_{\text{n darab}})=hÁm ekkor f művelettartó tulajdonsága miatt a baloldal átírható az alábbi módon:
\underbrace{f(g)\cdot f(g)\cdot \ldots f(g)}_{\text{n darab}}=(f(g))^n=hAzaz ebben az esetben h kifejezhető f(g) egész kitevős hatványaként.
Ha n negatív, akkor vezessük be a k=-n jelölést. Ilyenkor tehát k pozitív, és f(g^{-k})=h a 24.9. Definíció alapján így írható fel:
f(\underbrace{g^{-1}\cdot g^{-1}\cdot \ldots g^{-1}}_{\text{k darab}})=hAz f művelet- valamint inverzképzéstartó (lásd a 25.2. Lemma 2. pontját) tulajdonsága miatt a baloldal átírható az alábbi módon:
\underbrace{(f(g))^{-1}\cdot (f(g))^{-1}\cdot \ldots (f(g))^{-1}}_{\text{k darab}}=(f(g))^{-k}=hAzaz h ebben az esetben is kifejezhető f(g) egész kitevős hatványaként.
Végül ha n=0, akkor a 24.9. Definíció alapján g^n épp a G csoport egységeleme. Mivel a 25.2. Lemma 1. pontja alapján egységelem képe egységelem, ezért ebben az esetben h szükségképpen a H csoport egységeleme, amely nyilván kifejezhető f(g)-nek a nulladik hatványaként.
A H csoport tehát valóban ciklikus, melynek generátoreleme f(g).
∎Megjegyzés:
Figyelem, a tétel megfordítása nem igaz! Triviális ellenpéldaként tekintsünk egy olyan f:G\to H csoporthomomorfizmust, amely egy nem ciklikus G csoport elemeit egy olyan H csoportba képzi, amelynek mindössze egyetlen eleme van, méghozzá az egységelem. Ekkor a mindössze egyetlen elemből álló H csoport nyilvánvalóan ciklikus, ám G – mint említettük – nem az.
♣Végül ismertetjük a már említett, ciklikus csoportokra vonatkozó struktúratételünket, amely tehát kizárja a \Z^+ és a (\Z/m\Z)^+ additív csoportokon kívüli további ciklikus csoportok létezését.
25.22. Tétel (Ciklikus csoportok struktúratétele):
Egy G csoport akkor és csak akkor ciklikus, ha izomorf a \Z^+ vagy valamilyen m\geq 0 nemnegatív egész szám esetén a (\Z/m\Z)^+ csoporttal.
♣Bizonyítás:
A 25.20. Tétel alapján a \Z^+ illetve a (\Z/m\Z)^+ csoportok ciklikusak. Ezért ha G izomorf valamelyikükkel, akkor a 25.21. Lemma alapján G is ciklikus, hiszen a csoportizomorfizmus a 25.1. Definíció alapján egy szürjektív homomorfizmus.
Megfordítva: Tegyük fel, hogy G ciklikus, és legyen g egy generátorelem. Ekkor G minden eleme felírható g egész kitevős hatványaként.
1. eset – g rendje (lásd a 24.11. Definíciót) végtelen: Tekintsük azt az f:\Z^+\to G függvényt, amely minden n egész számhoz hozzárendeli a g^n elemet. Mivel a 24.12. Tétel alapján g bármely két hatványa különbözik, ezért ez a függvény injektív lesz, hiszen különböző egész számok képe különböző G-beli elem lesz. Továbbá, mivel G minden eleme felírható g egész kitevős hatványaként, ezért f egyben szürjektív is. Így már csak a művelettartó tulajdonságot kell igazolni. Ez viszont az egész kitevős hatványozás azonosságaiból (24.10. Tétel 3. pontja) következik:
f(n+k)=g^{n+k}=g^n\cdot g^k=f(n)\cdot f(k)Azaz G ebben az esetben izomorf a \Z^+ csoporttal.
2. eset – g rendje véges: Legyen g rendje m, és tekintsük azt az f:(\Z/m\Z)^+\to G függvényt, amely minden [n]_m maradékosztályhoz hozzárendeli a g^n elemet. Tekintsünk két tetszőleges maradékosztályt, legyenek ezek például [n]_m és [k]_m, és tegyük fel, hogy teljesülnek az alábbiak:
f([n]_m)=f([k]_m)Az f függvény definíciója alapján ez az egyenlet így írható fel:
g^n=g^kÁm mivel g rendje véges, ezért a 24.12. Tétel 1. pontja alapján ekkor teljesül az alábbi kongruencia:
n\equiv k\pmod mEz viszont azt jelenti, hogy n és k ugyanazt a modulo m maradékosztályt reprezentálják, azaz:
[n]_m=[k]_mVagyis különböző maradékosztályok képei nem lehetnek azonosak, így az f függvény injektív. Továbbá, mivel G minden eleme felírható g egész kitevős hatványaként, és bármely egész szám reprezentál valamilyen modulo m maradékosztályt, ezért f egyben szürjektív is. Így már csak a művelettartó tulajdonságot kell igazolni. Ez viszont ismét az egész kitevős hatványozás azonosságaiból (24.10. Tétel 3. pontja), továbbá a maradékosztályok közötti összeadás műveletének definíciójából (20.5. Tétel) következik:
f([n]_m+[k]_m)=f([n+k]_m)=g^{n+k}=g^n\cdot g^k=f([n]_m)\cdot f([k]_m)Azaz G ebben az esetben izomorf a (\Z/m\Z)^+ csoporttal.
∎Láthattuk tehát, hogy a \Z/m\Z maradékosztálygyűrűk additív csoportjai minden nemnegatív m esetén ciklikusak. Jogosan merülhet fel a kérdés, hogy vajon mi a helyzet ugyanezen gyűrűk multiplikatív csoportjaival ebben a tekintetben. Nézzük meg például a \Z/8\Z maradékosztálygyűrű esetét. Ennek multiplikatív csoportja a modulo 8 redukált maradékosztályokból áll, amelyek az alábbiak:
(\Z/8\Z)^{\times}=\{[1]_8; [3]_8; [5]_8; [7]_8\}Ezek hatványait az alábbi táblázatban foglaltuk össze, ahol az egyes sorokban e maradékosztályok hatványai szerepelnek az első néhány pozitív kitevőre, amely kitevőknek az egyes oszlopok felelnek meg:
\begin{array}{c|cccccc} &1&2&3&4&5&6 \\ \hline [1]_{8} & [1]_{8} & [1]_{8} & [1]_{8} & [1]_{8} & [1]_{8} & [1]_{8} \\ [3]_{8} & [3]_{8} & [1]_{8} & [3]_{8} & [1]_{8} & [3]_{8} & [1]_{8} \\ [5]_{8} & [5]_{8} & [1]_{8} & [5]_{8} & [1]_{8} & [5]_{8} & [1]_{8} \\ [7]_{8} & [7]_{8} & [1]_{8} & [7]_{8} & [1]_{8} & [7]_{8} & [1]_{8} \end{array}Látható, hogy egyetlen csoportelem sem tölti be a generátorelem szerepét, hiszen egyiknek az egész kitevős hatványai sem állítják elő az összes többi redukált maradékosztályt. A (\Z/8\Z)^{\times} multiplikatív csoport tehát NEM ciklikus.
Tekintsük most a (\Z/10\Z)^{\times} multiplikatív csoport elemeinek hatványait, amelyet az alábbi táblázatban foglaltunk össze:
\begin{array}{c|cccccc} &1&2&3&4&5&6 \\ \hline [1]_{10} & [1]_{10} & [1]_{10} & [1]_{10} & [1]_{10} & [1]_{10} & [1]_{10} \\ [3]_{10} & [3]_{10} & [9]_{10} & [7]_{10} & [1]_{10} & [3]_{10} & [9]_{10} \\ [7]_{10} & [7]_{10} & [9]_{10} & [3]_{10} & [1]_{10} & [7]_{10} & [9]_{10} \\ [9]_{10} & [9]_{10} & [1]_{10} & [9]_{10} & [1]_{10} & [9]_{10} & [1]_{10} \end{array}Látható, hogy ennek a csoportnak két generátoreleme is van, méghozzá a [3]_{10} és a [7]_{10} redukált maradékosztályok, így a (\Z/10\Z)^{\times} csoport bizony ciklikus. A maradékosztálygyűrűk multiplikatív csoportjai esetén tehát a kérdés már nem ennyire egyértelmű, ám ezzel a következő részben fogunk bővebben foglalkozni.
Ebben a részben tehát némileg kibővítettük csoportelméleti eszköztárunkat. A 18. részben megismert gyűrűhomomorfizmusok mintájára bevezettük a csoporthomomorfizmus fogalmát, valamint pontosan jellemeztük ezek magjait. Fontos párhuzamokat felfedve megmutattuk, hogy ezeknek is – a gyűrűhomomorfizmusok kapcsán bevezetett ideálokhoz hasonlóan – bizonyos speciális tulajdonságoknak kell megfelelniük. Így jutottunk el a normálosztó és a faktorcsoport fogalmához, majd ismertettük a csoportok homomorfizmustételét és további struktúratartó tulajdonságokat igazoltunk. Végül megismerkedtünk a generálás és az ehhez kapcsolódó ciklikus csoportok fogalmával.
Ezeket a csoportelméleti ismereteket a következő részben a Miller-Rabin-prímteszt hibavalószínűség-becslésének javítására fogjuk felhasználni. A cikksorozat lezárásaként igazolni fogjuk ugyanis, hogy a redukált maradékosztályoknak nemhogy a fele, de legalább a háromnegyede Miller-Rabin-tanú, így a prímteszt még gyorsabban ad majdnem biztos eredményt.
A következő részt itt találod…



