Az előző részben megismerkedtünk napjaink egyik legfontosabb aszimmetrikus kulcsú rejtjelezési eljárásával, az RSA-algoritmussal. Ehhez alapvetően három összetevőre volt szükség. Először is hatékonyan kell tudni megoldani lineáris kongruenciákat, amelyhez bemutattuk az euklidészi algoritmus kibővített változatát. Másodszor hatékonyan kell tudni kiszámítani az Euler-féle \varphi-függvény értékét. Láttuk, hogy a bemeneti szám prímtényezőinek ismeretében ez gyerekjáték. Megemlítettük ugyanakkor, hogy a prímtényezők ismerete nélkül jelenlegi tudásunk szerint ez gyakorlatilag kivitelezhetetlen, amennyiben ezek a prímtényezők kellően nagyok. Ez adja az RSA-eljárás biztonságát. Harmadszor a kódoló és dekódoló függvények elvégzéséhez hatékonyan kell tudni moduláris hatványozást végezni, amelyhez az ismételt négyzetreemelések módszerével ismerkedtünk meg. Végül egy konkrét példán ki is próbáltuk az eljárást, és megmutattuk, hogy a kulcspár egyik tagjával kódolt üzenetet varázslatos módon a kulcspár másik tagjával lehet dekódolni.
De vajon varázslat helyett valójában mi áll az RSA-algoritmus helyes működésének hátterében? Mit állít a kis Fermat-tétel és a kínai maradéktétel, és mi közük van ehhez az egészhez? Mit értünk egy maradékosztálygyűrű dekompozíciója alatt? Hogyan lehet ennek segítségével lényegesen felgyorsítani az RSA-dekódolási algoritmust? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 20., és 21. részekben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Legyen adva egy tetszőleges m\geq 0 nemnegatív egész szám. A 20.1. Tételben bevezetett modulo m kongruencia egy ekvivalenciareláció az egész számok \Z gyűrűjén. Az ehhez tartozó ekvivalencia-osztályokat modulo m kongruenciaosztályoknak vagy modulo m maradékosztályoknak nevezzük.
Ha m\gt 0, akkor pontosan m darab modulo m maradékosztály létezik. Legyen a egy tetszőleges egész szám. Ekkor az a-t tartalmazó modulo m maradékosztály bármely eleme felírható km + a alakban valamilyen alkalmas k egész számmal. Visszafelé: Minden k egész szám esetén a km + a egész szám benne van az a-t tartalmazó modulo m maradékosztályban.
Ha m=0, akkor végtelen sok modulo m maradékosztály létezik, és minden ilyen maradékosztályban pontosan egy egész szám van.
Legyen m\geq 0 egy tetszőleges nemnegatív egész szám, és jelöljük \Z/m\Z-vel azt a halmazt, amelynek elemei a 20.4. Tételben definiált modulo m maradékosztályok. Ha a valamilyen egész szám, akkor jelöljük [a]_m-mel az a-t tartalmazó modulo m maradékosztályt. Ilyenkor azt mondjuk, hogy az a egész szám reprezentálja az [a]_m maradékosztályt. Vezessünk be e maradékosztályok között két műveletet az alábbiak szerint:
- Ha [a]_m és [b]_m két maradékosztály, akkor ezek összege legyen az [a]_m\oplus [b]_m=[a+b]_m maradékosztály.
- Ha [a]_m és [b]_m két maradékosztály, akkor ezek szorzata legyen az [a]_m\odot [b]_m=[a\cdot b]_m maradékosztály.
Ekkor a \Z/m\Z halmaz ezzel a két művelettel egy kommutatív és egységelemes gyűrűt alkot, amelyet modulo m maradékosztálygyűrűnek nevezünk. E gyűrű nulleleme a [0]_m, egységeleme pedig az [1]_m maradékosztály.
Tekintsük továbbá azt az f:\Z\to \Z/m\Z függvényt, amely minden a egész számhoz az [a]_m maradékosztályt rendeli hozzá. Ekkor f egy gyűrűhomomorfizmus \Z és \Z/m\Z között, melynek magja az m egész szám többszöröseinek halmaza. Ennek a neve természetes gyűrűhomomorfizmus.
Legyen a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám. Ekkor az alábbi kongruenciaegyenletet lineáris kongruenciának nevezzük:
a\cdot x\equiv b\pmod mEgy lineáris kongruencia egy megoldásán egy olyan modulo m maradékosztályt értünk, amelynek tetszőleges elemét x helyére behelyettesítve a kongruencia teljesül.
Egy lineáris kongurencia megoldásszáma alatt azon modulo m maradékosztályok számát értjük, amelyek megoldásai az adott lineáris kongruenciának.
Legyen m\gt 0 tetszőleges pozitív, a pedig egy m-hez relatív prím egész szám. Ekkor teljesül az alábbi kongruencia:
a^{\varphi(m)} \equiv 1\pmod mItt az a^{\varphi(m)} kifejezés alatt egy olyan \varphi(m) tényezős szorzatot értünk, amelynek minden tényezője a.
Legyen a és b két tetszőleges pozitív egész szám. Tegyük fel továbbá, hogy a és b egymáshoz relatív prímek (lásd a 17.10. Definíciót). Ekkor teljesül az alábbi:
\varphi(ab)=\varphi(a) \cdot \varphi(b)Legyen p\gt 0 valamilyen pozitív prímszám, k\gt 1 pedig tetszőleges, 1-nél nagyobb pozitív egész. Ekkor teljesül az alábbi:
\varphi(p^k)=p^k-p^{k-1}Speciálisan prímszámokra az Euler-féle \varphi-függvény értéke:
\varphi(p)=p-1Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 20. és 21. részeket, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Az RSA-algoritmus lépéseit tehát már ismerjük. Mutattunk is egy konkrét példát az alkalmazására. Ebben a példában először Bob generált magának egy RSA kulcspárt, amelynek publikus részét elérhetővé tette Alice – illetve bárki más – számára, a titkos részét viszont nem adta ki a kezéből. Alice ezután a sziabobmiahelyzet üzenetet kódolta Bob publikus kulcsával, a titkosított üzetetet pedig átküldte a nembiztonságos csatornán. Ezt az üzenetet egy támadó, de még maga Alice sem tudja dekódolni. Arra ugyanis csak Bob képes, mivel nála van az ehhez szükséges titkos kulcs.
Úgy tűnik tehát, hogyha egy üzenetet egy kulcspár valamelyik tagjával – legyen az akár a publikus, akár a titkos kulcs – kódolunk, majd az így kapott eredményt dekódoljuk a kulcspár másik tagjával, akkor varázslatos módon az eredeti üzenetet kapjuk vissza. Most azt fogjuk megmutatni, hogy ez az összefüggés bármilyen, az ismertetett kritériumoknak megfelelő kulcspár, továbbá bármilyen üzenet esetén valóban fennáll. Ehhez azonban szükségünk lesz két nagyon fontos tételre. Ismerkedjünk is meg az elsővel.
A kis Fermat-tétel
A kis Fermat-tétel egy fontos számelméleti tétel, amelyet Pierre de Fermat fedezett fel 1636-ban. Fermat-nak bosszantó szokása volt, hogy bizonyítás nélkül közölte felfedezéseit kortársaival, mintegy kihívást intézve hozzájuk: jöjjenek rá ők is a bizonyításra. Fermat szokásához híven a kis Fermat-tételre sem adott bizonyítást. Ezt bizonyíthatóan elsőként Gottfried Wilhelm Leibniz német matematikus írta le egy dátumozatlan kéziratban, ahol azt is állította, hogy már 1683 előtt is ismert bizonyítást e tételre. A tétel nevében szereplő „kis” jelzőt a híres nevezetes nagy Fermat-tételtől való megkülönböztetés miatt szokás használni. Ez utóbbi egészen 1995-ig „nagy Fermat-sejtés” néven volt ismeretes, mivel csak ekkor – mintegy 350 évvel később – sikerült bizonyítást adni rá.
Visszatérve a kis Fermat-tételre, az egy viszonylag egyszerű számelméleti tétel, amely moduláris hatványokról szól, méghozzá azokban az esetekben, amikoris a modulus egy valamilyen pozitív p prímszám. Fermat azt vizsgálta, hogy egy tetszőleges a egész szám moduláris hatványai hogyan alakulnak ebben a modulo p óraaritmetikában. Észrevette, hogy minden olyan esetben, amikor a kitevő megegyezik a p modulussal, akkor az a egész szám p-edik moduláris hatványa is épp megegyezik a-val.
Vizsgáljuk meg például, hogy az a=2 egész szám moduláris hatványai hogyan alakulnak a kitevőknek megfelelő óraaritmetikákban. Nyilakkal jelöltük meg azokat a sorokat, amelyekben a kitevő és a modulus prímszám:
\begin{aligned}\to 2^2&\equiv 2\pmod 2 \\ \to 2^3&\equiv 2\pmod 3 \\ 2^4&\equiv 0\pmod 4 \\ \to 2^5&\equiv 2\pmod 5 \\ 2^6&\equiv 4\pmod 6 \\ \to 2^7&\equiv 2\pmod 7 \\ 2^8&\equiv 0\pmod 8 \\ 2^9&\equiv 8\pmod 9 \\ 2^{10}&\equiv 4\pmod{10} \\ \to 2^{11}&\equiv 2\pmod{11} \\ &\vdots \end{aligned}Valóban úgy tűnik, hogy a prím kitevők esetében a 2 hatványai mindig kongruensek lesznek 2-vel a kitevőnek megfelelő óraaritmetikában.
Az alábbi tétel második állítása éppen azt fogalmazza meg, hogy ez bármilyen alap – tehát nem csak a 2 –, továbbá bármilyen pozitív prím kitevő esetén így van. Amennyiben a és p relatív prímek, akkor érvényes az első állítás is, amely a kis Fermat-tétel gyakoribb alakja.
22.1. Tétel (A kis Fermat-tétel):
Legyen p\gt 0 egy tetszőleges pozitív prím, továbbá a egy tetszőleges egész szám, amely relatív prím p-hez. Ekkor teljesül az alábbi kongruencia:
a^{p-1}\equiv 1\pmod pAz alábbi kongruencia tetszőleges a egész számra – tehát nem csak a p-hez relatív prímekre – teljesül:
a^p\equiv a\pmod p ♣Bizonyítás:
Amennyiben a relatív prím a p modulushoz, akkor alkalmazható az Euler-Fermat tétel (20.19. Tétel). Eszerint teljesül az alábbi kongruencia:
a^{\varphi(p)}\equiv 1\pmod pA 21.5. Tétel alapján az Euler-féle \varphi-függvény értéke ebben az esetben p-1. Ebből a tétel első állítása adódik:
a^{p-1}\equiv 1\pmod pÁm ebben az esetben a 20.2. Tétel 7. pontja miatt a kongruencia mindkét oldalát megszorozhatjuk a-val. Így teljesül az alábbi kongruencia is, amely a tétel második állítása:
a^p\equiv a\pmod pMár csak annyit kell megmutatni, hogy ez a második állítás abban az esetben is teljesül, ha a és p NEM relatív prímek. A 21.4. Lemma alapján ebben az esetben teljesül a p|a oszthatóság. Ez viszont a 20.1. Tétel 3. pontja alapján épp az alábbi kongruenciát jelenti:
a\equiv 0\pmod pÁm ekkor a 20.2. Tétel 8. pontja alapján a kongruencia mindkét oldalát p-edik hatványra emelhetjük. Így teljesül az alábbi kongruencia is:
a^p\equiv 0\pmod pMivel tehát a is és a^p is 0-val kongruens modulo p, ezért a 20.2. Tétel 3. pontja alapján ők egymással is kongruensek modulo p, épp ahogyan a tétel állítja:
a^p\equiv a\pmod p ∎Megjegyzés:
Ez a tétel magától Fermat-tól származik 1636-ból. A bizonyításban felhasználtuk, hogy a kis Fermat-tétel az Euler-Fermat tétel (20.19. Tétel) egy speciális esete, amikoris a modulus egy p prímszám, és így a \varphi(p) kitevő p-1-gyel egyezik meg. Megemlítjük azonban, hogy az Euler-Fermat tételt Leonhard Euler mintegy 100 évvel a kis Fermat-tétel felfedezése után publikálta, méghozzá éppen annak tetszőleges – tehát nem csak prím – kitevőkre történő általánosításaként. A kis Fermat-tétel közvetlenül – tehát az Euler-Fermat tétel felhasználása nélkül – is viszonylag könnyen bizonyítható. Erre vonatkozóan itt találhatunk további részleteket.
Vigyázat! Attól még, hogy valamely a és n egész számokra teljesülnek a tételben szereplő kongruenciák, még nem biztos, hogy n prímszám. Ez azonban elsőre nem látszik. Például a=2 esetén a 2^n\equiv 2\pmod n kongruenciák látszólag csak azokban az esetekben teljesülnek, amikor az n kitevő prím. Az első ellenpéldára csak az n=341 kitevőnél bukkanunk rá. Ekkor teljesül ugyan a 2^{341}\equiv 2\pmod{341} kongruencia, a 341 azonban nem prím, hiszen 341=11\cdot 31. A következő ellenpélda n=561=3\cdot 11\cdot 17-nél következik. Néhány továbbit találunk ebben a listában.
♣Ráadásul az iménti megjegyzésben szereplő n=561 ellenpélda különleges abból a szempontból, hogy esetében nemcsak az a=2, hanem tetszőleges a alap esetén is teljesül az a^n\equiv a\pmod n kongruencia, ennek ellenére mégsem prím. Ez egyben azt is jelenti, hogy a tétel megfordítása nem igaz!
Azon túlmenően, hogy a most ismertetett kis Fermat-tétel fontos szerepet játszik az RSA-algoritmus helyességének igazolásában, Alice-nak és Bob-nak is nagy hasznára lesz a kulcsgeneráláshoz szükséges óriási – a gyakorlatban többszázjegyű – prímszámok kereséséhez. Erről a következő részben lesz szó, most azonban ismerkedjünk meg egy másik, az RSA működése szempontjából fontos kérdéssel.
Kongruenciarendszerek
A 20. részben megismerkedtünk az úgynevezett kongruenciaegyenletekkel. Ezek olyan kongruenciák, amelyekben valamilyen x ismeretlen is szerepel, a feladatunk pedig az egész számok egy olyan részhalmazának (vagy részhalmazainak) meghatározása, amelynek (vagy amelyeknek) elemeit behelyettesítve az x ismeretlen helyére a kongruencia teljesül. E kongruenciaegyenletek legegyszerűbb képviselői az úgynevezett lineáris kongruenciák voltak, így a továbbiakban elsősorban ezeket fogjuk példaként felhozni. Legyen például a és b tetszőleges, m\gt 0 pedig valamilyen pozitív egész szám, és tekintsük az alábbi lineáris kongruenciát:
a\cdot x\equiv b\pmod mA 20.8. Definíció utáni megjegyzés alapján egy ilyen kongruenciaegyenletnek a megoldásai teljes modulo m maradékosztályok lesznek – amennyiben persze létezik megoldás.
Most bonyolítsuk meg a dolgot egy kicsit. A hagyományos egyenletekhez hasonlóan a kongruenciaegyenletek esetén is előfordulhat, hogy ugyanarra az ismeretlenre egyidejűleg több, különböző modulus szerinti kongruenciafeltételt is előírunk. Ezeket kongruenciarendszereknek nevezzük. A példa kedvéért továbbra is a lineáris kongruenciáknál maradva tegyük fel, hogy most az egész számoknak azon részhalmát (vagy részhalmazait) keressük, amelynek (vagy amelyeknek) elemei egyszerre elégítik ki az alábbi mindkét kongruenciát:
\begin{aligned}3x&\equiv 2\pmod 5 \\ 6x&\equiv 4\pmod 8\end{aligned}Nyilvánvalóan egy ilyen rendszer megoldhatóságának szükséges feltétele, hogy a benne szereplő kongruenciák külön-külön megolhatók legyenek. Ez ebben a példában természetesen a 20.12. Tétel alapján teljesül, mivel a (3,5)=1 és a (6,8)=2 kitüntetett közös osztók osztói a megfelelő kongruenciák jobboldalainak, azaz rendre a 2 és a 4 egész számoknak.
A 20.13. Tétel 1. pontja alapján az első kongruenciának (3,5)=1 darab modulo 5 maradékosztály, míg a másodiknak (6,8)=2 darab modulo 8 maradékosztály lesz a megoldása. Ezek megtalálásához előszöris a 20.12. Tétel alapján az alábbi két lineáris diofantoszi egyenletet kell megoldani:
\begin{aligned}3x+5y&=2 \\ 6x+8y&=4\end{aligned}Ezt a 21.2. Tétel 1. pontja alapján a kibővített euklidészi algoritmussal tudjuk megtenni. Az így kapott megoldásokat a 20.12. Tételben leírtaknak megfelelően visszafordítva a kongruenciák nyelvére azt kapjuk, hogy a 3x\equiv 2\pmod 5 kongruenciának a [4]_5 modulo 5 maradékosztály, míg a 6x\equiv 4\pmod 8 kongruenciának a [6]_8 modulo 8 maradékosztály egy-egy megoldása lesz. Előbbinek ugye nincs más megoldása, míg utóbbinak a 20.13. Tétel 2. pontja alapján egy további megoldása lesz a [2]_8 modulo 8 maradékosztály.
A fenti kongruenciarendszerben szereplő két lineáris kongruencia megoldásait az alábbiakban foglaltuk össze a 19.1. Definícióban és a 19.3. Definícióban tanult halmazelméleti jelölésekkel:
\begin{aligned}3x\equiv 2\pmod 5 &\to x\in [4]_5 \\ 6x\equiv 4\pmod 8 &\to x\in [6]_8 \cup [2]_8\end{aligned}Olyan egész számokat keresünk tehát, amelyek 5-tel osztva 4 maradékot, és 8-cal osztva 6 vagy 2 maradékot adnak. Azaz tulajdonképpen az alábbi két kongruenciarendszer megoldásait keressük:
\begin{array}{c} \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 6\pmod 8\end{aligned}} \\ \\ \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 2\pmod 8\end{aligned}} \end{array}Az ilyen jellegű kérdések megválaszolására siet segítségünkre a most bemutatásra kerülő nagyon fontos összefüggés.
A kínai maradéktétel
Azt a kérdést szeretnénk tehát megválaszolni, hogy melyek azok az egész számok, amelyek adott modulusokkal osztva adott maradékokat adnak. Itt most csak azzal a számunkra fontos esettel foglalkozunk, amikor ezek a modulusok páronként relatív prímek egymáshoz – azaz bármely két modulus egymáshoz relatív prím. Ilyen például az előző szakaszban felmerülő két példa, hiszen az 5 és 8 modulusok egymáshoz relatív prímek.
Az írásos emlékek alapján az alábbi tételt már mintegy 2000 évvel ezelőtt is ismerte egy bizonyos Szun Cu nevű kínai matematikus, ezért ezt kínai maradéktétel néven szoktuk emlegetni.
22.2. Tétel (Kínai maradéktétel):
Legyen a és b tetszőleges, p\gt 0 és q\gt 0 pedig valamilyen pozitív egész számok. Tegyük fel továbbá, hogy p és q egymáshoz relatív prímek. Ekkor az alábbi kongruenciarendszer megoldható, és a megoldás egyetlen modulo pq maradékosztály lesz:
\begin{aligned}x&\equiv a\pmod p \\ x&\equiv b\pmod q\end{aligned}Más megfogalmazásban minden, a fenti két kongruenciát egyszerre kielégítő egész szám ugyanabba az egyetlen modulo pq maradékosztályba esik, továbbá ennek a bizonyos maradékosztálynak minden eleme kielégíti a fenti két kongruenciát.
♣Bizonyítás:
Először a kongruenciarendszer megoldhatóságát igazoljuk. Az első kongruencia a 20.12. Tétel alapján pontosan akkor oldható meg, ha az (1,p) kitüntetett közös osztónak többszöröse a jobboldalon álló a egész szám. Ehhez hasonlóan a második kongruencia pontosan akkor oldható meg, ha (1,q)-nak többszöröse a b egész szám. A tételben szereplő kongruenciarendszer tehát pontosan akkor oldható meg, ha mindkét alábbi oszthatóság teljesül:
\begin{aligned}(1,p)&|a \\ (1,q)&|b\end{aligned}Az oszthatóságok baloldalain álló kitüntetett közös osztók a 17.5. Tétel 4. pontja miatt 1-gyel egyeznek meg. Minthogy az 1 egész szám egység (16.3. Definíció), így ezek az oszthatóságok nyilván teljesülnek, a tételben szereplő kongruenciarendszer tehát valóban megoldható.
Másodszor azt mutatjuk meg, hogy minden megoldás ugyanabból a modulo pq maradékosztályból származik. Legyen ezért x_1 és x_2 két tetszőleges egész, amelyek mindkét kongruenciát kielégítik. Azaz egyrészt:
\begin{aligned}x_1&\equiv a\pmod p \\ x_1&\equiv b\pmod q\end{aligned}Másrészt:
\begin{aligned}x_2&\equiv a\pmod p \\ x_2&\equiv b\pmod q\end{aligned}Ez a 20.2. Tétel 3. pontja alapján azt jelenti, hogy az x_1 és x_2 egész számok kongruensek egymással mindkét modulus szerint, azaz:
\begin{aligned}x_1&\equiv x_2\pmod p \\ x_1&\equiv x_2\pmod q\end{aligned}Ez a 20.1. Tétel 3. pontja alapján azt jelenti, hogy az x_1-x_2 különbség többszöröse p-nek is és q-nak is, azaz:
\begin{aligned}p&|x_1-x_2 \\ q&|x_1-x_2\end{aligned}Azaz x_1-x_2 prímtényezős felbontásában szerepel p és q összes prímtényezője, valamint esetlegesen egyéb prímtényezők is. Tegyük fel, hogy p és q prímtényezős felbontásai a következők:
\begin{aligned}p&=p_1p_2\ldots p_k \\ q&=q_1q_2\ldots q_n\end{aligned}Mivel p és q egymáshoz relatív prímek, ezért nincs két egyforma prímtényezőjük. Azaz p egyetlen prímtényezője sem szerepel q prímtényezői között, valamint q egyetlen prímtényezője sem szerepel p prímtényezői között. Így tehát az x_1-x_2 különbség így írható fel:
x_1-x_2=\underbrace{p_1p_2\ldots p_k}_{=p}\cdot \underbrace{q_1q_2\ldots q_n}_{=q}\cdot \underbrace{r_1r_2\ldots r_l}_{\text{egyéb}}Azt kaptuk tehát, hogy teljesül az alábbi oszthatóság:
pq|x_1-x_2Ez ismét a 20.1. Tétel 3. pontja alapján az alábbi kongruenciát jelenti:
x_1\equiv x_2\pmod{pq}Tehát valóban igaz, hogy bármely két, a tételben szereplő kongruenciarendszert kielégítő egész szám ugyanabba a modulo pq maradékosztályba esik.
Végül azt kell igazolni, hogy ennek a bizonyos maradékosztálynak minden eleme kielégíti a kongruenciarendszert. Tegyük fel ezért, hogy s egy olyan egész szám ebben a maradékosztályban, amelyre teljesül a kongruenciarendszer, azaz:
\begin{aligned}s&\equiv a\pmod p \\ s&\equiv b\pmod q\end{aligned}Tegyük fel ezenkívül indirekt, hogy létezik olyan t egész szám ugyanebben a maradékosztályban, amelyre viszont nem teljesül legalább az egyik a tételben szereplő kongruenciák közül. Mivel t ugyanabban a modulo pq maradékosztályban van, mint s, ezért igaz az alábbi:
s\equiv t\pmod{pq}Minthogy a p|pq valamint a q|pq oszthatóságok nyilvánvalóan teljesülnek, ezért a 20.2. Tétel 9. pontja miatt teljesülnek az alábbi kongruenciák is:
\begin{aligned}s&\equiv t\pmod p \\ s&\equiv t\pmod q\end{aligned}Azaz t egyrészt ugyanabba a modulo p maradékosztályba esik, mint s, vagyis a 20.8. Definíció utáni megjegyzés alapján ő megoldása az x\equiv a\pmod p kongruenciának. Másrészt ehhez hasonlóan t ugyanabba a modulo q maradékosztályba is esik, mint s, ezért ő megoldása az x\equiv b\pmod q kongruenciának is. Így tehát t mégiscsak megoldása a tételben szereplő kongruenciarendszernek, ami ellentmond az indirekt feltételezésünknek. Az [s]_{pq} maradékosztálynak tehát valóban minden eleme megoldás, ahogyan a tétel állítja.
∎Az előző szakaszban közölt példánál maradva keressük tehát két kongruenciarendszer megoldásait. Ezek az alábbiak:
\begin{array}{c} \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 6\pmod 8\end{aligned}} \\ \\ \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 2\pmod 8\end{aligned}} \end{array}Az első kongruenciarendszer megoldáshalmaza a [4]_5 és a [6]_8 maradékosztályok közös része, azaz metszete lesz. Mivel az 5 és a 8 modulusok egymáshoz relatív prímek, ezért alkalmazhatjuk a kínai maradéktételt. Eszerint a keresett halmaz épp egy modulo 5\cdot 8=40 maradékosztály lesz. Ellenőrizzük is le, azaz írjuk fel egymás alá a [4]_5 és a [6]_8 maradékosztályokat, és keretezzük be a közös elemeiket:
\begin{aligned}[4]_5&=\{\ldots; 4;9;\boxed{14};19;24;29;34;39;44;49;\boxed{54};59;\ldots\} \\ [6]_8&=\{\ldots; 6;\boxed{14};22;30;38;46;\boxed{54};62;\ldots\} \end{aligned}Látható, hogy a felső sorban az elemek – modulo 5 maradékosztályról lévén szó – 5-ösével követik egymást, és minden 8-adik elem lett bekeretezve. Ezzel szemben az alsó sorban az elemek – modulo 8 maradékosztályról lévén szó – 8-asával követik egymást, és minden 5-ödik elem lett bekeretezve. Ha tehát kigyűjtjük a bekeretezett elemeket egy halmazba, akkor azok épp 40-esével fogják egymást követni, tehát ők valóban egy modulo 40 maradékosztályt alakotnak, méghozzá a következőt:
[14]_{40}=\{\ldots; 14;54;94;134;174;214;\ldots\}Ezek – és a kínai maradéktétel alapján csak ezek – az egész számok elégítik ki tehát az első kongruenciarendszert.
A második kongruenciarendszer esetén a [4]_5 és a [2]_8 maradékosztályok metszetét keressük. Ezt az előzőhöz hasonló módszerrel kaphatjuk meg:
\begin{aligned}[4]_5&=\{\ldots; 4;9;14;19;24;29;\boxed{34};39;44;49;54;59;64;69;\boxed{74};\ldots\} \\ [2]_8&=\{\ldots; 2;10;18;26;\boxed{34};42;50;58;66;\boxed{74};\ldots\} \end{aligned}Ha ismét kigyűjtjük a bekeretezett elemeket egy halmazba, akkor azok szintén 40-esével fogják egymást követni, tehát ők ugyancsak egy modulo 40 maradékosztályt alakotnak, méghozzá a következőt:
[34]_{40}=\{\ldots; 34;74;114;154;194;234;\ldots\}Az alábbiakban összefoglaltuk a két kongruenciarendszer megoldását, amely tehát egy-egy modulo 40 maradékosztály:
\begin{array}{ccc} \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 6\pmod 8\end{aligned}} & \to & [14]_{40} \\ \\ \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 2\pmod 8\end{aligned}} & \to & [34]_{40} \end{array}Kongruenciarendszerek megoldása
Most megmutatjuk, hogy ez a „bekeretezős” módszer mindig működik, és eljárást is adunk a keresett maradékosztály kiszámítására. Tulajdonképpen az a feladat, hogy adva van egy modulo p maradékosztályból (jelöljük ezt A-val) és egy modulo q maradékosztályból (jelöljük ezt B-vel) álló úgynevezett „rendezett pár”, ahol p és q egymáshoz relatív prímek. A feladat megtalálni azt az X-szel jelölt halmazt, amely épp a megadott két maradékosztály metszetével egyezik meg:
X=A\cap BA kínai maradéktétel tehát azt állítja, hogy amennyiben p és q egymáshoz relatív prímek, akkor az X-szel jelölt halmaz éppenséggel egy modulo pq maradékosztály lesz. Hamarosan látni fogjuk, hogy ennél jóval több is igaz.
Ehhez először ismételjük át a „rendezett pár” fogalmát, amelyről néhány korábbi részben már volt szó. Elsőként a kétváltozós művelet fogalmának bevezetésekor találkoztunk vele a 11. részben. Ezt a fogalmat a 11.3. Definícióban egy olyan függvényként definiáltuk, amely egy valamilyen H halmaz elemeiből alkotott párokhoz a H halmaz elemeit rendeli hozzá. Például az egész számok \Z halmazán értelmezett szokásos összeadás művelet, mint függvény a (3;2) rendezett párhoz az 5 egész számot rendeli hozzá.
Másodszor a 12. részben definiált kétváltozós reláció kapcsán került elő ez a fogalom. Egy szintén valamilyen H halmazon értelmezett kétváltozós relációt a 12.7. Definícióban a H elemeiből alkotott párok halmazának egy részhalmazaként definiáltuk. Azt mondtuk, hogy egy R reláció akkor áll fenn két H-beli a és b elem között, ha az (a;b) rendezett pár eleme az R halmaznak. Például a \Z halmazon értelmezett \leq relációnak, mint halmaznak eleme a (2;3) rendezett pár – hiszen 2\leq 3 –, de nem eleme a (3;2) rendezett pár – hiszen 3\nleq 2.
Végül a 13. részben magukat az egész számokat is a természetes számok \N halmazának elemeiből alkotott rendezett párok segítségével definiáltuk.
A felsorolt példákban egyrészt PÁRokról, azaz kétkomponensű objektumokról volt szó, másrészt pedig a PÁR két komponense ugyanabból a halmazból került ki. Egy ennél általánosabb fogalomhoz jutunk, ha ezeket a megszorításokat elhagyjuk.
22.3. Definíció (Halmazok direkt szorzata):
Legyenek A és B tetszőleges halmazok. Ekkor az A és B halmazok direkt szorzatának (vagy Descartes-szorzatának) nevezzük azt a halmazt, amely az összes olyan rendezett párt tartalmazza, amelynek első komponense valamilyen A-beli, második komponense pedig valamilyen B-beli elem. Ezt a halmazt A\times B-vel jelöljük (ejtsd: „A kereszt B”). Speciálisan ha a két halmaz azonos, akkor A\times A helyett az A^2 jelölést is használhatjuk. Ha a\in A és b\in B, akkor az a-ból és b-ből álló rendezett párt (a;b)-vel jelöljük.
Általánosabban legyenek A_1, A_2, ..., A_n tetszőleges halmazok. Ekkor ezen halmazok direkt szorzatának (vagy Descartes-szorzatának) nevezzük azt a halmazt, amely az összes olyan rendezett n-est tartalmazza, amelynek első komponense valamilyen A_1-beli, második komponense valamilyen A_2-beli, ..., n-edik komponense pedig valamilyen A_n-beli elem. Ezt a halmazt így jelöljük:
A_1\times A_2\times \ldots \times A_nTegyük fel, hogy a_1\in A_1, a_2\in A_2, ..., a_n\in A_n. Ekkor az ezekből az elemekből álló rendezett n-est így jelöljük:
(a_1;a_2;\ldots;a_n) ♣Egy kézenfekvő példa direkt szorzatra a sík pontjainak halmaza. Ezeket általában egy derékszögű koordinátarendszerben szoktuk ábrázolni. Ilyenkor felrajzolunk két egymásra merőleges számegyenest, amelyek a 0-nál metszik egymást. Ezek után egy síkbeli pontot egy számpárral írhatunk le, amelynek komponenseit a pont koordinátáinak nevezzük. Az első koordináta azt adja meg, hogy a két számegyenes metszéspontjából kiindulva mennyit kell haladni az első – általában vízszintes – számegyenes mentén, míg a második koordináta azt adja meg, hogy innen mennyit kell továbbhaladni a másik – általában függőleges számegyenes irányával párhuzamosan. Ezt mutatja az alábbi ábra:
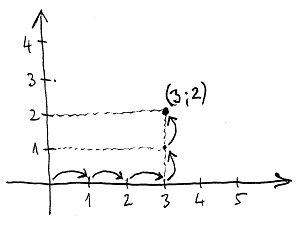
A számegyenes pontjainak halmazát \R-rel szoktuk jelölni, a sík pontjainak halmaza pedig ennek megfelelően az \R\times \R, vagy másként az \R^2 direkt szorzat lesz. Ehhez hasonlóan a 3, 4, …, n dimenziós tér pontjainak halmazát \R^3, \R^4, …, \R^n jelöli.
Egy másik kézenfekvő példa direkt szorzatra az 52 lapos franciakártya. Egy ilyen pakliban minden kártyalapnak van valamilyen „színe” (angolul „suit”) és „értéke” (angolul „rank”). Jelöljük a lehetséges színek halmazát S-sel, a lehetséges értékek halmazát pedig R-rel:
\begin{aligned}S&=\{\clubs;\diamonds;\spades;\hearts\} \\ R&=\{2;3;4;5;6;7;8;9;10;\text{J};\text{Q};\text{K};\text{A}\}\end{aligned}Mivel a kártyapakliban lévő lapok minden lehetséges színt és értéket felvehetnek, ezért e lapok halmaza tulajdonképpen az S\times R direkt szorzat lesz. Ekkor egy kártyalapot egy olyan rendezett pár reprezentál, amelynek első komponense az S, a második komponense pedig az R halmaz eleme. Például a „treff hetest” reprezentáló rendezett pár a (\clubs;7) lesz.
Most vonatkoztassuk a direkt szorzat fogalmát a kínai maradéktétel állítására. A szakasz elején szereplő A-ból és B-ből álló rendezett pár első komponense tehát a modulo p, míg a második komponense a modulo q maradékosztálygyűrű eleme. Maga az (A;B) rendezett pár tehát eleme e két maradékosztálygyűrű direkt szorzatának. Azaz a 20.5. Tételben szereplő és a most bevezetett jelölésekkel:
\begin{aligned}A &\in \Z/p\Z \\ B &\in \Z/q\Z \\ (A;B) &\in \Z/p\Z \times \Z/q\Z\end{aligned}Ezek után az alábbi tételben megadjuk a kínai maradéktétel egy alternatív megfogalmazását, valamint egy eljárást is mutatunk a tételben szereplő A\cap B halmaz előllítására:
22.4. Tétel (A kínai maradéktétel alternatív megfogalmazása):
Legyenek p\gt 0 és q\gt 0 valamilyen pozitív egész számok, továbbá tegyük fel, hogy p és q egymáshoz relatív prímek. Ekkor minden (A;B)\in \Z/p\Z \times \Z/q\Z rendezett pár esetén A\cap B\in \Z/pq\Z.
Tegyük fel, hogy az x_1 és x_2 egész számok kielégítik az alábbi kongruenciákat:
\begin{aligned}p\cdot x_1&\equiv 1\pmod q \\ q\cdot x_2&\equiv 1\pmod p\end{aligned}Amennyiben az A és B maradékosztályokat rendre valamilyen a és b egész számokkal reprezentáljuk – azaz A=[a]_p és B=[b]_q –, akkor az alábbi képlet az A\cap B maradékosztály egy reprezentánselemét szolgáltatja:
A\cap B=[a\cdot q\cdot x_2 + b\cdot p\cdot x_1]_{pq} ♣Bizonyítás:
Az A=[a]_p és B=[b]_q maradékosztályok metszete pontosan azokat az egész számokat fogja tartalmazni, amelyek mindkét maradékosztályban benne vannak. Ezek az alábbi kongruenciarendszert kielégítő egész számok lesznek:
\begin{aligned}x&\equiv a\pmod p \\ x&\equiv b\pmod q\end{aligned}A kínai maradéktétel (22.2. Tétel) alapján ezek az egész számok pontosan egy modulo pq maradékosztályt alkotnak, azaz valóban A\cap B\in \Z/pq\Z.
Most igazoljuk, hogy a tételben megadott képlet valóban az A\cap B maradékosztály egy reprezentánselemét adja. Ehhez azt kell megmutatni, hogy az aqx_2 + bpx_1 egész szám benne van ebben a halmazban. A halmazműveletekről szóló 19.3. Definíció alapján ez pontosan akkor teljesül, ha teljesül az alábbi két feltétel:
\begin{aligned}aqx_2 + bpx_1 &\in A \\ aqx_2 + bpx_1 &\in B\end{aligned}Nézzük először az első feltételt! Mivel az A halmaz egy modulo p maradékosztály, amelynek az a egész szám egy reprezentánsa, ezért ez a feltétel pontosan akkor teljesül, ha fennáll az alábbi kongruencia:
aqx_2 + bpx_1 \equiv a\pmod pA kongruencia baloldalán szereplő összeg második, bpx_1 tagja ugye p-nek többszöröse, így ő 0-val kongruens modulo p. Az összeg első, aqx_2 tagjában viszont a qx_2 tényező a tétel szövege alapján 1-gyel, és így ez a tag a-val kongruens modulo p. Összefoglalva tehát valóban teljesül a fenti kongruencia:
a\cdot \underbrace{qx_2}_{\equiv 1} + \underbrace{bpx_1}_{\equiv 0} \equiv a\pmod pMost nézzük a második feltételt! Mivel a B halmaz egy modulo q maradékosztály, amelynek a b egész szám egy reprezentánsa, ezért ez a feltétel pontosan akkor teljesül, ha fennáll az alábbi kongruencia:
aqx_2 + bpx_1 \equiv b\pmod qA kongruencia baloldalán szereplő összeg első, aqx_2 tagja ugye q-nek többszöröse, így ő 0-val kongruens modulo q. Az összeg második, bpx_1 tagjában viszont a px_1 tényező a tétel szövege alapján 1-gyel, és így ez a tag b-vel kongruens modulo q. Összefoglalva tehát valóban teljesül a fenti kongruencia:
\underbrace{aqx_2}_{\equiv 0} + b\cdot \underbrace{px_1}_{\equiv 1} \equiv b\pmod qA aqx_2 + bpx_1 összeg tehát benne van az A\cap B metszetben, amely – mint láttuk – egy modulo pq maradékosztály, és így valóban annak egy reprezentánselemét adja.
∎Megjegyzés:
A tételben szereplő p\cdot x_1\equiv 1\pmod q és q\cdot x_2\equiv 1\pmod p kongruenciáknak a 20.12. Tétel alapján létezik megoldása, hiszen p és q a tétel szövege alapján relatív prímek. Ugyanezen okból a 20.13. Tétel 1. pontja miatt a megoldás mindkét kongruencia esetén egy-egy maradékosztály lesz. Ezek megtalálásához a 20.12. Tétel alapján az alábbi lineáris diofantoszi egyenleteket kell megoldani:
\begin{aligned}px_1+qy_1&=1 \\ qx_2+py_2&=1\end{aligned}Ezeket a 21.2. Tétel 1. pontja alapján a 21.1. Tétel bizonyításában ismertetett kibővített euklidészi algoritmus segítségével tehetjük meg.
Azaz valóban egy eljárást kaptunk az A\cap B maradékosztály egy reprezentánselemének meghatározásához.
♣Most térjünk vissza az előző szakaszban szereplő példára, amelynek során a „bekeretezős” módszerrel az alábbi két kongruenciarendszer megoldását kerestük meg:
\begin{array}{ccc} \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 6\pmod 8\end{aligned}} & \to & [14]_{40} \\ \\ \boxed{\begin{aligned}x&\equiv 4\pmod 5 \\ x&\equiv 2\pmod 8\end{aligned}} & \to & [34]_{40} \end{array}Az első rendszernek tehát a [14]_{40}, a másodiknak pedig a [34]_{40} maradékosztály volt a megoldása. Ez a módszer azonban a gyakorlatban nem használható, így most próbáljuk meg megtalálni a megoldásokat a 22.4. Tételben ismertetett eljárás segítségével.
Az első kongruenciarendszer esetén keressük tehát az A=[4]_5 és a B=[6]_8 maradékosztályok metszetét. Ehhez a tétel szerint kell keresnünk olyan x_1 és x_2 egész számokat, amelyek kielégítik az alábbi kongruenciákat:
\begin{aligned}5\cdot x_1&\equiv 1\pmod 8 \\ 8\cdot x_2&\equiv 1\pmod 5\end{aligned}Ezeket az előző részben ismertetett kibővített euklidészi algoritmussal megoldva például az alábbi számokat választhatjuk x_1-nek és x_2-nek:
\begin{aligned}x_1&=5 \\ x_2&=2\end{aligned}Ezután a tételben szereplő képletet alkalmazva az A\cap B maradékosztály alábbi reprezentánselemét kapjuk:
4\cdot 8\cdot 2 + 6\cdot 5\cdot 5=64+150=214Valóban, az eredményül kapott 214 egész szám benne van a [14]_{40} maradékosztályban, amelyet a „bekeretezős” módszerrel kaptunk az első kongruenciarendszerre az előző szakaszban.
Most nézzük meg a második kongruenciarendszert. Ebben az esetben az A=[4]_5 és a B=[2]_8 maradékosztályok metszetét keressük. Az előző példánál már megkaptuk az 5\cdot x_1\equiv 1\pmod 8 és a 8\cdot x_2\equiv 1\pmod 5 kongruenciák megoldásait, így azokat most is használhatjuk. A tételben szereplő képletet alkalmazva most az alábbi reprezentánselemét kapjuk meg az A\cap B halmaznak:
4\cdot 8\cdot 2 + 2\cdot 5\cdot 5=64+50=114Valóban, az eredményül kapott 114 egész szám benne van a [34]_{40} maradékosztályban, amelyet a „bekeretezős” módszerrel kaptunk a második kongruenciarendszerre az előző szakaszban.
A most tanult eljárás tehát tulajdonképpen egy függvényt valósít meg, amely a \Z/p\Z \times \Z/q\Z halmazt képezi le a \Z/pq\Z halmazra, méghozzá minden maradékosztálypárt e párban szereplő maradékosztályok metszetére. Kérdés, hogy vajon ez a leképezés bijektív-e, azaz vajon minden modulo pq maradékosztály pontosan egy \Z/p\Z \times \Z/q\Z-beli maradékosztálypárnak a metszete-e? Az alábbi ábrák mutatják, hogy mi lenne a helyzet nemleges és igenlő válasz esetén:
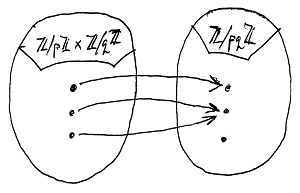
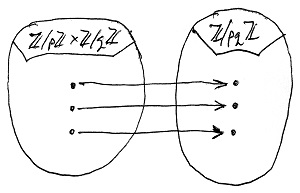
Most igazoljuk, hogy az utóbbi a helyzet. Hamarosan kiderül, hogy ez miért olyan fontos.
22.5. Tétel:
Legyenek p\gt 0 és q\gt 0 valamilyen pozitív egész számok, továbbá tegyük fel, hogy p és q egymáshoz relatív prímek. Ekkor minden X\in \Z/pq\Z maradékosztályhoz pontosan egy olyan (A;B)\in \Z/p\Z\times \Z/q\Z maradékosztálypár létezik, amelynek X a metszete, azaz amelyre teljesül az alábbi:
X=A\cap BAmennyiben az X maradékosztályt egy valamilyen s egész számmal reprezentáljuk – azaz X=[s]_{pq} –, akkor s egyúttal a keresett A és B maradékosztályok reprezentánseleme is:
\begin{aligned}A&=[s]_p \\ B&=[s]_q\end{aligned} ♣Bizonyítás:
A tétel bizonyításához az alábbi két állítást kell igazolni:
- Az X maradékosztály valóban az (A;B)\in \Z/p\Z\times \Z/q\Z maradékosztálypár metszete, azaz X=A\cap B.
- Nincs másik olyan maradékosztálypár a \Z/p\Z\times \Z/q\Z halmazban, amelynek X a metszete lenne.
Az 1. állítás: A 19.2. Definíció utáni megjegyzés 5. pontja alapján X és A\cap B akkor és csak akkor egyezik meg, ha egymásnak részhalmazai, azaz teljesülnek az alábbiak:
\begin{aligned}X&\sube A\cap B \\ A\cap B &\sube X\end{aligned}Az X\sube A\cap B tartalmazási reláció a 19.2. Definíció alapján azt jelenti, hogy az X=[s]_{pq} maradékosztály minden eleme egyúttal az A=[s]_p-nek is és B=[s]_q-nak is eleme.
Legyen például t\in X egy tetszőleges elem az X=[s]_{pq} maradékosztályban. Ezt úgy is megfogalmazhatjuk, hogy t ugyanúgy az X maradékosztályt reprezentálja, mint s. Azaz [s]_{pq}=[t]_{pq}, ami ugye az alábbi kongruenciát jelenti:
s\equiv t\pmod{pq}Mivel azonban a p|pq és q|pq oszthatóságok nyilvánvalóan teljesülnek, ezért a 20.2. Tétel 9. pontja miatt teljesülnek az alábbi kongruenciák is:
\begin{aligned}s&\equiv t\pmod p \\ s&\equiv t\pmod q\end{aligned}Tehát t benne van az A=[s]_p és B=[s]_q maradékosztályokban, azaz valóban teljesül az X\sube A\cap B tartalmazási reláció.
Most az A\cap B\sube X tartalmazási relációt igazoljuk. Ez a 19.2. Definíció alapján azt jelenti, hogy az A=[s]_p és B=[s]_q maradékosztályok közös elemei egyúttal az X=[s]_{pq} maradékosztálynak is elemei.
Legyen például t\in A\cap B egy tetszőleges elem az A=[s]_p és B=[s]_q maradékosztályok metszetében. Ezt úgy is megfogalmazhatjuk, hogy t ugyanúgy benne van mind az A, mind pedig a B maradékosztályokban, mint s.
Az A=[s]_p maradékosztályba pontosan azok az egész számok tartoznak bele, amelyeket az alábbi kongruenciába az x ismeretlen helyére behelyettesítve a kongruencia teljesül:
x\equiv s\pmod pEhhez hasonlóan a B=[s]_q maradékosztályba pontosan azok az egész számok tartoznak bele, amelyeket az alábbi kongruenciába az x ismeretlen helyére behelyettesítve a kongruencia teljesül:
x\equiv s\pmod qA fentebb említett t tehát s-sel karöltve kielégíti az iménti két kongruenciából álló rendszert. Ám a kínai maradéktétel (22.2. Tétel) állítása szerint minden ilyen tulajdonságú egész szám ugyanabba az egyetlen modulo pq maradékosztályba esik. Az nyilvánvaló, hogy s\in X, hiszen a tétel szövege alapján ő épp az X maradékosztály reprezentánseleme. Következésképp t is szükségképpen X-ben van, azaz valóban teljesül az A\cap B\sube X tartalmazási reláció.
Mivel mindkét irányú tartalmazási reláció teljesül X és A\cap B között, ezért a két halmaz az 1. állításnak megfelelően megegyezik.
A 2. állítás: Tegyük fel indirekt, hogy létezik egy (A;B)-től különböző (C;D) maradékosztálypár a \Z/p\Z\times \Z/q\Z halmazban, amelynek X a metszete, azaz:
C\cap D=XTegyük fel továbbá, hogy a C maradékosztályt a c egész számmal, míg a D maradékosztályt a d egész számmal reprezentáljuk, azaz:
\begin{aligned}C&=[c]_p \\ D&=[d]_q\end{aligned}Legyen t egy tetszőleges elem az X=[s]_{pq} maradékosztályban. Egyrészt a fentebb egyszer már leírt gondolatmenetet megismételve ez az alábbi kongruenciákat jelenti:
\begin{aligned}s&\equiv t\pmod p \\ s&\equiv t\pmod q\end{aligned}Másrészt viszont az indirekt feltételezésünk miatt X a C=[c]_p és D=[d]_q maradékosztályok metszete. Emiatt t ugyanúgy benne van a C=[c]_p maradékosztályban, mint c, valamint ugyanúgy benne van a D=[d]_q maradékosztályban, mint d. Teljesülnek tehát az alábbi kongruenciák:
\begin{aligned}t&\equiv c\pmod p \\ t&\equiv d\pmod q\end{aligned}A kongruencia tranzitivitása miatt (20.2. Tétel 3. pontja) teljesülnek tehát az alábbi kongruenciák is:
\begin{aligned}s&\equiv c\pmod p \\ s&\equiv d\pmod q\end{aligned}Azaz egyrészt az s által reprezentált modulo p maradékosztály (ez ugye az A halmaz) megegyezik a c által reprezentált modulo p maradékosztállyal (ez pedig ugye a C halmaz). Másrészt az s által reprezentált modulo q maradékosztály (ez ugye a B halmaz) megegyezik a d által reprezentált modulo q maradékosztállyal (ez pedig ugye a D halmaz).
Minthogy A=C és B=D, ezért indirekt feltételezésünkkel ellentétben az (A;B) maradékosztálypár mégiscsak megegyezik a (C;D) maradékosztálypárral. Azaz a 2. állításnak megfelelően az (A;B) páron kívül nincs másik olyan maradékosztálypár a \Z/p\Z\times \Z/q\Z halmazban, amelynek X a metszete lenne.
∎Ez azt bizonyítja, hogy a \Z/p\Z \times \Z/q\Z és a \Z/pq\Z halmazok közötti függvény egy kölcsönösen egyértelmű leképezés. Ha úgy tetszik egy kétirányú híd képezhető a két halmaz között. Ez azt jelenti, hogy az egyik halmazban lévő bármely elemnek egyértelműen megvan a párja a másik halmazban és viszont. A \Z/p\Z \times \Z/q\Z halmazból a \Z/pq\Z halmazba a 22.4. Tétel, visszafelé pedig a 22.5. Tétel biztosítja ezt a fajta átjárást.
Például egyrészt a \Z/5\Z\times \Z/8\Z halmazban lévő ([4]_5;[6]_8) maradékosztálypárnak a [14]_{40} maradékosztály, míg a ([4]_5;[2]_8) párnak a [34]_{40} maradékosztály a megfelelője a \Z/40\Z halmazban. Másrészt pedig biztosak lehetünk benne, hogy a [14]_{40} és a [34]_{40} maradékosztályok csakis ezekhez a párokhoz vannak ilymódon hozzárendelve.
Az RSA-algoritmus helyes működésének bizonyítása
Az előző részben megismertük napjaink egyik legfontosabb felfedezését, az RSA nevű aszimmetrikus kulcsú rejtjelezési eljárást. Ebben a szakaszban törlesztjük végre az adósságunkat, és igazolni fogjuk, hogy az RSA valóban mindig helyesen működik. Ezért most ismételjük át röviden, hogyan is történik a kulcsok generálása, majd az üzenetek titkosítása és dekódolása.
Az RSA biztonsága a nagy számok prímtényezős felbontásának algoritmikus nehézségén alapul. Egy kulcspár generálásához ezért először is választani kell két egymástól különböző óriási prímszámot – jelöljük ezeket p-vel és q-val –, majd képezni kell ezek szorzatából az m=pq modulust, és ki kell számítani a \varphi(m) értéket (20.7. Definíció). Ezután választunk egy tetszőleges \varphi(m)-hez relatív prím e számot a \Z_{\varphi(m)} gyűrűből, amely a kulcspár publikus része lesz, és kiszámítjuk e multiplikatív inverzét ebben a gyűrűben. Az így kapott d szám lesz a kulcspár titkos része. A publikus és titkos kulcsok közötti számelméleti kapcsolatot tehát a \Z_{\varphi(m)} gyűrű jelenti, amely gyűrű ismeretlen marad a támadó számára. Ennek oka, hogy \varphi(m) értéke jelenlegi számelméleti ismereteink szerint csak m prímtényezőinek ismeretében számítható ki hatékonyan.
Ezután részletesen leírtuk, és egy példával szemléltettük, hogyan történik egy üzenet titkosítása az adó, és dekódolása a vételi oldalon. Ehhez az elküldeni kívánt üzenetet valamilyen szabványos módon a \Z_m gyűrű elemeinek sorozatává kell alakítani, majd a sorozat tagjaira külön-külön kell alkalmazni a kódoló és dekódoló függvényeket. Legyen az üzenetet leíró számsorozat következő tagja x. Ennek titkosítása az alábbi \Z_m-beli moduláris hatványozás elvégzését jelenti:
y=x^eAz így képzett y szám nyugodtan átküldhető a kommunikációs csatornán. Ebből ugyanis csak a d titkos kulcs ismeretében állítható vissza „varázslatos módon” az eredeti x üzenet. Ehhez az alábbi, szintén \Z_m-beli moduláris hatványozást kell elvégezni:
x=y^dMost igazolni fogjuk, hogy ez a „varázslat” tényleg mindig teljesül. Az y helyére behelyettesíthetjük az őt képző, kódolófüggvény szerinti kifejezést. Ekkor az alábbit kapjuk:
x=({\underbrace{x^e}_{=y}})^d=x^{ed}A 20. részben láthattuk, hogy a \Z_m gyűrű izomorf a \Z/m\Z maradékosztálygyűrűvel. Így tehát a fenti kifejezést tulajdonképpen úgy is értelmezhetjük, hogy az x egész számnak ugyanabba az m modulus szerinti maradékosztályba kell esnie, mint az x^{ed} egész számnak. Ez az alábbi kongruencia teljesülését jelenti:
x\equiv x^{ed}\pmod mMost igazolni fogjuk, hogy ez a kongruencia valóban teljesül tetszőleges, a megadott kritériumoknak megfelelő e, d, m és x egész számokra.
22.6. Tétel (Az RSA algoritmus helyes működése):
Tegyük fel, hogy teljesülnek az alábbi feltételek:
- Legyen adott két tetszőleges, egymástól különböző pozitív prímszám: p és q.
- Képezzük ezekből az m=p\cdot q modulust.
- Képezzük az Euler-féle \varphi-függvény értékét az m modulusra, azaz kiszámítjuk a \varphi(m)=(p-1)\cdot (q-1) egész számot (erre vonatkozóan lásd a 21.3. Tételt és a 21.5. Tételt).
- Legyen adott egy tetszőleges e egész szám, amely relatív prím \varphi(m)-hez.
- Keressünk egy olyan d egész számot, amelyre teljesül az alábbi kongruencia:
Ekkor tetszőleges x egész szám esetén teljesül az alábbi kongruencia is:
x^{e\cdot d}\equiv x\pmod m ♣Bizonyítás:
Mivel teljesül az e\cdot d\equiv 1\pmod{\varphi(m)} kongruencia, ezért a 20.1. Tétel 3. pontja alapján teljesül az alábbi oszthatóság:
\varphi(m)|e\cdot d-1Az oszthatóság 16.1. Definíciója alapján ekkor létezik olyan k egész szám, amelyre teljesül az alábbi egyenlet:
k\cdot \varphi(m)=e\cdot d-1Mindkét oldalhoz 1-et adva:
k\cdot \varphi(m) + 1=e\cdot dAzt kell tehát bizonyítani, hogy tetszőleges x esetén teljesül az alábbi kongruencia:
x^{\overbrace{k\cdot \varphi(m)+1}^{=ed}}\equiv x\pmod mItt két eset lehetséges. Az első (és legvalószínűbb) esetben x relatív prím m-hez. Ekkor közvetlenül alkalmazható az Euler-Fermat tétel (20.19. Tétel). Ehhez alakítsuk át a kongruencia baloldalán álló kifejezést a 18.8. Tétel 2. és 3. pontjának megfelelően:
(x^{\varphi(m)})^k\cdot x\equiv x\pmod mAz Euler-Fermat tétel miatt az x^{\varphi(m)} kifejezés 1-gyel kongruens modulo m. Így a 20.2. Tétel 5. és 8. pontja alapján a fenti kongruencia egyszerűsíthető:
\underbrace{1^k\cdot x}_{=x}\equiv x\pmod mEz a kongruencia viszont nyilvánvalóan teljesül a 20.2. Tétel 1. pontja alapján.
Most nézzük meg, hogy mi a helyzet abban a nem túl gyakori esetben, ha x NEM relatív prím m-hez, azaz x-nek és m-nek van egységtől különböző közös osztója. Mivel az m=pq modulusnak csak két prímtényezője van (p és q), ezért ez csak az alábbi három esetben fordulhat elő:
1. eset: Az x többszöröse p-nek is és q-nak is, azaz magának az m=pq modulusnak. Ilyenkor tehát teljesül az alábbi kongruencia:
x\equiv 0\pmod mEkkor a 20.2. Tétel 8. pontja alapján mindkét oldalt a k\cdot \varphi(m)+1-edik hatványra emelve teljesül az alábbi kongruencia is:
x^{k\cdot \varphi(m)+1}\equiv 0\pmod mA két kongruenciát összevetve a 20.2. Tétel 2. és 3. pontjai alapján valóban teljesül a tétel állítása, azaz:
x^{k\cdot \varphi(m)+1}\equiv x\pmod m2. eset: Az x többszöröse p-nek, de nem többszöröse q-nak. Azaz teljesül a p|x oszthatóság, de nem teljesül a q|x oszthatóság. Ebben az esetben a 21.4. Lemma alapján x relatív prím q-hoz. Mivel \varphi(m)=(p-1)\cdot (q-1), ezért teljesül az alábbi:
x^{k\cdot \varphi(m) +1}=x^{k\cdot \overbrace{(p-1)\cdot (q-1)}^{=\varphi(m)} + 1}Felhasználva a hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontját, ez a hatványkifejezés az alábbi alakba írható:
(x^{q-1})^{k\cdot (p-1)}\cdot xMivel x relatív prím q-hoz, ezért a kis Fermat-tétel (22.1. Tétel) miatt teljesül az alábbi kongruencia:
x^{q-1}\equiv 1\pmod qA 20.2. Tétel 8. pontja alapján mindkét oldalt a k\cdot (p-1)-edik hatványra emelve továbbra is érvényes kongruenciát kapunk:
(x^{q-1})^{k\cdot (p-1)}\equiv 1\pmod qÍgy tehát a x^{k\cdot \varphi(m) +1} = (x^{q-1})^{k\cdot (p-1)}\cdot x kifejezésre teljesül az alábbi kongruencia:
x^{k\cdot \varphi(m) +1}\equiv x\pmod qTovábbá nyilván teljesül az alábbi kongruencia is, mivel x többszöröse p-nek, és így mindkét oldal 0-val kongruens modulo p:
x^{k\cdot \varphi(m) +1}\equiv x\pmod p3. eset: Az x többszöröse q-nak, de nem többszöröse p-nek. Azaz teljesül a q|x oszthatóság, de nem teljesül a p|x oszthatóság. Ebben az esetben az x egész szám q helyett p-hez lesz relatív prím. Ekkor az előző gondolatmenet szinte szóról szóra megismételhető, pusztán a p és q szerepét kell felcserélni.
Mivel ed=k\cdot \varphi(m)+1, ezért a 2. és 3. esetben is tulajdonképpen azt kaptuk, hogy teljesül az alábbi két kongruencia:
\begin{aligned}x^{ed}&\equiv x\pmod p \\ x^{ed}&\equiv x\pmod q\end{aligned}Ez a \Z/p\Z és a \Z/q\Z maradékosztálygyűrűkben az alábbiakat jelenti:
\begin{aligned}[x^{ed}]_p &= [x]_p \\ [x^{ed}]_q &= [x]_q\end{aligned}Ennek megfelelően ezt így írhatjuk fel a \Z/p\Z \times \Z/q\Z direkt szorzat egy elemeként:
([x^{ed}]_p; [x^{ed}]_q) = ([x]_p; [x]_q)A 22.4. Tétel és a 22.5. Tétel alapján azonban tudjuk, hogy a \Z/p\Z \times \Z/q\Z elemei kölcsönösen egyértelműen megfeleltethetők a \Z/pq\Z maradékosztálygyűrű elemeivel. Ez a leképezés a fenti egyenlet bal és jobboldalához a 22.5. Tételben szereplő képlet alapján az alábbiakat rendeli hozzá:
\begin{aligned}([x^{ed}]_p; [x^{ed}]_q) &\to [x^{ed}]_{pq} \\ ([x]_p; [x]_q) &\to [x]_{pq}\end{aligned}Mármost ha itt a nyilak baloldalán álló objektumok megegyeznek, akkor a leképezés kölcsönösen egyértelműsége miatt a nyilak jobboldalán álló objektumok is meg kell egyezzenek, azaz:
[x^{ed}]_{pq}=[x]_{pq}Ugyanezt kongruenciával megfogalmazva megkapjuk a tétel állítását:
x^{ed}\equiv x\pmod{\underbrace{pq}_{=m}} ∎Maradékosztálygyűrűk dekompozíciója
Az RSA-algoritmussal főként az a probléma, hogy szimmetrikus kulcsú társaihoz képest relatíve lassú. Ezt elsősorban a moduláris hatványozás okozza. Ez némileg ellentmond annak, amit az előző részben állapítottunk meg erről a műveletről. Akkor ugyanis azt mondtuk, hogy az ismételt négyzetreemelések módszerével rendkívül gyorsan elvégezhető a moduláris hatványozás. Ez algoritmuselméleti értelemben valóban így van, hiszen láttuk, hogy az elvégzendő moduláris szorzások száma legfeljebb a kitevő bináris számjegyei számának a kétszerese lehet. Márpedig egy ilyen jellegű skálázódás a 7. részben leírtak fényében bőven hatékony algoritmusnak tekinthető.
Igenám, csakhogy hiába a megfelelő skálázódás, amennyiben eleve nagyméretű bemenetekről van szó. A gyakorlatban ugyanis több ezer bites számokon kell több ezer moduláris szorzást elvégezni. Az ismételt négyzetreemelések módszerét vizsgálva megállapítottuk, hogy a szükséges moduláris szorzások száma attól függ, hogy a kitevő bináris számábrázolásában hány 1-es bit szerepel. Az RSA esetén a publikus kulcsban szereplő, kódoláshoz használt e kitevő megválasztásától nem függ az eljárás biztonsága. Emiatt általában olyan publikus e kitevőt választanak a kulcsgeneráláskor, amelyben minimális számú 1-es számjegy van. Célszerű például valamilyen 2-hatványnál 1-gyel nagyobb számot választani, hiszen ebben az esetben csak az első és az utolsó számjegy nem 0. Következésképp a kódoláskor elvégzendő moduláris hatványozás mindössze egy-két moduláris szorzásból megúszható.
A probléma érezhetően a dekódoláskor, vagy digitális aláírások képzésekor jön elő, amikor is a titkos d kitevőt kell használni. Ez ugyanis az e publikus kitevő multiplikatív inverze a \Z_{\varphi(m)} gyűrűben. Itt m ugye a kulcsgeneráláskor véletlenszerűen választott p és q prímszámok szorzata. Mivel emiatt a \varphi(m) is gyakorlatilag véletlenszerű lesz, ezért nemigazán lehet szabályozni, hogy a \Z_{\varphi(m)} gyűrűben az e multiplikatív inverzének éppenséggel milyen számjegyei lesznek. Emiatt pedig a fogadó oldal által elvégzendő RSA-dekódolás általában sokkal lassabb művelet, mint a küldő által elvégzett kódolás.
Ezért most a kínai maradéktétel egy nagyon praktikus alkalmazását mutatjuk be, amelynek a segítségével Alice és Bob a nekik küldött üzenetek dekódolását az előző részben leírtakhoz képest sokkal gyorsabban is el tudja végezni. Ehhez a kulcspár generálásakor választott titkos p és q prímszámokat is fel kell használni, így ezt a módszert csak a titkos kulcs birtokában lehet alkalmazni. Az eljárásban kulcsszerepe lesz a fentebb már sokat emlegetett \Z/p\Z \times \Z/q\Z halmaznak.
Most e halmaz elemei között fogunk két műveletet értelmezni. Az egyiket „összeadásnak”, a másikat pedig „szorzásnak” fogjuk nevezni, és rendre a \oplus és a \odot szimbólumokkal fogjuk őket jelölni. A \Z/p\Z \times \Z/q\Z halmaz elemei ugye olyan maradékosztálypárok, amelyeknek első komponense egy modulo p, második komponense pedig egy modulo q maradékosztály. Adja magát a kérdés, hogy vajon mi legyen két ilyen maradékosztálypár „összege” és „szorzata”:
\begin{aligned}(A;B)\oplus (C;D)&=\text{???} \\ (A;B)\odot (C;D)&=\text{???}\end{aligned}Az ötletet a fentebb már említett síkbeli pontok derékszögű koordinátáit leíró számpárok adhatják. Amennyiben a koordinátarendszer kezdőpontjából egy (a;b) számpárral megadott pontba képzeletben egy „nyilacskát” rajzolunk, akkor mondhatjuk azt is, hogy az (a;b) számpár tulajdonképpen ezt a „nyilacskát”, vagy tudományosabb nevén vektort reprezentálja. E vektorok között az alábbi kézenfekvő módon értelmezhető az összeadás művelete: két vektor „összege” legyen az a vektor, amelynek koordinátáit úgy kapjuk, hogy az eredeti két vektor megfelelő koordinátáit egymással összeadjuk. Azaz:
(a;b)\oplus (c;d)=(a+c;b+d)Itt a vektorok közötti összeadást a \oplus, míg az egyes koordináták közötti összeadást a + szimbólummal jelöltük. Ezzel azt próbáljuk kihangsúlyozni, hogy ez a két művelet nagyon nem ugyanaz. Nyilván, hiszen teljesen más halmazokon vannak értelmezve: a \oplus művelet az \R\times\R, míg a + művelet az \R halmazon.
Az alábbi ábrán az imént definiált vektorok közötti összeadás intuitív értelmezése látható:
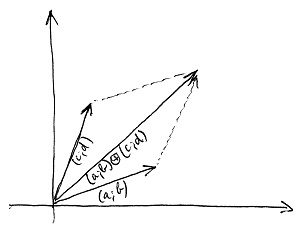
Eszerint tehát a két vektor összege épp abba a pontba mutat, amelybe úgy juthatunk el, hogy az egyik vektor végpontjába toljuk a másik vektor kezdőpontját, majd a koordinátarendszer kezdőpontjából végigmegyünk az így kijelölt útvonalon.
Visszatérve a \Z/p\Z \times \Z/q\Z halmazhoz, adja magát az ötlet, hogy ezen a halmazon is hasonlóképpen, azaz „koordinátánkénti” műveletvégzésként definiáljuk a két kérdéses műveletet. Nevezetesen:
\begin{aligned}(A;B)\oplus (C;D)&=(A+C;B+D) \\ (A;B)\odot (C;D)&=(A\cdot C;B\cdot D)\end{aligned}A vektorok között definiált összeadáshoz képest itt mindössze annyi a különbség, hogy az egyes „koordináták” nem feltétlenül azonos gyűrűkből származnak. Például jelen esetben az eredmény első „koordinátáját” adó A+C összeadást a modulo p, míg a második „koordinátát” adó B+D összeadást a modulo q maradékosztálygyűrűben kell elvégezni. A szorzásokra természetesen ugyanez vonatkozik.
Ezután minden bizonnyal nem lesz túl meglepő, hogy a \Z/p\Z \times \Z/q\Z halmaz az imént értelmezett \oplus és \odot műveletekkel egy gyűrűt alkot. Az alábbi tételben ezt ennél általánosabban igazoljuk.
22.7. Tétel (Gyűrűk direkt szorzata, szorzatgyűrű):
Legyenek R_1, R_2, ..., R_n tetszőleges gyűrűk, és értelmezzünk két műveletet az R_1\times R_2\times \ldots \times R_n halmaz tetszőleges (a_1;a_2;\ldots;a_n) és (b_1;b_2;\ldots;b_n) elemei között az alábbi módon:
\begin{aligned}(a_1;a_2;\ldots;a_n)\oplus (b_1;b_2;\ldots;b_n)&=(a_1+b_1;a_2+b_2;\ldots;a_n+b_n) \\ (a_1;a_2;\ldots;a_n)\odot (b_1;b_2;\ldots;b_n)&=(a_1\cdot b_1;a_2\cdot b_2;\ldots;a_n\cdot b_n)\end{aligned}Azaz a \oplus illetve a \odot műveleteket úgy kell elvégezni, hogy az azonos pozícióban lévő komponensek összegeit illetve szorzatait képezzük a megfelelő gyűrűkben.
Ekkor az R_1\times R_2\times \ldots \times R_n halmaz szintén egy gyűrűt alkot ezzel a két művelettel. Ezt a gyűrűt az R_1, R_2, ..., R_n gyűrűk direkt szorzatának, vagy szorzatgyűrűjének nevezzük.
A szorzatgyűrű nulleleme egy olyan rendezett n-es, amelynek minden komponensében a megfelelő gyűrű nulleleme áll. Azaz:
0_{R_1\times R_2\times \ldots \times R_n}=(0_{R_1};0_{R_2};\ldots;0_{R_n})A szorzatgyűrű egy tetszőleges (a_1;a_2;\ldots;a_n) elemének \ominus (a_1;a_2;\ldots;a_n)-nel jelölt ellentettjét úgy kapjuk meg, hogy vesszük minden komponens ellentettjét a megfelelő gyűrűben. Azaz:
\ominus (a_1;a_2;\ldots;a_n)=(-a_1;-a_2;\ldots;-a_n) ♣Bizonyítás:
A 14.12. Definícióban felsorolt gyűrűaxiómákat kell ellenőrizni:
A \oplus művelet kommutativitása könnyedén adódik az R_1, R_2, ..., R_n gyűrűkön értelmezett összeadások ugyanezen tulajdonságából:
\begin{aligned}(&a_1;\ldots;a_n)\oplus(b_1;\ldots;b_n)=\\ &= (a_1+b_1;\ldots;a_n+b_n) =\\&=(b_1+a_1;\ldots;b_n+a_n) =\\&= (b_1;\ldots;b_n) \oplus (a_1;\ldots;a_n)\end{aligned}Hasonlóképpen adódik a \oplus művelet asszociativitása:
\begin{aligned}((&a_1;\ldots;a_n)\oplus(b_1;\ldots;b_n))\oplus(c_1;\ldots;c_n) =\\&= (a_1+b_1;\ldots;a_n+b_n)\oplus(c_1;\ldots;c_n) =\\&=((a_1+b_1)+c_1;\ldots;(a_n+b_n)+c_n) =\\&= (a_1+(b_1+c_1);\ldots;a_n+(b_n+c_n)) =\\&=(a_1;\ldots;a_n)\oplus(b_1+c_1;\ldots;b_n+c_n)=\\&=(a_1;\ldots;a_n)\oplus((b_1;\ldots;b_n)\oplus(c_1;\ldots;c_n))\end{aligned}És a \odot művelet asszociativitása is:
\begin{aligned}((&a_1;\ldots;a_n)\odot(b_1;\ldots;b_n))\odot(c_1;\ldots;c_n) =\\&= (a_1\cdot b_1;\ldots;a_n\cdot b_n)\odot(c_1;\ldots;c_n) =\\&=((a_1\cdot b_1)\cdot c_1;\ldots;(a_n\cdot b_n)\cdot c_n) =\\&= (a_1\cdot (b_1\cdot c_1);\ldots;a_n\cdot (b_n\cdot c_n)) =\\&=(a_1;\ldots;a_n)\odot(b_1\cdot c_1;\ldots;b_n\cdot c_n)=\\&=(a_1;\ldots;a_n)\odot((b_1;\ldots;b_n)\odot(c_1;\ldots;c_n))\end{aligned}Továbbá a két művelet közötti mindkét oldali disztributivitás is teljesül. Nézzük először a baloldali disztributivitást, a jobboldali disztributivitás ugyanígy igazolható:
\begin{aligned}(&a_1;\ldots;a_n)\odot((b_1;\ldots;b_n)\oplus(c_1;\ldots;c_n))=\\&=(a_1;\ldots;a_n)\odot (b_1+c_1;\ldots;b_n+c_n)=\\&=(a_1\cdot(b_1+c_1);\ldots;a_n\cdot (b_n+c_n))=\\&=(a_1b_1+a_1c_1;\ldots;a_nb_n+a_nc_n)=\\&=(a_1b_1;\ldots;a_nb_n)\oplus (a_1c_1;\ldots;a_nc_n)=\\&=((a_1;\ldots;a_n)\odot (b_1;\ldots;b_n))\oplus ((a_1;\ldots;a_n)\odot (c_1;\ldots;c_n))\end{aligned}Végül igazoljuk a nullelemre és az ellentett elemre vonatkozó állításokat. Legyen (a_1;\ldots;a_n) az R_1\times \ldots \times R_n halmaz egy tetszőleges eleme. Ezt az (0_{R_1};\ldots;0_{R_n}) elemmel összeadva az eredmény valóban nem változik, hiszen minden komponensben a megfelelő gyűrű nullelemével való összeadás fog szerepelni:
\begin{aligned}(&a_1;\ldots;a_n)\oplus(0_{R_1};\ldots;0_{R_n})=\\&=(a_1+0_{R_1};\ldots;a_n+0_{R_n})=\\&=(a_1;\ldots;a_n)\end{aligned}Ehhez hasonlóan az (a_1;\ldots;a_n) elemet a (-a_1;\ldots;-a_n) elemmel összeadva az eredmény valóban a (0_{R_1};\ldots;0_{R_n}) elem lesz, hiszen minden komponensben az adott komponens és annak a megfelelő gyűrűben vett ellentettjének összege fog szerepelni:
\begin{aligned}(&a_1;\ldots;a_n)\oplus(-a_1;\ldots;-a_n)=\\&=(a_1-a_1;\ldots;a_n-a_n)=\\&=(0_{R_1};\ldots;0_{R_n})\end{aligned} ∎E tételből következően a \Z/p\Z \times \Z/q\Z halmaz a komponensenkénti moduláris összeadásra és szorzásra nézve valóban egy gyűrűt alkot. Például a fentebbi példákban szereplő ([4]_5;[6]_8) és ([4]_5;[2]_8) maradékosztálypárok „összegét” és „szorzatát” az alábbiak módon kapjuk meg:
\begin{aligned}([4]_5;[6]_8)\oplus ([4]_5;[2]_8) &= ([4]_5+[4]_5; [6]_8+[2]_8) = ([3]_5; [0]_8) \\ ([4]_5;[6]_8)\odot ([4]_5;[2]_8) &= ([4]_5\cdot [4]_5; [6]_8\cdot [2]_8) = ([1]_5; [4]_8) \end{aligned}A szakasz elején említett RSA-dekódolást gyorsító eljárás működésének a kulcsa az a tény, hogy szoros kapcsolat áll fenn a \Z/p\Z \times \Z/q\Z és a \Z/pq\Z gyűrűk között. Olyannyira szoros, hogy az alábbi tétel szerint lényegében ugyanannak a gyűrűnek csupán két megjelenési formájáról van szó.
22.8. Tétel (Maradékosztálygyűrűk dekompozíciója):
Legyenek p\gt 0 és q\gt 0 valamilyen pozitív egész számok, továbbá tegyük fel, hogy p és q egymáshoz relatív prímek. Ekkor a 22.7. Tétel szerint értelmezett \Z/p\Z \times \Z/q\Z gyűrű izomorf a \Z/pq\Z maradékosztálygyűrűvel (lásd a 18.6. Definíciót). Azaz:
\Z/p\Z \times \Z/q\Z\simeq \Z/pq\ZLegyenek a, b és c tetszőleges egész számok, továbbá tegyük fel, hogy az x_1 és x_2 egész számok kielégítik az alábbi kongruenciákat:
\begin{aligned}p\cdot x_1&\equiv 1\pmod q \\ q\cdot x_2&\equiv 1\pmod p\end{aligned}Ekkor az alábbi f:\Z/p\Z \times \Z/q\Z \to \Z/pq\Z és g:\Z/pq\Z \to \Z/p\Z \times \Z/q\Z leképezések épp egymás megfordításai, továbbá mindketten gyűrűizomorfizmusok a két gyűrű között:
\begin{aligned}f(([a]_p;[b]_q))&=[a\cdot q\cdot x_2 + b\cdot p\cdot x_1]_{pq} \\ g([c]_{pq})&=([c]_p;[c]_q)\end{aligned} ♣Bizonyítás:
Az f függvényről a 22.4. Tételben igazoltuk, hogy minden \Z/p\Z \times \Z/q\Z-beli rendezett párhoz pontosan egy \Z/pq\Z-beli maradékosztályt rendel hozzá. Méghozzá azt a maradékosztályt, amely a rendezett pár két komponensének a metszete.
A 22.5. Tételben pedig azt mutattuk meg, hogy ilymódon minden \Z/pq\Z-beli maradékosztály pontosan egy \Z/p\Z \times \Z/q\Z-beli rendezett párhoz lehet hozzárendelve, amelyet ráadásul épp a g függvény segítségével kaphatunk meg.
Ez egyrészt azt jelenti, hogy a \Z/p\Z \times \Z/q\Z halmaz elemei kölcsönösen egyértelmű megfeleltetésben állnak a \Z/pq\Z halmaz elemeivel. Másrészt pedig azt jelenti, hogy e kölcsönösen egyértelmű megfeleltetést az f függvény segítségével az egyik, míg a g függvény segítségével a másik irányban kaphatjuk meg. Más szavakkal az f és g függvények épp egymás megfordításai. Ezt az alábbi ábra mutatja:

Így már csak azt kell igazolni, hogy f és g művelettartó leképezések (lásd a 18.6. Definíciót). Annak érdekében, hogy világos legyen, melyik műveletet melyik gyűrűben kell elvégezni, a \Z/pq\Z maradékosztálygyűrű összeadását és szorzását jelöljük a \boxplus és \boxdot, míg a \Z/p\Z \times \Z/q\Z gyűrű összeadását és szorzását a \oplus és \odot szimbólumokkal. Ezeket a jelöléseket bevezetve azt kell igazolni, hogy tetszőleges a, b, c és d egész számokra teljesülnek az alábbiak:
\begin{aligned}f(([a]_p;[b]_q) \oplus ([c]_p;[d]_q)) &= f(([a]_p;[b]_q))\boxplus f(([c]_p;[d]_q)) \\ f(([a]_p;[b]_q) \odot ([c]_p;[d]_q)) &= f(([a]_p;[b]_q))\boxdot f(([c]_p;[d]_q)) \\ g([a]_{pq} \boxplus [b]_{pq}) &= g([a]_{pq})\oplus g([b]_{pq}) \\ g([a]_{pq} \boxdot [b]_{pq}) &= g([a]_{pq})\odot g([b]_{pq})\end{aligned}Kezdjük a g függvénnyel. Az erre vonatkozó két állítás baloldalait a 20.5. Tétel és a g függvény képletének felhasználásával az alábbi módon lehet kifejteni (itt a + és \cdot szimbólumok a szokásos egészek közötti összeadást és szorzást jelölik):
\begin{aligned}g([a]_{pq} \boxplus [b]_{pq}) &= g([a+b]_{pq})=([a+b]_p;[a+b]_q) \\ g([a]_{pq} \boxdot [b]_{pq}) &= g([a\cdot b]_{pq})=([a\cdot b]_p;[a\cdot b]_q)\end{aligned}Míg a jobboldalakból ezt kapjuk:
\begin{aligned}g([a]_{pq})\oplus g([b]_{pq}) &= ([a]_p;[a]_q)\oplus ([b]_p;[b]_q) \\ g([a]_{pq})\odot g([b]_{pq}) &= ([a]_p;[a]_q)\odot ([b]_p;[b]_q)\end{aligned}A 22.7. Tétel alapján a kapott rendezett párokat komponensenként kell összeadni illetve összeszorozni. Az első komponenshez szükséges összeadást és szorzást a modulo p, míg a második komponenshez szükséges összeadást és szorzást a modulo q maradékosztálygyűrűben kell elvégezni. Ismételten a 20.5. Tétel felhasználásával így az alábbit kapjuk:
\begin{aligned}g([a]_{pq})\oplus g([b]_{pq}) &= ([a+b]_p;[a+b]_q) \\ g([a]_{pq})\odot g([b]_{pq}) &= ([a\cdot b]_p;[a\cdot b]_q)\end{aligned}A g-re vonatkozó két állítás bal- és jobboldalai tehát megegyeznek, azaz a g függvény tartja mindkét műveletet, így ő egy gyűrűizomorfizmus \Z/pq\Z és \Z/p\Z \times \Z/q\Z között.
Mivel az f függvény a g függvény megfordítása, ezért a 18.6. Definíció utáni megjegyzés alapján ő is egy gyűrűizomorfizmus a két gyűrű között, csak épp a másik irányba képez.
∎Tekintsük ismét példaként a már sokat emlegetett ([4]_5;[6]_8) és ([4]_5;[2]_8) maradékosztálypárokat a \Z/5\Z\times \Z/8\Z gyűrűben. Ezek összege és szorzata ebben a gyűrűben az alábbiak voltak:
\begin{aligned}([4]_5;[6]_8)\oplus ([4]_5;[2]_8) &= ([3]_5; [0]_8) \\ ([4]_5;[6]_8)\odot ([4]_5;[2]_8) &= ([1]_5; [4]_8) \end{aligned}Fentebb már láttuk, hogy az imént tanult gyűrűizomorfizmusok – és persze az ezek hátterében lévő kínai maradéktétel – alapján az ő párjaik a \Z/40\Z gyűrűben rendre a [14]_{40} és a [34]_{40} maradékosztályok. Most nézzük meg ezek összegét és szorzatát a \Z/40\Z gyűrűben:
\begin{aligned}[14]_{40}\boxplus [34]_{40} &= [48]_{40}=[8]_{40} \\ [14]_{40}\boxdot [34]_{40} &= [476]_{40}=[36]_{40}\end{aligned}Valóban, a fenti tételben szereplő g gyűrűizomorfizmus a [8]_{40} maradékosztályhoz a ([8]_5;[8]_8)=([3]_5;[0]_8), míg a [36]_{40} maradékosztályhoz a ([36]_5;[36]_8)=([1]_5;[4]_8) maradékosztálypárt rendeli hozzá. Azaz tényleg egy művelettartó leképezésről van szó a \Z/40\Z és a \Z/5\Z \times \Z/8\Z gyűrűk között.
Tulajdonképpen az történt, hogy a \Z/40\Z gyűrűt felbontottuk két kisebb gyűrű direkt szorzatára. A két algebrai struktúra izomorfiája miatt bármelyikben elvégezhetjük a szükséges számításokat, és az egyikben kapott eredményt könnyedén áttranszformálhatjuk a másik struktúrába a gyűrűizomorfizmusok segítségével. Az utolsó szakaszban megvizsgáljuk, hogy mégis miért jó ez Alice és Bob számára.
Az RSA-dekódolás gyorsítása
Térjünk most vissza az előző részben közölt példára, amikoris Alice az RSA-algoritmussal rejtjelezett sziabobmiahelyzet üzenetet küldte el Bob-nak. Bob a kulcsgenerálás során a p=211 és q=139 prímszámokat választotta, és ezek segítségével az m=29329 modulust, az e=187 publikus, valamint a d=11623 titkos kitevőt állította elő.
Alice a példában leírt módon a \Z_{29329} gyűrű elemeinek sorozatává alakította az elküldendő üzenetet, melyek közül az első az x_1=9620 volt. Ebből a rejtjelezett számsorozat első tagja a \Z_{29329} gyűrűben végrehajtott alábbi moduláris hatványozás eredményeként állt elő:
\Z_{29329} \text{: } 9620^{187}=7812=y_1Bob ebből a d=11623 kitevő segítségével az alábbi, szintén a \Z_{29329} gyűrűben végrehajtott moduláris hatványozással kaphatja vissza az eredeti x_1 számot:
\Z_{29329} \text{: } 7812^{11623}=9620=x_1A 20. részben az egész számok maradékosztályai kapcsán szó volt róla, hogy a gyűrűk homomorfizmustétele (18.25. Tétel) miatt tetszőleges n\gt 0 pozitív egész szám esetén a \Z_n gyűrű izomorf a \Z/n\Z maradékosztálygyűrűvel. Következésképp a maradékosztálygyűrűk dekompozíciójáról szóló 22.8. Tétel miatt a \Z_p \times \Z_q gyűrű is izomorf a \Z_{pq}=\Z_m gyűrűvel.
Emiatt Bob a p és q prímszámok ismeretében megteheti, hogy a dekódoláskor elvégzendő moduláris hatványozást a \Z_m gyűrű helyett a \Z_p \times \Z_q gyűrűben végzi el, majd az eredményt visszatranszformálja a \Z_m gyűrűbe. Kérdezhetnénk, hogy ez miért jó neki, amikor így egy helyett gyakorlatilag két moduláris hatványozást kell elvégeznie? Igenám, csakhogy ezeknél már nem m, hanem a nagyságrendileg feleannyi számjegyből álló p és q lesz a modulus. A moduláris hatványozás sebessége pedig a kitevő méretén kívül erőteljesen függ a modulus méretétől is. Ráadásul a modulus méretét megfelezve a moduláris hatványozás futásideje kevesebb mint a felére csökken. Így két feleakkora modulussal elvégzett hatványozás összességében hatékonyabb, mintha csak egyet végeznénk el ugyan, de az eredeti modulussal.
A fenti példában ez azt jelenti, hogy megérkezik Bob-hoz az y_1=7812 rejtjelezett szám, amely ugye a \Z_{29329} gyűrű egy eleme. Ezt Bob a 22.8. Tételben megadott g izomorfizmus segítségével áttranszformálja a \Z_{211}\times \Z_{139} gyűrűbe, azaz veszi a két prímmel való osztási maradékát:
g(7812)=(5; 28)Ezután elvégzi a dekódolást ebben a gyűrűben, azaz kiszámítja az alábbi két moduláris hatványt:
\begin{aligned}\Z_{211} &\text{: } 5^{11623} \\ \Z_{139} &\text{: } 28^{11623}\end{aligned}Itt tehát az első moduláris hatványozást a \Z_{211}, míg a másodikat a \Z_{139} gyűrűben kell végrehajtani. Ez hatékonyabban végrehajtható, mintha csak a 7812^{11623} moduláris hatványozást hajtanánk végre ugyan, viszont a jóval nagyobb modulusú \Z_{29329} gyűrűben. Az előző részben megismert ismételt négyzetreemelések módszerével Bob az alábbi eredményt kapja:
\begin{aligned}\Z_{211} &\text{: } 5^{11623}=125 \\ \Z_{139} &\text{: } 28^{11623}=29\end{aligned}A kapott pár tehát a (125;29). Ahhoz, hogy Bob ebből megkapja az Alice által küldött eredeti x_1 üzenetet, vissza kell transzformálja ezt a \Z_{211}\times \Z_{139}-beli elemet a \Z_{29329} gyűrűbe. Ezt a 22.8. Tételben megadott f izomorfizmussal teheti meg:
f((125;29))=9620=x_1A kapott x_1=9620 eredmény helyességét könnyen leellenőrizhetjük. Ha ugyanis alkalmazzuk rá a g függvényt, akkor vissza kell kapnunk a (125;29) számpárt, hiszen a g függvény épp az f függvény megfordítása. Valóban: a 9620 egész számnak a p=211-gyel való osztási maradéka 125, míg a q=139-cel való osztási maradéka 29. Vagyis a (125;29) valóban az x_1=9620 üzenet párja a két gyűrű közötti izomorfizmus szerint.
Végezetül a kis Fermat-tétel egy egyszerű következményét ismertetjük, aminek a segítségével Alice és Bob nemcsak a dekódolás során használt modulus, hanem a d titkos kitevő méretét is jelentősen képes lecsökkenteni.
22.9. Tétel:
Legyen d\gt 0 egy tetszőleges pozitív egész szám, p\gt 0 pedig egy tetszőleges pozitív prímszám. Tegyük fel továbbá, hogy d_p egy olyan egész szám, amelyre teljesül az alábbi kongruencia:
d_p\equiv d\pmod{p-1}Ekkor minden y egész szám esetén teljesül az alábbi kongruencia is:
y^d\equiv y^{d_p}\pmod{p} ♣Bizonyítás:
A d_p\equiv d\pmod{p-1} kongruencia a 20.1. Tétel 3. pontja alapján az alábbi oszthatóság teljesülését jelenti:
p-1|d_p-dEz az oszthatóság a 16.1. Definíció alapján azt jelenti, hogy létezik olyan k egész szám, amelyre teljesül az alábbi egyenlet:
k\cdot (p-1)=d_p-dAz egyenlet mindkét oldalához d-t adva az alábbi kifejezést kapjuk d_p-re:
d_p=k(p-1)+dEz alapján az y^d\equiv y^{d_p}\pmod p kongruencia így írható fel:
y^d\equiv y^{\overbrace{k(p-1)+d}^{=d_p}}\pmod pEz a hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontjai alapján az alábbi alakra hozható:
y^d\equiv (y^{p-1})^k \cdot y^d\pmod pAmennyiben y relatív prím p-hez, akkor alkalmazható a kis Fermat-tétel, amely alapján a fenti kongruencia jobboldalán szereplő y^{p-1} tényező 1-gyel kongruens modulo p:
y^d\equiv 1^k \cdot y^d\pmod pÍgy tehát a kongruencia jobboldala a 20.2. Tétel 5. és 8. pontja alapján valóban y^d-vel kongruens modulo p.
Amennyiben y NEM relatív prím p-hez, akkor a 21.4. Lemma alapján többszöröse neki, azaz teljesül a p|y oszthatóság. Ilyenkor tehát ugyancsak teljesül a fenti kongruencia, hiszen mindkét oldal 0-val kongruens modulo p.
∎A fenti példánál maradva Bob-nak tehát a dekódoláshoz végre kéne hajtania az alábbi moduláris hatványozásokat a \Z_{211} és a \Z_{139} gyűrűben:
\begin{aligned}\Z_{211} &\text{: } 5^{11623}=125 \\ \Z_{139} &\text{: } 28^{11623}=29\end{aligned}Az iménti tétel alapján ezen a ponton megteheti, hogy veszi a d=11623 kitevő p-1=210-zel és q-1=138-cal való osztási maradékait, és d helyett ezeket az osztási maradékokat használja kitevőként. Jelöljük az így kapott új kitevőket d_p-vel és d_q-val. Jelen esetben ezek az alábbiak lesznek:
\begin{aligned}d_p&=\bmod_{210}(11623)=73 \\ d_q&=\bmod_{138}(11623)=31\end{aligned}A moduláris hatványozásokat ezekkel az eredeti d-nél jóval kisebb kitevőkkel elvégezve valóban ugyanazt az eredményt kapjuk:
\begin{aligned}\Z_{211} &\text{: } 5^{73}=125 \\ \Z_{139} &\text{: } 28^{31}=29\end{aligned}Ráadásul a d_p és d_q kitevők csak a választott p és q prímszámoktól függenek, azaz Alice és Bob megteheti, hogy már a kulcsgenerálás során előállítják ezeket.
Ebben a részben tehát megismerkedtünk a kis Fermat-tétellel és a több kongruenciából álló kongruenciarendszerek egyértelmű megoldhatóságát biztosító kínai maradéktétellel. Ezek segítségével igazoltuk, hogy az RSA-algoritmus valóban mindig helyesen működik. Ezután megismerkedtünk egy olyan konstrukcióval, amelynek a segítségével kettő vagy több gyűrűből egy újabb gyűrűt tudunk létrehozni azok direkt szorzataként. A kínai maradéktétel következményeként megmutattuk, hogy ezen a módon bármely összetett modulusú maradékosztálygyűrű felbontható egymáshoz relatív prím modulusú maradékosztálygyűrűk direkt szorzatára, amely ráadásul izomorf lesz az eredeti gyűrűvel. Ezt és a kis Fermat-tétel egy következményét kihasználva Alice és Bob jelentősen gyorsítani tudja az RSA dekódolási eljárást.
Történetünk hátralévő néhány részében megtudjuk, hogy hogyan lehet az RSA kulcsokhoz szükséges óriási prímszámokat találni anélkül, hogy az idők végezetéig osztáspróbákat kelljen végezni. Ezenkívül megismerkedünk néhány olyan módszerrel, amellyel a gonosz Eve képes feltörni az RSA-algoritmust, amennyiben Alice és Bob nem kellő körültekintéssel jár el a kulcsgenerálás során. Végezetül elkalandozunk egy kicsit a – talán nem is olyan távoli – jövőbe, amikor a kvantumszámítógépek korában az RSA már fabatkát sem fog érni.
A következő részt itt találod…




Ez a kód gyerekes , mert nincs benne emberi tényező .
Tudomásul kell venni , a gépek lebírnak minket , és az ilyeneket meg fogják fejteni .
Írtam egy kódot , a számológép azt írta ki , hogy 8 szorosan nem tudja kiszámolni ,
a lehetséges megoldások számát sem .
19X18X17X16X15X14X13X12X11X10X9x8X7X6X5X4X3X2X 19X18X17X16X15X14X13X12X11X10X9x8X7X6X5X4X3X2X
19X1440X95X6-ezt számold ki . És nem akartam sokat írni , mert a számokkal
együtt 29 -ről kéne visszaszorozni ezek csak a betűk .
És a visszafejtett szöveget is csak Magyarul jól beszélő ember érti meg .
És több emberi tényező is van benne , amire egy gép nagyon nehezen jön rá .
Ugyanazt leírhatom számmal , és betűvel is .
Sőt írhatok számmal , és betűvel vegyesen , lusta vagyok leírni , akkor mennyi varáció lehetséges .
Ezt melyik kódra értetted?
A 8 tácsás Enigma kódot sem feltörték , 2 Milliárd megoldása van .
Szereztek egy gépet , meg egy kódkönyvet (3 tengerész fulladt vízbe ezért) .
Csak nagypályáztak utána , hogy feltörték .
Való igaz, hogy többen az életüket adták azért, hogy a német rejtjelezéshez használt eszközöket ellopják. Elképzelhető, hogy ezeket konkrét üzenetek visszafejtésére is használták. De elsősorban ahhoz kellettek, hogy Alan Turing és csapata információkat szerezzen magáról a kódolási eljárásról, amely ugye ebben az esetben egy elektromechanikus szerkezetként volt implementálva. Ezen információk birtokában ugyanis képesek voltak egy olyan gépet létrehozni (Colossus), amely 1943-ra már pár perc alatt képes volt megtalálni az aznapi kulcsot, és így a továbbiakban nem volt szükség a megszerzett és semmilyen további kódkönyvre a német katonai kommunikáció tartalmának megismeréséhez.
Erről itt olvashatsz pár érdekességet: https://youproof.hu/kriptografia/1-alapfogalmak-caesar-vigenere-enigma-kulcsmegosztas/