Az előző részben kibővítettük csoportelméleti eszköztárunkat, és megismerkedtünk a csoporthomomorfizmusok, a normálosztók és a faktorcsoportok fogalmával. Ezek tárgyalása során fontos párhuzamokra világítottunk rá, hiszen a 18. részben gyakorlatilag pontosan ugyanezt az utat jártuk végig a gyűrűhomomorfizmusok, az ideálok és a faktorgyűrűk (vagy maradékosztálygyűrűk) ismertetésekor. Kitértünk továbbá az úgynevezett ciklikus csoportokra, és teljes mértékben feltártuk ezek szerkezetét. Ebben a részben a megismert csoportelméleti eszközök egy fontos alkalmazását mutatjuk be. Lényegesen javítani fogunk ugyanis a Miller-Rabin-tanúk számára vonatkozó eddigi alsó becslésünkön, amelyet a 24. részben adtunk meg.
De vajon mit nevezünk primitív gyöknek, és mi köze ennek a Diffie-Hellman kulcscsere protokollhoz? Milyen esetekben ciklikus egy maradékosztálygyűrű multiplikatív csoportja? Mit állít az úgynevezett Korselt-kritérium a Carmichael-számokról? Hogyan lehet igazolni, hogy a redukált maradékosztályoknak legalább a háromnegyede Miller-Rabin-tanú? Mi a következménye, ha az RSA kulcsok generálásához véletlenül prímek helyett Carmichael-számokat használunk? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 24. és 25. részben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Tegyük fel, hogy adva van egy valamilyen G halmaz, amelyen értelmezve van egy kétváltozós művelet. Nevezzük ezt a műveletet szorzásnak és jelöljük \cdot-tal, vagy egymás után írással. Például egy a és egy b elem szorzatát jelöljük a\cdot b-vel vagy ab-vel.
Az így kapott (G,\cdot ) algebrai struktúrát félcsoportnak nevezzük, amennyiben az említett művelet asszociatív. Azaz tetszőleges a, b és c elemek esetén teljesül az alábbi:
(a\cdot b)\cdot c = a\cdot (b\cdot c)Csoportnak nevezzük az olyan félcsoportokat, amelyek esetén az asszociativitáson kívül a műveletre nézve létezik neutrális elem is (14.7. Definíció), továbbá a művelet invertálható (14.9. Definíció). Egy csoport esetén a neutrális elemet általában e-vel vagy 1-gyel szoktuk jelölni, és ilyenkor egységelemről beszélünk. Egy a elem inverzét a^{-1}-gyel szoktuk jelölni. Tetszőleges a elem esetén teljesülnek tehát az alábbiak:
\begin{aligned}a\cdot e &= e\cdot a = a \\ a\cdot a^{-1} &= a^{-1}\cdot a = e\end{aligned}Amennyiben a művelet a fentieken felül még kommutatív is, úgy Abel-csoportról vagy kommutatív csoportról beszélünk. Abel-csoportok esetén a csoportműveletet tipikusan a + szimbólummal, a neutrális elemet 0-val, egy a elem inverzét pedig -a-val szoktuk jelölni. Ilyenkor a neutrális elemet nullelemnek, az a elem inverzét pedig a ellentettjének nevezzük.
Ha egy G csoport valamely H részhalmaza maga is csoport a G műveletére nézve, akkor azt mondjuk, hogy H részcsoport G-ben. Ezt így jelöljük: H\leq G.
Ha H részcsoport G-ben, de H\neq G, akkor azt mondjuk, hogy H valódi részcsoport G-ben. Ezt így jelöljük: H\lt G.
Legyen G tetszőleges csoport, H pedig valamilyen részcsoport G-ben. Definiáljunk egy \sim szimbólummal jelölt relációt a G csoport elemei között a következőképpen: a\sim b akkor és csak akkor, ha a^{-1}b\in H.
Ekkor a \sim reláció egy ekvivalenciareláció a G csoport elemei között. Az ehhez tartozó ekvivalencia-osztályokat a G csoport H részcsoportja szerinti baloldali mellékosztályoknak nevezzük. Ha g egy tetszőleges elem a G csoportban, akkor a g elemet tartalmazó H szerinti baloldali mellékosztály épp a 18.19. Definícióban bevezetett komplexusszorzással képzett gH halmaz lesz.
Ehhez hasonlóan, ha az a\sim b relációt úgy definiáljuk, hogy akkor és csak akkor teljesüljön, ha ba^{-1}\in H, akkor ugyanígy egy ekvivalenciarelációt kapunk. Ebben az esetben az ekvivalencia-osztályokat a H részcsoport szerinti jobboldali mellékosztályoknak nevezzük, a g elemet tartalmazó jobboldali mellékosztály pedig a Hg halmaz lesz.
Tegyük fel, hogy adva van egy (G,\cdot) és egy (H,\odot) csoport. Ekkor egy f:G\to H függvényt csoporthomomorfizmusnak nevezünk, amennyiben tetszőleges G-beli a és b elemekre teljesül az alábbi művelettartó tulajdonság:
f(a\cdot b)=f(a)\odot f(b)Amennyiben H minden eleme legalább egy G-beli elemhez hozzá van rendelve, akkor f-et szürjektív csoporthomomorfizmusnak vagy csoportráképzésnek nevezzük.
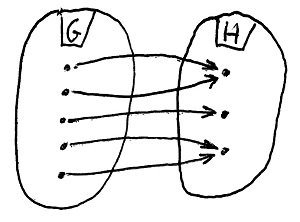
Amennyiben H minden eleme legfeljebb egy G-beli elemhez van hozzárendelve, akkor f-et injektív csoporthomomorfizmusnak vagy csoportbeágyazásnak nevezzük.
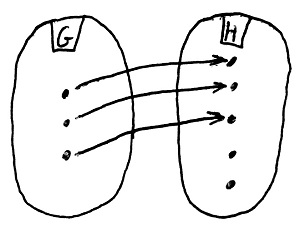
Amennyiben H minden eleme pontosan egy G-beli elemhez van hozzárendelve, akkor f-et bijektív csoporthomomorfizmusnak vagy csoportizomorfizmusnak nevezzük.
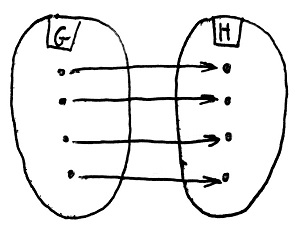
Ilyenkor azt mondjuk, hogy a G és a H csoport izomorf egymással. Ezt így jelöljük: G\simeq H.
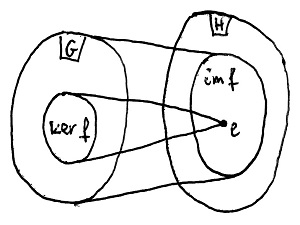
Legyenek G és H tetszőleges csoportok, valamint legyen adva közöttük egy f:G\to H csoporthomomorfizmus. Ekkor az f csoporthomomorfizmus magjának nevezzük azon G-beli elemek halmazát, melyeknek f szerinti képe a H csoport egységeleme. Az f magját – az angol „kernel” szóból eredeztetve – így jelöljük: \ker f.
Az f csoporthomomorfizmus képének nevezzük azoknak a H-beli elemeknek a halmazát, amelyek képei legalább egy G-beli elemnek. Az f képét – az angol „image” szóból eredeztetve – így jelöljük: \text{im} f.
Az alábbi ábra szemlélteti a fenti fogalmakat:
Legyen adva egy G csoport, valamint egy N részcsoport G-ben. Tegyük fel továbbá, hogy az N részcsoport szerinti bal- és jobboldali mellékosztályok megegyeznek, azaz minden a\in G esetén teljesül az alábbi:
aN=NaEkkor azt mondjuk, hogy az N részcsoport normálosztó G-ben. Ezt így jelöljük: N\triangleleft G.
Az a részcsoport, amely csak G egységeleméből áll, illetve maga a teljes G nyilvánvalóan normálosztók G-ben. Ezeket triviális normálosztóknak nevezzük.
Legyen G egy tetszőleges csoport, és tegyük fel, hogy N normálosztó G-ben. Jelöljük G/N-nel azt a halmazt, amelynek elemei a 24.7. Tételben definiált N szerinti baloldali mellékosztályok.
Vezessük be ezek között az alábbi műveletet: Ha A=aN és B=bN két baloldali mellékosztály, akkor ezek szorzata legyen az A\odot B=(a\cdot b)N baloldali mellékosztály.
Ekkor a G/N halmaz ezzel a művelettel csoportot alkot, amelyet a G csoport N normálosztó szerinti faktorcsoportjának nevezünk.
Ha e_G jelöli a G csoport egységelemét, akkor a G/N faktorcsoport egységeleme az e_GN baloldali mellékosztály.
Ha a^{-1} jelöli a G csoport egy a elemének inverzét, akkor a G/N faktorcsoport aN elemének inverze az (a^{-1})N baloldali mellékosztály.
Ha G kommutatív csoport (vagy más néven Abel-csoport), akkor G/N is az.
Tekintsük továbbá azt az f:G\to G/N függvényt, amely minden G-beli a elemhez az aN baloldali mellékosztályt rendeli hozzá a G/N faktorcsoportból. Ekkor f egy csoporthomomorfizmus G és G/N között, melynek magja N. Ennek a neve természetes csoporthomomorfizmus.
Legyenek A és B tetszőleges halmazok, továbbá tegyük fel, hogy értelmezve van egy f:A\to B függvény, amely tehát az A halmaz minden eleméhez hozzárendel egy elemet a B halmazból.
Legyen adott egy C\sube A halmaz. Ekkor B-nek azt a – 19.7. Definíció szerinti értelemben vett – legszűkebb részhalmazát, amely minden C-beli elem f szerinti képét tartalmazza, a C halmaz f szerinti képének (vagy értékkészletének) nevezzük és f(C)-vel jelöljük. Ezt az elrendezést mutatja az alábbi ábra:
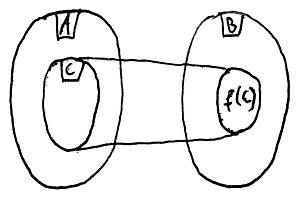
Legyen adott egy D\sube B halmaz. Ekkor A-nak azt a – 19.7. Definíció szerinti értelemben vett – legbővebb részhalmazát, amelynek f szerinti képe D, a D halmaz f szerinti teljes inverz képének nevezzük és f^{-1}(D)-vel jelöljük. Ezt az elrendezést mutatja az alábbi ábra:
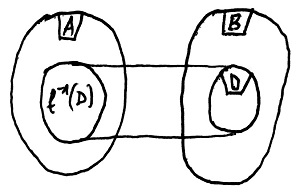
Legyenek G és H tetszőleges csoportok, f:G\to H pedig egy szürjektív csoporthomomorfizmus e két csoport között, és vezessük be az N=\ker f jelölést. Ekkor teljesülnek az alábbiak:
- A H részcsoportjai kölcsönösen egyértelmű megfeleltetésben állnak G azon részcsoportjaival, amelyek N-et teljes egészében tartalmazzák. Egy L\leq H részcsoporthoz az f^{-1}(L) teljes inverz kép, mint G-beli, N-et tartalmazó részcsoport tartozik. A továbbiakban legyenek K\leq G és L\leq H ebben az értelemben egymásnak megfelelő részcsoportok.
- A K szerinti baloldali mellékosztályok az L szerinti baloldali mellékosztályok teljes inverz képei f szerint, és ez a megfeleltetés szintén kölcsönösen egyértelmű.
- Ugyanez mondható el a jobboldali mellékosztályokról is.
- Az L részcsoport akkor és csak akkor normálosztó H-ban, ha K normálosztó G-ben, és ilyenkor a G/K és H/L faktorcsoportok izomorfak.
Legyen G tetszőleges csoport, H pedig valamilyen részcsoport G-ben. Amennyiben G-ben létezik olyan g elem, hogy az egyelemű X=\{g\} halmaz generálja H-t – azaz \lang X\rang = H –, akkor azt mondjuk, hogy H ciklikus részcsoport G-ben, amelynek generátoreleme (vagy primitív eleme) g.
Amennyiben maga a teljes G – mint triviális részcsoport – generálható egyetlen elemmel, akkor G-t ciklikus csoportnak nevezzük.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 24. és 25. részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Az előző rész végén igazoltuk, hogy az egész számok \Z gyűrűjének, valamint tetszőleges m\geq 0 esetén a \Z/m\Z maradékosztálygyűrűnek az additív csoportja ciklikus, továbbá, hogy ezeken kívül – izomorfiától eltekintve – nem is létezik más ciklikus csoport. Előbbit az 1 egész szám, utóbbit pedig az [1]_m maradékosztály generálja. Nyilván, hiszen ezeknek vagy ellentettjeiknek az önmagukkal való valahányszori összeadása előállítja az adott gyűrű minden elemét.
Felmerült azonban a kérdés, hogy vajon mi a helyzet ugyanezen gyűrűk multiplikatív csoportjával. A \Z gyűrű esetén ebben a tekintetben egyszerű a dolgunk. A 24.3. Definíció utáni megjegyzés alapján ugyanis egy kommutatív, egységelemes gyűrű multiplikatív csoportja pontosan az egységekből áll. Ezek a \Z gyűrűben a +1 és -1 egész számok lesznek. Az Olvasó a 24.1. Definíció és a 25.19. Definíció alapján könnyedén leellenőrizheti, hogy ez a kételemű halmaz egy ciklikus csoportot alkot az egészek közötti szorzással, mint művelettel. A generátorelem ebben az esetben a -1 egész szám, hiszen ennek hatványai kiadják a teljes csoportot. Ezzel szemben a +1 egész szám nem generátorelem, mivel az csak az egyelemű triviális részcsoportot generálja – azt, amelyikben csak a +1 szerepel.
Mármost ha a \Z^{\times} kételemű multiplikatív csoport ciklikus, akkor a 25.22. Tétel alapján izomorf a \Z^+ vagy a (\Z/m\Z)^+ additív csoportok valamelyikével. A \Z^+ csoport rendje végtelen, így ezt kizárhatjuk. A 20.4. Tétel alapján m=0 esetén végtelen sok, míg m\gt 0 esetén pontosan m darab modulo m maradékosztály létezik. Ez alapján tehát kizárásos alapon csak az m=2 eset lehetséges, azaz fennáll az alábbi izomorfia:
\Z^{\times} \simeq (\Z/2\Z)^+A \Z^{\times} multiplikatív csoport műveleti tábláját az alábbi táblázatban láthatjuk:
\begin{array}{c|cc} \cdot & 1 & -1 \\ \hline 1 & 1 & -1 \\ -1 & -1 & 1 \end{array}A (\Z/2\Z)^+ additív csoport műveleti táblája pedig a következő:
\begin{array}{c|cc} + & [0]_2 & [1]_2 \\ \hline [0]_2 & [0]_2 & [1]_2 \\ [1]_2 & [1]_2 & [0]_2 \end{array}Látható, hogy mindössze az elemek és a művelet elnevezésében van különbség a két csoport között, de ettől eltekintve teljesen ugyanúgy viselkednek, azaz izomorfak egymással.
Primitív gyök
A \Z gyűrű multiplikatív csoportja tehát ciklikus, ezért most térjünk rá arra a kérdésre, hogy vajon milyen m\gt 0 esetén lesz a \Z/m\Z gyűrű multiplikatív csoportja is ciklikus? Ez rögtön elvezet minket az alábbi fontos fogalomhoz.
26.1. Definíció (Primitív gyök):
Legyen m\gt 0 valamilyen pozitív egész szám. Amennyiben a \Z/m\Z gyűrű multiplikatív csoportja – azaz a (\Z/m\Z)^{\times} csoport – ciklikus, akkor azt mondjuk, hogy létezik primitív gyök modulo m.
Legyen [a]_m egy modulo m redukált maradékosztály, azaz a (\Z/m\Z)^{\times} multiplikatív csoport egy eleme. Amennyiben [a]_m generálja a teljes (\Z/m\Z)^{\times} csoportot a 25.19. Definíció szerinti értelemben, akkor az [a]_m maradékosztályt modulo m primitív gyöknek nevezzük.
♣Megjegyzés:
A 24.6. Definícióban bevezettük a csoport rendjének fogalmát, amely az adott csoport elemeinek a számát adja meg. Ez a (\Z/m\Z)^{\times} multiplikatív csoport esetén a 20.7. Definíció alapján épp az Euler-féle \varphi-függvény értékével egyezik meg, azaz:
|(\Z/m\Z)^{\times}|=\varphi(m)Ezután a 24.11. Definícióban definiáltuk a csoportelem rendjének a fogalmát, amely azt mondja meg egy csoportelemről, hogy hány különböző hatványa létezik az adott csoportban. Ez egy tetszőleges [a]_m\in (\Z/m\Z)^{\times} redukált maradékosztály esetén tehát az a legkisebb o([a]_m)-mel jelölt pozitív egész kitevő, amelyre fennáll az alábbi kongruencia:
a^{o([a]_m)} \equiv 1\pmod mAz Euler-Fermat-tétel (20.19. Tétel) alapján azonban tudjuk, hogy az alábbi kongruencia minden [a]_m redukált maradékosztályra teljesül:
a^{\varphi(m)}\equiv 1\pmod mAz [a]_m maradékosztály rendje tehát \varphi(m)-nél biztosan nem lehet nagyobb, azaz:
o([a]_m)\leq \varphi(m)Az iménti definícióból következik, hogy a modulo m primitív gyökök pontosan azok a redukált maradékosztályok lesznek, amelyeknél itt történetesen egyenlőség áll fenn. Nyilván, hiszen épp ez jelenti azt, hogy az adott maradékosztály különböző hatványaiként megkapjuk a (\Z/m\Z)^{\times} csoport összes – azaz mind a \varphi(m) darab – elemét, vagy más szavakkal az adott maradékosztály generálja a teljes (\Z/m\Z)^{\times} csoportot.
A definícióból és a 25.22. Tételből továbbá az is következik, hogy ha modulo m létezik primitív gyök, akkor a (\Z/m\Z)^{\times} multiplikatív csoport izomorf a (\Z/\varphi(m)\Z)^+ additív csoporttal, azaz:
(\Z/m\Z)^{\times} \simeq (\Z/\varphi(m)\Z)^+ ♣Az előző rész végén megállapítottuk, hogy a (\Z/10\Z)^{\times} csoport ciklikus, mivel a [3]_{10} és a [7]_{10} maradékosztályok külön-külön generálják a teljes csoportot. A mostani szóhasználattal élve tehát a [3]_{10} és a [7]_{10} maradékosztályok mindketten primitív gyökök modulo 10, továbbá az iménti megjegyzés alapján \varphi(10)=4 miatt fennáll az alábbi izomorfia:
(\Z/10\Z)^{\times} \simeq (\Z/4\Z)^+A primitív gyökök valamelyikét felhasználva az előző rész végén megadott hatványtáblázat segítségével könnyen meg is adhatunk egy f:(\Z/10\Z)^{\times} \to (\Z/4\Z)^+ izomorfizmust is a két csoport között. Ehhez csupán a táblázatban meg kell nézni, hogy egy adott [a]_{10} redukált maradékosztály a kiválasztott primitív gyöknek hanyadik hatványa. Ezután az f izomorfizmus az [a]_{10}-hez azt a modulo 4 maradékosztályt fogja hozzárendelni, amelybe az így kapott hatványkitevő esik. Például a [3]_{10} primitív gyök felhasználásával az f izomorfizmus az alábbi lesz:
\begin{aligned}[3]_{10} &\xmapsto{f} [1]_4 \\ [1]_{10} &\xmapsto{f} [0]_4 \\ [7]_{10} &\xmapsto{f} [3]_4 \\ [9]_{10} &\xmapsto{f} [2]_4\end{aligned}Az Olvasó is könnyen leellenőrizheti, hogy valóban minden esetben teljesül az f függvény művelettartó tulajdonsága a két csoport között. Például:
\begin{aligned}&f([9]_{10}\odot [7]_{10})=f([63]_{10})=f([3]_{10})=[1]_4 \\ &f([9]_{10}) \oplus f([7]_{10}) = [2]_4 \oplus [3]_4=[5]_4=[1]_4\end{aligned}Természetesen ha a [3]_{10} helyett a [7]_{10} primitív gyököt használtuk volna, akkor pedig az alábbi g:(\Z/10\Z)^{\times} \to (\Z/4\Z)^+ izomorfizmust kapjuk a hatványtáblázat alapján:
\begin{aligned}[7]_{10} &\xmapsto{g} [1]_4 \\ [1]_{10} &\xmapsto{g} [0]_4 \\ [3]_{10} &\xmapsto{g} [3]_4 \\ [9]_{10} &\xmapsto{g} [2]_4\end{aligned}Ez – habár különbözik az előzőtől – szintén egy izomorfizmus, mivel ebben az esetben is teljesül a művelettartó tulajdonság. Például:
\begin{aligned}&g([9]_{10}\odot [7]_{10})=g([63]_{10})=g([3]_{10})=[3]_4 \\ &g([9]_{10}) \oplus g([7]_{10}) = [2]_4 \oplus [1]_4=[3]_4\end{aligned}Ezzel szemben a (\Z/8\Z)^{\times} multiplikatív csoport nem ciklikus, mivel ebben a csoportban minden elem rendje 2 – az egységelemet kivéve, amelynek rendje 1 –, ugyanakkor magának a csoportnak a rendje \varphi(8)=4. A mostani szóhasználattal élve tehát nem létezik primitív gyök modulo 8, és így a 25.22. Tétel alapján nem létezik olyan m\gt 0 pozitív egész szám sem, amely esetén a (\Z/8\Z)^{\times} multiplikatív csoport izomorf lenne a (\Z/m\Z)^+ additív csoporttal.
Érdekes kérdés tehát, hogy pontosan mely m\gt 0 pozitív egész számok esetén létezik primitív gyök modulo m, és melyek esetén nem létezik. Az alábbiakban felsoroltuk az első néhány ilyen m-et (egy hosszabb sorozat található itt):
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, \ldotsLátható, hogy ebben a sorozatban egyaránt előfordulnak prímek és összetett számok is. Egyáltalán nem nyilvánvaló tehát, hogy pontosan mi a szabály. Nekünk ebben a részben csak egy speciális esetre lesz szükségünk, így az általános szabályt – amely a számelmélet egy nevezetes tétele – az alábbiakban bizonyítás nélkül mondjuk ki.
26.2. Tétel (Primitív gyökökről szóló tétel):
Egy m\gt 0 pozitív egész szám esetén akkor és csak akkor létezik primitív gyök modulo m, ha m az alábbiak valamelyike, ahol p tetszőleges pozitív, páratlan prímszám, k pedig tetszőleges pozitív kitevő:
1,2,4,p^k,2p^k ♣Az m=1,2,4 esetek nyilvánvalóak, ezt az Olvasó akár próbálgatással is leellenőrizheti. A tétel többi részéhez egyrészt azt kéne bizonyítani, hogy minden páratlan prímhatvány, továbbá ezek kétszerese esetén létezik primitív gyök. Másrészt azt is meg kéne mutatni, hogy ez nem csak elégséges, hanem szükséges feltétel is, azaz hogy a tételben felsoroltakon kívül semmilyen más esetben nem létezik primitív gyök. Számunkra elegendő lesz annyit igazolni, hogy bármilyen pozitív p prím esetén létezik modulo p primitív gyök. Ez tehát az m=2 és m=p^k eseteket fedi le a k=1 kitevőre – és annak is csak az elégségességét. A tétel többi részének bizonyítására ebben a cikksorozatban nem térünk ki, cserébe viszont nem is fogjuk felhasználni őket. Először azonban további fontos fogalmakkal kell megismerkednünk.
Polinomok
A 24. részben ismerkedtünk meg bizonyos típusú egyenletekkel, amelyekhez a matematikusok akkoriban lázasan keresték az úgynevezett megoldóképleteket, és amely problémakör tüzetesebb vizsgálata végül elvezetett a csoportelmélet megszületéséhez. Ezek az úgynevezett első-, másod-, harmad- vagy általánosságban n-edfokú egyenletek a következőképpen néztek ki:
\begin{aligned}a_0+a_1x&=0 \\ a_0+a_1x+a_2x^2&=0 \\ a_0+a_1x+a_2x^2+a_3x^3&=0 \\ &\vdots \\ a_0+a_1x+a_2x^2+a_3x^3+\ldots +a_nx^n&=0 \\ &\vdots\end{aligned}Egy ilyen egyenletben az a_0, a_1, a_2, …, a_n számok – amelyeket együtthatóknak nevezünk – konkrétan meg vannak adva, és a feladat megtalálni az összes olyan számot, amelyeket az x ismeretlen helyére beírva az adott egyenlőség fennáll. Ezeket a számokat az egyenlet megoldásainak vagy tudományosabban gyökeinek nevezzük.
Vegyük észre, hogy még ha nem is ismerjük egy-egy ilyen egyenlet konkrét megoldásait, magukkal az egyenletek baloldalain álló kifejezésekkel formálisan is „számolhatunk”. Például beszélhetünk két ilyen kifejezés „összegéről” vagy „szorzatáról”, amennyiben ezen „összeadás” vagy „szorzás” során betartjuk a „szokásos számolási szabályokat”. Ekkor az eredmény szintén egy hasonló alakban felírható kifejezés lesz:
\begin{aligned}(1+2x) \oplus (2+x) &= 3+3x \\ (1+2x) \odot (2+x) &= 2+x+4x+2x^2 = 2+5x+2x^2\end{aligned}Az „összeadás” viszonylag egyszerű, mivel ilyenkor csak az „azonos pozíciókban” álló együtthatókat kell összeadni egymással. Tegyük fel például, hogy egy n-edfokú és egy m-edfokú kifejezést szeretnénk egymással összeadni, és legyen n\leq m. Írjuk fel egymás alá a két összeadandó kifejezést az egyes tagokat az x ismeretlen hatványai szerint sorbarendezve. Az a_0 tagot – amelyben tehát x egyáltalán nem szerepel – a 24.9. Definícióval összhangban x-nek a nulladik hatványaként fogjuk fel:
\begin{alignedat}{100} &a_0+a_1\cdot &x + &\ldots + a_n\cdot &x^n +\overbrace{0}^{=a_{n+1}}\cdot &x^{n+1} + &\ldots + \overbrace{0}^{=a_m}\cdot &x^m \\ &b_0+b_1\cdot &x + &\ldots + b_n\cdot &x^n +b_{n+1}\cdot &x^{n+1} + &\ldots + b_m\cdot &x^m\end{alignedat}Itt n\leq m miatt az első kifejezésben az n-nél nagyobb indexű együtthatók nullák lesznek. Ezeket a tagokat és az esetleges többi nulla együtthatójú tagot nem kötelező kiírni, praktikussági okokból azonban ezt mi mégis megtettük, amit a fenti felírásban szemléltettük is. Ekkor, ha ezt a két kifejezést „összeadjuk” a „szokásos számolási szabályok” betartásával, akkor eredményül az alábbi kifejezést kapjuk, amelyben minden együttható a két eredeti kifejezés „azonos pozíciókban” lévő együtthatóinak összege:
(a_0+b_0)+(a_1+b_1)\cdot x + (a_2+b_2)\cdot x^2 + \ldots + (a_m+b_m)\cdot x^mÉrtelemszerűen n\geq m esetén ugyanígy kell eljárni, csak ekkor a második kifejezésben az m-nél nagyobb indexű tagok lesznek nullák.
A „szorzás” esetén már egy kicsit bonyolultabb dolgunk van. Ha ugyanis követni szeretnénk a „szokásos számolási szabályokat”, akkor a disztributivitási szabály (lásd a gyűrűk és testek 14.12. Definíciójának 5. pontját) szerint az első kifejezés minden tagját a második kifejezés minden tagjával össze kell szorozni, és az így kapott eredmény tagjait x hatványai szerint kell összevonni és sorbarendezni. Ezt a fentebbi konkrét számpéldában már láttuk, ezért most nézzük meg általánosságban is. Ismét legyen n\leq m, és írjuk fel egymás alá a két „összeszorzandó” kifejezést az egyes tagokat az x ismeretlen hatványai szerint sorbarendezve:
\begin{alignedat}{100} &a_0+a_1\cdot &x + &\ldots + a_n\cdot &x^n +\overbrace{0}^{=a_{n+1}}\cdot &x^{n+1} + &\ldots + \overbrace{0}^{=a_m}\cdot &x^m \\ &b_0+b_1\cdot &x + &\ldots + b_n\cdot &x^n +b_{n+1}\cdot &x^{n+1} + &\ldots + b_m\cdot &x^m\end{alignedat}Nézzük meg általánosságban, hogy tetszőleges k kitevő esetén mi lesz az x^k tényezőt tartalmazó tag együtthatója az eredményben. Ehhez a taghoz nyilván pontosan azok az a_ix^i és b_jx^j tagok fognak „hozzájárulni” az eredeti két kifejezésből, amelyek esetén i+j=k, hiszen két ilyen tag szorzata a 24.10. Tétel 3. pontja alapján az alábbi lesz:
a_ib_j\cdot x^ix^j=a_ib_j\cdot x^{\overbrace{i+j}^{=k}}Az eredményben tehát az x^k tag együtthatóját úgy kapjuk meg, hogy az összes olyan a_i és b_j együtthatót összeszorozzuk az eredeti kifejezésekből, amelyek esetén i+j=k, és az így kapott szorzatokat összeadjuk. Jelöljük ezt az együtthatót c_k-val. Ekkor a c_k együttható képlete az alábbi:
c_k=a_0b_k+a_1b_{k-1}+a_2b_{k-2}+\ldots +a_kb_0Ez látszólag egy k+1 tagú összeg, azonban k-tól függően bizonyos tagok nullák lesznek.
Most, hogy vázlatosan ismertettük, hogyan is kell elvégezni formálisan az ilyen kifejezések „összeadását” és „szorzását”, jogosan merülhet fel az Olvasóban a kérdés, hogy vajon pontosan hogyan fog alakulni az eredményül kapott kifejezés foka. Erre hamarosan rátérünk, most azonban adunk egy precíz matematikai definíciót is az eddigiekre.
Ennek a definíciónak első olvasásra semmi köze nem lesz az eddig tárgyaltakhoz. Itt a fentiekhez hasonló kifejezések lényegét próbáljuk ugyanis megragadni, és ezáltal kizárni bármiféle kétértelműséget a közöttük lévő műveletek értelmezésének, a fok fogalmának vagy bármi egyébnek a tekintetében. Márpedig egy ilyen kifejezésről kizárólag az együtthatói, illetve azok sorrendje hordoz érdemi információt. Az alábbi definícióban is ezt állítjuk a középpontba, a definíció utáni megjegyzésben pedig további intuitív magyarázatot fogunk adni erre az absztrakcióra.
26.3. Definíció (Polinomok):
Legyen R tetszőleges kommutatív gyűrű (lásd a 14.12. Definíciót). Legyen továbbá f egy végtelen sorozat, amelynek tagjai az R gyűrű elemei:
f=(a_0, a_1, a_2, \ldots)Amennyiben az f sorozatnak csak véges sok tagja nem az R gyűrű nulleleme, akkor f-et az R gyűrű feletti polinomnak, az a_i gyűrűelemeket az f polinom együtthatóinak, speciálisan az a_0 gyűrűelemet az f polinom konstans tagjának nevezzük. Az R gyűrű feletti polinomok halmazának jele: R[x].
Jelöljük az R gyűrű nullelemét 0_R-rel. Ha valamilyen n\geq 0 nemnegatív egész esetén a_n \neq 0_R, de minden k\gt n esetén a_k=0_R, akkor f-et n-edfokú polinomnak nevezzük, vagy azt mondjuk, hogy f foka n. Ezt így jelöljük: \deg(f)=n. Ilyenkor az a_n gyűrűelemet az f polinom főegyütthatójának nevezzük. A nulladfokú polinomokat konstans polinomoknak nevezzük.
Ha minden k\geq 0 esetén a_k=0_R, akkor f-et nullapolinomnak nevezzük és a 0 szimbólummal jelöljük. A nullapolinomnak nincs foka, azaz ebben az esetben \deg(f) nem értelmezhető.
Az f=(a_0,a_1,\ldots) és g=(b_0,b_1,\ldots) polinomokra azt mondjuk, hogy egyenlőek, ha minden k\geq 0 esetén a_k=b_k, azaz ha az őket reprezentáló két sorozat teljesen megegyezik. Ezt így jelöljük: f=g
Az f=(a_0,a_1,\ldots) és g=(b_0,b_1,\ldots) polinomok összegén azt az f+g=(c_0,c_1,\ldots) polinomot értjük, amelynek tagjait minden k\geq 0 esetén az alábbi képlet állítja elő:
c_k=a_k+b_kUgyanezen polinomok szorzatán azt az f\cdot g=(c_0,c_1,\ldots) polinomot értjük, amelynek tagjait minden k\geq 0 esetén az alábbi képlet állítja elő:
c_k=a_0b_k+a_1b_{k-1}+a_2b_{k-2}+\ldots +a_kb_0 ♣Megjegyzés:
Tekintsük például az alábbi egész számokból álló végtelen sorozatot, amely tehát a definíció alapján egy \Z feletti harmadfokú polinom, hiszen a 4-es indexű tagjától kezdve csupa 0 számokból áll (ne feledjük, a számozás a nulladik indextől indul):
(1,3,0,1,0,0,0,\ldots)Ez a polinom tulajdonképpen az 1+3x+0x^2+x^3 kifejezést reprezentálja, de ugyanúgy reprezentálja az x^3+3x+1 és az 1+x+2x^3+2x-x^3 kifejezéseket is, hiszen ezek csupán a tagok sorrendjében és az x hatványainak csoportosításában különböznek egymástól, lényegüket tekintve viszont mind ugyanannak a polinomnak a különböző megnyilvánulásai.
Amikor polinomokkal számolunk, sok esetben kézenfekvőbb a definícióhoz képest ebben a kevésbé szigorú formájukban gondolnunk rájuk. Azt, hogy intuitív módon a „szokásos szabályok” szerint lehet ezekkel a kifejezésekkel „számolni” az a kikötés biztosítja, hogy a polinom együtthatói valamilyen kommutatív gyűrűből kell származzanak, és hogy a definícióban lévő képletekben szereplő összeadások illetve szorzások alatt e gyűrű műveleteit kell érteni. Ettől függetlenül a kellő precizitás érdekében mi továbbra is a definícióban szereplő, végtelen sorozatokkal történő reprezentációt fogjuk használni.
Ezen túlmenően a végtelen sorozatokkal történő reprezentációnak praktikussági okai is vannak. Így ugyanis a polinomok összegének illetve szorzatának definiálásakor nem kell foglalkozni azzal, hogy a két összeadandó vagy összeszorzandó polinomnak mi a foka. A képletek ugyanis ettől függetlenül működnek, hiszen minden polinomot egységesen, egy végtelen, gyűrűelemekből álló sorozatként képzelhetünk el ilyenkor.
Nagyon fontos kikötés azonban, hogy nem minden végtelen sorozatot tekintünk polinomnak, hanem csak azokat, amelyek esetén véges sok tag után a sorozat minden további tagja a gyűrű nulleleme. Ez biztosítja azt, hogy nem léteznek végtelen fokú polinomok. Ezenkívül a fok tekintetében különbséget kell tennünk a nulladfokú polinomok és a nullapolinom között. A definíció szerint előbbieknek létezik foka (ami nevezetesen nulla), míg a utóbbinak nem. Ennek a megkülönböztetésnek fontos szerepe van bizonyos további tételekben is.
Végül tartsuk szem előtt, hogy a konstans polinomok jellegüket tekintve teljesen más matematikai objektumok, mint magának az R gyűrűnek az elemei, noha kifejezésként felírva őket ez nem látszik elsőre. Például a 3 jelölhet egy \Z[x]-beli konstans polinomot leíró kifejezést is, továbbá egy \Z-beli egész számot is. Előbbi esetben tulajdonképpen az alábbi végtelen sorozatról van szó, ami nagyon nem ugyanaz, mint maga a 3 egész szám:
(3,0,0,0,\ldots)Ez azonban mégsem okoz zavart, ugyanis tetszőleges R kommutatív gyűrű beágyazható (lásd a 18.6. Definíciót) az R[x] halmazba. Az f:R\to R[x] beágyazófüggvényt tetszőleges r\in R gyűrűelem esetén az alábbi hozzárendelés valósítja meg:
r\xmapsto{f} (r,0_R,0_R,0_R,\ldots)Ez nyilvánvalóan egyrészt egy kölcsönösen egyértelmű megfeleltetés R elemei és a konstans polinomok között, másrészt tartja az R gyűrű összeadását és szorzását. Ilyen értelemben tehát R elemei azonosíthatók a nekik megfelelő konstans polinomokkal. Vagyis az R gyűrűt gyakorlatilag tekinthetjük az R[x] halmaz részének is, habár szigorúan matematikai értelemben nem erről van szó. Ez nagyon hasonló ahhoz, mint ahogy a természetes számok \N halmazát a rajta értelmezett két művelettel és a rendezési relációval együtt az egész számok \Z halmazába ágyaztuk be (lásd az erről szóló 13.13., 14.5. valamint 15.19. Tételeket).
♣Az iménti megjegyzésben szereplő beágyazófüggvény jóvoltából tehát egy tetszőleges R kommutatív gyűrű esetén az R[x] halmazban lévő konstans polinomok szintén gyűrűt alkotnak a polinomok között definiált összeadás és szorzás műveletekkel. Hamarosan igazoljuk, hogy ez bizony szerencsére nem csak a konstans polinomokra, hanem a teljes R[x] halmazra is igaz. Előbb azonban korábbi ígéretünknek megfelelően egy hasznos összefüggést bizonyítunk az összeg- és szorzatpolinomok fokaival kapcsolatban.
26.4. Tétel:
Legyen R tetszőleges kommutatív gyűrű, és jelölje R[x] az R feletti polinomok halmazát, továbbá legyenek f és g tetszőleges nemnulla polinomok. Ekkor a 26.3. Definícióban bevezetett polinomok közötti műveletekre teljesülnek az alábbiak:
- Ha \deg(f)\gt \deg(g), akkor \deg(f+g)=\deg(f).
- Ha \deg(f)=\deg(g), akkor \deg(f+g)\leq \deg(f).
- Ha f\cdot g\neq 0, akkor \deg(f\cdot g)\leq \deg(f)+\deg(g).
- Ha R nullosztómentes (lásd a 15.3. Definíciót), akkor \deg(f\cdot g)= \deg(f)+\deg(g).
- Ha R egységelemes, és f vagy g főegyütthatója az egységelem, akkor \deg(f\cdot g)= \deg(f)+\deg(g).
Bizonyítás:
Legyen 0_R az R gyűrű nulleleme, továbbá vezessük be az alábbi jelöléseket:
\begin{aligned}\deg(f)&=n \\ \deg(g)&=m\end{aligned}Ennek megfelelően f és g az alábbi sorozatokkal reprezentálhatók:
\begin{aligned}f&=(a_0,a_1,\ldots,\overbrace{a_n}^{\neq 0_R}, 0_R, 0_R, \ldots) \\ g&=(b_0,b_1,\ldots,\underbrace{b_m}_{\neq 0_R}, 0_R, 0_R, \ldots)\end{aligned}Az 1. állítás: Mivel n=\deg(f)\gt \deg(g)=m, vagyis az n index nagyobb g fokánál, emiatt b_n=0_R, tehát az összegpolinom n-edik tagja a_n+b_n=a_n. Az n index viszont megegyezik f fokával, így ez az n-edik tag biztosan nem 0_R. Az összegpolinom további tagjai viszont már mind nullák, mivel az n-nél nagyobb indexek nagyobbak f és g fokánál is. Ez a 26.3. Definíció alapján azt jelenti, hogy \deg(f+g)=n=\deg(f).
A 2. állítás: Az továbbra is igaz, hogy az n-nél nagyobb indexek nagyobbak f és g fokánál is, így az ilyen indexű tagok biztosan nullák mindkét polinomban, ami természetesen az összegükre is igaz, azaz \deg(f+g) legfeljebb akkora lehet, mint f (vagy g) foka. Ennél többet viszont nem is mondhatunk, mivel attól még, hogy sem a_n sem pedig b_n nemnulla, az összegük még lehet az – történetesen ha épp egymás ellentettjei az R gyűrűben.
A 3. állítás: Az f\cdot g szorzatpolinom együtthatóira vezessük be az alábbi jelölést:
f\cdot g=(c_0,c_1,c_2,\ldots)Azt kell bizonyítani, hogy ennek a szorzatpolinomnak a \deg(f)+\deg(g)=n+m-nél nagyobb indexű tagjai mind nullák (hiszen ekkor lesz a szorzatpolinom foka legfeljebb n+m). Legyen ezért k egy tetszőleges ilyen index (azaz k\geq n+m+1), és mutassuk meg, hogy ekkor c_k=0_R. A 26.3. Definíció alapján a c_k együttható olyan a_ib_j szorzatok összegéből áll, ahol i+j=k. Igaz tehát a következő:
\underbrace{i+j}_{=k}\geq n+m+1Ha i\leq n, akkor ez a 15.18. Definíció alapján azt jelenti, hogy létezik olyan nemnegatív l\geq 0 egész szám, hogy i+l=n. Ezt behelyettesítve a fenti egyenlőtlenségbe az alábbit kapjuk:
i+j\geq \underbrace{i+l}_{=n}+m+1Mindkét oldalból i-t levonhatunk:
j\geq l+m+1Mivel l+1 pozitív – hiszen l legalább 0 –, ezért ez az egyenlőtlenség ugyancsak a 15.18. Definíció alapján azt jelenti, hogy j\gt m. Ám ekkor az a_ib_j szorzatban a b_j tényező nulla, mivel m a g polinom foka. Ha viszont i\gt n, akkor meg az a_i tényező nulla, mivel n viszont az f polinom foka. Azt kaptuk tehát, hogy a szorzatpolinom c_k tagját előállító képletben minden tag nulla, vagyis maga c_k is.
Végül a 4. és 5. állítás: Az előző ponthoz hasonló gondolatmenetet fogunk követni. Azt a 3. állításban már megmutattuk, hogy a szorzatpolinomban az n+m-nél nagyobb indexű tagok mind nullák. Legyen most k=n+m, és mutassuk meg, hogy ekkor viszont c_k\neq 0_R. A c_k együttható olyan a_ib_j szorzatok összegéből áll, ahol i+j=k. Igaz tehát a következő:
\underbrace{i+j}_{=k}=n+mHa i\lt n, akkor ez a 15.18. Definíció alapján azt jelenti, hogy létezik olyan pozitív l\gt 0 egész szám, hogy i+l=n. Ezt behelyettesítve a fenti egyenletbe az alábbit kapjuk:
i+j=\underbrace{i+l}_{=n}+mMindkét oldalból i-t levonhatunk:
j=l+mLétezik tehát olyan pozitív egész szám, amelyet m-hez adva j-t kapunk (nevezetesen l), ami azt jelenti, hogy j\gt m. Ám ekkor az a_ib_j szorzatban a b_j tényező nulla, mivel m a g polinom foka. Ha viszont i\gt n, akkor meg az a_i tényező nulla, mivel n viszont az f polinom foka.
Egyedül i=n esetben lesz nemnulla az a_ib_j szorzat, hiszen ekkor j=m, és sem a_n, sem pedig b_m nem lehet nulla, mivel az f polinom foka n, a g polinom foka pedig m. De a tételben szereplő feltételek esetén az ő szorzatuk sem lehet nulla: ha R egységelemes és a_n vagy b_m az egységelem, akkor azért, ha pedig R nullosztómentes, akkor pedig azért. Vagyis c_k=a_nb_m\neq 0_R. Ez viszont azt jelenti, hogy az f\cdot g szorzatpolinom foka épp k=n+m=\deg(f)+\deg(g).
∎Ez alapján már igazolni tudjuk az R[x]-re vonatkozó alábbi fontos tételt.
26.5. Tétel (Polinomgyűrű):
Legyen R tetszőleges kommutatív gyűrű, és jelölje R[x] az R feletti polinomok halmazát. Ekkor az R[x] halmaz a 26.3. Definícióban bevezetett műveletekkel szintén egy kommutatív gyűrűt alkot, amelyet az R feletti polinomgyűrűnek nevezünk. Ezt a gyűrűt az alaphalmazához hasonlóan szintén R[x]-szel jelöljük.
Az R[x] gyűrű nulleleme a nullapolinom, továbbá tetszőleges f=(a_0,a_1,\ldots) polinom -f-fel jelölt ellentettje az alábbi polinom:
-f=(-a_0,-a_1,-a_2,\ldots)Ha R egységelemes gyűrű (lásd a 14.12. Definíciót), melynek egységelemét 1_R-rel, nullelemét pedig 0_R-rel jelöljük, akkor R[x] is egységelemes, melynek egységeleme az alábbi konstans polinom:
(1_R,0_R,0_R,0_R,\ldots)Végül ha R nullosztómentes, akkor R[x] is nullosztómentes.
♣Bizonyítás:
Előszöris megmutatjuk, hogy a 26.3. Definícióban bevezetett műveletek nem vezetnek ki az R[x] halmazból, azaz algebrai értelemben is műveletek (lásd a 11.3. Definíciót).
A 26.4. Tétel 1. és 2. pontjai alapján ugyanis nemnulla polinomok összegének foka legfeljebb a polinomok fokainak maximuma, továbbá ugyanezen tétel 3. pontja alapján nemnulla polinomok szorzatának foka legfeljebb a polinomok fokainak összege, hacsak az eredmény nem maga a nullapolinom. Ezekben az esetekben tehát ha egy összeg tagjainak vagy egy szorzat tényezőinek foka véges, akkor az eredmény foka is véges, vagy az eredmény a nullapolinom. Emiatt R[x] valóban zárt a nemnulla polinomok összeadására és szorzására nézve.
Az nyilvánvaló, hogy a polinomok összeadása kommutatív és asszociatív, hiszen a 26.3. Definíció alapján azt tagonként kell elvégezni az R gyűrűben, ahol teljesül ez a két tulajdonság. Ezenkívül ha egy polinomhoz akár jobbról, akár balról a nullapolinomot adjuk, akkor az eredmény nem változik, hiszen a nullapolinom minden tagja az R gyűrű nulleleme, ezért a tagonkénti összeadás egyetlen tagot sem változtat meg. Egyrészt tehát az R[x] halmaz a nullapolinommal való összeadásra nézve is zárt, másrészt a nullapolinom valóban neutrális elem az R[x]-beli összeadásra nézve. A tételben szereplő -f-fel jelölt polinomra továbbá teljesül az alábbi, amennyiben az R gyűrű nullelemét 0_R-rel jelöljük:
f+(-f)=(a_0-a_0, a_1-a_1,\ldots)=(0_R,0_R,\ldots)A már bizonyított kommutativitás miatt a másik irányú összeadásra ugyanez teljesül. Az f-et -f-fel akár jobbról, akár balról összeadva tehát a nullapolinomot kapjuk, amely emiatt f ellentettje a polinomok összeadására nézve.
Továbbá ha egy polinomot jobbról vagy balról a nullapolinommal szorozzuk, akkor az eredmény tetszőleges k-adik tagja a 26.3. Definícióban szereplő képlet alapján az alábbiak szerint alakul:
\begin{aligned}&a_0\cdot 0_R+a_1\cdot 0_R+\ldots +a_k\cdot 0_R = 0_R \\ &0_R\cdot a_k + 0_R\cdot a_{k-1} + \ldots + 0_R\cdot a_0 = 0_R\end{aligned}Ilyenkor az eredmény tehát a nullapolinom, és így R[x] zárt a nullapolinommal való szorzásra nézve is.
Igazoltuk tehát a műveleti zártságot, továbbá a 14.12. Definícióban szereplő 1., 2. és 3. gyűrűaxiómákat. Így annak igazolásához, hogy R[x] gyűrű, már csak a szorzás kommutativitását, asszociativitását és a disztributivitási tulajdonságot kell ellenőrizni. A továbbiakban ezért legyenek f=(a_0,a_1,\ldots), g=(b_0,b_1,\ldots) és h=(c_0,c_1,\ldots) az R[x] halmaz tetszőleges elemei. A kommutativitás igazolásához írjuk fel az f\cdot g és a g\cdot f szorzatpolinomok tetszőleges k-adik tagját a 26.3. Definícióban szereplő képlettel:
\begin{aligned}&a_0b_k+a_1b_{k-1}+\ldots +a_kb_0 \\ &b_0a_k + b_1a_{k-1}+ \ldots + b_ka_0\end{aligned}Mivel az R gyűrűben a szorzás kommutatív, ezért ez a két kifejezés azonos, így tehát az R[x]-beli szorzás is kommutatív.
Az asszociativitáshoz írjuk fel először az f\cdot g szorzatpolinom tagjait:
\begin{array}{rl}\text{0. tag:} & a_0b_0 \\ \text{1. tag:} & a_0b_1 + a_1b_0 \\ \text{2. tag:} & a_0b_2+a_1b_1+a_2b_0 \\ & \vdots \\ \text{k. tag:} & a_0b_k + a_1b_{k-1} + a_2b_{k-2} +\ldots +a_kb_0 \\ & \vdots \end{array}Ha ezt a szorzatpolinomot megszorozzuk jobbról a h polinommal, akkor az (f\cdot g)\cdot h szorzatpolinomot kapjuk, amelynek tetszőleges k-adik tagja a 26.3. Definíció alapján az alábbi összeg lesz:
\begin{aligned}&a_0b_0c_k + \\ + &a_0b_1c_{k-1} + a_1b_0c_{k-1} + \\ + &a_0b_2c_{k-2} + a_1b_1c_{k-2} + a_2b_0c_{k-2} + \\ &\vdots \\ + &a_0b_kc_0 + a_1b_{k-1}c_0 + a_2k_{k-2}c_0 + \ldots + a_kb_0c_0\end{aligned}Most írjuk fel a g\cdot h szorzatpolinom tagjait fordított sorrendben:
\begin{array}{rl}& \vdots \\ \text{k. tag:} & b_0c_k + b_1c_{k-1}+\ldots +b_kc_0 \\ \text{k-1. tag:} & b_0c_{k-1} + b_1c_{k-2} + \ldots + b_{k-1}c_0 \\ \text{k-2. tag:} & b_0c_{k-2} + b_1c_{k-3} +\ldots + b_{k-2}c_0 \\ & \vdots \\ \text{0. tag:} & b_0c_0 \end{array}Ha ezt a szorzatpolinomot megszorozzuk balról az f polinommal, akkor az f\cdot (g\cdot h) szorzatpolinomot kapjuk, amelynek tetszőleges k-adik tagja a 26.3. Definíció alapján az alábbi összeg lesz:
\begin{aligned}&a_0b_0c_k + a_0b_1c_{k-1}+\ldots +a_0b_kc_0 + \\ + &a_1b_0c_{k-1} + a_1b_1c_{k-2} + \ldots + a_1b_{k-1}c_0 + \\ + &a_2b_0c_{k-2} + a_2b_1c_{k-3} +\ldots + a_2b_{k-2}c_0 + \\ &\vdots \\ + &a_kb_0c_0 \end{aligned}Látható, hogy ennek az összegnek a soraiban pontosan ugyanazok a tagok szerepelnek, mint annak az összegnek az oszlopaiban, amelyet az (f\cdot g)\cdot h szorzatpolinom k-adik tagjára kaptunk. A két polinom tehát valóban megegyezik, azaz teljesül az alábbi asszociativitási tulajdonság:
(f\cdot g)\cdot h=f\cdot (g\cdot h)Ezután a disztributivitási tulajdonságot igazoljuk. Mivel a szorzás kommutativitását már megmutattuk, ezért elegendő a 14.12. Definícióban szereplő 5. gyűrűaxiómából csak az egyik diszributivitási szabállyal foglalkozni. Írjuk fel az f\cdot (g+h) polinom tetszőleges k-adik tagját a 26.3. Definícióban szereplő képletek alapján:
a_0(b_k+c_k)+a_1(b_{k-1}+c_{k-1})+\ldots +a_k(b_0+c_0)A zárójeleket felbonthatjuk, hiszen az R gyűrűben teljesülnek a disztributivitási szabályok:
\overbrace{a_0b_k + a_0c_k}^{=a_0(b_k+c_k)} + \overbrace{a_1b_{k-1} + a_1c_{k-1}}^{=a_1(b_{k-1}+c_{k-1})} + \ldots + \overbrace{a_kb_0 + a_kc_0}^{=a_k(b_0+c_0)}Ezután írjuk fel az f\cdot g + f\cdot h polinom tetszőleges k-adik tagját is szintén a 26.3. Definícióban szereplő képletek alapján:
\begin{aligned}&a_0b_k + a_1b_{k-1} +\ldots a_kb_0 + \\ + &a_0c_k + a_1c_{k-1} + \ldots + a_kc_0\end{aligned}Ugyanazokat a tagokat kaptuk, csak épp más sorrendben. Mivel azonban az R gyűrűben az összeadás kommutatív, ezért a két kapott kifejezés megegyezik, azaz valóban teljesül az alábbi disztributivitási szabály:
f\cdot (g + h)=f\cdot g + f\cdot hEzzel igazoltuk, hogy R[x] gyűrű a polinomok közötti műveletekkel. Most tegyük fel, hogy R egységelemes, és nézzük meg, hogy mi a helyzet, ha f-et akár balról, akár jobbról megszorozzuk a tételben szereplő (1_R,0_R,0_R,\ldots) polinommal. Mivel a szorzás ugye kommutatív, ezért elegendő csak az egyik, például a jobboldali szorzást ellenőrizni. E szorzat k-adik tagja a 26.3. Definícióban szereplő képlet alapján az alábbi lesz:
a_0\cdot 0_R + a_1\cdot 0_R + \ldots a_{k-1}\cdot 0_R + a_k\cdot 1_RLátható, hogy ebben az összegben a k-adik tagot kivéve minden tag 0_R lesz. Azaz az (1_R, 0_R, 0_R, \ldots) polinommal való szorzás f minden együtthatóját helybenhagyja, és így R[x] valóban egységelemes.
Végül tegyük fel, hogy R nullosztómentes. Ekkor a 26.4. Tétel 4. pontja alapján bármely két nemnulla polinom szorzatának foka pontosan a két polinom fokának összege lesz. Vagyis az eredménynek van foka, és így az semmiképpen sem lehet a nullapolinom, ami ugye a 15.3. Definíció alapján azt jelenti, hogy R[x] is nullosztómentes.
∎A következő szakaszban megvizsgáljuk, hogy mi a kapcsolat a 26.3. Definícióban szereplő végtelen sorozatokat használó reprezentáció, és a kevésbé szigorú x-et tartalmazó kifejezésekkel történő ábrázolásmód között.
Polinomfüggvények
Legyen adott továbbra is egy tetszőleges R kommutatív gyűrű. Az előző szakaszban tárgyalt R feletti polinomok felfoghatók olyan „gépek” leírásaként is, amelyek nagyon hasonlítanak a 11. részben definiált kétváltozós műveletekhez. A különbség pusztán annyi, hogy ebben az esetben egy ilyen „gép” tetején kettő helyett csak egy lyuk van. Ha például f egy R feletti polinom, azaz f\in R[x], akkor jelöljük F-fel az általa leírt „gépet”, amelyet tehát így tudunk elképzelni:
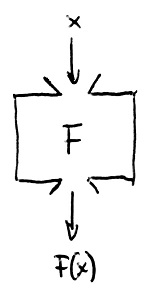
Ha most ennek az F-fel jelölt „gépnek” a tetején bedobunk egy valamilyen R-beli elemet, akkor ez a „gép” „végre fogja hajtani” az f polinom, mint az ő leírása által specifikált műveletsorozatot. Ennek az eredménye szintén az R gyűrű valamely eleme lesz, amely szépen kipottyan a „gép” alján.
Nézzünk is egy konkrét példát. Tekintsük például az alábbi f polinomot az egész számok \Z gyűrűje feletti \Z[x] polinomgyűrűben:
f=(1,2,3,0,0,0,\ldots)Itt szándékosan a 26.3. Definícióban szereplő végtelen sorozattal történő reprezentációt használtuk, mivel hangsúlyozni szeretnénk, hogy az f polinom csupán egy leírása az F-fel jelölt „gépnek”, nem pedig maga a „gép”. Az alábbi ábra mutatja, hogy mi történik, ha ennek a „gépnek” a felső nyílásába „bedobjuk” a 4\in \Z egész számot:

A „gép” alján tehát az 57\in \Z egész szám, mint eredmény fog kipottyanni. A „gép” működését könnyen megérthetjük, ha az f polinomot, mint e „gép” leírását a 26.3. Definícióban szereplő végtelen sorozat helyett kevésbé precízen a neki megfelelő alábbi kifejezésként képzeljük el, ahogyan azt az ábrán is feltüntettük:
f=1+2x+3x^2Valóban, a „gép” alján kipottyanó 57 egész szám úgy áll elő, hogy a tetején bedobott 4 egész számot behelyettesítjük ebbe a kifejezésbe az x ismeretlen helyére, és az így kapott műveletsorozatot végrehajtjuk a \Z gyűrűben. Ez az „algoritmus” nyilván bármilyen egész számra végrehajtható. Így az f polinom által leírt F „gép” tulajdonképpen nem más, mint egy F:\Z\to \Z függvény, amely tehát a \Z gyűrű minden eleméhez egyértelműen hozzárendel szintén egy \Z-beli gyűrűelemet. Méghozzá azt, amelyet az f polinom által leírt műveletsorozat végrehajtásával számítunk ki a bemeneti gyűrűelemből. Ez elvezet minket az alábbi fontos definícióhoz.
26.6. Definíció (Polinomfüggvény):
Legyen R egy tetszőleges kommutatív gyűrű, f\in R[x] pedig egy tetszőleges R feletti polinom. Tegyük fel, hogy f vagy a nullapolinom, vagy pedig a foka legfeljebb n, azaz reprezentálható az alábbi végtelen sorozattal, ahol 0_R jelöli az R gyűrű nullelemét:
f=(a_0,a_1,a_2,\ldots ,a_{n-1},a_n, 0_R, 0_R, 0_R, \ldots)Ekkor az f polinomhoz tartozó polinomfüggvénynek nevezzük azt az F:R\to R függvényt, amely tetszőleges x\in R gyűrűelemhez az alábbi F(x)-szel jelölt gyűrűelemet rendeli hozzá:
F(x)=a_0+a_1\cdot x+a_2\cdot x^2+\ldots + a_{n-1}\cdot x^{n-1} + a_n\cdot x^nAz ebben a képletben szereplő összeadások és szorzások alatt az R gyűrű összeadását és szorzását kell érteni.
♣Itt tehát az x már nem csupán egy szimbolikus változó, hanem egy konkrét R-beli gyűrűelemet jelöl. Fontos kihangsúlyozni, hogy egy polinom illetve a hozzátartozó polinomfüggvény két teljesen különböző fogalom, noha első látásra ez nem látszik. Például tekintsük az alábbi két \Z feletti polinomot és a hozzájuk tartozó polinomfüggvényeket:
\begin{aligned}f=(0,0,3,0,0,\ldots) &\to F(x)=3x^2 \\ g=(0,2,1,0,0,\ldots) &\to G(x)=2x+x^2\end{aligned}Mivel most az egész számok \Z gyűrűjéről van szó, ezért az F és G polinomfüggvények grafikonjait a középiskolában megszokott módon ábrázolhatjuk is két egymásra merőleges tengely segítségével, amelyek a nullánál metszik egymást. Az alábbi ábrán az F polinomfüggvény grafikonjának pontjait \bullet-okkal, a G polinomfüggvény grafikonjának pontjait pedig \circ-ökkel ábrázoltuk:
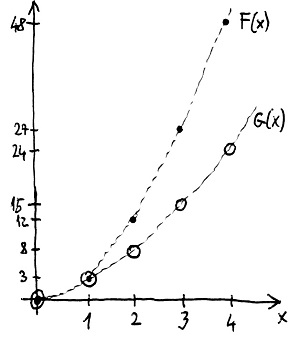
Látható, hogy jelen esetben az f és g polinomok egyértelműen azonosíthatók a hozzájuk tartozó F és G polinomfüggvényekkel, hiszen ezek grafikonjai is különböznek egymástól. Ezért egyesek hajlamosak arra gondolni, hogy gyakorlati szempontból nincs is különbség a két fogalom között.
Egy gondolatkísérlet erejéig azonban térjünk most át az egész számok \Z gyűrűjéről a 18.3. Definícióban definiált \Z_4 gyűrűre, és tegyük fel, hogy a fenti f és g polinomok most a \Z_4[x] polinomgyűrű elemei. Ezt nyugodtan megtehetjük, hiszen az őket reprezentáló végtelen sorozatok elemei 4-nél kisebb egész számok, vagyis mindannyian tekinthetők a \Z_4 gyűrű elemeinek is. Ekkor az f-hez és g-hez tartozó F és G polinomfüggvényeket a 26.6. Definíció alapján ugyanúgy a fenti két képlettel adhatjuk meg:
\begin{aligned}f=(0,0,3,0,0,\ldots) &\to F(x)=3x^2 \\ g=(0,2,1,0,0,\ldots) &\to G(x)=2x+x^2\end{aligned}A különbség pusztán annyi, hogy itt az F és G polinomfüggvények képletében szereplő összeadások és szorzások alatt most a \Z_4 gyűrű műveleteit, vagyis a 18.3. Definícióban definiált moduláris összeadást és szorzást kell érteni. Mivel a \Z_4 gyűrűnek mindössze 4 eleme van, ezért most az F és G polinomfüggvények „grafikonjait” az alábbi táblázatban adhatjuk meg:
\begin{array}{c||c|c}x & F(x)=3x^2 & G(x)=2x+x^2 \\ \hline 0 & 3\cdot 0^2=0 & 2\cdot 0+0^2=0 \\ 1 & 3\cdot 1^2=3 & 2\cdot 1+1^2=3 \\ 2 & 3\cdot 2^2=0 & 2\cdot 2+2^2=0 \\ 3 & 3\cdot 3^2=3 & 2\cdot 3+3^2=3\end{array}A példából jól látszik, hogy noha az f és g polinomok most is különböznek egymástól, a hozzájuk tartozó polinomfüggvények mégis ugyanazt a hozzárendelést valósítják meg, hiszen bármely x\in \Z_4 gyűrűelemhez mindketten ugyanazt a szintén \Z_4-beli gyűrűelemet rendelik hozzá. Ez a fenti táblázatból is látszik, hiszen a „grafikonjaikhoz” tartozó oszlopok azonosak, ami viszont azt jelenti, hogy a két polinomfüggvény megegyezik, függetlenül attól, hogy kétféle képlettel is le tudtuk írni őket a \Z_4 gyűrű műveleteit használva. Általánosságban tehát minden polinomhoz egyértelműen tartozik egy polinomfüggvény, azonban ugyanaz a polinomfüggvény tartozhat egynél több polinomhoz is.
A polinomok és polinomfüggvények tehát két nagyon különböző állatfaj. Van azonban közöttük egy fontos összefüggés, amelyre hamarosan rávilágítunk. Először azonban definiáljuk, hogy mit értünk két függvény (speciálisan két polinomfüggvény) pontonkénti összege illetve szorzata, vagy teljes általánosságban két függvény pontonkénti „összeműveletezése” alatt.
26.8. Definíció (Függvények közötti műveletek):
Legyen R egy tetszőleges gyűrű egy + szimbólummal jelölt összeadással és egy \cdot szimbólummal vagy egymás után írással jelölt szorzással. Legyenek továbbá f:R\to R és g:R\to R valamilyen R-en értelmezett és R-be képező függvények.
Ekkor az f+g-vel illetve f\cdot g-vel jelölt függvények alatt azokat a – szintén R-en értelmezett és R-be képző – függvényeket értjük, amelyek minden x\in R gyűrűelemhez rendre az f(x)+g(x) illetve az f(x)\cdot g(x) elemet rendelik hozzá. Előbbit az f és g függvények pontonkénti összegének, utóbbit pedig pontonkénti szorzatának nevezzük. Képlettel:
\begin{aligned}(f+g)(x)&=f(x)+g(x) \\ (f\cdot g)(x)&=f(x)\cdot g(x)\end{aligned}Általánosságban: Amennyiben R tetszőleges halmaz egy valamilyen * szimbólummal jelölt kétváltozós művelettel, akkor az f*g-vel jelölt függvény alatt azt a függvényt értjük, amely minden x\in R elemhez az f(x)*g(x) elemet rendeli hozzá. Képlettel:
(f*g)(x)=f(x)*g(x) ♣Ennek a fogalomnak a felhasználásával megfogalmazhatjuk a már említett, polinomok és polinomfüggvényeik közötti fontos összefüggést.
26.9. Tétel:
Legyen R tetszőleges kommutatív gyűrű, f és g pedig tetszőleges R feletti polinomok a hozzájuk tartozó F és G polinomfüggvényekkel. Az R gyűrű műveleteit jelöljük a szokásos módon, míg az R[x] polinomgyűrű műveleteit jelöljük a \oplus és \odot szimbólumokkal.
Ekkor az f\oplus g összegpolinomhoz az F+G, míg az f\odot g szorzatpolinomhoz az F\cdot G polinomfüggvény tartozik, melyek alatt a 26.8. Definíció szerinti értelemben vett pontonkénti összeg- illetve szorzatfüggvényeket értjük.
♣A bizonyításban a polinomokkal való számolás intuitív bevezetése során látott gondolatmenetet fogjuk követni.
Bizonyítás:
A továbbiakban reprezentáljuk az f és g polinomokat az alábbi végtelen sorozatokkal, ahol 0_R jelöli az R gyűrű nullelemét:
\begin{aligned}f&=(a_0,a_1,a_2,\ldots, a_n,0_R,0_R,0_R,\ldots) \\ g&=(b_0,b_1,b_2,\ldots, b_m,0_R,0_R,0_R,\ldots)\end{aligned}A 26.3. Definíció szerint e két polinom összegének k-adik tagját az alábbi képletből kapjuk:
c_k=a_k+b_kSzintén a 26.3. Definíció alapján a két polinom szorzatának k-adik tagját pedig az alábbi képlet szolgáltatja:
c_k=a_0b_k+a_1b_{k-1}+a_2b_{k-2}+\ldots+a_kb_0Az általánosság megsértése nélkül feltételezhetjük, hogy m=n. Ha ugyanis például m\leq n lenne a helyzet, akkor a g polinom tagjait az m+1-edik indextől kezdve, ha pedig m\geq n, akkor meg az f polinom tagjait az n+1-edik indextől kezdve 0_R-nek választva érvényes marad az alábbi gondolatmenet.
Ezek fényében a két polinomhoz tartozó polinomfüggények a 26.6. Definíció alapján minden x\in R gyűrűelemhez az alábbi kifejezések eredményét rendelik hozzá:
\begin{aligned}F(x)&=a_0+a_1x+a_2x^2+\ldots+a_nx^n \\ G(x)&=b_0+b_1x+b_2x^2+\ldots+b_nx^n\end{aligned}E két polinomfüggvény pontonkénti összege a 26.8. Definíció értelmében az alábbi lesz (miután a tagok sorrendjét az x hatványai szerint sorbarendeztük és csoportosítottuk):
(F+G)(x)=(a_0+b_0) + (a_1+b_1)x + (a_2+b_2)x^2 + \ldots + (a_n+b_n)x^nLátható, hogy itt tetszőleges k esetén az x^k tag együtthatója a_k+b_k alakban írható fel, vagyis ez a pontonkénti összegfüggvény a 26.6. Definíció értelmében valóban az f+g összegpolinomhoz tartozó polinomfüggvény lesz.
A két polinomfüggvény pontonkénti szorzatának kiszámításához az alábbi zárójeles kifejezést kell felbontani:
\begin{aligned}(F\cdot G)(x)=&(a_0+a_1x+a_2x^2+\ldots+a_nx^n)\cdot \\ \cdot &(b_0+b_1x+b_2x^2+\ldots+b_nx^n)\end{aligned}Ha most minden tagot minden taggal megszorzunk, akkor tetszőleges k esetén az x^k tag együtthatója azoknak az a_ib_j szorzatoknak az összege lesz, ahol i+j=k, azaz:
a_0b_k+a_1b_{k-1}+a_2b_{k-2}+\ldots+a_kb_0Vagyis ez a pontonkénti szorzatfüggvény a 26.6. Definíció értelmében valóban az f\cdot g szorzatpolinomhoz tartozó polinomfüggvény lesz.
∎Polinomok gyökei
Egy adott gyűrű feletti polinom szempontjából fontos szerepük van azoknak a gyűrűelemeknek, amelyekhez a polinomhoz tartozó polinomfüggvény a gyűrű nullelemét rendeli hozzá. Erről szól az alábbi definíció.
26.7. Definíció (Polinomok gyökei):
Legyen R egy tetszőleges kommutatív gyűrű, f\in R[x] egy tetszőleges R feletti polinom, F:R\to R pedig az f polinomhoz tartozó polinomfüggvény. Jelöljük továbbá az R gyűrű nullelemét 0_R-rel.
Ekkor az f polinom gyökeinek nevezzük azokat az x\in R gyűrűelemeket, amelyekhez az F polinomfüggvény az R gyűrű nullelemét rendeli hozzá. Azaz amelyekre teljesül az alábbi:
F(x)=0_RIlyenkor azt mondjuk, hogy x az f polinom gyöke az R gyűrűben.
♣A előző szakaszban szereplő f=(0,0,3,0,0,\ldots) polinomnak például az egész számok \Z gyűrűjében egyetlen gyöke van: a 0 egész szám, hiszen F(0)=3\cdot 0^2=0, de bármilyen más számot behelyettesítve az eredmény nem nulla. Ezzel szemben a \Z_4 gyűrűben van egy további gyöke is, méghozzá a 2, hiszen ebben a gyűrűben F(2)=3\cdot 2^2=0. A g=(0,2,1,0,0,\ldots) polinomnak \Z-ben már két gyöke is van, méghozzá a 0 és a -2 egész számok, míg a \Z_4 gyűrűben a 0 és a 2 egész számok teljesítik a feltételt.
Bármely R gyűrű felett a nullapolinomnak nyilván minden R-beli elem gyöke, hiszen a 26.6. Definíció alapján a hozzátartozó polinomfüggvény minden együtthatója 0_R, és így ő az R gyűrű minden eleméhez a nullelemet rendeli hozzá. Számunkra érdekesebb kérdés, hogy egy R feletti nemnulla polinomnak maximum hány gyöke lehet R-ben. A szakasz hátralévő részében meg fogjuk mutatni, hogy ez összefüggésben van a polinom fokával.
Előbb azonban szükségünk van egy fontos tételre. Felhívjuk a figyelmet, hogy a tétel megfogalmazásához felhasználhatjuk az oszthatóság 16.1. Definícióját, hiszen ez a fogalom minden gyűrűben, így természetesen a polinomgyűrűkben is értelmes. A továbbiakban csak azt az esetet fogjuk vizsgálni, amikoris a vizsgált gyűrű egységelemes.
26.10. Tétel:
Legyen R egy tetszőleges kommutatív, egységelemes gyűrű, f\in R[x] egy tetszőleges polinom a hozzátartozó F polinomfüggvénnyel, r\in R pedig egy tetszőleges gyűrűelem.
Ekkor létezik olyan q\in R[x] polinom, amelynek Q polinomfüggvényére teljesül az alábbi egyenlet:
F(x)=(x-r)\cdot Q(x)+F(r)Legyen most f_r\in R[x] az az elsőfokú polinom, amelyhez az F_r(x)=x-r polinomfüggvény tartozik. Ebben az esetben az r gyűrűelem akkor és csak akkor gyöke az f polinomnak, ha teljesül az f_r|f oszthatóság az R[x] polinomgyűrűben a 16.1. Definíció szerinti értelemben. Az f_r polinomot az f polinom r gyökéhez tartozó gyöktényezőjének nevezzük.
♣Bizonyítás:
Tegyük fel, hogy az F polinomfüggvény olyan, hogy tetszőleges x\in R gyűrűelemhez az alábbi kifejezés eredményét rendeli hozzá:
F(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0Ennek értékét x=r esetén tehát az alábbi kifejezés kiértékelésével számíthatjuk ki:
F(r)=a_nr^n+a_{n-1}r^{n-1}+\ldots+a_1r+a_0Emeljük ki r-et minden olyan tagból, amelyikből lehet:
F(r)=(a_nr^{n-1}+a_{n-1}r^{n-2}+\ldots+a_2r+a_1)r+a_0Ismételgessük ezt a képződő zárójelekre mindaddig, ameddig lehetséges:
\begin{aligned}F(r)&=((a_nr^{n-2}+a_{n-1}r^{n-3}+\ldots+a_3r+a_2)r+a_1)r+a_0=\\&=(((a_nr^{n-3}+a_{n-1}r^{n-4}+\ldots+a_4r+a_3)r+a_2)r+a_1)r+a_0=\\&\vdots\\&=((\ldots (a_nr+a_{n-1})r+a_{n-2})r+a_{n-3})r+\ldots +a_1)r+a_0\end{aligned}Az így kapott n-1 darab egymásba ágyazott zárójelből álló kifejezést kezdjük el kiértékelni „bentről kifelé” haladva zárójelenként, és a kapott részeredményekre sorban vezessük be a q_{n-1}, q_{n-2}, ..., q_0 jelöléseket az alábbi szisztéma szerint:
\begin{aligned}q_{n-1}&=a_n \\ q_{n-2}&=q_{n-1}r+a_{n-1} \\ q_{n-3}&=q_{n-2}r+a_{n-2} \\ &\vdots \\ q_i&=q_{i+1}r+a_{i+1} \\ &\vdots \\ q_1&=q_2r+a_2 \\ q_0&=q_1r+a_1\end{aligned}Végül az utolsó lépést is elvégezve megkapjuk az F(r) értékét:
F(r)=q_0r+a_0Vegyük észre, hogy az eljárással épp a keresett Q polinomfüggvény együtthatóit számítottuk ki. Ezt könnyen ellenőrizhetjük, ha felbontjuk az alábbi zárójelet:
(x-r)\cdot (\underbrace{q_{n-1}x^{n-1}+q_{n-2}x^{n-2}+\ldots+q_1x+q_0}_{=Q(x)})=\ldotsItt a baloldali zárójelben lévő mindkét tagot a jobboldali zárójelben lévő minden taggal meg kell szorozni. E beszorzás után az alábbi tagokat kapjuk, amelyek egy hiányzó a_0 tagot és egy felesleges -q_0r tagot leszámítva épp az F(x) polinomfüggvény tagjaival egyeznek meg:
\begin{aligned}\ldots &=\underbrace{q_{n-1}}_{=a_n}x^n+\\&+\underbrace{(q_{n-2}-q_{n-1}r)}_{=a_{n-1}}x^{n-1}+\\&+\underbrace{(q_{n-3}-q_{n-2}r)}_{=a_{n-2}}x^{n-2}+\\ &\vdots \\&+\underbrace{(q_0-q_1r)}_{=a_1}x-q_0r\end{aligned}Összefoglalva:
(x-r)\cdot Q(x)=F(x)-a_0-q_0rHa most mindkét oldalhoz hozzáadunk a_0+q_0r-t, akkor megkapjuk a tétel első állítását:
(x-r)\cdot Q(x)+\underbrace{a_0+q_0r}_{=F(r)}=F(x)A második állításhoz tegyük fel először, hogy teljesül az f_r|f oszthatóság az R[x] polinomgyűrűben. A polinomok közötti szorzást \odot-tal jelölve ezt azt jelenti, hogy létezik olyan q\in R[x] polinom, hogy teljesül az alábbi:
f=f_r\odot qA 26.9. Tétel alapján az f_r\odot q szorzatpolinomhoz tartozó polinomfüggvény az F_r és Q polinomfüggvények pontonkénti szorzata lesz. A polinomfüggvények szintjén tehát felírható az alábbi egyenlet:
F(x)=\underbrace{(x-r)}_{=F_r(x)}\cdot Q(x)Ám ekkor az F(x) polinomfüggvény az R gyűrű nullelemét rendeli r-hez, hiszen ebben az esetben az F_r(r) tényező épp nulla lesz:
F(r)=\underbrace{(r-r)}_{=F_r(r)}\cdot Q(r)=0_R\cdot Q(r)=0_RVagyis ha fennáll az f_r|f oszthatóság az R[x] polinomgyűrűben, akkor r valóban gyöke f-nek az R gyűrűben.
Megfordítva: Tegyük most fel, hogy r gyöke az f polinomnak az R gyűrűben. A tétel első állítása alapján létezik olyan q\in R[x] polinom, hogy a polinomfüggvények szintjén teljesül az alábbi egyenlet:
F(x)=\underbrace{(x-r)}_{=F_r(x)}\cdot Q(x)+F(r)Itt viszont a jobboldalon szereplő F(r) tag az R gyűrű nulleleme lesz, hiszen azt mondtuk, hogy r gyöke az f polinomnak. Azaz a fenti egyenlet az alábbira egyszerűsödik:
F(x)=F_r(x)\cdot Q(x)Ez viszont a 26.9. Tétel alapján a polinomok szintjén az alábbit jelenti:
f=f_r\odot qVagyis valóban teljesül az f_r|f oszthatóság az R[x] polinomgyűrűben.
∎Mostmár rátérhetünk arra, hogy egy nemnulla polinom gyökeinek száma milyen összefüggésben van a polinom fokával. Felhívjuk a figyelmet, hogy ez a tétel csak nullosztómentes gyűrűk esetén érvényes! Amennyiben ez nem teljesül, akkor meglehetősen furcsa dolgok történhetnek, amint azt a tétel igazolása után egy egyszerű példában látni fogjuk.
26.11. Tétel (Polinom gyökeinek száma):
Legyen R egy tetszőleges kommutatív, egységelemes és nullosztómentes gyűrű, legyen továbbá f\in R[x] egy tetszőleges nemnulla polinom, amelynek pontosan az r_1, r_2, ..., r_k gyűrűelemek a gyökei. Ha a \odot szimbólummal jelöljük az R[x] polinomgyűrű szorzását, akkor az f polinom felírható az alábbi alakban, ahol f_{r_1}, f_{r_2}, ..., f_{r_k} az f polinom minden gyökéhez tartozó egy-egy gyöktényezőjét, q pedig egy olyan polinomot jelöl, amelynek a fentieken kívül nincs további gyöke R-ben:
f=f_{r_1}\odot f_{r_2}\odot \ldots \odot f_{r_k}\odot qEbből következik, hogy f-nek legfeljebb annyi gyöke van R-ben, mint amennyi a foka.
♣Bizonyítás:
Tekintsük elsőként az f_{r_1} gyöktényezőt. A 26.10. Tétel alapján f felírható az alábbi alakban valamilyen alkalmas q_1\in R[x] polinommal:
f=f_{r_1}\odot q_1Mivel R egységelemes, továbbá az f_{r_1} gyöktényező főegyütthatója az egységelem – hiszen az ugye a 26.6. Definíció alapján megegyezik a hozzátartozó F_{r_1}(x)=x-r_1 polinomfüggvény elsőfokú tagjának, azaz x-nek az együtthatójával –, ezért a 26.4. Tétel 5. pontja alapján \deg(f)=\deg(f_{r_1})+\deg(q_1). Miután f_{r_1} egy gyöktényező, és így \deg(f_{r_1})=1, ezért a q_1 polinom foka eggyel kisebb f fokánál.
Továbbá a 26.10. Tétel alapján a polinomfüggvények szintjén az alábbi teljesül:
F(x)=(x-r_1)\cdot Q_1(x)De ugye r_2 is gyöke az f polinomnak, ezért őt behelyettesítve ebbe a polinomfüggvénybe az R gyűrű nullelemét kell kapnunk:
0_R=F(r_2)=(r_2-r_1)\cdot Q_1(r_2)A jobboldali első tényező biztosan nemnulla, ezért a nullosztómentesség miatt szükségképpen Q_1(r_2)=0_R, azaz r_2 gyöke a q_1 polinomnak. Ám ekkor a 26.10. Tétel alapján q_1-ből kiemelhető az f_{r_2} gyöktényező, azaz f felírható az alábbi alakban valamilyen alkalmas q_2\in R[x] polinommal, ahol q_2 foka a fentebb már ismertetett okok miatt már kettővel kisebb f fokánál:
f=f_{r_1}\odot f_{r_2}\odot q_2Ugyanilyen gondolatmenet alapján f-ből kiemelhető mind a k darab gyöktényező, és a fennmaradó q polinom foka k-val kisebb f fokánál:
f=f_{r_1}\odot f_{r_2}\odot \ldots \odot f_{r_k}\odot qMivel a fokszám nullánál nem lehet kisebb, ezért k valóban legfeljebb f foka lehet.
∎Most nézzünk egy egyszerű példát arra az esetre, ha a nullosztómentesség nem teljesülne. Például vegyük a \Z_8 gyűrűt a 18.3. Definícióban bevezetett moduláris összeadással és szorzással, és tekintsük azt a \Z_8 fölötti másodfokú polinomot, amelyhez az alábbi polinomfüggvény tartozik:
F(x)=x^2+7Mivel a \Z_8 gyűrűnek mindössze 8 eleme van, ezért próbálgatással könnyen megtalálhatjuk az összes gyököt:
\begin{aligned}F(0)&=0^2+7=0+7=7 \\ F(1)&=1^2+7=1+7=0 \\ F(2)&=2^2+7=4+7=3 \\ F(3)&=3^2+7=1+7=0 \\ F(4)&=4^2+7=0+7=7 \\ F(5)&=5^2+7=1+7=0 \\ F(6)&=6^2+7=4+7=3 \\ F(7)&=7^2+7=1+7=0\end{aligned}A gyökök tehát az 1, 3, 5 és 7 egész számok, azaz 4 darab van belőlük, pedig a polinom csak másodfokú volt. A problémát a nullosztómentesség hiánya okozza. Emiatt ugyanis nem mindegy, hogy milyen sorrendben emeljük ki a gyöktényezőket. Az iménti bizonyítás gondolatmenetét követve például emeljük ki elsőként az 1-hez tartozó gyöktényezőt, amelyhez ugye az F_1(x)=x-1 polinomfüggvény tartozik. Ekkor a polinomfüggvények szintjén az alábbi felbontást kapjuk:
F(x)=x^2+7=\underbrace{(x-1)}_{=F_1(x)}\cdot \underbrace{(x-7)}_{=Q_1(x)}Ebbe behelyettesítve a 3-at az eredmény valóban nulla, miközben a Q_1(3) tényező nemnulla:
F(3)=\underbrace{(3-1)}_{=F_1(3)=2}\cdot \underbrace{(3-7)}_{=Q_1(3)=4}=2\cdot 4=0Így viszont a 3-hoz tartozó gyöktényezőt már nem tudjuk kiemelni a q_1 polinomból, hiszen annak ő már nem gyöke. Az persze továbbra is igaz marad, hogy egy n-edfokú polinomból legfeljebb n darab gyöktényezőt lehet kiemelni, azonban a nullosztómentesség hiánya miatt ezeken kívül létezhetnek még további gyöktényezők is, amelyek tehát rejtve maradnak.
Primitív gyök létezése
Most a polinomokról eddig tanultakat arra fogjuk felhasználni, hogy igazoljuk az első szakaszban már említett nevezetes állítást, miszerint modulo p mindig létezik primitív gyök, amennyiben p egy tetszőleges pozitív prímszám. Ehhez először két segédtételt fogunk bizonyítani.
Az első segédtétel egy csoportelméleti állítás lesz. A 24.11. Definícióban bevezettük a csoportelem rendjének a fogalmát, amellyel kapcsolatban a 24.12. Tételben mondtunk ki néhány hasznos összefüggést. Most ezek felhasználásával megmutatjuk, hogy hogyan lehet kiszámolni egy csoportelem tetszőleges hatványának rendjét, ha egyébként magának a csoportelemnek a rendje már ismert.
26.12. Tétel (Csoportelem hatványának rendje):
Legyen G tetszőleges csoport, g pedig ennek egy tetszőleges eleme, amelynek rendje d, azaz:
o(g)=dEkkor g tetszőleges k-adik hatványának (lásd a 24.9. Definíciót) rendjét az alábbi képlet adja meg, ahol \frac{d}{(d,k)} azt az egész számot jelöli, amelyet a (d,k) kitüntetett közös osztóval megszorozva d-t kapunk:
o(g^k)=\frac{d}{(d,k)}A g^k hatvány rendje akkor és csak akkor egyezik meg g rendjével – azaz d-vel –, ha a k kitevő relatív prím d-hez.
♣Bizonyítás:
A 24.12. Tétel 4. pontja alapján tehát azt a legkisebb pozitív m kitevőt keressük, amellyel a g^k elemet hatványozva a csoport e-vel jelölt egységelemét kapjuk. Ez a hatvány a 24.10. Tétel 2. pontja alapján a g elem mk-adik hatványa lesz, azaz felírható az alábbi egyenlet:
(g^k)^m=g^{mk}=eEz a 24.12. Tétel 2. pontja alapján akkor és csak akkor teljesül, ha fennáll az alábbi kongruencia:
mk\equiv 0\pmod dMivel itt mind a baloldal, mind pedig a jobboldal osztható k-val, ezért alkalmazható a kongruenciák egyszerűsítéséről szóló 20.3. Tétel, miszerint fennáll az alábbi kongruencia is:
m\equiv 0\pmod{\frac{d}{(d,k)}}Ez a 20.1. Tétel 3. pontja alapján azt jelenti, hogy teljesül az alábbi oszthatóság:
\frac{d}{(d,k)}|mMármost azt mondtuk, hogy m az a legkisebb pozitív egész szám, amely teljesíti ezt az oszthatóságot. Így tehát ő nem más, mint maga \frac{d}{(d,k)}. Azaz g^k rendjére megkaptuk a tételben szereplő képletet:
o(g^k)=m=\frac{d}{(d,k)}Ez valóban akkor és csak akkor fog megegyezni o(g)=d-vel, ha a (d,k) kitüntetett közös osztó 1, azaz k relatív prím d-hez.
∎A második segédtétel egy nevezetes állítás az Euler-féle \varphi-függvénnyel kapcsolatban.
26.13. Tétel:
Legyen n\gt 0 tetszőleges pozitív egész szám, valamint \varphi a 20.7. Definíció szerinti Euler-függvény. Amennyiben d_1, d_2, ..., d_k az n egész szám összes pozitív osztója, akkor teljesül az alábbi összefüggés:
\varphi(d_1)+\varphi(d_2)+\ldots +\varphi(d_k)=n ♣A most következő bizonyítás gondolatmenete az lesz, hogy mutatunk két halmazt, amelyek közül az egyik egy n elemű halmaz lesz, a másiknak pedig annyi eleme lesz, mint a tételben szereplő összeg eredménye. Ezután e két halmaz elemei között egy kölcsönösen egyértelmű megfeleltetést fogunk mutatni, ami tulajdonképpen azt jelenti, hogy ugyanannyi elemük van. E megfeleltetés első ránézésre kissé mesterkéltnek fog tűnni, a mögötte lévő intuícióról azonban a bizonyítás utáni megjegyzésben szót ejtünk.
Bizonyítás:
Minden egyes, a tételben szereplő d_i osztóból állítsuk elő az összes olyan számpárt, amelynek első tagja d_i, második tagja pedig egy olyan d_i-nél kisebb nemnegatív egész szám, amely relatív prím d_i-hez. A 20.17. Következmény alapján pontosan \varphi(d_i) darab olyan számpárt tudunk előállítani, amelynek első tagja d_i, hiszen \varphi(d_i) épp azoknak az egészeknek a számát adja meg, amelyek a fenti szabály értelmében a számpár második tagjaként szerepelhetnek. Jelöljük S-sel az előállított számpárok halmazát, továbbá a_{ij}-vel a j-edik olyan számpárnak a második tagját, amelynek első tagja d_i. Ekkor S elemeit az alábbi lista sorolja fel:
\begin{aligned}S=\{&(d_1;a_{11}), (d_1;a_{12}), (d_1;a_{13}), \ldots, (d_1;a_{1\varphi(d_1)}), \\ &(d_2;a_{21}), (d_2;a_{22}), (d_2;a_{23}), \ldots, (d_2;a_{2\varphi(d_2)}), \\ &(d_3;a_{31}), (d_3;a_{32}), (d_3;a_{33}), \ldots, (d_3;a_{3\varphi(d_3)}), \\ &\vdots \\ &(d_k;a_{k1}), (d_k;a_{k2}), (d_k;a_{k3}), \ldots, (d_k;a_{k\varphi(d_k)}) \}\end{aligned}Látható, hogy az i-edik sorban \varphi(d_i) darab elem van, az S halmaz elemeinek a száma tehát épp a tételben szereplő összeg lesz, azaz:
\varphi(d_1)+\varphi(d_2)+\ldots+\varphi(d_k)Most képezzünk egy másik, T-vel jelölt halmazt, amelybe pakoljuk bele az egész számokat 0-tól n-1-ig, azaz:
T=\{0, 1, 2, \ldots, n-1\}Azt szeretnénk tehát igazolni, hogy az S és T halmazok elemei között egy kölcsönösen egyértelmű megfeleltetés létesíthető, hiszen ebből már következik, hogy mindketten ugyanannyi – azaz n darab – elemet tartalmaznak, ami épp a tétel állítása. Ehhez mutatunk egy f:S\to T és egy g:T\to S függvényt, amelyekről belátjuk, hogy egymás megfordításai.
Az f függvény legyen olyan, amely a fentiekben leírtaknak megfelelően konstruált tetszőleges (d;a)\in S számpárhoz az alábbi képlet jobboldalán szereplő egész számot rendeli hozzá. Itt a már megszokott jelölést alkalmazva \frac{n}{d} azt az egész számot jelöli, amelyet a d osztóval megszorozva az eredmény n:
f((d;a))=a\cdot \frac{n}{d}Most megmutatjuk, hogy a képlet jobboldalán szereplő kifejezés eredménye valóban a T halmazba esik. Az \frac{n}{d} egész szám nyilván pozitív, máskülönben őt a nemnegatív d osztóval megszorozva nem kaphatnánk eredményül a pozitív n-t. A (d;a) számpár konstrukciója miatt tudjuk, hogy teljesül az alábbi két egyenlőtlenség:
0\leq a\lt dEz a jobboldali \lt-vel jelölt szigorú rendezési reláció 15.18. Definíciója alapján azzal ekvivalens, hogy a\neq d, és teljesül az alábbi két egyenlőtlenség:
0\leq a \leq dA két egyenlőtlenség mindkét oldalát a pozitív \frac{n}{d}-vel megszorozva a 15.11. Definícióban szereplő 2. rendezési axióma alapján egyrészt ezt kapjuk:
0\leq a\cdot \frac{n}{d} \leq \overbrace{n}^{=d\cdot \frac{n}{d}}Másrészt pedig a\cdot \frac{n}{d}\neq n is teljesül, hiszen a\cdot \frac{n}{d}=n esetén mindkét oldalt d-vel szorozva an=nd, majd ezt a pozitív n-nel a 15.4. Tétel alapján egyszerűsítve a=d következne, ami ellentmondás. Vagyis az f függvény az S halmaz minden eleméhez valóban a T halmaz valamely elemét, azaz a 0, 1, ..., n-1 egész számok valamelyikét rendeli hozzá.
Most a másik irányba képző g:T\to S függvényt adjuk meg. Ez a függvény legyen olyan, hogy tetszőleges a\in T egész számhoz az alábbi képlet jobboldalán szereplő számpárt rendeli hozzá. Itt \frac{n}{(a,n)} illetve \frac{a}{(a,n)} azokat az egész számokat jelöli, amelyeket a pozitív (a,n) kitüntetett közös osztóval megszorozva az eredmény rendre n illetve a:
g(a)=(\frac{n}{(a,n)};\frac{a}{(a,n)})Most azt kell megmutatni, hogy a képlet jobboldalán szereplő számpár az S halmaz egy eleme, azaz hogy a g függvény valóban az S halmazba képez. A számpár első tagja nyilván osztója n-nek, hiszen őt megszorozva (a,n)-nel épp n az eredmény. Ráadásul szükségképpen pozitív is, máskülönben őt megszorozva a pozitív (a,n)-nel nem kaphatnánk eredményül a pozitív n-et. A számpár második tagja egyrészt ugyanilyen okok miatt nemnegatív, másrészt az első tagnál biztosan kisebb. Tegyük ugyanis fel indirekt, hogy nem ez a helyzet, azaz:
\frac{n}{(a,n)}\leq\frac{a}{(a,n)}Mindkét oldalt a pozitív (a,n)-nel szorozva n\leq a-t kapnánk, ami lehetetlen, hiszen a a T halmaz egy eleme, azaz biztosan kisebb n-nél. Végül azt kell megmutatni, hogy a számpár két tagja egymáshoz relatív prím. A kitüntetett közös osztó kiemelési tulajdonsága miatt (lásd a 17.9. Tételt) teljesül az alábbi asszociáció:
(\frac{n}{(a,n)},\frac{a}{(a,n)})\cdot (a, n) \sim (\underbrace{\frac{n}{(a,n)}\cdot (a,n)}_{=n},\underbrace{\frac{a}{(a,n)}\cdot (a,n)}_{=a})Azaz:
(\frac{n}{(a,n)},\frac{a}{(a,n)})\cdot (a, n) \sim \underbrace{(n,a)}_{=(a,n)}Minthogy a 16.10. Tétel alapján egy egységelemes integritástartományban valamely elem asszociáltjai pontosan az egységszeresei, emiatt a baloldalon tényezőként szereplő (\frac{n}{(a,n)},\frac{a}{(a,n)}) kitüntetett közös osztó szükségképpen egység kell legyen, és így a 17.10. Definíció utáni megjegyzés alapján az \frac{n}{(a,n)} valamint az \frac{a}{(a,n)} egész számok egymáshoz valóban relatív prímek. Ezzel tehát beláttuk, hogy a g függvény tényleg az S halmazba képez.
Utolsó lépésként azt kell megmutatni, hogy az f és g függvények kölcsönösen egymás megfordításai. Ez egyrészt azt jelenti, hogy tetszőleges a\in T esetén f(g(a))=a, másrészt pedig azt, hogy tetszőleges (d;a)\in S esetén g(f((d;a)))=(d;a) teljesül. Ellenőrizzük először az első azonosságot az f és g függvények fenti képleteibe való behelyettesítéssel:
f(g(a))=f(\underbrace{(\frac{n}{(a,n)};\frac{a}{(a,n)})}_{=g(a)})=\frac{a}{(a,n)}\cdot \frac{n}{\frac{n}{(a,n)}}Mindkét oldalt szorozzuk meg először (a,n)-nel, majd \frac{n}{(a,n)}-nel:
\underbrace{(a,n)\cdot \frac{n}{(a,n)}}_{=n}\cdot f(g(a))=a\cdot nMivel n pozitív, így biztosan nem nulla, azaz szabad vele egyszerűsíteni, amivel megkapjuk a kívánt azonosságot:
f(g(a))=aVégül a g(f((d;a)))=(d;a) azonosságot is a két függvény képletébe való behelyettesítéssel igazoljuk:
g(f((d;a)))=g(\underbrace{a\cdot \frac{n}{d}}_{=f((d;a))})=(\frac{n}{(a\cdot \frac{n}{d},n)};\frac{a\cdot \frac{n}{d}}{(a\cdot \frac{n}{d},n)})Azt kell megmutatnunk, hogy a jobboldalon szereplő bonyolult kifejezéssel megkapott számpár valójában megegyezik a kiindulási (d;a) számpárral, azaz hogy teljesül az alábbi két egyenlet:
\begin{aligned}d&=\frac{n}{(a\cdot \frac{n}{d},n)} \\ a&=\frac{a\cdot \frac{n}{d}}{(a\cdot \frac{n}{d},n)}\end{aligned}Az első egyenletből ekvivalens átalakításokkal a következőt kapjuk:
\begin{aligned}d&=\frac{n}{(a\cdot \frac{n}{d},n)} \\ d\cdot (a\cdot \frac{n}{d},n) &=n \\ (a\cdot n,d\cdot n) &=n \\ n\cdot (a,d)&=n \end{aligned}A második egyenletből pedig a következőt:
\begin{aligned}a&=\frac{a\cdot \frac{n}{d}}{(a\cdot \frac{n}{d},n)} \\ a\cdot (a\cdot \frac{n}{d},n) &=a\cdot \frac{n}{d} \\ (a\cdot \frac{n}{d},n) &= \frac{n}{d} \\ d\cdot (a\cdot \frac{n}{d}, n)&=n \\ (a\cdot n, d\cdot n) &=n \\ n\cdot (a,d)&=n\end{aligned}Mivel a (d;a) számpár az S halmaz egy eleme, ezért S definíciója miatt a relatív prím d-hez, vagyis (a,d)=1, és így mindkét azonosság teljesül.
Minthogy az f és g függvényekről megmutattuk, hogy egymás megfordításai, ezért ők egy kölcsönösen egyértelmű megfeleltetést létesítenek az S és a T halmazok elemei között, és ez az, amit bizonyítani akartunk.
∎Megjegyzés a bizonyításhoz:
A bizonyításban szereplő f és g függvények képlete első ránézésre kissé mesterkéltnek tűnhet. Ennek technikai oka van, ugyanis a szám fogalmát eddig csak a természetes és az egész számok körére korlátoztuk, az úgynevezett tört- vagy racionális számokat még nem vezettük be, így nem is tudunk hivatkozni rájuk. Az Olvasónak azonban az iskolából minden bizonnyal dereng valami a törtszámok egyszerűsítésének szabályaival kapcsolatban. Egy \frac{a}{b} alakban felírt törtszámot ugyanis adott esetben egyszerűbb alakban is fel lehet írni. Ha például az a számlálónak és a b nevezőnek van valamilyen 1-nél nagyobb közös osztója, akkor ezzel a közös osztóval elosztva mind a számlálót, mind a nevezőt ugyanazt a törtszámot tudjuk felírni, csak egyszerűbb alakban. Ezt egyszerűsítésnek nevezzük. Például:
\frac{231}{1001}=\frac{3}{13}A legegyszerűbb alakot akkor kapjuk, ha az egyszerűsítést a kitüntetett közös osztóval végezzük el, ami a fenti példában a 77. Most írjuk fel a \frac{0}{n}, \frac{1}{n}, \frac{2}{n}, ..., \frac{n-1}{n} törteket, majd ugyanezen törteket írjuk fel a legegyszerűbb alakjukban is. Például n=6 esetén ezek az egyszerűsítések a következőképpen néznek ki:
\begin{array}{cccccc}\frac{0}{6} & \frac{1}{6} & \frac{2}{6} & \frac{3}{6} & \frac{4}{6} & \frac{5}{6} \\ \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \\ \frac{0}{1} & \frac{1}{6} & \frac{1}{3} & \frac{1}{2} & \frac{2}{3} & \frac{5}{6}\end{array}A bizonyításban szereplő T halmaz elemeinek a felső sorban szereplő törtek számlálói, míg az S halmaz elemeinek az alsó sorban szereplő egyszerűsített törtek nevezőiből és számlálóiból alkotott számpárok felelnek meg. A g függvény ennek megfelelően minden a számlálójú törthöz az \frac{n}{(a,n)} nevezőjű és \frac{a}{(a,n)} számlálójú egyszerűsített törtet rendeli hozzá, míg az f függvény tulajdonképpen ennek az egyszerűsítésnek a megfordítása, amelyet egyébként bővítésnek nevezünk.
♣Ezek után már minden eszköz rendelkezésünkre áll ahhoz, hogy a primitív gyökök létezésére adjuk egy elégséges feltételt, amely kulcsfontosságú lesz ennek a résznek a második felében.
26.14. Tétel (Primitív gyök modulo p):
Legyen p\gt 0 valamilyen pozitív prímszám, (\Z/p\Z)^{\times} a modulo p maradékosztálygyűrű multiplikatív csoportja, d\gt 0 pedig tetszőleges pozitív egész szám. Ekkor d|p-1 esetén esetén a (\Z/p\Z)^{\times} csoportban pontosan \varphi(d) darab d rendű elem létezik, ha pedig d\nmid p-1, akkor egyáltalán nincs d rendű elem.
Következésképp d=p-1 esetén \varphi(p-1) darab p-1 rendű elem van – azaz létezik primitív gyök modulo p.
♣Vigyázzunk azonban, ez ugyanis csupán elégséges, de nem szükséges feltétel primitív gyök létezésére. Az első szakaszban például láttuk, hogy a (\Z/10\Z)^{\times} multiplikatív csoport is ciklikus, noha a 10 minden, csak nem prím.
Bizonyítás:
A (\Z/p\Z)^{\times} csoport a \Z/p\Z maradékosztálygyűrű redukált maradékosztályaiból áll, ezért a 20.7. Definíció alapján ennek a csoportnak a rendje \varphi(p), azaz a 21.5. Tétel miatt p-1. Mivel a 24.14. Következmény miatt bármely elem rendje osztója a csoport rendjének, ezért ha d\nmid p-1, akkor (\Z/p\Z)^{\times}-ben nincs d rendű elem.
Az általánosság megsértése nélkül feltehetjük tehát, hogy d|p-1. A d rendű redukált maradékosztályok a 24.12. Tétel 4. pontja szerint mind megoldásai a \Z/p\Z maradékosztálygyűrű elemein értelmezett alábbi egyenletnek:
x^d=[1]_pMindkét oldalból kivonva az [1]_p maradékosztályt az alábbi egyenletet kapjuk:
x^d-[1]_p=[0]_pVegyük észre, hogy ennek az egyenletnek a megoldásai a 26.7. Definíció alapján épp egy \Z/p\Z feletti d-edfokú polinom gyökei. Mivel \Z/p\Z izomorf \Z_p-vel, ami pedig a 18.5. Tétel alapján nullosztómentes, így \Z/p\Z is nullosztómentes. Emiatt viszont a 26.11. Tétel alapján ennek a bizonyos polinomnak legfeljebb d darab gyöke, azaz a fenti egyenletnek legfeljebb d darab megoldása van. Azt ugyan nem tudjuk még, hogy a (\Z/p\Z)^{\times} csoportban létezik-e egyáltalán d rendű redukált maradékosztály – hiszen épp ezt szeretnénk igazolni –, de ha igen, akkor ő mindenképpen megoldás. Tegyük fel tehát, hogy például az [a]_p redukált maradékosztály egy d rendű megoldás, azaz:
[a]_p^d=[1]_pMivel [a]_p rendje d, így a 24.12. Tétel 3. pontja szerint az ő [a]_p^0, [a]_p^1, [a]_p^2, ..., [a]_p^{d-1} hatványai mind különböznek egymástól, azaz különböző redukált maradékosztályok. Ezek a hatványok viszont szintén megoldásai a fenti egyenletnek, hiszen a hatványozás azonosságairól szóló 24.10. Tétel 2. pontja alapján tetszőleges k kitevő esetén teljesül az alábbi:
([a]_p^k)^d=[a]_p^{kd}=[a]_p^{dk}=(\underbrace{[a]_p^d}_{=[1]_p})^k=[1]_pMivel a megoldásszámról láttuk, hogy nem lehet d-nél nagyobb, így az [a]_p^0, [a]_p^1, ..., [a]_p^{d-1} hatványokon kívül nincs más megoldás. Kérdés, hogy ezek közül melyek azok, amelyek [a]_p-hez hasonlóan szintén d rendűek. A csoportelem hatványának rendjéről szóló 26.12. Tétel alapján tetszőleges i kitevő esetén [a]_p^i rendje akkor és csak akkor egyezik meg [a]_p rendjével (azaz d-vel), ha az i kitevő relatív prím d-hez. Így tehát a d rendű elemek száma megegyezik a 0, 1, ..., d-1 kitevők közül azoknak a számával, amelyek relatív prímek d-hez. Ez a 20.17. Következmény alapján épp \varphi(d).
Most foglaljuk össze az eddigieket: Az egyszerűség kedvéért jelöljük h(d)-vel a d rendű elemek számát. Eddig azt igazoltuk, hogy amennyiben d nem osztója p-1-nek, akkor h(d)=0, ha pedig d osztója p-1-nek, akkor az alábbi két eset lehetséges: h(d)=\varphi(d) vagy h(d)=0. A tétel bizonyításához azt kell belátnunk, hogy az utóbbi kizárt.
Tekintsük ezért p-1 összes pozitív osztóját: d_1, d_2, ..., d_k. Mivel a 24.14. Következmény alapján bármely elem rendje csak ezen számok közül kerülhet ki, továbbá ugye összesen p-1 darab elem van, ezért egyrészt igaz az alábbi:
h(d_1)+h(d_2)+\ldots+h(d_k)=p-1Másrészt a 26.13. Tétel alapján igaz az alábbi is:
\varphi(d_1)+\varphi(d_2)+\ldots+\varphi(d_k)=p-1Érvényes tehát az alábbi összefüggés:
h(d_1)+\ldots+h(d_k)=\varphi(d_1)+\ldots+\varphi(d_k)Az eddigiek alapján a baloldalon minden h(d_i) tag vagy 0-val vagy pedig \varphi(d_i)-vel egyezik meg. Ez az egyenlőség viszont csak ez utóbbi esetben teljesülhet, azaz p-1 minden d osztója esetén a d rendű elemek száma valóban \varphi(d).
A modulo p primitív gyökök épp azok az elemek, amelyeknek rendje p-1. A fentiek szerint ezekből \varphi(p-1) darab van, ami biztosan nagyobb 0-nál, azaz létezik primitív gyök modulo p.
∎Primitív gyökök és a Diffie-Hellman kulcscsere protokoll
Megjegyezzük, hogy a primitív gyököknek a 9. részben már ismertetett Diffie-Hellman kulcscsere protokoll kapcsán van nagy jelentőségük. Az eljárás részleteit nem ismételjük meg, de a lényeg ugye egy moduláris hatványozáson alapuló f egyirányú függvény, amelyet Alice és Bob használ egy közös titok (vagy ha úgy tetszik kulcs) meghatározásához. Ezt a hatványozást a 18.3. Definíció szerinti \Z_m gyűrűben, vagy az azzal izomorf \Z/m\Z maradékosztálygyűrűben kell végrehajtani az alábbi képlet alapján, ahol G egy tetszőlegesen választott maradékosztály, amelyet generátorelemnek nevezünk (az elnevezés oka rövidesen világos lesz):
f(n)=G^nAz eljárás biztonsága azon alapszik, hogy a támadónak a nyilvános G generátorelem, a használt gyűrűt azonosító szintén nyilvános m modulus és a kommunikációs csatornán elfogott G^n hatvány ismeretében kéne meghatároznia a titokban tartott n kitevőt. Ez az úgynevezett diszkrét logaritmus problémájának megoldását jelenti számára, amely algoritmikusan egy belátható időn belül kivitelezhetetlen feladat, feltéve persze, hogy a G maradékosztálynak elegendően sok hatványa létezik a \Z/m\Z gyűrűben.
Könnyen látszik, hogy e feltétel teljesítése érdekében generátorelemnek egy redukált maradékosztályt célszerű választani. Ha ugyanis G=[g]_m nem egy redukált maradékosztály, akkor a 20.14. Tétel alapján a g reprezentánselemnek és az m modulusnak van egységtől különböző közös osztója. Ez viszont igaz lesz bármelyik G^n hatvány reprezentánselemeire is, hiszen G^k=[g^k]_m, következésképp ekkor G hatványai szintén a nem redukált maradékosztályok közül kerülnek ki. Márpedig ezekből elenyészően kevés van a \Z/m\Z gyűrűben, és így a támadó akár próbálgatással is könnyedén célt érhet.
A redukált maradékosztályok viszont épp a (\Z/m\Z)^{\times} multiplikatív csoport elemei, amely csoport ugye zárt a szorzásra (és így a hatványozásra) nézve. Ezért Alice és Bob tulajdonképpen ebből a multiplikatív csoportból szeretne választani magának egy olyan elemet, amelynek lehetőleg minél több különböző hatványa van, azaz amelyiknek minél nagyobb a rendje (lásd a 24.11. Definíciót). Csoportelméleti terminológiával élve akkor vannak tehát a legnagyobb biztonságban, ha a (\Z/m\Z)^{\times} multiplikatív csoport ciklikus, G pedig ennek egy generátoreleme, azaz egy modulo m primitív gyök, ekkor ugyanis G hatványai kiadják a teljes (\Z/m\Z)^{\times} csoportot.
Az előző szakaszban bizonyított tétel alapján ha Alice és Bob egy p prímszámot használnak modulusként – amelyet az elmúlt részek fényében könnyedén találhatnak maguknak –, akkor a (\Z/p\Z)^{\times} csoport biztosan ciklikus lesz. Ami a rossz hír, hogy a tétel bizonyítása nem konstruktív, azaz nem szolgáltat konkrét eljárást primitív gyökök megkereséséhez, azoknak csupán a létezését bizonyítja. Ami még rosszabb hír, hogy erre a feladatra egyáltalán nem ismert (és minden jel arra mutat, hogy nem is várható) hatékony eljárás, így a modulo p primitív gyökök keresgélése nem egy járható út.
A gyakorlatban ehelyett egy olyan maradékosztály is megfelel a célnak, amely nem generálja ugyan a teljes (\Z/p\Z)^{\times} csoportot, hanem annak csak egy olyan részcsoportját, amely viszont már „kellően nagyméretű” a kívánt biztonsági szint eléréséhez. Ennek érdekében először ezt a „kellően nagy” méretet szokták meghatározni, majd ebből állítják elő a p modulust olymódon, hogy az egy úgynevezett „biztonságos prím” legyen. A részletek mellőzésével megemlítjük, hogy egy ilyen p biztonságos prímnek számos, kriptográfiai szempontból fontos tulajdonsága van. Többek között az, hogy „majdnem mindegyik” modulo p redukált maradékosztály „kellően nagyméretű” részcsoportot generál. Mivel ez hatékonyan ellenőrizhető, ezért Alice és Bob viszonylag gyorsan képes megfelelő biztonságú generátorelemet választani.
Carmichael-számok tulajdonságai
A primitív gyökökkel kapcsolatos eredmények felhasználásával ebben a szakaszban igazoljuk a 23.7. Definícióban megismert Carmichael-számok (vagy univerzális álprímek) néhány fontos tulajdonságát. Ezeknek szintén kulcsszerepük lesz a Miller-Rabin-tanúkra vonatkozó becslésünk javításában. Ehhez ismerkedjünk meg egy egyszerű fogalommal.
26.15. Definíció (Négyzetmentes szám):
Egy n egész számot négyzetmentesnek nevezünk, ha nem létezik olyan k egész szám, hogy teljesül a k^2|n oszthatóság.
♣Például az n=12 nem négyzetmentes, mivel osztható a 2 második hatványával. Ezzel szemben a 15 négyzetmentes, hiszen semmilyen egész szám második hatványával nem osztható. Most mutatunk egy egyszerű segédtételt, amely alapján elegendő csupán a pozitív prímosztókra ellenőrizni a feltételt.
26.16. Lemma:
Az n egész szám akkor és csak akkor négyzetmentes, ha nem létezik olyan pozitív p prímosztója, amely esetén teljesülne a p^2|n oszthatóság.
♣Bizonyítás:
Ha n négyzetmentes, akkor a 26.15. Definíció alapján nem osztható semmilyen egész szám négyzetével, így nyilván pozitív prímszámok négyzetével sem.
Megfordítva: Tegyük fel, hogy n nem négyzetmentes, azaz létezik olyan k egész szám, hogy k^2|n. Legyen p egy olyan prímszám, amely osztója k-nak. Ilyen biztosan létezik, hiszen 17.22. Tétel alapján \Z-ben teljesül a számelmélet alaptétele. Az általánosság megsértése nélkül feltételezhetjük, hogy p pozitív, hiszen ha negatív lenne, akkor az ő ellentettje lenne pozitív, ami a 16.2. Tétel 8. pontja alapján szintén osztója k-nak. A p|k oszthatóság a 16.1. Definíció alapján azt jelenti, hogy létezik olyan m egész szám, amelyre fennáll az alábbi:
k=p\cdot mEkkor a 18.8. Tétel 1. pontja alapján k^2 így írható fel:
k^2=p^2\cdot m^2Ez azt jelenti, hogy teljesül a p^2|k^2 oszthatóság. Azonban azt mondtuk, hogy teljesül a k^2|n oszthatóság is, amiből a 16.2. Tétel 5. pontja alapján következik, hogy teljesül a p^2|n oszthatóság.
∎Most egy olyan feltételt igazolunk, amely alapján egy adott összetett számról egyértelműen el lehet dönteni, hogy Carmichael-szám-e vagy nem. Ehhez mindössze a szám prímtényezős felbontására van szükség. Ezt a tételt Alwin Reinhold Korselt német matematikus fedezte fel 1899-ben, ő maga azonban nem talált egyetlen, a feltételnek eleget tevő egész számot sem. Ez dokumentáltan először Robert Daniel Carmichaelnek sikerült 1910-ben – innen ered a Carmichael-szám elnevezés. A teljességhez azonban hozzátartozik, hogy Václav Šimerka cseh matematikus már 25 évvel korábban felsorolta az első 7 univerzális álprímet egy kevésbé közismert cseh matematikai szaklapban, amely azonban akkoriban nem kapott túl nagy figyelmet.
26.17. Tétel (Korselt-kritérium):
Egy n pozitív összetett egész szám akkor és csak akkor Carmichael-szám, ha négyzetmentes és bármely pozitív p prímosztójára teljesül az alábbi oszthatóság:
p-1|n-1 ♣Például az 561 ez alapján Carmichael-szám, hiszen 561=3\cdot 11\cdot 17 és teljesülnek az alábbi oszthatóságok:
\begin{aligned}2&|560 \\ 10&|560 \\ 16&|560\end{aligned}Bizonyítás:
Elsőként azt mutatjuk meg, hogy ha n Carmichael-szám, akkor teljesíti a fenti két kritériumot. Először igazoljuk, hogy n négyzetmentes, ami a 26.16. Lemma alapján azt jelenti, hogy nem létezik olyan pozitív prímosztója, amelynek a négyzetével is osztható. Tegyük fel indirekt, hogy nem ez a helyzet, azaz p egy olyan galád pozitív prímosztó, amelynek a négyzete szintén n osztója. Ezt a 24.15. Definíció alapján úgy is mondhatjuk, hogy az n egész szám p-adikus rendje legalább 2. Azaz:
\begin{aligned}v_p(n)&=k \\ k&\geq 2\end{aligned}Ez azt jelenti, hogy n felírható az alábbi alakban, ahol m tovább már nem osztható p-vel:
n=p^kmMivel p prím, ezért az, hogy m nem osztható p-vel egyben azt is jelenti, hogy p^k és m relatív prímek, azaz (p^k,m)=1. Ekkor érvényes a kínai maradéktétel (22.2. Tétel), amelynek következményeként a 22.8. Tétel alapján fennáll az alábbi gyűrűizomorfizmus:
\Z/n\Z \simeq \Z/p^k\Z \times \Z/m\ZKövetkezésképp egyértelműen létezik olyan X maradékosztály a baloldali maradékosztálygyűrűben, amelyhez a 22.8. Tételben szereplő g gyűrűizomorfizmus az ([1+p]_{p^k};[1]_m) maradékosztálypárt rendeli hozzá a jobboldali szorzatgyűrűből. Legyen a ennek az X maradékosztálynak egy reprezentánseleme. Ekkor tehát az említett g gyűrűizomorfizmus az alábbi hozzárendelést valósítja meg:
[a]_n \xmapsto{g} (\underbrace{[1+p]_{p^k}}_{=[a]_{p^k}};\underbrace{[1]_m}_{=[a]_m})Azaz fennállnak a jobboldalon szereplő maradékosztályok közötti alábbi egyenlőségek:
\begin{aligned}[a]_{p^k}&=[1+p]_{p^k} \\ [a]_m&=[1]_m\end{aligned}A második egyenlőségből a 20.14. Tétel alapján következik, hogy a relatív prím m-hez. Az [a]_m=[1]_m maradékosztály ugyanis nyilván invertálható a \Z/m\Z gyűrűben, hiszen ő ennek a gyűrűnek az egységeleme, amelynek inverze önmaga. Az első egyenlőségből szintén a 20.14. Tétel alapján következik, hogy a pontosan akkor relatív prím p^k-hoz, ha 1+p is az, hiszen ők ugyanannak a modulo p^k maradékosztálynak a reprezentánselemei. Ez viszont nyilván teljesül, hiszen 1+p biztosan nem osztható p-vel, így annak semmilyen hatványával sem. Azt kaptuk tehát, hogy a-nak nincs közös prímtényezője sem m-mel, sem pedig p^k-val is, következésképp az ő szorzatukkal, azaz n-nel sem. Az a egész szám tehát relatív prím n-hez, azaz a 20.14. Tétel alapján [a]_n egy redukált maradékosztály.
Ugye n-ről most tudjuk, hogy Carmichael-szám, ami a 23.7. Definíció alapján azt jelenti, hogy egyetlen redukált maradékosztály sem lehet Fermat-tanú, ezért nyilván a most megkonstruált [a]_n sem az. Azaz a Fermat-tanúkra vonatkozó 23.3. Definíció alapján teljesül az alábbi kongruencia:
a^{n-1}\equiv 1\pmod nMivel azonban n=p^km, ezért nyilván teljesül a p^k|n oszthatóság, és így a 20.2. Tétel 9. pontja alapján az alábbi kongruencia is:
a^{n-1}\equiv 1\pmod{p^k}Az a egész számot viszont úgy választottuk ki, hogy kongruens legyen 1+p-vel modulo p^k, ezért a 20.2. Tétel 8. pontja alapján teljesül az alábbi kongruencia is:
(1+p)^{n-1}\equiv 1\pmod{p^k}Viszont indirekt feltételezésünk szerint a k kitevő legalább 2, és így teljesül a p^2|p^k oszthatóság, és így a 20.2. Tétel 9. pontja miatt az alábbi kongruencia is:
(1+p)^{n-1}\equiv 1\pmod{p^2}A kongruencia baloldalán tehát egy olyan n-1 tényezős szorzat szerepel, amelynek minden tényezője 1+p:
(1+p)^{n-1}=\underbrace{(1+p)\cdot (1+p)\cdot \ldots \cdot (1+p)}_{\text{(n-1) darab}}A 24.16. Lemma bizonyításának gondolatmenetéhez hasonlóan a 14.12. Definícióban szereplő disztributivitási szabályok alapján ezt az n-1 darab zárójelet úgy kell felbontani, hogy minden zárójelből az összes lehetséges kombinációban kiválasztunk pontosan egy tagot, ezeket összeszorozzuk egymással, és az így kapott szorzatokat összeadjuk. Így az alábbi tagok keletkeznek valamilyen A_0, A_1, A_2, ..., A_{n-1} szorzó tényezőkkel attól függően, hogy melyik kombinációt hányféleképpen lehet előállítani az n-1 darab zárójelből:
\begin{aligned}(1+p)^{n-1} &= A_0\cdot 1^{n-1}\cdot p^0 \\ &+ A_1\cdot 1^{n-2}\cdot p^1 \\ &+ A_2\cdot 1^{n-3}\cdot p^2 \\ &+ A_3\cdot 1^{n-4}\cdot p^3 \\ &\vdots \\ &+ A_{n-1}\cdot 1^0\cdot p^{n-1}\end{aligned}Itt az A_0 együttható nyilván 1 lesz, hiszen egyféleképpen lehet kiválasztani mind az n-1 darab zárójelből az 1 tagot. Ehhez hasonló okok miatt az A_1 együttható n-1 lesz, hiszen n-1-féleképpen lehet kiválasztani az n-1 darab zárójelből azt az egyet, amiből a p tagot vesszük az adott szorzathoz. A zárójelek felbontása után kapott kifejezés tehát így néz ki:
(1+p)^{n-1} = \underbrace{1}_{=A_0}p^0 + \underbrace{(n-1)}_{=A_1}p^1 + A_2p^2 + A_3p^3 + \ldots + A_{n-1}p^{n-1}Mivel minket ennek a kifejezésnek az értéke modulo p^2 érdekel minket, ezért nincs szükségünk az A_2, A_3, ..., A_{n-1} együtthatók pontos értékére – amelyeket egyébként a binomiális tétel alapján lehetne kiszámítani. Vegyük ugyanis észre, hogy a 3. tagtól kezdve minden tag osztható p^2-tel, vagy másként fogalmazva 0-val kongruens modulo p^2. Így az alábbi kongruenciát kapjuk:
(1+p)^{n-1}\equiv 1+(n-1)p\pmod{p^2}A baloldalon szereplő (1+p)^{n-1} már megmutattuk, hogy 1-gyel kongruens modulo p^2, emiatt a jobboldal is, azaz:
1\equiv 1+(n-1)p\pmod{p^2}Mivel n osztható p-vel (hiszen egy prímtényezőjéről van szó), így felírható n=t\cdot p alakban valamilyen alkalmasan választott t egész számmal:
1\equiv 1+(\underbrace{tp}_{=n}-1)p\pmod{p^2}A jobboldalon szereplő zárójelet felbontva az alábbi adódik:
1\equiv 1+\underbrace{tp^2}_{\equiv 0}-p\pmod{p^2}A középső tp^2 tag osztható p^2-tel, azaz 0-val kongruens modulo p^2, így az elhagyható a jobboldalról:
1\equiv 1-p\pmod{p^2}Ez viszont a 20.1. Tétel 3. pontja alapján azt jelentené, hogy teljesül az alábbi oszthatóság:
p^2|\underbrace{1-(1-p)}_{=p}Ez egyértelmű ellentmondás, ami az indirekt feltételezésünkből következne, ha igaz volna. Nem igaz tehát, hogy n osztható p^2-tel, vagy ugyanezen gondolatmenet alapján bármely más prímosztó négyzetével. Következésképp n valóban négyzetmentes.
Most a p-1|n-1 oszthatóságot igazoljuk. Legyen p továbbra is n tetszőleges pozitív prímtényezője. Az előzőekben tehát beláttuk, hogy az n egész szám p-adikus rendje 1, azaz n felírható az alábbi alakban, ahol m tovább már nem osztható p-vel:
n=pmMivel p prím, ezért az, hogy m nem osztható p-vel egyben azt is jelenti, hogy p és m relatív prímek, azaz (p,m)=1. Ismét érvényes tehát a kínai maradéktétel (22.2. Tétel), így a 22.8. Tétel alapján fennáll az alábbi gyűrűizomorfizmus:
\Z/n\Z \simeq \Z/p\Z \times \Z/m\ZTekintsük most a jobboldalon szereplő \Z/p\Z gyűrű multiplikatív csoportját, azaz a (\Z/p\Z)^{\times} csoportot. Ez a \Z/p\Z gyűrű invertálható elemeiből áll, amelyek épp a modulo p redukált maradékosztályok. Ezek számát a 20.7. Definíció alapján az Euler-féle \varphi-függvény adja meg. Mivel p prím, ezért ez a 21.5. Tétel alapján jelen esetben épp p-1, ami tehát a (\Z/p\Z)^{\times} multiplikatív csoport rendje.
A 26.14. Tétel alapján a (\Z/p\Z)^{\times} csoportban létezik primitív gyök, hiszen p prím. Azaz a 26.1. Definíció utáni megjegyzés szerint létezik olyan b egész szám, hogy az általa reprezentált [b]_p redukált maradékosztály rendje épp megegyezik a csoport rendjével, azaz:
o([b]_p)=p-1A fennálló gyűrűizomorfizmus miatt létezik olyan X maradékosztály a \Z/n\Z gyűrűben, amelyhez a 22.8. Tételben szereplő g gyűrűizomorfizmus a ([b]_p;[1]_m) maradékosztálypárt rendeli hozzá a \Z/p\Z \times \Z/m\Z szorzatgyűrűből. Legyen a ennek az X maradékosztálynak egy reprezentánseleme. Ekkor a g gyűrűizomorfizmus az alábbi hozzárendelést valósítja meg:
[a]_n \xmapsto{g} (\underbrace{[b]_p}_{=[a]_p};\underbrace{[1]_m}_{=[a]_m})Azaz fennállnak a jobboldalon szereplő maradékosztályok közötti alábbi egyenlőségek:
\begin{aligned}[a]_p&=[b]_p \\ [a]_m&=[1]_m\end{aligned}Az a egész szám tehát egyrészt relatív prím m-hez, mivel az általa reprezentált maradékosztály nyilván redukált, hiszen a \Z/m\Z maradékosztálygyűrű egységeleméről van szó. Másrészt relatív prím p-hez is, ugyanis a vele azonos modulo p maradékosztályban lévő b is az, hiszen ez a maradékosztály a (\Z/p\Z)^{\times} multiplikatív csoport egy eleme (konkrétan az egyik primitív gyök), azaz redukált maradékosztály. Következésképp a az n=pm szorzathoz is relatív prím, azaz (a,n)=1, és így [a]_n szintén redukált maradékosztály a \Z/n\Z gyűrűben.
Mivel azonban n ugye Carmichael-szám, ezért a 23.7. Definíció alapján [a]_n biztosan nem Fermat-tanú, azaz teljesül az alábbi kongruencia:
a^{n-1}\equiv 1\pmod nA 20.5. Tétel alapján a maradékosztályok közötti szorzást – és így a hatványozást is – a reprezentánselemeken kell végrehajtani. Ezért a fenti kongruencia baloldalán épp az [a]_n maradékosztály n-1-edik hatványának reprezentánseleme áll, amely hatvány tehát nem más, mint az [1]_n maradékosztály. Ám ekkor művelettartó tulajdonsága alapján a fenti g gyűrűizomorfizmus az alábbi hozzárendelést valósítja meg:
\underbrace{[a]^{n-1}_n}_{=[1]_n} \xmapsto{g} ([b]_p;[1]_m)^{n-1}A 22.7. Tétel alapján a jobboldali szorzatgyűrűben a hatványozást komponensenként kell végrehajtani, így valójában az alábbi hozzárendelésről van szó:
[1]_n \xmapsto{g} (\underbrace{[b]^{n-1}_p}_{=[1]_p};[1]_m)A jobboldal alapján tehát a \Z/p\Z maradékosztálygyűrűben fennáll az alábbi, maradékosztályok közötti egyenlőség:
[b]^{n-1}_p= [1]_pMinthogy [b]_p a (\Z/p\Z)^{\times} multiplikatív csoport egy eleme, amely csoportnak [1]_p épp a neutrális eleme, ezért a 24.12. Tétel 2. pontja alapján teljesül az alábbi oszthatóság:
o([b]_p)|n-1Azt azonban már korábban láttuk, hogy [b]_p rendje épp p-1, azaz valóban teljesül a p-1|n-1 oszthatóság n bármely pozitív p prímtényezőjére.
Végezetül megmutatjuk, hogy ha egy összetett számra teljesülnek a tételben szereplő kritériumok, akkor ő szükségképpen Carmichael-szám. Legyen ezért n tetszőleges összetett szám, amely négyzetmentes, és tegyük fel, hogy bármely pozitív p prímtényezőjére teljesül a p-1|n-1 oszthatóság. Válasszunk egy tetszőleges a egész számot, amely relatív prím n-hez. Mivel p az n egy prímtényezője, ezért a relatív prím p-hez is. Ekkor a kis Fermat-tétel alapján (22.1. Tétel) teljesül az alábbi kongruencia:
a^{p-1}\equiv 1\pmod pA feltételünk szerint azonban most fennáll a p-1|n-1 oszthatóság, azaz létezik olyan t egész szám, amelyre teljesül az alábbi:
(p-1)t=n-1A fenti kongruencia mindkét oldalát a t-edik hatványra emelve ezt kapjuk:
(a^{p-1})^t\equiv 1^t\pmod pA hatványozás azonosságairól szóló 18.8. Tétel 2. pontja alapján tehát:
a^{\overbrace{n-1}^{=(p-1)t}}\equiv 1\pmod pEz a 20.1. Tétel 3. pontja alapján azt jelenti, hogy teljesül az alábbi oszthatóság:
p|a^{n-1}-1Azt kaptuk tehát, hogy az n egész szám tetszőleges pozitív prímtényezőjére igaz, hogy ő az a^{n-1}-1 egész számnak is prímtényezője. Tekintsük most n egy olyan prímtényezős felbontását, amelyben minden tényező pozitív (ilyen nyilván létezik, hiszen maga n is pozitív):
n=p_1\cdot p_2\cdot p_3\cdot \ldots \cdot p_rA fenti gondolatmenet alapján eszerint a p_1, p_2, ..., p_r prímek mind az a^{n-1}-1 egész szám pozitív prímtényezői. Minthogy n-ről azt mondtuk, hogy négyzetmentes, ezért ezek a prímtényezők páronként különbözőek. Emiatt végülis az ő szorzatuk – azaz maga n – szintén osztója az a^{n-1}-1 egész számnak:
\underbrace{p_1\cdot p_2\cdot p_3\cdot \ldots \cdot p_r}_{=n}|a^{n-1}-1Ez a 20.1. Tétel 3. pontja alapján azt jelenti, hogy teljesül az alábbi kongruencia:
a^{n-1}\equiv 1\pmod nÍgy tehát semmilyen tetszőlegesen választott [a]_n redukált maradékosztály nem lehet Fermat-tanú, azaz a 23.7. Definíció alapján az n összetett szám valóban Carmichael-szám.
∎Most a Korselt-kritérium egy egyszerű következményét ismertetjük, amely a Carmichael-számok paritására és prímtényezőinek számára vonatkozik.
26.18. Következmény:
Minden Carmichael-szám páratlan és legalább 3 prímtényezője van.
♣Bizonyítás:
Először a Carmichael-számok paritására vonatkozó állítást igazoljuk.
Legyen n tetszőleges Carmichael-szám. Az n és az n-1 egész számok egymáshoz relatív prímek. Ugyanis bármilyen közös osztó a 16.2. Tétel 6. pontja alapján osztója e két szám különbségének, azaz 1-nek, és így a 16.5. Tétel miatt ez a közös osztó csak egység lehet. Így tehát az [n-1]_n egy redukált maradékosztály, és mivel n Carmichael-szám, ezért ez a maradékosztály a 23.7. Definíció alapján biztosan nem Fermat-tanú. Azaz a 23.3. Definíció értelmében teljesül az alábbi kongruencia:
(n-1)^{n-1}\equiv 1\pmod nAz n-1\equiv -1\pmod n kongruencia nyilván teljesül, ezért a fenti kongruenciát a 20.2. Tétel 8. pontja alapján a következőképpen írhatjuk át:
(-1)^{n-1}\equiv 1\pmod nAzt viszont tudjuk, hogy a -1 bármilyen hatványa +1 vagy -1 attól függően, hogy a kitevő páros vagy páratlan. Tegyük fel indirekt, hogy jelen esetben n-1 páratlan. Ekkor a fenti kongruencia így néz ki:
-1\equiv 1\pmod nEz a 20.1. Tétel 3. pontja alapján azt jelentené, hogy teljesül az alábbi oszthatóság:
n|\underbrace{1-(-1)}_{=2}Ez viszont lehetetlen, hiszen n Carmichael-szám, emiatt pozitív és összetett, következésképp biztosan nagyobb 2-nél, vagyis nem lehet osztója neki. Indirekt feltevésünk, miszerint n-1 páratlan hibás volt, azaz n-1 páros, és így n valóban páratlan.
Most igazoljuk a Carmichael-számok prímtényezőire vonatkozó állítást.
Legyen n továbbra is tetszőleges Carmichael-szám, de tegyük fel indirekt, hogy neki csak két prímtényezője van, azaz felírható n=pq alakban valamilyen alkalmasan választott p és q prímszámokkal. A Korselt-kritérium (26.17. Tétel) alapján n négyzetmentes, így e két prímtényező biztosan különbözik egymástól, azaz p\neq q. Ezenkívül az általánosság megsértése nélkül feltehetjük, hogy p\gt q, hiszen ha nem így lenne, akkor szerepük felcserélésével az alábbi gondolatmenet ugyanígy végigjátszható. Továbbá azt is feltehetjük, hogy mindkét prímtényező pozitív. Ha ugyanis nem így lenne, akkor az ő ellentettjükre ez már teljesül – hiszen n Carmichael-szám, és így pozitív –, és az alábbi gondolatmenetet rájuk alkalmazhatjuk.
Szintén a Korselt-kritérium (26.17. Tétel) alapján tudjuk, hogy teljesül az alábbi oszthatóság:
p-1|n-1Azaz létezik olyan k egész szám, amelyre teljesül az alábbi egyenlet:
(p-1)\cdot k=n-1Mivel azt feltételeztük, hogy n=pq, ezért ez így is írható:
(p-1)\cdot k=\underbrace{pq}_{=n}-1A jobboldal értéke nem változik, ha hozzá is adunk q-t és le is vonunk belőle q-t:
(p-1)\cdot k=pq-q+q-1A 14.12. Definícióban szereplő disztributivitási szabályok alapján ez így is írható:
(p-1)\cdot k=(p-1)\cdot q+q-1Mindkét oldalból levonhatunk (p-1)q-t:
(p-1)\cdot k - (p-1)\cdot q=q-1Most a baloldalra alkalmazhatjuk a disztributivitási szabályt:
(p-1)\cdot (k-q)=q-1Azt kaptuk tehát, hogy létezik olyan egész szám – nevezetesen a k-q – amellyel p-1-et megszorozva q-1-et kapunk. Teljesül tehát az alábbi oszthatóság:
p-1|q-1Mivel q egy pozitív prím, így q-1 is pozitív, ezért a 17.2. Lemma alapján ő legalább akkora, mint bármely osztója, azaz:
p-1\leq q-1A 15.11. Definícióban szereplő 1. rendezési axióma alapján mindkét oldalhoz 1-et adva ezt kapjuk:
p\leq qEz viszont ellentmondás, hiszen azt feltételeztük, hogy p\gt q. Ugyanilyen gondolatmenet alapján p\lt q-ból p\geq q következne, ami szintén ellentmondás. Indirekt feltételezésünk tehát hibás volt, és így n biztosan nem írható fel pq alakban, azaz szükségképpen valóban legalább 3 prímtényezője kell legyen.
∎A nem Miller-Rabin-tanúk csoportjának rendje
A 24. részben csoportelméleti eszközökkel igazoltuk, hogy a Miller-Rabin-prímtesztre nézve nem léteznek a Carmichael-számokhoz hasonló univerzális álprímek, amelyek becsaphatják a tesztet. Ennek keretében megmutattuk, hogy bármilyen n\gt 1 páratlan összetett szám esetén a modulo n redukált maradékosztályoknak legalább a fele Miller-Rabin-tanú (lásd a 24.20. Következményt). Most finomabb eszközökkel megjavítjuk ezt a becslésünket, és megmutatjuk, hogy ez a redukált maradékosztályoknak legalább a háromnegyedére igaz, azaz még sokkal jobb a helyzet, mint gondoltuk.
A stratégiánk azt volt, hogy a Miller-Rabin-tanúk helyett a nem Miller-Rabin-tanúkat vizsgáltuk, és megmutattuk, hogy ezek mind a (\Z/n\Z)^{\times} multiplikatív csoport egy valódi részcsoportjának elemei. Így viszont a Lagrange-tétel (24.8. Tétel) miatt legfeljebb feleannyian vannak, mint a redukált maradékosztályok, a többi redukált maradékosztály tehát Miller-Rabin-tanú. Külön kezeltük azt az esetet, amikor n valamilyen prímhatvány, és amikor nem.
A prímhatvány esetről a 24.18. Tétel 3. pontja szólt. Itt igazoltuk, hogy ebben az esetben a nem Miller-Rabin-tanúk egy olyan valódi részcsoportot alkotnak, amelynek rajtuk kívül nincs is más eleme. Most megadjuk ennek a bizonyos részcsoportnak a rendjét, amelyhez először egy segédtételre lesz szükségünk.
26.19. Lemma:
Legyen p egy pozitív, páratlan prímszám, c pedig egy pozitív kitevő, továbbá r egy tetszőleges olyan egész szám, amelyre teljesül az alábbi konguencia:
r^{p-1}\equiv 1\pmod{p^c}Jelöljük P_r-rel az összes olyan egész szám halmazát, amelyeket x helyére behelyettesítve fennáll mindkét alábbi kongruencia:
\begin{aligned}x&\equiv r\pmod{p^c} \\ x^{p-1}&\equiv 1\pmod{p^{c+1}}\end{aligned}Ekkor a P_r halmaz épp egy modulo p^{c+1} maradékosztállyal egyezik meg.
♣Bizonyítás:
A P_r megoldáshalmaz minden eleme kielégíti az első kongruenciát, azaz r-rel azonos modulo p^c maradékosztályban van. Következésképp a 20.4. Tétel alapján minden x\in P_r esetén létezik olyan y egész szám, hogy teljesül az alábbi egyenlet:
x=r+p^cyTehát tulajdonképpen azokat az y egész számokat keressük, amelyekre fennáll a második kongruencia is, azaz:
(\underbrace{r+p^cy}_{=x})^{p-1}\equiv 1\pmod{p^{c+1}}A baloldalon szereplő zárójeles kifejezést felbontva a Korselt-kritérium (26.17. Tétel) bizonyításánál látott gondolatmenet alapján az alábbi összeget kapjuk valamilyen A_2, A_3, ..., A_{p-1} együtthatókkal:
\begin{aligned}(r+p^cy)^{p-1}&=r^{p-1}+(p-1)r^{p-2}p^cy+\\&+A_2r^{p-3}p^{2c}y^2 + A_3r^{p-4}p^{3c}y^3+\ldots +A_{p-1}p^{(p-1)c}y^{p-1}\end{aligned}Ennek a kifejezésnek az értéke modulo p^{c+1} érdekel minket, emiatt nincs szükségünk az A_2, A_3, ..., A_{p-1} együtthatók pontos értékére – amelyeket egyébként a binomiális tétel alapján lehetne kiszámítani. A 3. tagtól kezdve ugyanis minden tag osztható p^{c+1}-gyel, vagy másként fogalmazva 0-val kongruens modulo p^{c+1}. Azaz tulajdonképpen az alábbi kongruencia megoldásait keressük:
\underbrace{r^{p-1}+(p-1)r^{p-2}p^cy}_{\equiv (r+p^cy)^{p-1}}\equiv 1\pmod{p^{c+1}}A tétel szövegéből tudjuk, hogy r-re teljesül az alábbi kongruencia is:
r^{p-1}\equiv 1\pmod{p^c}Azaz az r^{p-1} hatvány ugyanabban a modulo p^c maradékosztályban van, mint az 1 egész szám. Ám ekkor ugyancsak a 20.4. Tétel értelmében létezik olyan k_r egész szám, amelynek a segítségével az r^{p-1} hatvány felírható az alábbi alakban:
r^{p-1}=p^ck_r+1Ezt behelyettesíthetjük a kongruenciánkba, amelynek tehát a megoldásait keressük:
\underbrace{p^ck_r+1}_{=r^{p-1}}+(p-1)r^{p-2}p^cy\equiv 1\pmod{p^{c+1}}A 20.2. Tétel 6. pontja értelmében mindkét oldalból levonhatunk 1-et:
p^ck_r+(p-1)r^{p-2}p^cy\equiv 0\pmod{p^{c+1}}A zárójelet felbontva az alábbit kapjuk, ahol a második tag 0-val lesz kongruens modulo p^{c+1}, így az elhagyható:
p^ck_r+\underbrace{\cancel{r^{p-2}p^{c+1}y}}_{\equiv 0}-r^{p-2}p^cy\equiv 0\pmod{p^{c+1}}A maradék két tagból a p^c szorzótényezőt kiemelhetjük:
p^c\cdot (k_r-r^{p-2}y)\equiv 0\pmod{p^{c+1}}Ez a kongruencia viszont a kongruenciák egyszerűsítéséről szóló 20.3. Tétel alapján akkor és csak akkor teljesül, amikor az alábbi kongruencia is:
k_r-r^{p-2}y\equiv 0\pmod pMindkét oldalhoz r^{p-2}y-t adva tehát tulajdonképpen az alábbi lineáris kongruencia megoldásait keressük:
r^{p-2}y\equiv k_r\pmod pMivel a tétel szövegéből tudjuk, hogy teljesül az r^{p-1}\equiv 1\pmod{p^c} kongruencia, ezért a 24.18. Tétel 1. pontjának értelmében az [r]_{p^c} maradékosztály nem lehet Miller-Rabin-tanúja p^c-nek. Így viszont a 23.9. Definíció utáni megjegyzés értelmében [r]_{p^c} egy redukált maradékosztály, azaz r relatív prím p^c-hez. Ez egyben azt is jelenti, hogy r prímtényezős felbontásában biztosan nem szerepel a p prímszám, amely nyilván igaz lesz r bármely hatványára is. Így például az r^{p-2} hatványra – mint a fenti lineáris kongruencia együtthatójára – is, amely tehát relatív prím a p modulushoz, azaz (r^{p-2},p)=1.
Ez biztosan osztója a lineáris kongruencia jobboldalán lévő k_r-nek, így tehát a 20.12. Tétel értelmében szükségképpen létezik megoldás. Továbbá a megoldások száma a 20.13. Tétel alapján pontosan (r^{p-2},p)=1 darab modulo p maradékosztály.
Válasszuk ki ennek az eszerint egyetlen modulo p maradékosztálynak egy tetszőleges elemét, amelyet jelöljünk y_0-val. Ekkor tehát az y=y_0+pm képlet segítségével megkapjuk az (r+p^cy)^{p-1}\equiv 1\pmod{p^{c+1}} kongruenciát kielégítő összes egész számot (és csak azokat), amennyiben m-mel befutjuk a teljes \Z halmazt. Most alkalmazzuk visszafelé az x-re bevezetett jelölésünket:
x=r+p^c\cdot (\underbrace{y_0+pm}_{=y})=r+p^cy_0+p^{c+1}mEz tehát azt jelenti, hogy a tételben szereplő kongruenciarendszert kielégítő P_r megoldáshalmaz összes elemét (és csak azokat) megkapjuk, amennyiben a fenti képletben szereplő m-mel befutjuk a teljes \Z halmazt. Vagyis a 20.4. Tétel értelmében P_r valóban épp egy modulo p^{c+1} maradékosztály, melynek egyik reprezentánseleme r+p^cy_0.
∎Az iménti segédtételnek a felhasználásával mostmár igazolhatjuk a nem Miller-Rabin-tanúk csoportjának rendjéről szóló tételünket.
26.20. Tétel:
Legyen p tetszőleges pozitív, páratlan prímszám, c pedig tetszőleges pozitív kitevő. A 24.18. Tételnek megfelelően jelöljük G_{p^c}-vel azon modulo p^c maradékosztályok halmazát, amelyek NEM Miller-Rabin-tanúi p^c-nek. Ekkor G_{p^c} ugye a 24.18. Tétel 2. pontja alapján a (\Z/p^c\Z)^{\times} multiplikatív csoport egy részcsoportja. E részcsoport rendje minden pozitív c kitevő esetén p-1, azaz:
|G_{p^c}|=p-1 ♣Látható, hogy a kérdéses csoport mérete nem függ a c kitevő nagyságától, ezért prímhatvány esetben ez lesz majd a kulcs a Miller-Rabin-tanúk számára vonatkozó becslésünk javításához.
Bizonyítás:
A tételt a c kitevőre vonatkozó teljes indukcióval fogjuk igazolni.
Nézzük először a c=1 esetet! A 24.18. Tétel 3. pontja alapján ekkor G_p épp megegyezik a (\Z/p\Z)^{\times} multiplikatív csoporttal. Ennek rendje a modulo p redukált maradékosztályok számával, azaz \varphi(p)-vel egyezik meg, ami a 21.5. Tétel alapján valóban p-1.
Az indukció megindításához tegyük fel, hogy valamilyen c kitevő – mint például a most megmutatott c=1 – esetén a tétel igaz, azaz G_{p^c} elemszáma p-1. Azt kell igazolnunk, hogy ekkor G_{p^{c+1}} elemszáma is p-1. Rögzítsük G_{p^c} egy reprezentánsrendszerét, azaz válasszunk ki mindegyik G_{p^c}-beli nem Miller-Rabin-tanúból pontosan egy reprezentánselemet. Ekkor a G_{p^c} halmaz – amelynek tehát indukciós feltételezésünknek megfelelően p-1 eleme van – a következőképpen írható fel a most rögzített a_1, a_2, ..., a_{p-1} reprezentánselemek segítségével:
G_{p^c}=\{[a_1]_{p^c}; [a_2]_{p^c}; [a_3]_{p^c};\ldots ;[a_{p-1}]_{p^c}\}E reprezentánsrendszer felhasználásával most definiálunk egy f:G_{p^c}\to G_{p^{c+1}} függvényt, amely tehát a G_{p^c} halmaz minden eleméhez hozzárendel egy-egy elemet a G_{p^{c+1}} halmazból. Tekintsük a fenti reprezentánsrendszer szerinti bármelyik tetszőleges elemet, legyen ez például az [a_i]_{p^c}\in G_{p^c} nem Miller-Rabin-tanú. Ekkor a 24.18. Tétel 1. pontja alapján az a_i reprezentánselemre teljesül az alábbi kongruencia:
a_i^{p-1}\equiv 1\pmod{p^c}Ebben az esetben a 26.19. Lemma alapján pontosan egy olyan modulo p^{c+1} maradékosztály létezik, amelynek elemeire (és csak azokra) fennáll az alábbi mindkét kongruencia:
\begin{aligned}x&\equiv a_i\pmod{p^c} \\ x^{p-1}&\equiv 1\pmod{p^{c+1}}\end{aligned}Jelöljük ezt a modulo p^{c+1} maradékosztályt B_i-vel. Mivel tehát B_i elemeire teljesül a fenti kongruenciarendszer, és így az abban lévő második kongruencia is, ezért a 24.18. Tétel 1. pontja alapján a B_i maradékosztály nem Miller-Rabin-tanúja p^{c+1}-nek, azaz B_i\in G_{p^{c+1}}.
Ez tehát azt jelenti, hogy ha a keresett f függvényt az alábbi képlettel definiáljuk, akkor az valóban minden G_{p^c}-beli nem Miller-Rabin-tanúhoz egyértelműen hozzárendel egy-egy G_{p^{c+1}}-beli nem Miller-Rabin-tanút:
f([a_i]_{p^c})=B_iElőszöris azt mutatjuk meg, hogy az így definiált f függvény injektív, azaz különböző G_{p^c}-beli elemekhez különböző G_{p^{c+1}}-beli elemeket rendel hozzá. Indirekt tegyük fel, hogy nem ez a helyzet, azaz létezik olyan egymástól különböző a_i és a_j a fent rögzített reprezentánsrendszerben, amelyekre teljesül az alábbi:
f([a_i]_{p^c})=f([a_j]_{p^c})Az f függvény tehát indirekt feltételezésünk szerint az [a_i]_{p^c} és az [a_j]_{p^c} maradékosztályokhoz ugyanazt az alábbi ábrán B-vel jelölt modulo p^{c+1} maradékosztályt rendeli hozzá:
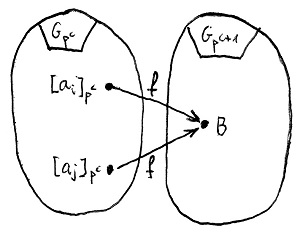
Tekintsük B-nek egy tetszőleges b reprezentánselemét. Ekkor b-re teljesülni fog a fenti kongruenciarendszer, és így az abban lévő első kongruencia a_i és a_j esetén is, azaz:
\begin{aligned}b&\equiv a_i\pmod{p^c} \\ b&\equiv a_j\pmod{p^c}\end{aligned}Ám ekkor a 20.2. Tétel 2. és 3. pontjai miatt teljesül az alábbi kongruencia is:
a_i\equiv a_j\pmod{p^c}Ám ez ellentmondás, hiszen indirekt feltételezésünkben azt mondtuk, hogy a_i és a_j egymástól különbözőek, és így – mivel ők a G_{p^c} halmaz egy reprezentánsrendszerének elemei – nem lehetnének azonos modulo p^c maradékosztályban. Az f függvény tehát valóban injektív, azaz különböző G_{p^c}-beli elemekhez szükségképpen különböző G_{p^{c+1}}-beli elemeket rendel hozzá.
Végül azt igazoljuk, hogy f az injektivitáson kívül szürjektív is, azaz nem létezik olyan G_{p^{c+1}}-beli elem, amely ne lenne hozzárendelve valamelyik G_{p^c}-beli elemhez. Indirekt tegyük fel, hogy nem ez a helyzet, vagyis létezik az alábbi ábrán látható B\in G_{p^{c+1}} maradékosztály, amely nincs hozzárendelve semelyik G_{p^c}-beli maradékosztályhoz f által:
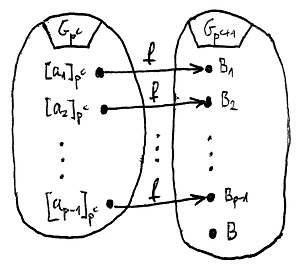
Tekintsük B egy tetszőleges b reprezentánselemét, azaz legyen B=[b]_{p^{c+1}}. Mivel [b]_{p^{c+1}}\in G_{p^{c+1}}, ezért a 24.18. Tétel 1. pontja alapján b-re teljesül az alábbi kongruencia:
b^{p-1}\equiv 1\pmod{p^{c+1}}Ám mivel a p^c|p^{c+1} oszthatóság nyilvánvalóan teljesül, ezért a 20.2. Tétel 9. pontja alapján teljesül az alábbi kongruencia is:
b^{p-1}\equiv 1\pmod{p^c}Ám ekkor a 24.18. Tétel 1. pontja szerint a b által reprezentált modulo p^c maradékosztály nem Miller-Rabin-tanúja p^c-nek, azaz [b]_{p^c}\in G_{p^c}. Mivel azonban a korábban rögzített a_1, a_2, a_3, ..., a_{p-1} egész számok a G_{p^c} halmaz egy reprezentánsrendszerét alkotják, ezért b szükségképpen azonos modulo p^c maradékosztályban van pontosan az egyikükkel. Azaz létezik olyan a_i ebben a reprezentánsrendszerben, amely esetén b-re teljesül az alábbi kongruencia is:
b\equiv a_i\pmod{p^c}Összegezve tehát b az egyike azon egész számoknak, amelyek kielégítik az alábbi kongruenciarendszert:
\begin{aligned}x&\equiv a_i\pmod{p^c} \\ x^{p-1}&\equiv 1\pmod{p^{c+1}}\end{aligned}Azt is láttuk, hogy b-re teljesül az alábbi kongruencia is:
b^{p-1}\equiv 1\pmod{p^c}Ekkor azonban a 26.19. Lemma alapján a fenti kongruenciarendszert kielégítő egész számok épp egy modulo p^{c+1} maradékosztályt alkotnak, amelyben ezek szerint b is benne van, így ez épp a B=[b]_{p^{c+1}} maradékosztály. Az f függvény viszont épp ezt a maradékosztályt rendeli hozzá [a_i]_{p^c}-hez, ami ellentmond indirekt feltételezésünknek, miszerint B egy olyan G_{p^{c+1}}-beli maradékosztály, amely nincs hozzárendelve semelyik G_{p^c}-beli maradékosztályhoz sem f által. Az f függvény tehát valóban szürjektív.
Mivel f-ről megmutattuk, hogy egyszerre injektív és szürjektív, ezért ő tulajdonképpen egy kölcsönösen egyértelmű megfeleltetést létesít G_{p^c} és G_{p^{c+1}} elemei között, így e két halmaznak pontosan ugyanannyi eleme van tetszőleges pozitív c kitevő esetén. A bizonyítás elején a c=1 kitevő esetén láttuk, hogy a G_p halmaznak p-1 eleme van. A most bizonyított indukció miatt ekkor p-1 eleme lesz G_{p^2}-nek is, majd emiatt G_{p^3}-nak is, stb. Tehát tetszőleges pozitív c kitevő esetén G_{p^c}-nek is valóban p-1 eleme lesz, ahogyan a tétel állítja.
∎Megjegyzés:
A bizonyításban megkonstruált f függvény által megvalósított leképezés természetesen függeni fog attól, hogy pontosan milyen reprezentánsrendszert választunk G_{p^c}-hez. Maga a tény azonban, hogy ez egy kölcsönösen egyértelmű megfeleltetés lesz G_{p^c} és G_{p^{c+1}} között, természetesen a reprezentánsrendszer megválasztásától függetlenül igaz lesz.
♣Most nézzük azt az esetet, amikor n nem prímhatvány. Erről az esetről a 24.19. Tétel szólt. Ebben az esetben a nem Miller-Rabin-tanúk ugyan nem alkotnak részcsoportot (\Z/n\Z)^{\times}-ben, azonban sikerült mutatnunk egy olyan valódi részcsoportot, amely minden nem Miller-Rabin-tanút magában foglalt, és így ugyancsak alkalmazni tudtuk a Lagrange-tételt a Miller-Rabin-tanúk számának becsléséhez. Most ezt a tételt továbbfejleszve tovább szűkítjük ennek a bizonyos valódi részcsoportnak a méretét.
26.21. Tétel:
Legyen n egy tetszőleges 1-nél nagyobb páratlan szám, amelynek legalább két egymástól különböző prímtényezője is van, azaz nem prímhatvány. Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyekre teljesül az alábbi:
n-1=2^ekA 24.19. Tétel szövegével megegyező módon legyen j_{\text{max}} a legnagyobb olyan j kitevő a \{0;1;2;\ldots;e-1\} egész számok között, amelyhez léteznek olyan x egész számok, hogy teljesül az x^{2^j}\equiv -1\pmod n kongruencia. Megjegyzés: Az említett 24.19. Tétel alapján legalább egy ilyen j kitevő biztosan létezik, tehát j_{\text{max}} is létezik.
Ugyancsak a 24.19. Tétel szövegével megegyezően jelöljük H_n-nel azon [a]_n maradékosztályok halmazát, amelyek esetén az a^{2^{j_{\text{max}}}k} hatvány 1-gyel vagy -1-gyel kongruens modulo n, azaz:
a^{2^{j_{\text{max}}}k} \equiv \pm 1\pmod nVégül jelöljük F_n-nel azokat a modulo n maradékosztályokat, amelyek nem Fermat-tanúi n-nek.
Ekkor H_n-hez hasonlóan F_n is részcsoportot alkot a (\Z/n\Z)^{\times} multiplikatív csoportban, valamint teljesülnek az alábbiak:
- Ha n nem Carmichael-szám, akkor H_n\lt F_n\lt (\Z/n\Z)^{\times}
- Ha n Carmichael-szám, akkor H_n\lt F_n=(\Z/n\Z)^{\times}.
Szavakkal ez így fogalmazható meg: H_n valódi részcsoport F_n-ben, amely viszont akkor és csak akkor valódi részcsoport (\Z/n\Z)^{\times}-ben, ha n nem Carmichael-szám (egyébként megegyezik vele).
♣Ez a tétel nyilván a nem Carmichael-számok esetén fogja lehetővé tenni a becslésünk javítását, hiszen tovább szűkíti a nem Miller-Rabin-tanúkat tartalmazó H_n részcsoport maximális méretét. Ezzel szemben a Carmichael-számok esetén nem kapunk újabb szűkítési lehetőséget, hiszen a 2. pont szerint ebben az esetben F_n=(\Z/n\Z)^{\times}. Ezért erre az esetre a következő szakaszban fogunk kitérni.
Bizonyítás:
A 23.3. Definíció utáni megjegyzés alapján nem Fermat-tanú csak redukált maradékosztály lehet, ezért fennáll az F_n\sube (\Z/n\Z)^{\times} tartalmazási reláció. Így az F_n\leq (\Z/n\Z)^{\times} részcsoport reláció igazolásához a 24.13. Következmény alapján csak azt kell megmutatni, hogy F_n nemüres és zárt a (\Z/n\Z)^{\times}-beli csoportműveletre nézve. Az első feltétel nyilván teljesül, hiszen 1^{n-1}\equiv 1\pmod n, és így az [1]_n maradékosztály a 23.3. Definíció értelmében nem Fermat-tanú, azaz benne van F_n-ben.
Legyen most [a]_n és [b]_n az F_n halmaz két tetszőleges eleme. Mivel ők nem Fermat-tanúk, ezért a 23.3. Definíció alapján teljesül az alábbi két kongruencia:
\begin{aligned}a^{n-1}&\equiv 1\pmod n \\ b^{n-1}&\equiv 1\pmod n\end{aligned}A két kongruenciát a 20.2. Tétel 5. pontja miatt összeszorozhatjuk. Alkalmazva a hatványozás azonosságairól szóló 18.8. Tétel 1. pontját, az alábbi kongruenciát kapjuk:
(ab)^{n-1}\equiv 1\pmod nÍgy a 23.3. Definíció alapján az [ab]_n maradékosztály szintén nem Fermat-tanú, azaz benne van F_n-ben. Mivel a 20.5. Tétel alapján az [ab]_n maradékosztály épp az [a]_n és [b]_n maradékosztályok szorzata, ezért F_n valóban zárt a (\Z/n\Z)^{\times} csoport műveletére nézve, azaz részcsoport (\Z/n\Z)^{\times}-ben.
Ha most n nem Carmichael-szám, akkor a 23.7. Definíció alapján létezik n-hez tartozó Fermat-tanú a redukált maradékosztályok között, vagyis a (\Z/n\Z)^{\times} csoportban, amely viszont így nincs benne F_n-ben. Ilyenkor tehát F_n valódi részcsoport. Ezzel szemben ha n Carmichael-szám, akkor egyik redukált maradékosztály sem Fermat-tanú, azaz ilyenkor F_n=(\Z/n\Z)^{\times}.
Azt kell még igazolni, hogy H_n valódi részcsoport F_n-ben. Azt a 24.19. Tétel 2. pontja alapján már tudjuk, hogy H_n részcsoport (\Z/n\Z)^{\times}-ben, ami a 24.13. Következmény értelmében azt jelenti, hogy H_n zárt a (\Z/n\Z)^{\times} csoport műveletére nézve. Így már csak azt kell megmutatni, hogy fennáll a H_n\sub F_n szigorú tartalmazási reláció.
Ehhez először azt igazoljuk, hogy H_n\sube F_n. Legyen ezért [a]_n a H_n halmaz tetszőleges eleme, és mutassuk meg, hogy [a]_n\in F_n. Mivel [a]_n\in H_n, ezért a tétel szövege alapján:
a^{2^{j_{\text{max}}}k} \equiv \pm 1\pmod nAkár 1, akár -1 szerepel a jobboldalon, a kongruenciát négyzetre emelve a következőt kapjuk:
a^{2^{j_{\text{max}}+1}k} \equiv 1\pmod nMivel a tétel szövegéből tudjuk, hogy j_{\text{max}}\leq e-1, ezért az egyenlőtlenség mindkét oldalához 1-et adva j_{\text{max}}+1\leq e adódik. Így ha a fenti kongruencia mindkét oldalát valahányszor négyzetre emeljük (sőt j_{\text{max}}+1=e esetén még csak nem is kell négyzetre emelnünk egyszer sem), akkor előbb-utóbb eljutunk az itt látható utolsó kongruenciáig:
\begin{aligned}a^{2^{j_{\text{max}}+1}}k &\equiv 1\pmod n \\ a^{2^{j_{\text{max}}+2}}k &\equiv 1\pmod n \\ a^{2^{j_{\text{max}}+3}}k &\equiv 1\pmod n \\ &\vdots \\ a^{2^ek} &\equiv 1\pmod n\end{aligned}Minthogy a tétel szövegéből tudjuk, hogy n-1=2^ek, ezért ez az utolsó kongruencia a 23.3. Definíció alapján épp azt jelenti, hogy [a]_n nem Fermat-tanú, azaz benne van F_n-ben, és így H_n\sube F_n.
Végezetül megmutatjuk, hogy ez valójában egy szigorú tartalmazási reláció, azaz mutatni fogunk egy olyan redukált maradékosztályt, amely benne van F_n-ben, de nincs benne H_n-ben. A munka felét már elvégeztük a 24.19. Tétel 4. állításának bizonyításában, ott ugyanis már mutattunk egy olyan [a]_n redukált maradékosztályt, amely nincs benne H_n-ben. Most igazoljuk, hogy ez a bizonyos [a]_n viszont benne van F_n-ben, azaz a következő a helyzet:

Ismételjük át az említett bizonyítás gondolatmenetét. Felhasználtuk, hogy n-nek legalább két prímtényezője van, hiszen nem prímhatvány. Azaz felírható n=p^cm alakban, ahol p az egyik prímtényező, c\geq 1 valamilyen pozitív kitevő, m\gt 1 valamilyen páratlan egész szám, továbbá p^c és m relatív prímek. Ekkor ugye érvényes a kínai maradéktétel (22.2. Tétel), amelynek következményeként a 22.8. Tétel alapján fennáll az alábbi gyűrűizomorfizmus:
\Z/n\Z \simeq \Z/p^c\Z \times \Z/m\ZA tétel szövegéből ugye azt is tudjuk, hogy a j_{\text{max}} kitevőhöz létezik olyan s egész szám, amelyre teljesül az alábbi kongruencia:
s^{2^{j_{\text{max}}}}\equiv -1\pmod nTovábbá az említett bizonyításban azt is megmutattuk, hogy ekkor az s^{2^{j_{\text{max}}}} hatvány -1-gyel kongruens modulo p^c is, azaz:
s^{2^{j_{\text{max}}}}\equiv -1\pmod{p^c}Ezt az s egész számot használtuk fel az említett [a]_n redukált maradékosztály megkonstruálásához. Azt mondtuk, hogy [a]_n legyen az a maradékosztály a \Z/n\Z gyűrűben, amelyhez a 22.8. Tételben szereplő g gyűrűizomorfizmus épp az ([s]_{p^c};[1]_m) maradékosztálypárt rendeli hozzá a \Z/p^c\Z \times \Z/m\Z szorzatgyűrűből, azaz:
[a]_n \xmapsto{g} ([s]_{p^c};[1]_m)Ha most a bal- és a jobboldalon álló kifejezést is 2^{j_{\text{max}}}k-adik hatványra emeljük, akkor g művelettartó tulajdonsága miatt érvényes lesz az alábbi hozzárendelés is:
[a^{2^{j_{\text{max}}}k}]_n \xmapsto{g} ([s^{2^{j_{\text{max}}}k}]_{p^c};[1^{2^{j_{\text{max}}}k}]_m)Mivel k páratlan, és az s^{2^{j_{\text{max}}}} hatvány -1-gyel kongruens modulo p^c, ezért ez teljesülni fog az s^{2^{j_{\text{max}}}k} hatványra is. Így tehát a fenti hozzárendelés az alábbira egyszerűsödik:
[a^{2^{j_{\text{max}}}k}]_n \xmapsto{g} ([-1]_{p^c};[1]_m)Ha most a bal- és jobboldalon álló kifejezéseket elkezdjük sorozatosan négyzetre emelni, akkor g művelettartó tulajdonsága miatt érvényesek lesznek az alábbi hozzárendelések is:
\begin{aligned}[a^{2^{j_{\text{max}}}k}]_n &\xmapsto{g} ([-1]_{p^c};[1]_m) \\ [a^{2^{j_{\text{max}}+1}k}]_n &\xmapsto{g} ([1]_{p^c};[1]_m) \\ [a^{2^{j_{\text{max}}+2}k}]_n &\xmapsto{g} ([1]_{p^c};[1]_m) \\ [a^{2^{j_{\text{max}}+3}k}]_n &\xmapsto{g} ([1]_{p^c};[1]_m) \\ &\vdots\end{aligned}A tétel szövegéből tudjuk, hogy j_{\text{max}}\lt e, ezért a sorozatos négyzetre emeléseket folytatva előbb-utóbb eljutunk az itt látható utolsó hozzárendelésig:
[a^{\overbrace{2^ek}^{=n-1}}]_n \xmapsto{g} ([1]_{p^c};[1]_m)Mivel a 22.8. Tétel alapján a g gyűrűizomorfizmus a jobboldalon látható ([1]_{p^c};[1]_m) maradékosztálypárt épp az [1]_n maradékosztályhoz rendeli hozzá, ezért a baloldalon álló [a^{n-1}]_n maradékosztály szükségképpen megegyezik az [1]_n maradékosztállyal, azaz teljesül az alábbi kongruencia:
a^{n-1}\equiv 1\pmod nÍgy az [a]_n maradékosztály a 23.3. Definíció értelmében nem Fermat-tanú, azaz benne van F_n-ben, tehát valóban fennáll a H_n\sub F_n szigorú tartalmazási reláció.
∎Mit kezdjünk a Carmichael-számokkal?
Az előző szakaszban igazolt tétel tehát a Carmichael-számok esetén közvetlenül nem ad lehetőséget a Lagrange-tétel alkalmazására, és ezáltal a nem Miller-Rabin-tanúkat tartalmazó valódi részcsoport további zsugorítására. Ezért most kénytelenek leszünk az előző részben megismert csoporthomomorfizmusok struktúratartó tulajdonságaira, valamint a Lagrange-tételben definiált részcsoportindex (lásd a 24.8. Tételt) fogalmára támaszkodni.
Az alábbi tételben azt mutatjuk meg, hogy ez a bizonyos valódi részcsoport annál kisebb (vagy más szavakkal annál nagyobb a részcsoportindexe), minél több prímtényezője van a vizsgált n összetett számnak. Ez azért lesz hasznos a Carmichael-számok esetén, mivel a Korselt-kritérium 26.18. Következménye alapján egy ilyen számnak legalább 3 prímtényezője van.
26.22. Tétel:
Legyen n egy tetszőleges 1-nél nagyobb páratlan szám, amelynek r darab különböző prímtényezője van, azaz prímtényezős felbontása az alábbi alakban írható fel valamilyen páronként egymástól különböző pozitív, páratlan p_1, p_2, ..., p_r prímszámokkal és valamilyen pozitív c_1, c_2, ..., c_r kitevőkkel:
n=p_1^{c_1}\cdot p_2^{c_2}\cdot \ldots \cdot p_r^{c_r}Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyekre teljesül az alábbi:
n-1=2^ekA 24.19. Tétel szövegével megegyező módon legyen j_{\text{max}} a legnagyobb olyan j kitevő a \{0;1;2;\ldots;e-1\} egész számok között, amelyhez léteznek olyan x egész számok, hogy teljesül az x^{2^j}\equiv -1\pmod n kongruencia. Megjegyzés: Az említett 24.19. Tétel alapján legalább egy ilyen j kitevő biztosan létezik, tehát j_{\text{max}} is létezik.
Ugyancsak a 24.19. Tétel szövegével megegyezően jelöljük H_n-nel azon [a]_n maradékosztályok halmazát, amelyek esetén az a^{2^{j_{\text{max}}}k} hatvány 1-gyel vagy -1-gyel kongruens modulo n, azaz:
a^{2^{j_{\text{max}}}k} \equiv \pm 1\pmod nVégül jelöljük D_n-nel azon [a]_n maradékosztályok halmazát, amelyek esetén az alábbi kongruenciák mindegyike teljesül:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_1^{c_1}} \\ a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_2^{c_2}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_r^{c_r}}\end{aligned}Ekkor teljesülnek az alábbiak:
- H_n\leq D_n\leq (\Z/n\Z)^{\times}
- |D_n:H_n|=2^{r-1}
Szavakkal ez így fogalmazható meg: H_n részcsoport D_n-ben, amely viszont részcsoport (\Z/n\Z)^{\times}-ben, és a H_n részcsoport D_n-beli indexe 2^{r-1}-gyel egyezik meg, ahol r az n egymástól különböző prímtényezőinek számát jelöli.
♣Bizonyítás:
Az 1. állítás bizonyításához először azt igazoljuk, hogy D_n részcsoport (\Z/n\Z)^{\times}-ben. A 24.13. Következmény alapján ez az alábbi 3 feltétel ellenőrzését jelenti:
- D_n nemüres
- Fennáll a D_n\sube (\Z/n\Z)^{\times} tartalmazási reláció
- D_n zárt a (\Z/n\Z)^{\times} csoport műveletére nézve.
Az első feltétel nyilván teljesül, hiszen teljesülnek az alábbi kongruenciák:
\begin{aligned}1^{2^{j_{\text{max}}}k} &\equiv 1\pmod{p_1^{c_1}} \\ 1^{2^{j_{\text{max}}}k} &\equiv 1\pmod{p_2^{c_2}} \\ &\vdots \\ 1^{2^{j_{\text{max}}}k} &\equiv 1\pmod{p_r^{c_r}}\end{aligned}Így tehát az [1]_n maradékosztály biztosan benne van D_n-ben.
A második feltételhez tekintsünk egy tetszőleges [a]_n\in D_n maradékosztályt, és igazoljuk, hogy ő egy redukált maradékosztály, azaz [a]_n\in (\Z/n\Z)^{\times}. Mivel [a]_n\in D_n, ezért a tétel szövege alapján tetszőleges p_i prímtényezőre teljesül az alábbi kongruencia:
a^{2^{j_{\text{max}}}k}\equiv \pm 1\pmod{p_i^{c_i}}Akár 1, akár -1 szerepel a jobboldalon, a kongruenciát négyzetre emelve az alábbit kapjuk:
a^{2^{j_{\text{max}}+1}k}\equiv 1\pmod{p_i^{c_i}}Találtunk tehát egy olyan pozitív kitevőt – nevezetesen 2^{j_{\text{max}}+1}k-t –, amelyre emelve a-t az eredmény kongruens lesz 1-gyel modulo p_i^{c_i}. Ebből viszont a 20.20. Tétel alapján következik, hogy a relatív prím p_i^{c_i}-hez, azaz prímtényezős felbontása nem tartalmazza a p_i prímtényezőt. Minthogy ez n összes prímtényezőjével végigjátszható, így azt kapjuk, hogy a prímtényezős felbontás nem tartalmazza n egyetlen prímtenyőjét sem, tehát relatív prím magához n-hez. Ez viszont a 20.14. Tétel értelmében azt jelenti, hogy [a]_n redukált maradékosztály, vagyis valóban benne van (\Z/n\Z)^{\times}-ben.
Végül a harmadik feltételhez tekintsünk két tetszőleges [a]_n és [b]_n maradékosztályt a D_n halmazban. A D_n definíciója alapján ekkor teljesülnek az alábbi kongruenciák:
\begin{array}{cc} \begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_1^{c_1}} \\ a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_2^{c_2}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_r^{c_r}}\end{aligned} & \begin{aligned}b^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_1^{c_1}} \\ b^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_2^{c_2}} \\ &\vdots \\ b^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_r^{c_r}}\end{aligned} \end{array}Ha az egymás mellett álló kongruenciákat összeszorozzuk, és alkalmazzuk a hatványozás azonosságairól szóló 18.8. Tétel 1. pontját, akkor az alábbi kongruenciákat kapjuk:
\begin{aligned}(ab)^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_1^{c_1}} \\ (ab)^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_2^{c_2}} \\ &\vdots \\ (ab)^{2^{j_{\text{max}}}k} &\equiv \pm 1\pmod{p_r^{c_r}}\end{aligned}Vagyis az [ab]_n maradékosztály szintén benne van D_n-ben. Mivel ez a 20.5. Tétel alapján épp az [a]_n és [b]_n maradékosztályok szorzata, ezért D_n valóban zárt a (\Z/n\Z)^{\times} csoport műveletére nézve. Minthogy a 24.13. Következmény mindhárom feltétele teljesül, ezért D_n részcsoport (\Z/n\Z)^{\times}-ben, azaz D_n\leq (\Z/n\Z)^{\times}.
Most az 1. állítás másik felét, azaz a H_n\leq D_n részcsoport relációt igazoljuk. A 24.19. Tétel 2. pontja alapján azt már tudjuk, hogy H_n részcsoport (\Z/n\Z)^{\times}-ban, azaz zárt a maradékosztályok közötti szorzásra nézve. Így már csak a H_n\sube D_n tartalmazási relációt kell igazolni. Legyen ezért [a]_n a H_n halmaz egy tetszőleges eleme és mutassuk meg róla, hogy ő egyúttal benne van D_n-ben is. Mivel [a]_n\in H_n, így a tétel szövege alapján a-ra teljesül az alábbi kongurencia:
a^{2^{j_{\text{max}}}k}\equiv \pm 1\pmod nÁm ekkor az n prímtényezős felbontásában szereplő összes p_i^{c_i} tényező esetén a 20.2. Tétel 9. pontja alapján teljesül az alábbi kongruencia is:
a^{2^{j_{\text{max}}}k}\equiv \pm 1\pmod{p_i^{c_i}}Ez viszont a tétel szövege alapján épp azt jelenti, hogy [a]_n\in D_n, azaz valóban teljesül a H_n\sube D_n tartalmazási reláció, és így H_n tényleg részcsoport D_n-ben. Ezzel igazoltuk a tétel 1. állítását.
A 2. állítás igazolásához ki kellene számítani a H_n részcsoport D_n-beli indexét. Ezt nem közvetlenül fogjuk megtenni, hanem a 25.14. Tétel alkalmazásával, méghozzá a következő lépésekben:
- Konstruálunk egy olyan I_n-nel jelölt csoportot, amelyben már könnyű kiszámítani a részcsoportindexeket.
- Konstruálunk egy D_n-ből I_n-be képző csoporthomomorfizmust.
- Megmutatjuk, hogy ez egy szürjektív csoporthomomorfizmus, azaz minden I_n-beli elem hozzá van rendelve legalább egy D_n-beli elemhez.
- Megmutatjuk, hogy a H_n részcsoport teljes egészében tartalmazza ennek a bizonyos csoporthomomorfizmusnak a magját.
- Megkeressük azt az I_n-beli részcsoportot, amelynek teljes inverz képe épp H_n.
- Ennek a részcsoportnak az I_n-beli indexe már könnyen kiszámítható lesz, amely a 25.14. Tétel 2. pontja alapján épp meg fog egyezni a H_n részcsoport D_n-beli indexével.
Kezdjük az 1. lépéssel! A kérdéses I_n csoport álljon az összes olyan r hosszú sorozatból – ahol ugye r a tétel szövege alapján az n egész szám különböző prímtényezőinek a számát jelöli –, amelyeknek mindegyik komponensében +1 vagy -1 áll. Azaz például az alábbi r darab komponensből álló sorozat legyen I_n egyik eleme:
\underbrace{(+1;-1;-1;+1;\ldots;-1)}_{r\ \text{darab komponens}}Az I_n tehát tulajdonképpen nem más, mint a \{+1;-1\} halmaz r-szer önmagával vett direkt szorzata (lásd a 22.3. Definíciót). Az I_n csoportművelete legyen a 25.15. Tételben definiált komponensenkénti szorzás. Azaz két ilyen +1-ekből és -1-ekből álló r hosszú sorozat szorzata legyen az a szintén r hosszú sorozat, amelynek mindegyik komponense a két bemeneti sorozat azonos pozícióban lévő komponenseinek szorzata.
Mivel a \{+1;-1\} halmaz épp az egész számok \Z gyűrűjének egységeiből áll, ezért ez a halmaz a szokásos szorzással tulajdonképpen \Z multiplikatív csoportját alkotja (lásd a 24.3. Definíció utáni megjegyzést). Ekkor azonban a 25.15. Tétel alapján I_n is csoport a komponensenkénti szorzással, mint művelettel. Minthogy az I_n csoport r hosszú sorozatokból áll, és egy-egy ilyen sorozat minden komponense +1 vagy -1 lehet, ezért I_n rendje 2^r.
Most 2. lépésként egy D_n-ből I_n-be képező f_n:D_n\to I_n csoporthomomorfizmust konstruálunk a következőképpen. Legyen [a]_n a D_n csoport egy tetszőleges eleme. Ekkor ugye a tétel szövege alapján az a^{2^{j_{\text{max}}}k} hatvány az n prímtényezős felbontásában szereplő minden p_i^{c_i} tényező esetén +1-gyel vagy -1-gyel lesz kongruens modulo p_i^{c_i}. Az f_n függvény tehát rendelje hozzá [a]_n-hez azt az I_n-beli sorozatot, melynek i-edik komponensében épp az ennek megfelelő +1 vagy -1 egész szám áll. Tegyük fel például, hogy a-ra az alábbi kongruenciák teljesülnek:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_1^{c_1}} \\ a^{2^{j_{\text{max}}}k} &\equiv -1\pmod{p_2^{c_2}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_3^{c_3}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv -1\pmod{p_r^{c_r}}\end{aligned}Ekkor az imént definiált f_n függvény az [a]_n\in D_n maradékosztályhoz az alábbi sorozatot rendeli hozzá az I_n csoportból:
[a]_n \xmapsto{f_n} (+1;-1;+1;\ldots;-1)Könnyen láthatóan f_n valóban egy csoporthomomorfizmus. Tekintsünk ugyanis két tetszőleges [a]_n és [b]_n maradékosztályt a D_n halmazban, és legyen p_i^{c_i} egy tetszőleges tényező az n prímtényzős felbontásában. Ekkor a tétel szövege alapján az a^{2^{j_{\text{max}}}k} és b^{2^{j_{\text{max}}}k} hatványok +1-gyel vagy -1-gyel lesznek kongruensek modulo p_i^{c_i}. Tegyük fel, hogy jelen esetben az alábbi kombináció teljesül, de természetesen a gondolatmenet a másik három kombinációra is végigjátszható:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_i^{c_i}} \\ b^{2^{j_{\text{max}}}k} &\equiv -1\pmod{p_i^{c_i}}\end{aligned}Ekkor az f_n([a]_n) sorozat i-edik pozíciójában +1, míg az f_n([b]_n) szorozat i-edik pozíciójában -1 fog szerepelni:
\begin{aligned}[a]_n &\xmapsto{f_n} (\ldots;+1;\ldots) \\ [b]_n &\xmapsto{f_n} (\ldots;-1;\ldots)\end{aligned}E két sorozat szorzatában pedig ennek megfelelően -1 lesz az i-edik pozícióban, hiszen 1\cdot (-1)=-1:
? \xmapsto{f_n} (\ldots;-1;\ldots)Azt kell igazolni, hogy f_n tartja a két csoport műveletét, azaz hogy a baloldali kérdőjel helyére behelyettesítve az [a]_n és [b]_n maradékosztályok szorzatát teljesül a fenti hozzárendelés. Mivel ez a szorzat a 20.5. Tétel alapján épp az [ab]_n maradékosztállyal egyezik meg, ezért az a kérdés, hogy teljesül-e az alábbi hozzárendelés:
[ab]_n \xmapsto{f_n} (\ldots;-1;\ldots)Vagyis az f_n függvény definíciója alapján az a kérdés, hogy teljesül-e az alábbi kongruencia:
(ab)^{2^{j_{\text{max}}}k} \equiv -1\pmod{p_i^{c_i}}Ez viszont nyilván teljesül, hiszen ezt a kongruenciát épp az a-ra és b-re vonatkozó két fentebbi kongruencia összeszorzásával kapjuk meg. Minthogy a fenti gondolatmenet az n prímtényezős felbontásában szereplő összes többi tényezőre is szóról-szóra megismételhető, ezért f_n valóban egy csoporthomomorfizmus D_n-ből I_n-be.
A 3. lépéshez meg kell mutatni, hogy az f_n csoporthomomorfizmus szürjektív. Azaz tetszőleges r hosszú, +1-ekből és -1-ekből álló sorozathoz létezik olyan [a]_n\in D_n maradékosztály, amely épp a kérdéses sorozatnak egy f_n szerinti ősképe. Nevezzük most bázissorozatoknak azokat a sorozatokat, melyeknek pontosan egy komponense -1, a többi viszont +1. Ezekből a bázissorozatokból szorzásokkal előállítható az I_n csoport tetszőleges X eleme, méghozzá a következő egyszerű eljárással:
- Vegyük az egyik tetszőleges bázissorozatot, és szorozzuk meg önmagával. Ekkor a csupa +1-ekből álló sorozatot kapjuk.
- Ezt szorozzuk meg azokkal a bázissorozatokkal, amelyeknél épp azokban a pozíciókban van -1, ahol a keresett X sorozatban is.
Az így megkapott X sorozatnak viszont f_n művelettartó tulajdonsága miatt épp az a D_n-beli maradékosztály lesz az ősképe, amelyet az X előállításához használt bázissorozatok ősképeinek D_n-beli szorzataként kapunk.
Például tegyük fel, hogy X előáll az X_1, X_2 és X_3 bázissorozatok szorzataként az I_n csoportban, azaz az iménti eljárással:
X_1\cdot X_1\cdot X_2\cdot X_3=XTegyük fel, hogy az X_1, X_2 és X_3 bázissorozatok f_n szerinti ősképei D_n-ben mondjuk rendre az A_1, A_2 és A_3 maradékosztályok, azaz:
\begin{aligned}f_n(A_1)&=X_1 \\ f_n(A_2)&=X_2 \\ f_n(A_3)&=X_3\end{aligned}Ekkor az f_n csoporthomomorfizmus művelettartó tulajdonsága miatt:
\underbrace{f_n(A_1)}_{=X_1}\cdot \underbrace{f_n(A_1)}_{=X_1}\cdot \underbrace{f_n(A_2)}_{=X_2}\cdot \underbrace{f_n(A_3)}_{=X_3}=\underbrace{f_n(A_1\cdot A_1\cdot A_2\cdot A_3)}_{=X}Elegendő tehát megmutatni, hogy a bázissorozatoknak létezik ősképe, ezek ismeretében ugyanis a fenti eljárással megtalálhatjuk tetszőleges X sorozat ősképét is. Ez a fenti példában nevezetesen az A_1\cdot A_1\cdot A_2\cdot A_3 szorzat lesz. Ha tehát megmutatjuk, hogy a bázissorozatokhoz létezik őskép, akkor azzal egyúttal azt is megmutattuk, hogy bármely I_n-beli sorozathoz is létezik őskép, azaz f_n valóban szürjektív.
Tekintsünk ezért most egy tetszőleges B_i bázissorozatot, amelynek tehát az i-edik pozíciójában -1, az összes többi pozíciójában pedig +1 szerepel. E sorozat ősképének előállításához lényegében a 24.19. Tétel 4. állításának bizonyításában szereplő gondolatmenetet fogjuk megismételni. Az n ugye felírható n=p_i^{c_i}m alakban, ahol p_i^{c_i} az n prímtényezős felbontásában szereplő i-edik tényező, az m pedig az összes többi tényező szorzata. Azaz p_i^{c_i} és m relatív prímek. Ekkor ugye érvényes a kínai maradéktétel (22.2. Tétel), amelynek következményeként a 22.8. Tétel alapján fennáll az alábbi gyűrűizomorfizmus:
\Z/n\Z \simeq \Z/p_i^{c_i}\Z \times \Z/m\ZA tétel szövegéből ugye azt is tudjuk, hogy a j_{\text{max}} kitevőhöz létezik olyan s egész szám, amelyre teljesül az alábbi kongruencia:
s^{2^{j_{\text{max}}}}\equiv -1\pmod nTovábbá az említett bizonyításban azt is megmutattuk, hogy ekkor az s^{2^{j_{\text{max}}}} hatvány -1-gyel kongruens modulo p_i^{c_i} is, azaz:
s^{2^{j_{\text{max}}}}\equiv -1\pmod{p_i^{c_i}}Ezt az s egész számot most felhasználjuk a keresett B_i bázissorozat ősképének előállításához. Legyen ez az őskép azon a egész szám által reprezentált [a]_n maradékosztály, amelyhez a 22.8. Tételben szereplő g gyűrűizomorfizmus épp az ([s]_{p_i^{c_i}};[1]_m) maradékosztálypárt rendeli hozzá a \Z/p_i^{c_i}\Z \times \Z/m\Z szorzatgyűrűből, azaz:
[a]_n \xmapsto{g} ([s]_{p_i^{c_i}};[1]_m)Ha most a bal- és a jobboldalon álló kifejezést is 2^{j_{\text{max}}}k-adik hatványra emeljük, akkor g művelettartó tulajdonsága miatt érvényes lesz az alábbi hozzárendelés is:
[a^{2^{j_{\text{max}}}k}]_n \xmapsto{g} ([s^{2^{j_{\text{max}}}k}]_{p_i^{c_i}};[1^{2^{j_{\text{max}}}k}]_m)Mivel k páratlan, és az s^{2^{j_{\text{max}}}} hatvány -1-gyel kongruens modulo p_i^{c_i}, ezért ez teljesülni fog az s^{2^{j_{\text{max}}}k} hatványra is. Így tehát a fenti hozzárendelés az alábbira egyszerűsödik:
[a^{2^{j_{\text{max}}}k}]_n \xmapsto{g} ([-1]_{p_i^{c_i}};[1]_m)A 22.8. Tétel alapján a g gyűrűizomorfizmus a baloldalon lévő [a^{2^{j_{\text{max}}}k}]_n maradékosztályhoz az ([a^{2^{j_{\text{max}}}k}]_{p_i^{c_i}};[a^{2^{j_{\text{max}}}k}]_m) maradékosztálypárt rendeli hozzá, amely maradékosztálypár tehát megegyezik a jobboldalon látható ([-1]_{p_i^{c_i}};[1]_m) maradékosztálypárral. Teljesülnek tehát az alábbi kongruenciák:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv -1\pmod{p_i^{c_i}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod m\end{aligned}Itt a második kongruencia m modulusa az n prímtényezős felbontásából minden p_i^{c_i}-n kívüli tényezőt tartalmaz, így tehát az a 20.2. Tétel 9. pontjának felhasználásával felbontható olyan kongruenciákra, amelyekben ezek a tényezők a modulusok. Azaz a fenti két kongruencia az alábbi r darab kongruenciával ekvivalens:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_1^{c_1}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_2^{c_2}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_{i-1}^{c_{i-1}}} \\ a^{2^{j_{\text{max}}}k} &\equiv -1\pmod{p_i^{c_i}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_{i+1}^{c_{i+1}}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_{i+2}^{c_{i+2}}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_r^{c_r}}\end{aligned}Ekkor az [a]_n maradékosztály egyrészt a tétel szövege alapján benne van D_n-ben, másrészt pedig az f_n csoporthomomorfizmus épp a B_i bázissorozatot rendeli hozzá, amelynek tehát az i-edik pozíciójában -1, az összes többi pozíciójában pedig +1 szerepel. Minthogy ilymódon tetszőleges bázissorozathoz találhatunk ősképet a D_n csoportban, ezért f_n valóban egy szürjektív csoporthomomorfizmus D_n-ből I_n-be.
A fentebb felvázolt stratégiánk 4. lépéseként megmutatjuk, hogy a tétel szövegében szereplő H_n részcsoport – amelynek tehát a D_n-beli indexét szeretnénk meghatározni – teljes egészében tartalmazza az f_n csoporthomomorfizmus magját. Ezt most jelöljük K_n-nel, azaz:
K_n=\ker{f_n}Azt szeretnénk tehát megmutatni, hogy a következő a helyzet:
Tekintsünk ezért egy tetszőleges [a]_n\in K_n maradékosztályt, és mutassuk meg, hogy ekkor [a]_n\in H_n is teljesül. Mivel [a]_n benne van az f_n csoporthomomorfizmus K_n-nel jelölt magjában, ezért az ő f_n szerinti képe épp az I_n csoport egységeleme lesz. Ez nem más, mint a csupa +1-esekből álló r hosszú sorozat, azaz:
[a]_n \xmapsto{f_n} (+1;+1;\ldots;+1)Az f_n csoporthomomorfizmus definíciójából adódik, hogy ekkor teljesülnek az alábbi kongruenciák:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_1^{c_1}} \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_2^{c_2}} \\ &\vdots \\ a^{2^{j_{\text{max}}}k} &\equiv +1\pmod{p_r^{c_r}}\end{aligned}Ez a 20.1. Tétel 3. pontja alapján azt jelenti, hogy az n prímtényezős felbontásában szereplő összes p_i^{c_i} tényezőre igaz, hogy ő osztója az a^{2^{j_{\text{max}}}k}-1 különbségnek is. Ekkor azonban nyilván maga n is osztója ennek a különbségnek, hiszen:
\underbrace{p_1^{c_1}\cdot p_2^{c_2}\cdot \ldots \cdot p_r^{c_r}}_{=n}|a^{2^{j_{\text{max}}}k}-1Ez viszont ismét a 20.1. Tétel 3. pontja alapján épp azt jelenti, hogy teljesül az alábbi kongruencia:
a^{2^{j_{\text{max}}}k}\equiv 1\pmod nTehát a tétel szövege alapján [a]_n\in H_n, azaz valóban teljesül a K_n\sube H_n tartalmazási reláció.
5. lépésként meghatározzuk azt az I_n-beli részcsoportot, amelynek teljes inverz képe épp H_n. Nézzük ezért először, hogy H_n elemei milyen I_n-beli sorozatokra képződnek le f_n által. Ha [a]_n a H_n részcsoport valamely eleme, akkor a tétel szövege alapján az alábbi kongruenciák közül teljesül valamelyik:
\begin{aligned}a^{2^{j_{\text{max}}}k} &\equiv +1\pmod n \\ a^{2^{j_{\text{max}}}k} &\equiv -1\pmod n\end{aligned}Ez viszont a 20.2. Tétel 9. pontja alapján azt jelenti, hogy az a^{2^{j_{\text{max}}}k} hatvány vagy +1-gyel, vagy pedig -1-gyel kongruens modulo p_i^{c_i} is az n egész szám prímtényezős felbontásában szereplő minden p_i^{c_i} tényező esetén. Az f_n függvény tehát a definíciója alapján H_n elemeihez vagy a csupa +1-esekből, vagy pedig a csupa -1-esekből álló sorozatot rendeli hozzá.
Azt kell még megmutatni, hogy ez csak a H_n-beli elemekre igaz. Legyen ezért [a]_n\in D_n most egy olyan maradékosztály, amely nincs benne H_n-ben. Tegyük fel indirekt, hogy az f_n függvény őt ennek ellenére a (+1;+1;\ldots;+1) vagy a (-1;-1;\ldots;-1) sorozatok valamelyikére képezi le. Ez az f_n függvény definíciója alapján azt jelentené, hogy az a^{2^{j_{\text{max}}}k} hatvány vagy +1-gyel, vagy pedig -1-gyel kongruens modulo p_i^{c_i} az n prímtényezős felbontásában szereplő minden p_i^{c_i} tényező esetén. Az előző gondolatmenet alapján tehát ez a hatvány +1-gyel vagy -1-gyel lenne kongruens modulo n is, ami azt jelentené, hogy [a]_n mégiscsak benne lenne H_n-ben, ami ellentmondás.
Összefoglalva tehát az 1. lépésben mutattunk egy csoportot, amelyben könnyű részcsoportindexeket számolni. Ez lenne az I_n csoport, amelynek tehát a rendje 2^r. Ezután a 2. lépésben egy f_n csoporthomomorfizmust mutattunk D_n és I_n között. Ezután 3. lépésként igazoltuk, hogy f_n szürjektív, majd 4. lépésként azt, hogy a D_n csoport H_n részcsoportja teljes egészében tartalmazza f_n magját. Végül az 5. lépésben igazoltuk, hogy H_n a teljes inverz képe I_n azon kételemű részcsoportjának, amely csak a csupa +1-ből és a csupa -1-ből álló sorozatból áll. Nevezzük most ezt a részcsoportot J_n-nek.
Minden adott tehát, hogy a 6. lépésben alkalmazzuk a 25.14. Tételt. Ez alapján a J_n szerinti baloldali mellékosztályok kölcsönösen egyértelmű megfeleltetésben állnak a H_n szerinti baloldali mellékosztályokkal, következésképp az |I_n:J_n| részcsoportindex épp megegyezik a |D_n:H_n| részcsoportindexszel. Mivel J_n rendje 2, I_n rendje pedig 2^r, ezért a Lagrange-tétellel (24.8. Tétel) összevetve megkapjuk a tétel 2. állítását:
|I_n:J_n|=|D_n:H_n|=2^{r-1} ∎Az eddigi eredmények összefoglalása
Így mostmár minden rendelkezésünkre áll a Miller-Rabin-tanúk számára vonatkozó, a 24.20. Következményben igazolt eredeti becslésünk javításához. Foglaljuk is össze ezeket az eredményeket. Megjegyezzük, hogy az alábbi becsléshez némileg szűkíteni kell a kört a 9-nél nagyobb páratlan összetett számokra, ám ez nyilvánvalóan nem jelent gyakorlati megszorítást, tekintve, hogy Miller-Rabin-prímtesztet ennél jóval nagyobb számtartományban használják.
26.23. Következmény:
Legyen n\gt 9 egy tetszőleges páratlan egész szám. Ha n összetett, akkor a modulo n redukált maradékosztályoknak legalább a háromnegyede Miller-Rabin-tanú.
♣Bizonyítás:
1. eset: n valamilyen prímhatvány
Ekkor tehát n=p^c, ahol p valamilyen páratlan prímszám, továbbá c\geq 2, máskülönben n=p nem lenne összetett. A modulo p^c redukált maradékosztályok a (\Z/p^c\Z)^{\times} multiplikatív csoport elemei, melynek rendjét a 20.7. Definíció alapján az Euler-féle \varphi-függvény adja meg. Ennek értéke a 21.5. Tétel szerint az alábbi:
|(\Z/p^c\Z)^{\times}|=\varphi(p^c)=p^c-p^{c-1}=p^{c-1}\cdot (p-1)Másrészt a nem Miller-Rabin-tanúk G_{p^c}-vel jelölt csoportjának rendje a 26.20. Tétel értelmében:
|G_{p^c}|=p-1Azt kell megmutatni, hogy (\Z/p^c\Z)^{\times} legalább négyszer annyi elemet tartalmaz, mint G_{p^c}, azaz:
\underbrace{p^{c-1}\cdot (p-1)}_{=|(\Z/p^c\Z)^{\times}|}\geq 4\cdot \underbrace{(p-1)}_{=|G_{p^c}|}Az n=p^c-ről ugye tudjuk, hogy ő egy 9-nél nagyobb prímhatvány, azaz p legalább 5 és c legalább 2. Az alábbi tehát biztosan teljesül:
p^{c-1}\geq 4Mindkét oldalt megszorozva p-1-gyel – ami a fentiek alapján biztosan pozitív – a 15.11. Definíció szerinti 2. rendezési axióma alapján megkapjuk a tétel állítását a prímhatványok esetére:
p^{c-1}\cdot (p-1)\geq 4\cdot (p-1)2. eset: n nem prímhatvány, és nem Carmichael-szám
Ekkor a nem Miller-Rabin-tanúk ugyan nem alkotnak részcsoportot (\Z/n\Z)^{\times}-ben, azonban a 26.21. Tétel 1. pontja alapján a nem Fermat-tanúk F_n-nel jelölt csoportja valódi részcsoport (\Z/n\Z)^{\times}-ben, továbbá az ugyanezen tételben H_n-nel jelölt csoport valódi részcsoport F_n-ben, amely viszont a 24.19. Tétel 1. pontja alapján minden nem Miller-Rabin-tanút tartalmaz. Azaz a következő a helyzet:

A Lagrange-tétel (24.8. Tétel) miatt azonban a redukált maradékosztályoknak legfeljebb a fele tartozhat F_n-be, amelyeknek legfeljebb a fele – köztük az összes nem Miller-Rabin-tanú – tartozhat H_n-be. Következésképp a redukált maradékosztályoknak ebben az esetben is legalább a háromnegyede Miller-Rabin-tanú.
3. eset: n nem prímhatvány, és Carmichael-szám
Ekkor a 26.21. Tétel 1. pontja helyett a 26.22. Tételt kell alkalmaznunk. Eszerint a nem Miller-Rabin-tanúkat tartalmazó H_n részcsoport indexe a tételben szereplő D_n részcsoportban 2^{r-1}, ahol r az n egész szám egymástól különböző prímtényezőinek számát jelöli. Továbbá, mivel D_n részcsoport (\Z/n\Z)^{\times}-ben, ezért a H_n részcsoport indexe (\Z/n\Z)^{\times}-ben legalább 2^{r-1}. Ez a Lagrange-tétel (24.8. Tétel) alapján azt jelenti, hogy (\Z/n\Z)^{\times} rendje legalább 2^{r-1}-szerese H_n rendjének, amely ugye a 24.19. Tétel 1. pontja alapján minden nem Miller-Rabin-tanút tartalmaz.
Mivel azonban n Carmichael-szám, ezért a Korselt-kritérium 26.18. Következménye alapján r\geq 3, és így ez a bizonyos 2^{r-1} szorzó tényező legalább 4. Most is azt kaptuk tehát, hogy a redukált maradékosztályoknak legalább a háromnegyede Miller-Rabin-tanú.
∎Az AKS-prímteszt
Általánosságban a prímteszteknek három fontos jellemzője van:
- Determinisztikusság: Egy determinisztikus prímteszt minden esetben egyértelműen választ ad arra a kérdésre, hogy a bemeneti szám prím-e vagy sem. Ilyen volt például a 23. részben ismertetett osztáspróbákon alapuló prímteszt. Ezzel szemben egy valószínűségi prímteszt – például a Fermat- vagy a Miller-Rabin-prímteszt – a gyakorlati alkalmazások szempontjából elhanyagolható valószínűséggel ugyan, de tévedhet.
- Hatékonyság: Egy prímtesztnél mindig fontos, hogy mennyire gyorsan, mennyire hatékonyan tudja megválaszolni a kérdést, ahol hatékonyság alatt algoritmikus hatékonyságot értünk. Erről a 7. részben volt szó bővebben. Az osztáspróbákon alapuló módszerről például láttuk, hogy nem nevezhető hatékonynak, ezzel szemben a Fermat- és Miller-Rabin-prímtesztek villámgyorsnak bizonyulnak.
- Feltétel nélküliség: Végül a harmadik szempont, hogy az adott prímteszt helyes működése és/vagy hatékonysága valamilyen még nem bizonyított matematikai sejtésen alapszik-e vagy sem.
Ez utóbbival kapcsolatban példaként megemlítjük, hogy a Miller-Rabin-prímteszt alapjául szolgáló úgynevezett Miller-prímtesztet eredetileg Gary Miller publikálta 1976-ban. Ez egy polinomiális időkomplexitású (azaz algoritmikusan hatékony) és determinisztikus eljárás, az első két feltétel tehát teljesül. Mindazonáltal az úgynevezett általánosított Riemann-hipotézis igazságán alapul, amely egy nagyon mély és messzemenő következményekkel járó, és egyben talán az egyik legfontosabb matematikai sejtés, amelyre ma még nem ismerjük a választ. Ennek a sejtésnek többek között az egyik következménye az lenne, hogy bármely összetett számnak mindenképpen létezne Miller-Rabin-tanúja egy nagyon kis számtartományban. Így elegendő lenne ezt a számtartományt szisztematikusan átvizsgálni, mivel ha itt nem találunk tanút, akkor az általánosított Riemann-hipotézisból következne, hogy máshol sem fogunk, azaz a bementi számunk biztosan prím.
Ez az egész azonban mit sem ér, ha az általánosított Riemann-hipotézisről végül kiderül, hogy mégsem igaz. Ezt a problémát megkerülendő Michael Oster Rabin 1980-ban publikálta a Miller-prímteszt módosított változatát, amely már nem függ az általánosított Riemann-hipotézis igazságától, cserében viszont ez a változat nemdeterminisztikus. Ez a már jól ismert Miller-Rabin-prímteszt, amelyet az elmúlt részekben részletesen ismertettünk.
Az eddigiekből úgy tűnik, hogy a prímtesztek a fenti három feltétel közül legfeljebb kettőt tudnak teljesíteni. Az osztáspróbákon alapuló teszt determinisztikus és feltétel nélküli, ugyanakkor nem hatékony. A Fermat- és Miller-Rabin-prímteszt hatékony és szintén feltétel nélküli, ugyanakkor nemdeterminisztikus. Végül a példaként imént felhozott Miller-prímteszt determinisztikus és hatékony, viszont az általánosított Riemann-hipotézis igazságától függ. Egészen a közelmúltig nyitott volt a kérdés, hogy vajon létezik-e olyan prímteszt, amely mindhárom kritériumnak megfelel. Ezt a 7. részben ismertetett algoritmuselméleti terminológiával élve úgy is kérdezhetnénk, hogy vajon a prímség vagy összetettség eldöntésének problémája a P problémaosztályba tartozik-e.
Erre a kérdésre három indiai matematikus, Manindra Agrawal, Neeraj Kayal, és Nitin Saxena adott igenlő választ 2002-ben, amikor publikálták az úgynevezett Agrawal-Kayal-Saxena-prímtesztet (rövidítve AKS-prímteszt). Ez az első olyan prímteszt, amely egyszerre determinisztikus, hatékony és nem függ semmilyen nem bizonyított sejtéstől.
Az AKS-prímteszt egy egyszerű összefüggésen alapszik, amelyet itt csak az érdekesség kedvéért, bizonyítás nélkül közlünk. Legyen n\geq 2 tetszőleges, a pedig egy szintén tetszőleges n-hez relatív prím egész szám. Ebben az esetben az n egész szám akkor és csak akkor prím, ha minden x esetén teljesül az alábbi kongruencia:
(x+a)^n\equiv x^n+a\pmod nEz a kongruencia tulajdonképpen az ebben a részben tanultak alapján felfogható egy egyenletnek a \Z/n\Z feletti polinomgyűrűben. Maga az összefüggés egyszerű, ugyanakkor a kiértékelése ebben a formában exponenciális időkomplexitású, hiszen mindkét oldalon szerepel egy-egy n darab tényezőből álló szorzat, márpedig n a számjegyei számának exponenciális függvénye. Az AKS-algoritmus bonyolultsága tehát nem az elméleti háttérből, hanem ennek a kiértékelési problémának a leküzdéséből ered, ám a részletektől itt eltekintünk.
Mindazonáltal megjegyezzük, hogy ennek a felfedezésnek főként elméleti jelentősége van, hiszen – mint már említettük – bizonyítja, hogy a prímség vagy összetettség eldöntése a P problémaosztályba tartozik. A gyakorlatban azonban továbbra is főként a nemdeterminisztikus algoritmusokat használják, mivel az AKS-teszt hatékonysága – noha polinomiális – messze elmarad ezektől.
Carmichael-számok és az RSA
Végezetül ejtünk még néhány szót arról, hogy miért volt olyan fontos kiküszöbölni az univerzális álprímek okozta kellemetlenséget a prímtesztek esetén. Azt a kérdést fogjuk megvizsgálni, hogy mi a helyzet az RSA-algoritmussal, ha a kulcsgeneráláshoz használt p és q pozitív egész számok közül legalább az egyik egy Carmichael-szám. A Fermat-prímteszt esetén – noha kicsi a valószínűsége, de – ez bizony előfordulhat, hiszen ez a teszt nem szűri ki a Carmichael-számokat. Emlékeztetnénk az Olvasót az RSA helyes működéséről szóló alábbi tételre, és javasoljuk, hogy tekintse át az ehhez kapcsolódó bizonyítást:
Most egy ehhez nagyon hasonló tételt igazolunk, amelyben azonban a p és q egészekről nem feltételezzük, hogy mindketten prímek. Például azért, mert szerencsétlen módon a Fermat-prímtesztet használtuk a megkeresésükre, és pont beletrafáltunk egy Carmichael-számba.
26.24. Tétel:
Tegyük fel, hogy teljesülnek az alábbi feltételek:
- Legyen adott két tetszőleges pozitív, egymáshoz relatív prím p és q egész szám, amelyek közül mindkettőre igaz, hogy vagy prím, vagy pedig Carmichael-szám.
- Képezzük ezekből az m=p\cdot q modulust.
- Képezzük a (p-1)\cdot (q-1) egész számot. Ha p és q mindketten prímek, akkor ez persze \varphi(m)-mel fog megegyezni, ám ezt ugye az 1. pont miatt most nem feltételezzük.
- Legyen adott egy tetszőleges e egész szám, amely relatív prím (p-1)\cdot (q-1)-hez.
- Keressünk egy olyan d egész számot, amelyre teljesül az alábbi kongruencia:
Ekkor tetszőleges x egész szám esetén teljesül az alábbi kongruencia is:
x^{e\cdot d}\equiv x\pmod m ♣Bizonyítás:
A d titkos kitevőt tehát alábbi lineáris kongruencia megoldásaként kapjuk:
e\cdot x\equiv 1\pmod{(p-1)\cdot (q-1)}Ennek a kongruenciának a 20.12. Tétel alapján természetesen létezik megoldása, amely a 20.13. Tétel 1. pontja szerint egyértelmű.
A továbbiakban azt szeretnénk igazolni, hogy tetszőleges x egész szám esetén teljesül az alábbi kongruencia:
x^{e\cdot d}\equiv x\pmod mA 22.6. Tétel bizonyításának gondolatmenetét követve az e\cdot d\equiv 1\pmod{(p-1)\cdot (q-1)} kongruenciából következik, hogy létezik olyan k egész szám, amelyre teljesül az alábbi:
k\cdot (p-1)\cdot (q-1)+1=e\cdot dA fenti bizonyítandó kongruencia tehát így is írható:
x^{\overbrace{k\cdot (p-1)\cdot (q-1)+1}^{=ed}}\equiv x\pmod mLegyen most r az m modulus egy tetszőleges pozitív prímosztója. Mivel p és q relatív prímek és m=pq, ezért r biztosan osztója p és q közül pontosan az egyiknek. Az általánosság megsértése nélkül feltehetjük, hogy p-nek osztója, máskülönben az alábbi gondolatmenet ugyanígy működik p és q szerepének felcserélésével. Ekkor az alábbi két eset lehetséges:
- Ha p prím, akkor r=p, és így r-1=p-1, azaz r-1|p-1.
- Ha p Carmichael-szám, akkor r|p, és így a Korselt-kritérium miatt r-1|p-1.
Mindkét esetben azt kaptuk tehát, hogy teljesül az r-1|p-1 oszthatóság, azaz létezik olyan egész szám, amivel r-1-et megszorozva p-1-et kapunk. Jelöljük ezt az egész számot \frac{p-1}{r-1}-gyel.
A kis Fermat-tételből (22.1. Tétel) tudjuk, hogy bármilyen r-hez relatív prím x egész szám esetén teljesül az alábbi kogruencia:
x^{r-1}\equiv 1\pmod rEkkor tetszőleges n pozitív egész esetén a 20.2. Tétel 8. pontja alapján teljesül az alábbi kongruencia is:
x^{n\cdot (r-1)}\equiv 1\pmod rSzorozzuk meg mindkét oldalt x-szel:
x^{n\cdot (r-1) + 1}\equiv x\pmod rVegyük észre, hogy ez a kongruencia már abban az esetben is teljesül, ha x nem relatív prím r-hez. Ilyenkor ugyanis x szükségképpen többszöröse r-nek – hiszen r ugye prím –, vagyis a kongruencia mindkét oldalán 0 áll ebben az esetben. Ha tehát ez a kongruencia minden x-re és minden pozitív egész n-re teljesül, akkor nyilván teljesül az alábbi speciális eseben is:
n=k\cdot \frac{p-1}{r-1}\cdot (q-1)Ez egy egész szám, méghozzá a korábban már igazolt r-1|p-1 oszthatóság miatt. Ezt behelyettesítve a fenti kongruencia kitevőjébe az alábbit kapjuk:
x^{\overbrace{k\cdot \frac{p-1}{r-1}\cdot (q-1)}^{=n}\cdot (r-1) + 1}\equiv x\pmod rElvégezve a kitevőben lévő r-1-gyel való szorzást az alábbi kongruenciát kapjuk:
x^{k\cdot (p-1)\cdot (q-1) + 1}\equiv x\pmod rEz tehát az m modulus minden pozitív r prímosztójára teljesül, ami viszont azt jelenti, hogy a 20.1. Tétel 3. pontja alapján teljesül az alábbi oszthatóság:
r|x^{k\cdot (p-1)\cdot (q-1)+1}-xFelhívnánk a figyelmet arra, hogy az m=pq modulus négyzetmentes. Ennek egyrészt az az oka, hogy p és q nem tartalmaznak közös prímtényezőket, hiszen azt mondtuk, hogy egymáshoz relatív prímek. Másrészt pedig mindkettőre igaz, hogy vagy prím, vagy pedig Carmichael-szám, márpedig egy prím nyilvánvalóan, egy Carmichael-szám pedig a Korselt-kritérium (26.17. Tétel) miatt négyzetmentes, így a relatív prímség miatt ezek szorzata is az, vagyis a 26.16. Lemma alapján m minden prímtényezője első hatványon szerepel.
Mármost ha m minden prímtényezőjére teljesül a fenti oszthatóság, akkor ezek szorzatára is teljesül. Mivel mindegyikük első hatványon szerepel m prímtényezős felbontásában, ezért ez a szorzat m-mel egyezik meg. Vagyis teljesül az alábbi oszthatóság is:
m|x^{k\cdot (p-1)\cdot (q-1)+1}-xEz viszont ismét a 20.1. Tétel 3. pontja alapján azt jelenti, hogy a bizonyítandó kongruencia is teljesül:
x^{k\cdot (p-1)\cdot (q-1)+1}\equiv x\pmod m ∎A tétel szerint tehát az RSA algoritmus sajnos ugyanúgy működőképes marad, ha prímek helyett Carmichael-számokat használuk a kulcsgeneráláshoz. Ennek súlyos következményei vannak a biztonságra nézve, hiszen a Korselt-kritérium 26.18. Következménye alapján egy Carmichael-számnak legalább 3 prímtényezője van. Ez viszont azt jelenti, hogy a kódoláshoz és dekódoláshoz használt m modulust jóval könnyebb prímtényezőire bontani, mintha p és q valóban prímszámok lettek volna, ezek a prímtényezők ugyanis jóval kisebbek lesznek, mint p és q. Ráadásul egyéb, itt nem részletezett összefüggések miatt egy Carmichael-szám prímtényezőire bontására létezik hatékony algoritmus, így viszont egy támadó is kiszámíthatja a d titkos kitevőt.
Ebben a részben megismerkedtünk a polinomok és polinomgyűrűk fogalmával. Az itt megismert összefüggéseket felhasználva igazoltuk, hogy prím modulus esetén mindig létezik primitív gyök. Ezután a Carmichael-számokat jellemeztük az úgynevezett Korselt-kritérium segítségével, majd ezt felhasználva lényegesen javítottunk a Miller-Rabin-prímteszt hibabecslésén. Végül megvizsgáltuk azt a kérdést, hogy miért jelent súlyos biztonsági kockázatot, ha az RSA kulcsok generálásakor véletlenül Carmichael-számokat használunk.
Ezzel számelméleti vizsgálataink végére értünk. A sorozat utolsó részében arról fogunk mesélni, hogy a talán nem is olyan távoli jövőben az úgynevezett kvantumszámítógépek milyen kihívások elé fogják állítani főhőseinket, és mik azok a módszerek, amelyek segítségével megbírkózhatnak e kihívásokkal.
Az utolsó részt itt találod…



