Az előző részben a Miller-Rabin-prímteszt hibázási valószínűségére vonatkozó becslésünket lényegesen megjavítottuk. Ennek során megismerkedtünk a primitív gyökök, a polinomok és a polinomfüggvények fogalmával, valamint az ezekhez kapcsolódó kulcsfontosságú tételekkel. Ezután említést tettünk az úgynevezett AKS-prímtesztről. Ez az elsőként felfedezett olyan hatékony prímteszt volt, amely minden esetben determinisztikus – tehát 100%-os valószínűségű – választ ad, és nem függ semmilyen, eddig nem bizonyított sejtéstől. Ezen elméleti jelentőségű eredmény alapján tehát a prímség vagy összetettség eldöntése furcsamód a P problémaosztályba tartozik (bővebben lásd a 7. részt), ugyanakkor a konkrét prímtényezők megtalálása egy ennél sokkal nehezebb feladatnak tűnik. Végül azt a kérdést vizsgáltuk meg, hogy mi történik akkor, ha az RSA-kulcsok generálásához prímek helyett véletlenül Carmichael-számokat használunk. Ezzel lezártuk számelméleti vizsgálatainkat, és a sorozat utolsó részében egy képzeletbeli időutazás keretében arra keressük a választ, hogy milyen kihívásokkal kell szembenéznie hőseinknek – és persze a kriptográfia tudományának – a jövőben.

Mi a probléma az RSA-algoritmussal, és miért fog elavulni a közeljövőben? Mik azok az elliptikus görbék, és mit állít róluk az egymillió dollárt érő Birch és Swinnerton-Dyer sejtés? Hogyan lehet az elliptikus görbékre újfajta titkosítási eljárásokat építeni? Mik azok a kvantumszámítógépek, és ha tényleg megvalósíthatók, akkor mire lesznek képesek a jövőben? Kell-e miattuk aggódnia Alice-nak és Bob-nak? Vajon a kriptográfusok, vagy a kiberbűnözők kerülnek ki győztesen ebből az emberiség egész történelmét végigkísérő kíméletlen háborúból? Az utolsó részben erről lesz szó…

Az elmúlt 26 részben az Olvasó vélhetően igen részletes képet kapott arról, hogy ez a bizonyos háború meglehetősen szokatlan természetű. Ez ugyanis a hagyományos háborúktól eltérően az elméleti matematika harcmezején zajlik, és olyan fegyverekkel vívják, amelyek csak a fejünkben léteznek. Ne legyenek kétségeink azonban afelől, hogy paradox módon ezeknek a képzeletbeli fegyvereknek bizony sokkal pusztítóbb hatásuk lehet a való világban, mint bármilyen hagyományos fegyvernek, legyen szó akár a legmodernebb termonukleáris robbanótöltetek kíméletlen arzenáljáról.

Mai világunkban ugyanis a legfontosabb erőforrás az a mérhetetlen mennyiségű adat, amelyet a legkülönfélébb elektronikus eszközeink megállás nélkül ontanak magukból a nap huszonnégy órájában az év minden napján. Aki ennek az erőforrásnak a birtokába kerül, és ki is tudja aknázni azt, az olyan elképesztő hatalomra tesz szert a világ felett, amilyenre talán még a legvadabb álmainkban sem mernénk gondolni, és amelyre az egész eddigi történelem során még nem volt példa.

Gondoljunk csak például a nagy techcégekre: a Google és a Facebook bizony többet tud rólunk, mint a saját családunk. Pontosan tudja, hogy mi az érdeklődési körünk, hogy mikor, hol és kivel találkozunk, hogy merre járunk, miket és hol vásárolunk, merre barangolunk az Interneten, mik a legféltettebb titkaink. Ezeknek az információknak a birtokában választások kimenetelét lehet befolyásolni még olyan nagyhatalmú országoknál is, mint az Egyesült Államok. Vagy akár gondoljunk csak arra, hogy lépten-nyomon egyre több és több intelligens eszköz vesz minket körbe, amelyek ráadásul az Interneten keresztül kommunikálnak egymással annak érdekében, hogy minket minél jobban kiszolgáljanak.

Az úgynevezett IoT (Internet of Things) technológiáknak köszönhetően rövidesen az életünk legalapvetőbb területein is a számítógépek fogják átvenni az irányítást. Okos otthonok, okos városok, önvezető autók, amelyek a közlekedési infrastruktúrától kapott információk alapján lesznek képesek döntéseket hozni a másodperc törtrésze alatt. A számítógép-hálózatok ma már teljes országok villamosenergia és egyéb ellátórendszereit képesek vezérelni. A világ pénzügyi folyamatait meghatározó döntéshozók a legkorszerűbb adatbányászati eszközökre támaszkodnak.

Ezek után nem nehéz elképzelni, hogy mekkora – akár világméretű – katasztrófákat lehet előidézni azáltal, ha bizonyos adatok vagy bizonyos rendszerekhez való hozzáférési jogosultságok illetéktelen kezekbe kerülnek. Az adatok és a kommunikációs csatornák kriptográfiai védelme tehát napjainkban fontosabbá vált, mint valaha a világtörténelemben. Sőt, talán nem túlzás azt állítani, hogy az egész emberi civilizáció törékeny léte többek között ezen áll vagy bukik.

Mi a probléma az RSA-val?

A korábbi részekben az RSA rejtjelezési eljárásról tanultak fényében talán egy kicsit félelmetes belegondolni abba, hogy a világ biztonsága – eléggé lesarkítva – mindössze olyan dolgokon múlik, minthogy például egy kellően nagy összetett szám prímtényezőit jelenlegi ismereteink alapján beláthatatlanul sok ideig tart megtalálni. Ráadásul nincs bizonyítva, hogy valóban nem is létezhet hatékony prímfaktorizációs eljárás, mint ahogy az sem, hogy az RSA feltöréséhez egyáltalán szükség van-e a prímtényezők kiszámítására. Mindazonáltal az RSA eddig kiállta az idők próbáját, ugyanakkor nincs kizárva, hogy valamikor a jövőben egy új számelméleti felfedezés végzetes csapást mér majd rá.

Azonban sajnos nem ez az egyetlen gond vele! A 21. részben ismertettük az RSA algoritmus részleteit, és láttuk, hogy a titkos kulcs kiszámításához elegendő a publikus kulcsban szereplő m modulus prímtényezőit megtalálni. Ezenkívül azt is megemlítettük, hogy erre a problémára jelenleg nem ismerünk polinomiális időkomplexitású algoritmust, és éppen ez adja az RSA biztonságát. Az persze igaz, hogy az úgynevezett Moore-törvény alapján a számítógépeink teljesítménye a hetvenes évek óta exponenciális növekedést mutat (a teljesítményük nagyjából kétévente megduplázódik). Ezért ami 10 évvel ezelőtt még elegendően nagy RSA-modulusnak számított, az ma már korántsem az. De semmi gond – mondhatnánk –, hiszen mindössze annyit kell tennünk, hogy megnöveljük az RSA-modulust, és újból biztosítva vannak az adataink jónéhány évig a prímfaktorizáció feladatának algoritmikus bonyolultsága miatt.

Ez kétségkívül így van, azonban a számelmélet fejlődésével sajnos napvilágot láttak olyan prímfaktorizációs algoritmusok, amelyek ugyan továbbra sem polinomiális időkomplexitásúak, viszont az exponenciális időkomplexitásnál lényegesen jobbak. Ezeket szubexponenciális időkomplexitású algoritmusoknak nevezzük. A jelenleg ismert legjobb prímfaktorizációs algoritmus az úgynevezett általános számtest-szita. Ez messze hatékonyabb, mint a 23. részben ismertetett osztáspróbákon alapuló iskolás módszer, amely – mint láttuk – exponenciális időkomplexitású. Ez azt jelenti, hogy egy-egy teljesítményduplázódás kiküszöböléséhez egyre nagyobb és nagyobb mértékben kell megnövelnünk az RSA-kulcsok bitjeinek számát. Ez viszont a dekódolás sebességére nincs túl jó hatással, mint ahogyan azt a 22. rész végén már megemlítettük.

Tegyük fel például, hogy folytatódik a Moore-törvény által leírt tendencia, és két év múlva a számítógépek teljesítménye ismét megduplázódik a jelenlegihez képest. Így a bűnözők kezében is kétszer akkora számítási kapacitás lesz, mint ma. A szubexponenciális prímfaktorizációs algoritmus miatt ahhoz, hogy a jelenlegivel megegyező biztonsági szintet el tudjuk érni az RSA-val, nagyobb mértékben kell megnövelnünk a kulcsok hosszát, mint amennyivel a két évvel ezelőtti állapothoz képest kellett megnövelnünk, és ez a mérték az évek előrehaladtával egyre nagyobb és nagyobb lesz. A teljesítménynövekedés nyilván pozitív hatással van a dekódoláshoz szükséges időre is, azonban az egyre gyorsuló kulcshossznövekedés miatt az RSA a jövőben egyre kevésbé lesz hatékony. Ha ehhez még hozzávesszük, hogy az információs társadalom hihetetlen mértékű fejlődése következtében a világban lévő érzékeny adatok mennyisége szintén exponenciálisan növekszik, akkor a nem is olyan távoli jövőben könnyen egy fenntarthatatlan szituációban találhatjuk magunkat. Annak érzékeltetésére, hogy mennyire valós problémáról van szó megemlítjük, hogy az RSA-dekódolás számításigénye már most problémát okoz az olyan eszközök esetén, amelyek kisebb memóriával és számítási kapacitással rendelkeznek.

A cikksorozat eddigi részeiben ismertetett kriptográfiai eljárások mind-mind egy-egy úgynevezett egyirányú függvényen alapultak. Ezek olyan függvények, amelyeket viszonylag könnyű kiszámítani az egyik irányban, azonban gyakorlatilag lehetetlen a másik irányban. Az RSA esetén például a kulcsgenerálás során lényegében két óriási prímszámot szorzunk össze egymással, és az így kapott m modulus, illetve egy ehhez szabadon választott relatív prím e kitevő adja a publikus kulcsot. Ahhoz, hogy a d titkos kitevőt meghatározza egy támadó, a műveletet visszafelé kéne végrehajtania, vagyis meg kéne határoznia az m modulus prímtényezőit. Mint említettük, erre létezik szubexponenciális algoritmus, amely ugyan még mindig nem elég hatékony, de arra elegendő, hogy hosszútávon fenntarthatatlanná tegye az RSA-t.

Ezért manapság egyre inkább kezd elterjedni egy ennél hatékonyabb egyirányú függvény, amelyet a következő szakaszokban vázlatosan ismertetünk.

A diszkrét logaritmus problémájának általánosítása

A 9. részben ismertetett Diffie-Hellman kulcscsere protokoll esetén az egyirányú függvényt az előző rész alapján lényegében egy speciális ciklikus csoportban, nevezetesen a (\Z/m\Z)^{\times} csoportban történő hatványozás jelenti, ahol a függvény megfordításaként a használt kitevő meghatározását kellene kiszámítania a támadónak. Ezt diszkrét logaritmus problémának (DLP) neveztük, és megemlítettük, hogy ez is egy roppant nehéz algoritmikus feladat. Vegyük észre, hogy a DLP megfogalmazható úgy is, hogy elvonatkoztatunk a konkrétan használt (\Z/m\Z)^{\times} csoporttól. Eszerint legyen G egy tetszőleges csoport, g pedig ennek egy tetszőleges eleme (lásd a 25.19. Definíciót), valamint tegyük fel, hogy ismerjük a g^k hatványt. A DLP ebben az általános esetben a k kitevő meghatározását jelenti.

Ennek a feladatnak az algoritmikus bonyolultsága nyilván erősen összefügg azzal, hogy konkrétan milyen csoportot használunk, vagy annak elemeit hogyan reprezentáljuk. Tekintsünk azonban most egy úgynevezett általános csoportot, azaz egyelőre vonatkoztassunk el az adott csoport konkrét reprezentációjától. Ezt úgy tudjuk modellezni, hogy feltételezzük egy olyan úgynevezett „orákulum” létezését, amely képes elvégezni a csoportműveletet, illetve két elemről el tudja dönteni, hogy megegyeznek-e vagy sem, azonban ennek az „orákulumnak” a válaszain kívül nincs semmilyen egyéb információnk a csoportról. Victor Shoup amerikai matematikus 1997-ben igazolta, hogy véges csoport esetén amennyiben p a csoport rendjének legnagyobb prímosztója, akkor legalább c\cdot \sqrt{p}-szer kell elvégezni a csoportműveletet a keresett kitevő kiszámításához, ahol c egy valamilyen alkalmasan választott konstans mennyiség. Ez a lépésszám nyilvánvalóan a csoport rendjének bináris hosszától exponenciálisan függ.

Ez persze nem azt jelenti, hogy egy konkrét csoport esetén ne lehetne ennél akár lényegesen jobb eredményt elérni, kihasználva annak speciális tulajdonságait. Gondoljunk csak például az alábbi lineáris kongruenciára, ahol keressük az n ismeretlent:

a\cdot n\equiv b\pmod m

A 21. részben megmutattuk, hogy egy ilyen kongruencia rendkívül hatékonyan megoldható a kibővített euklidészi algoritmus segítségével. Ez a hatékonyság kulcsfontosságú is, hiszen az RSA-hoz használt titkos kitevőt épp emiatt tudja kiszámítani az, aki birtokában van a modulus prímtényezőinek. Habár ez elsőre nem feltétlenül látszik, de tulajdonképpen itt is a DLP-ről van szó, csak éppenséggel a (\Z/m\Z)^+ additív csoportban. Valóban, hiszen a kérdés most is tulajdonképpen az, hogy az [a]_m maradékosztályt hányszor kell „összeműveleteznünk” önmagával ebben a csoportban ahhoz, hogy a [b]_m maradékosztályt kapjuk eredményül. Vagyis a (\Z/m\Z)^+ csoportban az alábbi egyenletet írhatjuk fel, ahol keressük az n „kitevőt”, csak épp ebben az esetben a 24.9. Definíció utáni megjegyzés szerinti additív irásmódot alkalmaztuk:

n[a]_m=[b]_m

Az additív csoporttal ellentétben szerencsére a (\Z/m\Z)^{\times} multiplikatív csoportban ennél lényegesen nehezebb ez a feladat. Sőt, ebben a csoportban jelenleg nem is ismeretes szubexponenciális időkomplexitású algoritmus a DLP-re, amely így alkalmasabbnak tűnik kriptográfiai primitívek képzésére, mint a prímfaktorizáció nehézségén alapuló módszerek. A kisteljesítményű eszközök számára azonban továbbra is problémát jelent, hogy a (\Z/m\Z)^{\times} csoportot használó eljárásokhoz nagy kulcsokat kell használni a kívánt biztonsági szint eléréséhez.

Ezért Neal Koblitz amerikai matematikus egy 1987-ben megjelent publikációjában a (\Z/m\Z)^{\times} helyett olyan csoportok használatát javasolta, amelyek esetén a DLP várhatóan jóval nagyobb komplexitású a hagyományos változathoz képest, és így kisebb méretű kulcsokkal is ugyanolyan biztonsági szintet lehet elérni. Egy-egy ilyen csoport elemei azonban nem számok, hanem a számelméletben az utóbbi évtizedekben intenzíven kutatott furcsa képződményeknek, az úgynevezett elliptikus görbéknek a „pontjai”.

Az elliptikus görbék elmélete az algebrai számelmélet egyik központi területe, melyhez számos jelentős és mély megoldatlan sejtés kapcsolódik. Mivel ez a témakör messze túlmutat e cikksorozat keretein, ezért itt csak vázlatosan tekintjük át az elliptikus görbékhez kapcsolódó alapfogalmakat. Előbb azonban vizsgáljuk meg, hogy tulajdonképpen mivel is foglalkozik az algebrai számelmélet.

Mivel foglalkozik az algebrai számelmélet?

Az algebrai számelmélet elsősorban olyan egy- vagy többváltozós egyenletekkel foglalkozik, amelyek felírhatók a négy alapművelet véges sokszori alkalmazásával, és célja ezeknek az egyenleteknek a megoldásait megtalálni egy megadott számhalmazban. Ezeket az egyenleteket algebrai egyenleteknek nevezzük. Általánosságban ugyanilyen értelemben beszélhetünk egy valamilyen T test feletti algebrai egyenletről is, hiszen a 14.12. Definíció alapján egy T testben korlátlanul elvégezhető a négy alapművelet T-beli megfelelője (kivéve persze a nullelemmel való osztást). Ilyenkor a megoldásokat a T testben keressük.

Ebben a cikksorozatban a szám fogalmát eddig csak az egész számok \Z gyűrűjéig bezárólag építettük fel. Ez azonban nyilván nem test, hiszen a +1-en és -1-en kívül semmilyen más egész számnak nem létezik inverze a szorzásra nézve, így az osztás ebben a számkörben egyáltalán nem értelmezhető. Ha nagyon precízek akarnánk lenni, akkor ezen a ponton egy ahhoz hasonló számkörbővítést kellene végrehajtanunk, mint amikor a 13., 14. és 15. részekben a természetes számok \N halmazát kibővítettük a negatív számoknak nevezett absztrakt objektumokkal annak érdekében, hogy a kivonást el lehessen végezni korlátlanul. Egy ehhez hasonló számkörbővítést most nem fogunk részletesen végigtárgyalni, ám az Olvasó minden bizonnyal sejti, hogy itt tulajdonképpen a törtszámok bevezetéséről van szó.

A törtszámokat tudományosabban racionális számoknak nevezzük, és az őket tartalmazó halmazt \mathbb{Q}-val jelöljük, utalva a latinból származó „quotient” szóra, amely „hányadost” jelent. Ezek tehát azok a számok, amelyek felírhatók \frac{a}{b} alakban, ahol a és b mindketten egész számok. Előbbit számlálónak, utóbbit nevezőnek hívjuk. A számkörbővítéshez a \mathbb{Q} számhalmazon be kellene vezetni egy összeadásnak és egy szorzásnak nevezett műveletet, valamint egy rendezési relációt. Méghozzá olymódon, hogy az egész számok \Z gyűrűje beágyazható legyen ebbe a bővebb struktúrába ahhoz hasonlóan, mint ahogyan a természetes számok \N halmazát ágyaztuk be a \Z gyűrűbe a 13. részben. Ezt most lazán átugorva kivételesen arra kérjük az Olvasót, hogy ezúttal támaszkodjon az általános iskolai tanulmányaira.

Könnyen látható, hogy \mathbb{Q} az egész számok \Z gyűrűjével ellentétben test, hiszen bármilyen nemnulla törtszámnak létezik inverze a szorzásra nézve, amelyet úgy kapunk meg, ha felcseréljük a számlálót és a nevezőt:

\frac{a}{b} \cdot \frac{b}{a}=\frac{a\cdot b}{b\cdot a}=1

Ezek után már beszélhetünk a \mathbb{Q} test feletti algebrai egyenletekről, azon belül is az úgynevezett polinomiális egyenletekről.

Polinomiális egyenletek alatt olyan speciális algebrai egyenleteket értünk, amelyekben csak az ismeretlenek egész kitevőjű hatványai, a \mathbb{Q} test elemei, valamint összeadások, kivonások és szorzások szerepelhetnek. Az osztás tehát ebben az esetben nem megengedett. Ezek közül a legegyszerűbbek az egyismeretlenes n-edfokú polinomiális egyenletek. Könnyű belátni, hogy ekvivalens átalakításokkal minden ilyen egyenlet az alábbi úgynevezett általános alakra hozható, ahol a_n\neq 0:

a_0+a_1x+a_2x^2+a_3x^3+\ldots +a_nx^n=0

Ehhez nagyon hasonlóval az előző részben lényegében már találkoztunk, hiszen ennek az egyenletnek a baloldalán épp az alábbi polinomnak a polinomfüggvénye szerepel:

f=(a_0, a_1, a_2, \ldots, a_n, 0, 0, \ldots)

Az egyetlen különbség mindössze annyi, hogy f most nem a \Z gyűrű, hanem a \mathbb{Q} test felett van értelmezve. Tehát az a_0, a_1, …, a_n együtthatók most a \mathbb{Q} test elemei, a fenti egyenlet megoldásai pedig az f polinom \mathbb{Q}-beli gyökei lesznek.

A kérdés tehát, hogy egy ilyen egyismeretlenes polinomiális egyenletnek létezik-e racionális megoldása, és ha igen, akkor hány darab, illetve hogyan lehet megtalálni ezeket. Nos, ezt a nem túl nehéz számelméleti problémát az úgynevezett racionális gyökteszt (vagy más nevén Rolle-féle gyöktétel) segítségével könnyedén megválaszolhatjuk. Ez egy elemi módszerekkel is nagyon könnyen igazolható tétel, így a részletektől most eltekintünk. A tétel azt mondja ki, hogy amennyiben minden együttható egész szám, akkor az összes racionális gyök felírható \frac{p}{q} alakban, ahol p és q egymáshoz relatív prím egész számok, és teljesítik az alábbi feltételeket:

• A p egész szám osztója az a_0 konstans tagnak.
• A q egész szám osztója az a_n főegyütthatónak.

Azt könnyen elérhetjük, hogy az egyenlet együtthatói egészek legyenek. Ha ugyanis mégsem lennének azok, akkor a nevezőikkel végigszorozva mindkét oldalt egy olyan egyenletet kapunk, amire ez a feltétel már teljesül. Ennek az új egyenletnek nyilván pontosan ugyanazok lesznek a gyökei, mint az eredeti egyenletnek. Ezután már alkalmazhatjuk a tételt, amely tehát egy viszonylag kisméretű véges halmazra szűkíti le a potenciális gyökök körét. Azt persze nem állítja, hogy minden, a fenti feltételeknek megfelelő \frac{p}{q} racionális szám valóban gyök lesz, ám ezeket behelyettesítéssel már könnyedén végigpróbálgathatjuk.

A Rolle-féle gyöktétel alapján tehát az egyismeretlenes esettel kapcsolatban felmerülő kérdéseket le is zárhatjuk, hiszen ez alapján egy ilyen egyenletnek vagy egyáltalán nincs racionális gyöke, vagy pedig csak véges sok van. Ennél némileg izgalmasabbak az egynél több ismeretlent tartalmazó polinomiális egyenletek. A továbbiakban minket a kétismeretlenes eset érdekel, amelyeket algebrai síkgörbéknek nevezünk.

Algebrai síkgörbék

Az algebrai síkgörbék olyan polinomiális egyenletekkel írhatók le, amelyekben két ismeretlen szerepel. Ezeket x-szel és y-nal fogjuk jelölni. Egy ilyen egyenlet általános alakjában tehát ax^ny^k alakú tagok szerepelnek a baloldalon, ahol n és k nemnegatív egész kitevők, az a együtthatók pedig valamilyen racionális számok (vagy általánosabban egy T test elemei), míg a jobboldalon 0 (vagy általánosabban a T test nulleleme) szerepel. Az együtthatókra – a matematikai részletek mellőzésével – mindössze annyi megkötést teszünk, hogy a görbe bizonyos „simasági” feltételeknek eleget tegyen, azaz ne legyenek rajta törések, önmetszések, izolált pontok, stb. Egy tag fokszáma alatt az n+k összeget, míg az egyenlet (vagy görbe) fokszáma alatt a legnagyobb fokú tag ilyen értelemben vett fokszámát értjük. Ennek megfelelően például egy első-, egy másod-, illetve egy harmadfokú algebrai síkgörbe egyenletének általános alakjai az alábbiak:

\begin{aligned}ax+by+c&=0 \\ ax^2+bxy+cy^2+dx+ey+f&=0 \\ ax^3+bx^2y+cxy^2+dy^3+ex^2+fxy+gy^2+hx+iy+j&=0\end{aligned}

Egy ilyen \mathbb{Q} felett értelmezett kétismeretlenes egyenlet megoldásai (vagy más szavakkal a görbe pontjai) alatt azokat az (x;y) racionális számpárokat értjük, amelyeket az egyenletbe behelyettesítve az egyenlőség fennáll a két oldal között.

A görbéket némi „csalással” ábrázolhatjuk is egy kétdimenziós koordináta-rendszerben, ahol a vízszintes tengely értelemszerűen az x, míg a függőleges tengely az y változónak felel meg. Tekintsük például az alábbi \mathbb{Q} feletti első- és másodfokú görbéket:

\begin{aligned}\frac{1}{2}x-y+1&=0 \\ x^2+y^2-1&=0\end{aligned}

Ha most a koordináta-rendszerünkben bejelöljük azokat és csakis azokat a pontokat, amelyeknek koordinátái kielégítik ezeket az egyenleteket, akkor a két görbe láthatóvá válik:

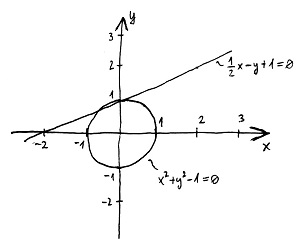
Általánosságban az elsőfokú görbék képe mindig valamilyen egyenes, míg a másodfokú görbék képe az együtthatóktól függően lehet kör, ellipszis, parabola vagy hiperbola, amelyeket összefoglaló néven kúpszeleteknek nevezünk.

A fenti ábrán a már említett „csalást” ott követtük el, hogy valójában nem ábrázolhattuk volna ezeket a görbéket folytonos vonallal, mivel ezeket a görbéket a racionális számok \mathbb{Q} teste felett értelmeztük, és így a megoldások (a görbe pontjainak koordinátái) is ebből a testből kell származzanak. Márpedig a koordináta-tengelyek pontjainak „nagyrésze” bizony nem racionális, azaz nem írható fel két egész szám hányadosaként. Ha például az egységoldalú négyzet átlójának hosszát (ami a pitagorasz-tétel alapján \sqrt{2} hosszúságú) felmérjük a számegyenesre, akkor kétségkívül egy létező távolságot kapunk, amely azonban nem írható fel tört alakban:

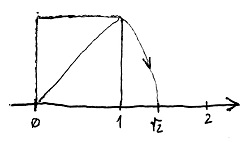
A koordináta-tengelyeken, és így a fenti görbéinken tehát „hézagok” vannak, azaz olyan pontok, amelyekhez nem lehet racionális koordinátákat rendelni. Ráadásul ez annak ellenére így van, hogy a racionális számok végtelenül sűrűn helyezkednek el a számegyenesen, azaz bármely két racionális szám között végtelen sok további található. Ha ez még nem lenne elég, az ilyen „hézagokról” elmondható, hogy „sokkal többen” vannak, mint a racionális számok. Úgy is fogalmazhatunk, hogy a számegyenes pontjai és a racionális számok között nem lehet kölcsönösen egyértelmű megfeleltetést létesíteni, azaz ilyen értelemben előbbiek „magasabb rendben” vannak végtelen sokan, mint a racionális számok. Ez egyrészt elvezet a számosság fogalmához, amelyet itt nem részletezünk. Másrészt pedig felveti annak szükségességét, hogy ezeket a „hézagokat” a számfogalom további bővítésével „betömködjük”, és a számegyenes minden pontját „számnak” tekintsük, ne pedig csak azt a „néhány” racionális számot, amelyek csak „elvétve” fordulnak elő közöttük. Így válna legálissá az, hogy a fenti görbéket folytonos vonallal rajzoltuk fel. Ez az úgynevezett valós számok bevezetéséhez vezet, amelyet szintén nem részletezünk.

Mindenesetre jogosan merül fel a kérdés, hogy vajon a fenti görbéink „eltalálnak-e” akárcsak egyetlen egy racionális pontot is – azaz olyan pontot, amelynek mindkét koordinátája racionális – a síkon? És ha igen, akkor mennyi van belőlük? Véges vagy végtelen sok? Hogyan lehet mindegyiket megtalálni? Az algebrai számelmélet elsősorban ezekkel a kérdésekkel foglalkozik. Az elsőfokú \mathbb{Q} feletti görbék (azaz az egyenesek) esetén a kérdés roppant egyszerű. Egy ilyen görbe ugyanis mindig végtelen sok racionális pontot tartalmaz. Az összes ilyen pontot megkaphatjuk, ha a görbe egyenletébe x helyére behelyettesítünk egy tetszőleges racionális számot, és az így kapott – immár egyismeretlenes – egyenletet megoldjuk y-ra. Általános iskolai módszerekkel könnyedén belátható, hogy minden ilyen esetben kapunk pontosan egy racionális megoldást, azaz bármilyen racionális x koordinátához pontosan egy racionális y koordináta tartozik. A \mathbb{Q} számtest elemei tehát kölcsönösen egyértelmű megfeleltetésben állnak az egyenes racionális pontjaival.

A másodfokú görbék, azaz a kúpszeletek esetén a helyzet egy fokkal bonyolultabb. Itt már két eset lehetséges: a görbének vagy egyáltalán nincs racionális pontja, vagy pedig végtelen sok van. De vajon hogyan lehet eldönteni, hogy a két eset közül melyikben vagyunk? Meglepő módon erre létezik hatékony eljárás, amelynek elméleti hátterét az úgynevezett Hasse-Minkowski tétel adja, ennek részletei azonban szintén túlmutatnak e cikksorozat keretein. Ha azonban ebből azt kaptuk, hogy végtelen sok racionális pont van, akkor egyetlen racionális pontból könnyen előállítható az összes többi. Az eljárást az egységkör esetére vázoljuk fel, de minden kúpszeletre nagyjából ugyanígy kell elképzelni:

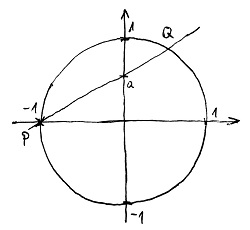
Ebben a példában a P=(-1;0) pontból indultunk ki, amelyről nyilvánvalóan látszik, hogy racionális. Válasszunk ki egy tetszőleges racionális koordinátát az y tengelyen – a fenti ábrán ezt a-val jelöltük –, és kössük össze ezzel a kiindulási P pontunkat. Az így kapott egyeneseket racionális meredekségű egyeneseknek nevezzük. Középiskolás módszerekkel viszonylag könnyen belátható, hogy egy racionális P ponton áthaladó racionális meredekségű egyenes egy szintén racionális Q pontban fogja metszeni az egységkört. Még könnyebben látható, hogy ennek megfordítása is igaz: ha az egységkör tetszőleges P-től különböző racionális pontját összekötjük P-vel, akkor az így kapott egyenes racionális meredekségű lesz, azaz az y tengelyt egy racionális koordinátánál fogja metszeni. Ebből következik, hogy az egységkörön elhelyezkedő racionális pontok a P pont kivételével kölcsönösen egyértelmű megfeleltetésbe hozhatók az y tengelyen elhelyezkedő racionális koordinátákkal, vagyis tulajdonképpen a \mathbb{Q} számtest elemeivel. Az egységkör azonban nem speciális ilyen értelemben, tehát a fenti eljáráshoz nagyon hasonlóan minden kúpszelet esetén található ilyen megfeleltetés a racionális pontok és \mathbb{Q} között.

A másodfokúnál magasabbfokú görbék racionális pontjainak kérdése az első- és másodfokú esetekhez képest jóval bonyolultabb, és jelenleg is csak részben tisztázott. Nagy meglepetést okozott, amikor Gerd Faltings német matematikus 1984-ben igazolta, hogy a legalább negyedfokú görbéknek csak véges sok racionális pontjuk lehet (beleértve azt az esetet is, amikor egyáltalán nincs racionális pont). Ez a nagyszerű eredmény Faltings-tétel néven ismeretes. Mindazonáltal jelenleg nem ismerünk olyan eljárást, amely ezeket a pontokat meg tudja határozni.

Összefoglalva az eddigieket: Az első- és másodfokú, valamint a legalább negyedfokú görbék esetén tehát a racionális pontok számára vonatkozó kérdést meg tudjuk válaszolni:

• Az elsőfokú görbéknek mindig végtelen sok racionális pontjuk van, amely általános iskolás módszerekkel is könnyen látható.
• A másodfokú görbéknek vagy egyáltalán nincs, vagy pedig végtelen sok racionális pontjuk van. Ennek eldöntésére ad módszert a Hasse-Minkowski tétel.
• A legalább negyedfokú görbéknek legfeljebb véges sok racionális pontjuk van a Faltings-tétel alapján.

De vajon mi a helyzet a harmadfokú görbékkel? Ezeket elliptikus görbéknek nevezzük, és az ő esetükben mindhárom lehetséges eset – nulla, véges illetve végtelen sok racionális pont – előfordulhat. Sajnos az a helyzet, hogy a harmadfokú esetben nem ismerünk olyan eljárást, amelynek segítségével el lehetne dönteni, hogy egy adott görbe melyik kategóriába tartozik, illetve amelynek segítségével meg lehetne határozni az összes racionális pontot egy görbén. Épp erről szól a számelmélet egyik mély és központi jelentőségű sejtése, amely egyrészt – ha igaznak bizonyul – választ ad ezekre a kérdésekre, másrészt messzemenő következményei vannak az egész számelméletben. Ez a Birch és Swinnerton-Dyer sejtés, amelyet az 1960-as évek első felében elliptikus görbéken végzett gépi számításaik alapján két brit matematikus, Bryan John Birch és Peter Swinnerton-Dyer vetett fel.

A Birch és Swinnerton-Dyer sejtés jelentőségét mi sem bizonyítja jobban, minthogy – a 7. részben ismertetett P\neq NP-sejtés mellett – ez is szerepel a Millenniumi Problémák között, amelyek megoldásáért egyenként egymillió amerikai dollár jutalom jár. A sejtés állítását némi előkészület után hamarosan ismertetjük.

Ehhez azonban előbb meg kell ismernünk az elliptikus görbék egy másik, kriptográfiai szempontból is fontos tulajdonságát, amely megkülönbözteti őket más algebrai görbéktől. Nevezetesen: az elliptikus görbék pontjai között egyedülálló módon egy olyan műveletet is lehet értelmezni, amellyel ezek a pontok egy kis kiegészítést követően csoportot (lásd a 24.1. Definíciót) alkotnak. Ilyen csoportot más fokszámú görbék esetén nem lehet létrehozni, és ez az a bizonyos csoport, amelyet Neal Koblitz a már említett 1987-es publikációjában kriptográfiai felhasználásra javasolt. Ahhoz azonban, hogy ezt a kis kiegészítést megtehessük, az elliptikus görbéket a szokásos kétdimenziós sík helyett az úgynevezett projektív síkra kell kiterjesztenünk.

A projektív sík

A hagyományos kétdimenziós síkkal az a probléma, hogy algebrailag nehezen kezelhető. Gondoljunk csak például arra az egyszerű esetre, amikor két elsőfokú görbe, azaz két egyenes metszéspontját szeretnénk meghatározni. Ez a látszattal ellentétben nem egy geometriai, hanem egy algebrai feladat, hiszen az egyenesek nyilván az egyenleteikkel vannak megadva. Nekünk pedig tulajdonképpen olyan (x;y) pontpárokat kell keresünk, amelyek mindkét egyenesen rajta vannak, következésképp mindkét egyenletet kielégítik. Ha egy olyan egyenletrendszer-megoldó algoritmust szeretnénk írni, amely a szokásos kétdimenziós síkon számol, akkor kapásból az alábbi három esetre kell felkészülnünk:

• Ha a két egyenes épp egybeesik, akkor végtelen sok metszéspont van.
• Ha a két egyenes nem esik egybe, viszont egymással párhuzamosak, akkor nincs metszéspont.
• Egyéb esetekben pontosan egy metszéspont van.

Márpedig egy algoritmus esetén nagyon nem szeretjük az esetszétválasztásokat, hiszen minél több van belőlük, annál valószínűbb, hogy valamire nem gondoltunk, és az algoritmusunk éles helyzetben elhasal. Ráadásul a helyzet tovább bonyolódhat, ha az egyeneseken kívül egyéb görbék is bejöhetnek a képbe. Kényelmesebb lenne tehát, ha ezeket a fentiekhez hasonló „elfajuló” eseteket a normál esetekkel azonos módon, algebrailag egységesen tudnánk kezelni.

Maradva az egyenesek metszéspontszámításáról szóló példánál, mondhatjuk például azt, hogy két egymástól különböző egyenesnek mindig pontosan egy metszéspontja van, csak épp párhuzamos egyenesek esetén ez a bizonyos metszéspont a „végtelenben” helyezkedik el. Az ilyen „végtelen távoli” pontokat ideális pontoknak nevezzük, és ezekkel kiegészítve a hagyományos kétdimenziós síkot egy olyan szerkezetű sík absztrakt modelljét kapjuk, amelyben a fentiekhez hasonló geometriai kérdések algebrailag sokkal kényelmesebben kezelhetők. Ezt az ideális pontokkal kiegészített síkot projektív síknak nevezzük.

Az alábbi ábrán látható e és f egyenesek például párhuzamosak egymással, így a hagyományos síkra felrajzolva őket azt kéne mondanunk, hogy ezek nem metszik egymást. Ezzel szemben a projektív sík esetén azt mondjuk, hogy ők egy P-vel jelölt ideális (végtelen távoli) pontban igenis metszik egymást. Ehhez hasonlóan az ábrán lévő g és h egyenesek is egy ideális Q pontban metszik egymást:

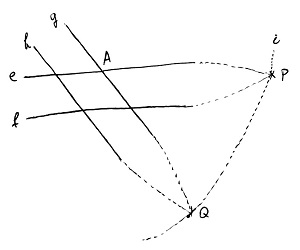
Természetesen továbbra is fenntartjuk azt a „játékszabályt” (vagy ha úgy tetszik axiómát), hogy két egymástól különböző egyenes nem metszheti egymást kétszer. Következésképp a P és Q pontoknak – noha mindkettőt a végtelenben elhelyezkedő ideális pontnak tekintjük – egymástól különbözőnek kell lenniük. Ha ugyanis nem így lenne – azaz P=Q lenne –, akkor például a g egyenes kétszer is metszené az e egyenest. Egyrészt a fenti ábrán jelölt hagyományos A pontban, másrészt pedig a P=Q ideális pontban.

Így tehát azt mondhatjuk, hogy a projektív sík ideális pontjai és a hagyományos síkon elképzelhető irányok között kölcsönösen egyértelmű megfeleltetés létesíthető. Sőt, a projektív sík geometriájának itt nem részletezett axiómarendszeréből következik, hogy az összes ideális pont tulajdonképpen egy „egyenesre” illeszkedik, amely azonban végtelen távol helyezkedik el. Ezt az ábrán szaggatott vonallal ábrázolt i „egyenest” ideális egyenesnek nevezzük. Az ilyen ideális objektumok bevezetésének nyilván akkor van értelme, ha nemcsak a képzeletünkben léteznek intuitív módon, hanem algebrailag is képesek vagyunk velük számolni.

Ezért most a projektív síknak egy olyan reprezentációját mutatjuk be, amelynek segítségével ezeket az ideális objektumokat is véges mennyiségekkel tudjuk leírni. Ennek alapötlete a következő: ha beágyazzuk a kétdimenziós síkot a háromdimenziós térbe úgy, hogy az ne illeszkedjen az origóra, akkor az origón átmenő térbeli egyenesek kölcsönösen egyértelműen megfeleltethetők lesznek egyrészt a beágyazott sík pontjaival (ezek lesznek a projektív sík hagyományos pontjai), valamint az ideális pontokkal. Ez azért jó, mert az origón átmenő térbeli egyeneseket tulajdonképpen egy-egy irányvektorral tudjuk leírni, amely már véges mennyiségeket tartalmaz. Ezt az ötletet mutatja az alábbi ábra:

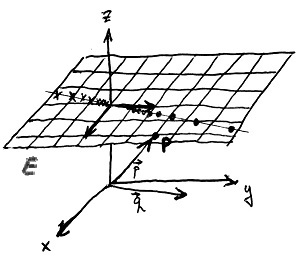
A négyzetráccsal ellátott E síkot tipikusan úgy szokták elhelyezni, hogy párhuzamos legyen a beágyazótér x és y tengelyei által kifeszített síkkal, és a z=1 magasságban helyezkedjen el. Ennek a választásnak mindössze praktikussági okai vannak, mint azt hamarosan látni fogjuk. Ekkor a beágyazótér origóján átmenő egyenesek két diszjunkt halmazra oszthatók:

• Azok az egyenesek, amelyek nem párhuzamosak az E síkkal, egyértelműen meghatároznak egy metszéspontot az E síkon. Ez egy hagyományos pont lesz az E által reprezentált projektív síkon.
• Azok az egyenesek, amelyek párhuzamosak az E síkkal, noha nem metszik azt, de egyértelműen meghatároznak egy irányt ezen a síkon. Ez egy ideális pont lesz az E által reprezentált projektív síkon.

Például az ábrán látható P pont a projektív sík egy hagyományos pontja, amely a hagyományos pontokat tartalmazó E síkon a (2;3) hagyományos koordinátákkal írható le. Ezt a pontot a beágyazótérben a \vec{p}=(2;3;1) irányvektorra illeszkedő térbeli egyenes jelöli ki ezen a síkon, így tehát a P pontot a (2;3;1) projektív koordinátákkal is leírhatjuk. Természetesen ugyanezt a P pontot kapjuk, ha a \vec{p} irányvektor mindhárom térbeli koordinátáját megszorozzuk egy tetszőleges c\neq 0 számmal. Vagyis a (2c;3c;c) projektív koordináták ugyanúgy a P pontot azonosítják minden c\neq 0 esetén.

Az ábrán látható \vec{q}=(1;4;0) irányvektor azonban párhuzamos a projektív sík hagyományos pontjait tartalmazó E síkkal, tehát nem metszi azt. Ez felfogható egyfajta határesetnek is, amikoris az (1;4;z) irányvektor harmadik koordinátájával egyre jobban és jobban közeledünk a z=0-hoz valamelyik irányból. Pozitív irányból közeledve a \bullet-tal, míg negatív irányból közeledve a \times-tel jelölt pontsorozatot kapjuk az E síkon, a z=0 koordinátát elérve pedig e pontsorozatok vonalában „kiszaladunk a végtelenbe”. Így az (1;4;0) projektív koordináták a projektív síknak azt az ideális pontját írják le, amely a kapott pontsorozat által kijelölt iránynak felel meg. Természetesen ugyanezt az irányt, azaz ideális pontot kapjuk, ha a \vec{q} irányvektor mindhárom térbeli koordinátáját megszorozzuk egy tetszőleges c\neq 0 számmal.

A fenti koncepciót továbbgondolva tehát tulajdonképpen arról van szó, hogy a projektív sík különböző objektumait a beágyazótér eggyel magasabb dimenziós objektumainak az E síkra vetített „árnyékaként” képzeljük el, de az algebrai feladatokban ezekkel a magasabb dimenziós objektumokkal számolunk. Így tehát a projektív sík pontjait (beleértve az ideális pontokat) a beágyazótérben egy-egy origón átmenő egyenesnek feleltetjük meg a fentiek szerint. Ehhez hasonlóan a projektív sík egyeneseihez (beleértve az ideális egyenest is) a beágyazótérben az origón átmenő síkokat rendeljük hozzá. Egy, az E síkon fekvő hagyományos egyenesnek az a sík fog megfelelni a beágyazótérben, amely az adott egyenesben metszi az E síkot, míg az ideális egyenest az x és y tengelyre illeszkedő síkkal azonosítjuk, amely tehát nem metszi az E síkot.

A fenti konstrukció természetesen magasabb dimenziókra is kiterjeszthető, ám ezt itt nem részletezzük. A kétdimenziós projektív sík helyett beszélhetünk például a háromdimenziós projektív térről is. Az persze igaz, hogy ekkor a fenti modell szerinti beágyazótér már négydimenziós, amelyet nemigazán tudunk elképzelni. Azonban algebrailag ugyanazok a szabályok fognak vonatkozni rá, mint a projektív síkra, csak épp a projektív térben három helyett már négy koordinátával kell dolgoznunk. Hogy ez mennyire nem elrugaszkodott a valóságtól, azt mi sem mutatja jobban, minthogy például a számítógépes grafikában használt hardverek is ilyen négydimenziós projektív koordinátákkal dolgoznak, és az ezekkel való műveletvégzésekre vannak optimalizálva.

Az elliptikus görbék csoportstruktúrája

Az elliptikus görbéknek mindössze az elnevezésükben van közük az ellipszisekhez, eredetileg ugyanis ellipszisek ívhosszának kiszámításához használtak hozzájuk hasonló egyenleteket. A matematikai részletek kidolgozását továbbra is mellőzve elliptikus görbének nevezünk tehát minden olyan harmadfokú algebrai görbét a projektív síkon, amely a már említett „símasági” feltételeknek eleget tesz. Ebben a szakaszban végig a \mathbb{Q} számtest feletti, tehát racionális elliptikus görbékről lesz szó. Egy ilyen görbe pontjai alatt mindig a racionális pontokat fogjuk érteni egy apró kiegészítéssel, amelyre hamarosan kitérünk. A harmadfokúságot már tisztáztuk az algebrai síkgörbék esetén. Eszerint egy elliptikus görbe egyenletének általános alakja az alábbi:

ax^3+bx^2y+cxy^2+dy^3+ex^2+fxy+gy^2+hx+iy+j=0

Mint már említettük, „símasági” feltételek alatt nem túl precízen azt értjük, hogy a görbe bizonyos értelemben „szép folytonos”, és „folytonosan is görbül”. Ezeket egészen pontosan a matematika analízis eszközeivel lehetne megfogalmazni, amitől most szintén eltekintünk.

Belátható, hogy egy ilyen görbének mindig van egy nyílt komponense, amely „végtelen távolról érkezik” egy jól meghatározott irányból, tesz néhány kanyart, majd az érkezésivel ellentétes irányban „távozik a végtelenbe”. Mivel a projektív síkon vagyunk, ezért ez az előző szakasz fényében azt jelenti, hogy a görbe mindig „áthalad” egy ideális ponton is, amelyet szintén a görbe egy pontjának, azaz racionális pontnak tekintünk. A paraméterektől függően továbbá a görbének lehet még egy különálló komponense is, ami egy zárt görbe.

A \mathbb{Q} számtest feletti elliptikus görbék egyenlete egy úgynevezett koordináta-transzformációval a fenti általános alakról minden esetben az alábbi jóval egyszerűbb, úgynevezett Weierstrass-féle normálalakra hozható, amelynek hatására a görbe szimmetrikus lesz az x tengelyre:

y^2=x^3+ax+b

Természetesen egy ilyen átalakítás során a görbe formája teljesen megváltozik, viszont az alapvető struktúrája – amelyre hamarosan rátérünk – lényegében azonos marad az eredeti görbe struktúrájával. Az alábbi ábrákon két elliptikus görbe látható különböző a és b paraméterekkel:

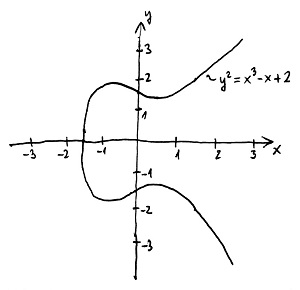
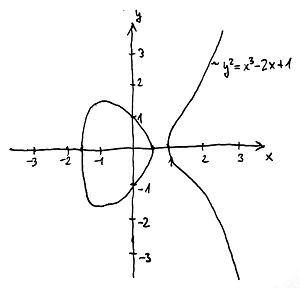
A másodfokú görbék esetén ha a görbének egy P racionális pontját már ismerjük, akkor ebből könnyen megtalálhatjuk az összes többit, ugyanis bármely P-re illeszkedő racionális meredekségű egyenes garantáltan egy másik racionális pontban metszi a görbét. Ezzel szemben egy elliptikus görbe racionális pontjainak megtalálása azért sokkal nehezebb, mivel egy adott racionális pontra illeszkedő egyenes két másik pontban is metszheti a görbét, és egyáltalán nem biztos, hogy bármelyikük is racionális pont lesz. Némi számolgatással belátható viszont, hogy amennyiben egy egyenes a görbét két racionális pontban is metszi, akkor a harmadik metszéspont szintén racionális lesz.

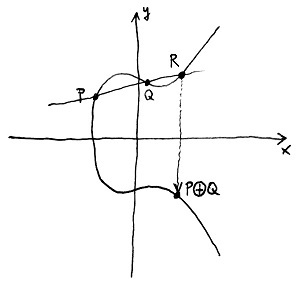
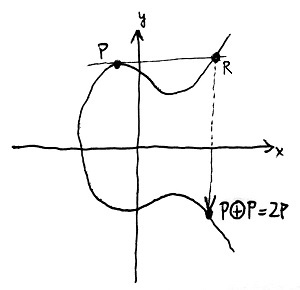
Ez elvezet minket egy furcsa, „összeadásnak” nevezett művelethez, amelyet az elliptikus görbe racionális pontjain fogunk értelmezni. Mint már említettük, ezek közé soroljuk azt az ideális pontot is, amelyen a görbe áthalad. Ez a Weierstrass-féle normálalak esetén a függőleges irányhoz tartozó ideális pont lesz. A pontok közötti „összeadást” a \oplus szimbólummal fogjuk jelölni annak érdekében, hogy megkülönböztessük a szokásos összeadástól, amelyhez természetesen nincs semmi köze. E művelet definíciójához szükségünk lesz a görbe egy tetszőlegesen választott \mathcal{O} pontjára, amelyet referenciapontnak fogunk nevezni. Ez tipikusan a görbe ideális pontja szokott lenni, és ebben az esetben egy P és Q pont összegén azt a P\oplus Q-val jelölt pontot értjük, amelyet az alábbi módon kapunk meg:

1. Kössük össze egymással a P és Q pontot egy egyenessel. Ha Q=\mathcal{O}, akkor értelemszerűen ez a P ponton átmenő függőleges egyenes lesz. Ha P=Q, akkor az egyenes legyen a görbe érintője a P=Q pontnál.
2. Az előző lépésben kapott egyenes egy további R pontban fogja metszeni a görbét, amely a fentebb leírtak alapján szintén egy racionális pont – vagy függőleges egyenes esetén az \mathcal{O} ideális pont – lesz.
3. Az előző lépésben kapott R pont x tengelyre vetített tükörképét nevezzük a P és Q pontok összegének. Ennek jele: P\oplus Q.

Az alábbi ábrákon két egymástól különböző pont összeadása, valamint egy úgynevezett „pontduplázás”, azaz egy pont önmagával való összeadása látható:

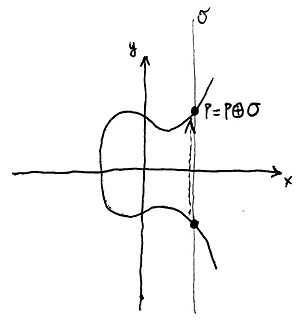
Ha az \mathcal{O} referenciapontnak nem a görbe ideális pontját választjuk, akkor a 3. lépést egy kicsit bonyolultabban kéne megfogalmazni. Ilyenkor ugyanis az R és \mathcal{O} által kijelölt egyenes és a görbe harmadik metszéspontja lenne a P\oplus Q összeg. Természetesen ha \mathcal{O} ideális pont, akkor ez az egyenes épp függőleges, és mivel a görbe szimmetrikus az x tengelyre, ezért ez valóban tükrözést jelent. Mi a továbbiakban az \mathcal{O} referenciapont alatt mindig a görbe ideális pontját fogjuk érteni.

Az nyilvánvaló, hogy a \oplus művelet kommutatív, hiszen teljesen mindegy, hogy az 1. lépésben a P pontot kötjük össze a Q ponttal, vagy fordítva, eredményként ugyanazt az R metszéspontot kapjuk, amelynek tükörképe – azaz P\oplus Q – ugyanaz lesz.

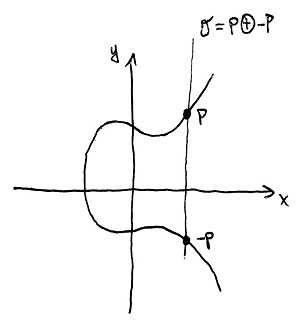
Ugyan elsőre nem látszik, de az \mathcal{O} referenciapont neutrális elemként viselkedik a \oplus műveletre nézve. Ezenkívül az is igaz, hogy a görbe bármely pontját összeadva az x tengelyre vetített tükörképével, eredményül az \mathcal{O} neutrális elemet kapjuk. Azaz minden pontnak van ellentettje a \oplus műveletre nézve:

A \oplus pontösszeadás tehát egy olyan kommutatív művelet, amelyre nézve létezik neutrális elem, és minden elemnek létezik ellentettje. Ezek a tulajdonságok a 24.1. Definícióben szereplő csoportaxiómákra emlékeztetnek minket, habár az asszociativitást még nem igazoltuk. Mivel ez egyáltalán nem magától értetődő, ezért ezt most nem is fogjuk megtenni. Mindenesetre a \oplus művelet valóban teljesíti az asszociativitást is, azaz a görbe tetszőleges A, B és C pontjaira teljesül az alábbi:

A\oplus (B\oplus C)=(A\oplus B)\oplus C

Így tehát elmondható, hogy minden racionális elliptikus görbe pontjainak halmaza a fent bevezetett \oplus műveletre nézve egy Abel-csoportot alkot. Természetesen egy olyan elliptikus görbén is szinte ugyanígy be lehetne vezetni a \oplus műveletet, amely a szakasz elején szereplő teljesen általános alakban van megadva. Az így kapott Abel-csoport azonban izomorf (lásd a 25.1. Definíciót) lenne azzal az Abel-csoporttal, amit akkor kapunk, ha a görbét a Weierstrass-féle normálalakba transzformáljuk.

Így tehát bármilyen elliptikus görbe vizsgálata visszavezethető egy Weierstrass-féle normálalakban megadott elliptikus görbe vizsgálatára. Ráadásul ez nem csak a racionális számtest, hanem – néhány kivételes esettől eltekintve – tetszőleges T test felett értelmezett elliptikus görbékre igaz. Kriptográfiai szempontból számunkra a véges testek feletti görbék lesznek érdekesek. Előbb azonban maradjunk még egy kicsit a racionális számtest feletti görbéknél, és ismerkedjünk meg a fentebb már említett egymillió dollárt érő Birch és Swinnerton-Dyer sejtés állításával egy kicsit részletesebben.

Mit állít a Birch és Swinnerton-Dyer sejtés?

Mint már említettük, továbbra is nyitott kérdés annak eldöntése, hogy egy adott E racionális elliptikus görbe vajon véges vagy végtelen sok racionális pontot tartalmaz-e. Ez a kérdés az előző szakasz fényében úgy is megfogalmazható, hogy a görbe által meghatározott E(\mathbb{Q})-val jelölt Abel-csoportnak véges vagy végtelen sok eleme van-e. Ez összefüggésben van az elliptikus görbe egy fontos tulajdonságával, amelyet E rangjának nevezünk. De mit is jelent ez pontosan?

Mint minden csoport esetében, így az E(\mathbb{Q}) csoport kapcsán is beszélhetünk a generálás fogalmáról. Ezt a fogalmat 25.18. Tételben vezettük be, amikoris azt mondtuk, egy bármilyen G csoport tetszőleges X részhalmaza egyértelműen meghatároz egy olyan legszűkebb részcsoportot G-ben, amely tartalmazza X összes elemét. Ezt a részcsoportot az X által generált részcsoportnak neveztük, és \lang X\rang-szel jelöltük. Amennyiben \lang X\rang = G, akkor azt mondjuk, hogy az X részhalmaz generálja a teljes G csoportot. Speciálisan végesen generált csoportoknak nevezzük az olyan csoportokat, amelyek generálhatók egy véges elemszámú részhalmazzal. Ennek egy még speciálisabb esetét a 25.19. Definícióban ciklikus csoportoknak neveztük, amikoris ez a véges elemszám konkrétan 1.

Sokáig nyitott volt a kérdés, hogy vajon létezik-e olyan E racionális elliptikus görbe, amely esetén az E(\mathbb{Q}) csoport nem generálható végesen. Ezt a kérdést Louis Mordell brit matematikus 1922-ben tisztázta a racionális számtest feletti elliptikus görbékre, amelyet Andé Weil francia matematikus 1928-ban megjelent doktori dolgozatában általánosított tetszőleges \mathbb{Q}-nál bővebb számtestekre is. Ez egy kiemelkedő eredmény volt a számelméletben, amely manapság Mordell-Weil tétel néven ismeretes. A tétel nemleges választ a fenti kérdésre, azaz kimondja, hogy minden racionális elliptikus görbe végesen generált. Ez azt jelenti, hogy mindig található véges sok olyan racionális pont a görbén, amelyekből a \oplus csoportművelet segítségével előállítható az összes többi – még ha azok végtelen sokan is vannak.

A Mordell-Weil tétel értelmében tehát a görbének mindig létezik véges generátorrendszere. Ekkor azonban nyilván létezik ezek között olyan is, amely minimális méretű. Ezeket független generátorrendszereknek nevezzük, utalva arra, hogy a csoportművelet segítségével egyik elemük sem kapható meg a többiből, vagyis független azoktól. Ha ugyanis nem így volna, akkor ezeket a nem független elemeket elhagyva a maradék rendszer továbbra is generálná a teljes csoportot, és így az eredeti generátorrendszer nem lett volna minimális méretű. Az E(\mathbb{Q}) csoport végessége nyilván attól függ, hogy egy ilyen független generátorrendszerben van-e végtelen rendű elem. A 24.11. Definíció alapján a görbe egy racionális pontja akkor végtelen rendű, ha önmagával akárhányszor összeadva mindig újabb és újabb pontokat kapunk a görbén.

Egy elliptikus görbe valamely független generátorrendszerében lévő végtelen rendű elemek száma egy olyan mennyiség, amely nem függ attól, hogy melyik generátorrendszert választottuk. Ezt a mennyiséget az elliptikus görbe rangjának nevezzük, amely tehát a Mordell-Weil tételből következően mindig véges. Egy racionális elliptikus görbe tehát pontosan akkor tartalmaz véges sok racionális pontot, ha a rangja 0 – hiszen ekkor a generátorrendszerben csak véges rendű elemek vannak –, és minden más esetben végtelen sok racionális pont van a görbén. Fontos lenne tehát, hogy ki tudjuk számolni a görbe rangját, azonban sajnos erre jelenleg nem ismert általános eljárás. Épp itt jön a képbe a Birch és Swinnerton-Dyer sejtés.

Az 1960-as években Bryan Birch és Peter Swinnerton-Dyer egy rendkívül érdekes felfedezésre jutottak, amikor elliptikus görbéket kezdtek el vizsgálni számítógéppel a \mathbb{Q} racionális számtest helyett különböző véges testek felett. Vegyük példának az alábbi racionális elliptikus görbét, amelynek a rangja ismert, történetesen 1, azaz végtelen sok racionális pontot tartalmaz:

y^2=x^3-5x

Ugyanezt a görbét tekintsük most a 18.3. Definícióban ismertetett \Z_p testek fölött különböző p prímszámokra. Könnyű belátni, hogy ezekben az esetekben \Z_p valóban nem csak gyűrű, hanem test is. Ekkor ugyanis a szorzásra nézve invertálható elemek száma a 21.5. Tétel alapján \varphi(p)=p-1, vagyis a nullán kívül minden elem invertálható, és így tényleg testet kapunk.

Vegyük példaként a fenti görbét a \Z_{17} test felett. Ilyenkor tehát a görbe pontjai olyan (x;y) számpárok lesznek, amelyeknek mindkét komponense a \Z_{17} testből való, és amelyeket behelyettesítve a görbe egyenletébe az egyenlet fennáll. Természetesen ilyenkor a hagyományos összeadások, szorzások és hatványozások helyett modulo 17 összeadásokat, szorzásokat és hatványozásokat kell érteni. Ezenkívül továbbra is a görbe pontjának tekintjük a „végtelen távol” lévő \mathcal{O} pontot, mint a görbe által meghatározott csoport egységelemét.

A pontokat – az \mathcal{O} pont kivételével – természetesen grafikonon is ábrázolhatjuk. Például a fenti y^2=x^3-5x elliptikus görbe grafikonja a \Z_{17} test felett így néz ki:

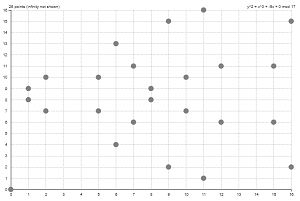
Az \mathcal{O} ponttal együtt tehát összesen 26 pontja van ennek a görbének. De ugyanígy megvizsgálhatjuk a pontok számát más és más \Z_p test felett különböző p prímekre. Az itt lévő oldalon minden ilyen görbének megtekinthetjük a grafikonját és a műveleti tábláját, valamint az adott görbe minden pontjának megnézhetjük az inverzét, a rendjét és az általa generált ciklikus részcsoportot is. Minket elsősorban a \Z_p feletti görbe pontjainak száma érdekel, amit jelöljünk N_p-vel. Az alábbi táblázat ezeket, valamint az \frac{N_p}{p} arányokat tartalmazza az első néhány p prímre:

\begin{array}{c|c|c}p & N_p & \frac{N_p}{p} \\ \hline 2 & 3 & 1.5 \\ \hline 3 & 4 & 1.33 \\ \hline 5 & 6 & 1.2 \\ \hline 7 & 8 & 1.14 \\ \hline 11 & 12 & 1.09 \\ \hline 13 & 18 & 1.38 \\ \hline 17 & 26 & 1.52 \\ \hline 19 & 20 & 1.05 \\ \hline & \vdots &\end{array}

Most a táblázat minden sorához képezzük a harmadik oszlopban lévő arányszámok szorzatait az adott sorig bezárólag. Például a fenti első néhány prímre az alábbi szorzatok képződnek:

\begin{aligned}p=2 &\to \frac{N_2}{2}=1.5 \\ p=3 &\to \frac{N_2}{2}\cdot \frac{N_3}{3}=2 \\ p=5 &\to \frac{N_2}{2}\cdot \frac{N_3}{3} \cdot \frac{N_5}{5}=2.4 \\ p=7 &\to \frac{N_2}{2}\cdot \frac{N_3}{3} \cdot \frac{N_5}{5} \cdot \frac{N_7}{7}=2.74 \\ p=11 &\to \frac{N_2}{2}\cdot \frac{N_3}{3} \cdot \frac{N_5}{5} \cdot \frac{N_7}{7}\cdot \frac{N_{11}}{11}=2.99 \\ p=13 &\to \frac{N_2}{2}\cdot \frac{N_3}{3} \cdot \frac{N_5}{5} \cdot \frac{N_7}{7}\cdot \frac{N_{11}}{11}\cdot \frac{N_{13}}{13}=4.14 \\ &\vdots \end{aligned}

Ez eddig látszólag pusztán játék a számokkal. A dolog akkor válik megdöbbentően érdekessé, amikor az így kapott értékeket elkezdjük felrajzolni egy megfelelően skálázott grafikonra:

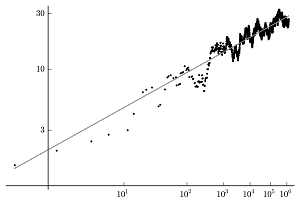
Ez a grafikon a fent leírt módon kiszámított szorzatokat tartalmazza az első 100000 prímszámra. A vízszintes tengely egy duplán, míg a függőleges tengely egy egyszeresen logaritmikus skálával van ellátva. Látható, hogy a kiszámított szorzatok eléggé hektikusan alakulnak, ahogy újabb és újabb p értékre számoljuk ki őket. A tapasztalat azonban azt mutatja, hogy ezen a furcsa logaritmikus skálán a felrajzolt pontok előbb-utóbb egy jól meghatározott egyenes körül kezdenek el egyre szorosabban csoportosulni. Ha megvizsgálnánk ennek a képzeletbeli egyenesnek a meredekségét, akkor 1-et kapnánk eredményül. Furcsamód ez épp megegyezik az eredeti racionális elliptikus görbe rangjával, ami szintén 1!

Ami még furcsább, hogy azóta rengeteg más, ismert rangú elliptikus görbére megvizsgálták ezt a jelenséget, és eddig minden egyes esetben azt tapasztalták, hogy a kapott egyenes meredeksége megegyezett a görbe rangjával. Az egymillió dollárt érő Birch és Swinnerton-Dyer sejtés némileg komplikáltabb megfogalmazásban lényegében azt állítja, hogy ez minden racionális elliptikus görbére igaz, vagyis tulajdonképpen egy eljárást ad a rang kiszámítására. Mintha valami nagyon mélyen gyökerező titokzatos kapcsolat lenne az eredeti racionális görbe és annak a \Z_p testek feletti változatai között. Az utóbbi évtizedek során rengeteg numerikus bizonyíték gyűlt össze, amely arra utal, hogy a sejtés igaz lehet. Ennek ellenére nagyrészt a mai napig fogalmunk sincsen, hogy mi állhat a háttérben, az állítás ugyanis csak a 0 és 1 rangú elliptikus görbékre van bizonyítva. Az 1-nél magasabb rangú görbékről semmit sem tudunk, noha a numerikus vizsgálatok eddig egyetlen ellenpéldát sem mutattak ki ezek közül.

Továbbá az sem ismert, hogy vajon van-e valamilyen felső korlát a rangra vonatkozóan, vagy az tetszőlegesen nagy is lehet. A vizsgálatok azt mutatják, hogy „majdnem minden” görbe rangja 0 vagy 1, méghozzá nagyjából 50-50% valószínűséggel, és ennél magasabb rangú görbék csak „elvétve” fordulnak elő. Ettől függetlenül persze ezekből is végtelen sok van, habár kimondottan nehéz magas rangú görbét találni. Az eddigi rekordot Noam Elkies amerikai matematikus tartja, aki 2006-ban az alábbi görbét fedezte fel:

y^2 + xy + y = x^3-x^2-20067762415575526585033208209338542750930230312178956502x + 34481611795030556467032985690390720374855944359319180361266008296291939448732243429

Ennek a görbének a pontos rangja nem ismert, mindössze annyit tudunk róla, hogy az legalább 28. A legfrissebb eredmény 2020-ból származik szintén Noam Elkies-től és Zev Klagsbrun-tól. Ennek a görbének a rangja pontosan 20:

y^2 + xy + y = x^3-x^2-244537673336319601463803487168961769270757573821859853707x + 961710182053183034546222979258806817743270682028964434238957830989898438151121499931

Látható, hogy ezek a rekordnak számító értékek sem túl magasak, bár a fenti első Elkies-féle görbe rangja lehet akármilyen magas is, hiszen arról csak annyit tudunk, hogy legalább 28. Ennek ellenére a legtöbben úgy gondolják, hogy nincs felső korlát a rangra vonatkozóan, ám a kérdés továbbra is nyitott.

Elliptikus görbék és kriptográfia

A Birch és Swinnerton-Dyer sejtéssel kapcsolatos kitérő után röviden ismertetjük, hogy hogyan lehet az elliptikus görbéket a kriptográfiában hasznosítani. Ehhez a szokásos racionális elliptikus görbék helyett véges testek feletti elliptikus görbéket kell használnunk. Véges testekre az előző szakaszban már láttunk példát. Ilyen véges test például a 18.3. Definíció szerinti \Z_p gyűrű, amennyiben p prímszám. Ebben a testben gyakorlatilag a 9. részben bemutatott óraaritmetika alapján kell számolni, és szerkezetileg teljesen megegyezik a 20.5. Tételben ismertetett \Z/p\Z maradékosztálygyűrűvel.

Lehet találni azonban olyan véges testet is, amelynek mérete nem prímszám, hanem valamilyen prímhatvány. Itt viszont már nem működik az óraaritmetika, ezért ebben az esetben egy némileg komplikáltabb konstrukcióra van szükség, amelynek részleteitől most eltekintünk. Továbbá azt is meg lehet mutatni, hogy minden véges test prím vagy prímhatvány méretű, sőt, minden azonos méretű véges test izomorf egymással. Ez tehát azt jelenti, hogy az elemek száma egyértelműen meghatározza a testet. Így például nincs értelme erről vagy arról a 8 elemet tartalmazó testről beszélni, hiszen ezek lényegében – izomorfiától eltekintve – ugyanazok.

Általánosságban ha q valamilyen prím vagy prímhatvány, akkor a q elemű testet \mathbb{F}_q-val jelöljük. Ennek megfelelően egy \mathbb{F}_q feletti E elliptikus görbe által meghatározott csoport jele E(\mathbb{F}_q). Az E(\mathbb{F}_q) csoport tehát egyrészt tartalmaz egy \mathcal{O}-val jelölt „végtelen távoli” pontot, amely a csoport neutrális eleme. Másrészt pedig azokat az (x;y) rendezett párokat tartalmazza, amelyeknek x és y komponensei az \mathbb{F}_q test elemei, és amelyek teljesítik az alábbi Weierstrass-egyenletet:

y^2=x^3+ax+b

Itt a és b a görbe paraméterei, amelyek szintén az \mathbb{F}_q test elemei, továbbá a képletben szereplő összeadások, szorzások és hatványozások alatt e test műveleteit kell érteni.

Egy ilyen véges test feletti elliptikus görbe pontjai között ugyanúgy értelmezni lehet a \oplus szimbólummal jelölt összeadást, mint a racionális elliptikus görbék esetén. A racionális esetben a koordinátáikkal adott P=(x_p;y_p) és Q=(x_q;y_q) pontok összegének kiszámítása egy egyszerű koordináta-geometriai feladat, amelynek itt csak a vázlatát ismertetjük. Az alábbi ábrán látható, hogy ehhez ki kell számítani a P és Q pontokra illeszkedő f egyenes és az elliptikus görbe R metszéspontját, majd ezt tükrözni kell az x tengelyre:

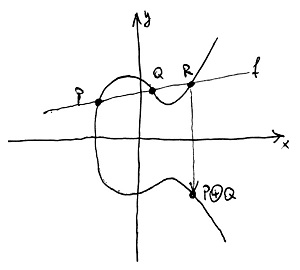
Előszöris fel kell írnunk az f egyenes egyenletét. Ez ugye egy elsőfokú síkgörbe, amely az alábbi alakban írható fel valamilyen c, d és e együtthatókkal:

cx+dy+e=0

A c és d együtthatók közül az egyik biztosan nemnulla, máskülönben a görbe nem lenne elsőfokú. Tegyük fel, hogy c\neq 0. Ha nem ez lenne a helyzet, akkor értelemszerűen a d\neq 0-val kell hasonlóan számolnunk. Az egyenlet mindkét oldalát c-vel elosztva az alábbit kapjuk, ahol D=\frac{d}{c} és E=\frac{e}{c}:

x+Dy+E=0

Mivel a P és Q pontok rajta vannak az egyenesen, ezért ezek koordinátái kielégítik ezt az egyenletet. Így őket behelyettesítve egy két egyenletből álló kétismeretlenes egyenletrendszert kapunk, amelyet megoldva megkapjuk a D és E együtthatókat. Az f egyenes és az elliptikus görbe keresett R metszéspontja egyrészt szintén kielégíti ezt az egyenletet, másrészt pedig kielégíti az elliptikus görbe egyenletét is. Ez ismét egy kétismeretlenes, két egyenletből álló rendszer, amelyet megoldva megkapjuk az R=(x_r;y_r) pont koordinátáit. Ezt kell tükröznünk az x tengelyre ahhoz, hogy megkapjuk a P\oplus Q pontot, ami annyit jelent, hogy vesszük az y_r koordináta ellentettjét.

Szokásos iskolás módszerekkel könnyen belátható, hogy az eljárás során végig olyan kifejezéseket kapunk, amelyekben csak a négy alapművelet szerepel. Még akkor is ez a helyzet, amikor P=Q, azaz amikor a görbe érintőjével kell számolnunk. További szélsőséges eset, amikor a kapott egyenes függőleges, mivel ekkor az ideális \mathcal{O} pontban fogja metszeni a görbét. Mindenesetre a P\oplus Q pontra kapott képletben minden esetben csak a négy alapművelet szerepel. Ha most elvonatkoztatunk a geometriai tartalomtól, valamint attól, hogy a racionális számok \mathbb{Q} testében számoltunk, akkor ezek a képletek nyilván átvihetők tetszőleges test feletti elliptikus görbékre is. Így az \mathbb{F}_q véges test feletti elliptikus görbék pontjai közötti összeadás képletét is megkaptuk, csak ilyenkor az adott test műveleteivel kell számolnunk. Ha például q prím – azaz \mathbb{F}_q\simeq \Z_q –, akkor az összeadásokat, és szorzásokat modulo q kell elvégeznünk, továbbá a kivonások és osztások alatt modulo q ellentett- és inverzképzést kell értenünk. Ha q nem prím, hanem valamilyen prímhatvány, akkor persze némileg bonyolultabb a helyzet, de a képletünk akkor is ugyanúgy működik.

E képlettel tehát tulajdonképpen az E(\mathbb{F}_q) csoport műveletének elvégzésére kaptunk egy eljárást. Ezt a csoportot kriptográfiai primitívek képzésére szeretnénk használni, ezért szükségünk lesz egy egyirányú függvényre, amely e csoport elemein, azaz a csoportot meghatározó elliptikus görbe pontjain van értelmezve. Ez az egyirányú függvény a következő: tegyük fel, hogy adva van egy P pont az elliptikus görbén, amelyet önmagával n-szer összeadunk, azaz:

\underbrace{P\oplus P\oplus \ldots \oplus P}_{\text{n darab}}=nP

Vegyük észre, hogy ez a 24.9. Definíció alapján tulajdonképpen a P pont n-edik „hatványa” az E(\mathbb{F}_q) csoportban, csak épp a definíció utáni megjegyzésben említett additív írásmódot alkalmaztuk, amikoris nem „hatványról”, hanem „többszörösről” beszélünk. Ha egy támadó csak a P és nP pontokat ismeri, akkor az n „kitevő” kiszámításához tulajdonképpen a diszkrét logaritmus problémájával (DLP) kell szembenéznie, ami – mint láttuk – reménytelen feladat, ha kellően nagy a csoport.

A 9. részben ismertettük a Diffie-Hellman kulcscsere protokollt, amelynek biztonságát tulajdonképpen a \Z_p test multiplikatív csoportján értelmezett DLP nehézsége adta. Most nézzük meg, hogyan néz ki ugyanez az eljárás, ha azt az E(\mathbb{F}_q) csoporton értelmezzük. Ezt az eljárást ECDH (Elliptic Curve Diffie-Hellman) protokollnak nevezzük:

1. Alice és Bob szeretnének egy nembiztonságos csatornán keresztül megállapodni egy közös titokban, amelyet egy titkosítási eljárás szimmetrikus kulcsaként használhatnának. Ez a közös titok egy véges test feletti elliptikus görbe egy pontja lesz. Először tehát megbeszélik, hogy pontosan melyik elliptikus görbét és melyik testet használják, továbbá megegyeznek egy kiindulási P pontban. Ezeket nem kell titokban tartaniuk, így ezt nyugodtan megtárgyalhatják a nembiztonságos csatornán keresztül is.
2. Mindketten választanak maguknak egy-egy egész számot, amelyet titokban tartanak, még egymással sem közlik azt. Tegyük fel, hogy Alice az n, Bob pedig az m egész számot választotta magának.
3. Alice kiszámítja az nP pontot a görbén, és az eredményt átküldi Bobnak. Bob ehhez hasonlóan kiszámítja az mP pontot, és az eredményt átküldi Alice-nak.
4. Alice a kapott mP pontból a titkos n szám ismeretében kiszámítja az n(mP) pontot. Ehhez hasonlóan Bob a kapott nP pontból a titkos m szám ismeretében kiszámítja az m(nP) pontot.
5. Az egész kitevős hatványozás azonosságairól szóló 24.10. Tétel 2. pontja miatt az előző lépésben kapott két pont meg fog egyezni, és ez lesz a közös titok. Persze itt az additív irásmód miatt hatvány helyett többszörösről beszélünk, de a 24.10. Tétel azonosságai ugyanúgy érvényesek, bárhogy is hívjuk ezt a műveletet.
6. Ha Eve időközben lehallgatja a csatornát, akkor mindössze a használt elliptikus görbét, a kiindulási P pontot, valamint a csatornán átküldött nP és mP pontokat ismeri meg. Ahhoz, hogy ő is birtokába kerüljön a közös titoknak, ki kéne számítania az n vagy az m egész számot, azaz egy DLP-feladatot kellene megoldania az E(\mathbb{F}_q) csoportban, amit belátható időn belül nem tud kivitelezni.

Ez mind szép és jó, viszont a 9. részben azt is megemlítettük, hogy egy úgynevezett közbeékelődéses támadással (man-in-the-middle attack) egy aktív támadó (például Mallory) el tudja hitetni Alice-szal és Bob-bal, hogy egymással állapodnak meg egy közös titokban, miközben valójában mindketten a támadóval beszélnek. Ez a támadás természetesen az ECDH esetén is ugyanúgy működik, azonban szerencsére létezik elliptikus görbéken alapuló digitális aláírás (ECDSA – Elliptic Curve Digital Signature Algorithm) is, amely partnerhitelesítést biztosít. Ismert továbbá elliptikus görbéken alapuló aszimmetrikus kulcsú rejtjelezési eljárás is. Ezek az eljárások szintén az E(\mathbb{F}_q) csoporton értelmezett DLP nehézségén alapulnak, a részletekre azonban nem térünk ki.

Az elliptikus görbéknek köszönhetően tehát Alice és Bob merőben újfajta, és – egyelőre legalábbis úgy tűnik – biztonságosabb eszközöket kapott a kezébe titkai elrejtéséhez. Az RSA-hoz képest az elliptikus görbéken alapuló kriptográfia (ECC – Elliptic Curve Cryptography) hosszabb távon is fenntartható a sokkal rövidebb kulcsméreteknek köszönhetően, emiatt napjainkban egyre inkább ez válik a de facto szabvánnyá az Interneten. Manapság már a legtöbb webböngésző is támogatja ezeket az algoritmusokat.

Nem lehetünk ugyanakkor teljesen nyugodtak, mivel a 20. század első felében az anyagot alkotó elemi részecskék elméletében egy addig soha nem látott forradalom kezdett el körvonalazódni. Megszületett ugyanis a kvantummechanika, amely abszolút felborította addigi világképünket, és úgy általában az egész fizikát. Ez az új tudomány olyan teljesen új elveken működő számítástechnikai eszközöket jósol, amelyeknek elképzelhetetlen számítási kapacitása a jelenlegi, algoritmikus bonyolultságon alapuló kriptográfiai eljárásaink végét fogja jelenteni.

A kétrés-kísérlet

Ebben a szakaszban a kvantummechanika egyik fontos kísérletét, az úgynevezett kétrés-kísérletet ismertetjük. A történet az 1600-as évekig, a fény természetéről folytatott első vitákig nyúlik vissza. Az egyik akkoriban uralkodó elmélet szerint a fény apró részecskékből, úgynevezett fotonokból áll, amelyek puskagolyókhoz hasonlóan haladnak előre a térben egyenes vonalban mindaddig, míg akadályba nem ütköznek. Innen aztán egy részük visszaverődik, más részük pedig elnyelődik. Ez az elmélet kiválóan megmagyarázta azokat a fényjelenségeket, amelyeket makroszkópikus világunkban tapasztalhatunk.

Képzeljünk el például egy fényforrást, amely fotonokat bocsájt ki magából, valamint egy ernyőt, amelyen a becsapódó fotonok intenzitásuktól függően nyomot hagynak. Helyezzünk a fényforrás és az ernyő közé egy olyan átlátszatlan lemezt, amelyen van egy rés. Ekkor értelemszerűen a fotonok az ernyőnek csak a rés mögé eső részén fognak nyomot hagyni, míg az árnyékban lévő részeken nem keletkezik nyom. Ez teljesen megfelel a puskagolyó-modellnek, vagyis úgy tűnik, hogy a fény valóban részecske természetű.

Most kezdjük el egyre jobban szűkíteni a rést. Egy idő után azt fogjuk tapasztalni, hogy a fotonok elkezdenek nyomot hagyni az ernyőn a rés mögötti résztől távolabb is, méghozzá egyre csökkenő intenzitással. Mintha az egyenesen haladó fotonok egy része a résen áthaladva irányt változtatna. Látszólag ugyanaz történik, mint amikor a vízben keltett síkhullámok egy, a hullámhosszukkal összemérhető szélességű résen keresztülhaladva a túloldalon koncentrikus félkörökként kezdenek továbbhaladni. Ez látható az alábbi ábrán:

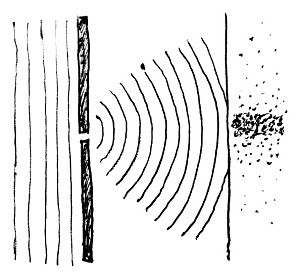
Az ernyő rés mögötti részén lesz a legnagyobb intenzitású a fény által hagyott nyom, hiszen ez a pont van a legközelebb a réshez. Oldalirányban távolodva viszont a hullámoknak egyre nagyobb utat kell megtenniük, amelynek során erősségük egyre jobban csökken. A fény tehát valójában hullám természetű, csak ez makroszkópikus méretekben nem látszik – mondhatnánk. Még inkább megerősíti ezt az elméletet, ha egy helyett két keskeny rést is nyitunk a lemezen. Az alábbi ábrán látszik, hogy mi történik ilyenkor:

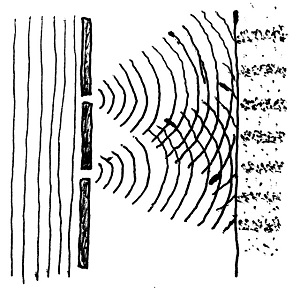
Ebben az esetben az ernyőn az ábrán látható furcsa csíkok fognak megjelenni. Ez azzal magyarázható, hogy a két résből kiinduló koncentrikus hullámok bizonyos helyeken erősítik, másutt pedig kioltják egymást, azaz interferencia lép fel. Ugyanúgy, mint amikor a vízbe egymás mellé két kavicsot dobunk, és a két becsapódás helyéről kiinduló körhullámok összetalálkoznak. A részecske-hullám vita tehát eldőlni látszott az utóbbi javára.

Volt azonban egy fotoeffektusnak nevezett jelenség, amelyet sehogyan sem lehetett megmagyarázni, ha a fényt egyszerűen csak valamiféle hullámnak tekintjük. A fotoeffektus során megfigyelték, hogy bizonyos fémekre ejtett fény elektromos áramot hozott létre egy alkalmas elektromos áramkörben. A feltételezés szerint a fény elektronokat ütött ki a fémből, amelyek így „folyni kezdtek” az áramkörben. Ugyanakkor azt is megfigyelték, hogy míg egy gyenge kék – azaz rövid hullámhosszú – fény elég volt az áram megindításához, addig egy erős vörös – azaz nagy hullámhosszú – fény nem. A hullámelmélet szerint ugyanakkor a fényhullám ereje a fényerősséggel, és nem pedig a hullámhosszal arányos, azaz egy erős fénynek elég erősnek kellett volna lennie az áramkeltéshez. Különös módon ez mégsem így volt. A jelenséget Albert Einstein azzal magyarázta, hogy a fény valóban fotonokból áll, amelyek ugyanakkor a fény hullámhosszától függő nagyságú energiával rendelkeznek, és csak bizonyos küszöbérték alatti hullámhosszal rendelkező fotonok képesek elektronokat kiszabadítani. Einstein a fotoeffektus magyarázatáért 1921-ben fizikai Nobel-díjat kapott.

Kezdték tehát felismerni, hogy a fény furcsamód kettős természetű: egyszerre mutat részecske- és hullámtulajdonságokat. Ezt azonban akkoriban azzal magyarázták, hogy a fény ugyan részecskékből áll, ám ezek valamilyen módon interferálnak egymással, amennyiben egyfajta tömegjelenségként vizsgáljuk őket. Időközben azonban fejlődött a technológia, és olyan eszközöket sikerült megalkotni, amelyek a hagyományos fényforrásokkal ellentétben képesek voltak egyesével is fotonokat kibocsájtani.

Ha a fenti kísérleti elrendezésben a fényforrást egy ilyen fotonágyúra cseréljük le, akkor értelemszerűen azt várnánk, hogy az egyenként kilőtt fotonok az ernyőnek a két rés mögötti részén fognak nyomot hagyni nagyjából fele-fele arányban, hiszen ebben az esetben nem tudnak interferálni más fotonokkal. Így tehát az interferenciára utaló csíkos mintázat helyett mindössze két csíknak kellene megjelennie az ernyőn a rések mögött. Megdöbbentő módon azonban nem ez történik: ebben az esetben is ugyanúgy megjelenik az interferenciakép. Mintha az egyes fotonok varázslatos módon egyszerre mindkét résen keresztülmennének, és a túloldalon valahogyan képesek volnának önmagukkal interferenciára lépni.

Az egyetlen mód, hogy megtudjuk, mi is történik valójában, ha detektorokat helyezünk el a résekhez – gondolnánk. Ezek ugyanis egyértelműen jeleznék, hogy egy-egy foton konkrétan melyik résen haladt át, vagy esetleg tényleg áthaladt-e mindkettőn egyszerre. Nos, miután elhelyezzük a detektorokat és megismételjük a kísérletet, egy még megdöbbentőbb dolog történik: interferenciakép helyett ezúttal valóban az eredetileg várt két csík fog megjelenni az ernyőn. Mintha a fotonok megfigyelése módosítaná az eredményt.

Most dobjuk félre egy picit a józat eszünket, és nézzük, milyen elképesztő magyarázatot ad erre a kvantummechanika.

Schrödinger macskája

A kvantummechanika egy rendszer pillanatnyi állapotát az úgynevezett hullámfüggvénnyel ábrázolja, ami a mérhető tulajdonságok valószínűségi eloszlását írja le. Például egy, a fenti kísérletben szereplő fotonnak nincs konkrét térbeli pozíciója, a hullámfüggvény ehelyett azt írja le, hogy hol milyen valószínűséggel van a foton. És itt nem arról van szó, hogy a mérőeszközök behatárolt pontosságát modelleznénk egy ilyenfajta matematikai leírással. Ehelyett a kvantummechanika azt állítja, hogy a foton a hullámfüggvény által leírt mértékekben egyszerre mindenhol jelen van.

Ezt a jelenséget szuperpozíciónak nevezzük. A kvantummechanika abból indul ki, hogy a kísérletben szereplő fotonról csak két dolgot tudunk: elhagyja a fotonágyút, és nekiütközik az ernyőnek. Minden, ami ezek között történt teljes rejtély. Sőt, a kvantummechanika szerint mindaddig, amíg nem tudjuk, hogy mit csinál egy részecske – azaz amíg meg nem mérjük –, addig tulajdonképpen mindent egyidejűleg csinál, azaz szuperpozíciós állapotban van. Azáltal, hogy detektort helyezünk a résekhez, tulajdonképpen egy mérést hajtunk végre, amely megváltoztatja a foton hullámfüggvényét. Ebben a pillanatban a hullámfüggvény egyetlen pontban, konkrétan a mért értéknél sűrűsödik össze, és minden egyéb helyen nulla lesz az értéke. Ezt a jelenséget a hullámfüggvény összeomlásának nevezzük. Ilyenkor tehát a szuperpozíciós állapot egyetlen konkrét állapotba roskad össze, és ez az oka annak, hogy az ernyőn érzékelt mintázat is teljesen más lesz, mint a detektorok nélküli esetben.

Ennek a meglehetősen őrültségnek tűnő elképzelésnek a szemléltetésére találta ki Erwin Schrödinger a „Schrödinger macskája” néven ismeretes gondolatkísérletet. Habár ez sem hangzik kevésbé őrültségnek, a kvantummechanika szerint az elemi részecskék szintjén valóban így működik a világunk. Képzeljünk el egy dobozban lévő macskát, amelynek két lehetséges állapota van: él vagy pedig halott. Amikor a láda még nyitva van, akkor egyértelműen látjuk, hogy a macska él, azaz ilyenkor nincs szuperpozíciós állapotban. Most beteszünk a macska mellé egy nagyon törékeny ciánfiolát, és lezárjuk a ládát. Ettől a pillanattól kezdve nem látjuk a macskát, nem tudjuk, hogy milyen állapotban van. Hétköznapi szóhasználattal élve vagy életben van, vagy halott, nem lehet tudni. Ezzel szemben a kvantummechanika szerint a macska egyszerre élő és halott, azaz szuperpozíciós állapotban van. Tegyük fel, hogy ismét kinyitjuk a ládát, hogy szemrevételezzük a macskát. Ekkor – és a kvantummechanika szerint csakis ekkor – a macska vagy az egyik, vagy a másik állapotba kerül, és ebben a pillanatban a szuperpozíció egyetlen konkrét állapotba roskad.

Noha mindez teljes képtelenségnek tűnik, ennek ellenére jelenleg ez minden idők legsikeresebb tudományos elmélete, ezért jobb ha megbarátkozik vele az Olvasó. Például ez teszi lehetővé, hogy a fizikusok képesek legyenek kiszámítani egy atomerőműben végbemenő nukleáris folyamatok következményeit. Csak ez az elmélet magyarázza az élőlények genetikai kódját tartalmazó DNS csodáit és a napsütést. Kizárólag ez teszi lehetővé annak a lézernek a megtervezését, amely a lejátszóba helyezett DVD és BluRay lemezeket elolvassa. Ez az alapja a tranzisztor és a dióda működésének, amelyek nélkülözhetetlenek az elektronikában, és amelyek az integrált áramkörök – és így a számítógépeink – építőkövei. És ez lehet az alapja egy olyan elképesző számítási kapacitással rendelkező eszköz, az úgynevezett kvantumszámítógép működésének is, amely eddig soha nem látott mértékű forradalmat hozhat főként a mesterséges intelligencia területén. Ez az eszköz azonban komoly fenyegetést is jelent az egész világ számára.

Kvantumszámítógépek

A 3. részben volt szó bővebben a hagyományos számítógépek működési elvéről. Itt került elő a kettes (bináris) számrendszer, amelyben ezek az eszközök dolgoznak. Ez azért előnyös, mert az ilyen számok csak 1-esekből és 0-ákból állnak, vagyis a számjegyeik könnyen reprezentálhatók valamilyen fizikai jel segítségével. Például folyik-e áram egy vezetékben vagy nem, van-e töltés egy kondenzátorban vagy nincs. A megfelelő elektronikus alkatrészek segítségével ezeket a fizikai jeleket azután manipulálni lehet. Képesek vagyunk tehát műveleteket végezni ezeken a számokon.

A bináris számjegyek reprezentációjához ugyanígy használhatunk elemi részecskéket is. Sok elemi részecske természeténél fogva rendelkezik egy tőle elválaszthatatlan tulajdonsággal, az úgynevezett perdülettel. Kelet vagy nyugat felé foroghatnak, mint az ujjhegyen megpörgetett labda. Állapodjunk meg abban, hogy egy kelet felé pörgő részecske 1-et, míg egy nyugat felé pörgő részecske 0-át jelent. Például egy öt darab, rendre kelet, kelet, nyugat, nyugat, nyugat irányba pörgő részecskéből álló rendszer a bináris 11000 számot jelképezi, amely tízes számrendszerben 24-et jelent. A következő példában ilyen pörgő részecskékkel fogjuk ábrázolni a számokat.

Tegyük fel, hogy meg kell keresnünk a legkisebb olyan egész számot, amelynek a négyzete és a harmadik hatványa együtt felhasználja 0-tól 9-ig az összes tízes számrendszerbeli számjegyet, méghozzá pontosan egyszer. Például a 23 nem elégíti ki ezt a feltételt, mivel 23^2=529 és 23^3=12167. Itt ugye az 1-es és a 2-es számjegy kétszer szerepel, míg a 0, 3, 4 és 8 számjegyek egyszer sem.

Hagyományos számítógéppel a feladat úgy oldható meg – noha biztosan nem ez a legokosabb módszer –, hogy elkezdjük szép sorban betáplálni a számjegyeknek megfelelő pörgő részecskékből álló sorozatokat egymás után, és megvárjuk, míg a számítógép leellenőrzi őket egyenként, hogy teljesítik-e a feltételt. Az 1-es nem teljesíti a követelményt, ezért betápláljuk a 2-est, és kivárjuk az újabb ellenőrzést. Aztán jön a 3-as, és így tovább, amíg a gép meg nem találja a megoldást, amely a 69-es lesz, hiszen 69^2=4761 és 69^3=328509. Ez a módszer elég sok időt emészt fel, hiszen a hagyományos számítógép egyszerre csak egy részecskesorozatot képes leellenőrizni, vagyis az egyes részfeladatokat sorba kell állítani. Így ha egy szám ellenőrzése 1 időegységig tart, akkor a teljes futási idő 69 időegységig fog tartani.

Ezzel szemben egy kvantumszámítógép dacol a józan ésszel, és képes ezt a feladatot egyetlen időegység alatt is elvégezni. A bináris számjegyeket reprezentáló részecskék perdülete ugyanis egy ugyanolyan kvantumtulajdonság, mint a kétrés-kísérletben szereplő fotonok pozíciója, azaz a megfelelő eszközökkel szuperpozícióba hozható. Ha például valamilyen módon sikerülne egy hét darab pörgő részecskéből álló rendszert szuperpozícióba hozni, akkor ezek a kelet és nyugat felé pörgés minden lehetséges kombinációját egyszerre reprezentálnák. Így egy kvantumszámítógép e szuperpozíciós állapotba került rendszer megfelelő manipulálásával képes lenne az összes lehetséges kombinációt egyszerre vizsgálni.

Hét bináris számjegyen összesen 2^7=128 féle számot lehet ábrázolni. Egy hagyományos számítógép ezek közül egyszerre csak az egyik kombináció által reprezentált számon képes műveletet végezni a számjegyek manipulációjával. Ilyenkor a számjegyeket biteknek nevezzük, ami a binary digit rövidítése. Ezzel szemben a kvantumszámítógép szuperpozícióban lévő számjegyeken, azaz úgynevezett kvantumbiteken vagy qubiteken (ejtsd: kjubit) végez műveleteket, tehát minden lehetséges kombináción egyidejűleg. Tekintsünk most egy mindössze 250 bináris számjegyből álló rendszert – ami hagyományos bitekből, valljuk be, nem túl sok. Ennyi számjegyen nagyjából 10^{75} darab különböző szám ábrázolható, amely több, mint a világegyetem atomjainak száma. Ha egy ilyen rendszert sikerülne valahogyan szuperpozícióba hozni, és persze ott is tartani, akkor a kvantumszámítógép egyidejűleg 10^{75} darab műveletet tudna végezni, és egyetlen időegység alatt be is fejezné őket. Ez eléggé félelmetesen hangzik, nemde?

Ha mindez nem lenne elég, az 1990-es években történt két olyan fejlemény, amely miatt Alice és Bob joggal kezdhetett el aggódni. Noha a kvantumszámítógép víziója már az 1980-as években napvilágot látott, a kutatók kezdetben nemigazán tudták, hogyan lehetne egy ilyen gépet programozni, hiszen teljesen más elveken működik, mint a hagyományos számítógépek. 1994-ben az AT&T Bell Laboratories egyik munkatársának, Peter Shor-nak sikerült egy olyan lépéssorozatot definiálnia, amelyet egy kvantumszámítógép képes lenne végrehajtani, és amely óriási számok prímtényezős felbontását számítja ki, méghozzá pillanatok alatt. Ez a Shor algoritmusnak nevezett kvantumszámítási eljárás tehát épp azt a feladatot oldja meg, amely az RSA-kód feltöréséhez szükséges, de ezenkívül alkalmas lenne az elliptikus görbéken alapuló kriptográfiai eljárások feltörésére is – habár ehhez több kvantumbitre lenne szükség, mint az RSA töréséhez.

1996-ban ugyancsak az AT&T Bell-nél Lov Grover-nek sikerült kidolgoznia egy másik kvantumeljárást, amely aggodalomra adhat okot. Ez a Grover algoritmusnak nevezett eljárás hihetetlenül nagy sebességgel képes kutakodni óriási listákban. Fogalmazhatnánk úgy is, hogy tűt keres a szénakazalban, és viszonylag gyorsan meg is találja. Vegyük észre, hogy egy szimmetrikus kulcsú titkosítás feltöréséhez pontosan ez kell: végignézni minden lehetséges kulcsot, míg elő nem kerül a megfelelő.

Noha ezek a fejlemények meglehetősen félelmetesen hangzanak, ám szerencsére egyelőre nem létezik még kvantumszámítógép, amelyen a fenti eljárásokat futtatni lehetne – gondolhatnánk. Ez azonban csak részben igaz! A nagy techcégek ugyanis már régóta kísérleteznek ilyen eszközök építésével, sőt, 2019-ben az IBM bemutatta a világ első kereskedelmi kvantumszámítógépét, az IBM Q System One-t, amely jó pénzért bárki számára elérhető egy felhőszolgáltatáson keresztül. Ez ugyanakkor egy mindössze 20 kvantumbites gép, amely csak néhány száz mikroszekundumig képes fenntartani a kvantumszámításokhoz szükséges szuperpozíciót. Így jelenleg még nem képes meghaladni a normál számítógépek teljesítményét, ehhez ugyanis a számítások szerint legalább 50 kvantumbitre lenne szükség. A fő problémát az okozza, hogy a szuperpozíció egy rendkívül instabil állapot. A legkisebb környezeti behatás – legyen az akárcsak egy kósza részecske jelenléte – a szuperpozíció összeomlását okozhatja, akárcsak a detektorok elhelyezése a kétrés-kísérlet esetén.

Mindezek ellenére az IBM bejelentése hatalmas mérföldkőnek számít, hiszen ezáltal a szélesebb tudományos közösség számára is elérhető a kvantumszámítógép – igaz, ez egyelőre még elsősorban csak kutatási célokat szolgál. Jelenleg még nem tudjuk, hogy a hagyományos számítógépekkel szembeni úgynevezett kvantumfölény elérése vajon pusztán illúzió, vagy már csak idő kérdése. Ha azonban ez valóban megtörténik, akkor egyrészt ma még elképzelhetetlen perspektívákat nyit a mesterséges intelligencia számára. Másrészt viszont komoly fenyegetést is jelent az egész emberiségre a fentebb már ismertetett okokból.

Kvantumkriptográfia

A kriptográfusoknak tehát az előző szakasz fényében fel kellett készülniük a kvantumfölény esetleges elérése utáni időkre is. Ekkor ugyanis az algoritmikus bonyolultságra építő kódjaink már fabatkát sem fognak érni. Szerencsére azonban az elemi részecskék szintjén tapasztalt furcsa jelenségeket nem csak kódok feltöréséhez, hanem teljesen újfajta kriptográfiai rendszerek létrehozásához is lehet használni. Ezzel foglalkozik a kvantumkriptográfia.

Az 5. részben volt szó róla, hogy elméletben létezik feltörhetetlen rejtjelező eljárás, méghozzá a one-time pad. Ez lényegében felfogható egy olyan Vigenére-kódnak, amely esetén a kulcs hossza megegyezik a nyílt szöveg hosszával, tökéletesen véletlenszerű, és minden egyes üzenethez új kulcsot használnak. Láttuk, hogy ez a kód abszolút értelemben feltörhetetlen, azaz egy támadó akkor sem fogja tudni megfejteni a nyílt szöveget, ha elegendő számítási kapacitás áll rendelkezésére az összes lehetséges kulcs végigpróbálásához. Az előző szakasz fényében a kvantumfölény korszakában ez egy teljesen reális feltételezés, így a jövőbeli Alice és Bob minden bizonnyal rá fog kényszerülni a one-time pad használatára.

Már csak az a kérdés, hogy ezt az óriási mennyiségű kulcsot hogyan fogják egymással megosztani anélkül, hogy találkozniuk kéne. Ne feledjük, erre a célra nem használhatnak RSA-t és semmilyen más olyan jelenlegi eljárást, amely az algoritmikus bonyolultságra épít. A kvantumszámítógépek korszakában ugyanis ezek többé már nem jelentenek védelmet számukra. Szerencsére a kvantummechanika lehetővé teszi Alice és Bob számára, hogy mégis megállapodjanak egy közös kulcsban, méghozzá teljes biztonságban. Ezt a kvantum-kulcsmegosztásnak nevezett eljárást fogjuk ismertetni ebben a szakaszban.

A kvantum-kulcsmegosztáshoz barátaink úgynevezett polarizált fotonokat, és polárszűrőket fognak használni. A fény ugye amellett, hogy fotonoknak nevezett részecskékből áll, hullámjelenségeket is mutat. Ezt úgy kell elképzelni, hogy a fotonok a térben utazva rezegnek egy adott sík mentén. Ennek a rezgésnek a síkját a foton polarizációjának nevezzük. Egy villanykörte által kibocsájtott fotonok a lehető legkülönfélébb polarizációval rendelkezhetnek. Egyesek függőlegesen, mások vízszintesen, megint mások tetszőleges egyéb szögben rezeghetnek. Az egyszerűség kedvéért tegyük fel, hogy csak függőleges, vízszintes, és átlós polarizációk léteznek, amelyeket az alábbi 4 szimbólummal fogunk jelölni: |, -, \backslash, /.

Ha azt szeretnénk, hogy minden foton azonos polarizációjú legyen, akkor egy úgynevezett polárszűrőt kell használnunk. Ezt egy adott szögben álló réssel ellátott lemezként lehet elképzelni. Ha például függőleges polárszűrőt alkalmazunk, akkor a függőleges polarizációjú fotonok akadálytalanul átjutnak, míg a vízszintes polarizációjú fotonok fennakadnak rajta. Az átlós polarizációjú fotonok azonban a kétrés-kísérlet detektoros változatához hasonlóan valamiféle „kvantumdilemmába” kerülnek, és azonos valószínűséggel vagy függőleges polarizációjú fotonná változva átjutnak a szűrőn, vagy pedig fennakadnak rajta. Ez látszik az alábbi ábrán:

Ezek után ismertetjük a kvantum-kulcsmegosztás alapgondolatát, amelyet Charles Bennett és Gilles Brassard dolgoztak ki az 1980-as években. Tegyük fel, hogy Alice titkos üzenetet szeretne küldeni Bobnak, amelyet a tökéletesen biztonságos one-time pad rejtjelezővel szeretne titkosítani. Ehhez előbb meg kell egyezniük egy, az üzenet hosszának megfelelő méretű véletlen kulcsban. Ez 3 szakaszban történik meg

1. szakasz: Alice generál egy 1-esekből és 0-ákból álló véletlen bitsorozatot. Tegyük fel, hogy ez a következő: 011000111010. Ezeket a biteket Alice polarizált fotonok formájában elküldi Bob-nak. Itt kétféle lehetősége van a bitek kódolására:

• Függőleges és vízszintes polarizációkat használ, azaz a | polarizáció fogja jelenteni az 1-est, a - polarizáció pedig a 0-ást.
• Átlós polarizációkat használ, azaz a / lesz az 1-es, míg a \backslash lesz a 0.

A trükk az, hogy Alice a bitek elküldésekor a kétféle polarizációs sémát véletlenszerűen váltogatja. Ennek jelentősége hamarosan világos lesz. Jelöljük a függőleges-vízszintes sémát +-szal, az átlós sémát pedig \times-tel. Tegyük fel, hogy Alice a fenti 12 bitet az alábbi táblázat szerint reprezentálja polarizált fotonokkal, majd az így kapott fotonokat elküldi Bob-nak:

\begin{array}{r|cccccccccccc}\text{bit} & 0&1&1&0&0&0&1&1&1&0&1&0 \\ \hline \text{séma} & +&\times& +&+&\times&\times&+&\times&+&+&+&\times \\ \hline \text{foton} & -&/&|&-&\backslash&\backslash&|&/&|&-&|&\backslash \end{array}

2. szakasz: A vételi oldalon Bob-nak meg kell állapítania a beérkező fotonok polarizációját. Ehhez kétféle polárszűrőt használhat, ezeken azonban egy helyett két rés van, amelyek egymásra merőlegesek. Ezt mutatja az alábbi ábra:

A baloldali + alakú polárszűrőn a függőleges vagy vízszintes síkban polarizált fotonok akadálytalanul áthaladnak. Ezzel szemben az átlósan polarizált fotonok az egyréses esethez hasonlóan azonos valószínűséggel vagy vízszintes, vagy pedig függőleges polarizációjú fotonokká változnak. Ugyanígy az \times alakú szűrőn az átlósan polarizált fotonok fognak akadálytalanul áthaladni, és a vízszintesen vagy függőlegesen polarizált fotonok fognak véletlenszerűen átlósan polarizálttá változni. Mivel Bob nem tudja, hogy Alice melyik fotont milyen sémával polarizálta, ezért nem tehet mást, minthogy tippel. Az alábbi táblázat mutatja a beérkező fotonokat, Bob-nak a sémára vonatkozó tippjeit, valamint az ilymódon detektált biteket:

\begin{array}{r|cccccccccccc}\text{foton} & -&/&|&-&\backslash&\backslash&|&/&|&-&|&\backslash \\ \hline \text{séma} & \times&\times&+&\times&\times&+&+&+&\times&\times&+&\times \\ \hline \text{bit} & \underline{0}&1&1&\underline{1}&0&\underline{1}&1&\underline{1}&\underline{0}&\underline{0}&1&0 \end{array}

Aláhúztuk azokat a biteket, amelyek esetén Bob rosszul tippelt, és nem a megfelelő sémát használta. Ez statisztikailag körülbelül az esetek felében fordul elő, és ilyenkor ugye véletlenszerű lesz a detektálás eredménye. Bob persze ezen a ponton még nem tudja, hogy melyek azok a bitek, amelyekhez nem jó sémát használt, és emiatt potenciálisan rosszul detektálta őket.

3. szakasz: Alice felhívja Bob-ot telefonon, és elmondja neki, hogy melyik fotont melyik séma szerint polarizálta, de azt nem árulja el, hogy konkrétan mi lett a fotonok polarizációja. Tehát például elmondja, hogy az első foton elküldésekor a + sémát használta, de azt nem, hogy függőlegesen vagy vízszintesen polarizált fotont küldött-e. Bob válaszában elmondja Alice-nak, hogy mely fotonoknál sikerült eltalálnia a megfelelő polárszűrőt, és mindketten eldobják azokat a biteket, amelyeknél Bob rosszul tippelt. A megmaradó bitek fogják alkotni a kulcsot. Ha esetleg ez még kevesebb, mint az Alice által küldeni kívánt üzenet hossza, akkor megismétlik az eljárást mindaddig, míg a megfelelő számú bit össze nem gyűlik a one-time pad rejtjelezéshez.

Ahhoz, hogy megértsük, miért is támadhatatlan ez a kulcsmegosztási eljárás, képzeljük magunkat Eve helyébe. Ő ugye lehallgatja a fotonok átküldésére szolgáló kvantumcsatornát és a főhőseink által használt telefonvonalat is. A fotonokat természetesen ő is megpróbálja detektálni, ám ezen a ponton ugyanabban a helyzetben van, mint Bob: kizárólag tippelni tud, hogy melyik fotonhoz milyen polárszűrőt használjon. Alice ezután elmondja ugyan Bob-nak, hogy melyik fotonnál melyik lett volna a helyes detektor, ám Eve-en ez nem segít, hiszen a Bob által helyesen bemért fotonoknak átlagosan a felénél ő rosszul tippelt. De azokkal a bitekkel sem ér sokat, ahol esetleg jól tippelt, hiszen ezek felénél viszont Bob tévedett, és ezeket a biteket főhőseink figyelmen kívül fogják hagyni. Eve tehát a kulcs bitjeinek körülbelül csak a felét fogja megismerni, amivel sajnos nem megy semmire.

Felfoghatjuk az egészet úgy is, mintha Alice különleges „kvantumkártyákat” küldene Bob-nak. Ezek olyan különleges kártyalapok, amelyeknél el kell döntenünk, hogy a színét, vagy az értékét szeretnénk megismerni, mivel egyszerre a kettőt nem lehet. Alice véletlenszerűen kiválaszt egyet ezek közül a különleges kártyák közül, legyen ez például a treff 6-os. Alice úgy dönt hogy a kártya színét nézi meg, és feljegyzi egy lapra, hogy treff, majd elküldi a kártyát Bob-nak. Eve persze lehallgatja a csatornát, de szerencsétlenségére ő az értékét leste meg, ami a 6-os. Alice ezután felhívja Bob-ot, és megbeszélik egymással, hogy egyezően tippeltek-e. Ha a válasz igenlő, akkor mindketten birtokában vannak egy közös titoknak, hiszen mindketten a treff-et írták fel. Eve ugyanakkor a 6-ost írta le, amivel nem megy semmire. Ha viszont Eve helyesen tippel, de Bob hibázik, akkor a fáradozása ugyancsak hiábavaló volt, hiszen ebben az esetben Alice és Bob a telefonos egyeztetés alapján el fogják vetni az Eve által helyesen bemért kártyalapot. Ráadásul Eve helyzete még ennél is rosszabb, hiszen egy 4. szakasz beiktatásával Alice és Bob képes detektálni, ha hallgatózik a csatornán.

4. szakasz: Miután megtörtént a kulcsmegosztás, Alice szúrópróbaszerűen kiválaszt néhány bitet, és ezeket leegyezteti Bob-bal a telefonvonalon keresztül. Amennyiben mindegyiknél egyezést találnak, az csak úgy lehetséges, hogy Eve nem hallgatózott, vagy ha igen, akkor olyan piszok nagy mázlija volt, hogy mindegyik fotonnál eltalálta a megfelelő polárszűrőt. Máskülönben ugyanis egy rosszul megválasztott polárszűrő megváltoztatta volna az adott foton polarizációját, és az ilyen esetek felében Bob a vételi oldalon hibásan detektálta volna a beérkező bitet annak ellenére, hogy ő viszont a megfelelő polárszűrőt választotta. Ha például Alice ilymódon 75 bitet egyeztet le Bob-bal, és nem találnak hibát, akkor körülbelül egy a milliárdhoz az esélye, hogy Eve lehallgatta a kvantumcsatornát. Ha azonban akárcsak egyetlen eltérést is találnak, akkor Eve lebukott, Alice és Bob pedig kénytelenek az egész kulcsot eldobni, átváltani egy másik csatornára, és elölről kezdeni a folyamatot. Barátaink a leegyeztetett biteket természetesen eldobják, hiszen azokat az egyeztetésre használt telefonvonal lehallgatásával bárki megismerhette.

Mindez persze elmélet, és az 1980-as években senki sem tudta, hogy vajon tényleg megvalósítható-e a gyakorlatban. Egészen 1989-ig kellett várni az áttörésre, amikor Bennett-nek egy történelmi léptékű kísérlettel sikerült igazolnia az elméletét: abszolút titkos kommunikációt hozott létre két, egymástól 30 centiméterre álló számítógép között. Azután a Genfi Egyetem tudósainak 1995-ben sikerült ugyanez a mutatvány, ám ezúttal az áthidalt távolság már 23 kilométer volt. A jelenlegi rekord 2018-ból származik, ami 421 kilométer. A végső cél azonban egy olyan rendszer kialakítása lenne, amely száloptika helyett műholdakon keresztül is működik, hiszen ez biztonságos kommunikációt biztosítana az egész Földön.

A most ismertetett kvantum-kulcsmegosztás természetesen csak a jéghegy csúcsa, amellyel pusztán ízelítőt kívántunk adni abból, hogy a kvantumkriptográfia valóban az abszolút biztonságot ígéri. A gyakorlati alkalmazhatóságig azonban még hosszú út áll a kutatók előtt. Egyelőre nincs szükség rá, hiszen az RSA és az elliptikus görbék révén rendelkezésünkre állnak azok az eljárások, amelyek a hagyományos számítógépek számára feltörhetetlenek. A versenyfutás azonban hatalmas, hiszen ez az előny azonnal szertefoszlik a kvantumszámítógépek megjelenésével. Ha a kvantumkriptográfia tényleg valósággá válik, akkor az információk védelme érdekében folytatott harc Alice és Bob győzelmével ér véget. Egy ilymódon titkosított üzenet feltörhetősége ugyanis azt jelentené, hogy hibás a kvantummechanika, amely az egész fizikát rombadöntené.

De vajon a kvantumkriptográfia idejében hozza el Alice és Bob számára a végső győzelmet? Vagy esetleg lesz egy olyan időszak, amikor a kvantumszámítógép már valóság, ám a világ még védtelen ellene egy ideig? Vajon a civilizációnk át fogja tudni vészelni ezt az átmeneti időszakot?

Reméljük, ám ez még a jövő zenéje…