Püthagorasz sötét oldala

Manapság talán nincs olyan ember a civilizált világban, aki ne hallott volna a Pitagorasz-tétel nevű összefüggésről. Ez olyan alaptétel, amelyet minden iskolás gyereknek meg kell tanulnia. Sőt, ez az egyike azon kevés matematikai állításnak, amelyet talán olyanok is viszonylag rendszeresen használnak, akiknek amúgy egész életükben nem sok közük van a matematikához. A tétel névadója egy bizonyos Püthagorasz nevű ókori filozófus, aki az Égei-tenger keleti partjánál fekvő aprócska Számosz szigetén született a Kr. e. 6. században. Mivel nincsenek hiteles beszámolók életéről és munkásságáról, ezért alakját rengeteg mítosz és legenda övezi. Tanítványaival máig ható eredményeket ért el a csillagászatban, a matematikában és a zeneelméletben. Mindazonáltal Püthagorasznak volt egy kevésbé közismert, ám igen dicstelen tette is, amellyel örökös szégyent hozott tulajdon nevére, és amely az ókori matematika egyik legnagyobb tragédiájaként vonult be a történelembe. Ebben a cikkben erről lesz szó…

A számtalan legenda ellenére a történészek körében mára egyetértés alakult ki abban a tekintetben, hogy Püthagorasz volt a számlogika atyja, és nevéhez fűződik a matematika első aranykora is. Felismerte, hogy a számokat nem csak dolgok megszámlálására és különböző számításokhoz lehet használni, hanem pusztán önmagukban is vizsgálni lehet őket. Eljutott arra az absztrakciós szintre, hogy a számok az érzékelhető világtól függetlenül léteznek. Tanulmányozásuk tehát minden mástól eltérő módon nincs kitéve az észlelés pontatlanságának. Emiatt képes volt olyan igazságokat felfedezni velük kapcsolatban, amelyek mindenféle véleménytől és előítélettől függetlenek, abszolút érvényűek, és sokkal tökéletesebbek, mint bármely addigi ismeret.

Püthagorasz beutazta szinte az egész ismert ókori világot, és húszéves utazgatása során összegyűjtötte az akkori világ összes matematikai ismeretét. Főként az egyiptomiaktól és a babiloniaktól vett át számos módszert és eszközt. Ezek a népek bonyolult számítási módszereket dolgoztak ki, ezekben azonban elsősorban csak a gyakorlati problémák megoldásának eszközét látták. Az egyiptomiak például szerették volna pontosan meghatározni a birtokhatárokat a Nílus folyó szokásos évi áradásai után, amelynek során tulajdonképpen a geometria alaptörvényeit fedezték fel. Maga a „geometria” szó is innen származik, amely „földmérést” jelent.

Püthagorasz megfigyelte, hogy ezek az ókori népek a bonyolult számítások során vakon követtek bizonyos szigorú szabályokat. Az azonban egyáltalán nem foglalkoztatta őket, hogy a képleteik miért adnak mindig jó eredményt. Ezek az ismeretek nemzedékről nemzedékre öröklődtek, soha nem volt velük semmi probléma, ezért soha senki nem vonta kétségbe őket. Püthagorasz azonban nem csak használni akarta a számokat, hanem meg is akarta érteni a bennük rejlő logikát és törvényszerűségeket. Húszéves utazgatás után azzal a céllal utazott haza Számosz szigetére, hogy iskolát alapítson, és ott az általa elsajátított ismeretek megértésének szenteljék az időt.

Időközben azonban az addig szabadszellemű Számoszt egy Polükratész nevű zsarnok kerítette hatalmába, és másságot nem tűrő konzervatív állammá változtatta. Püthagoraszt is meghívta az udvarába azzal a céllal, hogy elhallgattassa, ő azonban átlátott a szitán, és inkább elhagyta a várost. A sziget egy félreeső részén titokban alapított ugyan egy rövid életű iskolát, azonban az uralkodó a társadalmi reformokról vallott nézetei miatt végül menekülésre késztette a filozófust, aki a dél-itáliai Krotón városában telepedett le.

A Püthagoreus Testvériség

Itt lelkes patrónusra talált egy bizonyos Milón személyében, aki Krotón leggazdagabb embere – és nem mellesleg híres atléta – volt. Milón a filozófia és a matematika iránti lelkesedésétől vezérelve háza egy részét átengedte Püthagorasznak, aki új otthonának biztonságos falai között mintegy hatszáz követőjével megalapította iskoláját, a Püthagoreus Testvériséget.

A Testvériség tagjain kívül voltaképpen senkinek nem volt tudomása arról, hogy milyen horderejű eredményeket értek el. Az iskola tagjai ugyanis esküt tettek, hogy a világ előtt titokban tartják matematikai felfedezéseiket. Az esküszegést Püthagorasz halála után is keményen megtorolták. A Testvériség egyik tagja például esküjét megszegve nyilvánosságra hozta egy új szabályos test – a 12 szabályos ötszöglap által határolt dodekaéder – felfedezését, akit ezért vízbe fojtottak. Elsősorban e szigorú titoktartás miatt alakult ki oly sok mítosz a Testvériségről és különös szertartásaikról, és ez az oka annak, hogy kevés megbízható forrás maradt fenn matematikai eredményeikről.

Maga Püthagorasz az iskolán belül feltétlen, abszolút tekintélyt, és már-már isteni tiszteletet élvezhetett. Az iskola hallgatóit a beavatottság foka szerinti körökre osztották. A külsőbb tanítványok, az akuszmatikusok nem részesülhettek minden tudásban, ez a belsők, a mathématikusok kizárólagos joga volt. A legbelsőbb körökhöz tartozók öt év tanulás után állítólag beszélhettek is a mesterrel, de csak úgy, hogy annak alakját egy függöny rejtette előlük. Sokak életük végéig nem részesülhettek ebben a megtiszteltetésben. Kollektív intézmény lévén nem mindig világos, hogy a Püthagoreus Testvériség felfedezései és tanításai közül melyek köthetők személy szerint Püthagoraszhoz és melyek a tanítványaihoz.

A Pitagorasz-tétel

A Testvériség legfontosabb felfedezése magáról Püthagoraszról kapta a nevét. Ez a cikk elején már említett Pitagorasz-tétel, amely a derékszögű háromszögek oldalhosszai között mond ki egy fontos összefüggést.

Nevezetesen: minden derékszögű háromszögre teljesül, hogy a legnagyobb oldal (az úgynevezett átfogó) hosszának négyzete a másik két oldal (az úgynevezett befogók) négyzeteinek összegével egyezik meg. Az alábbi ábra szemlélteti ennek az állításnak a geometriai tartalmát:

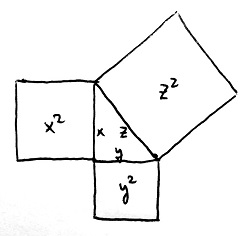
Itt x és y a két befogó, z pedig az átfogó hosszát jelöli. A tétel azt állítja, hogy ha a két befogóra felrajzolunk egy-egy négyzetet, akkor e négyzetek területének összege épp az átfogóra helyezett négyzet területével fog megegyezni. Ha például x=3, y=4 és z=5, akkor valóban teljesül az egyenlőség:

\begin{aligned}x^2+y^2&=z^2 \\ 3^2+4^2&=5^2 \\ 9+16&=25 \end{aligned}

Az igazsághoz hozzátartozik, hogy ezt az összefüggést már a kínaiak és a babiloniak is ismerték csaknem ezer évvel Püthagorasz előtt. Ők azonban nem tudták ennek okát, de nem is igazán foglalkoztak ezzel. Számukra ugyanis csak az volt a fontos, hogy a képlet valamilyen rejtélyes módon minden általuk megvizsgált derékszögű háromszögre működik. A tétel mégis joggal viseli Püthagorasz nevét, hiszen ő volt az első, aki teljesen biztos lehetett benne, hogy soha senki nem fog ellenpéldát találni, ameddig világ a világ. De vajon honnan lehetett ebben teljesen biztos, amikor nyilván nem vizsgálhatta végig az összes derékszögű háromszöget, hiszen végtelen sok van belőlük?

Ennek a bizonyosságnak a matematikai bizonyítás az alapja, amelyről ebben a cikkben volt szó bővebben. Egy matematikai állítás igazsága megcáfolhatatlan, és magasabbrendű minden másfajta állításnál, mert a logika szabályai szerint lépésről lépésre bizonyosodik be, amely folyamat végén kiderül, hogy nem is lehet másként. A Pitagorasz-tétel bizonyítása mérföldkőnek számított a matematikában, mert megmutatta, hogy a matematika segítségével olyan betonbiztos alap adható a tudomány számára, amelyre a tudósok nyugodtan ráépíthetik a maguk tökéletlen megfigyeléseit és pontatlan méréseit.

Most nézzük meg, hogy Püthagorasz hogyan gondolkodott. Vegyünk egy tetszőleges derékszögű háromszöget, amelynek befogóit jelöljük x-szel és y-nal, átfogóját pedig z-vel. Rajzoljuk fel ezt a háromszöget az alábbi ábrán látható elrendezés szerint 4 példányban, amelyek mindegyike 90 fokkal el van forgatva az előzőhöz képest:

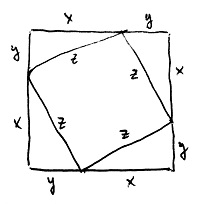
Az ábra közepén látható döntött síkidom egy négyzet, mivel mindegyik oldala z, és ezek derékszögeket zárnak be egymással, hiszen a háromszögünk 90 fokos elforgatásaival kaptuk őket. A bizonyítás kulcslépése, hogy a kapott nagy négyzet területét kétféleképpen is kiszámíthatjuk. Egyrészt, mivel minden oldalának hossza x+y, ezért a területe (x+y)^2. Másrészt ugyanezt a területet a darabjainak területéből is kiszámíthatjuk. A megdöntött négyzet területe ugye z^2, egy-egy derékszögű háromszög területe pedig \frac{xy}{2}. Mivel összesen 4 derékszögű háromszögünk van, ezért az ilymódon kiszámított teljes terület z^2+4\frac{xy}{2}. A kétféle területszámítási módszerrel ugyanannak a nagy négyzetnek a területét számítottuk ki, ezért fennáll az alábbi egyenlőség:

(x+y)^2=z^2+4\frac{xy}{2}

A baloldalon felbontva a zárójelet, a jobboldalon pedig a második tagot 2-vel egyszerűsítve a következőt kapjuk:

x^2+y^2+2xy=z^2+2xy

Mindkét oldalból levonhatjuk a 2xy tagot, így kapjuk a tétel állítását:

x^2+y^2=z^2

Mivel az x, y és z változók helyére bármilyen derékszögű háromszög oldalai beírhatók, ezért ez a bizonyítás általános érvényességű. Azaz a Pitagorasz-tétel valóban minden derékszögű háromszögre igaz.

A Pitagorasz-tétel megfordítása

Az előző szakaszban tehát azt igazoltuk, hogy ha egy háromszög derékszögű, akkor az oldalaira fennáll a tételben leírt egyenlet. Ebben a szakaszban azt fogjuk igazolni, hogy ez az egyenlet másfajta háromszögekre nem is teljesülhet. Másként fogalmazva: ha egy háromszög oldalaira teljesül a pitagorasz-féle egyenlet, akkor az a háromszög derékszögű. Ezt az állítást a Pitagorasz-tétel megfordításának nevezzük. Felhívjuk a figyelmet, hogy ez az állítás az előző szakaszban szereplő bizonyításból még nem következik, a megfordítás tehát nem azonos a Pitagorasz-tétellel. Most a megfordítást fogjuk igazolni.

Tegyük fel, hogy adva van egy tetszőleges háromszög, amelynek oldalhosszai rendre x, y és z. Tegyük fel továbbá, hogy ezekre az oldalhosszakra teljesül a pitagorasz-féle egyenlet, azaz:

x^2+y^2=z^2

Azt kell igazolnunk, hogy ez a háromszög derékszögű. Most rajzoljunk fel egy olyan háromszöget, amely valóban derékszögű, és a két befogójának hossza x-szel és y-nal egyezik meg. Jelöljük ennek a derékszögű háromszögnek az átfogóját w-vel. Az alábbi ábrán a két felrajzolt háromszöget láthatjuk:

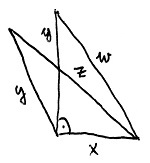
A kérdéses szabálytalan háromszögre tehát azt mondtuk, hogy teljesül rá a pitagorasz-féle egyenlet. A derékszögű háromszögről pedig a már bizonyított Pitagorasz-tétel miatt tudjuk ugyanezt, hiszen ez egy derékszögű háromszög. Ebből az alábbi két egyenletet írhatjuk fel:

\begin{aligned}x^2+y^2&=z^2 \\ x^2+y^2&=w^2 \end{aligned}

A két egyenlet baloldalai megegyeznek, így tehát a jobboldalak is:

z^2=w^2

Mivel z és w biztosan pozitív számok (hiszen oldalhosszakról van szó), ezért a négyzetük csak akkor lehet azonos, ha ők maguk is megegyeznek, azaz:

z=w

Azt kaptuk tehát, hogy az oldalhosszak azonosak, így a vizsgált háromszög valójában megegyezik a derékszögű háromszöggel.

Tökéletes számok

A Testvériség tulajdonképpen vallási közösség volt, és a számok képezték imádatuk egyik tárgyát. Úgy vélték, hogy a számok közötti kapcsolatok megértésével közelebb kerülhetnek az istenekhez, és megfejthetik a világmindenség spirituális titkait. A Püthagoreusok csak a pozitív egészeket, és az ezek hányadosaként előálló törteket – az úgynevezett racionális számokat – tanulmányozták. Ezek közül is főként a különleges jelentőségű számok érdekelték őket. Ilyenek például az úgynevezett tökéletes számok.

A Testvériség világképében egy egész szám tökéletessége az osztóitól, pontosabban azok összegétől függ. A mai szóhasználattal ellentétben a Püthagoreusok egy szám osztói alatt csak a pozitív osztókat értették, és nem sorolták közéjük magát a számot, csak a nála kisebb osztókat. Ha egy szám ilyen értelemben vett osztóinak összege nagyobb magánál a számnál, akkor őt bővelkedő, ha pedig kisebb, akkor hiányos számnak nevezték. Például a 10 hiányos szám, mivel osztóinak összege 1+2+5=8, ami kisebb 10-nél. Ezzel szemben a 12 bővelkedő szám, mivel az ő osztóinak összege 1+2+3+4+6=16, ami nagyobb 12-nél.

Észrevették, hogy ritkán ugyan, de előfordulnak olyan számok is, ahol az osztók összege épp megegyezik magával a számmal. Ezeket nevezték tökéletes számoknak. A legkisebb tökéletes szám a 6, mivel osztóinak összege 1+2+3=6. A második tökéletes szám a 28, hiszen 1+2+4+7+14=28. A Testvériségen kívül a történelem folyamán a tökéletes számokat más kultúrák is misztikus tulajdonságokkal ruházták fel. Szent Ágoston szerint például Isten egy pillanat alatt is megteremthette volna a világot, ám ő mégis 6 nap alatt tette ezt meg, méghozzá azért, hogy ezzel is kifejezésre juttassa a világegyetem tökéletességét.

Az ókori görögök további két tökéletes számot találtak, ezek a 496 és a 8128. Ezután egy nagy ugrás következik: az ötödik és hatodik tökéletes szám a 33\ 550\ 336 és a 8\ 589\ 869\ 056. A lista meglehetősen ritka, 2019-ig mindössze 51 tökéletes számot sikerült találni, a legnagyobb ezek közül 49\ 724\ 095 számjegyből áll, és nyitott kérdés, hogy vajon végtelen sok van-e belőlük. Ezenkívül minden ismert tökéletes szám páros, és a mai napig nem tudjuk, hogy egyáltalán létezik-e páratlan tökéletes szám. Már Euklidész felismerte, hogy az addig ismert tökéletes számok előállíthatók két olyan szám szorzataként, amelyek közül az egyik egy 2-hatvány, a másik pedig 1 híján a rákövetkező 2-hatvány. Például:

\begin{aligned}6&=2^1\cdot (2^2-1) \\ 28&=2^2\cdot (2^3-1) \\ 496&=2^4\cdot (2^5-1) \\ 8128&=2^6\cdot (2^7-1)\end{aligned}

Azt azonban, hogy minden páros tökéletes szám csakugyan előállítható ilyen alakban, Leonhard Euler-nek sikerült igazolnia mintegy 1500 évvel később.

Püthagoraszt rendkívül szórakoztatták ezek a számok, és szerette volna megérteni a különös természetüket. Észrevette, hogy a 2-hatványok „majdnem” tökéletesek, mivel az osztóik összege mindössze 1-gyel kisebb náluk. Például:

\begin{array}{c|c|r}n & 2^n & \text{osztók összege} \\ \hline 1 & 2^1=2 & 1 \\ 2 & 2^2=4 & 1+2=3 \\ 3 & 2^3=8 & 1+2+4=7 \\ 4 & 2^4=16 & 1+2+4+8=15 \\ 5 & 2^5=32 & 1+2+4+8+16=31 \end{array}

Az olyan számokat, amelyek csak 1-gyel nagyobbak az osztóik összegénél, kissé hiányos számoknak nevezzük, és ezekből végtelen sok van. Ezzel szemben kissé bővelkedő számot – tehát olyan számot, amelyek 1-gyel kisebbek az osztók összegénél – a görögök nem találtak, de azt sem tudták bebizonyítani, hogy nem is létezik. A Püthegoreusokat ilyesfajta rejtvények foglalkoztatták, mert a gyakorlati hasznosságtól függetlenül szerették volna megérteni a számok viselkedését. Mindazonáltal 2500 év elteltével a mai matematikusok még mindig nem tudják, hogy léteznek-e kissé bővelkedő számok. A tökéletes számokkal kapcsolatos további érdekességek itt találhatók.

Számok mindenütt

A fentieken túlmenően Püthagoraszt a számok és a természet kapcsolata is foglalkoztatta. Arra a következtetésre jutott, hogy a fizikai világ bizonyos szabályoknak engedelmeskedik, amelyek a matematika nyelvén írhatók le. Az egyik ilyen felfedezése a zenei harmónia és a számok közötti szoros kapcsolat felismerése volt.

Már az ókori zenészek is rájöttek arra, hogy bizonyos hangok együttesen kellemes hatást keltenek, míg mások bántják a fület. Ám nekik fogalmuk sem volt róla, hogy miért adnak bizonyos hangok harmonikus hangzást, ezért egyszerűen hallás után hangolták a hangszereiket. Ha egy húrt megpendítünk, akkor az egy alaphangon szólal meg, ha pedig bizonyos pontokon lerögzítjük, akkor az alaphangnál magasabb hangokat kelthetünk. Püthagorasz azonban észrevette, hogy csak bizonyos speciális helyzetű pontok lerögzítésekor keletkeznek olyan hangok, amelyek harmonizálnak az alaphanggal. Ezeket a hangokat felharmonikusoknak nevezzük, és akkor állnak elő, ha a húrt pontosan a felénél, harmadánál, negyedénél, ötödénél, stb. rögzítjük. Azaz a felharmonikusok frekvenciája mindig az alaphang frekvenciájának egész számú többszöröse kell legyen, máskülönben kellemetlen lesz a hangzás.

Püthagorasz tudományos forradalmat indított el annak felismerésével, hogy minden fizikai jelenség mögött számok rejlenek, a zenei harmóniától egészen a bolygópályákig. Ettől kezdve minden fontos matematikai eredmény újabb és újabb eszközöket adott a tudósoknak a világ jelenségeinek leírására. Püthagorasz világképében a világ tökéletessége arra a feltételezésre épült, hogy minden jelenség egész számokkal, illetve ezek arányaival – a már említett racionális számokkal – leírható, és ebbe a világképbe nem fért bele semmilyen, ettől az alapelvtől való eltévelyedés. Azokat a számokat, amelyek nem írhatók fel ilyen arányként tört alakban, irracionális számoknak nevezzük. Püthagorasz tehát tagadta az irracionális számok létezését.

Püthagorasz tragédiája

Volt azonban Püthagorasznak egy Hippaszosz nevű diákja, aki időtöltésként azzal játszadozott, hogy megpróbálta az egységnyi oldalú négyzet átlójának hosszát két egész szám hányadosaként, azaz törtalakban felírni. A Pitagorasz-tételből tudjuk, hogy az egységnyi oldalú négyzet átlója szükségképpen \sqrt{2}, hiszen ennek a négyzete 2, ami épp a két 1 hosszú befogó négyzetösszege:

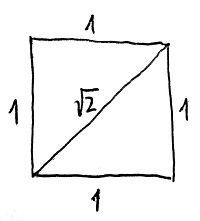
Hippaszosz végülis rájött, hogy ilyen tört nem létezik, és ezt be is tudta bizonyítani. Azaz kiderült, hogy a \sqrt{2} irracionális szám. Egy ilyen számban az a borzasztóan visszataszító, hogy a tizedesjegyeiben nem lehet találni semmilyen szabályosságot. Például a \sqrt{2} közelítő értéke 1.4142135623730950488. Ezzel szemben egy racionális számnak vagy véges sok tizedesjegye van, vagy ha végtelen sok, akkor viszont valahanyadik tizedesjegytől kezdve a számjegyek periodikusan ismétlődnek. Egy irracionális szám esetén azonban számolhatnánk bármeddig, ameddig csak a világegyetem erőforrásaiból futná, akkor sem juthatnánk el az adott szám pontos értékéhez, és szabályosságot sem tudnánk benne felfedezni. Így már talán felfoghatjuk, hogy Püthagorasz miért tartotta titokban ezeknek a matematikai szörnyetegeknek a létezését.

Hippaszosz azonban büszkén közölte a hírt mesterével, aki nagyon nem örült ennek a fejleménynek. A felfedezést hosszas vita és elmélkedés követte, és Püthagorasznak döntenie kellett: vagy elfogadja Hippaszosz megdönthetetlen logikán alapuló érveit, és elveti egész addigi világképét, vagy pedig saját tanításaival szembemenve megtagadja a logika erejét.

A logikus gondolkodás és a matematikai módszerek atyja szégyenteljes módon az utóbbi mellett döntött, és inkább erőszakhoz folyamodott, mintsem elismerje: nincs igaza. A világtörténelem egyik legnagyobb tudósa – dicstelen módon szégyent hozva saját nevére és eszméire – vízbefojtatta tanítványát. Az irracionális számokat csak Püthagorasz halála után lehetett újra életre kelteni.

Euklidész bizonyítása

Végezetül ismertetjük a matematikatörténet egyik leghíresebb bizonyítását, amelyet Euklidész írt le az Elemek című könyvében a Kr. e. 3. században, és amellyel szembenézett az irracionális számok kérdésével. Euklidész a reductio ad absurdum (bizonyítás ellentmondáson keresztül) elnevezésű logikai csavarral bizonyította a \sqrt{2} irracionalitását, amely azóta is a matematikusok egyik kedvenc fegyvere. Ennek a módszernek az a lényege, hogy először nyakatekert módon feltételezzük, hogy a bizonyítandó állítás hamis. Ezután feltárjuk, hogy ez a feltételezés milyen következményekkel járna. Végül a logikus érvelések sorozatában valahol egy feloldhatatlan ellentmondásba ütközünk más, korábban már bizonyított állításokkal, vagy nyilvánvaló tényekkel (például valahol azt kapjuk, hogy 1+1=1). A matematika azonban nem tűri az ellentmondásokat, amiből következik, hogy a bizonyítandó állítás semmiképpen sem lehet hamis – következésképp igaznak kell lennie.

G. H. Hardy angol matematikus a következőket mondta erről a módszerről: „Az ellentmondáson keresztül történő bizonyítás a matematikus részéről sokkal nagyszerűbb áldozat, mint amilyen egy sakkjátszmában lehetséges. A sakkjátékos feláldozhat egy gyalogot vagy egy tisztet, de a matematikus az egész játékot ajánlja fel.”. Ezek után nézzük meg, hogyan néz ki ez a gyakorlatban.

Tételezzük fel, hogy az állítással ellentétben a \sqrt{2} racionális, azaz léteznek olyan a és b egész számok, amelyekre teljesül az alábbi:

\sqrt{2}=\frac{a}{b}

Mindkét oldalt négyzetre emelve és megszorozva a jobboldalon kapott nevezővel az alábbit kapjuk:

\begin{aligned}2&=\frac{a^2}{b^2} \\ 2b^2&=a^2\end{aligned}

Eszerint tehát a jobboldalon szereplő a^2 páros szám, hiszen ő az egyenlet szerint a b^2 kétszerese. Mármost ha a^2 páros, akkor maga a is páros, máskülönben nem szerepelne a prímtényezői között a 2-es, és így az ő négyzetében sem szerepelhetne. Azaz létezik olyan c egész szám, hogy a=2c. Ezt visszahelyettesítve az egyenletbe az alábbit kapjuk:

\begin{aligned}2b^2&=(2c)^2 \\ 2b^2&=4c^2 \\ b^2&=2c^2\end{aligned}

Ugyanilyen megfontolásból most a baloldalon szereplő b^2-ről, és emiatt természetesen b-ről mondható el, hogy páros, azaz létezik olyan d egész szám, hogy b=2d. Ez azt jelenti, hogy a kiindulási feltétel szerinti \frac{a}{b} törtet egyszerűsíteni lehet 2-vel, hiszen:

\sqrt{2} = \frac{a}{b} = \frac{2c}{2d} = \frac{c}{d}

Vegyük észre azonban, hogy a fenti gondolatmenet megismételhető erre az egyszerűsítés után kapott \frac{c}{d} törtre is. Azaz találhatók olyan e és f egész számok, amelyekre c=2e és d=2f. Vagyis a \frac{c}{d} tört tovább egyszerűsíthető 2-vel:

\sqrt{2} = \frac{c}{d} = \frac{2e}{2f} = \frac{e}{f}

Ám most ezt az \frac{e}{f} törtet is tudjuk tovább egyszerűsíteni, és ez a folyamat nem szakad meg soha. Vagyis a kezdeti feltételezésünkből, miszerint a \sqrt{2} racionális, azaz felírható tört alakban, azt a következtetést vontuk le, hogy ekkor ezt a törtet a végtelenségig lehetne egyszerűsíteni 2-vel. Ez nyilvánvaló ellentmondás, ilyen nem lehetséges, egyetlen törtet sem lehet a végtelenségig egyszerűsíteni. Ebből az ellentmondásból következik, hogy a kezdeti feltételezésünk hamis volt, azaz a \sqrt{2} szükségképpen irracionális.

Az Olvasó is láthatja, hogy az iménti gondolatmenet teljességgel megcáfolhatatlan, és biztosak lehetünk benne, hogy soha senki nem fog találni két olyan egész számot, amelyek hányadosa előállítaná a \sqrt{2}-t, hiszen annak katasztrófális következményei lennének. Ráadásul ez a mennyiség az egységnyi oldalú négyzet átlójának a hossza, azaz nem valami elvont dologról van szó. Érthetetlen hát, hogy a logikus gondolkodás megalapozója hogyan söpörhette le magát a logikus gondolkodást az asztalról oly kegyetlenül pusztán azért, hogy ne kelljen beismernie: tévedett…