A végtelenen túl

Minden bizonnyal kevés olyan dolog van a matematikában, amely annyira megmozgatná az átlagemberek fantáziáját, mint a végtelen fogalma. Ehhez a szóhoz több egymástól elkülöníthető, a teológiában, a filozófiában és a matematikában előforduló jelentés is társítható. Itt csak az utóbbival fogunk foglalkozni, azaz szigorúan matematikai szempontból vizsgáljuk meg a végtelen fogalmát. 1878-ban egy Georg Cantor nevű német matematikus fölvetette annak gondolatát, hogy esetleg végtelen mennyiségek között is meglehetősen természetes módon értelmezni lehet a véges mennyiségek esetén már megszokott „kisebb”, „nagyobb” és „egyenlő” fogalmát. Ebben a cikkben vázlatosan végigvesszük azokat a gondolatokat, amelyek a 19. század végén Cantort elvezették ehhez a forradalmi felfedezéshez…

Georg Ferdinand Ludwig Philipp Cantor 1845. március 3-án született Szentpétervárott, Oroszországban. Apja, Georg Waldemar Cantor, sikeres nagybani kereskedő, majd a szentpétervári tőzsde brókere, rendkívül kulturált és a művészetek iránt fogékony ember volt. Anyja, Maria Anna Böhm osztrák zenész. Apja protestáns, anyja katolikus volt. Maga Cantor is mélyen vallásos hitben élt. Mivel apja egészségének nem tettek jót a hideg orosz telek, ezért a család 1856-ban Németországba költözött. Cantor a gimnáziumot Wiesbadenben kezdte, de később áttelepültek Frankfurtba, így tanulmányait a darmstadt-i gimnáziumban folytatta bentlakásos tanulóként. 1862-től Zürichben végezte felsőfokú tanulmányait, majd apja 1863-ban bekövetkezett halála után a Berlini Egyetem hallgatója lett. Itt 1867-ben doktorált a számelmélet témakörében, tanította őt többek között Weierstrass, Kummer és Kronecker is.

Cantor egyik legnagyobb érdeme az úgynevezett halmazelmélet megalkotása volt, amellyel az 1870-es években kezdett el foglalkozni. Ezzel gyökeresen megváltoztatta a matematika egész arculatát, hiszen segítségével gyakorlatilag a teljes matematika megalapozható. A halmazelméletről ebben a cikkben volt szó bővebben egy „gyorstalpaló” keretében. A jelen cikk megértéséhez szükséges alapfogalmakat vázlatosan itt is ismertetni fogjuk a megfelelő helyeken, ám mindenképpen javasoljuk az Olvasónak, hogy tekintse át a hivatkozott cikk megfelelő részeit.

A következő szakaszban egy érdekes gondolatkísérletre invitáljuk az Olvasót. Ennek keretében megpróbáljuk érzékeltetni azokat a furcsaságokat, amelyek látszólag ellentmondanak a józan észnek, de valójában teljesen normálisnak tekinthetők akkor, amikor végtelen mennyiségeket kezdünk vizsgálni.

A Hilbert-hotel

Ezt a gondolatkísérletet David Hilbert német matematikus vetette fel egy 1924-es tanulmányában, és George Gamow 1947-ben megjelent „One, Two, Three… Infinity” című könyvéből vált ismertté a szélesebb rétegek számára is.

A Hilbert-hotel egy olyan különleges képzeletbeli szálloda, amelyben végtelen sok szoba van. Az egyértelműség kedvéért ezalatt azt értjük, hogy a szobaszámok 1-től kezdve folyamatosan növekednek, és nincs olyan szoba, amelynél ne lenne nagyobb sorszámú szoba. A szállodának továbbá van egy olyan hangosbemondórendszere is, amelyen keresztül a portás egyszerre tud üzenni a szobákban lévő vendégeknek. Tegyük fel, hogy teltház van, azaz minden szoba foglalt.

Az első probléma: Képzeljük el, hogy egy új vendég érkezik. Vajon a portás kénytelen őt elküldeni, vagy valamilyen módon mégis el tudja helyezni annak ellenére, hogy a hotelben már nincs szabad szoba? Nos, a meglepő válasz az, hogy az új vendég minden további nélkül elhelyezhető. Ehhez a portásnak mindössze annyit kell tennie, hogy a hangosbemondón keresztül minden vendéget megkér, hogy költözzön át az 1-gyel nagyobb sorszámú szobába. Tehát az 1-es szoba lakói átköltöznek a 2-es szobába, amelynek a lakói átköltöznek a 3-as szobába, és így tovább. Ezt a költözési folyamatot mutatja az alábbi ábra:

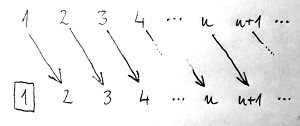
A költözködés után felszabadul az 1-es sorszámú szoba (az ábrán bekeretezve), ahová a portás minden gond nélkül beköltöztetheti az új vendéget.

A második probléma: Most képzeljük el azt, hogy 1 helyett végtelen sok új vendég érkezik. Vajon mit tud tenni a portás ebben a helyzetben? A megoldás egyszerű: megkér minden vendéget, hogy költözzön át abba a szobába, amelynek sorszáma az aktuális szobaszám kétszerese. Így tehát az 1-egy szoba lakói a 2-es szobába költöznek, a 2-es szoba lakói a 4-esbe, a 3-as szoba lakói a 6-osba, és így tovább. Ezt az alábbi ábrán láthatjuk:

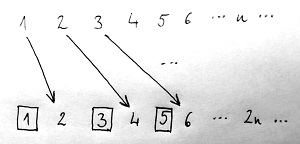
Ezáltal minden páratlan sorszámú szoba felszabadul (az ábrán bekeretezve), amelyekbe a portás beköltöztetheti a végtelen sok új vendéget.

A harmadik probléma: Vajon mi van akkor, ha még ennél is rosszabb a helyzet, és például hirtelen megérkezik végtelen sok autóbusz, amelyek mindegyikében végtelen sok vendég utazik? Azaz ezúttal végtelen sokszor végtelen sok vendéget kell elhelyezni az amúgy teltházas szállodában. Sorszámozzuk be a buszokat, és azokon belül az egyes utasokat. Ekkor az alábbi, mindkét dimenzió mentén végtelen táblázatban az összes utas szerepel:

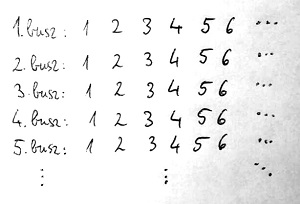
Meglepő módon ez a kétdimenziós probléma könnyedén visszavezethető az előző egydimenziós problémára, ahol csak egyetlen végtelen vendégsorozatunk volt. Ehhez mindössze annyit kell tenni, hogy a fenti táblázatban szereplő utasokat olymódon állítjuk sorba, ahogyan az alábbi vonal mentén követik egymást:

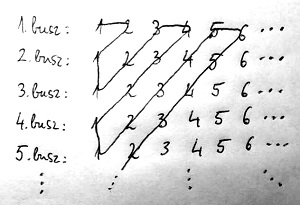
Ezt a sorbaállítási eljárást átlós módszernek nevezzük, amely Cantor nevéhez fűződik. Az ábráról is könnyen leolvasható, hogy így minden utas pontosan egyszer fog szerepelni ebben az új és immár egyetlen végtelen sorozatban. Őket pedig a portás természetesen minden gond nélkül el tudja helyezni a szállodában az előző probléma megoldásában leírtak alapján.

Hasonló a megoldás abban az esetben is, ha a „táblázat” dimenzióinak száma kettőnél nagyobb, azaz kettőnél többszintű végtelennel van dolgunk. Tegyük fel például, hogy a hotel egy óceán mellett van, és végtelen számú komp érkezik, amelyek mindegyike végtelen számú buszt szállít, és mindegyik buszon végtelen számú utas utazik. Ezt a háromdimenziós problémát az előzőleg már ismertetett kétdimenziós problémára vezethetjük vissza. Ehhez annyit kell tennünk, hogy átmenetileg csak az első két dimenziót vesszük figyelembe, azaz elsőként a kompokkal érkező buszokat állítjuk sorba a fent ismertetett átlós módszer segítségével, majd az eljárást megismételjük a buszokon helyetfoglaló utasok szintjén is.

A negyedik probléma: A portás ebben az esetben egy rendkívül kínos helyzetbe kerül, ugyanis napközben kap egy telefonhívást, miszerint az éjszaka folyamán új vendégek fognak érkezni, akik viszont mind egymás melletti szobákban szeretnének aludni. Természetesen a szálloda vendégeit éjszaka már nem lehet zavarni, így az egész költöztetést még este le kéne bonyolítani. Ugyanakkor a telefonáló azt nem tudja előre megmondani, hogy összesen hány vendég fog éjszaka érkezni, pusztán annyi tud, hogy ezek száma véges lesz. Vagyis most úgy kell a vendégeket átköltöztetni, hogy a költöztetés után legyen tetszőlegesen hosszú, egymással szomszédos üres szobákból álló szekció.

Szerencsére a portás – feltéve, hogy elég okos – még ebből a kínos szituációból is ki tudja magát vágni. Ezúttal arra kell megkérnie a vendégeket, hogy mindenki nézze meg, milyen sorszámú szobában lakik, ezt emelje négyzetre, és költözzön át az így kapott számú szobába. Tehát az 1-es szoba lakói helyben maradnak, a 2-es szoba lakói a 4-esbe költöznek, a 3-as szoba lakói a 9-esbe, a 4-es szoba lakói a 16-osba, és így tovább. A költözés után tehát pontosan azok a szobák lesznek foglaltak, amelyeknek a sorszáma négyzetszám. Mivel a négyzetszámok között egyre növekvő hézagok vannak, ezért tetszőlegesen sok, de véges számú új vendég számára lehet találni olyan egymás melletti szobákat, amelyek mindegyike szabad. Így az éjszaka folyamán megérkező vendégek minden probléma nélkül elhelyezhetők a kívánalmuknak megfelelően egymás melletti szobákba.

Ráadásul még egy csomó szabad szoba is marad, így ha esetleg végtelen sokszor érkezik további véges számú vendég az éjszaka közepén, a portás ugyanúgy el tudja őket helyezni további költöztetés nélkül.

A végtelen számosság fogalma

A józan ész azt diktálná, hogy egy teltházas hotelben egyetlen új vendéget sem lehet elhelyezni, nemhogy végtelenszer végtelen sokat. A fenti példák tehát látszólag ellentmondanak a józan észnek. Ez azonban csupán látszólagos ellentmondás, amit az okoz, hogy a rész és egész ismert logikája végtelen mennyiségek esetén összeomlik. Egy végtelen sok elemből álló sokaság vagy halmaz furcsamód elveszítheti néhány – sőt akár végtelen sok – tagját anélkül, hogy kisebbé válnék. Mint látni fogjuk, a halmazelmélet pontosan így definiálja a végtelen számosság fogalmát. De vajon mit jelent az a szó, hogy „számosság”, amelyet maga Cantor vezetett be?

Egy halmaz számossága, vagy tudományosabb nevén kardinalitása tulajdonképpen egy olyan „mennyiségi jellemző”, amely azt adja meg, hogy az adott halmaz „hány” elemet tartalmaz. Egy A halmaz számosságát így jelöljük: |A|. A számosság felfogható a szokásos számfogalom egyfajta általánosításaként, amelynek segítségével végtelen halmazokat is össze lehet egymással hasonlítani a méretük szerint. Ez első olvasatra értelmetlennek tűnik, hiszen azt gondolhatnánk, hogy valami vagy végtelen, vagy véges, s míg előbbi minden véges méretnél nagyobb, addig utóbbira ott vannak a pozitív egész számok. Cantor azonban észrevette, hogy a helyzet ennél jóval bonyolultabb: nem egyfajta végtelen kardinalitás létezik, és ezek között értelmezni lehet a „kisebb”, a „nagyobb” és az „egyenlő” fogalmát ugyanúgy, mint a véges számosságok esetén.

Először vizsgáljuk meg, hogy pontosan mit is értünk azalatt, hogy két halmaz egyenlő számosságú. Elsőként talán az juthat eszünkbe, hogy külön-külön megszámláljuk az elemeiket, és ha az így kapott számok egyeznek, akkor azt mondjuk, hogy a két halmaz azonos számosságú. Sajnos ez a módszer ebben a formában csak véges halmazok esetén fog működni, viszont a dolgot más megvilágításba helyezve könnyen átvihetjük azt akár végtelen számosságú halmazokra is. Mindössze azt kell végiggondolnunk, hogy a számlálás során tulajdonképpen mindkét halmaz elemeihez hozzárendeltünk egy-egy pozitív egész számot, méghozzá olymódon, hogy bármely pozitív egész számot a két halmaznak legfeljebb egy-egy eleméhez rendeltük hozzá. Ezt mutatja az alábbi ábra két véges halmazra:

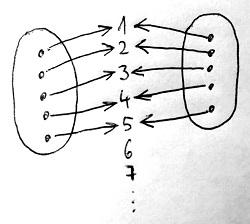
Itt tulajdonképpen arról van szó, hogy a baloldali halmaz elemeit kölcsönösen egyértelműen összepárosítottuk a jobboldali halmaz elemeivel. Azaz minden baloldali elemhez pontosan egy pár tartozik a jobboldalon, és fordítva, minden jobboldali elem pontosan egy baloldali elem párja. Vegyük észre, hogy ebben a párosítási folyamatban a középen lévő egész számoknak semmiféle szerepük nincs azonkívül, hogy egyfajta „címkeként” használtuk őket. Egy-egy elemet azáltal párosítottuk egymáshoz, hogy azonos címkét rendeltünk hozzájuk, de címkézés helyett megtehettük volna, hogy egyszerűen csak összekötjük őket egy-egy nyíllal. A kölcsönösen egyértelmű hozzárendeléseket bijekcióknak vagy bijektív leképezéseknek is nevezzük. A fenti címkézésnek megfelelő bijekció látható az alábbi ábrán:

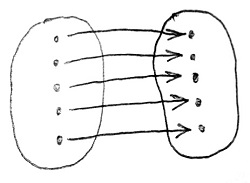
Így már végtelen halmazok esetén is definiálhatjuk az „egyező számosság” fogalmát: egy A és egy B halmazra akkor mondjuk, hogy számosságuk megegyezik, ha létezik bijekció az elemeik között. Ezt így jelöljük:

|A|=|B|

Ezek után a „végtelen számosság” Cantor szerinti definíciója így hangzik: egy halmazt akkor nevezünk végtelen számosságúnak, ha létezik bijektív leképezés saját maga és egy saját magánál szűkebb (vagy tudományosabb nevén valódi) részhalmaza között. Az előző szakaszban szereplő Hilbert-hotel esetén a portás a költöztetéssel épp ilyen bijekciókat jelölt ki az összes szobák halmaza és annak különböző valódi részhalmazai között. A végtelen számosság miatt képes volt tetszőlegesen csökkenteni a foglalt szobák halmazát anélkül, hogy ennek a halmaznak a számossága csökkent volna, és így nem kellett attól tartania, hogy bármely vendég szoba nélkül marad a költöztetés után. Ezt egy véges szobahalmazzal nyilván nem tehette volna meg.

Számosságok összehasonlítása

Cantor azonban továbbment a fenti gondolatmenetben, és a következő logikus kérdést kezdte el vizsgálni: vajon minden végtelen számosság megegyezik, vagy vannak olyanok, amelyek „nagyobbak” a többinél? Természetesen ehhez először az „egyenlőséghez” hasonlóan tisztázni kell a „nagyobb” és a „kisebb” fogalmát a számosságok tekintetében. Az előző szakaszban azt mondtuk, hogy két halmaz számossága akkor egyenlő, ha létezik bijektív leképezés közöttük. Ez ugye egy olyan leképezés létezését jelentette, amely esetén a jobboldali halmaz minden eleme pontosan egy baloldali elemhez van hozzárendelve.

Most gyengítsük ezt a feltételt. Továbbra is megköveteljük, hogy ha valamelyik jobboldali elem hozzá van rendelve baloldali elemhez, akkor egyértelmű legyen, hogy melyikhez. Most azonban megengedünk olyan elemeket is a jobboldalon, amelyek egyáltalán nincsenek hozzárendelve egyetlen baloldali elemhez sem. Azaz most a jobboldali elemek mindegyike „pontosan egy” helyett csupán legfeljebb egy baloldali elemhez kell legyen hozzárendelve. Az ilyen hozzárendeléseket injektív leképezéseknek nevezzük. Egy ilyen leképezést mutat az alábbi ábra:

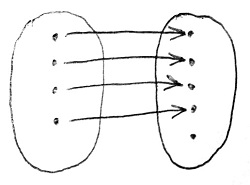
Ezek után már definiálhatjuk a számosságok közötti relációkat. Tegyük fel, hogy adott egy A és egy B halmaz, és létezik egy A-ból B-be mutató injektív leképezés. Ekkor azt mondjuk, hogy az A halmaz számossága legfeljebb akkora, mint a B halmaz számossága, vagy másként fogalmazva a B halmaz számossága legalább akkora, mint az A halmaz számossága. Ezt így jelöljük:

|A|\leq |B|

Az nyilvánvaló, hogy véges halmazok esetén ha |A|\leq |B| és |B|\leq |A| egyszerre teljesül, akkor |A|=|B| is teljesül. Ilyenkor ugyanis az előző szakaszban leírt módon 1-től kezdve növekvő pozitív egész számokkal címkézhetjük a két halmaz elemeit egyrészt az A-ból B-be mutató injektív leképezés mentén (amely ugye |A|\leq |B| miatt létezik), másrészt pedig a B-ből A-ba mutató injektív leképezés mentén (amely pedig |B|\leq |A| miatt létezik). Ez a címkézés lényegében nem más, mint a két halmaz elemeinek megszámlálása, melynek során azt kapjuk, hogy A legfeljebb és legalább annyi elemet tartalmaz, mint B. Ez csak úgy lehet, ha a két elemszám megegyezik, ami viszont azt jelenti, hogy mindkét injektív leképezés egyben bijektív is.

Ami azonban egyáltalán nem nyilvánvaló, hogy az iménti összefüggés végtelen számosságú halmazok esetén is érvényes. Ez Schröder-Bernstein tétel néven ismeretes, és csak a 19. század végén sikerült igazolni. A tétel tehát azt állítja, hogy tetszőleges – tehát nem feltétlenül csak véges – A és B halmazok esetén igaz, hogy amennyiben létezik injektív leképezés A-ból B-be, és létezik injektív leképezés B-ből A-ba, akkor bijektív leképezés is létezik a két halmaz között. A bizonyítás meglehetősen technikai jellegű, ezért itt nem részletezzük.

Az eddig definiált „egyenlő”, „legalább” és „legfeljebb” fogalmakból már könnyen adódik a „kisebb” és a „nagyobb” definíciója is. Ha |A|\leq |B|, de |A|\neq |B|, akkor azt mondjuk, hogy A számossága határozottan kisebb (vagy egyszerűen csak kisebb), mint B számossága, vagy másként fogalmazva a B halmaz számossága határozottan nagyobb (vagy egyszerűen csak nagyobb), mint az A halmaz számossága.

A megszámlálhatóan végtelen számosság

Ebben a szakaszban visszatérünk a Cantor által felvetett kérdésre: vajon tényleg létezik többféle végtelen számosság, vagy valójában bármely két végtelen halmaz számossága megegyezik? Ennek megválaszolásához most hasonlítsuk össze a különböző számhalmazok számosságát.

Az nyilvánvaló, hogy a nemnegatív egész (vagy más néven természetes) számok halmaza végtelen számosságú. Bővítsük ki ezt a számhalmazt a negatív egészekkel is, azaz tekintsük az összes egész számok halmazát. Így nyilván egy bővebb számhalmazt kapunk, de vajon ennek a számossága nagyobb-e a természetes számok számosságánál? A válasz nemleges, ugyanis tekintsük a két számhalmaz közötti alábbi leképezést:

\begin{aligned}0&\to 0 \\ 1&\to 1\\ 2&\to -1 \\ 3&\to 2 \\ 4&\to -2 \\ 5&\to 3\\ 6&\to -3 \\ &\vdots \end{aligned}

A leképezés jobboldalán nyilván minden egész szám pontosan egyszer szerepel, vagyis ez egy bijekció a két számhalmaz között, és így a számosságok megegyeznek.

Most bővítsük tovább a számhalmazunkat, és vizsgáljuk a két egész szám hányadosaként felírható úgynevezett tört-, vagy hivatalosabb nevükön racionális számok halmazát. Logikus azt gondolni, hogy ennek számossága már nagyobb kell legyen a természetes számokénál. Ezek elhelyezkedése ugyanis végtelenül „sűrű”, ami azt jelenti, hogy bármely két racionális szám között – legyenek azok akármennyire is közel egymáshoz a számegyenesen – további végtelen sok racionális szám van. Azonban jobban megvizsgálva a dolgot most is csalódnunk kell: a racionális számok pontosan ugyanannyian vannak, mint a természetes számok. Ezt a Hilbert-hotelnél már megismert úgynevezett átlós módszerrel láthatjuk be.

Mivel minden racionális szám felírható két egész szám hányadosaként, ezért mind a negatív, mind pedig a pozitív racionális számok egy-egy kétdimenziós táblázatba rendezhetők és egy vonal mentén sorbaállíthatók. Az alábbi ábra a pozitív racionálisok ilyen módon történő sorbaállítását mutatja:

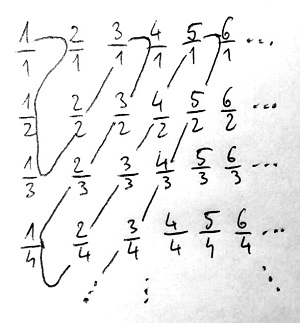
A vonal mentén haladva minden meglátogatott racionális számot címkézzünk fel egy-egy pozitív egész számmal. Ugyanígy a negatív racionálisokat tartalmazó táblázat mezőit pedig a negatív egészekkel címkézzük. Természetesen ha egy mezőhöz érve azt tapasztaljuk, hogy az ottlévő racionálisnak egy egyszerűbb alakját már meglátogattuk, akkor azt a mezőt hagyjuk ki a címkézésből. Például a \frac{2}{4}-hez érve ez a helyzet, hiszen ez a szám ugyanannyi, mint a korábban már felcímkézett \frac{1}{2}. Végül a 0 racionális számot címkézzük önmagával, mint egész számmal. Ez nyilvánvalóan egy bijekció az egészek és a racionálisok között, vagyis e két számhalmaz számossága is megegyezik egymással, és így persze a természetes számokéval is.

Azokat a halmazokat, amelyeknek számossága megegyezik a természetes számokéval, megszámlálhatóan végtelen halmazoknak nevezzük. Ez az elnevezés azt fejezi ki, hogy az adott halmaz elemeit „meg tudnánk számlálni” csak a természetes számokat használva, feltéve persze, hogy végtelen sok időnk van. Azaz az összes elemhez egy-egy sorszám rendelhető, méghozzá olymódon, hogy minden természetes szám pontosan egyszer szerepelhet sorszámként.

A kontinuum számosság

Eddig a pontig úgy tűnik tehát, hogy a megszámlálhatóan végtelennél nagyobb számosságú számhalmaz talán nem is létezik, és a „kisebb-nagyobb” fogalmának nincs is értelme végtelen kardinalitások esetén. Már az ókorban kiderült azonban, hogy furcsamód a számegyenesen a racionálisok mellett – noha végtelenül sűrűn helyezkednek el – további végtelen sok hely maradt az olyan számoknak, amelyek nem írhatók fel tört alakban. Ezekkel kibővítve a racionálisokat az úgynevezett valós számok halmazához jutunk. Itt már a számegyenes minden pontja megfeleltethető egy-egy valós számnak, vagyis a valós számok „folytonosan” töltik fel a számegyenest, azon nincs több hézag.

Vizsgáljuk meg most ennek a számhalmaznak azt a részét – az úgynevezett egységszakaszt –, amely a 0 és 1 közé esik a számegyenesen. Vajon az itt lévő valós számok párbaállíthatók-e a természetes számokkal? Cantor egy zseniális érveléssel megmutatta, hogy nemleges a válasz, vagyis az egységszakasz pontjainak számossága – és így persze a teljes valós számhalmaz számossága is – határozottan nagyobb, mint a természetes számoké.

Tegyük fel ugyanis, hogy nem ez a helyzet, azaz létezik bijekció a természetes számok és az egységszakasz pontjai által reprezentált valós számok között. Írjuk fel az összes hozzárendelést, amelyet ez a feltételezett bijekció megvalósít (itt a jobboldalakon szereplő valós számok tizedestört alakban láthatók):

\begin{aligned}0&\to 0.18276192\ldots \\ 1&\to 0.78298882\ldots \\ 2&\to 0.66176612\ldots \\ 3&\to 0.12345161\ldots \\ &\vdots \end{aligned}

Mivel a feltevésünk szerinti leképezés egy bijekció, ezért ebben a listában az egységszakaszon lévő összes valós számnak szerepelnie kéne. Mi azonban mégis mutatni fogunk egy olyan valós számot, amely bizony tuti nincs rajta a listán. Ennek a bizonyos valós számnak a tizedesjegyeit a következő algoritmus szerint írjuk fel:

• Ha a lista 1. pozíciójában lévő szám 1. tizedesjegye 1, akkor az új számunk 1. tizedesjegye legyen 0, egyébként 1.
• Ha a lista 2. pozíciójában lévő szám 2. tizedesjegye 1, akkor az új számunk 2. tizedesjegye legyen 0, egyébként 1.
• Ha a lista 3. pozíciójában lévő szám 3. tizedesjegye 1, akkor az új számunk 3. tizedesjegye legyen 0, egyébként 1.
• …
• Ha a lista n-edik pozíciójában lévő szám n-edik tizedesjegye 1, akkor az új számunk n-edik tizedesjegye legyen 0, egyébként 1.
• …

Ezt az algoritmust követve az alábbi valós számot kapjuk:

0.0101\ldots

Az 1. tizedesjegy azért lett 0, mert a fenti lista 1. pozíciójában lévő szám 1. tizedesjegye 1 volt, így az algoritmus szerint ide 0-t kellett írjunk. A 2. tizedesjegy azért lett 1, mert a lista 2. pozíciójában lévő szám 2. tizedesjegye 1-től különböző volt (konkrétan 8), tehát az algoritmus szerint ide 1-et kellett írjunk. A 3. tizedesjegy azért lett megint 0, mert a lista 3. pozíciójában lévő szám 3. tizedesjegye 1 volt. És így tovább folytatjuk az algoritmust a végtelenségig.

Ebből már könnyen látható, hogy ez a valós szám nem szerepel a listán, hiszen bármilyen n sorszámot tekintsünk is, a lista n-edik pozíciójában lévő számtól biztosan különbözni fog, méghozzá legalább az n-edik tizedesjegyben. Az eredeti feltételezésünk egy bijekció létezéséről tehát szükségképpen hibás volt, azaz az egységszakasz pontjainak halmaza nem megszámlálható, és így határozottan nagyobb, mint a természetes számok számossága.

Innen már csak egy lépés annak igazolása, hogy az egységszakasz és a teljes valós számhalmaz számossága között viszont egyenlőség van. Ehhez egy olyan bijektív leképezést kell mutatni, amely az egységszakaszt a teljes valós számhalmazra képezi le. Egy ilyen leképezést könnyen elő lehet állítani például a tangens függvény megfelelő torzításával, amelynek a grafikonja az alábbi ábrán látható (a pontos képlet kidolgozását az Olvasóra bízzuk):

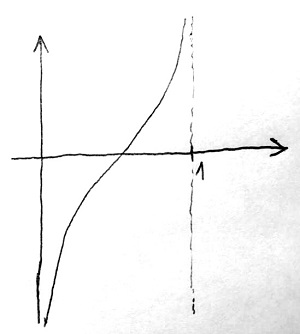
Ez a függvény szigorúan monoton növekszik, és így valóban egy bijektív leképezést valósít meg a vízszintes tengelyen lévő egységszakasz és a teljes függőleges tengely pontjai – azaz a valós számhalmaz – között. Emiatt a teljes valós számhalmaz és az egységszakasz számossága megegyezik. Azokat a halmazokat, amelyek számossága megegyezik a valós számokéval, kontinuum számosságú halmazoknak nevezzük.

„Látom, de nem hiszem”

Eddig tehát elmondhatjuk, hogy legalább kétféle végtelen kardinalitás létezik: a megszámlálhatóan végtelen és a kontinuum számosság, és – mint láttuk – az utóbbi határozottan nagyobb, mint az első. Cantor kíváncsi volt, hogy vajon itt vége is van-e a történetnek, vagy létezik még a kontinuum számosságnál is magasabbrendű végtelen? Ezek után kutatva első ötletként magasabb dimenziókat kezdett el vizsgálni. Bizonyos volt benne, hogy például a kétdimenziós síkban vagy a három- és magasabb dimenziós térben több pontnak kell lennie, mint az egydimenziós számegyenesen.

Azt gondolta – amire egy Dedekindnek írott levelében utalt is –, hogy erre a kérdésre annyira nyilvánvalóan nem a válasz, hogy ezt szinte bizonyítani is szükségtelen. Végül 1877-ben saját megdöbbenésére igazolta, hogy tetszőleges n esetén a teljes n-dimenziós térnek pontosan ugyanannyi pontja van, mint az egydimenziós számegyenesnek – vagy akár az egységszakasznak, ahogyan azt az előző szakasz végén láttuk. Az átlós módszer továbbfejlesztésével ugyanis sikerült egy bijektív leképezést adnia e két halmaz között. Ezen ő maga is annyira meglepődött, hogy egy ugyancsak Dedekindnek írott levelében így fogalmazott erről:

Látom, de nem hiszem.

Felfedezésének fontos következménye lett a dimenziófogalomra: jelezte, hogy a különböző dimenziós terek között nem a nagyság tesz különbséget. Úgy tűnt tehát, hogy a kontinuumnál magasabbrendű végtelenek utáni kutatás elakadt. De több, mint egy évtizeddel – és egy idegösszeomlás miatti szanatóriumi kezeléssel – később Cantor újabb áttörést ért el: rájött, hogy adott dolgok halmazaiból mindig több van, mint magukból a dolgokból.

Ez véges halmazok esetén eléggé nyilvánvaló. Ha van például egy olyan H halmazunk, amely az a, b és c betűkből áll, akkor ezekből a betűkből összesen nyolc különböző halmazt képezhetünk. Ezek a következők:

\begin{aligned}&\{\} \\ &\{a\} \\ &\{b\} \\ &\{c\} \\ &\{a;b\} \\ &\{a;c\} \\ &\{b;c\} \\&\{a;b;c\} \end{aligned}

Ezek tulajdonképpen az eredeti H halmaz összes lehetséges részhalmazai, beleértve természetesen az egyetlen elemet sem tartalmazó üreshalmazt, és magát az összes elemet tartalmazó teljes H halmazt is. Mivel a halmazelméletben semmi nem tiltja olyan halmazok konstruálását, amelyeknek elemei maguk is halmazok, ezért minden további nélkül beszélhetünk arról a halmazról is, amelynek ELEMEI nem mások, mint a H halmaz fent felsorolt részhalmazai. Ezt a halmazt a H halmaz hatványhalmazának nevezzük, és \mathcal{P}(H)-val jelöljük. Amennyiben az Olvasó nehezen emésztette meg a halmazokból álló halmazok gondolatát, javasoljuk, hogy olvassa át az itt leírtakat, ahol ezt részletesebben is kifejtettük.

Egyszerű kombinatorikai gondolatmenettel könnyen látható, hogy véges halmazok esetén a hatványhalmaz mindig több elemet fog tartalmazni, mint az eredeti halmaz. Tegyük fel ugyanis, hogy van egy n elemű H halmazunk, és szeretnénk ennek elemeiből képezni az összes lehetséges részhalmazt. Egy konkrét részhalmaz képzésekor tulajdonképpen H elemeiről egyenként el kell döntenünk, hogy beletegyük-e az adott részhalmazba, vagy ne. Minthogy összesen n elemünk van, és minden elemről kétféle döntést hozhatunk, ezért összesen 2^n különböző részhalmazt képezhetünk. Ez lesz tehát a \mathcal{P}(H) hatványhalmaz elemszáma, ami valóban minden esetben határozottan nagyobb, mint n.

Ami viszont nyilvánvaló véges halmazokra, az egyáltalán nem biztos, hogy teljesül végtelen halmazokra is – gondoljunk csak a Hilbert-hotel furcsaságaira. Cantor azonban egy újabb zseniális érveléssel megmutatta, hogy ez a szabály átvihető a végtelen számosságokra is.

A Cantor-tétel

Az iménti kombinatorikai érvelésünk itt nyilván csődöt mond, hiszen ha n tart a végtelenbe, akkor 2^n is tartani fog a végtelenbe, és semmi nem garantálja, hogy ez utóbbi végtelen magasabbrendű legyen az előbbinél. Ehelyett Cantornak azt kellett megmutatnia, hogy amennyiben egy végtelen halmaz és annak – szintén végtelen – hatványhalmaza között létezne bijektív leképezés, az végzetes logikai ellentmondáshoz vezetne.

Hogy a dolog egy fokkal kevésbé legyen absztrakt, tételezzük fel, hogy egy olyan világban élünk, ahol az emberek száma végtelen. Az emberek ugye szeretnek klubokba szerveződni. Mivel nem szeretnénk korlátok közé szorítani az ilyen jellegű szerveződést, ezért tekintsük most az összes lehetséges klubot, amely ebben a világban létezhet. E klubok közül a legkevésbé kirekesztő az Egyetemes Klub lesz, amelynek az összes ember tagja, míg a legexkluzívabb az úgynevezett Nullklub, amelynek egyetlen tagja sincs. A többi klub végtelen serege e két szélsőség közé esik, néhányuk sok – akár végtelen sok – taggal, mások kevesebbel. A kérdés, hogy vajon van-e arra mód, hogy az embereket és a klubokat bijektív módon összepárosítsuk egymással, és így kimutathassuk, hogy a két végtelen halmaz ugyanolyan méretű? Olyan párosítást keresünk tehát, amelyben minden emberhez pontosan egy klub van párosítva, és minden klub pontosan egy embernek a párja.

Figyelem! A most következő gondolatmenet a nyugalom megzavarására alkalmas!

Tételezzük fel, hogy ilyen párosítás létezik a két halmaz között. Az emberek némelyike olyan klubhoz lesz párosítva, amelynek egyébként tagja is. Ilyen például az a személy, amelynek a párja az Egyetemes Klub. Más emberek pedig olyan klubok párjai lesznek, amelyeknek nem tagjai. Ilyen például az a személy, amelynek a párja épp a Nullklub. Ez utóbbi emberek szintén egy klubot alkotnak, hiszen azt mondtuk, hogy emberek tetszőleges csoportját egy-egy klubnak tekintjük.

Nevezzük ezt a klubot a Kirekesztettek Klubjának: ez tehát pontosan azokból az emberekből áll, amelyek nem tagjai a velük párbaállított klubnak. Az a személy például, amelyik a Nullklubbal van összepárosítva – amely természetesen őt is kizárja – legalább azzal vígasztalódhat, hogy a Kirekesztettek Klubjának tagja. Mármost ugye azt feltételeztük, hogy az emberek és klubok közötti párosítás bijektív, ezért kell lennie pontosan egy fickónak, aki épp a Kirekesztettek Klubjának a párja ebben a párosításban. Hívjuk őt Bob-nak. A dolog akkor válik érdekessé, ha feltesszük az alábbi nagyon egyszerű kérdést: vajon Bob tagja-e a Kirekesztettek Klubjának vagy sem?

Tételezzük fel, hogy igen. Ez ugye a Kirekesztettek Klubjának definíciója szerint azt jelenti, hogy őt ki kell zárni abból a klubból, amelynek ő a párja. De az ő párja épp a Kirekesztettek Klubja, így tehát biztos, hogy Bob nem tagja ennek a klubnak, ami ellentmondás. Ha viszont Bob nem tagja a Kirekesztettek Klubjának, akkor ismét a Kirekesztettek Klubjának definíciója miatt tagja kell legyen annak a klubnak, amellyel párt alkot, márpedig az ő párja épp a Kirekesztettek Klubja. Ez ismét ellentmondás.

Mivel a fenti kérdésre adott mindkét lehetséges válasz ellentmondásra vezetett, ezért a logikai érvelésünk zsákutcába jutott. Ez csak úgy lehetséges, hogy a kiindulási feltételezésünk volt hibás, miszerint az emberek és a klubok között létezik bijektív leképezés. Ennek az állításnak tehát szükségképpen hamisnak kell lennie, ami azt jelenti, hogy ilyen leképezés nem létezhet: a dolgokból alkotott halmazok végtelensége nagyobb, mint maguknak a dolgoknak a végtelensége.

Átfogalmazva ezt a halmazelmélet nyelvére igaz tehát az alábbi, Cantor-tételnek nevezett állítás: tetszőleges H halmaz esetén a \mathcal{P}(H) hatványhalmaz számossága határozottan nagyobb magának a H halmaznak a számosságánál. Azaz:

|H| \lt |\mathcal{P}(H)|

Ennek a tételnek az a szépsége, hogy újra meg újra alkalmazható. Legyen szó bármilyen végtelen halmazról, mindig előhozakodhatunk egy ennél nagyobbrendű végtelennel azáltal, hogy képezzük ennek a halmaznak a hatványhalmazát. Cantor úttörő munkájában azt is bizonyította, hogy a valós számok halmazának számossága – azaz a kontinuum számosság – épp megegyezik a természetes számok hatványhalmazának számosságával, tehát szépen beleillik ebbe a sorba.

Cantor a fenti érveléssel a különböző végtelenek véget nem érő tornyát építette fel, és ezzel az új elmélettel egyúttal alapot adott a matematikusoknak ahhoz, hogy megtalálják a tudományuk biztos alapokra történő helyezéséhez szükséges forrásokat. David Hilbert így nyilatkozott erről:

Senki sem űzhet ki minket abból a paradicsomból, amelyet Cantor teremtett nekünk.

A kontinuum-hipotézis

Az eddigi szakaszokban a különböző számosságokat vagy kardinalitásokat csak funkcionálisan vizsgáltuk meg, de nem azonosítottuk őket önálló matematikai objektumokként. Ezalatt azt értjük, hogy képesek vagyunk halmazokat összehasonlítani a számosságuk, mint az ő egyik fontos jellemzőjük szempontjából, de mi van akkor, ha ezekről a számosságokról önmagukban is szeretnénk állításokat kimondani mindenféle konkrét halmaz megnevezése nélkül?

Ezt a problémát úgy hidalhatjuk át, hogy a halmazok között bevezetünk egy „azonos számosságúnak lenni” elnevezésű relációt. Azt, hogy egy A és B halmaz számossága megegyezik, így jelöljük:

|A|=|B|

Könnyen látható, hogy ez egy olyan reláció, amelyre tetszőleges A, B és C halmazok esetén igaz az alábbi négy alapvető tulajdonság:

1. |A|=|A|, azaz tetszőleges halmaz számossága megegyezik önmaga számosságával (reflexivitás).
2. Ha |A|=|B|, akkor |B|=|A|, azaz a reláció mindkét irányban teljesül (szimmetria).
3. Ha |A|=|B| és |B|=|C|, akkor |A|=|C|, azaz a reláció láncszerűen öröklődik (tranzitivitás).

Az ilyen tulajdonságú relációkat ekvivalenciarelációknak nevezzük. Ezekről bővebben ebben a cikkben volt szó, és arra használhatjuk őket, hogy úgynevezett ekvivalencia-osztályokba soroljuk azokat az objektumokat (jelen esetben az összes lehetséges halmazt), amelyeken a reláció értelmezve van. Belátható, hogy a halmazok egy ilyen osztályozásának megvan az a tulajdonsága, hogy egyrészt semelyik halmaz nem kerülhet egynél több osztályba, másrészt minden halmaz belekerül valamelyik osztályba. Ez azért jó, mert így a számosságokat azonosíthatjuk ezekkel az osztályokkal, mint matematikai objektumokkal, és állításokat tudunk tenni velük kapcsolatban anélkül, hogy az adott számossággal azonosított osztályon belül bármely konkrét halmazt meg kéne neveznünk.

Már csak valamilyen szimbólumokat kellene találni e számosságok, mint osztályok jelölésére. A véges számosságokkal könnyű a dolgunk, hiszen azokat jelölhetjük a nekik megfelelő egész számokkal. Például az 5 szimbólum ebben a kontextusban azoknak a halmazoknak az osztályát, mint számosságot jelöli, amelyek pontosan 5 darab elemből állnak. Az előző szakaszban azonban láttuk, hogy a véges számosságokon kívül végtelen számosságok egész sorozata létezik, így ezeknek is jó lenne találni valamilyen szimbólumokat.

A véges és a végtelen számosságokat, mint matematikai objektumokat együttesen kardinális számoknak nevezzük, amely tehát a számfogalom egyfajta általánosítása. A végtelen számosságok jelölésére a héber ábécé első betűjét, az úgynevezett „alef” szimbólumot használjuk, amely jelölést maga Cantor vezette be. Ezek „nagyság szerint” az alábbi módon követik egymást:

\alef_0 \lt \alef_1 \lt \alef_2 \lt \ldots

A legkisebb végtelen kardinális szám az \alef_0, amely tehát a megszámlálhatóan végtelen számosságot jelöli. Az \alef_1 a legkisebb olyan számosságot jelöli, amely nagyobb, mint \alef_0. Ezt követi az \alef_2, majd az \alef_3, és így tovább. Ha egy halmaz számossága \alef_i valamilyen i indexszel, akkor a hatványhalmaz számosságát 2^{\alef_i} jelöli.

A kontinuum számosságot a gótikus \mathfrak{c} szimbólummal jelöljük. E jelölések fényében tehát a Cantor által bizonyított, az előző szakaszokban ismertetett állításokat így is megfogalmazhatjuk:

1. \alef_0 \lt \mathfrak{c}, azaz a kontinuum számosság határozottan nagyobb, mint a megszámlálhatóan végtelen számosság.
2. Minden i esetén \alef_i \lt 2^{\alef_i}, azaz bármely halmaz hatványhalmazának számossága határozottan nagyobb, mint az eredeti halmaz számossága.
3. 2^{\alef_0} = \mathfrak{c}, azaz bármely megszámlálhatóan végtelen halmaz hatványhalmazának számossága épp a kontinuum számossággal egyezik meg.

Az 1. állítás az i=0 behelyettesítéssel nyilván következik a 2. és 3. állításokból. A kardinális számok között ezenkívül értelmezhető az összeadás, a szorzás és a hatványozás művelete, sőt még a gyökvonás és a logaritmus is. Ennek részleteiről itt olvashatunk.

Ami számunkra most érdekes, az egy olyan kérdés, amelyet maga Cantor vetett fel még 1878-ban, de megválaszolni nem tudta. Cantor azt a kérdést feszegette, hogy vajon létezik-e olyan halmaz, amelynek a számossága nagyobb a megszámlálhatóan végtelen de kisebb a kontinuum számosságnál? Ő maga azt sejtette, hogy ilyen számosság nem létezik, azaz a kontinuum számosság a legkisebb olyan számosság, amely nagyobb \alef_0-nál. Ezt az állítást nevezzük kontinuum-hipotézisnek, amely a fenti jelölésekkel így fogalmazható meg:

2^{\alef_0}=\mathfrak{c}=\alef_1

Ez az állítás kiterjeszthető nagyobb kardinalitásokra is. Az így kapott általánosított kontinuum-hipotézis azt állítja, hogy egyáltalán nem létezik olyan számosság, amely egy halmaz és hatványhalmazának számossága közé esik. Azaz tetszőleges i index esetén igaz az alábbi:

2^{\alef_i}=\alef_{i+1}

A kérdés megválaszolására egészen 1963-ig várni kellett. A meglepő választ Paul Cohen amerikai matematikus adta meg, amiért 1966-ban Fields Érmet kapott (ez a Nobel-díjhoz hasonló jelentőségű elismerés a matematikusok körében).

A kontinuum-hipotézisre adott furcsa válasz a következő volt: a kérdéses állítás független a halmazelmélet alapját adó Zermelo-Fraenkel-féle axiómarendszertől.

Ennek megértéséhez persze nem árt, ha tisztában vagyunk azzal, hogy mik azok az axiómák és axiómarendszerek. A matematikai elméleteket úgy kell elképzelni, mint valamiféle hatalmas építményeket. Az elmélet által megfogalmazott matematikai állítások töltik be az építőkövek szerepét. Ezek ugyanúgy egymásra épülnek, mint a téglák a valódi épületekben: egy állítás bizonyításához azt kell megmutatni, hogy az adott állítás korábban már bizonyított állítások logikai következménye. De ezek a korábbi állítások szintén más állításokból eredeztethetők, és így tovább. Amennyiben elkezdjük visszafelé követni ezeket a logikai láncolatokat, előbb utóbb el kell érnünk olyan állításokhoz, ahonnan már nincs tovább. Ezeket az állításokat nevezzük axiómáknak, amelyek tehát az adott elmélet alapjait és játékszabályait jelölik ki. Az axiómarendszerekről ebben a cikkben olvashatunk bővebben.

Természetesen a halmazelmélet alapjait is néhány axióma alkotja, amelyeket igaznak fogadunk el, és ezekből kiindulva bizonyítunk más állításokat. A leggyakoribb axiómarendszer az úgynevezett Zermelo-Fraenkel-féle axiómarendszer, amely 9 axiómából áll. Megjegyzendő, hogy a halmazelméletnek számos variánsát dolgozták ki, azonban ezek gyakorlatilag egyenértékűek olyan értelemben, hogy ugyanazok az állítások lesznek bizonyíthatók ezekben az alternatív halmazelméletekben.

A kontinuum-hipotézis által megfogalmazott állítás függetlensége azt jelenti, hogy sem maga az állítás, sem pedig a tagadása nem bizonyítható a Zermelo-Fraenkel-féle axiómarendszerből kiindulva. Másként fogalmazva ha az állítást (vagy annak tagadását) egy új axiómaként hozzávennénk az axiómarendszerhez, akkor továbbra is egy ellentmondásmentes halmazelméletet kapnánk.

Feltéve persze, hogy maga a Zermelo-Fraenkel axiómarendszer ellentmondásmentes, amely nem mellesleg Gödel úgynevezett második nemteljességi tétele értelmében szintén nem bizonyítható magából az axiómarendszerből kiindulva. Ez azonban már a matematikai logika területe, amely túlnyúlik ennek a cikknek a keretein…