Kalandozások a logika határán

A logikával foglalkozó első dokumentumok egyike a Dissoi Logoi („ellentétes szavak”) néven ismert töredék, amelynek eredete a Kr.e. 5. és 4. század fordulójára keltezhető. A logika tudománya az ókori görög idők egyik legfontosabb tudományából, a szónoklattan vagy retorika tudományából ered. Az ókori görögök észrevettek olyan következtetési sémákat, amelyekbe bárhogy helyettesítve is szavakat az érvelés szinte mindenki számára meggyőző, mert ezek az igazságot megtartó összefüggések, azaz logikai összefüggések. Ezek az észrevételek a matematika számára alapvető jelentőségűek voltak, a matematikusok ugyanis évszázadok óta ismert dolgokból logikus érveléssel jutnak el ismeretlen dolgok felfedezéséhez. A 19. század vége felé azonban felmerült az igény a matematika alapjainak ellenőrzésére. A matematikusok biztosak akartak lenni abban, hogy minden addig felfedezett ismeret valóban logikai következménye-e ezeknek a legelső alapelveknek. De 1931-ben egy Kurt Gödel nevű 25 éves matematikus megjelentetett egy történelmi jelentőségű cikket, amely mindörökre véget vetett ezeknek a reményeknek…

A matematikai tudás logikus felépítését célző erőfeszítéseket ennek a korszaknak a legkiemelkedőbb matematikusa, David Hilbert irányította. Hilbert hitt abban, hogy a matematikában néhány egyszerű alapfeltevésből – az úgynevezett axiómákból – kiindulva mindent be lehet bizonyítani. Ez azzal kecsegtetett, hogy bebizonyosodik a különböző matematikai elméletek alapját adó axiómarendszerektől elvárt két legfontosabb tulajdonság: a teljesség és az ellentmondásmentesség. Egy axiómarendszer teljessége azt jelenti, hogy a logikai következtetés szabályait alkalmazva az axiómákból kiindulva minden matematikai állításról el lehet dönteni, hogy igaz-e vagy hamis. Az ellentmondásmentesség pedig azt követeli meg az adott axiómarendszertől, hogyha valamilyen módon belátjuk egy állítás igazát, akkor semmilyen úton-módon ne lehessen ugyanerről az állításról bebizonyítani, hogy hamis. Hilbert meg volt róla győződve, hogy csupán néhány axiómából kiindulva válaszolni lehet bármiféle elképzelhető matematikai kérdésre, és eközben nem kell ellentmondástól tartani.

1900. augusztus 8-án Hilbert történelmi jelentőségű előadást tartott Párizsban a Nemzetközi Matematikus Kongresszuson. Huszonhárom megoldatlan, általa elsőrendű fontosságúnak ítélt problémát sorolt fel, melyek legtöbbje a matematika logikai megalapozásával függött össze. Ezzel az volt a célja, hogy összpontosítsa a matematikusvilág figyelmét, és kutatási programot adjon. Hilbert fel akarta rázni a matematikusközösséget, hogy segítsenek valóra váltani elképzeléseit egy kétségektől és ellentmondásoktól mentes matematikai rendszerről. A következő két évtizedben a matematikusok igyekeztek megvetni egy hibátlan matematikai építmény alapjait. Seregnyi logikus vett részt a matematikai tudás rettentő bonyolult rendszerének lassú és keserves, csak minimális axióma alapján való újrafelépítésében. Hilbert 1930-ban azzal a meggyőződéssel vonulhatott nyugdíjba, hogy a matematika a gyógyulás útjára lépett. A következetes logikáról és a minden kérdést megválaszoló matematikáról alkotott álma a legjobb úton haladt a megvalósulás felé.

Kurt Gödel 1906. április 28-án született Morvaországban, az egykori Osztrák-Magyar Monarchia egyik tartományában. A tudományok és a matematika iránti tehetsége már gyermekkorában megnyilvánult, kíváncsisága miatt a „Herr Warum” (Miért úr) becenevet kapta. 18 évesen lett a Bécsi Egyetem hallgatója, ekkor már kitűnően ismerte az egyetemi szintű matematika tananyagot. Bár eredetileg elméleti fizikával akart foglalkozni, felvett matematikai és filozófiai kurzusokat is. Kollégáival együtt időnként résztvett egy filozófuscsoport, az úgynevezett Bécsi Kör összejövetelein is, ahol akkoriban a logika nagy és időszerű kérdéseit vitatták meg. Ebben az időben dolgozta ki azokat az elképzeléseket, amelyek megrengették a matematika alapjait, és szertefoszlatták Hilbert álmát. Eredményeit a következő két pongyolán megfogalmazott állítás foglalja össze.

Gödel első nemteljességi tétele: Ha egy „kellőképpen erős” matematikai elmélet axiómarendszere ellentmondásmentes, akkor megfogalmazhatók olyan állítások, amelyek nem bizonyíthatók és nem is cáfolhatók ebből az axiómarendszerből kiindulva.

Gödel második nemteljességi tétele: Egy ilyen axiómarendszer ellentmondásmentessége szintén nem bizonyítható és nem is cáfolható magából az axiómarendszerből kiindulva.

A „kellőképpen erős” kitétel nagyjából azt jelenti, hogy az elmélet alkalmas legalább arra, hogy a pozitív egész számokra vonatkozó állításokat megfogalmazzunk benne. Úgy is mondhatnánk, hogy olyan elméletekről van szó, amelyeknek „gyakorlati haszna” is van. Az első nemteljességi tétel lényegében arról szól, hogy akármilyen axiómarendszert is veszünk egy ilyen elméletből, az biztosan nem lehet egyszerre teljes és ellentmondásmentes. Azaz bármilyen „valamirevaló” axiómarendszer esetén a teljesség és az ellentmondásmentesség közül legalább az egyik sérül. Sőt, a második nemteljességi tétel szerint a helyzet még ennél is rosszabb. Ez ugyanis azt mondja ki, hogy itt nem „kizáró vagy” kapcsolat áll fenn, azaz még abban sem lehetünk biztosan, hogy axiómáink nem vezetnek ellentmondásra, mivel az ellentmondásmentességet sem lehet bizonyítani.

Ez persze nem jelenti szükségképpen azt, hogy ez vagy az az axiómarendszer valóban ellentmondásos. A szíve mélyén a legtöbb matematikus továbbra is hitt abban, hogy matematikájuk megmarad ellentmondásmentesnek, csak épp a logika eszközeivel ezt nem tudták megnyugtatóan igazolni. Jó néhány évvel később a kiváló számelmélész, André Weil ezt mondta erről:

Isten azóta létezik, mióta a matematika ellentmondásmentes. Az ördög pedig azóta, amióta ezt nem tudjuk belátni.

John D. Barrow pedig így fogalmazott:

Ha „vallás” alatt olyan gondolatrendszert értünk, amely bizonyíthatatlan állításokat tartalmaz, akkor Gödel megmutatta nekünk, hogy a matematika nem csak hogy vallás, hanem ez az egyetlen vallás, ami be is tudja bizonyítani magáról, hogy az.

Gödel tehát megmutatta, hogy Hilbert programja végrehajthatatlan. Ahhoz, hogy a nemteljességi tételek mélyebb tartalmát megértsük, illetve azt a fentieknél szabatosabban megfogalmazhassuk, tisztáznunk kell néhány matematikai logikai fogalmat.

Szemantikai modellek

A matematika a fizikai valóság egy-egy szeletét a maga sajátos eszközeivel vizsgálja. E vizsgálatok során elvonatkoztatunk a valóságnak az adott vizsgálat szempontjából nem lényeges részleteitől. Ezt a folyamatot absztrakciónak nevezzük, melynek során képzeletben létrehozunk egy úgynevezett szemantikai modellt, és a továbbiakban a valóság helyett ezt a modellt tesszük vizsgálatunk tárgyává. Például az euklidészi síkgeometriában úgynevezett pontokat, egyeneseket vagy még általánosabban a sík pontjainak egyes részhalmazait vizsgáljuk. Ezek idealizált objektumok, hiszen például egy pontnak semmilyen irányban nincs kiterjedése, egy egyenest pedig egy egydimenziós, mindkét irányban végtelen kiterjedésű ponthalmaznak képzeljük el. Nyilvánvalóan semmi közük nincs a valósághoz, és mégis, ez az idealizált világ tökéletesen alkalmas arra, hogy segítségükkel a valóságban nagyonis létező épületeket tervezzünk.

Az absztrakció előnye, hogy nagyon jól meghatározott keretek és játékszabályok közé kényszeríti aktuális vizsgálatunk tárgyát. Ezáltal pedig rendelkezünkre fog állni a matematikai logika teljes eszköztára, amelynek segítségével formális állításokat (úgynevezett formulákat) fogalmazhatunk meg, vizsgálhatjuk ezek igazságértékét a konkrét modellünkön, és az igaznak bizonyult formulákból újabb formulák igazságát bizonyíthatjuk. A logikai következtetési sémák igazságtartó tulajdonsága biztosítja számunkra, hogy a már bizonyított formulák igazságában soha többé nem kell kételkednünk.

Ebben a szakaszban a szemantikai modellek általános felépítését vizsgáljuk meg. Egy modell tulajdonképpen egy H alaphalmazból, valamint az ennek elemei között értelmezett úgynevezett relációkból áll. A H alaphalmazt szokás tárgyalási univerzumnak is nevezni, mivel ez tartalmazza azokat az objektumokat, amelyekkel kapcsolatban formális állításokat szeretnénk megfogalmazni. Például az euklidészi síkgeometria esetén különböző síkbéli alakzatokról szeretnénk kijelentéseket tenni, ezért ebben az esetben a tárgyalási univerzum a sík pontjainak részhalmazaiból áll.

Egy másik példaként tegyük fel, hogy az alábbi kijelentést szeretnénk formalizálni: „Nem minden fiatal tiszteli az időseket.” Ebben az esetben tárgyalási univerzumnak tekinthetjük azt a halmazt, amely az összes emberből áll, vagy legalábbis embereknek egy olyan meghatározott csoportjából, amely csoportot a matematikai logika eszközeivel vizsgálni szeretnénk.

Egy modellhez a H alaphalmazon kívül szükség van relációkra is. Egy reláció a H alaphalmaz valahány eleme között fennálló valamilyen kapcsolatot reprezentál. Ezeknek egy speciális fajtájáról, az úgynevezett kétváltozós relációkról ebben a cikkben már volt szó korábban. Példaként a jól ismert kő-papír-olló játék ütési szabályait modelleztük egy, a \text{kő}, a \text{papír} és az \text{olló} szavakat tartalmazó halmazon értelmezett kétváltozós relációval. Általánosságban egy H-n értelmezett kétváltozós reláción a H elemeiből képezhető összes lehetséges rendezett pár H\times H-val jelölt halmazának egy részhalmazát értjük. A H\times H halmazt a H halmaz önmagával vett direkt szorzatának nevezzük.

Ha például H a \text{kő}, a \text{papír} és az \text{olló} szavakat tartalmazó halmaz, akkor a H\times H halmaz összesen 9 rendezett pár alkot, hiszen egy rendezett pár mindkét pozíciójába 3 féle elem helyezhető el H-ból. Jelöljük a \succ szimbólummal azt a relációt, amely az összes rendezett pár közül a (\text{kő}; \text{olló}), (\text{olló}; \text{papír}) és (\text{papír}; \text{kő}) párokat tartalmazza. Ekkor azt mondjuk, hogy e párok elemei között fennáll a \succ reláció.

Ezt kétféleképpen jelölhetjük. Az úgynevezett infix jelölés esetén a reláció szimbólumát a két elem közé írjuk (például a\succ b), míg az úgynevezett prefix jelölés esetén először a reláció szimbólumát írjuk le, majd zárójelben felsoroljuk a relációban résztvevő elemeket (például \succ(a, b). Az alábbi táblázatban mindkét jelölést feltüntettük:

\begin{array}{cc}\begin{aligned}\text{kő} &\succ \text{olló} \\ \text{olló} &\succ \text{papír} \\ \text{papír} &\succ \text{kő}\end{aligned} & \begin{aligned}&\succ(\text{kő}, \text{olló}) \\ &\succ(\text{olló}, \text{papír}) \\ &\succ(\text{papír}, \text{kő})\end{aligned}\end{array}

Amennyiben az a \succ b reláció fennállását az a „üti” b-t jelentéssel interpretáljuk, akkor ez a reláció valóban a kő-papír-olló játék ütési szabályait reprezentálja.

De vehetünk példának egy, a fentebb már említett „nem minden fiatal tiszteli az időseket” jellegű kijelentések szemantikáját meghatározó modellt is. Itt az emberek H halmazát tekinthetjük alaphalmaznak, amelyen definiálhatunk egy T-vel jelölt kétváltozós relációt, amely két H-beli elem (azaz ember) között állhat fenn, és amelyet „tiszteletként” interpretálhatunk. Ekkor ha a és b két tetszőleges eleme a H alaphalmaznak, akkor a T(a,b) – vagy infix jelöléssel aTb – reláció fennállása azt fogja jelenteni, hogy a „tiszteli” b-t.

További példa kétváltozós relációra az euklidészi síkgeometria szemantikai modellje esetén az „illeszkedési” reláció. Itt a H tárgyalási univerzum a sík pontjainak részhalmazaiból áll, amelyek lehetnek például egyenesek, körök, egyedülálló pontok, vagy akár egyéb egzotikus alakzatok is. Ha mondjuk e\in H egy egyenes a síkon, p\in H pedig egy egyedülálló pont, akkor az I(p,e) relációt interpretálhatjuk úgy, hogy a p pont „illeszkedik” az e egyenesre.

Egy reláció azonban nemcsak kettő, hanem akárhány változós is lehet. Ilyenkor a H alaphalmaz elemeiből nem párokat, hanem úgynevezett n-eseket képzünk az összes lehetséges módon – ahol n a reláció változóinak száma –, és az így kapott n-esek halmazának egy részhalmazát azonosítjuk az adott relációval. Modellezzünk most például egy piacot, ahol a H tárgyalási univerzum a piacon lévő minden embert és árut – mint a vizsgálatunk szempontjából fontos objektumokat – tartalmazza. Ekkor tekinthetünk egy T-vel jelölt relációt, amely a piacon történt tranzakciókat fogja tartalmazni. Ez a reláció 3 változós lesz, hiszen az eladón és a vevőn kívül egy konkrét áru is résztvesz benne, mint a tranzakció tárgya. Például a T(a,b,c) reláció fennállását felruházhatjuk azzal a jelentéssel, hogy a „vásárolt” b-től egy c árut.

Speciálisan az egyváltozós relációk magának a H tárgyalási univerzumnak a részhalmazai lesznek. Egy ilyen relációval valamilyen konkrét tulajdonságot reprezentálhatunk, amellyel bizonyos H-beli elemeket felruházunk, másokat pedig nem. Például a „nem minden fiatal tiszteli az időseket” jellegű mondatok szemantikai értelmezéséhez szükség van egy F-fel és egy I-vel jelölt egyváltozós relációra, amelyek a tárgyalási univerzum bizonyos elemeit rendre az „idős” vagy a „fiatal” tulajdonságokkal ruházzák fel. Egy másik kézenfekvő példa a már említett síkgeometria, ahol az egyes ponthalmazokat ruházhatjuk fel például az „egyenes”, a „kör” vagy az „egyetlen pont” tulajdonságokkal.

Végül fontos megemlíteni, hogy az egy- és kétváltozós relációkat adott esetben grafikusan is tudjuk ábrázolni. Az idős emberek tiszteletével kapcsolatos példánknál maradva, ábrázoljuk az alaphalmazban lévő embereket kis pontokkal. Egy adott x pontból egy adott y pontba pontosan akkor húzzunk egy nyilat, ha az x által reprezentált ember tiszteli az y által reprezentált embert. Továbbá címkézzük fel I betűkkel az idős, F betűkkel pedig a fiatal embereket reprezentáló pontokat. Az alábbi ábrán egy konkrét modell látható ezekkel a jelölésekkel:

Mivel ez egy viszonylag kis számosságú alaphalmazzal rendelkező modell, ezért akár ránézésre is látható, hogy konkrétan ezen a modellen igaz a „nem minden fiatal tiszteli az időseket” állítás, hiszen például az a-val jelölt fiatalember nem tiszteli az f-fel jelölt öregurat. Ugyanakkor az is igaz, hogy az állítás nincs teljesen egyértelműen megfogalmazva. A „tiszteli az időseket” kitétel ugyanis jelentheti egyrészt azt, hogy az illetőnek szigorúan minden egyes idős ember iránt tiszteletet kell éreznie. Másrészt lehet ennél elnézőbb jelentése is, miszerint elég, ha úgy „általában” tiszteli valaki az időseket, de azért lehet néhány kivétel közöttük. Ennek a gyengébb kitételnek az a fiatalember egy kis túlzással megfelel, és ez egyből módosítja a fenti állítás igazságértékét, amely tehát ez utóbbi interpretáció mellett már hamis ugyanezen a modellen.

Az elsőrendű logika nyelve

Az iménti példa érzékelteti, hogy a matematikában mennyire fontos az egyértelmű megfogalmazás. Ez különösen így van a logikában. Egy logikai állítás kellően pontos megfogalmazására az emberi kommunikációban használt nyelvek nem éppen a legalkalmasabbak. Ezért most megismerkedünk egy úgynevezett formális nyelvvel, amelyet az elsőrendű logika nyelvének nevezünk. A formális nyelvekkel kapcsolatos alapfogalmakról ebben a cikkben volt szó bővebben, így azokat itt nem ismételjük meg, de mindenképpen javasoljuk az Olvasónak, hogy fussa át őket.

Egy formális nyelvet általánosságban egy megadott szimbólumkészletből – a nyelv ábécéje – alkotott jelsorozatok konkrét halmazaként definiáljuk, és mondatoknak nevezzük azokat a jelsorozatokat, amelyek elemei ennek a halmaznak. A logikában használt elsőrendű nyelvek esetén a mondatokat formuláknak szokás nevezni. Ahogy minden formális nyelv esetén, itt is adva van egy szabálykészlet, mely megadja, hogy a szimbólumokat milyen sorrendben lehet és kell összerakni ahhoz, hogy formulákat kapjunk. Ezeket a nyelvtani szabályokat a nyelv szintaxisának nevezzük.

Ebben a cikkben a könnyebb megértést elősegítendő a szintaxist nem fogjuk teljes precízitással specifikálni, ám általánosságban elmondható, hogy egy elsőrendű nyelv szimbólumkészlete az alábbi nagyobb csoportokra osztható:

• Logikai szimbólumok: Ezek a különböző logikai műveleteket, illetve az úgynevezett kvantorokat jelölő szimbólumok. Ezekről hamarosan szó lesz, most csak felsoroljuk őket. A \land, \lor, \lnot, \implies és \iff szimbólumok rendre az „és”, a „vagy”, a „nem” illetve az úgynevezett implikáció (következmény) és ekvivalencia műveleteket, a \forall és \exists szimbólumok pedig rendre az úgynevezett univerzális („minden”) és egzisztenciális („létezik”) kvantorokat jelölik.
• Individuumváltozók: Ezek segítségével a modell tárgyalási univerzumának elemeire hivatkozhatunk a formuláinkban, és általában az ábécé kisbetűivel szoktuk jelölni őket, esetleg valamilyen indexszel ellátva. Például: x_1, x_2, x_3, …
• Nemlogikai szimbólumok: Mivel a nyelv formuláival egy adott szemantikai modellel kapcsolatos állításokat szeretnénk megfogalmazni, ezért szükség van arra, hogy a modellben szereplő konkrét relációkat valahogyan jelölni is tudjuk a formuláinkban. Ezért a nyelv szimbólumkészletébe fel kell venni ezeket a relációkat jelölő szimbólumokat. Ezekre használhatunk speciális szimbólumokat is, de általános tárgyalás esetén az ábécé nagybetűivel szoktuk őket jelölni, szintén esetleg valamilyen indexszel ellátva. Például: R_1, R_2, R_3, stb. Speciálisan bevezethetünk egy = szimbólummal jelölt kétváltozós relációjelet is, amelyet úgy fogunk interpretálni, hogy pontosan akkor teljesül, ha a két bemeneti individuumváltozó ugyanazt az elemet jelöli a modell tárgyalási univerzumában.
• Segédjelek: A formulák szintaktikai összetevőinek elválasztásához szükségünk lesz zárójelekre, vesszőkre, illetve adott esetben egyéb szintaktikai jelekre is. Például ha x és y két individuumváltozó, R pedig egy kétváltozós relációt jelölő nemlogikai szimbólum egy formulában, akkor azt az állítást, hogy x és y között fennáll az R reláció így fogjuk kifejezni a nyelv szimbólumkészletével: R(x,y)

Ezek után megadjuk a formulák képzésének szabályait, azaz lényegében a szintaxist, majd példaként az idősek tiszteletéről szóló mondatot fogjuk megfogalmazni az elsőrendű logika nyelvén. Az itt leírt szabályok alapján képzett formulák pontos jelentésével egy kicsit később fogunk foglalkozni. Egy formula ugyanis csak akkor kap konkrét jelentést (és persze igazságértéket), amikor azt egy konkrét szemantikai modellen interpretáljuk. Egy valamilyen szimbólumkészlettel rendelkező elsőrendű nyelv esetén tehát az alábbi szabályok véges sokszori alkalmazásával nyert jelsorozatokat nevezzük formuláknak:

1. Ha R egy valamilyen n-változós relációt jelölő szimbólum – beleértve az egyenlőségjelet is, mint kétváltozós relációjelet –, valamint x_1, x_2, …, x_n individuumváltozók, akkor az R(x_1,x_2,\ldots,x_n) jelsorozat formula. Az így képzett formulákat atomi formuláknak nevezzük.
2. Ha \alpha és \beta valamilyen formulák, akkor a \lnot \alpha, \alpha \land \beta, \alpha \lor \beta, \alpha \implies \beta és \alpha \iff \beta jelsorozatok is formulák. Az így képzett formulákat összetett formuláknak, az \alpha és \beta formulákat pedig ezen összetett formula részformuláinak nevezzük.
3. Ha \alpha valamilyen formula, és x tetszőleges individuumváltozó, akkor a \exists x \alpha és \forall x \alpha jelsorozatok is formulák. Ilyenkor azt mondjuk, hogy az x individuumváltozó kvantált (vagy kötött) az \alpha részformulában, amely részformulát pedig az adott kvantor hatáskörének nevezzük.

Noha az iménti nyelvtani szabályok alapján képzett formuláknak ezen a ponton még nincs semmi jelentésük, azt azonban megköveteljük ezektől a szabályoktól, hogy egyrészt ezek alapján egy tetszőleges jelsorozatról algoritmikusan el lehessen dönteni, hogy formula-e – azaz mondata-e az adott elsőrendű nyelvnek – vagy sem. Az algoritmikusan eldönthető halmazokat (vagy nyelveket) rekurzív halmazoknak (vagy nyelveknek) nevezzük, a velük kapcsolatos elméleti kérdésekről ebben a cikkben volt szó bővebben. Másrészt pedig azt is megköveteljük e szabályoktól, hogy bármely formula egyértelműen dekódolható legyen, azaz csak egyféleképpen lehessen előállítani a fenti szabályok alkalmazásával. Belátható, hogy a fenti szabályrendszer eleget tesz mindkét követelménynek, ám ennek részleteitől itt eltekintünk.

Most példaként vizsgáljuk meg, hogyan tudjuk leírni ezen a nyelven a „nem minden fiatal tiszteli az időseket” mondatot a fentebb már megadott relációjeleket használva:

\lnot\forall x(F(x)\implies \forall y(I(y)\implies T(x,y)))

A belső zárójelben lévő I(y)\implies T(x,y) részformulát két atomi formulából kaptuk a 2. szabály felhasználásával. Ez így olvasható: „ha y idős, akkor x tiszteli y-t”. Ebben a részformulában sem az x, sem pedig az y individuumváltozó nem kvantált. Ilyenkor őket szabad változóknak nevezzük. Nyíltnak nevezzük azokat a formulákat, amelyekben vannak szabad változók, és zártnak azokat, amelyek nem nyíltak. A későbbiek során a formulák igazságértékelésénél látni fogjuk, hogy a nyílt formulák igazsága egy adott modellen attól fog függeni, hogy konkrétan mely elemeket helyettesítjük be a szabad változókba a modell tárgyalási univerzumából.

Következő lépésként a 3. szabályt alkalmazzuk, amikoris az univerzális kvantor segítségével kvantáljuk az y változót. Ezzel a lépéssel kapjuk a \forall y(I(y)\implies T(x,y)) részformulát, amely így olvasható: „minden y-ra igaz, hogyha y idős, akkor x tiszteli y-t”. Ebben a részformulában már csak x lesz a szabad változó, hiszen y-t megkötöttük a kvantor segítségével.

Ismét a 2. szabályt alkalmazva az F(x)\implies \forall y(I(y)\implies T(x,y)) részformulát kapjuk, amely így olvasható: „ha x fiatal, akkor minden y-ra igaz, hogyha y idős, akkor x tiszteli y-t”. Itt az x változó még mindig szabad.

Végül a 3. és 2. szabályokat alkalmazva megkapjuk a végső \lnot\forall x(F(x)\implies \forall y(I(y)\implies T(x,y))) formulát, amely így olvasható: „nem igaz az, hogy minden x-re igaz, hogyha x fiatal, akkor minden y-ra igaz, hogyha y idős, akkor x tiszteli y-t”. Ez már zárt formula, hiszen mindegyik individuumváltozó csak valamely rá vonatkozó kvantor hatáskörén belül fordul elő.

Megjegyezzük, hogy az egzisztenciális kvantor segítségével megfogalmazhatunk egy olyan formulát is, amely az előbbivel „logikailag ekvivalens” jelentéssel bír. Ezalatt azt értjük, hogy ez a formula pontosan akkor lesz igaz, amikor az előző is. Ez a változat így néz ki:

\exists x(F(x) \land \exists y(I(y) \land \lnot T(x,y)))

Ez így olvasható: „létezik olyan x fiatal, hogy létezik olyan y idős ember, hogy x nem tiszteli y-t”. Vagy kicsit hétköznapibban fogalmazva: „van olyan fiatal, aki legalább egy időst nem tisztel”.

Most nézzünk egy másik példát: „Ha bármely két nő beszélget egymással, akkor egy harmadik csuklik.”

Most a tárgyalási univerzum a nők halmaza, amelyen az alábbi két relációt értelmezzük:

• B(x,y) jelölje azt a kétváltozós relációt, hogy x beszélget y-nal.
• C(x) jelölje azt az egyváltozós relációt, hogy x csuklik.

A fenti mondat ezekkel a jelölésekkel az elsőrendű logika nyelvén így írható le:

\forall x \forall y(B(x,y) \implies \exists z C(z))

Az igazság fogalma

Az előző két szakaszban áttekintettük, hogy egyrészt egy elsőrendű nyelv szimbólumkészletéből milyen szabályok szerint lehet formulákat előállítani. Másrészt pedig azt, hogy mik azok a szemantikai modellek, amelyeken ezeket a formulákat interpretálni lehet annak érdekében, hogy az adott modellen felvett igazságértéküket meg lehessen határozni. És ezzel elérkeztünk a logika központi jelentőségű fogalmának, az igazságnak a definíciójához, amelyet ebben a szakaszban tárgyalunk.

Az eddigiek szellemében mégegyszer fontos kihangsúlyozni, hogy egy adott formula igazságáról vagy hamisságáról önmagában nincs értelme beszélni. Azt, hogy egy formula igaz-e vagy hamis, az a modell határozza meg, amelyen a formulát interpretáljuk. Elképzelhető, hogy egy formula igaz egy adott modellen, ugyanakkor hamis egy másik modellen. Sőt, az előző szakaszban látott nyílt formulák igazsága még attól is függhet, hogy a bennük szereplő individuumváltozóknak milyen konkrét értékeket adunk az interpretáció alapját adó modell tárgyalási univerzumából.

A most következő szemantikai igazságfogalommal kapcsolatos definíciók első olvasatra talán bonyolultnak fognak tűnni, ám itt pusztán a hétköznapokból ismert igazságfogalom matematikai megfogalmazásáról van szó. Egy hétköznapi nyelven megfogalmazott állításra akkor mondjuk, hogy igaz, ha az a valóságban „ténylegesen is úgy van”. Ehhez hasonlóan egy elsőrendű logikai formula igazsága is azon múlik, ha az a konkrét szemantikai modell, amelyen őt interpretáljuk, „ténylegesen úgy viselkedik”, ahogyan az a formulában le van írva. A következő bekezdésekben ezt próbáljuk meg szabatosan megfogalmazni, majd a könnyebb érthetőség érdekében egy konkrét példán is illusztráljuk. Érdemes ezért a most következő, némileg nehezen emészthető bekezdésekhez többször is visszatérni, amennyiben szükséges.

Tegyük fel tehát, hogy adva van egy \mathcal{H}-val jelölt szemantikai modell a H tárgyalási univerzummal, valamint a rajta értelmezett konkrét relációkkal. Tegyük fel továbbá, hogy definiáltunk egy elsőrendű nyelvet, amelynek nemlogikai szimbólumaival a modell minden relációját jelölni tudjuk a formulákban. Ha például R egy ilyen szimbólum a nyelv ábécéjében, akkor R^{\mathcal{H}}-val fogjuk jelölni az \mathcal{H} modellnek azt konkrét relációját, amelynek leírására az R szimbólumot használjuk a formulákban. Ezzel azt szeretnénk kihangsúlyozni, hogy két teljesen különböző fogalomról van szó, amelyek között csak az teremt kapcsolatot, hogy az adott formulát most éppen a \mathcal{H} szemantikai modellen szeretnénk interpretálni.

Most bevezetünk egy olyan jelölést, amely azt fejezi ki, hogy egy formula igazságértékelésekor a benne szereplő individuumváltozóknak konkrét értékeket adunk a H tárgyalási univerzumból. Tegyük fel, hogy az \alpha formulában az x_1, x_2, …, x_n individuumváltozók fordulnak elő, amelyeknek meg kell adnunk egy konkrét kiértékelését. Jelöljük \sigma-val azt a kiértékelést, amely rendre a H-beli h_1, h_2, …, h_n értékeket párosítja ezekhez a változókhoz, vagyis \sigma az alábbi értékpárosításokat végzi el:

\begin{aligned}x_1 &\gets h_1 \\ x_2 &\gets h_2 \\ &\vdots \\ x_n &\gets h_n\end{aligned}

Az \alpha formula igazságértékét e \sigma kiértékelés mellett így jelöljük: \alpha_{\sigma}.

Végül a kvantort is tartalmazó formulák igazságértékeléséhez szükségünk van még egy jelölésre. Tegyük fel, hogy már rendelkezésünkre áll egy, a fentiek szerinti konkrét \sigma kiértékelés. Erről a kiértékelésről áttérhetünk egy olyan kiértékelésre, amely az i-edik individuumváltozóhoz – azaz x_i-hez – valamilyen új g értéket párosít a H tárgyalási univerzumból az eredeti h_i érték helyett, de egyébként minden más értékpárosítást helybenhagy. Ezt a kiértékelést \sigma(i, g)-vel fogjuk jelölni, amely tehát az alábbiak szerint módosítja az eredeti \sigma kiértékelést:

\begin{aligned}x_1 &\gets h_1 \\ x_2 &\gets h_2 \\ &\vdots \\ x_{i-1} &\gets h_{i-1} \\ x_i &\gets g \\ x_{i+1} &\gets h_{i+1} \\ &\vdots \\ x_n &\gets h_n\end{aligned}

Az \alpha formula igazságértékét e \sigma(i, g) kiértékelés mellett így jelöljük: \alpha_{\sigma(i, g)}.

Ezek után már – a képzési szabályokhoz hasonló módon – definiálhatjuk, hogy pontosan mit értünk egy formula igazsága alatt egy adott \sigma kiértékelés mellett:

1. Ha R egy relációt jelölő szimbólum, akkor R(x_1,x_2,\ldots,x_n)_{\sigma} pontosan akkor igaz, ha teljesül az R^{\mathcal{H}}(h_1, h_2, \ldots, h_n) reláció a \mathcal{H} szemantikai modellen.
2. Tegyük fel, hogy az \alpha_{\sigma} és a \beta_{\sigma} igazságértékek már ismertek. Ekkor:
   • (\lnot\alpha)_{\sigma} pontosan akkor igaz, ha \alpha_{\sigma} hamis (vagyis nem igaz).
   • (\alpha \land \beta)_{\sigma} pontosan akkor igaz, ha \alpha_{\sigma} igaz és \beta_{\sigma} is igaz.
   • (\alpha \lor \beta)_{\sigma} pontosan akkor hamis, ha \alpha_{\sigma} hamis és \beta_{\sigma} is hamis.
   • (\alpha \implies \beta)_{\sigma} pontosan akkor hamis, ha \alpha_{\sigma} igaz és \beta_{\sigma} hamis.
   • (\alpha \iff \beta)_{\sigma} pontosan akkor igaz, ha (\alpha\implies \beta)_{\sigma} igaz és (\beta\implies \alpha)_{\sigma} is igaz.
3. Tegyük fel, hogy valamilyen i indexre az \alpha_{\sigma(i, g)} igazságértékek már ismertek minden H-beli g elem esetén. Ekkor:
   • (\forall x_i\alpha)_{\sigma} pontosan akkor igaz, ha minden H-beli g elem esetén \alpha_{\sigma(i, g)} igaz.
   • (\exists x_i\alpha)_{\sigma} pontosan akkor igaz, ha létezik olyan H-beli g elem, amelyre \alpha_{\sigma(i, g)} igaz.

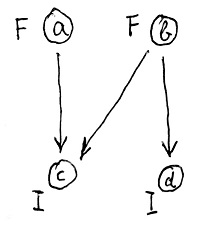
Most vizsgáljuk meg a már jól bejáratott „nem minden fiatal tiszteli az időseket” állítás igazságát az alábbi \mathcal{H} egyszerűsített modellen, ahol a „tiszteletet” jelentő, a formulákban T-vel jelölt relációt nyilakkal, az időseket I betűkkel, a fiatalokat pedig F betűkkel jelöltük:

Az alábbi ábrán a fenti állításnak megfelelő kiértékelendő formulánk úgynevezett szintaxisfája látható az egyes részformulákhoz rendelt azonosítószámokkal együtt:

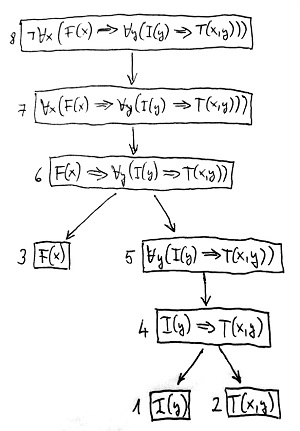
Először a szintaxisfa „alján” elhelyezkedő 1-es, 2-es és 3-as számú atomi formulák igazságértékeit kell meghatározni az x és y individuumváltozók minden lehetséges kiértékelésére, majd a szintaxisfában „felfelé” haladva az összetett részformulák igazságértékeléseit kell elvégezni a részeredmények (részigazságok) rendelkezésre állásának sorrendjében. Az alábbi táblázat sorai az egyes változókiértékeléseket, az oszlopai pedig az egyes részformulákat tartalmazzák. Minden mezőben az adott oszlopnak megfelelő részformula igazságértéke szerepel az adott sornak megfelelő változókiértékelés mellett:

\begin{array}{cc||ccccccccc} x & y & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline a & a & - & - & + & + & - & - & - & + \\ a & b & - & - & + & + & - & - & - & + \\ a & c & + & + & + & + & - & - & - & + \\ a & d & + & - & + & - & - & - & - & + \\ b & a & - & - & + & + & + & + & - & + \\ b & b & - & - & + & + & + & + & - & + \\ b & c & + & + & + & + & + & + & - & + \\ b & d & + & + & + & + & + & + & - & + \\ c & a & - & - & - & + & - & + & - & + \\ c & b & - & - & - & + & - & + & - & + \\ c & c & + & - & - & - & - & + & - & + \\ c & d & + & - & - & - & - & + & - & + \\ d & a & - & - & - & + & - & + & - & + \\ d & b & - & - & - & + & - & + & - & + \\ d & c & + & - & - & - & - & + & - & + \\ d & d & + & - & - & - & - & + & - & + \end{array}

Az 1-es, 2-es és 3-as oszlopokban szereplő igazságértékeket úgy kaptuk, hogy az 1. szabály szerint megvizsgáltuk rendre az I^{\mathcal{H}}(y), T^{\mathcal{H}}(x,y) és F^{\mathcal{H}}(x) relációk teljesülését a modellben. A 4-es oszlopba a 2. szabály \implies logikai műveletre vonatkozó pontja alapján pontosan azokhoz a kiértékelésekhez írtunk hamis értéket, ahol az 1-es oszlopban igaz érték, a 2-esben pedig hamis érték szerepel.

Az 5-ös oszlopban a 3. szabály univerzális kvantorra vonatkozó pontja szerint jártunk el. Itt csak azoknál kiértékeléseknél szerepel igaz érték, ahol az x individuumváltozó a b értéket kapta, hiszen pontosan ezek azok a kiértékelések, amiknél az y individuumváltozó értékétől függetlenül mindenhol igaz érték szerepel a 4-es oszlopban.

A 6-os oszlopba ismét a 2. szabály \implies logikai műveletre vonatkozó pontja alapján pontosan azokhoz a kiértékelésekhez írtunk hamis értéket, ahol a 3-as oszlopban igaz érték, az 5-ösben pedig hamis érték szerepel.

A 7-es oszlopban megint a 3. szabály univerzális kvantorra vonatkozó pontját kellett alkalmazni. Itt mindenhová hamis érték került, hiszen nincs az y individuumváltozónak olyan értéke, amely mellett az x individuumváltozó értékétől függetlenül mindenhol igaz érték szerepelne a 6-os oszlopban.

Végül a 8-as oszlopnak a 2. szabály \lnot logikai műveletre vonatkozó pontja alapján mindenhol a 7-es oszlophoz képest ellentétes, azaz jelen esetben igaz értéket kell felvennie.

Feljutottunk tehát a szintaxisfa tetejére, és azt kaptuk, hogy a „nem minden fiatal tiszteli az időseket” állítás igaz a \mathcal{H} szemantikai modellen, méghozzá az individuumváltozók kiértékelésétől függetlenül. Ez nem is meglepő, hiszen ez egy zárt formula, mivel minden benne szereplő individuumváltozó kvantált. Megállapíthatjuk tehát, hogy a zárt formuláknak önmagukban is van igazságértékük egy szemantikai modellen, az nem függ semmiféle konkrét kiértékeléstől. Azt, hogy egy \alpha zárt formula igaz a \mathcal{H} modellen – vagy más szavakkal \mathcal{H} modellje \alpha-nak – így jelöljük:

\mathcal{H} \models \alpha

A logikában általában nem egyetlen zárt formulát, hanem zárt formulák valamilyen halmazát (például egy egész axiómarendszert) szokás vizsgálni. Egy \Sigma-val jelölt, zárt formulákból álló halmazra akkor mondjuk, hogy van modellje, ha létezik olyan \mathcal{H} modell, amelyen \Sigma minden formulája igaz. Ezt így jelöljük:

\mathcal{H} \models \Sigma

Speciálisan egy \mathcal{H} modell elmélete alatt azoknak a zárt formuláknak a halmazát értjük, amelyek igazak \mathcal{H}-n. Ezt az angol „theory” kifejezésből eredően így jelöljük:

\text{Th}(\mathcal{H})

A logikai következmény fogalma

Az igazságfogalom után ebben a szakaszban a logika egy másik lényeges fogalmával, a logikai következmény fogalmával – és még néhány egyéb kapcsolódó definícióval – ismerkedünk meg. A továbbiakban formulák alatt minden esetben zárt formulákat fogunk érteni.

Azt mondjuk, hogy egy \alpha formula logikai következménye egy \Sigma formulahalmaznak, ha \Sigma minden modellje egyúttal \alpha-nak is modellje. Ezt így jelöljük:

\Sigma \models \alpha

Ezzel ekvivalens megfogalmazás: \Sigma \models \alpha pontosan akkor teljesül, ha a \Sigma \cup \{\lnot \alpha\} formulahalmaznak nincs modellje, azaz nincs olyan modell, amelyen \Sigma összes formulája és az \alpha formula tagadása egyaránt igaz.

Vegyük észre, hogy egy \Sigma\models\alpha következmény helyessége vagy helytelensége nem függ semmiféle szemantikai modelltől, hanem csakis az adott formulák logikai szerkezetétől. Ez a tulajdonság jelenti az alapját a logika másik nagy fejezetének, az úgynevezett bizonyításelméletnek, amelyről hamarosan szó lesz. Egy helyes \Sigma\models\alpha logikai következmény segítségével egy konkrét struktúrán újabb és újabb igaz állításokat nyerhetünk. Ha ugyanis egy \mathcal{H} modellről tudjuk, hogy modellje \Sigma-nak, akkor a logikai következmény definíciója szerint egyúttal \alpha-nak is modellje lesz. Vigyázzunk azonban, mert hiába helyes egy \Sigma\models\alpha logikai következmény, attól még kaphatunk hamis állításokat egy konkrét \mathcal{H} modellen, amennyiben maga \Sigma tartalmaz olyan állításokat, amelyek hamisak \mathcal{H}-n – azaz ha eleve hamis állításokból indulunk ki.

Most felsoroljuk a két legfontosabb úgynevezett következménysémát. Egy következményséma abban tér el egy logikai következménytől, hogy akkor helyes, ha a benne szereplő formulákat jelölő szimbólumok – az úgynevezett formulaváltozók – helyére tetszőleges formulákat írva helyes logikai következményt kapunk.

Modus ponens következtetés: \{\alpha \implies \beta; \alpha\} \models \beta

Ez az egyik legtermészetesebb következményséma. Tegyük fel például, hogy a baloldalon az alábbi konkrét formulák szerepelnek:

\begin{aligned}&\overbrace{\text{Ha dolgozom,}}^{\alpha} \ \overbrace{\text{akkor}}^{\implies} \ \overbrace{\text{stresszes vagyok.}}^{\beta} \\ &\underbrace{\text{Dolgozom.}}_{\alpha}\end{aligned}

A szemantikai igazság előző szakaszban közölt definíciójából következik, hogy minden olyan modellen, amelyen ez a két állítás igaz, igaz lesz a következményséma jobboldalán szereplő alábbi állítás is:

\underbrace{\text{Stresszes vagyok.}}_{\beta}

Most egy másik, a matematikában gyakran használt következtetési sémát, az úgynevezett indirekt következtetést ismertetjük.

Indirekt következtetés: \{\lnot\beta \implies \lnot\alpha; \alpha\} \models \beta

Sok matematikai bizonyítás használja ezt a következménysémát, amikoris feltesszük, hogy a bizonyítandó állítás – jelen esetben \beta – hamis, majd megmutatjuk, hogy ez ellentmondana egy korábban már bizonyított állításnak – jelen esetben \alpha-nak. Az előző példánál maradva a következményséma baloldalán most az alábbi két állítás szerepel:

\begin{aligned}&\overbrace{\text{Ha nem vagyok stresszes,}}^{\lnot\beta} \ \overbrace{\text{akkor}}^{\implies} \ \overbrace{\text{nem dolgozom.}}^{\lnot\alpha} \\ &\underbrace{\text{Dolgozom.}}_{\alpha}\end{aligned}

Következésképp ha egy modellen igaz ez a két állítás, akkor igaz lesz az alábbi, jobboldalon szereplő állítás is:

\underbrace{\text{Stresszes vagyok.}}_{\beta}

Most kimondunk a következményfogalomhoz kapcsolódó néhány fontos definíciót.

Azt a formulahalmazt, amely egy \Sigma formulahalmaz logikai következményeiből áll, az angol „consequence” kifejezésből eredően így jelöljük:

\text{Cons}(\Sigma)

Tegyük fel, hogy egy \Gamma formulahalmaz zárt a logikai következményre nézve, azaz igaz az alábbi:

\Gamma = \text{Cons}(\Gamma)

Ekkor a \Gamma formulahalmazt elméletnek nevezzük. Egy elmélet tehát zárt abban értelemben, hogy őt nem lehet „elhagyni” logikai következményeken keresztül.

Azt mondjuk, hogy egy \Gamma elmélet axiomatizálható, ha létezik olyan \Sigma formulahalmaz, amely egyrészt algoritmikusan eldönthető, azaz rekurzív halmaz – az ezzel a fogalommal kapcsolatos elméleti kérdésekről ebben a cikkben volt szó bővebben. Másrészt a \Sigma formulahalmaz logikai következményei kiadják a teljes \Gamma elméletet, azaz:

\Gamma = \text{Cons}(\Sigma)

A \Sigma formulahalmazt a \Gamma elmélet axiómarendszerének nevezzük. Ha \Sigma csak véges sok formulát tartalmaz, akkor azt mondjuk, hogy a \Gamma elmélet végesen axiomatizálható.

Azt mondjuk, hogy egy \Gamma elmélet eldönthető, ha ő maga, mint formulahalmaz algoritmikusan eldönthető, azaz rekurzív. Egy elméletre azt mondjuk, hogy eldönthetetlen, ha nem eldönthető.

Egy \Sigma formulahalmazra akkor mondjuk, hogy ellentmondásos (inkonzisztens), ha létezik olyan \alpha formula, amely esetén a \Sigma \models \alpha és \Sigma \models \lnot \alpha logikai következmények egyaránt helyesek. Ebben az esetben a \Sigma formulahalmaznak nyilván nem létezhet modellje, máskülönben \alpha és \lnot \alpha is igaz lenne ezen a modellen, ami lehetetlen. Egy formulahalmazt ellentmondásmentesnek (konzisztens) nevezünk, ha nem ellentmondásos.

Egy \beta formulára akkor mondjuk, hogy független a \Sigma formulahalmaztól, ha \Sigma\models\beta és \Sigma\models\lnot\beta egyike sem teljesül, azaz sem \beta, sem pedig a tagadása nem logikai következménye \Sigma-nak.

Egy \Gamma elméletre akkor mondjuk, hogy teljes (komplett), ha nincs \Gamma-tól független formula. Másként fogalmazva ha bármely \alpha formula esetén vagy \alpha, vagy pedig \lnot\alpha benne van a \Gamma elméletben. Egy elmélet inkomplett, ha nem teljes.

Vegyük észre, hogy az előző szakasz végén említett \text{Th}(\mathcal{H})-val jelölt formulahalmaz – amelyet a \mathcal{H} modell elméletének neveztünk – valóban elmélet az itt definiált értelemben is, amely ráadásul teljes és ellentmondásmentes.

Tegyük fel ugyanis, hogy \text{Th}(\mathcal{H})-nak létezik olyan logikai következménye – jelöljük ezt a formulát mondjuk \alpha-val –, amely nincs benne \text{Th}(\mathcal{H})-ban. Ekkor a logikai következmény definíciója miatt \alpha igaz a \mathcal{H} modellen, azaz mégiscsak benne van \text{Th}(\mathcal{H})-ban, ami ellentmondás, azaz \text{Th}(\mathcal{H}) valóban egy elmélet. Az nyilvánvaló, hogy \text{Th}(\mathcal{H}) ellentmondásmentes és teljes, hiszen ennek az elméletnek \mathcal{H} egy modellje, amelyen tetszőleges formula egyértelműen vagy igaz, vagy pedig hamis.

Valamilyen adott \mathcal{H} modell esetén a \text{Th}(\mathcal{H}) az elméletek egy fontos esete, hiszen hozzá kapcsolódik a logika talán két legfontosabb kérdése:

• Axiomatizálható-e a \text{Th}(\mathcal{H}) elmélet?
• Eldönthető-e a \text{Th}(\mathcal{H}) elmélet?

Tekintsük példaként a számelmélet (vagy aritmetika) modelljének \Pi_P-vel jelölt elméletét, amelynek axiómarendszere – a tágabb értelemben vett Peano-axiómarendszer – tulajdonképpen a számegyenes szerkezetét (lásd itt), az azon értelmezett összeadás (lásd itt) és szorzás műveletek (lásd itt) tulajdonságait, valamint a szokásos „kisebb-nagyobb” fogalmát (lásd itt) határozza meg. Az axiomatizálhatóság kérdése ebben az esetben gyakorlatilag így hangzik: vajon az összes számelmélettel kapcsolatos igaz állítás logikai következménye-e a Peano-axiómarendszernek? Az elmélet eldönthetőségének kérdése pedig: vajon bármely formula \Pi_P halmazba tartozása – azaz egy tetszőleges számelmélettel kapcsolatos állítás igazsága – algoritmikusan eldönthető-e. Mint azt látni fogjuk, sajnos mindkét kérdésre nemleges a válasz.

Megjegyezzük még, hogy a Peano-axiómarendszer tulajdonképpen végtelen sok axiómából áll, mivel tartalmaz egy úgynevezett indukciós axiómasémát, amelybe tetszőleges elsőrendű formula behelyettesíthető. Ez a séma azt állítja, hogy amennyiben a 0 természetes számra igaz egy \alpha elsőrendű formula (ide helyettesíthető bármilyen formula), továbbá \alpha igazsága a „rákövetkezésen” keresztül öröklődik, akkor igaz lesz minden természetes számra. Ez teszi lehetővé az úgynevezett teljes indukciós bizonyításokat, amelyekre néhány remek példát találhatunk itt. Amennyiben ezt az axiómasémát elhagyjuk – lemondva így a teljes indukció fegyveréről –, akkor az így kapott „szűkebb” elméletet végesen axiomatizált számelméletnek nevezzük, és \Pi-vel jelöljük – amelynek axiómarendszere tehát már véges.

Mint azt látni fogjuk, az imént ismertetett \Pi_P és \Pi elméletek lesznek a főszereplői a jelen cikk tárgyát képező és hamarosan ismertetett, az egész matematikát megrengető Gödel-féle inkomplettségi (nemteljességi) tételeknek.

Bizonyításelmélet és a teljességi tétel

A szemantikai igazságfogalom definíciójával van egy nagy probléma, méghozzá az, hogy algoritmikusan nem kezelhető.

Egyrészt nem alkalmazható arra, hogy formulák igazságértékeit egy adott modellen meghatározzuk, hiszen a modellen definiált relációk általában már maguk sem feltétlenül algoritmikusan eldönthetők, a kvantorok pedig általában végtelen tárgyalási univerzumon futnak végig, így sem a „minden”, sem pedig a „létezik” kvantor igazságértéke nem meghatározható. Például a számelmélet nyelvén viszonylag könnyen megfogalmazhatunk egy olyan formulát, amelynek interpretációja a „végtelen sok ikerprím számpár létezik” állítás. Ez azonban a matematika egy nevezetes, máig megoldatlan problémája, a definíció alapján igazságértékét természetesen nem tudjuk meghatározni, azaz nem tudjuk, hogy vajon az ennek megfelelő formula benne van-e a \Pi_P elméletben vagy sem.

Másrészt a szemantikai igazságfogalom arra sem alkalmazható, hogy egy logikai következmény helyességét vizsgáljuk. Ehhez ugyanis elvben minden modellen vizsgálnunk kell a következményben szereplő formulák igazságát, ami nyilván még inkább lehetetlen, mintha csak egyetlen formula igazságát vizsgálnánk egyetlen modellen.

A logikának ezért létezik egy másik felépítése, amely a logika fontos problémáit másfelől közelíti meg, mint a szemantika, ám a háttérben szorosan összefonódik vele. Ezt a területet nevezzük bizonyításelméletnek, amely az úgynevezett levezetési (bizonyítási) rendszerek vizsgálatával foglalkozik, és amelyet itt csak vázlatosan tekintünk át.

A bizonyításelmélet tulajdonképpen abból indul ki, hogy egy bizonyítás során valamilyen formális nyelven megfogalmazott formulákon véges sok manipulációt hajtunk végre – szemben a szemantikai modellek általában végtelen halmazaival és relációival – annak érdekében, hogy végül a bizonyítani kívánt formulát kapjuk eredményül. Egy konkrét levezetési rendszer tulajdonképpen azt határozza meg, hogy milyen manipulációs lépéseket lehet végrehajtani a formulákon, illetve hogy mikor mondjuk azt, hogy egy adott \alpha formula e megengedett lépések felhasználásával bizonyítható egy adott \Sigma formulahalmazból. Azt, hogy \alpha bizonyítható \Sigma-ból így jelöljük:

\Sigma \vdash \alpha

Azt a formulahalmazt, amely egy \Sigma formulahalmazból az adott levezetési rendszer szerint bizonyítható formulákból áll, az angol „deduction” kifejezésből eredően így jelöljük:

\text{Ded}(\Sigma)

Ezen a ponton az előző szakaszban szereplő definíciók sorra megismételhetők lennének, csak épp ezúttal erre a \vdash szimbólummal jelölt bizonyíthatósági kapcsolatra. Ugyanúgy definiálhatjuk az elmélet, az axiomatizálhatóság, az eldönthetőség, az ellentmondásmentesség, a függetlenség és a teljesség fogalmát, mint a \models szimbólummal jelölt logikai következmény esetén. Kérdés, hogy ezek a bizonyításelméleti változatok vajon egybeesnek-e a szemantikai párjukkal, és ha igen, akkor pontosan mely esetekben?

E kérdés elvezet minket a levezetési rendszerekkel szemben támasztott két fontos követelményhez. Vegyük észre, hogy a \vdash bizonyíthatósági kapcsolattal tulajdonképpen az a célunk, hogy a \models szimbólummal jelölt logikai következmény kapcsolatot „szimuláljuk”. Ezért egy levezetési rendszerrel (vagy más néven logikai kalkulussal) szemben minimálisan elvárható követelmény, hogy helyes legyen. Ezalatt azt értjük, hogy csak olyan \alpha formulák legyenek bizonyíthatók egy \Sigma formulahalmazból, amelyek egyben logikai következményei is \Sigma-nak, azaz teljesüljön a következő: Ha \Sigma\vdash\alpha, akkor \Sigma\models\alpha.

Ilyenkor tehát a \text{Ded}(\Sigma) és a \text{Cons}(\Sigma) halmazok egymáshoz való viszonya az alábbi:

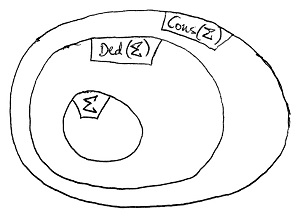
Egy levezetési rendszerrel szemben a helyességen kívül általában egy másik fontos tulajdonságot is elvárunk, ez pedig az úgynevezett teljesség, amely nem keverendő össze egy elmélet teljességével. Ez a tulajdonság azt is megköveteli a levezetési rendszertől, hogy egy \Sigma formulahalmaz minden logikai következményét lehessen is bizonyítani, ami tehát a helyességi követelmény megfordítása: Ha \Sigma\models\alpha, akkor \Sigma\vdash\alpha.

Ilyenkor a \text{Ded}(\Sigma) és a \text{Cons}(\Sigma) halmazok pontosan megegyeznek egymással, továbbá a felsorolt fogalmak épp egybeesnek a szemantikai értelemben vett változatukkal. Ebből az is következik, hogy ilyen értelemben bármely helyes és teljes logikai kalkulus egymással teljesen ekvivalens, azaz mindegy, hogy melyiket használjuk.

Kurt Gödel egyik rendkívül fontos eredménye az úgynevezett teljességi tétel, amely az egyik gyakran használt logikai kalkulus, a Hilbert-féle levezetési rendszer helyességét és teljességét mondja ki. Ennek jelentőségét nehéz túlbecsülni, hiszen a teljességi tétel a matematika motorját jelentő elsőrendű logika erejét bizonyítja, mivel azt állítja, hogy a szemantikai logikai következmény és a bizonyíthatóság egymással ekvivalens fogalmak. Igazolja azt a sejtést, hogy egy \Sigma\models\alpha logikai következmény helyességének vizsgálata történhet a formális nyelvet és a következtetésben előforduló formulák szerkezetét felhasználva pusztán szintaktikai manipulációkkal.

A teljességi tétel egy fontos ekvivalens megfogalmazása, hogy egy \Sigma formulahalmaz akkor és csak akkor ellentmondásmentes, ha van modellje. Úgy is fogalmazhatnánk, hogy egy elmélet logikai ellentmondásmentességének fogalma ekvivalens azzal, hogy az elmélet valamilyen modellben „fizikailag meg is valósul”.

Gödel nemteljességi tételei és a logika korlátai

Az előző szakaszban a Hilbert-féle logikai kalkulus teljességéről szóló tétel jóvoltából a bizonyításelmélet erejét „ünnepelhettük”, most azonban rátérünk az árnyoldalakra is. Az alábbi, Gödeltől származó, történelmi jelentőségű tételek két főszereplője a \Pi_P-vel jelölt szokásos, valamint a \Pi-vel jelölt végesen axiomatizált számelmélet. Sajnos azonban ezek a negatív eredmények nemcsak ezt a két elméletet, hanem ezek minden axiomatizálható, ellentmondásmentes kiterjesztéseit is érintik – azaz gyakorlatilag a legtöbb hasznos elméletet.

Gödel I. nemteljességi tétele: A \Pi elmélet, valamint minden axiomatizálható, ellentmondásmentes kiterjesztése inkomplett.

Következmények:

• Sem maga \Pi, sem pedig annak ellentmondásmentes kiterjesztései nem lehetnek egyszerre axiomatizálhatók, és teljesek.
• A természetes számok szokásos modelljének elméletét nem lehet a bizonyításelmélet eszközeivel teljes egészében „megragadni”. Ez az elmélet ugyanis \Pi-nek nyilván kiterjesztése, amely ráadásul teljes és ellentmondásmentes, és így az I. nemteljességi tétel értelmében nem axiomatizálható.
• Másként megfogalmazva bármilyen axiómarendszert állítunk is fel a számelmélet „lefedésére”, mindig megfogalmazható lesz olyan \alpha formula, amely független ettől az axiómarendszertől. Ezen a ponton választanunk kell, hogy \alpha-val vagy a tagadásával bővítjük ki az axiómarendszerünket. Mivel mindkét esetben egy ellentmondásmentes axiómarendszert kapunk – feltéve, hogy az eredeti axiómarendszer is az volt –, ezért ezen a ponton a számelmélet tulajdonképpen „kettéválik”. Ráadásul mindkét változatra szintén érvényes lesz az I. nemteljességi tétel.
• A Peano-axiómák által generált \Pi_P elmélet sem lehet teljes, hiszen ő \Pi ellentmondástalan kiterjesztése. Az ellentmondástalanságot Gerhard Gentzen német matematikus igazolta 1936-ban.

Gödel II. nemteljességi tétele: Létezik olyan formula, amely a \Pi_P elmélet ellentmondásmentességét állítja, és ez a formula független a \Pi_P elmélettől. Továbbá \Pi_P minden axiomatizálható, ellentmondásmentes kiterjesztéséhez is létezik ilyen tulajdonságú formula.

Következmények:

• A \Pi_P ellentmondásmentességét tehát \Pi_P-ben nem, legfeljebb egy alkalmas kiterjesztésében lehet bizonyítani, ahogyan azt – mint már említettük – Gentzen 1936-ban meg is tette. Azonban természetesen ekkor ennek a kiterjesztett elméletnek az ellentmondásmentességének igazolása ugyanebbe a problémába ütközik.
• A \Pi_P keretében tehát nem tudjuk bizonyítani, hogy \Pi_P-nek egyáltalán van-e modellje. A teljességi tétel értelmében ugyanis ez pontosan akkor teljesül, ha \Pi_P ellentmondásmentes, amely a II. nemteljességi tétel értelmében nem bizonyítható.
• Ezek a következmények öröklődnek \Pi_P-ről annak minden kiterjesztésére is.

A nemteljességi tételek bizonyítása meglehetősen technikai jellegű, amelynek itt csak az alapgondolatát ismertetjük. Gödel a bizonyításhoz egy igen furfangos konstrukciót vezetett be, az úgynevezett Gödel-számozást. Ennek segítségével mind a formulákhoz, mind pedig a levezetésekhez egyértelműen dekódolható módon természetes számokat rendelt hozzá. Ilymódon lehetőség nyílik olyan formulák konstrukciójára, amelyek saját magukról tesznek kijelentést. Ez úgy lehetséges, hogy a formulába a saját Gödel-számát helyettesítjük. Speciálisan Gödelnek sikerült megadnia egy olyan formulát, amely pontosan akkor igaz, ha nem bizonyítható.

Régen felfigyeltek a logikában és a filozófiában az önmagukra utaló állításokra. Ilyen például a híres hazug paradoxon, amikoris egy hazug ember az alábbi kijelentést teszi: „Hazudok”.

A kérdés: vajon igaz-e ez a kijelentés? Ha igaz, akkor az, aki ezt állítja – lévén, hogy ő maga hazug – nem ejthet ki igazságot a száján, vagyis a kijelentés mégsem igaz. Saját maga rögtön ellenpéldaként szolgált volna állítása igazságára, mivel legalább ebben az egy esetben igazat mondott. Ha viszont hamis az állítás, akkor a kijelentő hazudott, vagyis a mondat nem lehet hamis, tehát igaz.

Gödel tulajdonképpen újraértelmezte a hazug paradoxont, és belefoglalta a bizonyíthatóság fogalmát. Eredményül ezt kapta: „Ez az állítás nem bizonyítható”.

Ha ez az állítás hamis lenne, akkor bizonyítható lenne, és ez ellentmondana a benne foglaltaknak. Következésképpen csak igaznak tekinthetjük, hogy elkerüljük az ellentmondást. Ha azonban az állítás igaz, akkor egyszersmind igazsága a benne foglaltak szerint nem bizonyítható.

Noha a logikusok belterjes vitákat folytattak az eldönthetetlenség kérdéseiről, a matematikustársadalom többi tagja ezzel a legkevésbé sem törődött. Sok matematikus volt azon a véleményen, hogy Gödel eldönthetetlen állításai csak a matematika félreeső, halandó számára soha nem látogatott egzotikus területein fordulhatnak elő, és ezért ők maguk soha nem fognak beléjük botlani. Elvégre Gödel pusztán annyit állított, hogy léteznek eldönthetetlen állítások, de ténylegesen egyet sem tudott megnevezni. Legalábbis attól eltekintve, hogy a formális logika nyelvén nyakatekert módon képes volt kierőltetni magából egy ilyen formulát, amelynek pusztán filozófiai jelentősége van – gondolták.

Ám 1963-ban Gödel elméleti rémálma véres valósággá vált, amikor Paul Cohen amerikai matematikus elsőként fedezett fel olyan eldönthetetlen kérdéseket, amelyek közül némelyik központi helyet foglal el a matematikában. Ezek közül a leghíresebb az úgynevezett kontinuum-hipotézis, amelyről az előző cikk szólt.

Gödel nemteljességi tételei nagy csapást jelentettek a teljes matematikára. Ha elfogadjuk, hogy egy kijelentés igazságértéke felderítésének lényegében egyedüli útja az, hogy találunk-e hozzájuk bizonyítást, akkor súlyos episztemológiai állítással kerülünk szembe. Eszerint minden elég erős elméletben lesz olyan állítás, melynek igazságáról nem fogunk tudni meggyőződni. Azaz egyik (elég erős) formális-axiomatikus rendszer sem lesz képes arra, hogy maradéktalanul minden eldöntendő kérdésre válaszoljon. Eszerint tehát eleve lehetetlen minden állítás igazságát levezetéssel megállapítani, azaz a formális rendszerek inkompetensek az összes kijelentés igazságának eldöntése dolgában…