Az előző részben intuitív módon kiterjesztettük a szorzás műveletét is az egész számok \Z halmazára. Ezzel többnyire teljessé vált a Peano-axiómarendszer (11.1. Definíció) által definiált természetes számok \N halmazának beágyazása ebbe a bővebb, már a negatív számokat is tartalmazó számkörbe. Ezután megmutattuk, hogy mind az összeadás, mind pedig a szorzás művelete ugyanúgy viselkedik az eredeti \N halmazon, mint annak a beágyazófüggvény szerinti képén. Ez a képhalmaz a \Z-nek azon részhalmaza, amely a pozitív egész számokat és a 0 egész számot tartalmazza. Ebben tehát ugyanúgy érvényes a Peano-axiómarendszer, így mostantól ezt fogjuk a természetes számok halmazának tekinteni. Ezután megvizsgáltuk, hogy mit értünk azalatt, hogy teljesülnek a „szokásos számolási szabályok”. Ennek keretében megismerkedtünk a „neutrális elem”, az „inverz elem”, a „gyűrű” és a „test” fogalmával. Végül megmutattuk, hogy az egész számok halmaza az összeadás és szorzás műveletével egy kommutatív, egységelemes gyűrűt alkot.
De vajon mit jelent a „nullosztómentesség” és az „integritástartomány” fogalma? Hogyan terjesszük ki a „kisebb-nagyobb” fogalmát az egész számok körére is, és miért fontos ez a kriptográfiai eljárások szempontjából? Milyen absztrakt algebrai megfontolások állnak ennek hátterében, és mit jelent ez általános gyűrűk esetén? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít az előző részben bevezetett alábbi definíciókra és a hozzájuk kapcsolódó tételekre:
A \Z halmazon az alábbi képlet szerint értelmezett \odot-tal jelölt kétváltozós műveletet szorzásnak nevezzük:
[(a;b)] \odot [(c;d)] = [(ac+bd; ad+bc)]A fentiekben + a 11.4. Definíció szerinti Peano-összeadást, az egymás után írás a 12.1. Definíció szerinti Peano-szorzást, [(x;y)] pedig a \Z halmaznak azon elemét jelöli, amelynek – mint ekvivalencia-osztálynak – eleme az (x;y) természetes számpár.
Legyen adott egy R halmaz és egy ezen értelmezett *-gal jelölt kétváltozós művelet, valamint legyen n az R halmaz egy eleme.
Az n elemet jobboldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
a*n=aAz n elemet baloldali neutrális elemnek nevezzük a * műveletre nézve, amennyiben tetszőleges R-beli a elemre teljesül az alábbi:
n*a=aHa egy n elem egyszerre jobb- és baloldali neutrális elem, akkor őt kétoldali neutrális elemnek, vagy egyszerűen csak neutrális elemnek nevezzük.
A szakirodalomban sok helyen találkozhatunk még a semleges elem, a nullelem, a zéruselem vagy az egységelem kifejezésekkel, valamint a 0 illetve az 1 jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
Legyen adott egy R halmaz egy rajta értelmezett * művelettel. Létezzen továbbá neutrális elem erre a műveletre nézve, amelyet jelöljünk n-nel.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b*b^{-1}=n, akkor b^{-1}-et a b elem jobboldali inverzének nevezzük a * műveletre nézve.
Ha egy adott b elemhez létezik olyan b^{-1}-gyel jelölt elem, amelyre b^{-1}*b=n, akkor b^{-1}-et a b elem baloldali inverzének nevezzük a * műveletre nézve.
Ha b^{-1} egyszerre jobb- és baloldali inverz, akkor őt a b elem kétoldali inverzének, vagy egyszerűen csak inverzének nevezzük a * műveletre nézve. Azt mondjuk, hogy a b elem invertálható, amennyiben létezik hozzá inverz elem a * műveletre nézve. Azt mondjuk, hogy a * művelet invertálható, ha minden R-beli elemhez létezik inverz erre a műveletre nézve.
A szakirodalomban sok helyen találkozhatunk még az ellentett elem vagy a reciprok kifejezésekkel, valamint a -b illetve az \frac{1}{b} jelölésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat és/vagy jelöléseket, ettől függetlenül ezek mind ugyanazt jelentik.
A \Z halmazon az alábbi képlet szerint értelmezett \ominus-szal jelölt kétváltozós műveletet kivonásnak nevezzük:
[(a;b)] \ominus [(c;d)] = [(a;b)] \oplus [(d;c)]Vagy a hagyományos jelölésekkel:
n - k = n + (-k)Ez tehát azt jelenti, hogy egy n egész számból egy k egész számot úgy vonunk ki, hogy hozzáadjuk az ellentettjét.
Tegyük fel, hogy adva van egy valamilyen R halmaz, amelyen értelmezve van két darab kétváltozós művelet. Az egyiket nevezzük összeadásnak és jelöljük +-szal. A másikat nevezzük szorzásnak és jelöljük \cdot-tal. Az így kapott (R,+,\cdot ) algebrai struktúrát gyűrűnek nevezzük, amennyiben teljesülnek rá az alábbi tulajdonságok – az úgynevezett gyűrűaxiómák:
- A + művelet kommutatív és asszociatív.
- A + műveletre nézve létezik neutrális elem. Ezt a gyűrű nullelemének nevezzük és 0-val jelöljük.
- A + művelet invertálható. Egy tetszőleges a elem +-ra vonatkozó inverzét -a-val jelöljük és a additív inverzének vagy ellentettjének nevezzük.
- A \cdot művelet asszociatív.
- Tetszőleges R-beli a, b és c elemekre teljesülnek az alábbi disztributivitási szabályok:
Amennyiben a \cdot művelet is kommutatív, úgy (R,+,\cdot )-et kommutatív gyűrűnek nevezzük.
Amennyiben a \cdot műveletre nézve is létezik neutrális elem, úgy ezt az elemet a gyűrű egységelemének nevezzük és 1-gyel jelöljük, (R,+,\cdot )-et pedig egységelemes gyűrűnek nevezzük.
Azt a gyűrűt, amely kizárólag a 0 elemet (azaz a gyűrű nullelemét) tartalmazza, nullgyűrűnek nevezzük. Ezt definíció szerint nem tekintjük egységelemes gyűrűnek annak ellenére, hogy a 0 ebben az elfajult esetben nyilvánvalóan neutrális elem az összeadáson kívül a szorzásra nézve is.
Ferdetestnek nevezzük azokat az egységelemes gyűrűket, amelyekben a \cdot műveletre nézve a gyűrű nullelemén kívül minden elemnek létezik inverze. Ha emellett a \cdot művelet még kommutatív is, akkor (R,+,\cdot )-et kommutatív ferdetestnek vagy egyszerűen csak testnek nevezzük (a nullgyűrű tehát nem test, mivel nem is egységelemes a definíció szerint). Egy tetszőleges a elem \cdot-ra vonatkozó inverzét ebben az esetben \frac{1}{a}-val vagy a^{-1}-gyel jelöljük és a multiplikatív inverzének nevezzük.
A 13.7. Definícióban bevezetett \Z halmaz egy kommutatív, egységelemes gyűrűt alkot a 13.12. Definíció szerinti \oplus és a 14.3. Definíció szerinti \odot műveletekkel.
E definíciók kontextusba helyezése, valamint a hozzájuk kapcsolódó tételek és egyéb fogalmak megismerése miatt erőteljesen ajánlott elolvasni az előző és az azelőtti részt, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
A bevezetőben azt írtuk, hogy a természetes számok beágyazása \Z-be „többnyire” teljessé vált. Ami még hátra van, és ami a továbbiakban szintén fontos lesz számunkra, az a 12.13. Definíció szerinti \leq rendezési reláció kiterjesztése erre a számhalmazra. Szeretnénk azonban ezt a problémakört minél általánosabban – lehetőleg az előző részben megismert gyűrűk szintjén – tárgyalni. Ehhez először a gyűrűk néhány alapvető tulajdonságával fogunk megismerkedni.
Gyűrűk alapvető tulajdonságai
A gyűrűaxiómákat a 14.12. Definícióból már ismerjük. Ezek mindössze annyit követelnek meg, hogy legyen egy halmazunk két művelettel, amelyeket most önkényesen „összeadásnak” és „szorzásnak” nevezünk. Az „összeadás” legyen kommutatív és asszociatív, létezzen rá nézve neutrális elem (amelyet nullelemnek nevezünk és 0-val jelölünk), valamint minden a elemnek létezzen inverze erre a műveletre nézve (amelyet a ellentettjének nevezünk és -a-val jelölünk). Ezen kívül a „szorzásnak” asszociatívnak kell lennie, valamint teljesülnie kell a két disztributivitási szabálynak. Mivel az ellentett létezése követelmény, ezért minden gyűrűben korlátlanul el lehet végezni a „kivonást”.
Egy általános gyűrű mindössze „ennyit tud”. Azaz esetében még a „szorzás” sem feltétlenül kommutatív. Ezért kellett rögzíteni két disztributivitási szabályt is. Továbbá egységelem sem feltétlenül létezik rá nézve. Attól függően, hogy ezen extra tulajdonságok közül melyik teljesül pluszban, beszélhetünk rendre kommutatív gyűrűről, egységelemes gyűrűről vagy kommutatív és egységelemes gyűrűről. Végül az olyan kommutatív és egységelemes gyűrűket testnek neveztük, amelyekben „osztani” is lehet minden nem 0 elemmel (azaz amelyben minden nem 0 elemnek létezik inverze a szorzásra nézve is).
Azt ugye már tudjuk, hogy az egész számok egy kommutatív, egységelemes gyűrűt alkotnak a szokásos műveletekkel (14.13. Tétel). Ez a gyűrű azonban nem test, hiszen csak az egységelemnek és ellentettjének (azaz az 1 és a -1 egész számoknak) létezik multiplikatív inverze: méghozzá önmaga. Azt javasoljuk az Olvasónak, hogy ezt saját maga is gondolja végig a 14.3. Definíció és a 13.10. Definíció alapján.
Most néhány, az általános iskolából már jól ismert összefüggést fogunk bizonyítani, ám ezúttal általános gyűrűkre. Ne feledjük azonban, hogy ezen az absztrakciós szinten a gyűrűaxiómákon kívül nem feltételezhetünk semmi egyebet ezekkel az algebrai struktúrákkal kapcsolatban. Még azt sem, hogy egyáltalán számokról van-e szó. Az alábbi – sokak számára jól ismert – összefüggések tehát csak és kizárólag a gyűrűaxiómák logikai következményei.
15.1. Tétel:
Legyen (R, +, \cdot ) tetszőleges gyűrű a szokásos jelölésekkel. Ekkor tetszőleges a és b elemekre teljesülnek az alábbiak:
- 0a=a0=0
- -(-a)=a
- a(-b)=(-a)b=-(ab)
- (-a)(-b)=ab
- -(a+b)=(-a)+(-b)
Bizonyítás:
Igazoljuk először az 1. állítást. Mivel 0 a gyűrű nulleleme, ezért a 2. gyűrűaxióma miatt 0+0=0, és így a disztributivitási szabály miatt:
0a = (\underbrace{0+0}_{=0})a = 0a+0aMindkét oldalhoz hozzáadva 0a ellentettjét (amely ugye a 3. gyűrűaxióma miatt létezik) a tétel 1. állítását kapjuk:
0 = 0aA 0=a0 azonosság ugyanilyen módon igazolható, csak ekkor a másik oldali disztributivitási szabályt kell alkalmazni.
A 2. állítás baloldalán -(-a) szerepel, amely nem más, mint -a ellentettje. Ezért a 3. gyűrűaxióma miatt kettejük összege épp a nullelem kell legyen:
-(-a)+(-a)=0Mindkét oldalhoz hozzáadva a-t a következőt kapjuk:
-(-a)+\underbrace{0}_{=(-a)+a}=0+aA keletkező 0-kat mindkét oldalról elhagyhatjuk a 2. gyűrűaxióma miatt, megkapva így a tétel 2. állítását:
-(-a)=aMost a 3. állítást igazoljuk. Az 1. állítás miatt 0=0b, de mivel 0 a gyűrű nulleleme, ezért a 3. gyűrűaxióma miatt -a+a=0, és így a disztributivitási szabály miatt:
0=0b=(\underbrace{-a+a}_{=0})b=(-a)b + abMivel ab-hez (-a)b-t adva épp a nullelemet kapjuk, ezért (-a)b valóban ab ellentettje. Ez viszont a 14.10. Tétel miatt egyértelmű, így tehát:
(-a)b = -(ab)Az a(-b)=-(ab) azonosság ugyanilyen módon igazolható, csak ekkor a másik oldali disztributivitási szabályt kell alkalmazni.
A 4. állítás könnyen adódik az előző 3 állításból. Az 1. állítás miatt 0=0(-b), de mivel 0 a gyűrű nulleleme, ezért a 3. gyűrűaxióma miatt -a+a=0, és így a disztributivitási szabály miatt:
0=0(-b)=(\underbrace{-a+a}_{=0})(-b)=(-a)(-b) + a(-b)A 3. állítás miatt a fenti egyenlet jobboldalán lévő második tag -(ab)-vel egyenlő, azaz:
0=(-a)(-b) + \underbrace{(-(ab))}_{=a(-b)}Mivel (-a)(-b)-hez -(ab)-t adva épp a nullelemet kapjuk, ezért (-a)(-b) valóban -(ab) ellentettje. Ez viszont a 14.10. Tétel miatt egyértelmű, így tehát:
(-a)(-b) = -(-(ab))Az egyenlet jobboldalát viszont a 2. állítás miatt átírhatjuk a következőképpen, megkapva a tétel 4. állítását:
(-a)(-b) = \overbrace{ab}^{=-(-(ab))}Végül az 5. állításhoz azt kell belátnunk, hogy az (a+b) ellentettje – azaz a -(a+b) elem – valóban megegyezik a (-a)+(-b) elemmel. A 14.10. Tétel miatt az ellentettképzés asszociatív művelet esetén egyértelmű, így ez pontosan akkor teljesül, ha:
(a+b)+((-a)+(-b))=0Az 1. gyűrűaxióma alapján ez a kifejezés tetszőlegesen átzárójelezhető (asszociatív) és átsorrendezhető (kommutatív), így felírható így is:
\underbrace{(a+(-a))}_{=0}+\underbrace{(b+(-b))}_{=0}=0+0=0Így tehát (a+b) ellentettje – azaz a -(a+b) elem – tényleg megegyezik a (-a)+(-b) elemmel, ahogyan a tétel állítja.
∎Az alábbi egyszerű tétel a nullelem és az egységelem egymáshoz való viszonyáról szól:
15.2. Tétel:
Legyen (R, +, \cdot ) tetszőleges egységelemes gyűrű a szokásos jelölésekkel. Ekkor 0\neq 1, azaz az egységelem biztosan különbözik a nullelemtől.
♣Bizonyítás:
Tegyük fel, hogy létezik olyan gyűrű, amelyben 0=1. Mivel 1 neutrális elem a szorzásra nézve, ezért tetszőleges a elemre igaz az alábbi:
a=a\cdot 1=a\cdot \underbrace{0}_{=1}Ez viszont a 15.1. Tétel 1. állítása miatt 0-val egyenlő. Ez azt jelentené, hogy egy ilyen gyűrűnek valójában egyetlen eleme lenne, méghozzá a nullelem. A 14.12. Definícióban ezt a gyűrűt nullgyűrűnek neveztük, amelyet nem tekintünk egységelemesnek.
∎Az előző rész elején azt vizsgáltuk, hogy vajon a természetes számok \N halmazán érvényesek-e a szokásos egyenletrendezési szabályok. Ennek kapcsán merült fel az a kérdés, hogy vajon egy egyenlet mindkét oldalát el lehet-e „osztani” egy adott nem nulla természetes számmal annak ellenére, hogy az osztás művelete nem értelmezhető ezen a számhalmazon. Ezt a 14.1. Lemma következményeként a 14.2. Lemma tette lehetővé számunkra.
Most általános gyűrűkre is megvizsgáljuk ezt a kérdést. Az nyilvánvaló, hogy egy tetszőleges gyűrűn értelmezett egyenlet mindkét oldalából „ki lehet vonni” ugyanazt az elemet. A gyűrűkben ugyanis korlátlanul elvégezhető a „kivonás”. Az „osztás” azonban csak testekben értelmezhető korlátlanul, általános gyűrűkben nem. Ennek ellenére vannak olyan gyűrűk, amelyek nem testek ugyan, ám a természetes számokhoz hasonlóan egy rajtuk értelmezett egyenlet mindkét oldalát bizonyos esetekben „el lehet osztani” ugyanazzal a nem 0 elemmel. Ezeknek a gyűrűknek speciális nevük van:
15.3. Definíció (Nullosztómentes gyűrű):
Legyen (R,+,\cdot ) tetszőleges gyűrű a szokásos jelölésekkel, valamint legyen a és b a gyűrű két tetszőleges eleme. Ha a\cdot b=0, de sem a\neq 0, sem pedig b\neq 0, akkor azt mondjuk, hogy a baloldali nullosztó, b pedig jobboldali nullosztó.
Másként fogalmazva egy a elemet akkor nevezünk baloldali nullosztónak, ha a\neq 0, és létezik olyan b\neq 0 elem, amelyre a\cdot b=0 teljesül. Megint másként fogalmazva egy b elemet akkor nevezünk jobboldali nullosztónak, ha b\neq 0, és létezik olyan a\neq 0 elem, amelyre a\cdot b=0 teljesül.
Az (R,+,\cdot ) gyűrűt nullosztómentes gyűrűnek hívjuk, ha nincs benne sem jobb-, sem pedig baloldali nullosztó. Másként fogalmazva egy nullosztómentes gyűrűben a\cdot b=0-ból következik, hogy a=0 vagy b=0.
A szakirodalomban sok helyen találkozhatunk még a zérusosztó, illetve a zérusosztómentes gyűrű kifejezésekkel is. Kontextustól függően mi is felváltva fogjuk használni ezeket a fogalmakat, ettől függetlenül ezek mind ugyanazt jelentik.
♣Ez a definíció elsőre furcsának tűnhet. Az általános iskolából ugyanis megszokhattuk, hogy egy szorzat csak úgy lehet 0, ha legalább az egyik tényezője 0. Gyűrűk esetén – mint hamarosan látni fogjuk – ez általánosságban nem igaz. Ezért mindig körültekintően kell eljárnunk, amikor egyenleteket oldunk meg valamilyen gyűrűben. A nullosztómentes gyűrűkben azonban az alábbi tétel alapján nyugodtan alkalmazhatjuk a szokásos egyenletrendezési szabályokat.
15.4. Tétel:
Legyen (R, +, \cdot ) tetszőleges (nem feltétlenül kommutatív) nullosztómentes gyűrű a szokásos jelölésekkel. Ekkor bármely a, b és c\neq 0 elemek esetén teljesülnek az alábbiak:
- Ha a\cdot c = b\cdot c, akkor a=b.
- Ha c\cdot a = c\cdot b, akkor a=b.
Igaz a tétel megfordítása is: Amennyiben tetszőleges a, b és c\neq 0 elemek esetén teljesül a fenti két tulajdonság, akkor az (R,+,\cdot ) gyűrű nullosztómentes.
♣Bizonyítás:
Nézzük az 1. tulajdonság bizonyítását. Az ac=bc egyenlet mindkét oldalához adjuk hozzá bc ellentettjét (amely ugye a 3. gyűrűaxióma miatt létezik):
ac+(-(bc))=0A baloldal második tagja a 15.1. Tétel 3. pontja miatt így is írható:
ac+(-b)c=0Az egyenlet baloldala az 5. gyűrűaxióma miatt átírható erre:
(a+(-b))c=0Mivel a gyűrű nullosztómentes, ezért nem létezik benne jobboldali nullosztó, így c sem lehet az. Ez a 15.3. Definíció miatt azt jelenti, hogy nem létezik olyan nem 0 elem, amelyet c-vel jobbról megszorozva a nullelemet kapnánk. Másként fogalmazva a fenti egyenlet csak akkor teljesülhet, ha a+(-b)=0. Mindkét oldalhoz b-t adva megkapjuk a tételben szereplő 1. tulajdonságot: a=b.
A 2. tulajdonság ugyanezen a módon igazolható, csak ekkor a baloldali disztributivitást és a baloldali nullosztó fogalmát kell felhasználni.
Most bizonyítjuk a tétel megfordítását. Ez ugye azt állítja, hogyha teljesül a tételbeli mindkét tulajdonság egy gyűrűre, akkor a gyűrű nullosztómentes. Vizsgáljuk meg külön-külön, mi a következménye az 1. és a 2. tulajdonság teljesülésének.
Ha az 1. tulajdonság teljesül, akkor az azt jelenti, hogy tetszőleges a, b és c\neq 0 elemek esetén az ac=bc állításból következik az a=b állítás. Speciálisan, ha b történetesen épp a gyűrű nulleleme, akkor tetszőleges a és c\neq 0 elemek esetén az ac=0c állításból következne az a=0 állítás. Ezt a 15.1. Tétel 1. pontja miatt úgy is megfogalmazhatjuk, hogy tetszőleges a és c\neq 0 elemek esetén az ac=\underbrace{0}_{=0c} állításból következne az a=0 állítás. A 15.3. Definíció miatt ez épp azt jelenti, hogy a gyűrűben nem létezik jobboldali nullosztó.
Ha a 2. tulajdonság teljesül, akkor ugyanilyen gondolatmenetet követve azt kapjuk, hogy a gyűrűben nem létezik baloldali nullosztó.
Ha tehát mindkét tulajdonság teljesül, akkor a gyűrű nullosztómentes.
∎Végezetül érdemes megismerkedni még egy fogalommal, amely gyakran fordul elő a szakirodalomban.
15.5. Definíció (Integritástartomány):
A nullosztómentes és kommutatív gyűrűket integritástartományoknak nevezzük.
Megjegyezzük, hogy ez a definíció nem követeli meg egységelem – azaz a szorzásra nézve neutrális elem – létezését. Sajnos a magyar terminológiában sincs külön neve az egységelemmel is rendelkező integritástartományoknak, ezért a továbbiakban mi is kénytelenek leszünk körülírni az ilyen eseteket, amennyiben az szükséges.
♣Egy integritástartományban tehát minden „ugyanúgy működik”, ahogy az általános iskolában megszokhattuk. Ez a fogalom az egész számok szokásos műveletekkel alkotott algebrai struktúrájának általánosítása, mint ahogyan az alábbi tétel is mutatja.
15.6. Tétel:
Az egész számok \Z halmaza egy egységelemet tartalmazó integritástartományt alkot a szokásos összeadás (13.12. Definíció) és a szokásos szorzás (14.3. Definíció) műveletekkel.
♣Bizonyítás:
A korábban már bizonyított 14.13. Tétel szerint az egész számok szorzása kommutatív, valamint létezik egységelem, ezért csak a nullosztómentességet kell bizonyítani.
Egy pillanatra térjünk vissza a 13.7. Definícióban bevezetett jelölésekre, amikoris az egész számokat még természetes számpárok ekvivalencia-osztályaiként jelöltük [(a;b)] alakban. A 13.10. Definícióban három részre osztottuk az egész számokat. A pozitív egész számokat [(n;0)], a negatív egész számokat [(0;n)], végül a nulla egész számot [(0;0)] alakban írtuk fel. Ezt a 13.9. Tétel alapján tehettük meg, amely szerint minden egész szám felírható e három közül valamelyik alakban.
Az egész számok szorzásának 14.3. Definíciója alapján ekkor bármely két nemnulla egész szám szorzata az alábbi két alak valamelyikére hozható, ahol n és k valamilyen nemnulla természetes számok:
\begin{aligned}&[(nk;0)]\\&[(0;nk)]\end{aligned}A 14.1. Lemma alapján nemnulla természetes számok szorzata nem lehet 0, azaz ebben az esetben nk \neq 0. Ebből viszont a 13.9. Tétel alapján az következik, hogy sem [(nk;0)], sem pedig [(0;nk)] nem lehet a nulla egész szám.
Azt kaptuk tehát, hogy nemnulla egész számok szorzata nem lehet a nulla egész szám, azaz a (\Z , +, \cdot ) gyűrű valóban nullosztómentes.
∎A szokásos egyenletrendezési játékszabályokat tehát az általános gyűrűk szintjén tisztáztuk. Most nézzük meg, hogy mi a helyzet az úgynevezett egyenlőtlenségek esetén ugyanezen az absztrakciós szinten.
Relációk és műveletek kapcsolata gyűrűkben
A 12. részben tisztáztuk az úgynevezett rendezési relációk és a rendezett halmazok fogalmát. Ezeknek a fogalmaknak a segítségével absztrakt szinten tudunk beszélni „kisebb-nagyobb”-jellegű viszonyokról tetszőleges halmaz elemei között. Most ezt a kérdéskört szeretnénk kiterjeszteni általános gyűrűkre – és természetesen speciálisan az egész számok gyűrűjére – is. Azt javaslom az Olvasónak, hogy a folytatás előtt ismételje át az alábbi kapcsolódó fogalmakat:
Ha H egy tetszőleges halmaz, akkor a H\times H halmaz egy valamilyen R részhalmazát kétváltozós relációnak nevezzük. Ha a és b a H halmaz két tetszőleges – nem feltétlenül különböző – eleme, és az (a; b) rendezett pár benne van az R halmazban, akkor azt mondjuk, hogy a és b között fennáll az R reláció. Ezt így jelöljük: aRb.
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció. Ha H minden a elemére teljesül, hogy aRa, akkor azt mondjuk, hogy az R reláció reflexív.
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a és b a H halmaz tetszőleges, de egymástól különböző elemei – azaz a\neq b. Ha minden ilyen esetben aRb és bRa közül legfeljebb az egyik teljesül, akkor azt mondjuk, hogy az R reláció antiszimmetrikus.
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a, b és c a H halmaz tetszőleges elemei. Ha minden ilyen esetben aRb és bRc együttes teljesülése esetén aRc is teljesül, akkor azt mondjuk, hogy az R reláció tranzitív.
Legyen adott egy H halmaz és egy ezen a halmazon értelmezett R reláció, valamint tegyük fel, hogy a és b a H halmaz tetszőleges elemei. Ha minden ilyen esetben aRb és bRa közül legalább az egyik teljesül, akkor azt mondjuk, hogy az R reláció trichotóm.
Tegyük fel, hogy adott egy H halmaz, és egy rajta értelmezett R reláció. Amennyiben R egyszerre reflexív, antiszimmetrikus és tranzitív, úgy R-et H feletti részbenrendezésnek hívjuk, vagy pedig azt mondjuk, hogy a H egy részbenrendezett halmaz az R relációval.
Az R relációt teljes rendezésnek nevezzük H felett, ha a fentieken kívül a trichotómia is teljesül rá. Ilyenkor azt mondjuk, hogy a H egy rendezett halmaz az R relációval.
A 12.12. Definíció alapján rendezett halmaz alatt tehát dióhéjban egy olyan, kétváltozós relációval (12.7. Definíció) ellátott halmazt értünk, amelynek elemei között e reláció segítségével valamilyen egyértelmű sorrend állítható fel. Mivel egy gyűrű is tulajdonképpen egy halmaz, így ez a fogalom nyilván ezekre is értelmezhető. Csakhogy a gyűrűk rendelkeznek két művelettel is. Ezért az ő esetükben egy rendezési relációtól azt is elvárjuk, hogy bizonyos értelemben „jól viselkedjenek” ezekkel a műveletekkel.
Hogy ez alatt pontosan mit értünk, azt egy példán keresztül világítjuk meg. Vizsgáljuk meg például, hogy a természetes számok \N halmazán értelmezett 12.13. Definíció szerinti rendezési reláció milyen kapcsolatban van az összeadás és a szorzás műveletével. Erről szól az alábbi tétel.
15.7. Tétel:
A természetes számok \N halmazán tetszőleges a, b és c számokra igazak az alábbiak:
- Ha a\leq b akkor a+c \leq b+c.
- Ha a\leq b akkor ac \leq bc.
Ha tehát egy egyenlőtlenség mindkét oldalához hozzáadjuk ugyanazt a természetes számot, vagy mindkét oldalát megszorozzuk ugyanazzal a természetes számmal, akkor az egyenlőtlenség továbbra is érvényben marad.
♣Bizonyítás:
Az a\leq b reláció a 12.13. Definíció miatt azt jelenti, hogy létezik olyan k természetes szám, amelyre teljesül az alábbi:
a+k=bAz egyenlet mindkét oldalához c-t hozzáadva, illetve mindkét oldalt c-vel megszorozva ezeket kapjuk:
\begin{aligned}(a+k)+c &= b+c \\ (a+k)c &= bc\end{aligned}A két egyenlet baloldalai a Peano-összeadás asszociativitása (11.8. Tétel) és kommutativitása (11.7. Tétel), valamint a Peano-szorzás disztributivitása (12.5. Tétel) miatt így írhatók:
\begin{aligned}(a+c)+k &= b+c \\ ac+kc &= bc\end{aligned}Egyrészt létezik tehát olyan természetes szám (nevezetesen k), amelyet a+c-hez adva b+c-t kapunk. Másrészt pedig létezik olyan természetes szám is (nevezetesen kc), amelyet ac-hez adva bc-t kapunk. Ez a 12.13. Definíció alapján éppen azt jelenti, hogy:
\begin{aligned}a+c &\leq b+c \\ ac &\leq bc\end{aligned} ∎Egy ehhez hasonló tulajdonság általánosságban is hasznos lehet egy műveletekkel ellátott algebrai struktúra alaphalmazán értelmezett reláció esetén. Erről szól az alábbi definíció.
15.8. Definíció:
Legyen H egy tetszőleges halmaz, amelyen értelmezve van egyrészt egy *-gal jelölt kétváltozós művelet, másrészt pedig egy valamilyen \simeq-val jelölt kétváltozós reláció. Amennyiben H tetszőleges a, b és c elemeire az a\simeq b reláció teljesülése esetén az a*c \simeq b*c reláció is teljesül, akkor azt mondjuk, hogy a \simeq reláció kompatibilis a * művelettel.
♣Ezzel a szóhasználattal élve tehát a fenti tétel úgy is megfogalmazható, hogy a természetes számok rendezési relációja kompatibilis a Peano-összeadás és a Peano-szorzás műveletével.
Most nézzük, mit tudunk elmondani egy gyűrű alaphalmazán értelmezett rendezési reláció és a gyűrű két műveletének viszonyáról. Tegyük hát fel, hogy (R,+,\cdot ) egy gyűrű. Kérdés, hogy vajon létezhet-e olyan részbenrendezés a gyűrű alaphalmazán, amely mindkét művelettel kompatibilis? Ennek megválaszolásához az alábbi segédtételre lesz szükségünk.
15.9. Lemma:
Tegyük fel, hogy (R,+,\cdot ) egy tetszőleges gyűrű, amelynek R alaphalmazán értelmezve van egy részbenrendezési reláció. Jelöljük ezt a relációt a \leq szimbólummal, és tegyük fel, hogy a \leq reláció kompatibilis a gyűrű + műveletével. Ekkor tetszőleges a, b és c elemekre igazak az alábbiak:
- Ha 0\leq a, akkor 0\geq (-a).
- Ha ac\leq bc, akkor a(-c)\geq b(-c).
- Ha ca\leq cb, akkor (-c)a\geq (-c)b.
Itt 0 jelöli a gyűrű nullelemét, -x pedig az x elem ellentettjét. Megjegyezzük még, hogy kommutatív gyűrű esetén természetesen a 2. és 3. tulajdonság egymással ekvivalens.
♣Bizonyítás:
Az 1. tulajdonság esetén tehát az a kiindulási feltételünk, hogy 0\leq a. Mivel a \leq reláció kompatibilis az összeadással, ezért mindkét oldalhoz a ellentettjét adva – amely a 3. gyűrűaxióma miatt létezik – továbbra is érvényes egyenlőtlenséget kapunk:
0+(-a)\leq a+(-a)Mivel 0 a gyűrű nulleleme, ezért a baloldali összegből őt elhagyhatjuk, a jobboldali összeg pedig épp a nullelemmel lesz egyenlő. Így tulajdonképpen megkapjuk az 1. állítást:
(-a)\leq 0A 2. tulajdonság esetén a kiindulási feltételünk az, hogy ac\leq bc. Mivel a \leq reláció kompatibilis az összeadással, ezért mindkét oldalhoz jobbról -(ac)-t, balról pedig -(bc)-t adva továbbra is érvényes egyenlőtlenséget kapunk:
(-(bc))+\underbrace{ac+(-(ac))}_{=0}\leq \underbrace{(-(bc))+bc}_{=0}+(-(ac))Mindkét oldalon a két egymásnak ellentett tag kiejti egymást, így ezt kapjuk:
-(bc)\leq -(ac)Ez viszont a 15.1. Tétel 3. pontja miatt így is írható, megkapva ezzel a 2. állítást:
b(-c)\leq a(-c)Végül a 3. tulajdonság ugyanilyen módon igazolható, csak ekkor a kiindulási feltétel mindkét oldalához -(ca)-t és -(cb)-t kell adni.
∎Ez alapján úgy néz ki, hogy nem mindegy, hogy egy egyenlőtlenség mindkét oldalát egy adott elemmel, vagy annak ellentettjével szorozzuk-e meg. Ezt a sajnálatos tényt fogalmazza meg az alábbi tétel.
15.10. Tétel:
Tegyük fel, hogy (R,+,\cdot ) egy kommutatív gyűrű, amelynek R alaphalmazán értelmezve van egy részbenrendezési reláció. Jelöljük ezt a relációt a \leq szimbólummal, és tegyük fel, hogy a \leq reláció kompatibilis a gyűrű + műveletével. Tételezzük fel továbbá, hogy a gyűrű valamilyen a és b elemei között fennál az a\leq b egyenlőtlenség. Ekkor teljesülnek az alábbiak:
- Ha minden c\geq 0 esetén ac\leq bc, akkor minden d\leq 0 esetén ad\geq bd.
- Ha minden c\geq 0 esetén ac\geq bc, akkor minden d\leq 0 esetén ad\leq bd.
Megjegyezzük, hogy a tétel elején azért korlátozódtunk kommutatív gyűrűkre, hogy ne kelljen a fordított sorrendű szorzásokra is megfogalmazni (és aztán persze bizonyítani) ugyanezt a két tulajdonságot. Az Olvasóra bízzuk annak átgondolását, hogy hogyan lehet ezt a tételt (és bizonyítását) kiterjeszteni a nemkommutatív esetekre is.
♣Bizonyítás:
Kezdjük az 1. tulajdonsággal. Itt a kiindulási feltételünk az, hogy az a\leq b egyenlőtlenség mindkét oldalát egy „legalább” 0 elemmel megszorozva a reláció iránya nem változik. Azt kell belátni, hogy ebben az esetben egy „legfeljebb” 0 elemmel való szorzás viszont megfordítja a relációt. A tételben ezt a „legfeljebb” 0 elemet d-vel jelöltük, azaz d\leq 0. Ebből viszont a 15.9. Lemma 1. pontja miatt következik, hogy (-d)\geq 0, azaz d ellentettje „legalább” 0.
A kiindulási feltételünk szerint viszont bármilyen „legalább” 0 elemmel szorozva az a\leq b relációt, annak iránya nem változik. Ez tehát igaz lesz (-d)-re is, és így:
a(-d)\leq b(-d)Ebből viszont a 15.9. Lemma 2. pontja miatt megkapjuk az 1. tulajdonságot:
ad\geq bdA 2. tulajdonság bizonyítása ehhez nagyon hasonló. Itt a kiindulási feltételünk az, hogy az a\leq b egyenlőtlenség mindkét oldalát egy „legalább” 0 elemmel megszorozva a reláció iránya megfordul. Azt kell belátni, hogy ebben az esetben egy „legfeljebb” 0 elemmel való szorzás viszont nem változtatja meg a reláció irányát. A tételben ezt a „legfeljebb” 0 elemet d-vel jelöltük, azaz d\leq 0. Ebből viszont a 15.9. Lemma 1. pontja miatt megintcsak következik, hogy (-d)\geq 0, azaz d ellentettje „legalább” 0.
A kiindulási feltételünk szerint viszont bármilyen „legalább” 0 elemmel szorozva az a\leq b relációt, annak iránya megfordul. Ez tehát igaz lesz (-d)-re is, és így:
a(-d)\geq b(-d)Ebből viszont a 15.9. Lemma 2. pontja miatt megkapjuk a 2. tulajdonságot:
ad\leq bd ∎Hogy ez miért sajnálatos?
Azért, mert ez azt jelenti, hogy egy gyűrűben egy rendezési reláció egyszerre nem lehet kompatibilis mindkét művelettel – legalábbis semmilyen gyakorlatilag hasznos esetben. Most megmutatjuk, miért.
Tekintsünk továbbra is egy (R,+,\cdot ) gyűrűt, amelyről az egyszerűség kedvéért most tételezzük fel, hogy kommutatív. Jelölje a rendezési relációnkat továbbra is a \leq szimbólum, és tegyük fel, hogy a\leq b teljesül valamilyen a és b gyűrűelemekre. Ha mármost \leq kompatibilis lenne mindkét művelettel, akkor ez egyrészt a szorzással való kompatibilitás miatt azt jelentené, hogy tetszőleges c esetén mindkét alábbi egyenlőtlenség teljesülne:
\begin{aligned}ac &\leq bc \\ a(-c) &\leq b(-c)\end{aligned}Másrészt az összeadással való kompatibilitás miatt a 15.9. Lemma továbbra is igaz lenne, ezért az a(-c)\leq b(-c) egyenlőtlenségből következne az ac\geq bc egyenlőtlenség, tehát végsősoron ezt kapnánk:
\begin{aligned}ac &\leq bc \\ ac &\geq bc\end{aligned}Mivel azonban a \leq reláció egy rendezési reláció, ezért a 12.12. Definíció miatt antiszimmetrikus. Ez viszont a 12.9. Definíció miatt épp azt jelenti, hogy a fenti két egyenlőtlenség csak abban az esetben teljesülhet egyszerre, ha ac=bc.
Összefoglalva tehát azt kapnánk, hogy tetszőleges a, b és c gyűrűelemekre a\leq b teljesülése esetén ac=bc is teljesülne. Ez például egy nullosztómentes gyűrűben a 15.4. Tétel miatt azt jelentené, hogy a\leq b-ből következne, hogy a=b. Így nem lenne túl sok értelme rendezésről beszélni.
Kénytelenek leszünk tehát a mindkét művelettel való kompatibilitásnál némileg gyengébb követelményeket támasztani a gyűrűkön „jól viselkedő” rendezési relációkkal szemben.
Gyűrűk rendezési axiómái
Az előző szakasz tanulságai alapján most a gyűrűaxiómák után megfogalmazunk két újabb axiómát. Ezeket egy gyűrűn értelmezett rendezési relációnak kell majd teljesítenie ahhoz, hogy őt „jól viselkedőnek” tekintsük. Ezeket rendezési axiómáknak nevezzük.
Az már fix, hogy az első rendezési axióma az összeadással való teljes kompatibilitás lesz. A szorzásra sajnos a 15.10. Tétel miatt ilyet nem tudunk előírni. Eszerint ugyanis ha a c\geq 0 elemekkel való szorzásra követeljük meg azt, hogy a rendezés iránya megmaradjon, akkor a c\leq 0 elemekkel való szorzás rendezésfordító lesz. Ha viszont a c\leq 0 elemekkel való szorzásra szeretnénk megtartani a rendezés irányát, akkor viszont a c\geq 0 esetekben lesz rendezésfordító a szorzás. Választanunk kell tehát, hogy melyiket tekintsük axiómának e kettő közül.
Alapvetően ugye az a célunk, hogy a természetes számok rendezését terjesszük ki az egész számok (\Z ,+,\cdot ) gyűrűjére. Márpedig ebben a gyűrűben épp a pozitív egész számok és a 0 felelnek meg a természetes számoknak. Célszerű tehát, ha az ezzel analóg c\geq 0 esetekben követeljük meg a rendezés tartását az általános gyűrűk rendezési axiómáinak rögzítésekor is. Mivel nem akarunk kizárólag a kommutatív gyűrűkre szorítkozni, ezért mindkét irányú szorzásra elő kell írnunk ezt a feltételt. Így tehát a rendezési axiómákat a következőképpen célszerű megadni.
15.11. Definíció (Rendezett gyűrű):
Legyen (R,+,\cdot ) egy tetszőleges gyűrű, valamint a gyűrű R alaphalmazán legyen értelmezve egy részbenrendezési reláció, amelyet jelöljünk most a \leq szimbólummal. Tegyük fel, hogy tetszőleges a, b és c gyűrűelemek esetén teljesülnek az alábbi követelmények – az úgynevezett rendezési axiómák:
- Ha a\leq b, akkor a+c\leq b+c.
- Ha a\leq b és c\geq 0, akkor ac\leq bc és ca\leq cb.
Ekkor azt mondjuk, hogy (R,+,\cdot ) egy részbenrendezett gyűrű a \leq relációra nézve. Amennyiben a \leq reláció egy teljes rendezés – azaz bármely két gyűrűelem „összehasonlítható” egymással –, akkor azt mondjuk, hogy (R,+,\cdot ) egy teljesen rendezett gyűrű a \leq relációra nézve.
Egy (R,+,\cdot ) gyűrűre akkor mondjuk, hogy részbenrendezhető, ha létezik olyan részbenrendezési reláció a gyűrű R alaphalmazán, amely teljesíti a fenti két axiómát. Az (R,+,\cdot ) gyűrűre akkor mondjuk, hogy teljesen rendezhető, ha létezik a fenti axiómákat kielégítő teljes rendezés az R alaphalmazon.
♣Az egész számok gyűrűjét a 13.10. Definíció alapján három részre osztottuk. Megkülönböztettünk negatív és pozitív egész számokat, és a nulla egész számot, amelyet nem tekintettünk sem pozitívnak, sem pedig negatívnak. Habár ezeket a fogalmakat bármiféle rendezési relációtól függetlenül vezettük be a kapcsolódó cikkben, ám hamarosan látni fogjuk, hogy szoros összefüggésben van a most következő fogalmakkal.
15.12. Definíció (Pozitivitástartomány):
Tegyük fel, hogy (R,+,\cdot ) egy részbenrendezhető gyűrű, és legyen \leq egy olyan részbenrendezés a gyűrű R alaphalmazán, amely teljesíti a 15.11. Definíció szerinti rendezési axiómákat. Ekkor azoknak az a\neq 0 gyűrűelemeknek a halmazát, amelyekre teljesül az a\geq 0 reláció, a gyűrű pozitivitástartományának nevezzük a \leq rendezésre nézve, és P_{\leq}-vel jelöljük. A P_{\leq} halmazban lévő elemekre ilyenkor azt mondjuk, hogy pozitívak a \leq rendezésre nézve.
Ehhez hasonlóan azoknak az a\neq 0 gyűrűelemeknek a halmazát, amelyekre teljesül az a\leq 0 reláció, a gyűrű negativitástartományának nevezzük a \leq rendezésre nézve, és -P_{\leq}-vel jelöljük. A -P_{\leq} halmazban lévő elemekre ilyenkor azt mondjuk, hogy negatívak a \leq rendezésre nézve.
♣Megjegyzés:
A 15.9. Lemma 1. pontjából azonnal következik, hogy ha egy gyűrűelem pozitív egy rendezésre nézve, akkor az ellentettje negatív, illetve visszafelé: ha egy gyűrűelem negatív egy rendezésre nézve, akkor az ellentettje pozitív.
Igaz továbbá az is, hogy nem létezik egyszerre pozitív és negatív gyűrűelem semmilyen rendezésre nézve. Ha ugyanis valamilyen a gyűrűelem egyszerre lenne pozitív és negatív, akkor 0\leq a és a\leq 0 egyszerre teljesülne. Az antiszimmetria miatt azonban ekkor a=0 lenne, azonban ez ellentmondana annak, miszerint a nullelem definíció szerint se nem pozitív, se nem negatív.
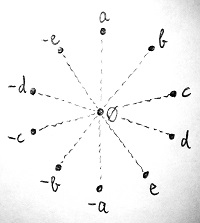
♣Vegyünk példaképp egy 11 elemű gyűrűt, és rajzoljuk fel az alaphalmazát a benne található elemekkel. Középen a gyűrű nulleleme, körülötte pedig a többi elem helyezkedjen el. Ezen kívül minden elem és az ő ellentettje legyen egymással szemben. Ez az elrendezés látható az alábbi ábrán:
Tegyük fel, hogy létezik ezen a gyűrűn 3 olyan rendezési reláció is, amelyek teljesítik a 15.11. Definíció szerinti rendezési axiómákat. Az alábbi ábrán egy példa látható arra, hogy az ezekhez tartozó pozitivitástartományok (P_1, P_2 és P_3) és negativitástartományok (-P_1, -P_2 és -P_3) hogyan helyezkedhetnek el a gyűrű alaphalmazán belül:
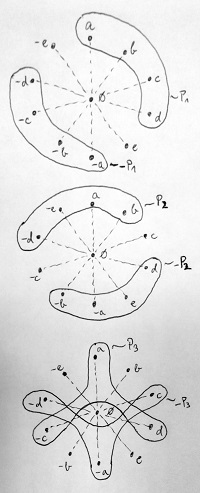
Megjegyzendő, hogy létezhet olyan elem a gyűrűben akár a nullelemen kívül is, amely se nem pozitív, se nem negatív egy adott rendezésre nézve. Ne felejtsük el ugyanis, hogy a részbenrendezés 12.12. Definíciója nem követeli meg a trichotómiát, vagyis azt, hogy bármely két elem összehasonlítható legyen. A fenti ábrán látható például, hogy az e elem és a 0 nem összehasonlítható a P_1 és a P_3 pozitivitástartományokhoz tartozó rendezési relációk szerint. A „nem összehasonlítható” itt azt jelenti, hogy közöttük egyik irányban sem teljesül a reláció. Ezzel szemben egy teljes rendezés megköveteli a trichotómiát. Következésképp ebben az esetben bármely gyűrűelem és a nullelem között legalább az egyik irányban teljesülni fog egy ilyen rendezési reláció.
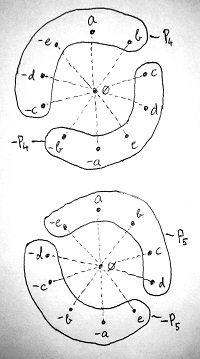
Tegyük most fel, hogy a fenti gyűrűn létezik 2 olyan rendezési reláció is, amelyek szintén teljesítik a 15.11. Definíció szerinti rendezési axiómákat, de ezen felül még teljes rendezések is. Az alábbi ábrán egy példa látható arra, hogy az ezekhez tartozó pozitivitástartományok (P_4 és P_5) és negativitástartományok (-P_4 és -P_5) hogyan helyezkedhetnek el a gyűrű alaphalmazán belül:
Az eddigiek alapján semmi nem zárja ki, hogy egy gyűrűn több olyan rendezés is létezzen, amelyek eleget tesznek a rendezési axiómáknak. Ha például \leq és \lesssim két ilyen, egymástól különböző rendezési reláció egy gyűrű alaphalmazán, akkor – mint azt a következő tételben látni fogjuk – a hozzájuk tartozó P_{\leq} és a P_{\lesssim} pozitivitástartományok is különbözni fognak. Következésképp mások lesznek a negatív és pozitív elemek a \leq rendezésre nézve, mint a \lesssim rendezésre nézve.
Nézzük tehát az erről szóló tételt.
15.13. Tétel:
Tegyük fel, hogy (R,+,\cdot ) egy részbenrendezhető gyűrű, valamint legyen \leq és \lesssim két tetszőleges részbenrendezési reláció, amelyek kielégítik a 15.11. Definícióban megfogalmazott rendezési axiómákat.
Amennyiben tetszőleges a és b gyűrűelemekre a\leq b pontosan akkor teljesül, amikor a\lesssim b is teljesül, úgy a két rendezés pozitivitástartománya megegyezik – azaz P_{\leq}=P_{\lesssim}.
Megfordítva: amennyiben a két rendezés pozitivitástartománya megegyezik – azaz P_{\leq}=P_{\lesssim} –, úgy tetszőleges a és b gyűrűelemekre a\leq b pontosan akkor teljesül, amikor a\lesssim b is teljesül.
♣Más szavakkal a pozitivitástartomány egyértelműen meghatározza a hozzá tartozó rendezést.
Bizonyítás:
Ha tetszőleges a és b gyűrűelemekre a\leq b pontosan akkor teljesül, amikor a\lesssim b is, akkor ez nyilván igaz lesz az a=0 speciális esetre is. Azaz ebben a speciális esetben igaz lesz, hogy tetszőleges b gyűrűelemre pontosan akkor teljesül a 0\leq b reláció, amikor a 0\lesssim b reláció is. Ez viszont azt jelenti, hogy tetszőleges gyűrűelem pontosan akkor van benne a \leq rendezés pozitivitástartományában, amikor a \lesssim rendezés pozitivitástartományában is benne van. A két pozitivitástartománynak tehát pontosan ugyanazok az elemeik, ami épp azt jelenti, hogy megegyeznek.
Megfordítva: az, hogy a két rendezés pozitivitástartománya megegyezik, úgy is megfogalmazható, hogy bármely gyűrűelem pontosan akkor van benne a P_{\leq} halmazban, ha benne van a P_{\lesssim} halmazban is. Ez nyilván igaz lesz minden olyan gyűrűelemre is, amelyet két tetszőleges a és b gyűrűelemből képzünk a b+(-a) összegzéssel – hacsak nem éppen az a=b esetről van szó, ám ekkor a reflexivitás miatt amúgyis mindkét reláció teljesül. Így tehát pontosan akkor fog teljesülni a 0\leq b+(-a) reláció, amikor teljesül a 0\lesssim b+(-a) reláció is. Mivel mindkét reláció teljesíti a rendezési axiómákat, ezért mindkettő kompatibilis az összeadás művelettel. Így e két egyenlőtlenség mindkét oldalához a-t adva megkapjuk a tétel állítását: a\leq b pontosan akkor teljesül, amikor a\lesssim b is, azaz a két reláció valójában – jelöléstől eltekintve – egy és ugyanaz.
∎Látható tehát, hogy egy gyűrűben önmagában nincs értelme pozitív vagy negatív elemekről beszélni. Azt ugyanis, hogy mely elemek pozitívak és melyek negatívak, az adott rendezési reláció, illetve az előző tétel alapján az adott pozitivitástartomány határozza meg.
Jogos a kérdés, hogy akkor a 13.10. Definíció alapján milyen jogon mondtuk azt bizonyos egész számokra, hogy pozitívak, másokra pedig azt, hogy negatívak anélkül, hogy megneveztünk volna egy konkrét rendezési relációt. Ezt a kérdést hamarosan megválaszoljuk, ehhez azonban szükségünk lesz két fontos tételre. Egyrészt szeretnénk egy könnyen ellenőrizhető kritériumot találni, amely alapján egy gyűrű alaphalmazának egy adott részhalmazáról eldönthetjük, hogy pozitivitástartománya-e egy rendezési relációnak vagy nem. Másrészt, miután ezt eldöntöttük egy részhalmazról, szeretnénk azt is könnyen eldönteni, hogy ez a rendezési reláció vajon egy teljes rendezés-e, vagy csak részbenrendezés.
Az alábbi tétel az első kérdésre ad egy könnyen ellenőrizhető kritériumot nullosztómentes gyűrűk esetén.
15.14. Tétel:
Tegyük fel, hogy (R,+,\cdot ) egy nullosztómentes gyűrű, valamint P a gyűrű alaphalmazának egy részhalmaza. A P halmaz akkor és csak akkor pozitivitástartománya valamilyen R-en értelmezett, a 15.11. Definíció szerinti rendezési axiómákat is kielégítő részbenrendezésnek, ha zárt az összeadásra és a szorzásra, valamint nem tartalmazza a gyűrű nullelemét.
Az összeadásra és szorzásra való zártságot úgy értjük, hogy ha a és b benne van a P halmazban, akkor az a+b összeg, valamint az ab és a ba szorzatok is benne vannak a P halmazban. Ne feledjük: nem feltételeztük, hogy a gyűrű kommutatív, ezért mindkét irányú szorzást külön meg kell említeni.
♣Bizonyítás:
Nézzük először a könnyebbik irányt. Azt kell belátnunk, hogy ha valamilyen P részhalmazhoz létezik olyan \leq részbenrendezés, amelynek épp P a pozitivitástartománya, és kielégíti a 15.11. Definíció szerinti rendezési axiómákat, akkor P zárt az összeadásra és a szorzásra, valamint nem tartalmazza a nullelemet.
Vegyünk két tetszőleges P-beli elemet, és jelöljük őket a-val és b-vel. Az, hogy ők P-ben vannak, a 15.12. Definíció miatt ezt jelenti:
\begin{aligned}a&\neq 0 \\ b&\neq 0 \\ a&\geq 0 \\ b&\geq 0\end{aligned}Az 1. rendezési axióma miatt az a\geq 0 egyenlőtlenség mindkét oldalához b-t adva az egyenlőtlenség továbbra is érvényes, azaz a+b\geq b. De mivel részbenrendezésről van szó, és b\geq 0 ugye teljesül, ezért a tranzitivitás miatt:
a+b\geq 0Igaz ugyanakkor az is, hogy a+b \neq 0, hiszen máskülönben a=-b lenne a helyzet, azaz a pozitivitástartomány 15.12. Definíciója utáni megjegyzés alapján egyiküknek a -P negativitástartományban kéne lennie. Ez ugye ellentmondana annak, hogy mindkettő P-ben van, így valóban a+b is benne van P-ben, azaz P zárt az összeadásra.
Most nézzük, mi a helyzet az ab és a ba szorzatokkal? A 2. rendezési axióma miatt az a\geq 0 egyenlőtlenség mindkét oldalát megszorozhatjuk a b\geq 0 elemmel jobbról is és balról is, azaz egyrészt ab\geq 0b, másrészt ba\geq b0. Mindkét egyenlőtlenség jobboldala a 15.1. Tétel 1. pontja alapján 0-val egyenlő, ezért:
\begin{aligned}ab&\geq 0 \\ ba&\geq 0\end{aligned}Tekintve, hogy a gyűrű a tétel feltétele miatt nullosztómentes, ezért e két szorzat közül egyik sem 0, és így mindkettő szintén benne van P-ben, azaz P zárt a szorzásra is.
Végül, mivel P-ről azt mondtuk, hogy pozitivitástartománya a \leq rendezési relációnak, ezért a 15.12. Definíció miatt nem tartalmazza a nullelemet.
Most nézzük a nehezebbik irányt. Itt azt kell belátnunk, hogy ha valamilyen P részhalmaz zárt az összeadásra és a szorzásra, valamint nem tartalmazza a gyűrű nullelemét, akkor létezik olyan részbenrendezés a gyűrűn, amelynek épp P a pozitivitástartománya, és kielégíti a 15.11. Definíció szerinti rendezési axiómákat.
Definiáljunk hát egy \lesssim szimbólummal jelölt relációt a gyűrű alaphalmazán a következőképpen: a \lesssim b akkor és csak akkor, ha a=b vagy pedig a b+(-a) elem benne van a P halmazban.
A feladatunk tehát megmutatni, hogy a P-re vonatkozó feltételek teljesülése esetén \lesssim valóban egy részbenrendezés (azaz reflexív, tranzitív és antiszimmetrikus), és ezen felül még a rendezési axiómákat is teljesíti. A reflexivitás azonnal látszik, hiszen a \lesssim reláció teljesülésének első feltétele épp a=b volt.
A tranzitivitás megmutatásához tegyük fel, hogy valamilyen a, b és c elemekre teljesülnek az a\lesssim b és a b\lesssim c relációk. Feladatunk megmutatni, hogy ekkor az a\lesssim c reláció is teljesül. Feltehetjük, hogy ez a 3 elem páronként különbözik, máskülönben bármelyik kettő egyezése esetén nyilvánvalóan fennáll a\lesssim c. Ha viszont páronként különböznek, akkor a\lesssim b és b\lesssim c épp azt jelenti, hogy a b+(-a) és a c+(-b) elemek benne vannak a P halmazban. Mivel azonban P zárt az összeadásra, ezért ezek összege is, azaz a (b+(-a))+(c+(-b)) elem is benne van a P halmazban. Az összeadásra vonatkozó gyűrűaxiómák miatt azonban ez a kifejezés c+(-a)-val egyenlő, amely épp azt jelenti, hogy a\lesssim c. A \lesssim reláció tehát valóban tranzitív.
Az antiszimmetria bizonyításához indirekt tegyük fel, hogy léteznek olyan galád a és b elemek, amelyekre a\lesssim b és b\lesssim a is teljesül, ugyanakkor a\neq b. Ebben az esetben a\lesssim b és b\lesssim a épp azt jelenti, hogy a b+(-a) és az a+(-b) elemek benne vannak a P halmazban. Mivel azonban P zárt az összeadásra, ezért ezek összege is, azaz a (b+(-a))+(a+(-b)) elem is benne van a P halmazban. Az összeadásra vonatkozó gyűrűaxiómák miatt azonban ez a kifejezés épp a gyűrű nullelemével egyenlő. Ez ellentmond annak, hogy P nem tartalmazza a nullelemet. A \lesssim reláció tehát szükségképpen antiszimmetrikus kell legyen.
Annyi van még hátra, hogy megmutassuk, hogy a \lesssim reláció teljesíti a 15.11. Definíció szerinti rendezési axiómákat is. Nézzük az 1. rendezési axiómát. Ehhez tegyük fel, hogy valamilyen a és b elemekre fennáll az a\lesssim b reláció, és legyen c egy tetszőleges gyűrűelem. Meg kell mutatnunk, hogy ekkor fennáll az a+c\lesssim b+c reláció is. Feltehetjük, hogy a\neq b, hiszen máskülönben nyilvánvalóan a \lesssim reláció már bizonyított reflexivitása miatt a+c\lesssim \underbrace{a}_{=b}+c is igaz. Ha viszont a\neq b, akkor a\lesssim b épp azt jelenti, hogy b+(-a) benne van a P halmazban. Ehhez a kifejezéshez hozzáadva a c elemet és annak ellentettjét, a kifejezés eredménye a gyűrűaxiómák miatt nem változik:
(b+(-a))+\underbrace{(c+(-c))}_{=0}Mivel az összeadás kommutatív és asszociatív, így ez a kifejezés átzárójelezhető és átsorrendezhető:
(b+c)+((-a)+(-c))Vegyük azonban észre, hogy a jobboldali (-a)+(-c) tag a 15.1. Tétel 5. pontja miatt így is írható: -(a+c). Így tehát azt kapjuk, hogy az alábbi elem szintén benne van a P halmazban:
(b+c)+(-(a+c))Ez viszont a \lesssim reláció definíciója miatt épp azt jelenti, hogy a+c\lesssim b+c.
Végül ellenőrizzük a 15.11. Definíció szerinti 2. rendezési axióma teljesülését is. Ehhez tegyük fel, hogy valamilyen a és b elemekre fennáll az a\lesssim b reláció, és legyen adva egy tetszőleges 0\lesssim c gyűrűelem. Meg kell mutatnunk, hogy ekkor fennállnak az ac\lesssim bc, valamint a ca\lesssim cb relációk is. Feltehetjük egyrészt, hogy c\neq 0, hiszen máskülönben nyilvánvalóan a \lesssim reláció már bizonyított reflexivitása miatt \underbrace{0}_{=a0=0a}\lesssim \underbrace{0}_{=b0=0b} is igaz. Másrészt azt is feltehetjük, hogy a\neq b, hiszen máskülönben ugyanezen okok miatt ac\lesssim \underbrace{a}_{=b}c és ca\lesssim c\underbrace{a}_{=b} szintén nyilvánvalóan teljesül.
Ha viszont a\neq b és c\neq 0, akkor egyrészt a\lesssim b épp azt jelenti, hogy b+(-a) benne van a P halmazban, másrészt pedig 0\lesssim c épp azt jelenti, hogy c+(-0)=c szintén benne van a P halmazban. Mivel azonban P zárt a szorzásra, ezért a (b+(-a))c valamint a c(b+(-a)) szorzatok szintén benne vannak a P halmazban. E két szorzat viszont a disztributivitási szabályok és a 15.1. Tétel 3. pontja miatt így írható fel:
\begin{aligned}(b+(-a))c &= bc+(-a)c = bc+(-(ac)) \\ c(b+(-a)) &= cb+c(-a) = cb + (-(ca)) \end{aligned}Az, hogy ezek a P halmazban vannak, a \lesssim reláció definíciója miatt épp azt jelenti, hogy ac\lesssim bc és ca\lesssim cb. Valóban teljesül tehát a 2. rendezési axióma is.
∎Most tehát már van egy szükséges és egyben elégséges feltételünk arra, hogy egy gyűrű alaphalmazának bármilyen részhalmazáról eldöntsük, vajon ő egy rendezési reláció pozitivitástartománya-e vagy sem. Ráadásul a bizonyításból az is könnyen látszik, hogy igenlő válasz esetén hogyan kaphatjuk meg magát a keresett rendezési relációt (ami a 15.13. Tétel miatt ugye egyértelmű).
A most következő tétel annak eldöntésére ad egy könnyen ellenőrizhető kritériumot, hogy ez a bizonyos rendezés vajon egy teljes rendezés-e vagy sem.
15.15. Tétel:
Tegyük fel, hogy (R,+,\cdot ) egy tetszőleges gyűrű, valamint P egy valamilyen, ezen a gyűrűn definiált, a 15.11. Definíció szerinti rendezési axiómákat kielégítő részbenrendezési reláció pozitivitástartománya. A P-hez tartozó részbenrendezési reláció akkor és csak akkor teljes rendezés, ha minden nemnulla elemre igaz, hogy vagy ő maga, vagy pedig az ellentettje benne van P-ben.
♣Bizonyítás:
Jelöljük a P pozitivitástartomány által meghatározott relációt a \leq szimbólummal. Mivel ez ismét egy „akkor és csak akkor” típusú állítás, ezért ezúttal is mindkét irányú következtetést bizonyítani kell.
Nézzük meg először, hogy mi következik P-re vonatkozóan abból, ha \leq egy teljes rendezés. Az ugye világos, hogy tetszőleges a\neq 0 elemre vagy teljesül a 0\leq a reláció, vagy pedig nem. Ha teljesül, akkor a 15.12. Definíció miatt maga a benne van a P halmazban. Ha nem teljesül, akkor viszont a rendezés trichotómiája miatt – lévén, hogy teljes rendezésről van szó – szükségképpen teljesül az a\leq 0 reláció. Ebben az esetben viszont a 15.9. Lemma 1. pontja miatt teljesül a 0\leq (-a) reláció is. Mivel a\neq 0, ezért (-a)\neq 0, és így a 15.12. Definíció miatt ekkor -a benne van a P halmazban. Teljes rendezés esetén tehát minden nemnulla elemre igaz, hogy vagy ő maga, vagy pedig az ellentettje benne van a rendezés pozitivitástartományában.
Most visszafele nézzük meg, hogy mi következik a \leq részbenrendezésre vonatkozóan abból, ha minden nemnulla elem vagy az ellentettje benne van a rendezés P pozitivitástartományában. Ez nyilván igaz lesz azokra az elemekre is, amelyeket valamilyen tetszőleges a és b elemekből képzünk a b+(-a) képlettel – kivéve persze, ha a=b, de ezekben az esetekben a rendezés reflexivitása miatt amúgyis teljesül mind az a\leq b, mind pedig a b\leq a reláció is. Ha tehát a\neq b, akkor vagy b+(-a), vagy pedig az ő ellentettje, azaz -(b+(-a)) benne van P-ben.
Ha b+(-a) van benne P-ben, akkor a 15.12. Definíció miatt 0\leq b+(-a). Az 1. rendezési axióma miatt mindkét oldalhoz a-t adva továbbra is érvényes egyenlőtlenséget kapunk, azaz a\leq b.
Ha viszont -(b+(-a)) van benne P-ben, akkor a 15.12. Definíció, valamint a 15.9. Lemma 1. pontja miatt a b+(-a)\leq 0 fog teljesülni, amiből viszont b\leq a következik.
Azt kaptuk tehát, hogyha tetszőleges nemnulla elem, vagy az ellentettje benne van egy rendezési reláció pozitivitástartományában, akkor a rendezési reláció legalább az egyik irányban bármely két elem között fennáll – azaz ő valóban egy teljes rendezés.
∎Teljes rendezés az egész számok gyűrűjében
A most következő szakaszban végre rátérhetünk arra a kérdésre, hogy a 13.10. Definícióban milyen jogon mondtuk azt bizonyos egész számokról, hogy pozitívak, másokról pedig, hogy negatívak. Ez pofátlanságnak tűnik a fentiek fényében, hiszen nem mondtuk meg, hogy melyik rendezési reláció szerint értjük őket pozitívnak illetve negatívnak. Most ezt a hiányosságunkat fogjuk pótolni.
Azt rögtön kijelenthetjük, hogy minket most csak a teljes rendezések érdekelnek. Szeretnénk ugyanis, ha bármely két egész számról eldönthető lenne, hogy melyik nagyobb a másiknál. Kérdés, hogy létezik-e egyáltalán olyan teljes rendezés az egész számok gyűrűjében, amely teljesíti a 15.11. Definíció szerinti rendezési axiómákat.
A következő tétel nullosztómentes gyűrűkre fogalmaz meg egy számunkra fontos észrevételt ezzel kapcsolatban.
15.16. Tétel:
Tegyük fel, hogy (R,+,\cdot ) egy olyan nullosztómentes gyűrű, amely teljesen rendezhető – azaz létezik legalább egy, a 15.11. Definíció szerinti rendezési axiómákat kielégítő teljes rendezés a gyűrű R alaphalmazán. Ekkor minden nemnulla elem önmagával vett szorzata, valamint az összes ilyen szorzatból képzett akárhánytagú összeg pozitív a gyűrű bármely teljes rendezésére nézve.
♣Bizonyítás:
Az 15.15. Tétel alapján minden a\neq 0 elemre teljesül, hogy vagy ő, vagy pedig az ellentettje benne van az összes olyan pozitivitástartományban, amely valamilyen, a rendezési axiómákat kielégítő teljes rendezéshez tartozik.
Az első esetben a\cdot a is benne van az összes ilyen pozitivitástartományban, hiszen azok – nullosztómentes gyűrűről lévén szó – a 15.14. Tétel miatt zártak a szorzás műveletére nézve.
Második esetben az a elem helyett a (-a) elem van benne ezekben a pozitivitástartományokban, de ekkor – szintén a 15.14. Tétel miatt – a (-a)\cdot (-a) szorzat is. Vegyük észre azonban, hogy ez a szorzat a 15.1. Tétel 4. pontja alapján épp a\cdot a-val egyenlő.
Azt kaptuk tehát, hogy minden a\neq 0 elem önmagával vett szorzata mindenképpen pozitív bármely teljes rendezésre nézve – még akkor is, ha ő maga negatív. De ekkor e szorzatok tetszőleges kombinációban felírt összegei is pozitívak, hiszen a 15.14. Tétel szerint egy nullosztómentes gyűrűben a pozitivitástartományok zártak az összeadásra nézve.
∎Most térjünk vissza az egész számok (\Z ,+,\cdot ) gyűrűjéhez. Mivel a 15.6. Tétel értelmében ő egy integritástartomány – azaz kommutatív és nullosztómentes –, így érvényes rá az imént bizonyított 15.16. Tétel tétel. Azt ugyan még nem tudjuk, hogy létezik-e rajta akárcsak egyetlen, a rendezési axiómákat kielégítő teljes rendezés is. Ám ha létezik ilyen, akkor annak pozitivitástartománya biztosan tartalmazni fogja az összes nemnulla elem önmagával vett szorzatát, és az ilyen szorzatok összegeit is. Ha több ilyen teljes rendezés is létezik, akkor minden ezekhez tartozó pozitivitástartomány tartalmazni fogja ugyanezeket az elemeket.
Tegyük fel például, hogy a (\Z ,+,\cdot ) gyűrűn 3 teljes rendezés is létezik. Az alábbi ábrán az ehhez a 3 hipotetikus rendezéshez tartozó pozitivitástartományok láthatók (P_1, P_2 és P_3):
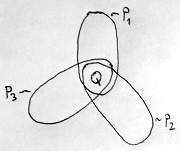
A 15.16. Tétel alapján tehát a 3 pozitivitástartomány Q-val jelölt közös része tartalmazza az összes nemnulla elem önmagával vett szorzatát, és az ilyen szorzatok összes lehetséges összegeit is. Kérdés, hogy vajon tartalmaznak-e a Q-beli elemeken kívül más elemeket is, vagy valójában az összes pozitivitástartomány egy és ugyanaz?
Úgy gondolom, a fentiek fényében már nem lesz meglepő az erre választ adó alábbi tétel.
15.17. Tétel:
Az egész számok (\Z ,+,\cdot ) gyűrűjének alaphalmazán pontosan egy olyan teljes rendezés létezik, amelyre teljesülnek a 15.11. Definícióban megfogalmazott rendezési axiómák. Ennek a rendezésnek a pozitivitástartománya épp a 13.10. Definíció szerinti pozitív, negativitástartománya pedig az ugyanezen definíció szerinti negatív egész számokból áll.
♣Bizonyítás:
A 13.10. Definícióban az egész számok halmazát 3 részre osztottuk: pozitív egész számok, negatív egész számok és a 0 egész szám. A pozitív egész számok halmazát jelöljük a továbbiakban P-vel, a negatív egész számok halmazát pedig -P-vel. A P halmaz nem tartalmazza a gyűrű nullelemét, azaz a 0 egész számot, valamint a 13.13. Tétel és a 14.5. Tétel miatt zárt a (\Z ,+,\cdot ) gyűrű összeadására és szorzására. Mivel a gyűrű nullosztómentes, ezért a 15.14. Tétel alapján annyi már bizonyos, hogy a P halmaz valóban egy részbenrendezés pozitivitástartománya.
A 14.13. Tétel bizonyítása alapján a P-ben lévő egész számok ellentettjei épp a -P-ben lévő egész számok. Így a 15.12. Definíció utáni megjegyzés miatt a P-hez tartozó rendezés negativitástartománya épp a -P halmaz, aminek tehát nincs közös eleme P-vel. Mivel a P és a -P halmazok ketten együtt tartalmazzák a 0 egész számon kívüli összes egész számot, így a 15.15. Tétel alapján a P halmazhoz tartozó rendezés valójában egy teljes rendezés.
Már csak azt kell belátni, hogy ez az egyetlen, a rendezési axiómákat is kielégítő teljes rendezés. Tegyük fel ezért indirekt, hogy egy másik ilyen teljes rendezés is létezik az egész számok gyűrűjén. Jelöljük az ehhez tartozó pozitivitástartományt Q-val, a negativitástartományt pedig -Q-val. Mivel rendezésről van szó, ezért a Q és a -Q halmazoknak szintén nincs közös elemük, továbbá – mivel ez a hipotetikus rendezés teljes – ketten együtt tartalmazzák a 0 egész számon kivüli összes egész számot. A 15.13. Tétel alapján az indirekt feltevésünk pontosan azt jelenti, hogy a P és Q pozitivitástartományok különbözőek.
Vegyük észre azonban, hogy a 15.16. Tétel alapján mindazon egész számok, amelyek felírhatók egy akármilyen egész szám önmagával vett szorzataként, vagy ilyen szorzatok akárhánytagú összegeként, benne vannak mind a P, mind pedig a Q halmazban. Ez viszont igaz minden P-beli egész számra. Az első néhány példa alapján az Olvasó is könnyen megértheti, miért:
\begin{aligned}1&=1\cdot 1 \\ 2&=1\cdot 1 + 1\cdot 1 \\ 3&=1\cdot 1 + 1\cdot 1 + 1\cdot 1 \\ &\ldots \end{aligned}Az tehát már bizonyos, hogy P része Q-nak. Ebből viszont következik, hogy -P is része -Q-nak. Hiszen ha egy tetszőleges a nemnulla egész szám benne van -P-ben, akkor az ellentettje benne van P-ben. Azonban P része Q-nak, így tehát ez az ellentett benne van Q-ban is. Ekkor viszont maga a benne van -Q-ban. A szituáció tehát valójában a következő:
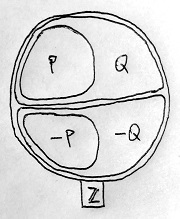
Az indirekt feltételezésünk ugye az volt, hogy a P és a Q halmazok különböznek. Azaz létezik olyan x nemnulla egész szám, amely benne van Q-ban, de nincs benne P-ben. Egyrészt, mivel Q-nak és -Q-nak nincs közös eleme, ezért ha x benne van Q-ban, akkor nincs benne -Q-ban. Másrészt, mivel P és -P ketten együtt tartalmazzák az összes nemnulla egész számot, ezért ha x nincs benne P-ben, akkor benne van -P-ben. Mivel azonban -P része -Q-nak, ezért ha x benne van -P-ben, akkor benne van -Q-ban is.
Az indirekt feltételezésünkből tehát az következik, hogy létezik olyan egész szám, amely benne is van -Q-ban, és nincs is benne. Ez teljes képtelenség, így csak az a feltételezésünk lehet hibás, miszerint P és Q különböznek, azaz valójában P és Q megegyeznek. Ekkor viszont a 15.13. Tétel miatt a hozzájuk tartozó teljes rendezések is megegyeznek. Az egész számok gyűrűje tehát valóban csak egyféleképpen rendezhető teljesen.
∎Most tehát már tudjuk, hogy az egész számok gyűrűjében pontosan egy olyan teljes rendezés létezik, amely teljesíti a 15.11. Definíció szerinti rendezési axiómákat. Ráadásul ennek a rendezésnek a pozitivitástartománya (vagy negativitástartománya) épp azokat az egész számokat tartalmazza, amelyeket a 13.10. Definícióban pozitív (vagy negatív) számoknak neveztünk. Jogos volt tehát az elnevezés annak ellenére, hogy akkor nem definiáltuk magát a rendezést, amely alapján ezt értettük.
Ezen a ponton fontos megjegyezni, hogy ez az egyértelműség az egész számok gyűrűjében pusztán egy szerencsés egybeesés eredménye. Léteznek például olyan gyűrűk is, amelyekben egyáltalán nem található a rendezési axiómákat is kielégítő teljes rendezés (például az úgynevezett komplex számok teste). Léteznek továbbá olyanok is, amelyekben végtelen sok ilyen teljes rendezés definiálható (például az úgynevezett valós polinomgyűrű).
Most azonban maradjunk továbbra is a (\Z ,+,\cdot ) gyűrűben. Nincs más hátra, mint megadni ezt az egyetlen teljes rendezést ezen a gyűrűn. A pozitivitástartományunk ugye már megvan, és ez a 15.13. Tétel alapján egyértelműen meghatározza a hozzátartozó rendezési relációt. Jelöljük a pozitivitástartományt P-vel, amely tehát a 13.10. Definíció szerinti pozitív egész számokat tartalmazza. A 15.14. Tétel bizonyításából már tudjuk, hogy P-ből hogyan kaphatjuk meg a rendezést.
Jelöljük ezt a rendezést a \leq szimbólummal. Eszerint tehát a\leq b-t úgy kell definiálnunk, hogy akkor és csak akkor teljesüljön, ha a=b vagy pedig a b+(-a) benne van P-ben.
Az első feltétel mindkét oldalához (-a)-t adva így azt kapjuk, hogy az a\leq b reláció pontosan akkor teljesüljön, ha a b+(-a) egész szám 0 vagy pozitív. Mivel az előző rész vége óta épp a 0 vagy pozitív egész számokat nevezzük természetes számoknak, így tehát a\leq b pontosan akkor teljesül, ha létezik olyan k természetes szám, hogy b+(-a)=k. Mindkét oldalhoz a-t adva megkapjuk az egész számok rendezésének definícióját, amely – vegyük észre – épp a természetes számok rendezésének (12.13. Definíció) kiterjesztése az egész számok \Z halmazára.
15.18. Definíció (Egész számok rendezése):
Amennyiben tetszőleges a és b egész számokhoz létezik olyan k természetes szám, amelyre teljesül, hogy a+k=b, akkor azt mondjuk, hogy a\leq b. Kiolvasva: „a legfeljebb b” vagy „b legalább a”.
Ha ezen kívül a\neq b is teljesül – azaz a nem azonos b-vel –, akkor azt mondjuk, hogy a\lt b. Kiolvasva: „a kisebb, mint b” vagy „b nagyobb, mint a”. Egy ezzel azonos megfogalmazás így hangzik: ha tetszőleges a és b egész számokhoz létezik olyan k\neq 0 természetes szám, amelyre teljesül, hogy a+k=b, akkor a\lt b.
Fordított irányú reláció esetén értelemszerűen használhatjuk a \geq vagy a \gt szimbólumokat is.
♣Egyszerűen adódik tehát, hogy a Peano-axiómarendszer (11.1. Definíció) által definiált – korábban természetes számoknak nevezett – halmaz 13. részben tárgyalt beágyazása az egész számok gyűrűjébe az összeadáson (13.13. Tétel) és a szorzáson (14.5. Tétel) kívül tartja a fenti rendezést is. Ezt fogalmazza meg az alábbi tétel.
15.19. Tétel:
E tétel megfogalmazásához az alábbi jelöléseket használjuk:
- \N_1-gyel a Peano-axiómarendszer (11.1. Definíció) szerint definiált halmazt jelöljük.
- Az egész számokra a 13.7. Definíció szerinti jelölést alkalmazzuk.
- A \Z halmazon értelmezett 15.18. Definíció szerinti teljes rendezést a \lesssim, az \N_1 halmazon értelmezett 12.13. Definíció szerinti teljes rendezést pedig a \leq szimbólummal jelöljük.
- A \Z halmazon értelmezett 13.12. Definíció szerinti összeadást a \oplus, az \N_1 halmazon értelmezett 11.4. Definíció szerinti Peano-összeadást pedig a + szimbólummal jelöljük.
Tegyük fel, hogy adva van egy f:\N_1 \to \Z függvény az alábbiak szerint:
f(n)=[(n;0)]Ekkor az \N_1 halmaz tetszőleges a és b elemeire igaz, hogy a\leq b pontosan akkor teljesül, ha f(a)\lesssim f(b) is teljesül. Más szavakkal f egy injektív homomorfizmus az (\N_1, \leq) és a (\Z ,\lesssim ) teljesen rendezett halmazok, mint algebrai struktúrák között.
♣Bizonyítás:
Ha a\leq b, akkor létezik olyan k elem az \N_1 halmazban, amelyre a+k=b. Mivel a 13.13. Tétel miatt az f függvény tartja a Peano-összeadást, ezért f(a+k)= f(a)\oplus f(k) = f(b). Tekintve, hogy az \N_1 halmaz minden elemének f szerinti képe a 13.10. Definíció értelmében pozitív vagy 0 a \Z halmazon belül (tehát természetes szám), így nyilván f(k) is az. Azaz a 15.18. Definíció értelmében f(a)\lesssim f(b).
Megfordítva: ha f(a)\lesssim f(b), akkor létezik olyan c természetes szám a \Z halmazon belül, amelyre f(a)\oplus c=f(b). Mivel c természetes szám, ezért csak pozitív vagy 0 lehet. Emiatt létezik az \N_1 halmazban olyan n elem, amelynek épp ő az f szerinti képe, azaz amelyre f(n)=c, és így f(a)\oplus f(n)=f(b). De mivel az f függvény tartja a Peano-összeadást, ezért f(a+n)=f(b) is teljesül. Tekintve, hogy az f függvény minden \Z-beli elemet legfeljebb egy \N_1-beli elemhez rendel hozzá, ezért ebből a+n=b következik. Ez viszont a 12.13. Definíció értelmében épp azt jelenti, hogy a\leq b.
∎Ebben a részben tehát definiáltuk a „kisebb-nagyobb” fogalmát az egész számok gyűrűjében is. Ezután megmutattuk, hogy az valóban a korábban csupán a természetes számok körében értelmezett hasonló reláció kiterjesztése. Megvizsgáltuk ezt a kérdéskört egy magasabb absztrakciós szinten általános gyűrűkre is. E vizsgálódásaink során sikerült megmutatni, hogy e reláció kiterjesztésének ez az egyetlen módja. Feltéve persze, ha bizonyos, az általános iskolából is jól ismert számolási szabályokat az egész számok halmazán is érvényben szeretnénk tartani.
A továbbiakban ennek a relációnak a felhasználásával meg fogunk ismerkedni az úgynevezett oszthatóság és a maradékos osztás fogalmával. Ezek végre elvezetnek majd minket a prímszámokkal kapcsolatos összefüggésekhez. Ezeket a kérdéseket továbbra is az általános gyűrűk szintjén fogjuk vizsgálni, már amennyire lehetséges. Ezáltal ugyanis átfogóbb képet kaphatunk a modern kriptográfiai eljárások mögött meghúzódó számelméleti gondolatokról.
A következő részt itt találod…



