Az előző részben igazoltuk, hogy az RSA rejtjelezési eljárás valóban minden esetben helyesen működik. Ezt alapvetően két fontos számelméleti összefüggés biztosította számunkra. Az első a kis Fermat-tétel (22.1. Tétel), amely a 20. részben ismertetett Euler-Fermat tétel (20.19. Tétel) következménye a prímekre nézve. A másik összefüggés pedig a kínai maradéktétel (22.2. Tétel), amely az úgynevezett kongruenciarendszerek megoldhatóságával, illetve a megoldások számával volt kapcsolatos. Végül egyrészt ennek következményeként egy – egyébként a számelmélet más területein is – rendkívül fontos gyűrűizomorfizmussal, másrészt a kis Fermat-tétel egy egyszerű következményével ismerkedtünk meg, amelyek együtt lehetővé teszik a kommunikáló felek számára az RSA-dekódolás felgyorsítását.
De vajon hogyan képes Alice és Bob az RSA-kulcsgeneráláshoz szükséges többszázjegyű prímszámokat találni? Hogyan tudják ezt megtenni anélkül, hogy az idők végezetéig osztáspróbákat kellene végezniük? Mik azok a prímtesztek, és pontosan hogyan működnek? Mely számokat nevezzük univerzális álprímeknek, és hogyan tudunk megszabadulni tőlük? Ebben a részben erről lesz szó…
Figyelem! Ez a rész erőteljesen épít a 16., 20. és 22. részekben felépített alábbi definíciókra, valamint a hozzájuk kapcsolódó tételekre:
Legyen R egy tetszőleges kommutatív gyűrű. Ha egy adott e gyűrűelem esetén minden a gyűrűelemre teljesül az e|a oszthatósági reláció, akkor az e elemet egységnek nevezzük.
Egy kommutatív gyűrű valamely a és b elemeire akkor mondjuk, hogy egymás asszociáltjai, ha pontosan ugyanazok a többszöröseik és az osztóik is. Pontosabban fogalmazva, ha tetszőleges r gyűrűelem esetén a|r akkor és csak akkor teljesül, amikor b|r is teljesül, valamint r|a akkor és csak akkor teljesül, amikor r|b is teljesül.
Azt, hogy a és b egymás asszociáltjai így jelöljük: a\sim b.
Legyen R egy tetszőleges kommutatív gyűrű. Ha valamely a, b és c elemekre a=b\cdot c teljesül, akkor a b\cdot c szorzatot az a elem felbontásának nevezzük. Azokat a felbontásokat, amelyekben b és c közül az egyik egység, a másik pedig a asszociáltja, triviális felbontásoknak nevezzük. Ha egy gyűrűelem saját maga nem egység és nem létezik nemtriviális felbontása (azaz ha létezik is felbontása, az csak triviális lehet), akkor őt felbonthatatlannak vagy irreducibilisnek nevezzük. Ha egy elem nem felbonthatatlan és nem egység, akkor őt összetett elemnek nevezzük. Az egységeket nem tekintjük sem felbonthatatlannak, sem pedig összetettnek.
Egy R kommutatív gyűrű valamely p elemét prímtulajdonságú elemnek (vagy egyszerűen csak prímnek) nevezzük, ha nem a nullelem, nem egység, és csak úgy lehet osztója két gyűrűelem szorzatának, ha legalább az egyik tényezőnek osztója. Azaz ha valamely a és b gyűrűelemekre teljesül a p|ab oszthatóság, akkor a p|a vagy p|b oszthatóságok közül legalább az egyik ugyancsak teljesül.
Legyen m\gt 0 egy tetszőleges pozitív egész szám. Ekkor a \Z/m\Z-vel jelölt modulo m maradékosztálygyűrű (lásd a 20.5. Tételt) invertálható elemeit modulo m redukált maradékosztályoknak nevezzük.
Legyen m\gt 0 tetszőleges pozitív egész szám. Ekkor a modulo m redukált maradékosztályok számát a \varphi(m)-mel jelölt függvény értéke adja meg. Ezt a függvényt Euler-féle \varphi-függvénynek (ejtsd: „fi”) nevezzük.
Legyen p\gt 0 egy tetszőleges pozitív prím, továbbá a egy tetszőleges egész szám, amely relatív prím p-hez. Ekkor teljesül az alábbi kongruencia:
a^{p-1}\equiv 1\pmod pAz alábbi kongruencia tetszőleges a egész számra – tehát nem csak a p-hez relatív prímekre – teljesül:
a^p\equiv a\pmod pLegyen a és b tetszőleges, p\gt 0 és q\gt 0 pedig valamilyen pozitív egész számok. Tegyük fel továbbá, hogy p és q egymáshoz relatív prímek. Ekkor az alábbi kongruenciarendszer megoldható, és a megoldás egyetlen modulo pq maradékosztály lesz:
\begin{aligned}x&\equiv a\pmod p \\ x&\equiv b\pmod q\end{aligned}Más megfogalmazásban minden, a fenti két kongruenciát egyszerre kielégítő egész szám ugyanabba az egyetlen modulo pq maradékosztályba esik, továbbá ennek a bizonyos maradékosztálynak minden eleme kielégíti a fenti két kongruenciát.
Ezek kontextusba helyezése miatt erőteljesen ajánlott elolvasni a 16., 20. és 22. részeket, mivel gyakran hivatkozni fogunk rájuk. A teljes cikksorozat elejét itt találod.
Alice és Bob tehát ott ülnek az RSA-algoritmus 21. részben ismertetett leírása felett, és mindketten szeretnének maguknak egy-egy kulcspárt generálni. Ezután ezek publikus részeit megosztják majd egymással, és indulhat a biztonságos kommunikáció, azaz mindenki boldog. Igenám, csakhogy a kulcsgenerálási eljárás első lépéseként először is mindkettejüknek kellene találnia két-két többszázjegyű prímszámot. Azt a 16.14. Tétel és a 17.12. Tétel következményeként tudják, hogy az egész számok \Z gyűrűjében a prímszámok (16.13. Definíció) és felbonthatatlan számok (16.11. Definíció) köre éppenséggel egybeesik. Emiatt a továbbiakban ezt a két – egyébként teljesen különböző – gyűrűelméleti fogalmat egymás szinonímájaként fogjuk használni.
A prímszámok keresése szempontjából lényeges kérdés, hogy azok mennyire gyakran fordulnak elő ebben a számtartományban. Az úgynevezett prímszámláló függvény egy olyan függvény, amely azt adja meg bármilyen n pozitív egészre, hogy mennyi az n-nél nemnagyobb pozitív prímek száma. Ezt a függvényt \pi-vel jelöljük. Az alábbiakban a prímszámláló függvény értékét láthatjuk néhány pozitív egész számra:
\begin{aligned}\pi(1)&=0 \\ \pi(2)&=1 \\ \pi(3)&=2 \\ \pi(3)&=2 \\ \pi(10)&=4 \\ \pi(100)&=25 \\ \pi(1000000)&=78498 \\ &\vdots \end{aligned}Az alábbi ábrán pedig a függvény grafikonja látható az első 60 pozitív egész számra:
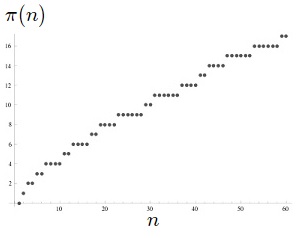
Sajnos a prímszámláló függvényre nincs képletünk, amelybe tetszőleges pozitív egész számot behelyettesítve varázslatos módon megkaphatnánk az értékét. Azonban az úgynevezett analitikus számelmélet egy nevezetes tétele szerint ez az érték viszonylag jól becsülhető egy másik, könnyen kiszámítható függvénnyel. Ez „nagy prímszámtétel” néven ismeretes, amelynek részleteire ebben a cikksorozatban nem térünk ki. Ez alapján kiszámítható, hogy a 300-600 számjegyből álló számok tartományában – amelyben Alice és Bob-nak prímeket kéne keresnie az RSA-kulcsokhoz – hogyan alakul a prímek eloszlása. Eszerint ha Alice és Bob teljesen véletlenszerűen kisorsol számokat ebből a tartományból, akkor nagyjából minden párszázadik próbálkozásnál belebotlanak egy-egy prímszámba.
Így már csak az a kérdés, hogy Alice és Bob hogyan tudja gyorsan eldönteni egy konkrét egész számról, hogy prím-e vagy sem. Az erre szolgáló algoritmusokat prímteszteknek nevezzük. A most következő prímtesztelő eljárás ismerős lehet az általános iskolából is.
Prímtesztelés osztáspróbákkal
Alice és Bob némi gondolkodás után néhány korábbi részben ismertetett összefüggés alapján az alábbi egyszerű, és mindenki számára jól ismert következtetésre jut a prímszámokkal kapcsolatban.
23.1. Tétel:
Legyen n\neq 0 egy tetszőleges nemnulla egész szám, amely nem egység. Ebben az esetben n akkor és csak akkor prím (azaz felbonthatatlan), ha nem létezik 1-nél nagyobb, de |n|-nél kisebb osztója.
Ezzel ekvivalens megfogalmazás: Az n akkor és csak akkor összetett (tehát nem prím, azaz nem felbonthatatlan), ha létezik 1-nél nagyobb, de |n|-nél kisebb osztója.
Itt |n| jelöli az n egész szám 17.18. Definíció szerinti abszolútértékét.
♣Bizonyítás:
Először nézzük azt az esetet, amikor n pozitív, azaz n\gt 0. Ekkor ugye |n|=n a 17.18. Definíció alapján.
Tegyük fel, hogy n-nek létezik 1-nél nagyobb, de |n|=n-nél kisebb osztója, amit jelöljünk k-val. Azaz egyrészt:
1\lt k\lt nMásrészt:
k|nEz az oszthatóság a 16.1. Definíció alapján azt jelenti, hogy létezik olyan l egész szám, hogy teljesül az alábbi egyenlet:
n=k\cdot lA felbonthatatlanság 16.11. Definíciója alapján azt kell bizonyítani, hogy ez a szorzat n-nek egy nemtriviális felbontása, azaz sem k, sem pedig l nem egység, és nem is asszociáltja n-nek.
Egyrészt a 16.5. Tétel alapján az egész számok \Z gyűrűjében az 1-en és a -1-en kívül nincs más egység. Mivel 1 pozitív, ezért a 15.12. Definíció utáni megjegyzés alapján -1 negatív. Emiatt k biztosan nem lehet egység, hiszen ő maga pozitív, továbbá határozottan nagyobb 1-nél.
Másrészt a 16.10. Tétel alapján n-nek mindössze két asszociáltja van, méghozzá önmaga, és az ellentettje, azaz -n. Mivel n pozitív, ezért a 15.12. Definíció utáni megjegyzés alapján -n negatív. Emiatt viszont k biztosan nem lehet n asszociáltja sem, hiszen ő maga pozitív, továbbá határozottan kisebb n-nél.
A k egész szám tehát egy olyan osztója n-nek, amely se nem egység, se nem asszociáltja n-nek. Most ugyanezt kellene megmutatni a fenti szorzat másik tényezőjéről, azaz l-ről is. Ez viszont automatikusan teljesül a 16.12. Tétel miatt. Ha ugyanis l egység lenne, akkor ez alapján k szükségképpen n-nek asszociáltja lenne. Ha viszont l asszociáltja lenne n-nek, akkor k szükségképpen egység lenne. Mindkét esetről láttuk, hogy nem ez a helyzet.
Megtaláltuk tehát n-nek egy nemtriviális felbontását, így ő a 16.11. Definíció alapján valóban összetett.
Visszafelé: Tegyük most fel indirekt, hogy n összetett ugyan, ám mégsem létezik olyan osztója, amely 1-nél nagyobb, de |n|=n-nél kisebb. Mivel összetett, így a 16.11. Definíció alapján létezik valamilyen nemtriviális felbontása. Például:
n=k\cdot lEgyrészt, mivel n\neq 0, ezért a 16.2. Tétel 4. pontja alapján k és l egyike sem lehet 0. Másrészt, mivel a fenti felbontás ugye nemtriviális, ezért egyikük sem lehet egység, továbbá egyikük sem lehet asszociáltja n-nek. Harmadrészt, indirekt feltevésünk miatt egyikük sem eshet az 1 és az |n|=n közötti számtartományba. Végül negyedrészt a 17.2. Lemma alapján egyikük sem lehet nagyobb n-nél. Összefoglalva tehát k és l mindketten negatívak, határozottan kisebbek -1-nél, továbbá -n-től különbözőek. Ezt mutatja az alábbi ábra:

Az n=k\cdot l egyenlet miatt azonban a 15.1. Tétel 4. pontja alapján teljesül az alábbi egyenlet is:
n=(-k)\cdot (-l)A k és l egész számok ellentettjei tehát szintén osztói n-nek, mindketten pozitívak, határozottan nagyobbak 1-nél, továbbá n-től különbözőek. Ezt az alábbi ábra mutatja:

A 17.2. Lemma miatt az n-nél nagyobb számtartományt ismételten kizárhatjuk. Így végülis indirekt feltételezésünkkel ellentétben mégiscsak találtunk két olyan osztót – nevezetesen a -k és -l egész számokat –, amelyek 1-nél nagyobbak, de |n|=n-nél kisebbek.
Végezetül nézzük most azt az esetet, amikor n negatív, azaz n\lt 0. Ekkor egyrészt a 15.12. Definíció utáni megjegyzés alapján -n pozitív. Másrészt pedig a 16.8. Tétel 1. pontja alapján ő n-nek asszociáltja, azaz pontosan ugyanazok az osztói, mint n-nek. Így n akkor és csak akkor prím, ha -n is, amelyre viszont pozitivitása miatt szóról szóra alkalmazható a fenti gondolatmenet.
∎Ez alapján tehát egy adott n egész szám esetén elegendő osztáspróbákkal ellenőrizni, hogy teljesül-e valamelyik oszthatóság az alábbiak közül:
\begin{aligned}2&|n \\ 3&|n \\ 4&|n \\ &\vdots \\ |n|-1&|n\end{aligned}Ha ezek közül akárcsak egyetlen oszthatóság is teljesül, akkor az iménti tétel alapján a prímtesztelő algoritmus leállhat azzal a válasszal, hogy n „biztosan összetett”. Ezzel szemben ha egyetlen oszthatóság sem teljesül a fentiek közül, akkor ugyancsak a fenti tétel alapján n „biztosan prím”.
Például az n=7 „biztosan prím”, hiszen:
\begin{aligned}2&\nmid 7 \\ 3&\nmid 7 \\ 4&\nmid 7 \\ 5&\nmid 7 \\ 6&\nmid 7\end{aligned}Ezzel szemben az n=35 „biztosan összetett”, hiszen:
\begin{aligned}2&\nmid 35 \\ 3&\nmid 35 \\ 4&\nmid 35 \\ 5&|35\end{aligned}Főhőseink tehát ez alapján bármilyen egész számról el tudják dönteni, hogy prímszám-e vagy sem. Csakhogy van egy kis probléma ezzel az eljárással, amely akkor jelentkezik, amikor a gyakorlatban előforduló nagyságrendű számokra kezdjük el lefuttatni. Vizsgáljuk ezért meg, hogy mekkora az eljárás számításigénye a bemenet méretének függvényében. A „bemenet mérete” alatt itt értelemszerűen a leírásához szükséges számjegyek számát fogjuk érteni. Jelöljük ezt a számot mondjuk k-val, és tegyük fel, hogy tizes számrendszerben dolgozunk.
A lehető legkisebb k számjegyből álló egész szám a 10^{k-1} lesz. Vagyis ha a bemenet történetesen prímszám, akkor ez nagyságrendileg legalább ennyi osztáspróba után fog csak kiderülni. Ez bizony a bemenet méretének exponenciális függvénye, és így az algoritmus sajnos a 7. részben tanultak alapján nem nevezhető hatékonynak. Nem sokkal jobb a helyzet akkor sem, ha a bemenet összetett szám, kivéve persze az olyan ritka eseteket, amikor viszonylag kicsi prímtényezője is van. A 21. részben már említettük, hogy az RSA esetén manapság tipikusan 300-600 számjegyből álló prímszámokat használnak, ezért az algoritmus futása ebben a számtartományban az idők végezetéig is eltarthat, és így a gyakorlatban nem használható.
Alice és Bob tehát tovább töri a fejét, hogyan tudnának ennél jóval kevesebb osztáspróbával is célt érni, és némi gondolkodás után az alábbi következtetésre jutnak.
23.2. Tétel:
Legyen n\neq 0 egy tetszőleges nemnulla egész szám, amely nem egység, valamint jelöljük r-rel a lehető legnagyobb olyan egész számot, amelyre r^2\leq |n| teljesül.
Ebben az esetben az n egész szám akkor és csak akkor prím (azaz felbonthatatlan), ha nem létezik olyan osztója, amely 1-nél nagyobb, de legfeljebb r.
Ezzel ekvivalens megfogalmazás: Az n egész szám akkor és csak akkor összetett (tehát nem prím, azaz nem felbonthatatlan), ha létezik olyan osztója, amely 1-nél nagyobb, de legfeljebb r.
♣Bizonyítás:
Előszöris az világos, hogy r nemnegatív, hiszen az ő és az ellentettjének a négyzete megegyezik, így ha negatív lenne, akkor nem ő lenne a legnagyobb olyan egész szám, amelyre r^2\leq |n| teljesül.
Másodszor r biztosan nem lehet nulla sem. A 17.19. Tétel alapján ugyanis az abszolútérték-függvény egy euklidészi norma az egész számok \Z gyűrűjén, és így a 17.16. Definíció 1. pontja alapján n\neq 0-ból |n|\neq 0, azaz végülis 1\leq |n| következik. Ha mármost r nulla lenne, akkor igaz ugyan, hogy a négyzete nem haladná meg |n|-t, ám ekkor lenne nála nagyobb ugyanilyen tulajdonságú szám is (például az 1).
Összefoglalva r-re teljesülni fog az 1\leq r egyenlőtlenség, ebből pedig a 15.11. Definícióban ismertetett 2. rendezési axióma alapján r\leq r^2 következik. Ezt összevetve a tétel szövegében szereplő r^2\leq |n| feltétellel teljesül az alábbi:
1\leq r\leq |n|Ennyi előkészület után igazoljuk a tétel állítását. Tegyük fel, hogy n prím. Ekkor a 23.1. Tétel alapján egyáltalán nincsen osztója 1 és |n| között. Következésképp az ennél szűkebb, 1 és r közötti szakaszon „méginkább” nincs osztója.
Visszafelé: Először azt az esetet igazoljuk, amikoris n pozitív. Tegyük fel, hogy n összetett, azaz létezik valamilyen n=k\cdot l nemtriviális felbontása. Az általánosság megsértése nélkül feltehetjük, hogy k és l mindketten pozitívak, máskülönben ellentettjüket véve ez az állapot elérhető. Azt kell igazolni, hogy k és l közül legalább az egyik nemnagyobb r-nél. Tegyük fel indirekt, hogy nem ez a helyzet, vagyis az alábbi két eset valamelyike áll fenn:
\begin{aligned}r&\lt k\leq l \\ r&\lt l\leq k\end{aligned}Első esetben a jobboldali egyenlőtlenség mindkét oldalát k-val megszorozva az alábbit kapjuk: k^2\leq k\cdot l=n. Ez viszont r\lt k miatt lehetetlen, hiszen a tétel szövege alapján r a legnagyobb olyan szám, amelynek négyzete |n|=n-t nem lépi túl.
Ehhez hasonlóan a második esetben a jobboldali egyenlőtlenség mindkét oldalát l-lel megszorozva ezt kapjuk: l^2\leq l\cdot k=n. Ez r\lt l miatt az előbb ismertetett okból szintén lehetetlen.
Indirekt feltételezésünk hibás volt, vagyis k és l közül az egyik biztosan nem lehet nagyobb r-nél, ahogyan a tétel állítja.
Végezetül nézzük most azt az esetet, amikor n negatív, azaz n\lt 0. Ekkor egyrészt a 15.12. Definíció utáni megjegyzés alapján -n pozitív. Másrészt pedig a 16.8. Tétel 1. pontja alapján ő n-nek asszociáltja, azaz pontosan ugyanazok az osztói, mint n-nek. Így n akkor és csak akkor prím, ha -n is, amelyre viszont pozitivitása miatt szóról szóra alkalmazható a fenti gondolatmenet.
∎Ez alapján tehát az osztáspróbákkal elegendő addig a számig elmenni, amelynek a négyzete még épp |n| alatt marad. Ha eddig nem találunk osztót, akkor ezután sem fogunk. Például az n=61 „biztosan prím”, hiszen:
\begin{aligned}2&\nmid 61 \\ 3&\nmid 61 \\ 4&\nmid 61 \\ 5&\nmid 61 \\ 6&\nmid 61 \\ 7&\nmid 61\end{aligned}A további osztáspróbákat már nem érdemes elvégezni, hiszen 8 négyzetével már túllépnénk a 61-et, így ha 7-ig bezárólag nincs osztója a 61-nek, akkor 7-nél nagyobb osztója sem lesz.
Ez első látásra lényeges gyorsításnak tűnik, de sajnos nem az. Most nem teljes matematikai precizitással felvázoljuk, hogy miért.
Tegyük fel ismét, hogy a bemeneti szám k darab számjegyből áll, és tizes számrendszerben dolgozunk. A lehető legkisebb k számjegyből álló szám a 10^{k-1}. Egy ekkora számnak a teszteléséhez az iménti tétel alapján nagyságrendileg r darab osztáspróbát kell elvégezni, ahol r a legnagyobb olyan szám, amelyre teljesül, hogy r^2\leq 10^{k-1}. Tegyük fel, hogy r a tizes számrendszerben l darab számjeggyel írható le, azaz r legalább 10^{l-1}. Ezt négyzetre emelve azt kapjuk, hogy r^2 legalább 10^{2\cdot (l-1)}. Összefoglalva:
10^{2\cdot (l-1)} \leq r^2 \leq 10^{k-1}Azaz:
10^{l-1} \leq r \leq 10^{\frac{k-1}{2}}Ez az exponenciális függvény tulajdonságai miatt azt jelenti, hogy r felírásához legalább feleannyi számjegy kell, mint ahány számjegyből a bemeneti szám áll. Mivel r az elvégzendő osztáspróbák számát jelenti, ezért ez sajnos még mindig a bemenet méretének exponenciális függvénye.
Alice és Bob tehát továbbra sem mennek sokra ezzel a prímtesztelési eljárással abban a számtartományban, ahol prímszámokat szeretnének keresni. Ezért most szintet lépünk, és egy lényegesen más elven működő prímtesztet ismertetünk.
A Fermat-prímteszt
Ennek a prímtesztelő eljárásnak az alapja az előző részben megismert kis Fermat-tétel. Ez a tétel azt állítja, hogy HA egy n\gt 0 pozitív egész szám prímszám, AKKOR minden n-hez relatív prím a egész szám esetén teljesülni fog az alábbi kongruencia:
a^{n-1} \equiv 1 \pmod nMás megfogalmazásban azt is mondhatjuk, hogy amennyiben akárcsak egyetlen olyan n-hez relatív prím a egész szám is létezik, amelyre nem teljesül a fenti kongruencia, akkor n biztosan nem prím (azaz összetett, vagy egység). Egy ilyen a egész szám tehát „leleplezi” vagy „tanúsítja” n összetettségét. Könnyen adódik, hogyha egy a egész szám tanú a fenti értelemben, akkor minden olyan b egész szám is tanú, amely a-val azonos modulo n maradékosztályban van. Ekkor ugyanis teljesül az a\equiv b\pmod n kongruencia, és így a 20.2. Tétel 8. pontja miatt teljesül az alábbi kongruencia is:
a^{n-1} \equiv b^{n-1} \pmod nMármost ha a baloldal nem kongruens 1-gyel – azaz a tanú –, akkor a jobboldal sem lehet kongruens 1-gyel – azaz b is tanú. Az alábbi definícióban tehát a fenti értelemben vett „tanú” fogalmát praktikus módon komplett maradékosztályokra vonatkoztatjuk.
23.3. Definíció (Fermat-tanú):
Legyen n\gt 1 egy tetszőleges pozitív, a pedig tetszőleges egész szám, amely nem többszöröse n-nek, azaz n\nmid a. Tegyük fel továbbá, hogy nem teljesül a kis Fermat-tételben (22.1. Tétel) szereplő kongruencia, azaz:
a^{n-1} \ \cancel{\equiv} \ 1 \pmod nEkkor az a egész szám által reprezentált [a]_n maradékosztályt az n egész szám Fermat-tanújának nevezzük.
♣Megjegyzés:
A definícióban nem kell külön kikötni, hogy a és n legyen relatív prím – ami a 20.14. Tétel értelmében azt jelentené, hogy [a]_n egy redukált maradékosztály –, hiszen ha nem ez lenne a helyzet, akkor az szintén tanúsítaná n összetettségét. Ez ugyanis egyrészt azt jelentené, hogy az (a,n) kitüntetett közös osztó különbözne az egységektől. Másrészt az n\nmid a feltételből az is következik, hogy ez a közös osztó n-től – és így n asszociáltjaitól – is különbözne. Ez nyilvánvaló is, hiszen (a,n)=n azt jelentené, hogy mégiscsak teljesül az n|a oszthatóság. Mármost ha az (a,n) kitüntetett közös osztó egyben n-nek is osztója, akkor n-nek lenne az egységektől és a saját asszociáltjaitól különböző osztója is, azaz nem lehetne prím.
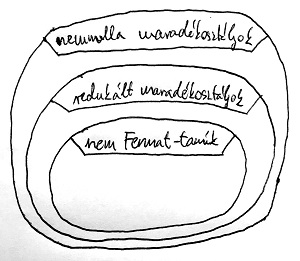
Nem mellesleg megjegyezzük, hogy az a^{n-1}\equiv 1\pmod n kongruencia a 20.20. Tétel értelmében amúgysem teljesülhetne, amennyiben [a]_n nem egy redukált maradékosztály, azaz (a,n)\neq 1. Ez tehát azt jelenti, hogy NEM Fermat-tanú csak redukált maradékosztály lehet. Az alábbi ábrán ezek elhelyezkedése látható az összes modulo n maradékosztályok között. Az összes többi maradékosztály Fermat-tanú, ami ezen a halmazon kívül van – kivéve persze a [0]_n maradékosztályt.
A kis Fermat-tétel eszerint úgy is megfogalmazható, hogy amennyiben egy n egész számnak létezik Fermat-tanúja, akkor „biztosan összetett”. Így ha n-ről szeretnénk eldönteni, hogy prím-e, akkor nincs más dolgunk, mint keresni egy Fermat-tanút a nemnulla modulo n maradékosztályok között. Igenám, csakhogy e maradékosztályok száma borzasztóan nagy – egészen pontosan n-1 –, így reménytelennek tűnik bármiféle ezek között való keresgélés. Az az érdekes, hogy ennek ellenére viszonylag gyorsan tudunk Fermat-tanút találni, amennyiben egyáltalán létezik ilyen. Most ennek okát fogjuk megvizsgálni.
Az alábbi táblázatban néhány adatot láthatunk az összes 500 és 600 közötti páratlan számról. A táblázat első oszlopa magát a vizsgált n számot tartalmazza. A második oszlopban azt láthatjuk, hogy összesen hány modulo n redukált maradékosztály létezik. Ez tehát a 20.7. Definíció alapján épp az Euler-féle \varphi-függvény értéke. A harmadik oszlop tartalmazza azt, hogy e \varphi(n) darab redukált maradékosztály között mennyi olyan van, amely nem Fermat-tanú. Ezt az értéket l(n)-nel jelöltük. Végül a negyedik oszlop azt tartalmazza, hogy n ténylegesen prím-e vagy sem:
\begin{array}{c||c}\begin{array}{c|c|c|c} n & \varphi(n) & l(n) & \text{prím} \\ \hline 501 & 332 & 4 & \text{nem} \\ 503 & 502 & 502 & \text{igen} \\ 505 & 400 & 16 & \text{nem} \\ 507 & 312 & 4 & \text{nem} \\ 509 & 508 & 508 & \text{igen} \\ 511 & 432 & 36 & \text{nem} \\ 513 & 324 & 4 & \text{nem} \\ 515 & 408 & 4 & \text{nem} \\ 517 & 460 & 4 & \text{nem} \\ 519 & 344 & 4 & \text{nem} \\ 521 & 520 & 520 & \text{igen} \\ 523 & 522 & 522 & \text{igen} \\ 525 & 240 & 16 & \text{nem} \\ 527 & 480 & 4 & \text{nem} \\ 529 & 506 & 22 & \text{nem} \\ 531 & 348 & 4 & \text{nem} \\ 533 & 480 & 16 & \text{nem} \\ 535 & 424 & 4 & \text{nem} \\ 537 & 356 & 4 & \text{nem} \\ 539 & 420 & 4 & \text{nem} \\ 541 & 540 & 540 & \text{igen} \\ 543 & 360 & 4 & \text{nem} \\ 545 & 432 & 16 & \text{nem} \\ 547 & 546 & 546 & \text{igen} \\ 549 & 360 & 8 & \text{nem} \end{array} & \begin{array}{c|c|c|c} n & \varphi(n) & l(n) & \text{prím} \\ \hline 551 & 504 & 4 & \text{nem} \\ 553 & 468 & 36 & \text{nem} \\ 555 & 288 & 8 & \text{nem} \\ 557 & 556 & 556 & \text{igen} \\ 559 & 504 & 36 & \text{nem} \\ 561 & 320 & 320 & \boxed{\text{nem}} \\ 563 & 562 & 562 & \text{igen} \\ 565 & 448 & 16 & \text{nem} \\ 567 & 324 & 4 & \text{nem} \\ 569 & 568 & 568 & \text{igen} \\ 571 & 570 & 570 & \text{igen} \\ 573 & 380 & 4 & \text{nem} \\ 575 & 440 & 4 & \text{nem} \\ 577 & 576 & 576 & \text{igen} \\ 579 & 384 & 4 & \text{nem} \\ 581 & 492 & 4 & \text{nem} \\ 583 & 520 & 4 & \text{nem} \\ 585 & 288 & 32 & \text{nem} \\ 587 & 586 & 586 & \text{igen} \\ 589 & 540 & 36 & \text{nem} \\ 591 & 392 & 4 & \text{nem} \\ 593 & 592 & 592 & \text{igen} \\ 595 & 384 & 24 & \text{nem} \\ 597 & 396 & 4 & \text{nem} \\ 599 & 598 & 598 & \text{igen} \end{array} \end{array}A táblázatból legalábbis úgy tűnik, hogy amennyiben egy n egész szám összetett, akkor ezt rendkívül sok, sőt „majdnem mindegyik” modulo n redukált maradékosztály tanúsítja. Ez abból látszik, hogy az összetett számok esetén a táblázat harmadik oszlopában lévő szám nagyon kicsi. Az egyetlen kakukktojás ebben a számtartományban az 561, akire hamarosan visszatérünk még. Ez azt is jelenti, hogy véletlenszerűen választott redukált maradékosztályok vizsgálatával jó eséllyel nagyon hamar „leleplezhetjük” n-t, amennyiben összetett, hiszen kicsi az esélye, hogy épp a néhány nem Fermat-tanú valamelyikét választjuk. Ráadásul egy-egy ilyen vizsgálatot a 21. részben tanult ismételt négyzetreemelések módszerével rettentően hamar el is tudunk végezni. Hamarosan általánosságban is igazolni fogunk egy alsó becslést a Fermat-tanúk számára vonatkozóan. Ez ugyan jóval szerényebb lesz annál, mint ami a táblázatból látszik, ám egy hatékonyan működő prímteszthez még ez is bőven elég lesz.
Ehhez azonban először két segédtételre lesz szükségünk. Az első arra vonatkozik, hogy egy Fermat-tanúból hogyan tudunk előállítani egy másik Fermat-tanút.
23.4. Lemma:
Legyen n\gt 1 tetszőleges pozitív egész szám. Tegyük fel, hogy adva van egy valamilyen a egész szám által reprezentált [a]_n redukált maradékosztály, amely Fermat-tanú. Legyen adott továbbá egy valamilyen b\neq 0 egész szám által reprezentált [b]_n redukált maradékosztály, amely nem Fermat-tanú.
Ekkor e két maradékosztály szorzata, vagyis az [a]_n \odot [b]_n maradékosztály egyrészt Fermat-tanú, másrészt szintén redukált maradékosztály.
Itt „szorzás” alatt a modulo n maradékosztálygyűrű \odot szimbólummal jelölt szorzás műveletét értjük (lásd a 20.5. Tételt).
♣Bizonyítás:
Képezzük e két maradékosztály szorzatát, azaz az [a]_n \odot [b]_n maradékosztályt. A \odot művelet 20.5. Tételben ismertetett definíciója alapján ez épp az [ab]_n maradékosztály lesz. Először azt kell bizonyítanunk, hogy ez a maradékosztály Fermat-tanú. Ez a 23.3. Definíció alapján az alábbit jelenti:
(ab)^{n-1} \ \cancel{\equiv} \ 1 \pmod nAz (ab)^{n-1} kifejezés a hatványozás azonosságairól szóló 18.8. Tétel 1. pontja alapján így is írható: a^{n-1}b^{n-1}. Mivel b\neq 0 és [b]_n nem Fermat-tanú, ezért a 23.3. Definíció alapján teljesül az alábbi kongruencia:
b^{n-1}\equiv 1\pmod nKövetkezésképp a 20.2. Tétel 5. pontja miatt teljesül az alábbi kongruencia is:
\underbrace{a^{n-1}b^{n-1}}_{=(ab)^{n-1}} \equiv a^{n-1} \pmod nMivel [a]_n Fermat-tanú, ezért ugyancsak a 23.3. Definíció alapján a jobboldali kifejezés biztosan nem kongruens 1-gyel modulo n. Így hát a baloldali kifejezés sem, azaz:
(ab)^n \ \cancel{\equiv} \ 1\pmod nEz tehát azt jelenti, hogy az [ab]_n=[a]_n\odot [b]_n maradékosztály valóban egy Fermat-tanú.
Most azt igazoljuk, hogy [ab]_n egy redukált maradékosztály. Mivel az [a]_n egy redukált maradékosztály, ezért a egy redukált maradékrendszer egyik eleme. Továbbá, mivel [b]_n szintén egy redukált maradékosztály, ezért b relatív prím n-hez. Így tehát az ab szorzat a 20.18. Tétel miatt szintén egy redukált maradékrendszer egyik eleme lesz. Ebből következően az [ab]_n maradékosztály egy redukált maradékosztály.
∎A második segédtétel arra vonatkozóan mond ki egy fontos állítást, hogy mi történik akkor, ha egymástól különböző maradékosztályokat egyesével végigszorozzuk ugyanazzal a redukált maradékosztállyal.
23.5. Lemma:
Ha bármely két egymástól különböző [a]_n és [b]_n maradékosztályt megszorzunk egy tetszőleges [c]_n redukált maradékosztállyal, akkor az így kapott maradékosztályok is különböznek egymástól.
Azaz ha [a]_n \neq [b]_n, akkor [c]_n \odot [a]_n \neq [c]_n \odot [b]_n.
♣Bizonyítás:
Tegyük fel indirekt, hogy nem ez a helyzet, vagyis annak ellenére, hogy [a]_n és [b]_n különböznek egymástól, mégiscsak teljesül az alábbi egyenlőség:
[c]_n \odot [a]_n = [c]_n \odot [b]_nA \odot művelet 20.5. Tételben ismertetett definíciója alapján ez az alábbit jelenti:
[ca]_n = [cb]_nAz egész számok maradékosztályainak 20.4. Tételben bevezetett definíciója alapján ugyanezt a kongruenciák nyelvén is kifejezhetjük:
ca\equiv cb\pmod nMivel [c]_n egy redukált maradékosztály, ezért a 20.14. Tétel alapján c relatív prím n-hez, és így a kongruencia a 20.3. Tétel utáni megjegyzés szerint minden további nélkül egyszerűsíthető c-vel. Ezt kapjuk tehát:
a\equiv b\pmod nEz viszont azt jelenti, hogy indirekt feltételezésünkkel ellentétben a és b mégiscsak ugyanazt a maradékosztályt reprezentálja, ami ellentmondás.
∎E két segédtétel segítségével mostmár könnyedén igazolhatjuk a Fermat-tanúk számára vonatkozó alsó becslésünket.
23.6. Tétel:
Legyen n\gt 1 egy tetszőleges pozitív egész szám. Amennyiben n-nek létezik Fermat-tanúja a redukált maradékosztályok között, akkor a modulo n redukált maradékosztályoknak legalább a fele Fermat-tanú.
♣Bizonyítás:
Tegyük fel, hogy összesen k darab olyan modulo n redukált maradékosztály van, amely nem Fermat-tanú. Legyenek például ezek az alábbiak, amelyek tehát páronként különböző redukált maradékosztályok:
\begin{aligned}&[a_1]_n \\ &[a_2]_n \\ &[a_3]_n \\ &\vdots \\ &[a_k]_n \end{aligned}Tegyük fel továbbá, hogy n-nek létezik legalább egy Fermat-tanúja a redukált maradékosztályok között. Legyen ez például az alábbi redukált maradékosztály:
[b]_nAmennyiben ezzel a [b]_n Fermat-tanúval végigszorozzuk a fenti k darab nem Fermat-tanút, akkor az alábbi maradékosztályokat kapjuk, amelyek a 23.4. Lemma alapján szintén mindannyian Fermat-tanúk és redukált maradékosztályok:
\begin{aligned}[b]_n &\odot [a_1]_n \\ [b]_n &\odot [a_2]_n \\ [b]_n &\odot [a_3]_n \\ &\vdots \\ [b]_n &\odot [a_k]_n \end{aligned}Mivel a szorzáshoz használt [b]_n egy redukált maradékosztály, továbbá az [a_1]_n, [a_2]_n, ..., [a_k]_n redukált maradékosztályok páronként különbözőek voltak, emiatt a 23.5. Lemma alapján az eredményül kapott szorzatok is páronként különböző redukált maradékosztályok. Ráadásul ezek az [a_1]_n, [a_2]_n, ..., [a_k]_n redukált maradékosztályoktól is biztosan különböznek, hiszen azok nem is voltak Fermat-tanúk.
Ha tehát teljesül a tétel feltétele, miszerint n-hez létezik legalább egy Fermat-tanú a redukált maradékosztályok között, akkor minden nem Fermat-tanúhoz elő tudunk állítani egy-egy újabb Fermat-tanút szintén a redukált maradékosztályok között. Más szavakkal a redukált maradékosztályok között minimum annyi Fermat-tanú van, mint ahány nem Fermat-tanú, ráadásul létezhetnek további Fermat-tanúk is. A modulo n redukált maradékosztályoknak tehát valóban legalább a fele Fermat-tanú.
∎Na és akkor mi van?! – kérdezhetné az Olvasó. Nos, az a helyzet, hogy ezt az első látásra nem túl érdekes tényt Alice és Bob egy meglehetősen pofátlan kis trükkel prímteszteléshez tudja felhasználni. Ezt az eljárást Fermat-prímtesztnek nevezzük, és a következőképpen néz ki:
- Az algoritmus bemenete egy n\gt 1 pozitív egész szám, amelyről el kellene dönteni, hogy prím-e vagy összetett.
- Válasszunk véletlenszerűen egy tetszőleges 1 és n közötti a egész számot, azaz 1\lt a\lt n.
- A 17.17. Tétel bizonyításában ismertetett euklidészi algoritmus segítségével számítsuk ki az (a,n) kitüntetett közös osztót. Ha (a,n)\neq 1, akkor az algoritmus leáll a következő válasszal: az n egész szám biztosan összetett, és az egyik osztója (a,n). Ha (a,n)=1, akkor folytassuk a 4. lépéstől.
- A 21. részben ismertetett ismételt négyzetreemelések módszerével ellenőrizzük le, hogy teljesül-e az a^{n-1}\equiv 1\pmod n kongruencia. Amennyiben nem teljesül a kongruencia, akkor az algoritmus leáll a következő válasszal: az n egész szám biztosan összetett, de nem találtuk meg egyetlen osztóját sem. Amennyiben teljesül a kongruencia, akkor az algoritmus a következő válasszal áll le: az n egész szám „valószínűleg” prím.
„Valószínűleg” prím?!
Ez az egész elsőre teljesen értelmetlennek tűnik, ezért most vizsgáljuk meg, hogy miről is van szó tulajdonképpen. Képzeljük el, hogy a bemenő n egész szám valójában összetett, ám ezt szeretné minél jobban eltitkolni előlünk. Mi azonban a kis Fermat-tételből (22.1. Tétel) tudjuk, hogy n esetleges összetettségét egy Fermat-tanú egyértelműen leleplezné.
Ezért az összes nemnulla modulo n maradékosztályt szépen bedobáljuk egy képzeletbeli kalapba, majd becsukjuk a szemünket, és teljesen véletlenszerűen kihúzunk közülük egyet. Olyan ez, akárcsak egy lottósorsolás. Ez lenne tehát az algoritmus 2. lépése. A 3. lépésben azt vizsgáljuk meg, hogy egy redukált maradékosztályt húztunk-e ki. Annak, hogy nem, gyakorlatilag 0 az esélye, de ha mégis, akkor ez leleplezi n-et, ráadásul még egy osztóját is megkapjuk. Majdnem biztos azonban, hogy tovább kell mennünk a 4. lépésre.
Ezen a ponton már tudjuk, hogy a kiválasztott maradékosztály egy redukált maradékosztály. Ebben a lépésben azt ellenőrizzük le, hogy véletlenül nem egy Fermat-tanút találtunk-e. Ha igen – azaz a vizsgált kongruencia nem teljesült – akkor n lelepleződött, hiszen a kis Fermat-tétel miatt biztosan összetett. Ha azonban nem Fermat-tanút fogtunk ki – azaz a vizsgált kongruencia teljesül –, akkor nem tudunk semmi biztosat mondani n-ről, ugyanis a kis Fermat-tétel megfordítása nem igaz.
Azt viszont az előző szakaszban bizonyított 23.6. Tétel alapján tudjuk, hogy a kalapban lévő redukált maradékosztályoknak legalább a fele – ám a tapasztalat alapján általában ennél jóval nagyobb része – Fermat-tanú. Így annak valószínűsége meglehetősen kicsi, hogy pont belehúztunk abba a néhány kósza nem Fermat-tanúba, miközben n összetett. Ennél sokkal valószínűbb, hogy n ténylegesen prím, és emiatt valóban nincs egyetlen Fermat-tanú sem abban a bizonyos kalapban. Ám biztosat ezen a ponton nem tudunk mondani, és ez az oka ennek a meglehetősen furcsán hangzó „valószínűleg prím” válasznak.
A Fermat-tanúk számára vonatkozó, a 23.6. Tételben bizonyított alsó becslés ugyan önmagában nem túl erős, azonban Alice és Bob megteheti, hogy többször is húz a kalapból. A Fermat-tanúság ellenőrzése ugyanis – mint említettük – az ismételt négyzetreemelések módszerével rendkívül gyorsan elvégezhető. Tegyük fel, hogy a lehető legrosszabb a helyzet, és a redukált maradékosztályoknak mindössze csak a fele Fermat-tanú. Ekkor 50% annak valószínűsége, hogy főhőseink egy véletlenszerű választással pont a másik feléből választanak egy redukált maradékosztályt. Annak pedig már csak 25%, hogy ez kétszer egymás után is megtörténik. Az, hogy egy újabb, harmadik húzással sem találunk Fermat-tanút, már csak 12.5% valószínűséggel következik be. És így tovább, minden újabb húzással megfeleződik annak valószínűsége, hogy tévesen prímszámmá nyilvánítjuk n-et.
Tegyük fel például, hogy 100 teljesen véletlenszerűen kiválasztott redukált maradékosztály egyike sem bizonyul Fermat-tanúnak. Ennek már csupán annyi az esélye, mint 100-szor zsinórban eltalálni, hogy egy feldobott pénzérme fej vagy írás lesz-e. Ez nagyságrendileg kevésbé valószínű, mint hogy valakinek 3-szor egymás után telitalálata lesz az 5-ös lottón.
Van azonban egy kis probléma ezzel a prímteszttel: sajnos léteznek olyan összetett számok, amelyeket nem lehet ilyen módon kiszűrni.
Univerzális álprímek
Térjünk vissza egy kicsit az előző szakasz elején szereplő táblázathoz. Itt a második oszlop a modulo n redukált maradékosztályok számát mutatja – ezt \varphi(n)-nel jelöltük –, a harmadik pedig azt, hogy ezek közül hány olyan van, amely NEM Fermat-tanú – ezt pedig l(n)-nel jelöltük.
Értelemszerűen a prímszámok esetén ez a két érték megegyezik, hiszen egy prímszámhoz nyilván nem létezik az összetettségét igazoló Fermat-tanú. Kérdés, hogy vajon létezik-e olyan összetett szám, amelyhez szintén nincs Fermat-tanú a redukált maradékosztályok között. A táblázatban felhívtuk a figyelmet az 561 egész számra, amely épp ezzel a szemtelen tulajdonsággal rendelkezik. Ezeknek a számoknak külön nevük is van.
23.7. Definíció (Univerzális álprímek, Carmichael-számok):
Legyen n\gt 1 tetszőleges pozitív, továbbá a egy n-hez relatív prím egész szám, és tegyük fel, hogy n összetett. Amennyiben az [a]_n redukált maradékosztály NEM Fermat-tanú, akkor azt mondjuk, hogy n álprím az a alapra nézve.
Amennyiben a modulo n redukált maradékosztályok között egyáltalán nem létezik Fermat-tanú, akkor n-et univerzális álprímnek vagy Carmichael-számnak nevezzük.
♣Ha tehát véletlenül épp egy Carmichael-számba botlunk, akkor a Fermat-prímteszt azt nagyon nagy valószínűséggel tévesen prímnek fogja minősíteni, hiszen akárhány redukált maradékosztályt is húzunk ki a kalapból, azokra mind teljesülni fog a Fermat-kongruencia. Az ilyen számok összetettségét egyedül akkor fogjuk tudni detektálni, ha sikerül épp egy nem redukált maradékosztályt kisorsolni a kalapból. Ilyenkor ugyanis a 3. lépésben végrehajtott euklidészi algoritmus 1-től különböző eredménye lebuktatja a számunkat. Erre azonban gyakorlatilag semmi esély nincs, hiszen egy nagy szám esetén a maradékosztályoknak általában csak elenyésző hányada nem redukált maradékosztály.
A figyelmes Olvasó észreveheti az említett táblázatból, hogy egy n univerzális álprímet mindössze az különbözteti meg egy valódi prímtől, hogy összetettsége miatt a [0]_n maradékosztályon kívül vannak még egyéb nem redukált maradékosztályok is. Ez onnan látszik, hogy a táblázat második oszlopában nem \varphi(n)=n-1 fog szerepelni, ahogyan a prímek esetében a 21.5. Tétel alapján elvárható, hanem egy ennél kisebb szám. Ez valóban lebuktatja álprímünket. A gond csak az, hogy – mint ahogyan a 21. részben már említettük – az Euler-féle \varphi-függvény kiszámítására csak n prímtényezőinek ismeretében van esélyünk, máskülönben az idők végezetéig is eltarthat. Így erre nem tudunk támaszkodni.
Érdekes kérdés, hogy vajon hány Carmichael-szám létezik? Ha esetleg ezek száma véges, akkor ezeket nyilvántarthatnánk a számítógép memóriájában, az algoritmus pedig leellenőrizhetné, hogy n véletlenül nem szerepel-e ebben a listában. Régóta ismeretes, hogy tetszőleges a\gt 1 egész szám esetén végtelen sok a alapú álprím létezik, az azonban sokáig nyitott kérdés volt, hogy vajon az univerzális álprímek száma is végtelen-e. Sajnálatos módon 1992-ben ezt is sikerült igazolni. Emiatt nem mehetünk el szó nélkül a probléma mellett, és az a^{n-1}\equiv 1\pmod n kongruencia ellenőrzésén kívül egyéb dolgokat is meg kell vizsgálnunk annak érdekében, hogy a Carmichael-számokat is ki tudjuk szűrni.
A Miller-Rabin prímteszt
Ebben a szakaszban a Fermat-prímtesztünket fogjuk egy kicsit feljavítani annak érdekében, hogy a Carmichael-számokat is ki tudjuk szűrni. Előszöris szögezzük le, hogy a továbbiakban csak a páratlan n-ekkel fogunk foglalkozni. Ez nem jelent tényleges megszorítást, hiszen az utolsó számjegyből azonnal látszik, hogy páratlan vagy páros-e a bemenetünk. Ez utóbbi esetben nyilván megállhatunk, és összetettnek nyilváníthatjuk a számunkat, hiszen az osztható 2-vel.
Az általánosság megsértése nélkül feltételezhetjük tehát, hogy n\gt 1 egy páratlan egész szám. Ekkor azonban az a^{n-1}\equiv 1\pmod n Fermat-kongruenciában szereplő n-1 kitevő biztosan páros lesz. Vagyis létezik olyan k_1 egész szám, amelyre teljesül az alábbi – és ezt meg is kapjuk, ha n-1-et „elosztjuk” 2-vel:
n-1 = 2\cdot k_1Ezután k_1-re vizsgáljuk meg, hogy páratlan-e vagy páros. Utóbbi esetben hasonlóképpen tovább bonthatjuk n-1-et, azaz létezni fog olyan k_2 egész szám, amelyre teljesül az alábbi:
n-1 = 2\cdot 2\cdot k_2És így tovább mindaddig bontjuk tovább a jobboldali tényezőt, amíg páratlan számot nem kapunk. Ez garantáltan be fog következni véges számú lépés után, máskülönben n-1 prímtényezős felbontásában végtelen sok 2-es tényező szerepelne, ami lehetetlen. Tegyük fel, hogy e darab lépés után egy valamilyen k páratlan számot kapunk. Ekkor n-1-re az alábbi kifejezést kaptuk:
n-1=\underbrace{2\cdot 2\cdot \ldots \cdot 2}_{e \text{ darab}}\cdot k=2^e\cdot kPéldául ha az n=561 Carmichael-szám a bemenetünk, akkor n-1=560-ra az iménti felbontás után e=4 és k=35 adódik, hiszen:
\begin{aligned}n-1=560&=2\cdot 280=\\&=2^2\cdot 140=\\&=2^3\cdot 70=\\&=2^4\cdot 35\end{aligned}Ilymódon kiszámítva az e és k értékét, a Fermat-tesztben használt a^{n-1}\equiv 1\pmod n kongruencia az alábbi alakot ölti:
a^{2^e\cdot k}\equiv 1\pmod nAmennyiben tehát [a]_n egy redukált maradékosztály és n prím, akkor teljesül a fenti kongruencia. Ez viszont a 20.1. Tétel 3. pontja alapján azt jelenti, hogy n osztója az alábbi kifejezésnek:
a^{2^e\cdot k}-1Most ezt a kifejezést fogjuk szorzattá alakítani a következő tétel segítségével.
23.8. Tétel:
Legyenek adottak valamilyen tetszőleges e\geq 1 és k\geq 1 egész számok. Ekkor bármilyen a egész szám esetén teljesül az alábbi összefüggés:
a^{2^e\cdot k}-1 = (a^k-1)\cdot (a^k+1)\cdot (a^{2k}+1)\cdot (a^{4k}+1)\cdot \ldots \cdot (a^{2^{e-1}k}+1) ♣Bizonyítás:
Azt a jól ismert azonosságot fogjuk használni, miszerint bármilyen kommutatív gyűrű tetszőleges x és y elemeire teljesül az alábbi:
x^2-y^2=(x-y)\cdot (x+y)Ez a 14.12. Definícióben szereplő gyűrűaxiómák közvetlen következménye, amelyet most le is ellenőrzünk. Rögtön alkalmazhatjuk az 5. pontban lévő első disztributivitási szabályt:
(x-y)\cdot (x+y)=(x-y)\cdot x + (x-y)\cdot y=\ldotsA kapott összeg két tagjára a második disztributivitási szabályt alkalmazhatjuk. Figyelembe véve a 15.1. Tétel 3. pontját valóban a fent szereplő kifejezést kapjuk:
\ldots = x^2-yx + xy-y^2 = x^2-y^2Ezek után alkalmazhatjuk ezt az azonosságot az a^{2^ek}-1 kifejezésre. Ez ugyanis a hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontjai alapján a következőképpen alakítható át:
a^{2^ek}-1=a^{2^{e-1}\cdot k\cdot 2}-1=(a^{2^{e-1}\cdot k})^2-1Erre már alkalmazhatjuk a fenti azonosságot x=a^{2^{e-1}\cdot k} és y=1 szereposztással:
(\underbrace{a^{2^{e-1}\cdot k}}_{=x})^2-(\underbrace{1}_{=y})^2=(\underbrace{a^{2^{e-1}\cdot k}}_{=x}-\underbrace{1}_{=y})\cdot (\underbrace{a^{2^{e-1}\cdot k}}_{=x}+\underbrace{1}_{=y})=\ldotsAmennyiben az e-1 kitevő még mindig nagyobb 0-nál, akkor a kapott szorzat első tényezőjére megismételhetjük a fenti eljárást:
\ldots=\underbrace{(a^{2^{e-2}\cdot k}-1)\cdot (a^{2^{e-2}\cdot k}+1)}_{=a^{2^{e-1}\cdot k}-1}\cdot (a^{2^{e-1}\cdot k}+1)=\ldotsHa még az e-2 kitevő is nagyobb 0-nál, akkor az első tényezőt ugyanígy tovább bonthatjuk. Minden lépésben tovább fog csökkenni a kitevő, és előbb-utóbb – egészen pontosan e lépés után – eléri a 0-t. Ekkor épp a tételben szereplő szorzatot fogjuk kapni.
∎Tegyük fel például, hogy továbbra is az n=561 Carmichael-szám a bemenetünk. Az n-1=560-ból ugye már korábban kiszámítottuk az e=4 és k=35 értékeket. Ekkor az a^{n-1}-1=a^{560}-1 kifejezés az iménti tétel alapján így alakítható szorzattá:
a^{560}-1=(a^{35}-1)\cdot (a^{35}+1)\cdot (a^{70}+1)\cdot (a^{140}+1)\cdot (a^{280}+1)Ha tehát [a]_{561} egy tetszőleges redukált maradékosztály, és az n=561 egy prímszám lenne, akkor ő garantáltan osztója lenne a baloldali a^{560}-1 kifejezésnek. Természetesen ez az oszthatóság teljesülhet egészen más okból is, és – minthogy az n=561 egy Carmichael-szám – jelen esetben teljesül is bármilyen [a]_{561} redukált maradékosztályra. A Fermat-prímteszt ezen a ponton annak rendje és módja szerint meg is bukik, hiszen néhány véletlenszerűen kiválasztott [a]_{561} redukált maradékosztály vizsgálata után tévesen arra a következtetésre jut, hogy az n=561 „valószínűleg prím”.
Ezen a ponton a Miller-Rabin-prímteszt továbbmegy, és az n=561 esetleges prímtulajdonságát (16.13. Definíció) próbálja meg cáfolni a kiválasztott [a]_{561} redukált maradékosztály segítségével. Ha ugyanis n=561 osztója a baloldali a^{560}-1 egész számnak, akkor a prímtulajdonság miatt a 16.13. Definíció utáni megjegyzés alapján osztója kell legyen legalább az egyik jobboldalon szereplő tényezőnek is. Azaz teljesülnie kell az alábbi oszthatóságok közül legalább egynek tetszőleges [a]_{561} redukált maradékosztály esetén:
\begin{aligned}561&|a^{35}-1 \\ 561&|a^{35}+1 \\ 561&|a^{70}+1 \\ 561&|a^{140}+1 \\ 561&|a^{280}+1\end{aligned}Ez viszont a 20.1. Tétel 3. pontja alapján azt jelenti, hogy teljesülnie kell legalább az egyik alábbi kongruenciának tetszőleges [a]_{561} redukált maradékosztály esetén:
\begin{aligned}a^{35}&\equiv +1\pmod{561} \\ a^{35}&\equiv -1\pmod{561} \\ a^{70}&\equiv -1\pmod{561} \\ a^{140}&\equiv -1\pmod{561} \\ a^{280}&\equiv -1\pmod{561} \end{aligned}Más megfogalmazásban ez azt jelenti, hogy amennyiben találunk egy olyan [a]_{561} redukált maradékosztályt, amely esetén a fenti kongruenciák közül egyik sem teljesül, akkor az n=561 biztosan nem lehet prím. Egy ilyen maradékosztály tehát „leleplezi” vagy „tanúsítja” az n=561 összetettségét. Vizsgáljuk meg például a [2]_{561} redukált maradékosztályt, azaz legyen a=2. Az itt lévő kalkulátor segítségével leellenőrizhetjük a fenti kongruenciákat:
\begin{aligned}2^{35} \equiv 263 \ &\cancel{\equiv}\ +1\pmod{561} \\ 2^{35} \equiv 263 \ &\cancel{\equiv}\ -1\pmod{561} \\ 2^{70}\equiv 166 \ &\cancel{\equiv}\ -1\pmod{561} \\ 2^{140}\equiv 67 \ &\cancel{\equiv}\ -1\pmod{561} \\ 2^{280}\equiv 1 \ &\cancel{\equiv}\ -1\pmod{561} \end{aligned}Minthogy egyetlen kongruencia sem teljesül, ezért az eddigi okfejtés alapján az n=561 Carmichael-szám biztosan összetett, azaz megbukott a Miller-Rabin-prímteszten.
Az eljárás általános megfogalmazásához most bevezetünk egy új tanú fogalmat.
23.9. Definíció (Miller-Rabin-tanú):
Legyen n\gt 1 egy tetszőleges páratlan szám, a pedig tetszőleges egész szám, amely nem többszöröse n-nek, azaz n\nmid a. Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyekre teljesül az alábbi:
n-1=2^e\cdot kTegyük fel továbbá, hogy az alábbi kongruenciák egyike sem teljesül:
\begin{aligned}a^k&\equiv +1\pmod n \\ a^k&\equiv -1\pmod n \\ a^{2k}&\equiv -1\pmod n \\ a^{4k}&\equiv -1\pmod n \\ &\vdots \\ a^{2^{e-1}\cdot k}&\equiv -1\pmod n\end{aligned}Ekkor az a egész szám által reprezentált [a]_n maradékosztályt az n egész szám Miller-Rabin-tanújának nevezzük.
♣Megjegyzés:
A Fermat-tanú 23.3. Definíciójához hasonlóan itt is teljes maradékosztályokra célszerű vonatkoztatni ezt a fogalmat. Ha ugyanis egy b egész szám a-val azonos modulo n maradékosztályban van, akkor teljesül az a\equiv b\pmod n kongruencia, és így a 20.2. Tétel 8. pontja alapján teljesülnek az alábbi kongruenciák is:
\begin{aligned}a^k&\equiv b^k\pmod n \\ a^{2k}&\equiv b^{2k}\pmod n \\ a^{4k}&\equiv b^{4k}\pmod n \\ &\vdots \\ a^{2^{e-1}\cdot k}&\equiv b^{2^{e-1}\cdot k}\pmod n\end{aligned}Mármost ha a baloldal nem kongruens a definícióban szereplő számokkal, akkor a jobboldal sem. Így tehát az [a]_n maradékosztálynak vagy minden eleme teljesíti a Miller-Rabin-tanúkkal szemben támasztott kritériumokat, vagy egyik sem.
Szintén a Fermat-tanú 23.3. Definíciójához hasonlóan itt sem kell kikötni, hogy [a]_n egy redukált maradékosztály, hiszen ha van egységtől különböző közös osztója a-nak és n-nek, akkor n nyilván összetett. Nem mellesleg itt is megjegyezzük, hogy a Miller-Rabin-kongruenciák amúgysem teljesülhetnének, amennyiben [a]_n nem egy redukált maradékosztály, azaz (a,n) nem egység. Ennek indoklása szinte szóról szóra megegyezik a 23.3. Definíció utáni megjegyzésben leírtakkal.
Ez tehát azt jelenti, hogy NEM Miller-Rabin-tanú csak redukált maradékosztály lehet. Ezen túlmenően a 23.8. Tétel miatt ha egy [a]_n redukált maradékosztály NEM Miller-Rabin tanú – azaz teljesül a definícióban szereplő kongruenciák közül legalább az egyik –, akkor Fermat-tanú SEM lehet. Ha ugyanis teljesül legalább az egyik kongruencia, akkor a 20.1. Tétel 3. pontja alapján n osztója az alábbi kifejezések közül legalább az egyiknek:
\begin{aligned}&a^k-1 \\ &a^k+1 \\ &a^{2k}+1 \\ &a^{4k}+1 \\ &\vdots \\ &a^{2^{e-1}\cdot k}+1\end{aligned}Ám e kifejezések szorzata a 23.8. Tétel alapján épp a^{n-1}-1, aminek n a 16.2. Tétel 7. pontja miatt szintén osztója. Azaz teljesül az a^{n-1}\equiv 1\pmod n kongruencia, és így az [a]_n redukált maradékosztály valóban nem Fermat-tanú. Másként fogalmazva ez azt jelenti, hogy minden Fermat-tanú egyúttal Miller-Rabin-tanú is, vagyis az új definíció tágítani igyekszik a lehetséges tanúk körét.
Az alábbi ábrán a NEM Miller-Rabin-tanúk és a NEM Fermat-tanúk elhelyezkedése látható a modulo n maradékosztályok között.

Felmerül a kérdés, hogy vajon a tanúk körének tágítását nem vittük-e túlzásba. Azaz nem lehetséges-e, hogy ha Fermat-tanúja nem is, de Miller-Rabin-tanúja már lehet esetleg prímszámoknak is. Az alábbi tétel szerint szerencsére nem ez a helyzet.
23.10. Tétel:
Semmilyen 1-nél nagyobb páratlan prímszámnak nincs Miller-Rabin-tanúja. Másként fogalmazva ha egy 1-nél nagyobb n páratlan számnak van Miller-Rabin-tanúja, akkor n összetett.
♣Bizonyítás:
Legyen n\gt 1 egy tetszőleges páratlan prímszám, továbbá legyen adva egy tetszőleges [a]_n redukált maradékosztály. Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyekre teljesülnek az alábbiak:
n-1=2^e\cdot kAzt kell igazolni, hogy [a]_n nem lehet Miller-Rabin-tanú, azaz az alábbi kongruenciák közül legalább az egyiknek teljesülnie kell:
\begin{aligned}a^k&\equiv +1\pmod n \\ a^k&\equiv -1 \\ a^{2k}&\equiv -1\pmod n \\ a^{4k}&\equiv -1\pmod n \\ &\vdots \\ a^{2^{e-1}\cdot k}&\equiv -1\pmod n\end{aligned}Mivel n prím, továbbá (a,n)=1 – hiszen [a]_n egy redukált maradékosztály –, ezért a kis Fermat-tétel (22.1. Tétel) miatt teljesül rá az alábbi kongruencia:
a^{\overbrace{2^e\cdot k}^{=n-1}}\equiv 1\pmod nEz a 20.1. Tétel 3. pontja alapján azt jelenti, hogy teljesül az alábbi oszthatóság:
n|a^{2^e\cdot k}-1Az oszthatóságban szereplő jobboldali kifejezést a 23.8. Tétel alapján szorzatba fejthetjük:
n|(a^k-1)\cdot (a^k+1)\cdot (a^{2k}+1)\cdot (a^{4k}+1)\cdot \ldots \cdot (a^{2^{e-1}k}+1)Mivel n prím, ezért a 16.13. Definíció utáni megjegyzés szerint legalább az egyik jobboldali tényezőnek osztója kell legyen. Azaz az alábbi oszthatóságok közül legalább az egyiknek teljesülnie kell:
\begin{aligned}n&|a^k-1 \\ n&|a^k+1 \\ n&|a^{2k}+1 \\ n&|a^{4k}+1 \\ &\vdots \\ n&|a^{2^{e-1}k}+1 \end{aligned}A 20.1. Tétel 3. pontja alapján ez tehát azt jelenti, hogy legalább az egyik kongruenciának teljesülnie kell az alábbiak közül:
\begin{aligned}a^k\equiv +1\pmod n \\ a^k\equiv -1\pmod n \\ a^{2k}\equiv -1\pmod n \\ a^{4k}\equiv -1\pmod n \\ &\vdots \\ a^{2^{e-1}k}\equiv -1\pmod n \end{aligned}Ez viszont a 23.9. Definíció szerint épp azt jelenti, hogy az [a]_n maradékosztály nem Miller-Rabin-tanú.
∎Ezekután ismertetjük a Miller-Rabin-prímtesztelő eljárást, amely tehát a Fermat-prímtesztnek a továbbfejlesztett változata:
- Az algoritmus bemenete egy n\gt 1 páratlan egész szám, amelyről el kellene dönteni, hogy prím-e vagy összetett.
- Válasszunk véletlenszerűen egy tetszőleges 1 és n közötti a egész számot, azaz 1\lt a\lt n.
- A 17.17. Tétel bizonyításában ismertetett euklidészi algoritmus segítségével számítsuk ki az (a,n) kitüntetett közös osztót. Ha (a,n)\neq 1, akkor az algoritmus leáll a következő válasszal: az n egész szám biztosan összetett, és az egyik osztója (a,n). Ha (a,n)=1, akkor folytassuk a 4. lépéstől.
- Képezzük azt az e\geq 1 kitevőt és k\geq 1 páratlan számot, amelyre n-1=2^e\cdot k teljesül.
- A 21. részben ismertetett ismételt négyzetreemelések módszerével ellenőrizzük le, hogy az [a]_n maradékosztályra teljesül-e legalább az egyik a 23.9. Definícióban felsorolt kongruenciák közül. Amennyiben nem teljesül egyetlen kongruencia sem, akkor Miller-Rabin-tanút találtunk, és az algoritmus leáll a következő válasszal: az n egész szám biztosan összetett, de nem találtuk meg egyetlen osztóját sem. Amennyiben teljesül legalább az egyik kongruencia, akkor az algoritmus a következő válasszal áll le: az n egész szám „valószínűleg” prím.
Már megint csak „valószínűleg” prím? – kérdezhetné teljes joggal az Olvasó. Látszólag valóban nem kerültünk közelebb a prímek azonosításához, hiszen ismét csak összetett számokat tudunk egyértelműen leleplezni. Ha azonban szerencsétlenül épp egy olyan maradékosztályt sikerült kihúzni a kalapból, amely nem Miller-Rabin-tanú, akkor ismét csak annyit mondhatunk, hogy a kérdéses szám „valószínűleg” prím.
Ez valóban így van, azonban a Fermat-prímteszthez hasonlóan itt is megtehetjük, hogy többször húzunk a kalapból. Ezen túlmenően a Miller-Rabin-tanú 23.9. Definíciója utáni megjegyzés alapján egy adott n-hez tartozó Miller-Rabin-tanúk köre biztosan nem szűkebb, mint az ugyanezen n-hez tartozó Fermat-tanúk köre. Sőt, azt is láthattuk, hogy az n=561-nek egyáltalán nincs Fermat-tanúja – hiszen Carmichael-számról van szó. Ezzel szemben például a [2]_{561} maradékosztály „lebuktatja” ezt a számot is, hiszen ő egy Miller-Rabin-tanú, amely bizonyítja az 561 összetettségét.
Úgy tűnik tehát, mintha a Miller-Rabin-prímteszt elől még a Carmichael-számok sem tudnának „elbújni”, ami kétségkívül hatalmas előrelépés. De vajon tényleg nem léteznek univerzális álprímek erre a tesztre nézve? Sajnos ahhoz, hogy ezt megválaszolhassuk, az absztrakt algebra egy rendkívül fontos ágának, nevezetesen az úgynevezett csoportelméletnek az eszköztárára lesz szükségünk. Így ezt csak a következő részben tudjuk majd igazolni.
Most azonban térjünk vissza egy kicsit az RSA-kulcsgenerálás kérdésköréhez. Nem árt ugyanis, ha felhívjuk Alice és Bob figyelmét néhány fontos dologra, amire vigyázniuk kell, ha nem akarják, hogy Eve és Mallory borsot törjön az orruk alá.
A Fermat-faktorizáció
Az RSA implementációja során sok apró részleten múlhat a biztonság. Számos hatékony támadás ismert ugyanis, amelyek az üzenethalmaz, a kulcsgeneráláshoz használt prímpár, valamint a kódoló és dekódoló kulcs nem elég körültekintő megválasztását használják ki. Ezt néhány példán keresztül illusztráljuk, amelyek közül az első az úgynevezett Fermat-faktorizációs algoritmus.
Ez az eljárás bizonyos körülmények között lehetővé teszi egy támadó számára, hogy hatékonyan kiszámíthassa a kódoláshoz és dekódoláshoz használt n modulus prímtényezőit, és így tulajdonképpen ő maga is a titkos kulcs birtokába juthasson. Erre akkor nyílik lehetősége, ha a prímtényezők közötti különbség nem eléggé nagy. Ebben az esetben a két prímtényező közel van a 23.2. Tételben szereplő r számhoz. Ez ugye a legnagyobb olyan egész szám, amelynek négyzete még éppen nemnagyobb n-nél. Így ennek a környékén jó eséllyel hamar megtalálhatjuk a prímtényezőket. Az erre szolgáló alább ismertetett módszer magától Pierre de Fermat-tól származik, amely a 23.8. Tétel bizonyításának elején már említett x^2-y^2 = (x+y)\cdot (x-y) összefüggésen alapul.
Képzeljük magunkat Eve helyébe, és tegyük fel, hogy az n=57\ 319\ 249\ 499 RSA-modulus prímtényezőit szeretnénk megtalálni. Azaz keressük azt a p és q prímszámot, amelyre teljesül az alábbi egyenlet – itt nyugodtan feltételezhetjük, hogy p\gt q, ha pedig mégsem, akkor nevezzük el őket fordítva:
n=p\cdot qEz első látásra reménytelennek tűnik, azonban abban reménykedhetünk, hogy az ismeretlen p és q prímtényezőket a kulcsgeneráláskor óvatlanul választották ki, és a különbségük kicsi. Most megmutatjuk, hogy mindig léteznek olyan a és b egész számok, amelyeknek összege p-vel, különbsége pedig q-val egyenlő. Azaz:
\begin{aligned}p&=a+b \\ q&=a-b\end{aligned}Adjuk össze, és vonjuk ki egymásból a két egyenletet:
\begin{aligned}p+q&=2a \\ p-q&=2b\end{aligned}Mivel p és q is biztosan páratlan – hiszen mindketten 2-től különböző prímek – ezért a fenti két egyenlet baloldalán álló p+q összeg és p-q különbség biztosan páros, azaz osztható 2-vel. A keresett a és b egész számok tehát valóban léteznek. Ekkor a fentebb említett összefüggés alapján:
n=(\underbrace{a+b}_{=p})\cdot (\underbrace{a-b}_{=q})=a^2-b^2Ha valóban igaz a feltételezésünk, miszerint a két prím egymáshoz közel van, akkor a p-q=2b összefüggés alapján b kicsi. Ha viszont b kicsi, akkor a négyzete is kicsi, amit az n=a^2-b^2 összefüggés jobboldaláról elhanyagolhatunk. Azaz feltételezhetjük, hogy a keresett a közel lesz a 23.2. Tételben szereplő r számhoz, ami ugye a legnagyobb olyan egész szám, amelynek a négyzete nemnagyobb n-nél. Ha most az n=a^2-b^2 összefüggésből kifejezzük b^2-et, akkor az alábbit kapjuk:
b^2=a^2-nFeladatunk a megkeresése. Azt tudjuk, hogy r környékén van, ezért innen kiindulva elkezdünk tippelni mindaddig, míg a jobboldali kifejezésre nem négyzetszámot kapunk.
A fenti példában tehát n=57\ 319\ 249\ 499. Ekkor r=239\ 414, mivel ez az a legnagyobb szám, amelynek a négyzete még nemnagyobb n-nél. Ebből kiindulva adunk tippeket a-ra, és vizsgáljuk, hogy az a^2-n négyzetszám-e:
\begin{array}{c|c|c}a & a^2-n & \text{négyzetszám?} \\ \hline 239\ 415 & 292\ 726 & \text{nem} \\ 239\ 416 & 771\ 557 & \text{nem} \\ 239\ 417 & 1\ 250\ 390 & \text{nem} \\ 239\ 418 & 1\ 729\ 225 & \text{igen} \end{array}Meglepően gyorsan, mindössze 4 lépés után négyzetszámot kaptunk a második oszlopban, amely tehát b^2-tel egyezik meg. Ebből b=1315 adódik, és mivel a-t is sikerült megtippelnünk, végülis megkaptuk a két prímtényezőt is:
\begin{aligned}p&=a+b=239\ 418 + 1315 = 240\ 733 \\ q&=a-b=239\ 418 - 1315=238\ 103\end{aligned}Látható, hogy eléggé hatékonyan sikerült prímtényezőire bontani a bemeneti számunkat. Mostmár látszik is, hogy miért: a két prím különbsége mindössze 2630 volt, ami nagyon kicsi a két prímhez képest.
Amikor tehát Alice és Bob kulcspárt generálnak maguknak, vigyázniuk kell, hogy a kiválasztott prímszámok átlagosan az őket leíró bitek felében különbözzenek egymástól. Ezzel viszonylag hamar elvehetik Eve kedvét a fenti eljárástól, a keresett a ugyanis ebben az esetben nagyon messze lesz r-től, amelyet így az idők végezetéig keresgélhet.
A kicsi kódoló kulcsok problémája
A 22. részben a RSA dekódolás gyorsítási lehetőségei kapcsán megemlítettük, hogy az RSA biztonsága nem függ a publikus e kódoló kitevő megválasztásától. Az ismételt négyzetreemelések módszerét vizsgálva a 21. részben megállapítottuk, hogy célszerű olyan kitevőt választani, amelynek bináris számábrázolásában kevés számú 1-es bit szerepel. Emiatt racionális megfontolásnak tűnhet, ha a megvalósítás során úgy döntünk, hogy egy viszonylag alacsony számtartományból választjuk ki a rendszer felhasználóihoz tartozó e publikus kitevőket a kulcsgenerálás során. Ez azonban bizonyos körülmények között a nyílt üzenet kiszámítására adhat lehetőséget egy támadó számára anélkül, hogy feltörné a titkosító kódolást.
Tegyük fel ugyanis, hogy egy sokfelhasználós rendszerről van szó, és kicsi az a számtartomány, amelyből kisorsoljuk a felhasználók számára a publikus e kitevőt. Ekkor előfordulhat, hogy több felhasználó is ugyanazt a kitevőt kapja. Tegyük fel, hogy k darab felhasználó kapta ugyanazt az e kitevőt. Szerencsétlen, ugyanakkor nem túl ritka esetekben még az is megeshet, hogy e\leq k is teljesül. Ez látszólag nem jelent problémát, hiszen természetesen más és más prímpárokat sorsolunk hozzájuk, tehát e k darab felhasználóhoz különböző modulusok és dekódoló kitevők fognak tartozni.
Képzeljük el azonban, hogy valaki egy bizalmas körlevelet küld felhasználók egy csoportjának, amelybe történetesen a fenti k darab felhasználó is beletartozik. Ebben az esetben tehát az x nyílt szöveg ugyanaz lesz. A küldő fél egyenként előkeresi a publikus kulcstárból a címzettek publikus kulcsait, és mindenki számára egyedileg kódolja az üzenetet a 21. részben leírt módon. A szerencsétlenül járt k darab felhasználónak kiküldött y_1, y_2, …, y_k rejtett üzenetekből a támadó az alábbi kongruenciarendszert tudja felírni:
\begin{aligned}y_1&\equiv x^e\pmod{m_1} \\ y_2&\equiv x^e\pmod{m_2} \\ &\vdots \\ y_k&\equiv x^e\pmod{m_k}\end{aligned}Ebben a kongruenciarendszerben a támadó számára egyedül az x nyílt üzenet ismeretlen, hiszen egyrészt a felhasználókhoz tartozó e kitevő és a modulusok számára is elérhetők a publikus kulcstárból, másrészt pedig az y_1, y_2, …, y_k rejtett üzeneteket a kommunikációs csatorna lehallgatásával ismeri meg. Most megmutatjuk, hogy a támadó a fent ismertetett szerencsétlen körülmények fennállása esetén ebből a kongruenciarendszerből egy pillanat alatt megkaphatja az x nyílt üzenetet.
Azt mindjárt az elején feltehetjük, hogy az m_1, m_2, …, m_k modulusok páronként relatív prímek. Ezek ugyanis véletlenszerűen sorsolt prímpárok szorzataiként állnak elő, így annak gyakorlatilag nincs esélye, hogy van közöttük két olyan, amelynek közös legalább az egyik prímtényezője. Emlékeztetnénk az olvasót a kínai maradéktételhez kapcsolódó 22.4. Tételre, valamint a 22.5. Tételre, amelyek így már alkalmazhatók.
Ezek többszöri alkalmazásával azt kapjuk, hogy a \Z/m_1\Z \times \Z/m_2\Z \times \ldots \times \Z/m_k\Z szorzatgyűrű (lásd a 22.7. Tételt) elemei kölcsönösen egyértelmű megfeleltetésben állnak a \Z/m_1m_2\ldots m_k\Z maradékosztálygyűrű elemeivel. A fenti kongruenciarendszer a szorzatgyűrűben tulajdonképpen az alábbi elemet írja le:
([x^e]_{m_1};[x^e]_{m_2};\ldots;[x^e]_{m_k})Ennek a \Z/m_1m_2\ldots m_k\Z maradékosztálygyűrűben a 22.5. Tétel alapján az alábbi maradékosztály felel meg:
[x^e]_{m_1\cdot m_2\cdot \ldots \cdot m_k}Vegyük észre azonban, hogy az x nyílt üzenetet a küldő az előkódolás során úgy választotta meg, hogy az 0 és a legkisebb modulus közé essen. Az előkódolásról a 21. részben írtunk bővebben. Teljesülnek tehát az alábbi egyenlőtlenségek:
\begin{aligned}0\leq x &\lt m_1 \\ 0\leq x&\lt m_2 \\ &\vdots \\ 0\leq x &\lt m_k\end{aligned}Mivel azt mondtuk, hogy szerencsétlen módon az e\leq k egyenlőtlenség is fennáll, ezért ebben az esetben nyilván teljesül az alábbi is:
0\leq x^e \lt m_1m_2\ldots m_kÍgy a támadó valójában az [x^e]_{m_1m_2\ldots m_k} maradékosztály legkisebb nemnegatív reprezentánselemét kapja meg, amely nem más, mint a nyílt üzenetnek ténylegesen az e-edik hatványa – és nem pedig annak modulo megfelelője. Ebből viszont az x nyílt üzenetet már egyszerűen megkaphatja.
Alice-nak és Bob-nak tehát azt javasolhatjuk, hogy a kulcsgeneráláskor semmiképpen se korlátozzák az e kitevőt egy szűk számtartományra, nehogy a fenti kellemetlenségben legyen részük. A kódolás gyorsasága szempontjából a lényeg úgyis az, hogy kevés számú 1-es legyen e bináris ábrázolásában, nem pedig az, hogy ő maga kicsi legyen. Ezen túlmenően amikor ugyanazt az üzenetet nagyszámú résztvevőnek továbbítjuk, akkor célszerű az üzenet egyes példányaiba valamilyen véletlentől függő elemet is belevinni. Például megtehetjük, hogy az utolsó valahány biten hasznos tartalom helyett elhelyezünk egy véletlenszámot.
Ennek az az előnye, hogy így az eredeti x üzenet egyes példányai különböző kódolandó nyílt üzenetekké válnak, amivel a fenti támadás lehetőségét egycsapásra kiiktattuk. Természetesen ekkor a küldő és fogadó félnek meg kell egyezniük egymással, hogy melyek lesznek a haszontalan bitek.
Közös modulus választásának hibája
Végül egy nagyon súlyos potenciális rendszertervezési hibára hívnánk fel a figyelmet. Mivel az RSA meglehetősen számításigényes, ezért csábító lehet az a gondolat, hogy a teljes rendszer számára egyetlen m modulust generálunk, és csak az egyes felhasználókhoz tartozó e publikus és d titkos kitevők lesznek különbözőek a kulcsgenerálás során. Ez látszólag előnyös lehet, hiszen így például előre le tudunk gyártatni egy célhardvert, amely a modulo m maradékosztálygyűrűben való számolásra van optimalizálva.
Képzeljük el, hogy az előző szakaszhoz hasonlóan ismét egy közös x üzenet – például egy körlevél – érkezik mondjuk két felhasználóhoz. Tegyük fel, hogy e két felhasználóhoz az e_1 és e_2 publikus kitevők vannak rendelve. Nagy az esély rá, hogy e két kitevő egymáshoz relatív prím, azaz (e_1,e_2)=1, és ebben az esetben egy támadó sajnos meg tudja fejteni az x nyílt üzenetet. Ő ugyanis az alábbi kongruenciákat írhatja fel:
\begin{aligned}y_1&\equiv x^{e_1}\pmod m \\ y_2&\equiv x^{e_2}\pmod m\end{aligned}Ebben a kongruenciarendszerben a támadó számára ismét egyedül az x nyílt üzenet ismeretlen, hiszen az összes többi paraméter a nyilvános kulcstárból, valamint a kommunikációs csatorna lehallgatásával megismerhető. Nézzük, hogy mihez kezd mindezzel a támadó.
A Bézout-lemmából (21.1. Tétel) tudjuk, hogy bármely két egész szám kitüntetett közös osztója kifejezhető a két szám lineáris kombinációjaként. Ezt jelen esetben az e_1 és e_2 kitevőkre alkalmazhatjuk. Mivel róluk azt mondtuk, hogy relatív prímek – azaz (e_1,e_2)=1 –, ezért a Bézout-lemma alapján léteznek olyan u és v egész számok, amelyekre teljesül az alábbi:
(e_1,e_2)=1=u\cdot e_1 + v\cdot e_2Ráadásul a támadó a keresett u és v egész számokat hatékonyan elő tudja állítani a kibővített euklidészi algoritmus segítségével, amelyről a 21. részben volt szó részletesen. Most vizsgáljuk meg, hogy a kiszámított u és v egész számokból, valamint a kommunikációs csatornán elfogott y_1 és y_2 kódszövegekből képzett alábbi kifejezés mivel kongruens modulo m:
y_1^u\cdot y_2^v \equiv ?\pmod mMivel y_1\equiv x^{e_1}\pmod m és y_2\equiv x^{e_2}\pmod m az RSA-kódolás alapján, ezért a kongruencia tulajdonságairól szóló 20.2. Tétel 8. és 5. pontjait alkalmazva ezt kapjuk:
(\underbrace{x^{e_1}}_{\equiv y_1})^u\cdot (\underbrace{x^{e_2}}_{\equiv y_2})^v \equiv \ ?\pmod mA baloldali kifejezést a hatványozás azonosságairól szóló 18.8. Tétel 2. és 3. pontjai alapján átírhatjuk az alábbi módon:
x^{u\cdot e_1 + v\cdot e_2}\equiv \ ?\pmod mA Bézout-lemma alapján a kitevőről viszont már tudjuk, hogy az az (e_1,e_2)=1 kitüntetett közös osztóval egyezik meg, azaz teljesül az alábbi:
x^{\overbrace{u\cdot e_1 + v\cdot e_2}^{=1}}\equiv x\pmod mA támadó tehát pusztán publikusan, illetve a csatorna lehallgatása által megszerezhető információkból ki tudja számítani az x nyílt szöveget anélkül, hogy feltörte volna az RSA-t. A fentiek alapján ugyanis nincs más dolga, mint kiszámítani az y_1^u\cdot y_2^v kifejezést, amely tehát biztosan az x nyílt üzenettel lesz kongruens modulo m.
Felhívnánk a figyelmet azonban egy apró „csalásra”, amelyet a fenti okfejtésben elkövettünk. Vizsgáljuk meg ugyanis jobban a Bézout-lemmából kapott u\cdot e_1 + v\cdot e_2=1 egyenletet. Mivel itt az e_1 és e_2 kitevők mindketten pozitívak, ezért ebből következik, hogy u és v közül pontosan az egyik szükségképpen negatív. Ők viszont a fenti y_1^u\cdot y_2^v kifejezésben kitevőkként szerepelnek. Márpedig ebben az esetben elvileg nem használhatnánk a hatványozás azonosságairól szóló 18.8. Tételt és a kongruencia tulajdonságairól szóló 20.2. Tételt, hiszen ezeket csak pozitív kitevőkre bizonyítottuk. Arról már nem is beszélve, hogy az eddigi definícióink alapján negatív kitevőket egyelőre nem is tudunk értelmezni.
Ennek a kis hiányosságnak a pótlását a következő részre halasztjuk, mivel ehhez fel kell építeni néhány újabb fontos algebrai fogalmat. Ám elöljáróban megjegyezzük, hogy a hatványozás azonosságai és a kongruenciák tulajdonságai ebben a kibővített értelmezésben is érvényben fognak maradni. Így válik majd a fenti érvelés teljessé. Konklúzióként azonban elmondhatjuk, hogy a közös modulus választását mindenképpen el kell kerülni az RSA-algoritmuson alapuló kriptográfiai rendszerekben.
Ebben a részben tehát főként azzal a problémával foglalkoztunk, hogy hogyan tud Alice és Bob az RSA-kulcsgeneráláshoz szükséges óriási prímszámokat találni. Ennek keretében megmutattuk, hogy a hagyományos, osztáspróbákon alapuló módszer a gyakorlatban a lassúsága miatt nem alkalmazható. Ezért bemutattunk két valószínűségi prímtesztet, amelyek a kis Fermat-tételen alapulnak. Az első a Fermat-prímteszt volt, amelynek fő hátránya, hogy léteznek olyan összetett számok, amelyeket nem tud kiszűrni. Ezeket univerzális álprímeknek vagy Carmichael-számoknak nevezzük, amelyekről a közelmúltban kimutatták, hogy sajnos végtelen sok van belőlük. Ezt a problémát kiküszöbölendő bemutattuk a Miller-Rabin-prímtesztet, amely – úgy tűnik – kiszűri az univerzális álprímeket is. Végül felhívtuk a figyelmet pár olyan dologra, amelyekre Alice-nak és Bob-nak oda kell figyelniük a kulcsgenerálás során.
A következő részben megismerkedünk az absztrakt algebra talán legfontosabb ágának, az úgynevezett csoportelméletnek az alapjaival. Ezután az így felépített eszközök segítségével igazolni fogjuk, hogy a Miller-Rabin-prímtesztre nézve valóban nem léteznek univerzális álprímek. Végül adunk egy felső korlátot is annak valószínűségére, hogy egy összetett számot tévesen prímmé nyilvánít ez a teszt.
A következő részt itt találod…



